人教版八年级下册第18章平行四边形——弦图模型和半角模型专题(Word版,无答案)

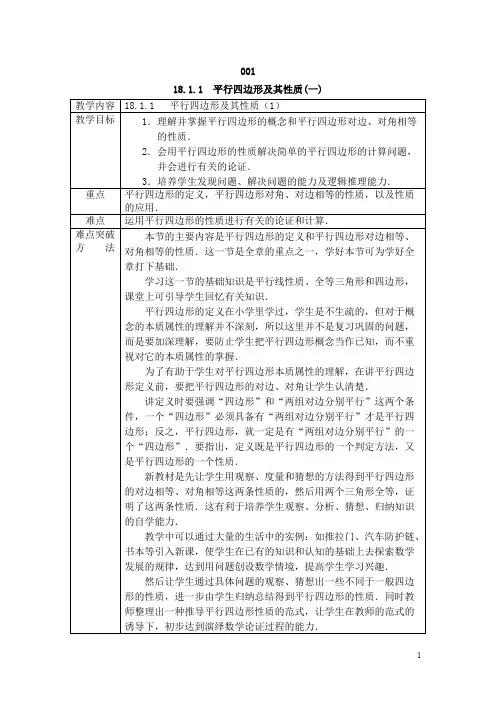
（一）弦图模型【基本图形】已知正方形ABCD,过B,D两点分别向过点C的直线作垂线,垂足分别为点E,F,则△BCE≌△CDF1.如图,l1,,l2,l3,l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,正方形ABCD的四个顶点分别在这四条直线上且正方形ABCD的面积是25(1)证明△ABE,△FBE△EDF,△CDF的面积相等； (2)求h的值。

2.已知:在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,设∠BCD=∝，以D为旋转中心,将腰DC逆时针旋转90°至DE,连接AE、CE(1)当a=45°时,求△EAD的面积(2)当a=30°时,求△EAD的面积(3)当0°<a<90时,猜想△EAD的面积与a大小有何关系?若有关,写出△EAD的面积S与a的关系式;若无关,请证明。

3.(1)已知:如图1,△ABC中,分别以AB、AC为一边向△ABC外作正方形ABGE和ACHF,直线AN⊥BC于N,若EP⊥AN 于P,FQ⊥AN于Q.①判断线段EP、FQ的数量关系,并证明;②求证：BC=2AP.(2)如图2,梯形ABCD中,AD∥BC,分别以两腰AB、CD为一边向梯形ABCD外作正方形ABGE和DCHF,线段AD的垂直平分线交线段AD于点M,交BC于点N,若EP⊥MN于P, FQ⊥MN于Q.(1)中结论还成立吗?请说明理由。

【变式训练】如图，分别以ABC ∆的AC 和BC 为一边，在ABC ∆的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．4．如图,直角梯形ABCD 中,AD/BC,∠ADC=90°,是AD 的垂直平分线,交AD 于点M,以腰AB 为边作正方形ABFE ， EP ⊥l 于点P.求证:2EP+AD=2CD（二）半角模型半角模型【用旋转和对称（翻折）的方法解决问题】ABCD 中，若M 、N 分别在边BC 、CD 上移动，且满足MN=BM +DN ， 则有以下基本结论（需记忆）：①.∠MAN=45°；②.；③.AM 、AN 分别平分∠BMN 和∠DNM.同样，在正方形ABCD 中,若已知∠MAN=45°，则会有：①.MN=BM +DN; ②;③.AM 、AN 分别平分∠BMN和∠DNM;④若继续作AH ⊥MN 于点H ,则有AH=AB.1.在正方形ABCD 中，已知∠MAN=45°，若M、N 分别在边CB 、DC 的延长线上移动，试探究线段MN 、BM 、DN 之间ABC CMN 2=∆ABC CMN 2=∆P C G F B Q A DE的数量关系.k、m、n为边长的三角形的形状是什么并试着证明你的猜想。

课程主题：平行四边形性质及判定教学内容1.平行四边形：两组对边分别平行的四边形是平行四边形．表示：平行四边形用符号“”来表示．如图，在四边形ABCD中，AB∥DC，AD∥BC，那么四边形ABCD是平行四边形．平行四边形ABCD记作“ ABCD”，读作“平行四边形ABCD”．注意：平行四边形中对边是指无公共点的边，对角是指不相邻的角，邻边是指有公共端点的边，邻角是指有一条公共边的两个角．而三角形对边是指一个角的对边，对角是指一条边的对角．2.平行四边形的性质：（1）边：平行四边形的对边平行且相等．（2）角：平行四边形的对角相等．邻角互补（3）对角线：平行四边形的对角线互相平分对称性：平行四边形是中心对称图形，两条对角线的交点是对称中心；【例题精讲】例1 ：如图，在平行四边形ABCD中，DB=DC、，CE BD于E，则．例2：如图，在□ABCD中，已知AD＝8㎝， AB＝6㎝，DE平分∠ADC交BC边于点E，则BE等于（）A.2cmB.4cmC.6cmD.8cm例3：如图，已知：平行四边形ABCD中，的平分线交边于，的平分线交于，交于．求证：．【课堂练习】（1）在ABCD 中，∠A= 50，则∠B= 度，∠C= 度，∠D= 度．（2）如果ABCD 中，∠A —∠B=24°，则∠A= 度，∠B= 度，∠C= 度，∠D= 度． （3）如果ABCD 的周长为28cm ，且AB ：BC=2∶5，那么AB= cm ，BC= cm ，CD= cm ，AD= cm ． 2．如图4.3－9，在ABCD 中，AC 为对角线，BE ⊥AC ，DF ⊥AC ，E 、F 为垂足，求证：BE ＝DF ．3．在平行四边形中，周长等于48，① 已知一边长12，求各边的长 ② 已知AB=2BC ，求各边的长③ 已知对角线AC 、BD 交于点O ，△AOD 与△AOB 的周长的差是10，求各边的长4．如图，ABCD 中，AE ⊥BD ，∠EAD=60°，AE=2cm ，AC+BD=14cm ，则△OBC 的周长是_______cm ． 5．ABCD 一内角的平分线与边相交并把这条边分成cm 5，cm 7的两条线段，则ABCD 的周长是_____cm ．6．ABCD 的周长为36，AB=8cm ，BC=________；当∠B=60°时，AD 、BC 的距离AE=________，ABCD 的面积ABCD S =________。