初中几何证明题思路及做辅助线总结.

初中数学做辅助线的方法总结
在初中数学中，做辅助线是解题的重要方法之一。

以下总结了几
种常见的做辅助线的方法：
1. 对称性辅助线法：当一个图形或方程式具有对称性时，可以
画出一条对称轴或一些对称线，从而利用对称性来简化问题。

例如，
在求三角形的中线长度相等定理时，可以描绘出三角形的垂直平分线，并在中点处作垂线，得到两个相等的直角三角形。

2. 垂线辅助线法：当一个角、线段或线段的垂线很难直接操作时，可以画出一条垂线，将问题转化为一个直角三角形问题。

例如，
在求一条线段的垂线长度时，可以先画出一条垂线与该线段相交，并
组成一个直角三角形。

3. 平移辅助线法：当一个几何图形或方程式涉及到平移时，可
以通过向图形或方程式添加平移线或平移量来使问题变得简单。

例如，在证明平行四边形对角线平分的定理时，可以平移一个平行四边形，
使其成为一个重合的平行四边形，从而使问题变得简单。

4. 分割辅助线法：当一个图形或方程式很复杂时，可以通过将
其分解成几个简单的部分来解题。

例如，在求多边形面积时，可以将
多边形分割成几个三角形或梯形，并将它们的面积相加，从而得到多
边形的面积。

总之，做辅助线的方法不只有以上四种，还可以根据具体问题的
不同情况选用其他的方法。

需要注意的是，在使用辅助线时，要注意
画出清晰的图形，并理解各种辅助线的作用，才能有效地解决问题。

几何证明题辅助线基本方法几何证明题是数学中的一种重要题型，需要通过逻辑推理和几何知识来证明给定的几何关系。

在解决几何证明题时，辅助线是一种常用的策略，可以帮助我们简化问题、构建更简洁的证明过程。

本文将介绍几何证明题中常用的辅助线基本方法。

1. 平行辅助线法当我们需要证明两条线段平行时，可以在图形中引入一条辅助线来构建平行关系。

具体步骤如下：1. 观察图形，找到可能存在平行关系的线段。

2. 在相应的位置引入一条辅助线。

3. 利用平行线的性质进行推理，证明所需的平行关系。

2. 相等辅助线法当我们需要证明两个线段相等时，可以通过引入一条相等的辅助线来简化证明过程。

具体步骤如下：1. 观察图形，找到可能具有相等关系的线段。

2. 在相应的位置引入一条相等的辅助线。

3. 利用等边、等角等性质进行推理，证明所需的相等关系。

3. 垂直辅助线法当我们需要证明两条线段垂直时，可以通过引入一条垂直的辅助线来简化证明过程。

具体步骤如下：1. 观察图形，找到可能具有垂直关系的线段。

2. 在相应的位置引入一条垂直的辅助线。

3. 利用垂直线的性质进行推理，证明所需的垂直关系。

4. 同位角辅助线法当我们需要证明两条直线的同位角相等时，可以通过引入同位角的辅助线来简化证明过程。

具体步骤如下：1. 观察图形，找到可能存在同位角的直线。

2. 在相应的位置引入同位角的辅助线。

3. 利用同位角的性质进行推理，证明所需的同位角相等关系。

5. 其他辅助线方法除了上述介绍的常用辅助线方法外，还可以根据具体的几何证明题目选择其他辅助线的方法。

例如，可以利用中位线、角平分线、内切圆、外接圆等辅助线，根据题目要求灵活运用。

综上所述，几何证明题辅助线基本方法包括平行辅助线法、相等辅助线法、垂直辅助线法、同位角辅助线法等。

通过合理引入辅助线，可以帮助我们简化问题、构建更简洁的证明过程，提高解题效率。

在实际解题中，我们需要综合运用不同的辅助线方法，根据题目要求灵活选择适合的策略。

初中数学几何证明题怎么做辅助线，怎么做好辅助线
这个不能一概而论。

至于几何证明问题，每个问题都有解决方案，因问题而异。

如果在证明问题中不知道怎么做辅助线，多练习去发现这类问题，多练习多看，自然就能发现辅助线这类问题的一定规律。

此外，老师应该谈论这类话题的一些常见类型。

你应该从根本上理解这些常见的类型。

遇到类似的题目，可以依靠这些辅助线的常用做法。

初中数学没那么复杂，常见的题也就那么几个。

你可以对它们进行分类总结。

我知道我朋友的孩子数学也不太好。

他刚刚在快乐学网上找到苏航老师辅导，初三面临中考。

听朋友讲，苏航老师讲的很仔细很认真，主要是老师把常见的问题总结的很到位，正好解决了你不会做辅助线的问题。

老师会总结常见的辅助线，你可以认真背，老师会用大量的练习巩固。

学数学，了解了课文的基础知识，掌握了常见题的做法，再刷很多题，多做，多看，自然就有了题感，数学教程好，很容易出成绩，加油。

完整)初中数学几何辅助线技巧
几何常见辅助线口诀
三角形
在三角形中，可以使用角平分线来构造垂线，也可以将图形对折以后进行对称，从而得到更多的关系。

同时，角平分线还可以和平行线一起使用，来构造等腰三角形。

另外，在线段问题中，垂直平分线常常被用来将线段连接起来，而线段和差的问题可以通过延长或缩短线段来解决。

四边形
在处理平行四边形时，可以使用对称中心和等分点来进行计算。

对于梯形问题，可以将其转换为三角形或平行四边形，然后利用已有的知识来解决。

如果出现腰中点，可以连接中位线来解决问题。

如果以上方法都无法奏效，可以尝试使用全等来解决问题。

在证明相似时，可以使用比例和平行线的关系来辅助证明。

圆形
在圆形问题中，可以利用半径和弦长来计算弦心距。

如果出现切线，可以使用勾股定理来计算其长度。

要想证明一条线段是切线，需要利用半径垂线进行辨别。

在处理弧的问题时，需要记住垂径定理和圆周角的性质。

如果要作出内接或外接圆，需要将各边的中垂线或角平分线连起来。

如果遇到相交圆，需要注意作出公共弦。

最后，如果要证明等角关系，可以使用角平分线来构造辅助线。

由角平分线想到的辅助线
在使用角平分线时，可以通过截取构造全等来解决问题。

也可以在角分线上的点向两边作垂线，来构造全等三角形。

同时，三线合一也可以用来构造等腰三角形。

最后，在处理角平分线和平行线问题时，可以使用线段的加减和移动来解决问题。

几何证明题辅助线经典方法
引言
几何证明题是数学中常见的题型，也是学生们认识几何图形、发现几何规律的重要手段。

辅助线是解决几何证明题时常用的方法之一，本文将介绍几种经典的辅助线方法。

方法一：画垂直平分线
对于某些几何图形中的线段，我们可以通过画垂直平分线来辅助证明。

垂直平分线将线段分成两等分，从而在几何证明过程中起到重要的辅助作用。

方法二：画过顶点的高
在证明三角形相等或等腰三角形时，辅助线中的高是常见的方法之一。

通过画一条从顶点到对边的垂线，我们可以将几何图形转化为更容易处理的形式，从而证明所需结论。

方法三：画过顶点的中位线
在证明平行四边形或矩形时，辅助线中的中位线是一种常见的
方法。

通过画一条从顶点到对边中点的线段，我们可以将问题简化，并且利用矩形或平行四边形的性质得到所需结论。

方法四：画三角形的内切圆
在证明三角形的某些性质时，画三角形的内切圆是一种常见的
辅助线方法。

内切圆与三角形的各边均相切，通过利用内切圆的性质，我们可以得到有关三角形的一些重要结论。

方法五：画过顶点的角平分线
在证明两角相等或证明某些三角形相似时，画过顶点的角平分
线是一种常见的辅助线方法。

通过将角细分为两等分，我们可以得
到有关角度的一些重要关系，从而得到所需结论。

结论
辅助线方法在解决几何证明题时起到了重要的作用。

以上介绍
的几种经典辅助线方法仅是其中的一部分，通过熟练掌握这些方法，并结合具体问题，我们可以更好地解决几何证明题，提高数学水平。

初中几何辅助线思路
在初中几何中，当我们遇到一些看似复杂的问题时，常常需要添加辅助线来帮助我们解决问题。

以下是一些常见的添加辅助线的思路：
1. 构造中点：通过构造中点，我们可以利用中点定理来解决问题。

中点定理告诉我们，如果一条线段的中点被找到，那么可以通过这条中点作一条垂线或平行线，将问题简化为一个更简单的问题。

2. 延长或截取：在某些情况下，通过延长或截取线段，我们可以使图形的形状更加明显，从而更容易找到解题思路。

3. 平行线构造：平行线的性质可以为我们提供很多有用的信息。

通过构造平行线，我们可以利用平行线的性质来解决问题。

4. 作垂线：在处理与矩形、菱形等四边形有关的问题时，我们可以通过作垂线来构造直角三角形，从而利用勾股定理等三角函数性质来解决问题。

5. 利用30度角：在一些与30度角有关的问题中，我们可以构造一条过30度角的线段，从而利用30度角的一些特殊性质来解决问题。

6. 连接两点：连接两点构造一条线段，可以通过这条线段找到一些与问题相关的信息，从而更容易解决问题。

7. 作平行四边形：通过作平行四边形，我们可以利用平行四边形的性质来解决问题。

8、在添加辅助线时，我们需要注意以下几点：
要明确添加辅助线的目的，不要为了添加而添加。

要根据题目的条件和要求，选择合适的方法添加辅助线。

在添加辅助线后，要仔细分析图形的形状和性质，从而找到解决问题的关键点。

总之，在初中几何中添加辅助线是一项非常重要的技能。

通过不断练习和掌握常见的辅助线方法，我们可以更好地解决各种几何问题，提高自己的数学水平。

中考几何题证明思路总结一、证明两线段相等1.两全等三角形中对应边相等;2.同一三角形中等角对等边;3.等腰三角形顶角的平分线或底边的高平分底边;4.平行四边形的对边或对角线被交点分成的两段相等;5.直角三角形斜边的中点到三顶点距离相等;6.线段垂直平分线上任意一点到线段两段距离相等;7.角平分线上任一点到角的两边距离相等;8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等;二、证明两角相等1.两全等三角形的对应角相等;2.同一三角形中等边对等角;3.等腰三角形中,底边上的中线或高平分顶角;4.两条平行线的同位角、内错角或平行四边形的对角相等;5.同角或等角的余角或补角相等;6.同圆或圆中,等弦或弧所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角;三、证明两直线平行1.垂直于同一直线的各直线平行;2.同位角相等,内错角相等或同旁内角互补的两直线平行;3.平行四边形的对边平行;4.三角形的中位线平行于第三边;5.梯形的中位线平行于两底;6.平行于同一直线的两直线平行;7.一条直线截三角形的两边或延长线所得的线段对应成比例,则这条直线平行于第三边;四、证明两直线互相垂直1.等腰三角形的顶角平分线或底边的中线垂直于底边;2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角;3.在一个三角形中,若有两个角互余,则第三个角是直角;4.邻补角的平分线互相垂直;5.一条直线垂直于平行线中的一条,则必垂直于另一条;6.两条直线相交成直角则两直线垂直;7.利用到一线段两端的距离相等的点在线段的垂直平分线上;8.利用勾股定理的逆定理;9.利用菱形的对角线互相垂直;10.在圆中平分弦或弧的直径垂直于弦;11.利用半圆上的圆周角是直角;五、证明线段的和、差、倍、分1.作两条线段的和,证明与第三条线段相等;2.在第三条线段上截取一段等于第一条线段,证明余下部分等于第二条线段;3.利用一些定理三角形的中位线、含30度的直角三角形、直角三角形斜边上的中线、三角形的重心、相似三角形的性质等;六、证明角的和、差、倍、分1.作两个角的和,证明与第三角相等;2.作两个角的差,证明余下部分等于第三角;3.利用角平分线的定义;4.三角形的一个外角等于和它不相邻的两个内角的和;第一讲：如何做几何证明题例题精讲专题一证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系;很多其它问题最后都可化归为此类问题来证;证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到;例1已知：如图所示,∆A B C 中,∠=︒===C AC BC AD DB AE CF 90，，，; 求证：DE ＝DF巩固如图所示,已知∆A B C 为等边三角形,延长BC 到D,延长BA 到E,并且使AE ＝BD,连结CE 、DE;求证：EC ＝ED例2已知：如图所示,AB ＝CD,AD ＝BC,AE ＝CF; 求证：∠E ＝∠FF EDC BA ACEDFBABDCE专题二证明直线平行或垂直在两条直线的位置关系中,平行与垂直是两种特殊的位置;证两直线平行,可用同位角、内错角或同旁内角的关系来证,也可通过边对应成比例、三角形中位线定理证明;证两条直线垂直,可转化为证一个角等于90°,或利用两个锐角互余,或等腰三角形“三线合一”来证; 例3如图所示,设BP 、CQ 是∆A B C 的内角平分线,AH 、AK 分别为A 到BP 、CQ 的垂线; 求证：KH ∥BC例4已知：如图所示,AB ＝AC,∠，，A A E B F B D D C =︒==90; 求证：FD ⊥ED专题三证明线段和的问题一在较长线段上截取一线段等一较短线段,证明其余部分等于另一较短线段;截长法 例5如图,四边形ABCD 中,AD ∥BC,点E 是AB 上一个动点,若∠B ＝60°,AB ＝BC, 且∠DEC ＝60°； 求证：BC ＝AD ＋AE巩固已知：如图,在∆A B C 中,∠=︒B 60,∠BAC 、∠BCA 的角平分线AD 、CE 相交于O; 求证：AC ＝AE ＋CDABCDEF E DCBAAOE BDABQP HCK二延长一较短线段,使延长部分等于另一较短线段,则两较短线段成为一条线段,证明该线段等于较长线段;补短法例6 已知：如图7所示,正方形ABCD 中,F 在DC 上,E 在BC 上,∠=︒E A F 45; 求证：EF ＝BE ＋DF专题四证明几何不等式：例7已知：如图所示,在∆A B C 中,AD 平分∠BAC,AB AC >; 求证：B DD C>拓展∆A B C 中,∠=︒⊥B A C A D B C 90，于D,求证：()A D AB AC B C <++14FED CBAAC BDBCDA基本图形的辅助线的画法1.三角形问题添加辅助线方法方法1：有关三角形中线的题目,常将中线加倍;含有中点的题目,常常利用三角形的中位线,通过这种方法,把要证的结论恰当的转移,很容易地解决了问题;方法2：含有平分线的题目,常以角平分线为对称轴,利用角平分线的性质和题中的条件,构造出全等三角形,从而利用全等三角形的知识解决问题;方法3：结论是两线段相等的题目常画辅助线构成全等三角形,或利用关于平分线段的一些定理;方法4：结论是一条线段与另一条线段之和等于第三条线段这类题目,常采用截长法或补短法,所谓截长法就是把第三条线段分成两部分,证其中的一部分等于第一条线段,而另一部分等于第二条线段;2.平行四边形中常用辅助线的添法平行四边形包括矩形、正方形、菱形的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种,举例简解如下：1连对角线或平移对角线：2过顶点作对边的垂线构造直角三角形3连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线4连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形;5过顶点作对角线的垂线,构成线段平行或三角形全等.3.梯形中常用辅助线的添法梯形是一种特殊的四边形;它是平行四边形、三角形知识的综合,通过添加适当的辅助线将梯形问题化归为平行四边形问题或三角形问题来解决;辅助线的添加成为问题解决的桥梁,梯形中常用到的辅助线有：1在梯形内部平移一腰;2梯形外平移一腰3梯形内平移两腰4延长两腰5过梯形上底的两端点向下底作高6平移对角线7连接梯形一顶点及一腰的中点;8过一腰的中点作另一腰的平行线;9作中位线当然在梯形的有关证明和计算中,添加的辅助线并不一定是固定不变的、单一的;通过辅助线这座桥梁,将梯形问题化归为平行四边形问题或三角形问题来解决,这是解决问题的关键;。

初中数学辅助线应用技巧总结数学是一门需要逻辑思维和推理能力的学科，而辅助线是在解决数学问题时起到辅助作用的直线。

学会灵活运用辅助线可以帮助我们更好地理解和解决数学问题。

本文将总结几种初中数学辅助线的应用技巧。

一、应用技巧1：利用垂直线垂直线是辅助线中最常见的一种。

在解决几何问题时，垂直线可以帮助我们确定几何图形的性质。

例如，在求解平面几何问题时，我们可以利用垂直线来证明两条直线垂直。

在作图时，通过画出垂直线可以辅助我们队几何图形进行分析。

二、应用技巧2：运用平行线平行线也是常用的辅助线之一。

在解决平面几何问题时，可以利用平行线的特性来求解未知角度、边长或形状。

例如，当我们需要求解两条直线平行时，可以通过与这两条直线交叉的另一条直线来构造平行线，从而帮助我们解决问题。

三、应用技巧3：利用等腰三角形等腰三角形是一个重要的几何图形，其辅助线的运用可以帮助我们解决关于三角形的问题。

例如，在求解三角形的面积或者角度时，我们可以构造等腰三角形，从而简化问题的解决。

另外，等腰三角形的对称性质也在解决证明问题时起到重要作用。

四、应用技巧4：利用垂直平分线垂直平分线是连接线段的中点并垂直于该线段的直线。

在解决几何问题时，利用垂直平分线可以帮助我们证明角的相等、线段的相等以及几何图形的对称性质。

例如，当我们需要证明一个四边形是矩形时，可以利用垂直平分线来证明其中的两个角相等。

五、应用技巧5：利用相似三角形相似三角形是指形状相似但大小不同的三角形。

在解决几何问题时，我们可以通过构造相似三角形来求解未知边长或者角度。

例如，在利用勾股定理求解三角形问题时，常常需要使用相似三角形的性质进行推导和证明。

六、应用技巧6：使用角平分线角平分线是将一个角分成两个相等的角的直线。

在解决几何问题时，角平分线可以帮助我们证明角的相等或者构造特定的几何图形。

例如，在求解两个角相等时，可以通过画出角平分线来帮助我们得出证明结果。

七、应用技巧7：利用直行线直行线是指两条相交直线间的形成的四个角中有两个是相等的。

作辅助线的方法一：中点、中位线，延线，平行线。

如遇条件中有中点，中线、中位线等，那么过中点，延长中线或中位线作辅助线，使延长的某一段等于中线或中位线；另一种辅助线是过中点作已知边或线段的平行线，以达到应用某个定理或造成全等的目的。

二：垂线、分角线，翻转全等连。

如遇条件中，有垂线或角的平分线，可以把图形按轴对称的方法，并借助其他条件，而旋转180度，得到全等形，，这时辅助线的做法就会应运而生。

其对称轴往往是垂线或角的平分线。

三：边边若相等，旋转做实验。

如遇条件中有多边形的两边相等或两角相等，有时边角互相配合，然后把图形旋转一定的角度，就可以得到全等形，这时辅助线的做法仍会应运而生。

其对称中心，因题而异，有时没有中心。

故可分“有心”和“无心”旋转两种。

四:造角、平、相似，和、差、积、商见。

如遇条件中有多边形的两边相等或两角相等，欲证线段或角的和差积商，往往与相似形有关。

在制造两个三角形相似时，一般地，有两种方法：第一，造一个辅助角等于已知角；第二，是把三角形中的某一线段进行平移。

故作歌诀：“造角、平、相似，和差积商见。

”托列米定理和梅叶劳定理的证明辅助线分别是造角和平移的代表）五：两圆若相交，连心公共弦。

如果条件中出现两圆相交，那么辅助线往往是连心线或公共弦。

六：两圆相切、离，连心，公切线。

如条件中出现两圆相切（外切，内切），或相离（内含、外离），那么，辅助线往往是连心线或内外公切线。

七：切线连直径，直角与半圆。

如果条件中出现圆的切线，那么辅助线是过切点的直径或半径使出现直角；相反，条件中是圆的直径，半径，那么辅助线是过直径（或半径）端点的切线。

即切线与直径互为辅助线。

如果条件中有直角三角形，那么作辅助线往往是斜边为直径作辅助圆，或半圆；相反，条件中有半圆，那么在直径上找圆周角——直角为辅助线。

即直角与半圆互为辅助线。

八：弧、弦、弦心距；平行、等距、弦。

如遇弧，则弧上的弦是辅助线；如遇弦，则弦心距为辅助线。

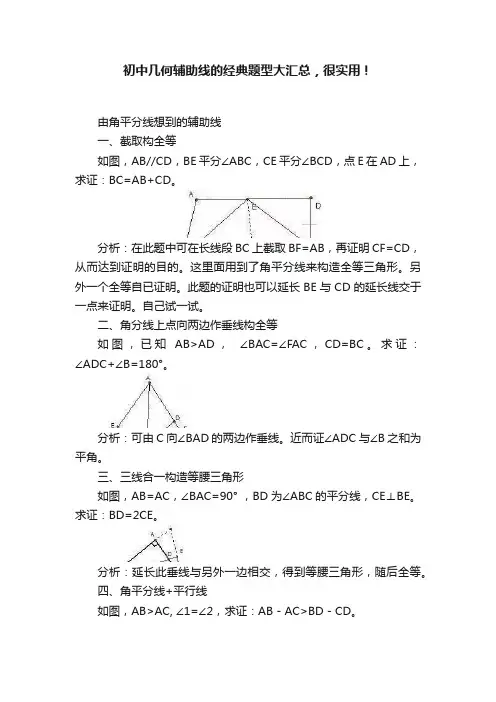
初中几何辅助线的经典题型大汇总，很实用！由角平分线想到的辅助线一、截取构全等如图，AB//CD，BE平分∠ABC，CE平分∠BCD，点E在AD上，求证：BC=AB+CD。

分析：在此题中可在长线段BC上截取BF=AB，再证明CF=CD，从而达到证明的目的。

这里面用到了角平分线来构造全等三角形。

另外一个全等自已证明。

此题的证明也可以延长BE与CD的延长线交于一点来证明。

自己试一试。

二、角分线上点向两边作垂线构全等如图，已知AB>AD，∠BAC=∠FAC，CD=BC。

求证：∠ADC+∠B=180°。

分析：可由C向∠BAD的两边作垂线。

近而证∠ADC与∠B之和为平角。

三、三线合一构造等腰三角形如图，AB=AC，∠BAC=90° ，BD为∠ABC的平分线，CE⊥BE。

求证：BD=2CE。

分析：延长此垂线与另外一边相交，得到等腰三角形，随后全等。

四、角平分线+平行线如图，AB>AC, ∠1=∠2，求证：AB－AC>BD－CD。

分析：在AB上截取AE=AC，通过全等和组成三角形的三边关系可证。

由线段和差想到的辅助线截长补短法AC平分∠BAD，CE⊥AB，且∠B+∠D=180°，求证：AE=AD+BE。

分析：过C点作AD垂线，得到全等即可。

由中点想到的辅助线一、中线把三角形面积等分如图，ΔABC中，AD是中线，延长AD到E，使DE=AD，DF是ΔDCE的中线。

已知ΔABC的面积为2，求ΔCDF的面积。

分析：利用中线平分三角形的面积求解。

二、中点联中点得中位线如图，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，BA、CD的延长线分别交EF的延长线于点G、H。

求证：∠BGE=∠CHE。

分析：取BD的中点M，连接ME、MF，通过中位线得平行传递角度。

三、倍长中线如图，已知ΔABC中，AB=5，AC=3，连BC上的中线AD=2，求BC的长。

分析：倍长中线得到全等易得。