平行四边形的面积(完美版)
- 格式:ppt
- 大小:2.14 MB
- 文档页数:28

ppt课件•平行四边形基本概念与性质•平行四边形面积计算公式推导•实际应用举例与计算技巧•常见误区及纠正方法目录•拓展延伸:其他相关几何图形面积计算•总结回顾与课堂互动环节平行四边形基本概念与性质01定义及特点定义两组对边分别平行的四边形叫做平行四边形。
特点对角线互相平分;对边平行且相等;对角相等,邻角互补。
平行四边形与矩形、正方形关系矩形有一个角是直角的平行四边形是矩形。
矩形具有平行四边形的所有性质,同时其对角线相等且互相平分。
正方形一组邻边相等的矩形是正方形。
正方形具有矩形和平行四边形的所有性质,同时其对角线相等、互相垂直且互相平分。
010204性质总结平行四边形的对边平行且相等。
平行四边形的对角相等,邻角互补。
平行四边形的对角线互相平分。
平行四边形的面积等于底和高的乘积,即S=ah(其中a为底,h为高)。
03平行四边形面积计算公式推导02基于矩形面积公式推导割补法将平行四边形沿高线切割成两部分,通过平移和旋转拼成一个矩形,从而得出平行四边形的面积等于底乘以高。
等积变形法通过等积变形,将平行四边形转化为一个与其面积相等的矩形,从而推导出平行四边形的面积公式。
基于三角形面积公式推导三角形面积公式三角形的面积等于底乘以高的一半。
对于平行四边形,可以将其划分为两个等底等高的三角形,因此平行四边形的面积等于两个三角形面积之和,即底乘以高。
间接推导法通过证明平行四边形的对角线将其分成两个面积相等的三角形,再利用三角形面积公式推导出平行四边形的面积公式。
不同方法比较与优缺点分析方法比较基于矩形面积公式推导的方法更加直观易懂,适用于初学者;而基于三角形面积公式推导的方法则更加严谨,但需要一定的几何基础。
优缺点分析基于矩形面积公式推导的方法优点是简单易懂,缺点是对于某些特殊情况可能不太适用;而基于三角形面积公式推导的方法优点是严谨性强,适用范围广,缺点是对于初学者可能较难理解。
在实际应用中,可以根据具体情况选择合适的方法进行计算。


平行四边形面积计算公式全部咱先来说说平行四边形面积计算公式这事儿哈。
要说平行四边形的面积计算,那可是数学里挺重要的一块知识呢!就拿我之前教过的一个学生小明来说吧。
有一次上课,我正讲到平行四边形面积的计算,小明那一脸迷茫的样子,让我印象特别深。
咱们来瞧瞧平行四边形,它就像一个会变形的家伙,一会儿歪这边,一会儿歪那边。
但是不管它怎么歪,咱们要算出它的面积,就得有个固定的办法。
平行四边形的面积计算公式是:面积 = 底 ×高。
这个公式看起来简单,但是要真理解透,还得费点心思。
比如说,有一个平行四边形,底是 6 厘米,高是 4 厘米。
那它的面积就是 6×4 = 24 平方厘米。
那为啥是底乘高呢?咱们来想想哈,其实可以把平行四边形沿着高剪开,然后平移,就能拼成一个长方形啦。
这个长方形的长就是原来平行四边形的底,宽就是原来平行四边形的高。
而咱们都知道长方形的面积是长乘宽,所以平行四边形的面积就是底乘高咯。
再回到小明那,我发现他不明白,就给他拿了一张纸,剪成一个平行四边形,然后当着他的面,沿着高剪开再拼成长方形。
他眼睛一下子亮了,说:“老师,我懂啦!”看着他那恍然大悟的样子,我心里可美了。
在实际生活中,平行四边形面积的计算也经常能用到。
就像咱们盖房子的时候,要是有个平行四边形的窗户,那要知道用多少玻璃,就得算出它的面积。
还有,做家具的时候,比如一张平行四边形的桌面,要给它铺上桌布,也得先知道面积大小,才能买到合适的桌布。
咱们在做数学题的时候,可不能死记硬背这个公式。
得真正理解为啥是这样,这样不管题目怎么变,咱们都能轻松应对。
总之,平行四边形面积计算公式虽然简单,但要真正掌握,还得多多练习,多多思考。
就像小明,经过那次的亲手操作,后来遇到平行四边形面积的题目,再也不犯迷糊啦。
希望大家也都能像小明一样,把这个知识牢牢掌握,在数学的世界里畅游无阻!。
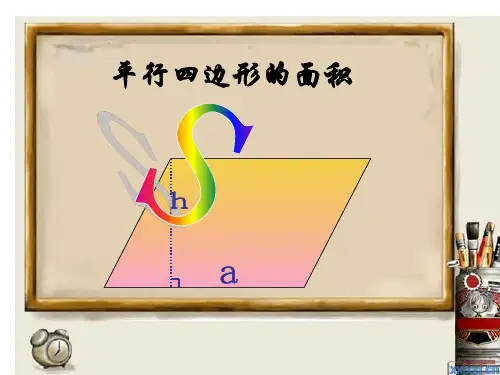

平行四边形的面积的公式平行四边形是一种常见的几何形状,它有着特殊的几何属性和数学规律。
在计算平行四边形的面积时,需要用到特定的公式,并掌握正确的计算方法。
下面就为大家详细介绍平行四边形的面积公式及其应用。
首先,我们需要知道什么是平行四边形。
平行四边形是有两组平行的边所组合成的四边形,它拥有四个顶点、四条边和四个角。
根据几何定理,平行四边形的相邻角是补角,相邻边的夹角相等。
平行四边形的对角线互相平分,且对角线长度相等。
接下来,让我们来了解平行四边形的面积公式。
对于任意一个平行四边形,其面积可以通过底边长度与高的乘积来计算。
因此,平行四边形的面积公式为S = b × h,其中b为底边的长度,h为该平行四边形的高度。
在计算平行四边形面积时,需要注意底边和高的长度单位必须相同,否则计算结果将会产生误差。
如果所给的底边长度和高度单位不同,需要先将它们转换成相同的单位,然后再进行计算。
除了通过公式计算平行四边形的面积之外,还可以通过图形构建法进行计算。
具体方法为:在平行四边形的任意一边上作一条垂线,以该垂线的长度作为高,再通过对垂线的长度和底边的长度进行计算,得出平行四边形的面积。
最后,需要强调的是,在应用平行四边形面积公式时,必须保证所计算的四边形是平行四边形。
如果所给出的四边形并非平行四边形,则不能使用该公式进行计算。
总之,平行四边形是一种简单而又重要的几何形状,它有着特殊的几何属性和数学规律。
正确掌握平行四边形的面积公式及其应用方法,有助于提高我们的几何思维能力,进一步了解数学美妙的世界。

可编辑修改精选全文完整版《平行四边形面积》说课稿《平行四边形面积》说课稿(精选12篇)作为一位优秀的人民教师,总归要编写说课稿,说课稿有助于顺利而有效地开展教学活动。
怎样写说课稿才更能起到其作用呢?以下是小编为大家整理的《平行四边形面积》说课稿(精选12篇),欢迎大家借鉴与参考,希望对大家有所帮助。
《平行四边形面积》说课稿篇1一、说教材。
《平行四边形的面积》是北师大版小学数学五年级上册第二单元的内容。
它是在学生已经掌握了长方形和正方形的面积计算、面积概念和面积单位,以及认识了平行四边形,清楚了其特征及底和高的概念的基础上来进行教学的。
学生学了这部分内容,能为以后学习三角形和梯形的面积公式打下基础。
为了更好地体现《数学课程标准》的理念,通过学习来解决生活中的实际问题,让学生感受到数学就在身边,人人学有价值的数学。
根据以上对教材的理解与内容的分析,按照新课程标准中掌握4~6学段空间与图形的要求,我将本节课的教学目标定为:1、知识目标:能应用公式计算平行四边形的面积;2、能力目标:理解推导平行四边形面积计算公式的过程,培养学生抽象概括的能力。
3、情感目标:发展学生的空间观念,培养学生的思维能力;在解决实际问题的过程中体验数学与生活的联系。
根据新课程标准中的教学内容和学生的认知能力,我将本节课的教学重点定为:能应用公式计算平行四边形的面积。
教学难点定为:理解平行四边形面积的推导过程,并能运用公式解决实际问题。
二、说教法、学法。
根据本节课的教学内容和学生的思维特点,以及新课程理念学生是学习的主体,教师是引导者、组织者、合作者,我准备采用以下几种教法和学法:1、教学中,我将通过生活情境的创设,利用多媒体教学课件,引发学生学习数学的兴趣和积极思维的动机,引导学生主动地探索。
2、动手实践、主动探索、合作交流是学生学习数学的重要方式。
由直观到抽象,层层深入,遵循了概念教学的原则和学生的认知规律。
通过动手操作,把平行四边形转化成长方形,再现已有的表象,借助已有的知识经验,进行观察、分析、比较、推理、概括出平行四边形面积的计算公式。



