编译原理课件 语法分析_自下而上__LALR

动作
移进 S5 归约 r4 Li
移进 S6 移进 S4 移进 S5 归约 r4 归约 r5 归约 r3 归约 r5 归约 r1 接受
Li RL L*R RL S L=R
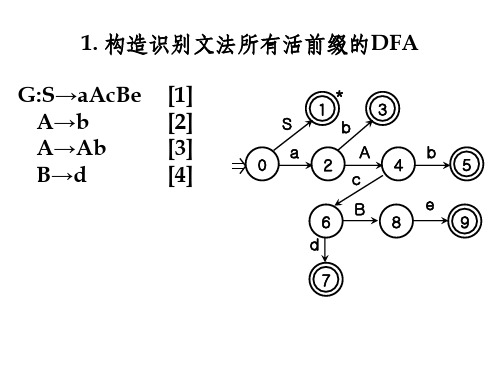
i = * i # 的LR分析过程
步骤 1 0 状态 符号栈 # 剩余输入串 动作 i=*i# 移进 S5 =*i# 归约 r4 Li =*i# 移进 S6 *i# 移进 S11 i# 移进 S12 # 归约 r4 Li # 归约 r5 RL # 归约 r3 L*R # 归约 r5 RL # 归约 r1 S L=R # 接受
结论
• 对于错误的输入串,LALR会比LR执行一些多余 归约,但不会比LR移进更多的符号. • 对于正确的输入串,LR和LALR分析器始终如影 相随
例
G[S']: (0) S' S (1) S L=R (2) S R (3) L *R (4) L i (5) R L • 写出此文法的LALR分析表 • 并根据文法的LALR分析表分析输入串 “ i=*i= # ”
i = * i # 的LALR分析过程
步骤 1 2 3 4 5 6 7 8 9 10 11 状态
0 05
02 026 0264 02645 02648 02647 0268 0269 01
符号栈 # #i #L #L= #L=* #L=*i #L=*L #L=*R #L= L #L= R #S
剩余输入串 i=*i# =*i# =*i# *i# i# # # # # # #
1 2
LALR分析表
ACTION GOTO
2 3 4 5 6 7 8 9
r1
s7 r3
r2
r2
r2
是 5 否 2 会 36 8 产 47 生 5 冲 89 9 突 ？
0 1
a b s36 s3 s47 s4
s36 s6 s36 s47 s7 s47
#
acc
S 1
B 2 5 89
r3
r3
r3 r1
r2
LALR分析表
ACTION a b # s3 s47 s4 s36 acc s36 s6 s47 s7 s36 s47 r3 r3 r2 r2 r3 r1 r2 5 89 GOTO S B 1 2
36 47 5
89
9
r2
(0)S' S (1)S BB (2)B aB (3)B b
＃aab＃的分 析过程见黑板
I6：B →a· B, # B →· aB, # B →· b, #
I36: B→a· B , a/b/# B→· aB , a/b/# B→· b , a/b/#
LR分析表
状 态 0 1 ACTION
a s3 s6 s3 r3
s6
b s4 s7 s4 r3
#
acc
合 并 GOTO 同 状 心 态 S B 集
I0初态 S' •S, # S•L=R, # S•R, # L•*R, =/# L •i, =/# R•L, #
I3: Go(I0 , R) SR •, # I4: Go(I0 , *) L* • R, =/# R • L, =/# L • *R, =/# L • i•, =/# I5: Go(I0 , i) L i •, =/#
2 3 4 5 6 7 8 9 10 11
05 02 026 026 11 026 11 12 026 11 10 026 11 13 026 10 0269 01
#i #L #L= #L=* #L=*i #L=*L #L=*R #L= L #L= R #S
LR分析小结
• • • • • • • • 规范 归约过程 LR分析过程是______ 活前缀 符号栈中的符号串被定义为__________ 分析过程中依据________________________ 栈顶状态和现行输入符号 查分析表 识别活前缀的 为构造LR分析表，可先构造________________DFA 分析表的构造 LR分析器的关键是_______________ 逐个增强 LR(0) 、SLR 、 LALR 、 LR 功能_________ 真包含 关系 四种LR类型的文法是________ LR类型文法一定是非二义的吗? 是
i = * i = # 的LR分析过程
步骤 1 0 2 3 4 5 6 05 02 026 026 11 026 11 12 状态 符号栈 # #i #L #L= #L=* #L=*i 剩余输入串 动作 i=*i=# 移进 S5 =*i=# 归约 r4 Li =*i=# 移进 S6 *i=# 移进 S11 i=# 移进 S12 =# 报错
定义
• LALR文法 - LALR分析表不含多重定义 • LALR分析表和LR(0)以及SLR分析表永远具有相 同数目的状态。
例: 写出输入串＃aab＃的LR分析过程和LALR分析过程
(0)S' S (1)S BB (2)B aB (3)B b
分析表
LR分析表
状 态 0 1 2 3 4 5 6 7 8 ACTION a b # s3 s4 acc s6 s3 r3 s6 r2 s7 s4 r3 r1 s7 r3 r2 9 5 8 GOTO S B 1 2 状 态 0 1 2
5
6 7 8 9 10 11 12
r4
S12 S11 r3 r5
r4
10 r3 r5 r1 r5 S12 S11 r4 10 13
5
6 7
r4
S5 S4 r3
r4
8 r3
8
9
r5
r5
r1
LALR分析表
13
r3
i = * i = # 的LALR分析过程
步骤 1 2 3 4 5 6 7 8 9 10 0 05 02 026 0264 02645 02648 02647 0268 0269 状态 符号栈 # #i #L #L= #L=* #L=*i #L=*L #L=*R #L= L #L= R 剩余输入串 动作 i=*i=# 移进 S5 =*i=# 归约 r4 Li =*i=# 移进 S6 *i=# 移进 S4 i=# 移进 S5 =# 归约 r4 Li =# 归约 r5 R L =# 归约 r3 L *R =# 归约 r5 R L =# 报错
B
I ：B →b·, a/b 4 b
I ：B →a·B, a/b 3 B →·aB, a/b B →·b, a/b B
b
I ：B →aB·, a/b 8
I ：B →aB·, # 9
LALR方法 : 在LR(1)项目集规范族基础上, 合并同心集
合并同心集
I4：B →b· , a/b I7：B →b· , # I8：B →aB· , a/b I9：B →aB· , # I3：B →a· B, a/b B →· aB, a/b B →· b, a/b I47: B→b·, a/b/# I89: B→aB·, a/b/#
LALR(1)分析
• 对 LR(1) 来说, 存在着某些状态, 这些状态除向前搜 索符不同外, 其核心部分都是相同的. • 同心集: 两个LR(1)项目集具有相同的心, 即除去搜索符 之后, 这两个集合是相同的。
该文法产生的是语言 a*ba*b
a
I ：S′ →·S, 0 S →·BB, B →·aB, B →·b,
ACTION GOTO 状 态 = i * # S L R
0 S5 S6 S5 S4 S4 1 2 3
GOTO 状 ACTION 态 = i * # S L R
0 S5 S4 1 2 3
1
acc
r5 r2 8 7 9
1
2 3 4 S5 S4 S6
ቤተ መጻሕፍቲ ባይዱ
acc
r5 r2 8 7 9
原 LR 分 析 表
2 3 4
Go(I11 , i) 同 I12
LR(1)项目集规范族
合并同心集
合并 I4与I11 I4,11: L* • R, =/# R • L, =/# L • *R, =/# L • i, =/# 合并 I5与I12 I5,12: L i •, =/# 合并 I7与I13 I7,13: L* R •, =/# 合并 I8与I10 I8,10: R L •, =/#
r2
r2
LALR的能力弱于LR 合并同心项目集可能会引起冲突 同心集的合并不会引起新的 移进归约冲突 (课下自行证明) 同心集的合并有可能产生新的 归约归约冲突 G : (0) S S (1) S aAd (2) S bBd (3) S aBe (4) S bAe (5) A c (6) B c 构造LR(1)项目集规范族 (见黑板) 对ac有效的项目集 合并同心集 A c ·, d 产生归约-归约冲突 B c ·, e 对bc有效的项目集 A c ·, e B c ·, d A c ·, d/e B c ·, d/e 该文法是LR(1)文法 但不是LALR(1)文法
I1: Go(I0 , S) S S • , #
I6: Go(I2 , =) SL= • R, # I2: Go(I0 , L) R • L, # SL • =R, # L • *R, # RL •, # L • i•, #
I7: Go(I4 , R) I11: Go(I6 , *) L* R •, =/# L* • R, # R • L, # I8: Go(I4 , L) L • *R, # R L •, =/# L • i•, # Go(I4 , *) I12: Go(I6 , i) 同 I4 L i •, # Go(I4 , i) 同 I5 I13: Go(I11 , R) L* R •, # I9: Go(I6 , R) Go(I11 , L) SL=R•, # 同 I10 I10: Go(I6 , L) Go(I11 , *) R L •, # 同 I11