物理化学课后答案-热力学第二定律-精选.pdf

物理化学-课后答案-热力学第二定律-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第三章 热力学第二定律【复习题】【1】指出下列公式的适用范围。

（1）min ln BB BS Rnx ∆=-∑;（2）12222111lnln ln ln P v p T V T S nR C nR C p T V T ∆=+=+; （3）dU TdS pdV =-； （4）G Vdp ∆=⎰（5）,,S A G ∆∆∆作为判据时必须满足的条件。

【解】 （1）封闭体系平衡态，理想气体的等温混合，混合前后每种气体单独存在时的压力都相等，且等于混合后气体的总压力。

（2）非等温过程中熵的变化过程，对一定量的理想气体由状态A （P 1、V 1、T 1）改变到状态A （P 2、V 2、T 2）时，可由两种可逆过程的加和而求得。

（3）均相单组分（或组成一定的多组分）封闭体系，非体积功为0的任何过程；或组成可变的多相多组分封闭体系，非体积功为0的可逆过程。

（4）非体积功为0，组成不变的均相封闭体系的等温过程。

（5）S ∆：封闭体系的绝热过程，可判定过程的可逆与否； 隔离体系，可判定过程的自发与平衡。

A ∆：封闭体系非体积功为0的等温等容过程，可判断过程的平衡与否； G ∆：封闭体系非体积功为0的等温等压过程，可判断过程的平衡与否；【2】判断下列说法是否正确，并说明原因。

（1）不可逆过程一定是自发的，而自发过程一定是不可逆的； （2）凡熵增加过程都是自发过程； （3）不可逆过程的熵永不减少；（4）系统达平衡时，熵值最大，Gibbs 自由能最小；（5）当某系统的热力学能和体积恒定时，S ∆<0的过程不可能发生；（6）某系统从始态经过一个绝热不可逆过程到达终态，先在要在相同的始、终态之间设计一个绝热可逆过程；（7）在一个绝热系统中，发生了一个不可逆过程，系统从状态1变到了状态2，不论用什么方法，系统再也回不到原来状态了；（8）理想气体的等温膨胀过程，0U ∆=，系统所吸的热全部变成了功，这与Kelvin 的说法不符；（9）冷冻机可以从低温热源吸热放给高温热源，这与Clausius 的说法不符； （10）p C 恒大于V C 。

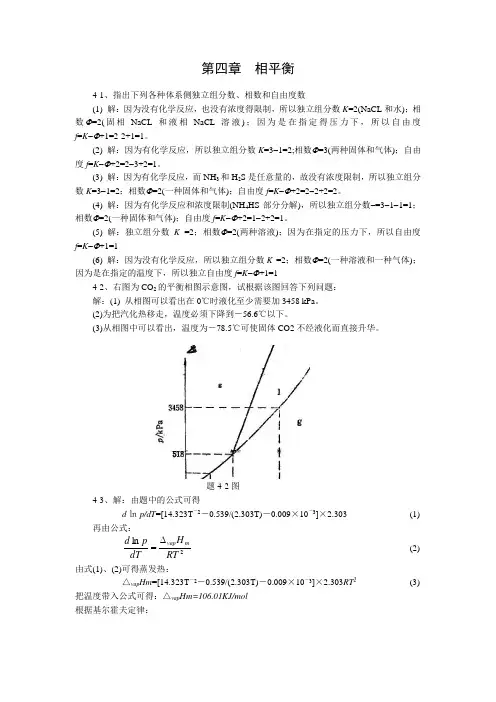
第四章 相平衡4-1、指出下列各种体系侧独立组分数、相数和自由度数(1) 解：因为没有化学反应，也没有浓度得限制，所以独立组分数K =2(NaCL 和水)；相数Φ=2(固相NaCL 和液相NaCL 溶液)；因为是在指定得压力下，所以自由度f =K -Φ+1=2-2+1=1。

(2) 解：因为有化学反应，所以独立组分数K =3-1=2;相数Φ=3(两种固体和气体)；自由度f =K -Φ+2=2-3+2=1。

(3) 解：因为有化学反应，而NH 3和H 2S 是任意量的，故没有浓度限制，所以独立组分数K =3-1=2；相数Φ=2(一种固体和气体)；自由度f =K -Φ+2=2-2+2=2。

(4) 解：因为有化学反应和浓度限制(NH 4HS 部分分解)，所以独立组分数-=3-1-1=1；相数Φ=2(一种固体和气体)；自由度f =K -Φ+2=1-2+2=1。

(5) 解：独立组分数K =2；相数Φ=2(两种溶液)；因为在指定的压力下，所以自由度f =K -Φ+1=1(6) 解：因为没有化学反应，所以独立组分数K =2；相数Φ=2(一种溶液和一种气体)；因为是在指定的温度下，所以独立自由度f =K -Φ+1=14-2、右图为CO 2的平衡相图示意图，试根据该图回答下列问题：解：(1) 从相图可以看出在0℃时液化至少需要加3458 kPa 。

(2)为把汽化热移走，温度必须下降到－56.6℃以下。

(3)78.5℃可使固体CO2不经液化而直接升华。

题4-2图4-3、解：由题中的公式可得d ㏑p/dT =[14.323T －2－0.539/(2.303T)－0.009×10－3]×2.303 (1) 再由公式：2ln RTH dT p d m vap ∆= (2) 由式(1)、(2)可得蒸发热： △vap Hm =[14.323T －2－0.539/(2.303T)－0.009×10－3]×2.303RT 2 (3) 把温度带入公式可得：△vap Hm=106.01KJ/mol根据基尔霍夫定律：︒︒∆=⎥⎥⎦⎤⎢⎢⎣⎡∂∆∂p C T H )( … (4) ∴△C p =(－0.539T/2.303－0.009×10－3×2T)×R … (5) 把温度带入式(5)可得热熔差：△C p =－7.694J.mol -1K -14-4、解：V T H dT dp ∆∆=，两边进行定积分得：△=P VH ∆∆12T T Ln △=P mg/s=4104490-⨯=1.225×106Pa , V H ∆∆ =12311104.334ρρ-⨯=－3.01×1094kJ ·kg －1·m －3T1=273K, ∴T2=272K,温度要低于零下1度4-5、解：由已知条件：T 1=398.15K , P 1=101.325Kpa , P 2=233KPa再由公式： ⎪⎪⎭⎫ ⎝⎛-∆=211211ln T T R H p p m vap 得T 2=399K 此时水得沸点：t=299℃4-6、解：△=P V H ∆∆12T T Ln ，△=P =gh ρ10×9.8×14.6×103=1430.8×103Pa ∴T2=247.32K4-7、解：(2) 从图中作垂线可知泡点温度为110.2℃(3) 从图中作垂线可知露点温度为112.8℃(4) 经过105.0︒C 点作平行线，可知组成为y B =0.417, x B =0.544(5) 此体系中X B =0.769，由杆杆规则可得w (g )×(X B －y B )= w (l )×(x B －X B )而w (g)+w (l)= 39kg ，∴w (g )=12.31kg, w (l )=26.69kg (6) 从理论上说应该降低醋酸溶液得温度4-8解：线abc是三相平衡线，此时的相数为3，独立组分数为2，自由度为0区域1：熔液，此时的相数为2，独立组分数为2，自由度为1区域2：熔液和固体Pb，相数为3，自由度为2区域3：熔液和固体Sb，相数为3，自由度为2区域4：固体Pb和固体Sb，相数为2，自由度为14-9、解：从图中可以知道，这是形成稳定化合物体系。

第三章热力学第二定律3.1卡诺热机在的高温热源和的低温热源间工作。

求（1）热机效率；（2）当向环境作功时，系统从高温热源吸收的热及向低温热源放出的热。

解：卡诺热机的效率为根据定义3.5高温热源温度，低温热源。

今有120 kJ的热直接从高温热源传给低温热源，龟此过程的。

解：将热源看作无限大，因此，传热过程对热源来说是可逆过程3.6不同的热机中作于的高温热源及的低温热源之间。

求下列三种情况下，当热机从高温热源吸热时，两热源的总熵变。

（1）可逆热机效率。

（2）不可逆热机效率。

（3）不可逆热机效率。

解：设热机向低温热源放热，根据热机效率的定义因此，上面三种过程的总熵变分别为。

3.7已知水的比定压热容。

今有1 kg，10 ︒C的水经下列三种不同过程加热成100 ︒C的水，求过程的。

（1）系统与100 ︒C的热源接触。

（2）系统先与55 ︒C的热源接触至热平衡，再与100 ︒C的热源接触。

（3）系统先与40 ︒C，70 ︒C的热源接触至热平衡，再与100 ︒C的热源接触。

解：熵为状态函数，在三种情况下系统的熵变相同在过程中系统所得到的热为热源所放出的热，因此3.8已知氮（N, g）的摩尔定压热容与温度的函数关系为2(g)置于1000 K的热源中，将始态为300 K，100 kPa下1 mol的N2求下列过程（1）经恒压过程；（2）经恒容过程达到平衡态时的。

解：在恒压的情况下, g）看作理想气在恒容情况下，将氮（N2体将代替上面各式中的，即可求得所需各量3.9始态为，的某双原子理想气体1 mol，经下列不同途径变化到，的末态。

求各步骤及途径的。

（1）恒温可逆膨胀；（2）先恒容冷却至使压力降至100 kPa，再恒压加热至；（3）先绝热可逆膨胀到使压力降至100 kPa，再恒压加热至。

解：（1）对理想气体恒温可逆膨胀， U = 0，因此（2）先计算恒容冷却至使压力降至100 kPa，系统的温度T:（3）同理，先绝热可逆膨胀到使压力降至100 kPa时系统的温度T:根据理想气体绝热过程状态方程，各热力学量计算如下2.12 2 mol双原子理想气体从始态300 K，50 dm3，先恒容加热至400 K，再恒压加热至体积增大到100 dm3，求整个过程的。

第二章热力学第二定律练习题一、判断题（说法正确否）：1．自然界发生的过程一定是不可逆过程。

2．不可逆过程一定是自发过程。

3．熵增加的过程一定是自发过程。

4．绝热可逆过程的∆S= 0，绝热不可逆膨胀过程的∆S> 0，绝热不可逆压缩过程的∆S< 0。

5．为了计算绝热不可逆过程的熵变，可以在始末态之间设计一条绝热可逆途径来计算。

6．由于系统经循环过程后回到始态，∆S = 0，所以一定是一个可逆循环过程。

7．平衡态熵最大。

8．在任意一可逆过程中∆S = 0，不可逆过程中∆S > 0。

9．理想气体经等温膨胀后，由于∆U = 0，所以吸的热全部转化为功，这与热力学第二定律矛盾吗10．自发过程的熵变∆S > 0。

11．相变过程的熵变可由计算。

12．当系统向环境传热时(Q < 0)，系统的熵一定减少。

13．一切物质蒸发时，摩尔熵都增大。

14．冰在0℃，p下转变为液态水，其熵变>0，所以该过程为自发过程。

15．自发过程的方向就是系统混乱度增加的方向。

16．吉布斯函数减小的过程一定是自发过程。

17．在等温、等压下，吉布斯函数变化大于零的化学变化都不能进行。

18．系统由V1膨胀到V2，其中经过可逆途径时做的功最多。

19．过冷水结冰的过程是在恒温、恒压、不做其他功的条件下进行的，由基本方程可得∆G = 0。

20．理想气体等温自由膨胀时，对环境没有做功，所以 -p d V= 0，此过程温度不变，∆U= 0，代入热力学基本方程d U = T d S - p d V，因而可得d S = 0，为恒熵过程。

21．是非题：⑴“某体系处于不同的状态，可以具有相同的熵值”，此话对否⑵“体系状态变化了，所有的状态函数都要变化”，此话对否⑶绝热可逆线与绝热不可逆线能否有两个交点⑷自然界可否存在温度降低，熵值增加的过程举一例。

⑸ 1mol理想气体进行绝热自由膨胀，体积由V1变到V2，能否用公式：计算该过程的熵变22．在100℃、p时，1mol水与100℃的大热源接触，使其向真空容器中蒸发成100℃、p的水蒸气，试计算此过程的∆S、∆S(环)。

第二章 热力学第二定律练习题一、判断题（说法正确否）：1．自然界发生的过程一定是不可逆过程。

2．不可逆过程一定是自发过程。

3．熵增加的过程一定是自发过程。

4．绝热可逆过程的∆S = 0，绝热不可逆膨胀过程的∆S > 0，绝热不可逆压缩过程的∆S < 0。

5．为了计算绝热不可逆过程的熵变，可以在始末态之间设计一条绝热可逆途径来计算。

6．由于系统经循环过程后回到始态，∆S = 0，所以一定是一个可逆循环过程。

7．平衡态熵最大。

8．在任意一可逆过程中∆S = 0，不可逆过程中∆S > 0。

9．理想气体经等温膨胀后，由于∆U = 0，所以吸的热全部转化为功，这与热力学第二定律矛盾吗?10．自发过程的熵变∆S > 0。

11．相变过程的熵变可由T H S ∆=∆计算。

12．当系统向环境传热时(Q < 0)，系统的熵一定减少。

13．一切物质蒸发时，摩尔熵都增大。

14．冰在0℃，pT H S ∆=∆>0，所以该过程为自发过程。

15．自发过程的方向就是系统混乱度增加的方向。

16．吉布斯函数减小的过程一定是自发过程。

17．在等温、等压下，吉布斯函数变化大于零的化学变化都不能进行。

18．系统由V 1膨胀到V 2，其中经过可逆途径时做的功最多。

19．过冷水结冰的过程是在恒温、恒压、不做其他功的条件下进行的，由基本方程可得∆G = 0。

20．理想气体等温自由膨胀时，对环境没有做功，所以 -p d V = 0，此过程温度不变，∆U = 0，代入热力学基本方程d U = T d S - p d V ，因而可得d S = 0，为恒熵过程。

21．是非题：⑴“某体系处于不同的状态，可以具有相同的熵值”，此话对否？ ⑵“体系状态变化了，所有的状态函数都要变化”，此话对否？ ⑶ 绝热可逆线与绝热不可逆线能否有两个交点？⑷ 自然界可否存在温度降低，熵值增加的过程？举一例。

⑸ 1mol 理想气体进行绝热自由膨胀，体积由V 1变到V 2，能否用公式：⎪⎪⎭⎫⎝⎛=∆12ln VV R S计算该过程的熵变？22．在100℃、p 时，1mol 水与100℃的大热源接触，使其向真空容器中蒸发成 100℃、p 的水蒸气，试计算此过程的∆S 、∆S (环)。

物理化学-课后答案-热力学第二定律(总25页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除第三章 热力学第二定律【复习题】【1】指出下列公式的适用范围。

（1）min ln BB BS Rnx ∆=-∑;（2）12222111lnln ln ln P v p T V T S nR C nR C p T V T ∆=+=+; （3）dU TdS pdV =-； （4）G Vdp ∆=⎰（5）,,S A G ∆∆∆作为判据时必须满足的条件。

【解】 （1）封闭体系平衡态，理想气体的等温混合，混合前后每种气体单独存在时的压力都相等，且等于混合后气体的总压力。

（2）非等温过程中熵的变化过程，对一定量的理想气体由状态A （P 1、V 1、T 1）改变到状态A （P 2、V 2、T 2）时，可由两种可逆过程的加和而求得。

（3）均相单组分（或组成一定的多组分）封闭体系，非体积功为0的任何过程；或组成可变的多相多组分封闭体系，非体积功为0的可逆过程。

（4）非体积功为0，组成不变的均相封闭体系的等温过程。

（5）S ∆：封闭体系的绝热过程，可判定过程的可逆与否； 隔离体系，可判定过程的自发与平衡。

A ∆：封闭体系非体积功为0的等温等容过程，可判断过程的平衡与否； G ∆：封闭体系非体积功为0的等温等压过程，可判断过程的平衡与否；【2】判断下列说法是否正确，并说明原因。

（1）不可逆过程一定是自发的，而自发过程一定是不可逆的； （2）凡熵增加过程都是自发过程； （3）不可逆过程的熵永不减少；（4）系统达平衡时，熵值最大，Gibbs 自由能最小；（5）当某系统的热力学能和体积恒定时，S ∆<0的过程不可能发生；（6）某系统从始态经过一个绝热不可逆过程到达终态，先在要在相同的始、终态之间设计一个绝热可逆过程；（7）在一个绝热系统中，发生了一个不可逆过程，系统从状态1变到了状态2，不论用什么方法，系统再也回不到原来状态了；（8）理想气体的等温膨胀过程，0U ∆=，系统所吸的热全部变成了功，这与Kelvin 的说法不符；（9）冷冻机可以从低温热源吸热放给高温热源，这与Clausius 的说法不符； （10）p C 恒大于V C 。

第三章热力学第二定律三．思考题参考答案1．自发过程一定是不可逆的，所以不可逆过程一定是自发的。

这说法对吗？ 答：前半句是对的，但后半句是错的。

因为不可逆过程不一定是自发的，如不可逆压缩过程就是一个不自发的过程。

2．空调、冰箱不是可以把热从低温热源吸出、放给高温热源吗，这是否与热力学第二定律矛盾呢？答：不矛盾。

Claususe 说的是：“不可能把热从低温物体传到高温物体，而不引起其他变化”。

而冷冻机系列，把热从低温物体传到了高温物体，环境做了电功，却得到了热。

而热变为功是个不可逆过程，所以环境发生了变化。

3．能否说系统达平衡时熵值最大，Gibbs 自由能最小？答：不能一概而论，这样说要有前提，即：绝热系统或隔离系统达平衡时，熵值最大。

等温、等压、不做非膨胀功，系统达平衡时，Gibbs 自由能最小。

也就是说，使用判据时一定要符合判据所要求的适用条件。

4．某系统从始态出发，经一个绝热不可逆过程到达终态。

为了计算熵值，能否设计一个绝热可逆过程来计算？答：不可能。

若从同一始态出发，绝热可逆和绝热不可逆两个过程的终态绝不会相同。

反之，若有相同的终态，两个过程绝不会有相同的始态。

所以只有设计一个除绝热以外的其他可逆过程，才能有相同的始、终态。

5．对处于绝热钢瓶中的气体，进行不可逆压缩，这过程的熵变一定大于零，这说法对吗？答：对。

因为是绝热系统，凡是进行一个不可逆过程，熵值一定增大，这就是熵增加原理。

处于绝热钢瓶中的气体，虽然被压缩后体积会减小，但是它的温度会升高，总的熵值一定增大。

6．相变过程的熵变，可以用公式H S T∆∆=来计算，这说法对吗？ 答：不对，至少不完整。

一定要强调是等温、等压可逆相变，H ∆是可逆相变时焓的变化值（,R p H Q ∆=），T 是可逆相变的温度。

7．是否,m p C 恒大于,m V C ?答：对气体和绝大部分物质是如此。

但有例外，4摄氏度时的水，它的,m p C 等于,m V C 。

第二章 热力学第二定律 一、基本公式和基本概念 基本公式1. 热力学第二定律的数学表达式----克劳修斯不等式 ()0A B A B QS Tδ→→∆-≥∑2. 熵函数的定义 ()R QdS Tδ=， ln S k =Ω3. 熵变的计算理想气体单纯,,p V T 变化22,1122,1122,,11ln ln ln ln lnln V m p m p m V m T V S C R T V T p S C R T p V p S C C V p ∆=+∆=-∆=+理想气体定温定压混合过程ln i i iS R n x ∆=-∑封闭系统的定压过程21,d T p m T C S n T T∆=⎰封闭系统定容过程 21,d T V m T C S n T T∆=⎰可逆相变 m n H S T∆∆=标准状态下的化学反应 ,()r m Bm B BS S T θθν∆=∑定压下由1T 温度下的化学反应熵变求2T 温度下的熵变 21,21()()d T p m r m r m T C S T S T T T∆∆=∆+⎰4. 亥姆霍兹函数 A U TS ≡-5. 吉布斯函数 G H TS ≡-6. G ∆和A ∆的计算(A ∆的计算原则与G ∆相同，做相应的变换即可)定温过程G H T S ∆=∆-∆组成不变的均相封闭系统的定温过程 21d p p G V p ∆=⎰理想气体定温过程 21ln p G nRT p ∆= 7. 热力学判据熵判据：,()0U V dS ≥亥姆霍兹函数判据：,,'0(d )0T V W A =≤ 吉布斯函数判据：,,'0(d )0T p W G =≤8. 热力学函数之间的关系组成不变，不做非体积功的封闭系统的基本方程d d d d d d d d d d d d U T S p V H T S V pA S T p V G S T V p=-=+=--=-+麦克斯韦关系S VpS T Vp TT p V S T V p S S p V T S V p T ∂∂⎛⎫⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭⎛⎫∂∂⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭∂∂⎛⎫⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭⎛⎫∂∂⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭9. 吉布斯-亥姆霍兹方程2()pG HT T T ∆⎡⎤∂⎢⎥∆=-⎢⎥∂⎢⎥⎣⎦ 基本概念1. 热力学第二定律在研究化学或物理变化驱动力来源的过程中，人们注意到了热功交换的规律，抓住了事物的共性，提出了具有普遍意义的熵函数。

第三章 热力学第二定律一、选择题1. 系统经历一个不可逆循环后：A. 系统的熵增加B. 环境热力学能减少C. 环境的熵一定增加D. 系统吸热大于对外做功2. 理想气体与温度为T 的大热源接触作等温膨胀吸热Q ，所作的功是变到相同终态的最大功的25%，则系统的熵变为：A. 0B. Q /TC. - Q /TD. 4Q /T3. 下列四个关系式中，不是麦克斯韦关系式的是：A. (∂S /∂p )T =- (∂V /∂T )pB. (∂T /∂p )s = (∂V /∂S )pC. (∂S /∂V )T =(∂p /∂T )VD. (∂T /∂V )s = (∂V /∂S )p4. 封闭系统中，若某过程的ΔA = 0，最可能的情况是：A. 绝热可逆，且 W f = 0B. 等容等压可逆，且W f = 0C. 等温等容，且 W f = 0的可逆过程D. 等温等压，且W f = 0的可逆过程5. 从热力学基本关系式可导出 (∂U /∂S )V 等于：A. (∂A /∂V )TB. (∂H /∂S )pC. (∂U /∂V )SD. (∂G /∂T )p6. 可逆机的效率最高，在其它条件相同的情况下，假设火车由可逆机牵引，其速度将： A. 最慢 B. 中等 C. 最快 D. 不能确定7. 在 100℃ 和 25℃ 之间工作的热机，其最大效率为：A. 100 %B. 75 %C. 25 %D. 20 %8. 对1mol 理想气体，温度由T 1变到T 2，等压可逆过程系统熵变为❒S p ，等容可逆过程系统熵变为❒S V ，则❒S p :❒S V 为：A. 1:1B. 2:1C. 3:5D. 5:39. 某气体状态方程为p = f (V )·T ，则恒温下该气体的熵是随体积的增加而： A. 增加 B. 不变 C. 减小 D. 不能确定10. 求任一不可逆绝热过程的熵变ΔS 时，可以通过 途径求得：A. 始终态相同的可逆绝热过程B. 始终态相同的可逆非绝热过程C. 始终态相同的可逆恒温过程D. B 和C 均可11. 一定量的理想气体向真空绝热膨胀，体积由V 1变到V 2，则熵变求算公式为： A. ΔS =0 B. 21lnV S nR V ∆= C. 21ln pS nR p ∆= D. 无法求算 12. 298K 时，1 mol 理想气体等温可逆膨胀，压力从1000kPa 变到100kPa ，系统的吉布斯自由能变化值为：A. 0.04kJB. -12.4kJC. 5.7kJD. -5.7kJ13. 热力学第三定律也可表示为：A. 在0K 时，任何晶体的熵等于零B. 在0℃时，任何晶体的熵等于零C. 在0K 时，任何完整晶体的熵等于零D. 在0℃时，任何完整晶体的熵等于零14. 在273.15K 、101325Pa 的条件下，水凝结成冰，系统的热力学量变化一定为；零的是： A. ❒H B. ❒U C. ❒S D. ❒G15. 在-10℃、101325Pa 下，1mol 水凝结为冰的过程中，下列公式扔适用的是：A. ❒U =T ❒SB. H GS T∆-∆∆=C. ❒H =T ❒S + V ❒pD. ❒G T ,p =0二、填空题1. 对于孤立系统，∆S = 0表示 过程；∆S < 0 表示________过程；∆S >0表示__________过程。

第七章7-1、证明对于二级反应，当反应物的原始浓度相同时，作用掉3/4原始反应物所需时间等于此反应半衰期的三倍． 证明：对于二级反应000][3)14311(][1)111(][1A k A k A k t ααθαθ=--=--= 02/1][1A k t α=2/13t t =∴θ7-2、反应A ２+B ２→2AB 若为基元反应，速率方程应当怎样？只根据速率方程能否确定是否基元反应？ 解：速率方程为]][[22B A k r =只根据速率方程不能确定是基元反应。

例如: H 2+I 2=2HI 的速率方程为 ]][[22I H k r =,但H 2+I 2=2HI 的反应并不是基元反应。

所以只跟据速率 方程不能确定是基元反应。

7-3、试证明一级反应在其原始反应物的转化率从0→50%，50→75%及75→87.5%所需的每段反应时间都等于ln2/k 。

解：对于一级反应：0→50%的时间： k t 2ln 1=50→75%的时间：k k k t 2ln 2ln 4311ln 1=--= 75→87.5%的时间：k k k t 2ln 4311ln 18711ln 1=---= 7-4、反应(CH 3)2CHN=NCH(CH 3)2(g) →N 2(g)+C 6H 12(g)为一级反应。

若反应在恒容反应器中进行，则体系的压力逐渐增大。

假设t =0时，(CH 3)2CHN=NCH(CH 3)2(g)的压力为P i ，此时没有产物。

在t =t 时，反应体系的压力为P 。

证明k =1/t ln[P i /（2P i –P ）]解：设(CH 3)2CHN=NCH(CH 3)2(g) , N 2(g), C 6H 12(g)分别为A, B, C A → B + Ct=0 P A,0 0 0 t=t P A,0-P B P B P c =P B 系统总压力 P= P A,0-P B +(P B+ P B )= P A,0+P B 反应物A 的分压P A = P A,0-P B = P A,0-(P- P A,0)=2P A,0-P一级反应⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=P P P t P P t k i i A A 2ln 110, 7-5、温度升高，反应速率为什么增大？从阿仑尼乌斯公式和碰撞理论来解释。

热力学第二定律课后习题答案习题1在300 K ，100 kPa 压力下，2 mol A 和2 mol B 的理想气体定温、定压混合后，再定容加热到600 K 。

求整个过程的∆S 为若干？已知C V ,m ,A = 1.5 R ，C V ,m ,B = 2.5 R[题解]⎪⎩⎪⎨⎧B(g)2mol A(g)2mol ，，纯态 3001001K kPa，（）−→−−−−混合态，，2mol A 2mol B100kPa 300K 1+==⎧⎨⎪⎪⎩⎪⎪p T 定容（）−→−−2混合态，，2mol A 2mol B 600K 2+=⎧⎨⎪⎩⎪T ∆S = ∆S 1 + ∆S 2，n = 2 mol∆S 1 = 2nR ln ( 2V / V ) = 2nR ln2 ∆S 2 = ( 1.5nR + 2.5nR ) ln （T 2 / T 1）= 4nR ln2 所以∆S = 6nR ln2= ( 6 ⨯ 2 mol ⨯ 8.314 J ·K -1·mol -1 ) ln2 = 69.15 J ·K -1 [导引]本题第一步为理想气体定温定压下的混合熵，相当于发生混合的气体分别在定温条件下的降压过程，第二步可视为两种理想气体分别进行定容降温过程，计算本题的关键是掌握理想气体各种变化过程熵变的计算公式。

习题22 mol 某理想气体，其定容摩尔热容C v ，m =1.5R ，由500 K ，405.2 kPa 的始态，依次经历下列过程：(1)恒外压202.6 kPa 下，绝热膨胀至平衡态； (2)再可逆绝热膨胀至101.3 kPa ； (3)最后定容加热至500 K 的终态。

试求整个过程的Q ，W ，∆U ，∆H 及∆S 。

[题解] （1）Q 1 = 0，∆U 1 = W 1， nC V ,m （T 2－T 1）)(1122su p nRT p nRT p --=， K400546.2022.405)(5.11221211212====-=-T T kPa p kPa p T p T p T T ，得，代入，（2）Q 2 = 0，T T p p 3223111535325=-=-=--()γγγγ，， T T 320.42303==-()K（3）∆V = 0，W 3 = 0，Q U nC T T V 3343232831450030314491==-=⨯⨯⨯-=∆,()[.(.)].m J kJp p T T 434350030310131671==⨯=(.).kPa kPa 整个过程：Q = Q 1 + Q 2+ Q 3 =4.91kJ ，∆U = 0，∆H = 0，Q + W = ∆U ，故W =－Q =－4.91 kJ∆S nR p p ==⨯=--ln (.ln ..).141128314405616711475J K J K ··[导引]本题的变化过程为单纯pVT 变化，其中U 、H 和S 是状态函数，而理想气体的U 和H 都只是温度的函数，始终态温度未变，故∆U = 0，∆H = 0。

第二章 热力学第二定律练习题一、判断题（说法正确否）：1．自然界发生的过程一定是不可逆过程。

2．不可逆过程一定是自发过程。

3．熵增加的过程一定是自发过程。

4．绝热可逆过程的S = 0，绝热不可逆膨胀过程的S > 0，绝热不可逆压缩过程的S < 0。

5．为了计算绝热不可逆过程的熵变，可以在始末态之间设计一条绝热可逆途径来计算。

6．由于系统经循环过程后回到始态，S = 0，所以一定是一个可逆循环过程。

7．平衡态熵最大。

8．在任意一可逆过程中S = 0，不可逆过程中S > 0。

9．理想气体经等温膨胀后，由于U = 0，所以吸的热全部转化为功，这与热力学第二定律矛盾吗10．自发过程的熵变S > 0。

11．相变过程的熵变可由T HS ∆=∆计算。

12．当系统向环境传热时(Q < 0)，系统的熵一定减少。

13．一切物质蒸发时，摩尔熵都增大。

14．冰在0℃，p 下转变为液态水，其熵变T HS ∆=∆>0，所以该过程为自发过程。

15．自发过程的方向就是系统混乱度增加的方向。

16．吉布斯函数减小的过程一定是自发过程。

17．在等温、等压下，吉布斯函数变化大于零的化学变化都不能进行。

18．系统由V 1膨胀到V 2，其中经过可逆途径时做的功最多。

19．过冷水结冰的过程是在恒温、恒压、不做其他功的条件下进行的，由基本方程可得G = 0。

20．理想气体等温自由膨胀时，对环境没有做功，所以 -p d V = 0，此过程温度不变，U = 0，代入热力学基本方程d U = T d S - p d V ，因而可得d S = 0，为恒熵过程。

21．是非题：⑴“某体系处于不同的状态，可以具有相同的熵值”，此话对否⑵“体系状态变化了，所有的状态函数都要变化”，此话对否⑶ 绝热可逆线与绝热不可逆线能否有两个交点⑷ 自然界可否存在温度降低，熵值增加的过程举一例。

⑸ 1mol 理想气体进行绝热自由膨胀，体积由V 1变到V 2，能否用公式：⎪⎪⎭⎫⎝⎛=∆12ln VV R S计算该过程的熵变22．在100℃、p时，1mol 水与100℃的大热源接触，使其向真空容器中蒸发成100℃、p 的水蒸气，试计算此过程的S 、S (环)。