积分白噪声随机路面谱的生成

一、白噪声模型建立白噪声模型是由白噪声经过积分后得到的，是一种描述路面形态的最常用的数学模型。

通常把路面相对于基准平面的高度q ，沿道路走向长度I 的变化q(t)，称为路面纵断面曲线，它服从高斯分布。

作为车辆输入的路面不平度，主要采用路面功率谱密度描述其统计特性。

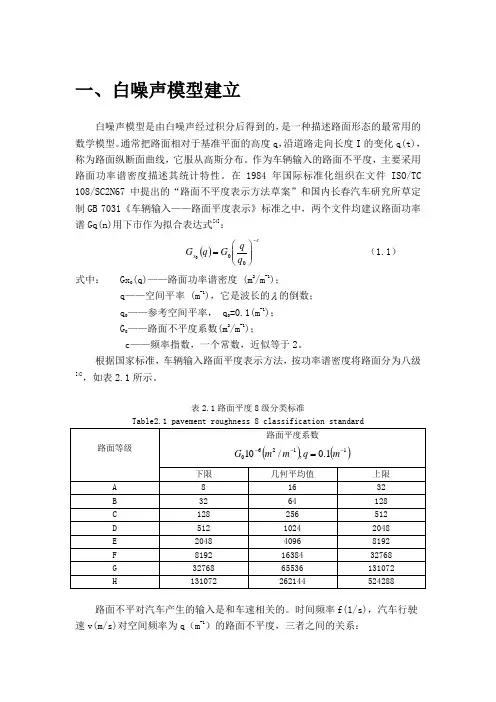
在1984年国际标准化组织在文件ISO/TC 108/SC2N67中提出的“路面不平度表示方法草案”和国内长春汽车研究所草定制GB 7031《车辆输入——路面平度表示》标准之中，两个文件均建议路面功率谱Gq(n)用下市作为拟合表达式[4]：()cx q q G q G -⎪⎪⎭⎫⎝⎛=000 （1.1）式中： Gx 0(q)——路面功率谱密度 (m 2/m -1)； q ——空间平率 (m -1)，它是波长的λ的倒数； q 0——参考空间平率， q 0=0.1(m -1)； G 0——路面不平度系数(m 2/m -1)；c ——频率指数，一个常数，近似等于2。

根据国家标准，车辆输入路面平度表示方法，按功率谱密度将路面分为八级[4]，如表2.1所示。

表2.1路面平度8级分类标准Table2.1 pavement roughness 8 classification standard路面不平对汽车产生的输入是和车速相关的。

时间频率f(1/s)，汽车行驶速v(m/s)对空间频率为q （m -1）的路面不平度，三者之间的关系：qv f = (1.2)空间频率谱函数转化为与速度有关的时间频谱函数，有关系式()()Vq G f G x x 00=(1.3)将式（2.2）和式（2.3）代入上（2.1）最后推到的式：()cc cx f V q G f G 1000-=（1.4） 垂直位移的功率谱密度与垂直速度的功率谱密度的关系，如式()()()f G f f G x x 0022π= （1.5）如果c=2，则地面垂直速度功率谱密度描述为()()()V q G f G f f G x x 20224200ππ== (1.6)由上式(1.6)看出，如果w 一定，则地面垂直功率谱密度就是一个常数，可以看做是白噪声的过程。

σ 2 , ω ≤ ω0 （ ω0 为给定的远大于过程的截止频率） 谱密度： SW (ω ) = 0, ω > ω0 σ 2ω0 sin ω0τ 相关函数： RW (τ ) = ⋅
π
ω0τ
讨论白噪声时，还要涉及到白噪声的概率分布，服从正态分布的白噪声称为 高斯白噪声。 n 维白噪声：一个 n 维随机过程 W (t ) 满足： E{W (t )} = 0 Cov{W (t ),W (t + τ )} = E{W (t )W (t + τ )} = Qδ (τ ) 其中 Q 为正定常数矩阵，则称 W (t ) 为 n 维白噪声过程。 ● 白噪声序列 白噪声序列是白噪声过程的离散形式。如果序列 {W (k )} 满足： 相关函数： RW (l ) = σ 2δ l , l = 0,±1,±2,L 则称为白噪声序列。 谱密度： SW (ω ) =
N 2 = i =1 N / 12
∑ξ
N
i
−
N 12 2 由此可得正态分布η ~ N ( µη ,σ η ) 的随机数。
取 N = 12 时，有
η = µη + σ η
∑ξ
i =1
N
i
−
N 2
η = µη + σ η ∑ ξi − 6
i =1
● 变换抽样法 理论依据：设 ξ1 和 ξ 2 是相互独立的（0，1）均匀分布随机变量，则
● M 序列的生成结构图 ● M 序列的波形 1.2.3 特征多项式 解决如何选取反馈通道的问题，以保证生成 M 序列。 ● 定义多项式： G ( s ) = ∑ x i s i （无限阶）
i =0 P 1 , F ( s ) = 1 ⊕ ∑ a j s j （有限阶） F ( s) j =1 称 F ( s ) 为 M 序列的特征多项式。 注意 1：此时选取 M 序列初始状态为： x1 = 1, x 2 = 0, L , x P = 0 。 注意 2：生成 M 序列的结构图完全由特征多项式 F ( s ) 确定。 ∞

滤波白噪声法生成随机路面1.原理200()()()1()()n Gq n Gq n nf unGq f Gq n uf un===ω=2π=2π22002()()()uGq n n ω=2πω (1)设截止频率为0ω，则1式变换成220022()()()u Gq Gq n n ω=2πω+ω (2)假设2式是白噪声激励下一阶线性系统的响应，设频率响应函数()aH j b j ω=+ω（a,b 为未知常数） (3)2()()Gq H j S ω=ωω （S ω为白噪声信号，设1S ω=） (4)连理式2、3、4解得a nb =2π=ω该线性系统的频率响应函数为0()H j ω=系统的微分方程为0()()()n w t q t q t 2π=ω+（()w t 为白噪声的时域信号，()q t为激励，即为路面谱时域信号）状态方程0()()()q t q t n w t =-ω+2π由于000n u ω=2π得00()()()q t n uq t n w t =-2π+2π2.simulink 仿真输入参数u=10; % 速度（单位m/s ）Gqn0=4096e-6; % E 级路面的路面功率谱密度 down=2048; % E 级路面不平度下限 up=8192; % E 级路面不平度上限白噪声信号属性注意：采样周期为0.001s ，采样频率为f=1/0.001=1000Hz,路面频率f1=un<1000/2,满足采样定理。

采样频率过低，可能引起低频功率下降。

时域路面信号生成模型验证y=simout;Fs=1000; %采样频率[pxx,f]=pwelch(y,[],[],[],Fs); %功率谱密度函数n=f/u; %时间频率转换成空间频率 pxx=pxx*u;loglog(n,pxx);grid on;hold on;y1=down.*1e-8./n.^2; %注意单位y2=up.*1e-8./n.^2;loglog(n,y1);loglog(n,y2);z=std(y)验证结果可见路面谱大部分落在了E级路面的区域内！！！完！！。

滤波白噪声法生成随机路面1.原理200()()()1()()n Gq n Gq n nf unGq f Gq n uf un===ω=2π=2π22002()()()uGq n n ω=2πω (1)设截止频率为0ω，则1式变换成220022()()()u Gq Gq n n ω=2πω+ω (2)假设2式是白噪声激励下一阶线性系统的响应，设频率响应函数()aH j b j ω=+ω（a,b 为未知常数） (3)2()()Gq H j S ω=ωω （S ω为白噪声信号，设1S ω=） (4)连理式2、3、4解得a nb =2π=ω该线性系统的频率响应函数为0()H j ω=系统的微分方程为0()()()n w t q t q t 2π=ω+（()w t 为白噪声的时域信号，()q t为激励，即为路面谱时域信号）状态方程0()()()q t q t n w t =-ω+2π由于000n u ω=2π得00()()()q t n uq t n w t =-2π+2π2.simulink 仿真输入参数u=10; % 速度（单位m/s ）Gqn0=4096e-6; % E 级路面的路面功率谱密度 down=2048; % E 级路面不平度下限 up=8192; % E 级路面不平度上限白噪声信号属性注意：采样周期为0.001s ，采样频率为f=1/0.001=1000Hz,路面频率f1=un<1000/2,满足采样定理。

采样频率过低，可能引起低频功率下降。

时域路面信号生成模型验证y=simout;Fs=1000; %采样频率[pxx,f]=pwelch(y,[],[],[],Fs); %功率谱密度函数n=f/u; %时间频率转换成空间频率 pxx=pxx*u;loglog(n,pxx);grid on;hold on;y1=down.*1e-8./n.^2; %注意单位y2=up.*1e-8./n.^2;loglog(n,y1);loglog(n,y2);z=std(y)验证结果可见路面谱大部分落在了E级路面的区域内！！！完！！。

一、白噪声模型建立白噪声模型是由白噪声经过积分后得到的，是一种描述路面形态的最常用的数学模型。

通常把路面相对于基准平面的高度q ，沿道路走向长度I 的变化q(t)，称为路面纵断面曲线，它服从高斯分布。

作为车辆输入的路面不平度，主要采用路面功率谱密度描述其统计特性。

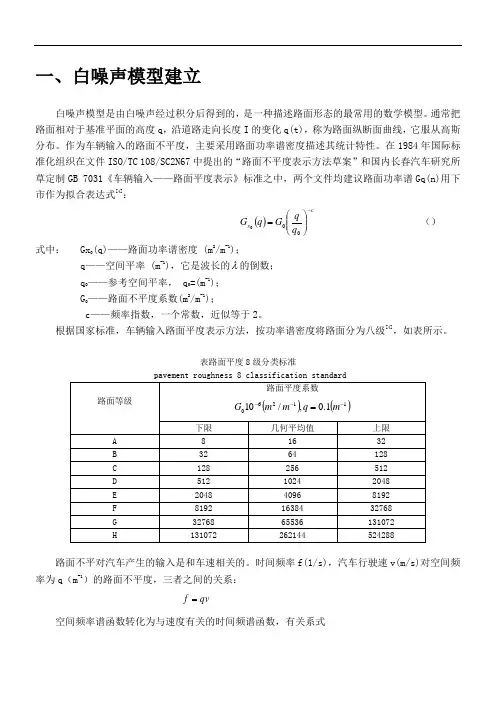
在1984年国际标准化组织在文件ISO/TC 108/SC2N67中提出的“路面不平度表示方法草案”和国内长春汽车研究所草定制GB 7031《车辆输入——路面平度表示》标准之中，两个文件均建议路面功率谱Gq(n)用下市作为拟合表达式[4]：()cx q q G q G -⎪⎪⎭⎫⎝⎛=000 （）式中： Gx 0(q)——路面功率谱密度 (m 2/m -1)； q ——空间平率 (m -1)，它是波长的λ的倒数； q 0——参考空间平率， q 0=(m -1)； G 0——路面不平度系数(m 2/m -1)；c ——频率指数，一个常数，近似等于2。

根据国家标准，车辆输入路面平度表示方法，按功率谱密度将路面分为八级[4]，如表所示。

表路面平度8级分类标准路面不平对汽车产生的输入是和车速相关的。

时间频率f(1/s)，汽车行驶速v(m/s)对空间频率为q （m -1）的路面不平度，三者之间的关系：qv f =空间频率谱函数转化为与速度有关的时间频谱函数，有关系式()()Vq G f G x x 00=将式（）和式（）代入上（）最后推到的式：()cc cx fV q G f G 1000-= （） 垂直位移的功率谱密度与垂直速度的功率谱密度的关系，如式()()()f G f f G x x 0022π= （）如果c=2，则地面垂直速度功率谱密度描述为()()()V q G f G f f G x x 20224200ππ==由上式看出，如果w 一定，则地面垂直功率谱密度就是一个常数，可以看做是白噪声的过程。

通过()dt t w c t x t⎰=)(0就可以得到白噪声路面干扰模型，其中C=4π2G 0q 20V ，w 0(t)是单位白噪声。

白噪声积分，并计算方差和均值
白噪声积分是指对白噪声进行积分得到的过程。

白噪声是一种
具有平坦功率谱密度的随机信号，其在不同频率上具有相等的能量。

对白噪声进行积分可以得到随机过程，通常称为随机游走过程或布
朗运动。

在数学上，对白噪声进行积分可以用随机过程的角度来理解，即在每个时间点上，随机游走的位置是前一时刻位置的累积和，因此可以看作是一个连续的累积过程。

要计算白噪声积分的方差和均值，首先需要明确白噪声的性质。

白噪声的方差是无穷大，因为其功率谱密度在所有频率上都是常数，所以方差是无穷大。

但是对于白噪声的积分，情况会有所不同。

具
体计算白噪声积分的方差需要考虑积分的时间范围，通常情况下，
对于有限时间范围内的积分，可以计算其方差。

假设我们对白噪声进行积分得到随机过程X(t)，则X(t)的均值
可以表示为E[X(t)]，方差可以表示为Var[X(t)]。

在这种情况下，
我们需要使用随机过程的性质和积分的定义来计算均值和方差。

具
体的计算方法会涉及到随机过程的理论和积分的性质，需要进行一
定的数学推导和计算。

总的来说，白噪声积分的方差和均值的计算涉及到随机过程的
性质和积分的定义，需要根据具体的情况进行计算。

在实际应用中，可以通过数值模拟或者利用随机过程的性质进行估计。

希望这个回
答能够帮助你理解白噪声积分的方差和均值的计算方法。

在计算机上用数学方法产生随机数，是目前使用较广，发展较快 的一种方法。它利用数学递推公式来产生随机数，通常把这样得到的 随机数称为伪随机数。
由于这种方法属于半经验性质，只能近似地具备随机性质。但是 只要产生伪随机数的递推公式选得较好，由此产生的随机数序列的独 立性是可以近似得到满足的。而且只要公式的参数选得适当，就可以 保证所得到的随机数循环周期有足够长。若所使用的随机数总数不超 过伪随机数序列的循环周期时，使用要求即可得到满足。理论定量分 析结果表明，为保证随机数学期望的最大容量（对应循环周期）、独 立性及均匀性，递推公式及其有关参数的正确选择是极为重要的。
➢ 物理方法——真随机数
所谓物理方法就是在电子计算机上装一台物理随机数发生器， 它是把具有随机性质的物理过程直接在机器上变换为随机数字。例 如：以放射性物质为随机源的放射型随机数发生器、以电子管或晶 体的固有噪声为随机源的随机数发生器。主要的物理方法有： 放射性物质、电子管或晶体管噪声、锁相环噪声源、量子模型、混 沌模型
➢数学方法——伪随机数
2、联合法（组合发生器）
混和同余法实际上是通过同余等运算打乱数列0，1，…，m-1的次 序，来达到产生随机序列的目的。“打乱数列的次使之排列无规则”是 设计发生器的一个可依据的原则，基于此产生联合法：
3、各种分布白噪声的产生
➢均匀分布白噪声的产生
1、物理方法 2、数学方法
线性同余法、联合法、反馈位移寄存器法
➢非均匀分布白噪声的产生
1、理论方法 反变换法、舍选抽样法、复合法、变换法、查表法
2、常用的连续分布及其产生 均匀分布、指数分布、 正态分布、 对数正态分布、威布尔分布、 瑞利分布 3、常用的离散分布及其产生
3、建立各种估计量
具有各种分布随机序列的模拟是计算机模拟及系统仿真的基础，广 泛地应用于雷达、通信、声呐、机械振动、核物理、自动控制、金融分 析、数值计算、贝叶斯统计等许多领域，例如雷达/声呐回波中的杂波和 噪声的模拟、机械振动噪声的模拟、随机测量误差的模拟等。

白噪声的研究与生成目录白噪声的研究与生成 (1)目录 (1)1. 白噪声的定义 (2)2. 统计特性 (2)3. 白噪声的生成 (3)3.1 高斯白噪声的生成 (3)3.1.1. WGN：产生高斯白噪声 (3)3.1.2. AWGN：在某一信号中加入高斯白噪声 (3)3.1.3.注释 (4)3.2 均匀分布的白噪声的产生 (5)4.白噪声的应用 (6)1.白噪声的定义白噪声是指功率密度在整个频域内均匀分布的噪声。

所有频率具有相同能量的随机噪声称为白噪声。

从我们耳朵的频率响应听起来它是非常明亮的“咝”（每高一个八度，频率就升高一倍。

因此高频率区的能量也显著增强）。

即，此信号在各个频段上的功率是一样的。

由于白光是由各种频率（颜色）的单色光混合而成，因而此信号的这种具有平坦功率谱的性质被称作是“白色的”，此信号也因此被称作白噪声。

相对的，其他不具有这一性质的噪声信号被称为有色噪声。

理想的白噪声具有无限带宽，因而其能量是无限大，这在现实世界是不可能存在的。

实际上，我们常常将有限带宽的平整信号视为白噪声，以方便进行数学分析。

2.统计特性术语白噪声也常用于表示在相关空间的自相关为0的空域噪声信号，于是信号在空间频率域内就是“白色”的，对于角频率域内的信号也是这样，例如夜空中向各个角度发散的信号。

右面的图片显示了计算机产生的一个有限长度的离散时间白噪声过程。

需要指出，相关性和概率分布是两个不相关的概念。

“白色”仅意味着信号是不相关的，白噪声的定义除了要求均值为零外并没有对信号应当服从哪种概率分布作出任何假设。

因此，如果某白噪声过程服从高斯分布，则它是“高斯白噪声”。

类似的，还有泊松白噪声、柯西白噪声等。

人们经常将高斯白噪声与白噪声相混同，这是不正确的认识。

根据中心极限定理，高斯白噪声是许多现实世界过程的一个很好的近似，并且能够生成数学上可以跟踪的模型，这些模型用得如此频繁以至于加性高斯白噪声成了一个标准的缩写词：AWGN。

导师姓名 及 职 称： 陈虹 教授
论文起止年月：2001 年 9 月 至 2003 年 2 月 |
I
提要
悬架系统是汽车的重要组成部分， 关系车辆振动与操控问题， 悬架设计是 车辆设计的重要部分。 悬架系统的设计为控制理论的应用提供了一个广泛的研 究领域。本文以二分之一车为对象，利用鲁棒控制理论与 LMI（线性矩阵不等 式）理论，进行主动悬架控制系统的分析与设计，使其满足车辆系统的性能要 求。 本文首先给出了悬架系统的数学模型， 利用鲁棒控制理论， 将车辆在行驶 中的参数变化描述为系统的结构不确定性。 随后给针对悬架系统性能出了三种 、RMS 增益法和传递函数法。本 分析与评价的方法， µ 分析（结构奇异值法） 文以二分之一车模型为基础， 考虑车辆的乘坐舒适性、 稳定性与物理系统的约 束，利用鲁棒控制理论，设计 H ∞ 与 H 2 主动悬架控制器，并对闭环系统进行分 析与评价。最后，针对悬架控制的多目标性，利用 LMI 理论，进行系统性能的 分析与状态反馈控制器的综合，对闭环系统进行分析与仿真。 本文的研究工作受教育部科学技术研究项目 “约束不确定鲁棒优化控制的 LMI 方法及其滚动时域实现”资助。
吉林大学硕士学位论文
论文分类号 密 级
TP273 内 部
单 位 代 码 研 究 生 学 号
10183 2200721
吉
林
大
学
硕 士 学 位 论 文
基于二分之一车的主动悬架设计
Active Suspension Control Based On a Half-Car Model
作者姓名： 专 业：
刘淳 控制理论与控制工程车体的姿态控制 乘员乘坐舒适性悬架工作行程
轮胎动载荷的控制
图 1-1 车辆行驶动力学的主要性能指标

基于联合仿真的主动悬架自适应模糊PID控制研究陈传灿;朱哈福【摘要】利用ADAMS建立了1/4车辆主动悬架的机械模型,运用MATLAB设计了基于自适应模糊PID控制算法的主动悬架控制系统,通过ADAMS/Control模块与MATLAB的接口实现了基于车辆悬架多体模型的主动控制联合仿真.仿真结果表明,采用自适应模糊PID控制能取得很好的控制效果,与被动悬架相比显著地降低了车身加速度和轮胎动位移,大大提高了车辆的乘坐舒适性和操纵稳定性.【期刊名称】《农业装备与车辆工程》【年(卷),期】2012(050)008【总页数】5页(P33-37)【关键词】联合仿真;主动悬架;自适应模糊PID控制【作者】陈传灿;朱哈福【作者单位】201804 上海市同济大学汽车学院;201804 上海市同济大学汽车学院【正文语种】中文【中图分类】U463.330 引言悬架系统是车辆底盘的重要组成部分，它与车辆行驶的平顺性和稳定性紧密相关。

传统被动悬架的阻尼和刚度系数一般按经验和优化设计方法选择，一经选定，在车辆行驶过程中就无法进行调节，当面对复杂多变的工况时，被动悬架很难兼顾平顺性和稳定性。

主动悬架能主动实时地产生和调整所需悬架控制力，使悬架总是处于较佳的减振状态，可以大幅度改善车辆的乘坐舒适性和操纵稳定性。

近年来，随着汽车工业的飞速发展，主动悬架已越来越多地用于车辆当中，寻找一种较佳的控制策略成为了主动悬架研究的重要内容和亟待解决的问题。

目前对车辆主动悬架控制策略的研究大都是建立在悬架系统数学模型基础之上[1～3] ，利用MATLAB软件对车辆进行仿真，得到最终减震效果。

然而，精确数学模型不易建立，且由于机械设计师和控制工程师使用不同的软件对同一车辆模型进行重复建模，一旦出现问题，机械系统和控制系统都要重新设计，势必带来繁重的工作量。

将ADAMS和MATIAB结合起来进行联合仿真，可以很好地解决上述问题。

它能直接从ADAMS生成仿真模型导入MATLAB中进行仿真，而无需推导、列写复杂的动力学方程描述机械系统，大大简化了建模过程；同时，它可以在ADAMS机械系统模型上实现复杂的控制策略，并进行交互式仿真，遇到问题，可从机械系统和控制系统协调的角度来解决。

Matlab实现ADAMS三维随机路面建模黄志强;郑旺辉【摘要】根据谐波叠加法得到二维随机路面谱,通过改进的谐波叠加法将二维路面谱扩展到三维,形成三维随机路面谱的建模方法.详解了ADAMS中三维随机路面文件的编制规则,通过Matlab编程计算出路面文件中的路面点高程值阵列,生成ADAMS三维随机路面模型文件,仿真计算过程表明路面可用于仿真计算研究.【期刊名称】《现代防御技术》【年(卷),期】2018(046)003【总页数】6页(P165-170)【关键词】谐波叠加法;路面谱;三维路面;仿真;建模;模型文件【作者】黄志强;郑旺辉【作者单位】北京机械设备研究所,北京100854;北京机械设备研究所,北京100854【正文语种】中文【中图分类】TJ812;N945.120 引言随机路面中激励点的高程值变化可以用另一个词汇来表达：路面不平度。

路面不平度[1]定义为道路表面相对于理想平面的偏离，它描述了随机路面下车辆的振动输入。

同时，相较于车辆发动机等激励源，路面不平度是车辆振动系统的主要振源，在建立车辆系统整车数学或者仿真模型进行平顺性分析时，可以忽略发动机等激励源，而将路面不平度激励作为唯一的激励源施加在车上。

路面不平度通常用来描述路面的起伏程度[1]。

对路面谱的研究首先在于获取路面谱，最直接的方法就是测量，为此，研究者们发明了多种路面谱测量设备。

近年来，随着传感器技术、计算机技术和信号处理技术的飞速发展, 人们对路面不平度的采集、测量和各种试验方法也在不断的更新和改进[1],这一领域已经涌现出了多种测量和试验分析的新方法。

一般按照测量原理的不同可分为直接接触式测量仪和非接触式测量仪(响应式测量仪)等。

国内直接接触式测量仪的典型代表是1979年, 国内长春汽车研究所的赵继海等人发明的拖车式真实路形仪[1], 通过测量拖车上前后轮与拖臂等部件之间的角度变化来获得路面的真实路形。

在对一定道路的测量和分析研究中，学者们发现路面不平度虽然不能够用普通数学函数描述，但是其具有随机、平稳、各态历经的特征[1],这些特征在统计学意义上具有完整的理论描述方法，研究发现路面不平度可以用平稳随机过程理论来分析描述。

，A不能 的伪随机数
• 不同的A值对应的随机序列的周期：
• T=
• 64 NaN 3 5 11 13 19 21 … A=4*i-2-(-1)^i
• 32 NaN 7 9 23 25 39 41 … A=8*i-4-(-1)^i*3
• 16 NaN 15 17 47 49 79 81 … A=16*i-8-(-1)^i*7
白噪声的产生和应用
组员：黄健 张颖 蔡朋飞 主讲人：黄 健
白噪声的产生方法
1.均匀随机数的产生 • 乘同余法 • 混合同余法 2.正态随机数的产生 • 统计近似抽样法 • 变换抽样法 3.M序列
均匀随机数的产生
1.乘同余法 第一步：递推式 其中 太小。初值 取正奇数。 第二步： 为伪随机数，周期为
接收 E ＋ X1 用户
Y m序列 产生器
原始信码 X1 m序列 Y
加密输出 E 解密输出 X1
10 110 100 11 11 000 010 11 01 110 110 00 10 110 100 11
3.误码率的测量
m序列 发生器
数传机 发送端
信道
数传机 接收端
＋
误码 计数器
m序列 发生器
A=256*i+1
A=179时产生的随机序列，周期：T =64
2.混合同余法 第一步：递推式 其中： c为正整数，初值 为非负整数 第二步： 是周期为 的伪随机数
M=2^8时，不同的c值对应的随机序列的周期：
• T=
• 256 NaN 10 14 18 22 …c=4*i-2
Ci
M序列
n级线性移位寄存器的如图：
＋
＋
＋
c0＝1
c1

Matlab中白噪声的时间积分在Matlab中，对白噪声进行时间积分是一个常见且重要的过程。

白噪声是一种频谱特性非常均匀的噪声信号，其功率谱密度在所有频率上都是恒定的。

在实际应用中，我们经常需要对白噪声进行时间积分，以得到随机游走过程或布朗运动过程，这在金融工程、信号处理等领域具有重要意义。

对于Matlab用户来说，如何进行白噪声的时间积分是一个常见问题。

在Matlab中，可以通过以下步骤实现这一过程。

1. 生成白噪声信号我们需要生成一个白噪声信号。

在Matlab中，可以使用awgn函数生成均值为0、方差为1的高斯白噪声信号，具体代码如下：```matlabN = 1000; % 信号长度white_noise = randn(1, N); % 生成白噪声信号```2. 对白噪声进行时间积分接下来，我们需要对生成的白噪声进行时间积分。

在Matlab中，可以使用cumsum函数对信号进行累积和运算，实现时间积分的过程，具体代码如下：```matlabintegrated_noise = cumsum(white_noise); % 对白噪声进行时间积分```3. 绘制结果并分析我们可以将生成的白噪声信号和对其进行时间积分后的信号进行绘图，以便更直观地观察时间积分的效果。

还可以对结果进行进一步分析，比如计算信号的均值、方差等统计特性，以及观察信号的频谱特性等。

个人观点和理解对于白噪声的时间积分，在Matlab中的实现过程相对简单，但在实际应用中具有重要意义。

通过对白噪声进行时间积分，可以得到随机游走过程或布朗运动过程，这对于模拟金融资产价格、分析信号处理中的随机干扰等问题具有重要意义。

掌握在Matlab中实现白噪声的时间积分是非常有益的。

总结本文通过介绍在Matlab中对白噪声进行时间积分的方法，以及对结果进行分析的过程，希望读者能够对这一问题有所了解。

在实际应用中，对白噪声进行时间积分是一个常见且重要的过程，通过本文的介绍，希望读者能够掌握这一技能，并在实际工程中加以应用。

一、实验背景白噪声是一种具有平坦频谱特性的噪声，其功率谱密度在所有频率范围内均相等。

白噪声在信号处理、通信、噪声控制等领域具有广泛的应用。

本实验旨在通过搭建实验装置，产生白噪声，并对其进行测量和分析。

二、实验目的1. 了解白噪声的产生原理；2. 掌握白噪声的产生方法；3. 学习白噪声的测量方法；4. 分析白噪声的特性。

三、实验原理白噪声的产生原理是通过随机信号源产生具有平坦频谱特性的噪声。

在实验中，我们可以通过以下方法产生白噪声：1. 采用随机噪声发生器，将随机信号经过滤波器处理后，得到具有平坦频谱特性的白噪声；2. 利用数字信号处理技术，通过随机信号生成算法产生白噪声。

四、实验仪器与设备1. 随机噪声发生器；2. 滤波器；3. 信号分析仪；4. 示波器；5. 数据采集卡；6. 计算机。

五、实验步骤1. 连接实验装置，将随机噪声发生器的输出信号输入滤波器；2. 调整滤波器参数，使滤波器输出信号具有平坦频谱特性；3. 将滤波器输出信号输入信号分析仪，进行频谱分析；4. 使用示波器观察白噪声的波形；5. 使用数据采集卡采集白噪声信号，进行进一步分析。

六、实验结果与分析1. 频谱分析通过信号分析仪对白噪声进行频谱分析，得到白噪声的功率谱密度。

从分析结果可以看出，白噪声的功率谱密度在所有频率范围内均相等，符合白噪声的特性。

2. 波形观察使用示波器观察白噪声的波形，可以看到白噪声的波形具有随机性，无明显规律。

3. 数据分析使用数据采集卡采集白噪声信号，进行进一步分析。

通过分析白噪声的时域特性、频域特性等，可以进一步了解白噪声的特性。

七、实验结论1. 成功搭建了白噪声产生实验装置，并产生了具有平坦频谱特性的白噪声；2. 掌握了白噪声的产生方法、测量方法和特性分析；3. 为后续白噪声在信号处理、通信、噪声控制等领域的应用奠定了基础。

八、实验总结本实验通过对白噪声的产生、测量和分析，使我们了解了白噪声的特性及其应用。

积分白噪声随机路面谱的生成本文介绍的是用MATLAB6.5生成随机数据，导入并应用于ADAMS20050.0版本的汽车悬架联合仿真的路面输入。

首先在MATLAB中按图1所示创建有限带宽随机数据产生模块：图1框图中，两个增益的值分别为：k=0.1303，k1=13.89。

点击仿真开始后，在MATLAB的工作空间（Workspace）会得到两组数据tout,yout，是106×1的数组，分别打开并复制到一个新的文本文件里，tout 作为第一列，yout作为第二列，保存为英文文件名，以备稍候导入到ADAMS中。

由于ADAMS不识别中文字符，建议最好连文件夹的储存路径都用英文的。

打开ADAMS/View中所建立的悬架模型，在主菜单选File----Import，出现图2对话框:图2“FileType”项选“TestData”；选生成样条“CreateSpline”；在“FileToRead”项单击鼠标右键，选择上个步骤所储存的文本数据文件。

点“OK”完成数据导入。

打开ADAMS的数据库浏览器，可以看到生成的样条曲线数据。

在以后定义驱动方程时就可以用这个样条曲线数据了。

定义驱动方程。

在给路面施加驱动时，定义随机路面输入的步骤如下：1.右击驱动，选择“Modify”，出现图3对话框，在“Function（time）”框内输入：100*AKISPL(time,0,SPLINE_2,0)。

AKISPL（）是ADAMS的一个函数，表示按Akima 插值方法将样条数据“SPLINE_2”拟合成以时间为横轴的函数曲线。

这样，汽车悬架随机路面谱驱动生成了。

必须再次说明，这是在MATLAB6.5版中做的结果，在7.0或其他版本做出的结果可能有所不同，请大家注意。

一、白噪声模型建立白噪声模型是由白噪声经过积分后得到的，是一种描述路面形态的最常用的数学模型。

通常把路面相对于基准平面的高度q ，沿道路走向长度I 的变化q(t)，称为路面纵断面曲线，它服从高斯分布。

作为车辆输入的路面不平度，主要采用路面功率谱密度描述其统计特性。

在1984年国际标准化组织在文件ISO/TC 108/SC2N67中提出的“路面不平度表示方法草案”和国内长春汽车研究所草定制GB 7031《车辆输入——路面平度表示》标准之中，两个文件均建议路面功率谱Gq(n)用下市作为拟合表达式[4]：()cx q q G q G -⎪⎪⎭⎫⎝⎛=000 （1.1）式中： Gx 0(q)——路面功率谱密度 (m 2/m -1)； q ——空间平率 (m -1)，它是波长的λ的倒数； q 0——参考空间平率， q 0=0.1(m -1)； G 0——路面不平度系数(m 2/m -1)；c ——频率指数，一个常数，近似等于2。

根据国家标准，车辆输入路面平度表示方法，按功率谱密度将路面分为八级[4]，如表2.1所示。

表2.1路面平度8级分类标准Table2.1 pavement roughness 8 classification standard路面不平对汽车产生的输入是和车速相关的。

时间频率f(1/s)，汽车行驶速v(m/s)对空间频率为q （m -1）的路面不平度，三者之间的关系：qv f = (1.2)空间频率谱函数转化为与速度有关的时间频谱函数，有关系式()()Vq G f G x x 00=(1.3)将式（2.2）和式（2.3）代入上（2.1）最后推到的式：()cc cx f V q G f G 1000-=（1.4） 垂直位移的功率谱密度与垂直速度的功率谱密度的关系，如式()()()f G f f G x x 0022π= （1.5）如果c=2，则地面垂直速度功率谱密度描述为()()()V q G f G f f G x x 20224200ππ== (1.6)由上式(1.6)看出，如果w 一定，则地面垂直功率谱密度就是一个常数，可以看做是白噪声的过程。

驾驶员座椅悬架模糊控制的联合仿真研究孟杰;陈庆樟;张凯【摘要】根据某车型参数，运用Adams/View 建立了驾驶员座椅悬架系统的虚拟样机模型。

应用模糊逻辑控制理论，进行了针对该悬架模糊控制模型的设计，并在Matlab/Simulink 环境下控制系统实现了联合仿真。

同时，将该控制方式、被动控制以及 PID控制器控制的半主动座椅悬架系统做了性能对比分析。

仿真结果证明，相对于其它两种悬架来说，具有模糊控制器作用的主动悬架在降低座椅悬架振动加速度、速度和动行程等性能方面效果明显，有效改善了乘坐舒适性。

%According to the parameters of a vehicle , this paper builds a virtual prototyping for the driver ’ s seat suspen-sion system usingAdams/View.Based on the theory of the fuzzy logic control , this paper also provides such a control system design , and carries out a co-simulation under the environment of Matlab/Simulink .Meanwhile , this paper com-pares the fuzzy controller to the passive and PID one .The simulation results show that such a fuzzy controller can greatly better the performance of the acceleration , velocity and the dynamic travel of the seat suspension , and the sitting comfort .【期刊名称】《农机化研究》【年(卷),期】2013(000)008【总页数】5页(P212-216)【关键词】车辆;座椅;悬架;模糊控制器;联合仿真【作者】孟杰;陈庆樟;张凯【作者单位】常熟理工学院机械工程学院，江苏常熟 215500;常熟理工学院机械工程学院，江苏常熟 215500;常熟理工学院机械工程学院，江苏常熟 215500【正文语种】中文【中图分类】U4630 引言以农用车辆和工程车辆为代表的非道路车辆，其减振装置简陋、道路条件差及车辆的振动问题较为突出，对车辆的乘坐舒适性和驾驶员的健康造成影响[1]；而车辆座椅是车辆减振系统的最后环节，它可以减少司乘人员所受的振动。