慈溪中学苗孟义

慈溪市三山高级中学2007学年第一学期高三理科第一次月考数学卷命题：苗孟义 审题：王叶岐 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．第I 卷（选择题 共50分）一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知全集{1,2,3,4,5}U =，集合,A B U ⊆，若}4{=B A ，()U A B =ð{2, 5}，则集合B 等于 （ ） A ．{2, 4, 5}B ．{2, 3, 5}C ．{3, 4, 5}D ．{2, 3, 4}2．已知条件x x p =|:|，条件x x q -≥2:，则p 是q 的 （ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分又不必要条件3．已知,αβ均为第二象限角，且sin sin αβ>，则下列不等式成立的是 （ ）A ．tan tan αβ>B ．cot cot αβ<C ．cos cos αβ>D ．sec sec αβ>4．已知tan θ、tan()4πθ-是方程02=++n mx x 的两根，则n m -的值为 （ ）A ．1B ．2C ．1-D ．2-5．在等差数列{}n a 中，2616a a a ++为定值，记数列{}n a 的前n 项和为n S ，则一定是 常数的是 （ ）A ．17SB ．15SC ．8SD ．7S6．如果直线1y kx =+与圆2240x y kx my +++-=交于M 、N 两点，且M 、N 关于 直线01=-+y x 对称，则k -m 的值为 （ ）A ．4B ．2C ．-2D ．-47．已知函数2()f x ax x c =--，若不等式()0f x >的解集为{|21}x x -<<，则函数 ()y f x =-的大致图象是 （ ）8．已知a 、b 、c 是互不相等的正数，则下列不等式中不恒成立．．．．的是 （ ） A ．| a －b |≤| a －c | + | b －c | B ．221a a +≤aa 1+C ．1||||a b a b -+-≥2D ．13+-+a a ≤a a -+29．设平面向量11(,)x y =a ，22(,)x y =b ，若||2=a ，||3=b ，6⋅=-a b ，则1122x y x y ++=（ ） A ．23 B ．23- C ．56 D ．56-10．已知定义域为R 的函数()f x 满足(2)(2)f x f x +=--，当2x <时，函数()f x单调递增，如果124x x +<，且12(2)(2)0x x --<，则12()()f x f x + （ ）A ．可能为0B ．恒大于0C ．恒小于0D ．可正可负第Ⅱ卷（非选择题 共100分）二、填空题（本大题共7小题，每小题4分，共28分，把答案填在答题卡的相应位置）11．直线:(2)l y k x =+被圆224C :x y +=截得线段长为k = ．12．已知A 、B 、C 为△ABC 的三内角，且其对边分别为a 、b 、c ，若120A =,a =4b c +=，则ABC ∆的面积为 ．13．已知实数,x y 满足10,10,10,x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩则2x y -的最大值为 ．14．不等式1||121≥-++x x x 的解集为 ．15．函数log (3)1a y x =+-(01)a a >≠且，的图象恒过定点A ，若定点A 在直线10(0)mx ny mn ++=>上，则12m n+的最小值为 ． 16．已知函数3)(+=x x f ，x x g -=3)(，构造函数)(x F y =定义如下：当)()(x g x f ≥时，)()(x g x F =；当)()(x g x f <时，)()(x f x F =，则)(x F 的最大值为__________． 17．有下列四个命题：①xx y 22sin 3sin +=的最小值是32； ②已知1011)(--=x x x f ，则)3()4(f f <；③)1,0)(2(log ≠>+=a a a y x a 在定义域R 上是增函数；④定义在实数集R 上的奇函数()f x 满足(1)()f x f x +=-，则(2)0f =． 其中，真命题的序号是 ．（把你认为正确命题的序号都填上） 三、解答题(本大题共5小题，共72分，解答应写出文字说明，证明过程或演算步骤) 18．（本题满分14分）已知函数()2f x kx =+，不等式|()|6f x <的解集为(1,2)-．试求不等式6log log (1)(01)()a a x a f x <-<<的解集．19．（本题满分14分）已知函数2()6sin cos 1f x x x x =+． ⑴求函数()f x 的最大值及相应的x 值的集合；⑵写出函数()f x的图象是由函数y x =的图象经过怎样的变换得到的？ ⑶若()f x 的图象按向量(,2)3π=-a 平移，得到函数()g x ，求()g x 的单调递增区间． 20．（本题满分14分）已知||=a ，||3=b ，a 与b 的夹角为45．⑴求⋅a b 及|a -b |；⑵若λa +b 与λa +b 的夹角为锐角，求实数λ的取值范围．21．（本题满分14分）已知函数321()(0)3F x ax bx cx d a =-++≠的图象过原点，设()()f x F x '=，且(1)0f =．⑴若函数()y F x =在1x =-处取得极大值2，试求函数()y F x =的单调区间； ⑵设()()g x f x '=，函数()y f x =与()y g x =的图象交于不同的两点A 、B ， 若使()0g x =成立的x 满足11[,]22x ∈-，求线段AB 在x 轴上的射影长的取值范围．22．（本题满分16分）已知数列{}n a 的首项114a a =≠，且11,21,4nn n a n a a n +⎧⎪⎪=⎨⎪+⎪⎩为偶数，为奇数.设2114n n b a -=-，1,2,3,n =．⑴求23,a a ；⑵判断数列{}n b 是否为等比数列，并证明你的结论； ⑶求12lim()n n b b b →∞+++．[参考答案]一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)二、填空题（本大题共7小题，每小题4分，共28分，把答案填在答题卡的相应位置） 11．．1 14．1{|}3x x >-15．8 16．2 17．②③④ （填写②③或②④或③④得2分） 三、解答题(本大题共5小题，共72分，解答应写出文字说明，证明过程或演算步骤) 18．（本题满分14分）解：由|2|6kx +<得，84kx -<<，由于解集为(1,2)-．若0k >，则84x k k -<<，故8142k k⎧-=-⎪⎪⎨⎪=⎪⎩ 无解；若0k <，则48x k k <<-，故8241k k⎧-=⎪⎪⎨⎪=-⎪⎩ ∴4k =-∴ ()42f x x =-+ 故原不等式可化为3og og (1)12aa l l x x<-- ∴ 3012103112x x xx⎧>⎪-⎪->⎨⎪⎪>--⎩∴ 12122x x ⎧<⎪⎪⎨⎪-<<⎪⎩ ∴1122x -<< ∴解集为11(,)22-19．（本题满分14分）解：由于1cos 2()3sin 212xf x x +=+-3sin 21x x =+)16x π=++⑴ 当22()62x k k Z ππ+=π+∈时，即当()6x k k Z π=π+∈时，有max ()1f x =，此时{|,}6x x k k Z π=π+∈⑵ 变换：()()2)6I II y x y x y x π=−−→=−−→=+())16III y x π−−−→=++ ()I 图象上各点的横坐标缩小到原来的12倍（纵坐标不变）； ()II 图象上各点向左平移12π； ()III 图象上各点向上平移1个单位．⑶ 由于()))]1236g x x ππ=-++-)12x π=--1x =--令222k x k π≤≤π+π得()2k x k k Z ππ≤≤π+∈ ∴ 增区间为[,]()2k k k Z πππ+∈． 20．（本题满分14分）解：⑴ ⋅a b 332=⨯=；222()+229-235=+⋅=+⨯=a -b a b a b ，∴=|a -b |．⑵若λa +b 与λa +b 平行时，有11λ=λ，∴1λ=±当1λ=时，λa +b 与λa +b 的夹角为0； 当1λ=-时，λa +b 与λa +b 的夹角为π；∵ λa +b 与λa +b 的夹角为锐角，则()()0⋅>λλa +b a +b ，∴ 222(λ+1)0λ⋅λ>a +a b+b∴ 22λ+3(λ+1)+9λ>0 ，即23λ+11λ+3>0∴λ<或λ>且1λ≠ 21．（本题满分14分）解：⑴c bx ax x F x f +-='=2)()(2 ,∴(1)20(1)20f a b c f a b c =-+=⎧⎨-=++=⎩又根据已知得(0)0(1)23F d aF b c d ==⎧⎪⎨=-++=⎪⎩解得330a c b d =-⎧⎪=⎨⎪==⎩∴3()3F x x x =-+（Ⅱ）b ax x f x g 22)()(-='= )0(≠a ，∴方程0)(=x g 的解为a b x =∴⎥⎦⎤⎢⎣⎡-∈=21,21a b x 由2()2()22f x ax bx c g x ax b⎧=-+⎨=-⎩化简得02)(22=+++-c b x b a ax (0)a ≠ 再由0)1(=-f 得b a c 2--=,∴04)(4)2(4)(4222>++=+-+=∆a b a c b a b a . 设),(),,(2211y x B y x A ,∴222221)22(4)(4)2(4)(4a a b b a b a a c b a b a x x ---+=+-+=- 2)(2)(24882222++=++=a ba b ab ab a . ⎥⎦⎤⎢⎣⎡-∈21,21a b ,∴∈-21x x ]13,5[. 即线段AB 在x 轴上的射影长的取值范围是]13,5[22．（本题满分16分）解：⑴ 211144a a a =+=+； 32111228a a a ==+；⑵ 由于111144b a a =-=+，23111428b a a =-=-，∵212212112121212111111111()()142424424111124444n n n n n n n n n n a a a a b b a a a a +--+------+--=====---- ∴ 数列{}n b 是以14a +为首项，以12为公比的等比数列．⑶ 112114lim()211212n n a b b b b a q →∞-+++===---。

关于公布2013年宁波市高一化学竞赛获奖名单的通知各县(市)、区教研室、直属中学：2013年宁波市高一化学竞赛在各县（市）、区教研室的大力支持下已于5月26日顺利进行。

本次竞赛有5000余名学生参加，共评出：（1）A组团体优胜奖4名，B组团体优胜5名；（2）A组个人一等57名，二等奖107名，三等奖126名；（3）B组个人一等奖52名，二等奖88名，三等奖126名。

现将名单予以公布（详见附件）。

附件一：A组获奖名单附件二：B组获奖名单宁波市教育局教研室宁波市化学会宁波教育学会中学化学分会2013年6月1日附件一：A组获奖名单一等奖（57名）郑宇镇海中学陈鼎镇海中学陈智健象山中学金旭统镇海中学黄镭慈溪中学吴田波镇海中学胡佳聪慈溪中学孙暄镇海中学郑毓宁镇海中学刘敏超宁海中学徐子云镇海中学周彬象山中学林友宇镇海中学王波镇海中学黄刚慈溪中学黄海文镇海中学陆莹莹镇海中学李尚霖镇海中学王秦松宁海中学温东晟镇海中学胡桐玮宁海中学徐甬嘉镇海中学张定余镇海中学沈运浩效实中学叶宇航慈溪中学伍哲彬镇海中学孙家平镇海中学施博文镇海中学史挺镇海中学蔡丹杰镇海中学林少植慈溪中学刘盛旺宁海中学姜河之是慈溪中学柴恒镇海中学徐晴慈溪中学厉宏宇镇海中学童翔宇宁海中学马天放镇海中学谢茂林余姚中学李嘉楠镇海中学叶威镇海中学徐贝贝慈溪中学岑佳辉慈溪中学严清余姚中学陈齐斌慈溪中学王涛镇海中学胡益慈溪中学陈楚天镇海中学周涵慈溪中学周子逸镇海中学王雯宇宁海中学林远帆镇海中学章剑鸿宁海中学邱宇珩镇海中学尤亚颖宁海中学王竹阳镇海中学邵涵余姚中学二等奖（107名）戎誉慈溪中学陈珊珊宁海中学林挺慈溪中学夏启铭余姚中学毛凯天慈溪中学吴亦全余姚中学应焕钦慈溪中学汪畅镇海中学徐翯晟北仑中学严勇杰宁海中学孟子羽效实中学何柯琪余姚中学张瀚岑效实中学诸清源镇海中学沈敏哲慈溪中学施亦凡镇海中学徐斌奉化中学张腾辉北仑中学陈昊哲效实中学崔嘉彦鄞州中学王刚华慈溪中学徐帅余姚中学费楠益慈溪中学蒋之成镇海中学陈欢宁海中学徐梦凡镇海中学王朝骅宁海中学叶庭葳镇海中学朱元昊象山中学潘晓宇效实中学孙晨航慈溪中学叶唯简镇海中学张冰宇象山中学朱国友效实中学韦祎象山中学王玥慈溪中学高洁锋慈溪中学蓝天翔镇海中学吕勇奉化中学吴心宇镇海中学赵程浩余姚中学陈鑫犇镇海中学郑登超余姚中学叶鸿远北仑中学陈瑶北仑中学杨明杰镇海中学钟妤婕慈溪中学唐翀铖镇海中学周国立奉化中学王屹昂镇海中学王哲思宁海中学李瑞栋镇海中学朱林圣宁海中学岑宇航龙赛中学程俊渝余姚中学陈嘉伟镇海中学陈奕霖余姚中学姚嘉哲慈溪中学俞佳烨慈溪中学娄鼎革宁海中学李文韬慈溪市浒山中学卢晨象山中学陈琪午奉化中学张好雨鄞州中学杨浏奉化中学魏杰超余姚中学蓝金晶宁海中学吴必升镇海中学郑荣宁海中学林靖坤镇海中学邬俊俊宁海中学张煜皓镇海中学张文雅宁海中学杨智宇效实中学张芝晗效实中学倪当午知恩中学韩超慈溪中学邵海磊象山中学童章彬宁海中学何天泽余姚中学童宇亮宁海中学杨鈜毅余姚中学袁文琳宁海中学吴仁柯余姚中学陈羽楠宁海中学崔健镇海中学彭李军宁海中学张哲豪镇海中学陈泽华宁海中学周旭波鄞州中学袁霜宁波中学林奕人象山中学张楠宁波中学武晓俊象山中学何璇效实中学俞冠丞余姚中学张蔚奉化中学方铃亚余姚中学陈旭东奉化中学张颂北仑中学沈哲怡北仑中学徐祺鄞州中学傅莹北仑中学鲁勇杰鄞州中学李宇龙北仑中学王璐余姚中学毛灵栋效实中学三等奖（126名）刘韬北仑中学朱嘉聪效实中学谢磊北仑中学张幼翟效实中学居钰乔宁波中学吴振贤象山中学鞠朵宁波中学董靖鄞州中学徐程程效实中学夏潜北仑中学蒋雨晨北仑中学徐邵行鄞州中学沈昊效实中学虞浩磊鄞州中学梁晓莹奉化中学陈智岚姜山中学龚学平象山中学金荣璐鄞州中学孙梓涵象山中学叶旭枫余姚中学叶哲宇象山中学袁逸凡余姚中学曾庆敏北仑中学王昂泽奉化中学庄心昊北仑中学吴浩鄞州中学李书尧北仑中学徐佳豪鄞州中学倪乐天效实中学施洌聪余姚中学张震祺效实中学王瀚文余姚中学庄雨虹奉化中学赵越北仑中学刘泽南北仑中学杨亦臻奉化中学易磊宁波中学袁寅申奉化中学罗文菁效实中学周家腾奉化中学陈澹宁效实中学胡崇泽奉化中学任航效实中学谢其宸象山中学项望效实中学尹一帆象山中学施韬宁波中学陈宇昂象山中学沈威力奉化中学胡梦梦余姚中学孙蕴妍北仑中学屠若文效实中学虞子健北仑中学郑滢效实中学戴博纬北仑中学梁鑫科奉化中学史雨阳效实中学周阳象山中学练恩魁效实中学施洁钻余姚中学陈怡北仑中学陈为治宁波二中王纪恩北仑中学叶凯效实中学江梦倩北仑中学朱泉松奉化中学林思远效实中学吕旭浩象山中学周凌峰效实中学郑浩鄞州中学胡琼效实中学龚泽宁鄞州中学陈焯效实中学王文嘉鄞州中学赵逸文效实中学林恒余姚中学杨哲涵宁波二中胡烨北仑中学贺泽博北仑中学余府臻奉化中学乐协辉宁波二中蒋文灏奉化中学刘仲禹效实中学丁雷杰奉化中学施敏效实中学戴拓鄞州中学石守珂效实中学冯金宣余姚中学邱悦效实中学郑浙舜余姚中学王珂宇效实中学符浩铖余姚中学吴昕炜宁波二中江梦芸北仑中学邬家琪北仑中学施放效实中学贺顺杰北仑中学徐琛杰奉化中学钱宇效实中学陈诗蝶鄞州中学周家瑜效实中学包旭东余姚中学王书迪效实中学洪启洋余姚中学朱乾麒效实中学张毅恺效实中学俞嘉力鄞州中学童旻鄞州中学郑可鄞州中学石晨磊正始中学蒋增鄞州中学林鹤峰鄞州中学夏佳能正始中学周威涛正始中学宋世威鄞州中学楼立诚鄞州中学宋锦浩姜山中学陈卫正始中学周昱伟鄞州中学章佳杰正始中学徐毅晖姜山中学张之远鄞州中学朱力鄞州中学蒋挺正始中学陈杰姜山中学郑书晟姜山中学A组团体优胜奖:镇海中学慈溪中学宁海中学象山中学附件：B组获奖名单一等奖（52名）陈凯浪慈溪市实验高中赵鼎蛟川书院王泽辉慈溪市实验高中黄郅栋慈溪市实验高中陈再宏慈溪市实验高中范天立慈溪市实验高中朱镒栋慈溪市实验高中詹洲翔蛟川书院陈奕瑞慈溪市实验高中夏宇鑫慈溪市实验高中方昊天慈溪市慈中书院宋杰慈溪市实验高中姜港宁波外国语学校沈鑫慈溪市实验高中徐圣涛宁波外国语学校叶浩桢慈溪市实验高中马商瑜慈溪市育才中学虞倩慈溪市实验高中马梦叶慈溪市实验高中施湛慈溪市实验高中胡炀慈溪市实验高中胡蒙福慈溪市实验高中张浩东宁波外国语学校於姝怡慈溪市实验高中蔡望勇慈溪市实验高中余升宇蛟川书院周士钧宁波外国语学校应哲栋慈溪市慈中书院朱子航慈溪市实验高中邹殷辞蛟川书院苗科泽慈溪市实验高中沃思奇蛟川书院范一丰宁波外国语学校邹锴慈溪市实验高中孙珂璐慈溪市实验高中褚博煜蛟川书院张楚人慈溪市实验高中吴善平象山三中王程永康惠贞书院罗世晨姚中书院黄晟慈溪市实验高中刘双劼蛟川书院沈云青慈溪市实验高中高源象山三中王迪晟奉化高级中学张旭豪象山三中李琦刚柴桥中学陈家洛宁波外国语学校王逸群惠贞书院龚不破慈溪市实验高中吕道桓宁波外国语学校王铭君蛟川书院二等奖（88名）吴俊彦泰河中学吴铖澄慈溪市实验高中高克威慈溪市育才中学马云天慈溪市慈中书院胡晨翔慈溪市实验高中赵阳姚中书院胡亮慈溪市实验高中郑一尔象山三中黄群佳慈溪市实验高中章俊逸惠贞书院邵威慈溪市实验高中童铖昊鄞州高级中学沈林坤慈溪市实验高中马怡斌高风中学陆镥桑慈溪市慈中书院颜敏杰蛟川书院王凤泰河中学张延蛟川书院余伟成慈溪市育才中学胡一帆惠贞书院周琦慈溪市观城中学董韬鄞州高级中学庄杰栋慈溪市慈中书院王译博涵鄞州高级中学梁浩威奉化高级中学梅清远蛟川书院杨楷雯鄞州高级中学王嘉豪蛟川书院龚拾贝宁波外国语学校唐杰慈溪市慈中书院毛仁义慈溪市三山中学范君杰蛟川书院宓宏潮慈溪市育才中学吴洁莹象山三中楼栽赟慈溪市育才中学章绥原柔石中学张子凌泰河中学宣铭杨余姚二中徐昱雷泰河中学唐佳乐余姚二中曹旭东泰河中学阮怡婷蛟川书院张思源慈溪市三山中学何莺蛟川书院潘鲁青鄞州高级中学鲍立晟柔石中学朱文韬泰河中学邹子尧宁波外国语学校张晓栋泰河中学蔡路鄞州高级中学熊子韬惠贞书院汪涛航高风中学邵灵蓉惠贞书院孙瑜彬蛟川书院张璟瑞柴桥中学吴思尉鄞州高级中学胡华松泰河中学周军彬蛟川书院顾文益泰河中学吴俊哲蛟川书院徐吉祥慈溪市育才中学潘璐象山三中崔博彦鄞州高级中学俞涵泰河中学沃英杰泰河中学李昊昶蛟川书院贺犇兴宁中学徐鸿达蛟川书院黄鸣柳惠贞书院蔡鲁建蛟川书院龚佳楠惠贞书院舒平平蛟川书院徐文歆惠贞书院章鼎蛟川书院邵智辰惠贞书院阮蒙蛟川书院胡易韬宁波外国语学校王羽蛟川书院徐标鄞州高级中学包伊莉象山三中龚豪辉余姚二中石荣浩象山三中汪哲柴桥中学杨斌象山三中陈磊咸祥中学郑安旦象山三中郑科航鄞州高级中学郑嘉晗宁波滨海学校三等奖（126名）王恩伟泰河中学钱一运惠贞书院庄潮霖柴桥中学沈烨钦宁波外国语学校邱添柴桥中学王圣杰奉化高级中学郑军杰柴桥中学应欣芷奉化高级中学陈茹怡柴桥中学俞辉鄞州高级中学郭佳唯泰河中学周磊象山三中忻犁兴宁中学邱启杭象山港书院厉鼎惠贞书院魏延延柔石中学林丽慧柔石中学沈宁宁鄞州高级中学王至立柴桥中学许异川鄞州高级中学黄颖磊柴桥中学马嘉飞余姚二中马祥明港中学傅彦程余姚四中屠家祺泰河中学张呈姚中书院王思羽鄞州高级中学邵鑫辉柔石中学王樟敏柔石中学翟程涛鄞州高级中学徐珊珊柴桥中学张屠桥鄞州高级中学鄢恩南柴桥中学谭妍鄞州高级中学谢森明港中学韩思佳余姚二中郝子烨泰河中学王朱斌姚中书院胡绪晗奉化高级中学张程杰姚中书院杨泽林奉化高级中学徐遵涵姚中书院郑泽源五乡中学沈琪超余姚七中徐哲轩咸祥中学葛浩凡柔石中学史佩元咸祥中学唐超杰鄞州高级中学张庭源鄞州高级中学陈锡冬余姚二中沈王杰鄞州高级中学王磊柔石中学马云飞柔石中学郑文涛鄞州区同济中学毛芸生奉化高级中学汪淼森余姚四中卢裕昶桃源书院陈挺鄞州高级中学吴林伟桃源书院李科峰鄞州高级中学毛萍萍柔石中学曹天择余姚二中陈芝铭柔石中学董佳玮余姚二中娄伟斌柔石中学姜杭杰余姚二中王丹娜柔石中学毛银宁高风中学王嘉雄鄞州高级中学王蕴初桃源书院陈家晟柔石中学马罗泽余姚四中俞鸿涛柔石中学舒棋余姚四中周来杰奉化高级中学潘迪涵余姚七中谢林昕奉化高级中学俞霖高风中学蒋莹奉化高级中学杨妮莎高风中学宋艺杰奉化高级中学徐金余姚二中谢尘锴奉化高级中学冷钦余姚二中夏彭奎奉化高级中学茅崇腾余姚二中刘浩栋奉化高级中学徐聪余姚二中朱林奉化高级中学张思争高风中学邢劲松余姚二中刘煜奉化高级中学董宇奉化高级中学童锦奇余姚二中陈家顺奉化高级中学屠浩杨姚中书院郑向荣余姚二中夏栋雪余姚四中高瑛余姚二中蔡文彬余姚七中邵晓枫余姚二中袁盛钦余姚七中范启立余姚二中倪锞莹高风中学程冰锋余姚二中翁州姚高风中学王杉荣奉化高级中学姚锦权余姚二中丁沈威奉化高级中学俞海霞余姚二中许开磊奉化高级中学李钊余姚四中邬雯雅奉化高级中学潘凯航余姚四中朱佳洁余姚二中楼婷婷余姚七中黄依峰余姚二中严霜云高风中学郑益涛余姚二中冯乐乐高风中学汪双雷奉化高级中学叶其晟奉化高级中学周伟峰奉化高级中学缪水康江口中学钱源益奉化高级中学金洲洲余姚七中B组团体优胜奖：慈溪实验高中蛟川书院宁波外国语学校慈中书院Power by YOZOSOFT。

对“人教A版数学必修系列（1-5）”教学的若干认识慈溪市三山高级中学苗孟义摘要：浙江省普通高中新课程第一阶段实施已开展一年半，笔者作为新课程实验的参与者和广大一线教师共同努力，在省数学专业指导小组和人民教育出版社章建跃博士等一批专家的帮助下，积极开展教学实验，积累了丰富的素材和成果.现结合人教A版数学必修系列（1-5）在教学顺序安排、教学衔接、教材个别内容的调整，配套练习的开发研制，模块评价和能力测试，教材钻研和校本教材开发，教师培训等七个方面进行论述，希望对推进我省普通高中新课程第一阶段教学的实践有所帮助.浙江省普通高中新课程数学学科实施（必修系列）已全部结束．回顾这一年多来的实践，结合参加宁波市教研室组织的在宁海与奉化溪口的两次新课程研讨活动，在杭州省委党校和舟山中学的两次省级培训，谈谈对“人教A版数学必修系列”教学的若干认识，一来可以作为“人教A版数学必修系列”教学实践的总结，二来可以为新一届实践教师传经送宝．一、关于“人教A版数学必修系列（1-5）”的教学顺序安排《普通高中数学课程标准（实验）》（以下简称《课标》）认为：“一标多版”下的任何一种教材，只要学完模块必修1后，其它模块的教学顺序是学校根据自己的教学实际情况来定的，可以选择任意一种顺序开展教学，这样就打乱了大纲模式下的教学顺序，让我们教师很难接受，所以我省统一采用了“1-4-5-2-3”的做法．这样考虑主要有四点：①这个顺序基本上与旧人教版相同，教师们在思想上容易接受；②必修3中的算法是“新增内容”，教师们不熟悉，放到最后来教学；③其他试验区的经验教训在间接影响；④可以不受教材和教辅改动的影响（由学校自己选择教学顺序，需要征订齐必修系列的全部教材和配套资料，教材一改，配套跟着改）．通过一年零三个月的教学实践之后，我们对这种教学顺序的科学性进行了调研与反思，认为：“1-4-5-2-3”的顺序是可以的，但也存在不足：①由于这种教学安排的顺序与《课标》对教学内容的安排顺序是不一致，导致教材内容个别问题在分析方法上呈现跳跃性．如：必修4平面向量的坐标表示的教学，就会遇到需要用解析法的思想来分析问题，在应用信息技术制作三角函数表时需要用算法思想分析解决问题的程序．因此给教学带来了一定的麻烦，教师必须通过引导学生用已经掌握的知识和方法去分析这些问题，这也正是调整教学内容顺序，带来的弊端．②将必修3的学习排在最后，失去了高中五大重要思想——必修3中“算法思想”的应用机会．《课标》在必修3中增设“算法”的意图之一，就是要学会用算法思想来指导后续课程的学习和数学问题的解决．这样一来没有很好体现《课标》的一番苦心．③调研中发现：有86%的学生认为算法的学习是在快乐中进行的，学生们很喜欢“读程序，完善程序”，对“写程序（给出问题让学生设计程序）”时有点困惑，因此有98%的学生认为必修3在高一下开设比较好，因为这个学期学生有每周二次的信息技术课，学生可以上机实践、得到信息技术教师的帮助．现在有82%的学生反映，算法课堂根本和计算机脱节，没见过老师演示程序，更谈不上让学生上机调试、动手练习．另外，大部分学生感觉必修3的学习较为容易，原因是题型的变化不太多.④调研中还发现：教师对算法的态度也在逐渐改变，正由原先对算法的恐惧渐渐对算法产生了兴趣．那些一开始算法课程让信息技术教师上的老师逐渐感到了后悔，因为他们失去了一次很好的近距离接触——算法亲身体验的机会．因此，采用哪种教学顺序更能体现《课标》的一番苦心，这个问题值得研究，我们通过实践以后，偏向《课标》的原有顺序“1-2-3-4-5”．右图是人民教育出版社在全国调研统计的教学顺序中发现，采用《课标》的原有顺序“1-2-3-4-5”是一种方向．二、关于“人教A版数学必修系列（1-5）”的教学衔接笔者在《初高中数学衔接中的问题分析和对策探索》一文中有比较详细的阐述，刊登在浙江师范大学主办的“中学教研(数学)”2007年第9期上．目前初高中衔接主要存在两个问题：①初中内容的不适当删减、降低要求，导致学生“双基”无法达到高中教学要求；②高中教学不顾学生的基础，任意拔高教学要求，繁琐的、高难度的运算充斥课堂．针对这两个困扰着高中教学的问题，我们通过实践发现，整体把握和微观调整很重要，教学要体现知识的完整性，过程的人性化、方法的通俗化、学生的有兴趣接受．针对以上情况，我们着重对以下20个知识点进行衔接，这里我推荐《新课程初高中衔接》数理化40课：1．分母有理化；2．二次根式；3．十字相乘法；4．判别式；5．韦达定理；6．乘法公式；7．解方程；8．解方程组；9．恒等变形；10．一次分式函数；11．二次函数；12．比例线段；13．解直角三角形；14．三角形的“心”；15．四点共圆；16．圆幂定理；17．基本轨迹；18．统计图表；19．反证法；20．分类讨论．在知识衔接的同时，需要教学方法的衔接，考试评价的衔接，师生情感的衔接，这一些是新课程带来的新的课题．三、关于“人教A版数学必修系列（1-5）”的个别内容的调整我们使用教材的同时，吸取和借鉴其他兄弟学校的成功做法，对教材进行了创造性的发挥和自我升值．必修1模块中的适当调整：在必修1的第一章中，先讲集合，补充一元二次方程，韦达定理等衔接内容，把必修5中的一元二次不等式提前到集合后面，注意难度不要升得太高(要螺旋上升)，简单的绝对值不等式，分式不等式不要补充(标准中已删除)，再讲函数及其表示和函数的基本性质．必修4模块中的适当调整：先学三角函数及三角恒等变换，再进入平面向量的学习，然后学习解三角形（老教材顺序）；学习三角函数，再学习平面向量，最后学习三角恒等变换及必修5中的解三角形（新课标顺序）．两种顺序各有特色，新课标为何把“平面向量”放在“三角恒等变换”之前是再三考虑的：要突出三角函数的函数特征，要突出向量工具的重要性，要正确认识三角恒等变换及解三角形是平面向量的应用.我们通过实践对比发现：老教材顺序实施感觉上课很累，特别在教材处理上，教师为了能开展好课堂教学另起炉灶，搬出老教材体系给学生上课，这样一来削弱了向量的工具特征，很难体现向量法解决数学问题的基本思想，向量在物理、几何中的应用，用向量方法推导两角差的余弦公式等很难开展；新课标顺序可以完全避开这些问题．必修5模块和必修2模块中的适当调整：解三角形，数列，不等关系与不等式，直线与方程，圆的方程，直线、圆的位置关系，线性规划，基本不等式，空间几何体，点、线、平面之间的位置关系，空间直角坐标系．必修3模块中的适当调整：文科顺序按“算法，统计，两个计数原理（比较简单的应用），概率”；理科顺序按“算法，统计，计数原理（选修2-3），概率”．关于理科顺序的最佳方案我们做了实验：到目前为止，采用调整后顺序的学生对知识的学习和掌握来的比较顺利，在平行班考试中，调整顺序的班级单元测试成绩比没有调整顺序的班级要高出3.72分．因此，适当的对教材内容的调整是广大的一线教学工作者对教材改革的大胆尝试和优化，是教学大纲到课程标准平稳过渡的一个必不可少的环节．四、关于“人教A版数学必修系列（1-5）”配套练习的开发研制关于配套练习的开发和研制，这是一个迫在眉睫的问题．目前市场上关于人教A版数学必修系列（1-5）和选修系列的配套练习，如雨后春笋般冒出来，这个信号值得我们警惕．我在这一年零三个月中，花了633元钱买了103本关于人教A版数学必修系列（1-5）的参考书，在仔细阅读以后发现，大部分是书与书之间对抄，很多超范围，超要求，和我们浙江省普通高中新课程学科实施指导意见不符合，因此这些参考书可以参考借鉴，不能直接用于教学，教师渴望有一本能适合自己学生水平的教学参考书．目前全省各县市中考招生政策的影响，使得生源的分布可以形象地比喻为呈“五国趋势”：第一层次（超级大国）：省一级重点；第二层次（发达国家）：高考业绩好的学校；第三层次（一般国家）：高考业绩一般的学校；第四层次（落后国家）：高考业绩在同类学校中倒数的学校；第五层次（剩下国家）：综合高中与职高．省教研室编写的浙江省普通高中新课程作业本（数学）和普通高中新课程模块学习三级跳（数学）这两本书，在使用以后感到比较适合第一、二层次的学生，对其它层次的学生不适宜，使用面不广．浙江教育出版社出版的《新课标新精编》A组题比较适合二、三层次，B组题比较适合一、二层次，对其它层次学生不适宜．浙江教育出版社出版的学能同步训练（数学）比较适合一、二层次．慈溪市教研室编写的高中新课程同步练习（数学）比较适合二、三、四层次．因此，一本适合多层次学生选择的数学习题集的研制和开发势在必行，在一个学校，一个班级，学生的中考排名由前2000名的，也有7000名后的，如何让学生在学习中得到知足，真正体现课标的精神，配套练习的作用功不可没．五、关于“人教A版数学必修系列（1-5）”模块评价和能力测试2006年秋开始入学的高一新生，在初中三年的考试试题很简单，再加上中考可以带计算器进考场，中考成绩个个都是三位数，自我感觉很好，教师在平时命题时要注意不能用老“眼光(历届高一)”来衡量这届学生，否则会考得很惨，要把握好试卷整体的难度系数，在新课程开展刚刚起步阶段切忌“教考分离即交叉命题”，随着学生的习惯的养成，有意识地降低难度系数，从而和高考水平接轨．部分生源较高的学校出台了“双评价”制度，即每个模块教学结束以后进行模块评价（试卷的难度系数控制在0.75—0.85），在两个模块结束以后，进行能力测试（两个模块的内容合在一起，试卷的难度系数控制在0.65左右）．近3年的中考数学平均分较高(以我市为例)，在学生心目中，他们是数学的天才，进入高中，几次考试下来，好多学生有失落感，甚至从此数学成绩就会一落千丈，因此在高一第一学期各类练习编写、试题命题时要注意难度，注意平时练习和试题的积累，特别是错题，好题，“双评价”制度值得借鉴．六、关于“人教A版数学必修系列（1-5）”教材钻研和校本教材开发教材有章引言、章头图、章头语，几乎每节有旁批，有阅读材料等．人教A版十分重视探究性题目，通过对问题的探究，让学生自己发现、总结有关规律，这是新课程的理念，也是教师在课改中得以施展潜能的舞台．通过教学实践，我们对人教A版数学必修系列（1-5）中的133个思考、15个观察，91个探究、83个云图（大耳朵）、23个阅读与思考、9个信息技术应用、5个实习作业、7个探究与发现进行了创造性的发挥和开拓，收到了良好的效益，在提高学生成绩的同时，使学生对数学的学习兴趣倍增．我们根据学生的基础特点，针对不同层次的学生，积累了人教A版数学必修系列（1-5）中实践的第一手资料编写成校本教材，为推动新课程改革具有不可替代的作用．七、从“人教A版数学必修系列（1-5）”的三次集训谈教师培训我们说教师是新课程实践得以开展的战斗员，那么教师培训是新课程开展的指挥员．教师培训应分为集中培训和定时培训．集中培训：省级培训主要对象是地县两级教研员，省数学专业指导委员会成员，地县两级骨干教师代表，新课程样本学校教师代表；地区培训主要对象是全体新课程实施的参与者．分析这里的二级（省级、地区级）培训，考虑到大部分培训对象不熟悉新课程内容，因此培训的效果不够理想，在调研中还发现，专家在报告中强调的，部分教师因听报告时打瞌睡、讲空话、做其它事情，没有注意报告中强调的重要信息，导致了在新课程实施中走弯路．定时培训：这个是为了弥补集中培训不足而出台的新的培训方式．在教师拿到教材，对教材有初步熟悉的情况下，通过教研活动或备课组活动，定时培训，可以请外校的“土专家”上辅导课，或自己备课组选派一名教师做专题讲座，或收看网络培训教程．目前，收看网络教程是一种新的培训方式，这有助于教师能进一步理解和把握教材，少走弯路，推进课程改革．网络教程主要包括：对每个模块教材的整体把握，每个章节的教材处理，典型课程的课堂实录，教材中信息技术的使用技巧等．以上关于“人教A版数学必修系列（1-5）”的七点，是这一年半以来，我们课改一线教师集体的反思、探索的一些想法，希望能为下一届新课程的改革有所帮组．参考文献：[1]普通高中《数学课程标准》（实验），人民教育出版社，2003年4月出版．[2]浙江省普通高中新课程（实验）数学学科教学指导意见，浙江省普通高中新课程实验专业指导委员会数学专业指导小组，2006年12．[3]浙江省高中新课程课前培训资料汇编高中数学（高一下），浙江省教育厅教研室编印，2007年1月．[4]2006年宁波地区高中数学新课程研讨资料汇编，宁波市教育局教研室．[5]浙江省高中新课程课前培训资料汇编光盘高中数学（高二上），浙江省教育厅教研室编印，2007年7月．[6]宁波地区高中新课程课前培训资料高中数学（高二上），宁波市教育局教研室．[7]新课程实践中的“三个关于、八条建议”，苗孟义，人民教育出版社．2010-08-10 人教网【上一篇】校本课程开发与数学课堂教学融合的尝试与思考【下一篇】高考复习中应重视数学思想方法的渗透。

当
a

0 时，
f
(x)
|
4 x

a|
x

a

x
4 x, x 4
x
a
4 2a, x
4
x
a
若1 4 4 即1 a 4 ，必满足 f (x) 在区间[1,4] 上先减再增，故有 2a 3 5 ，即 a 1 a
若 0 4 1 时，即 a 4 ， f (x) 在区间 [1,4] 上递增，故有 2a 3 5 ， a 1不符题意 a
ln x ln x (x2 1)2
x2
1
令 h(x) x2 ln x ln x
x2
1， h'(x)
2x ln x
x
1 x
， (h' (x))'
2 ln x 1
1 x2
0(x
1)
可知 h' (x) 递减，h' (x) h' (1) 0 ，即 h(x) 递减，h(x) h(1) 0 ，可知 g(x) 递减，g(x) g(1)

x ln x 1 ，所以 (x 1)2
f (1)
1. 2
(Ⅱ)由于定义域为 (0, ) ，令 g(x) x ln x 1 ，
函数 g(x) x ln x 1 在 (0, ) 上单调递增，
因为
g(
1 e2
)

1 e2
1 0 ， g(1) e
1 e
4 （将 a 看成主元，后同法一）
【题 2】（2019 学年杭州第四中学下沙校区第一次月考卷，21）

甬教研〔2007〕132号关于公布2007年宁波市高二学生物理竞赛结果的通知各县（市、区）教育局教研室，各有关中学：经宁波市教育局批准，在各县（市、区）教育局教研室的大力支持下，宁波市高二物理竞赛在2007年12月3日如期举行。

在本次竞赛中，镇海中学史寒朵等同学获得省一级重点中学高中组一等奖，慈溪育才中学王科柯等同学获得非省一级重点中学高中组一等奖，现将竞赛结果公布如下。

（省一级重点中学组见附件1，非省一级重点中学组见附件2），请通知有关单位和获奖学生，并请各有关学校继续做好对优秀学生的教学指导工作，使得优秀学生能有一个更大的成长空间。

附件1：2007年宁波市高二物理竞赛学生获奖名单（省一级重点中学组）附件2：2007年宁波市高二物理竞赛学生获奖名单（非省一级重点中学组）附件3：2007年宁波市高二物理竞赛城区获奖名单宁波市教育局教研室2007年12月25日附件1：2007年宁波市高二物理竞赛学生获奖名单（省一级重点中学组）一等奖（14名）镇海中学史寒朵余姚中学徐彬镇海中学杨起帆效实中学童精中慈溪中学张哨波北仑中学林琪佶北仑中学张玉苗效实中学沈云骢镇海中学张峰北仑中学包思遥慈溪中学陈嗣栋效实中学项长铖余姚中学周轶柯效实中学叶轲二等奖（31名）镇海中学李沛九北仑中学汪思遥镇海中学张天侃北仑中学周松盛余姚中学张蒙北仑中学刘琳刚余姚中学魏宇峰效实中学黄毳晨之镇海中学许成述效实中学沈典迪镇海中学赵原慈溪中学黄润镇海中学陈磊余姚中学李雯琦鄞州中学杨雄慈溪中学张泽琛北仑中学汪啸龙北仑中学林春儿效实中学赵鸿宇宁海中学葛飞镇海中学李扬帆效实中学王一耀效实中学闵兆飞余姚中学徐磊镇海中学唐良晓宁海中学王益行余姚中学谢堞江北仑中学邵觊杰慈溪中学郑伟伟效实中学叶向阳效实中学王羚捷三等奖（72名）北仑中学王崇宇效实中学陈诗佳音奉化中学唐君宁海中学杨一鸣北仑中学郭俊杰镇海中学包磊杰北仑中学王俊宁波中学龚炎斌宁波中学夏本炎效实中学邵董宁宁波中学杨一盼余姚中学史浩业效实中学杨骥雷知恩中学林凯余姚中学陈蕾安宁海中学张鑫满镇海中学毛卿卿慈溪中学虞郁磊效实中学韩劼群北仑中学姚明峰姜山中学张若蒙北仑中学刘觊峰镇海中学毕迢盈效实中学金钱琛效实中学陈彦余姚中学张迪宁海中学严宇成宁海中学葛添星慈溪中学郑晨鄞州中学周行浩姜山中学沈文欢镇海中学范悦象山中学陈良威宁海中学储锡君慈溪中学施思知恩中学王心颂北仑中学郑宇豪正始中学谢逸坤宁波中学许铮效实中学丁巍巍余姚中学史杰昊余姚中学胡佳慈溪中学金河余姚中学黄柯效实中学张天昊姜山中学倪建梁效实中学郭家胤镇海中学扬栋元效实中学冯洋淼效实中学杨翔宇象山中学何天宇宁海中学杨晓锋效实中学高立镇海中学杨阳余姚中学童舒宁镇海中学庞雨廷余姚中学严余伟宁波中学周宇峰宁海中学王葳韡效实中学盛静远宁海中学葛明辉效实中学任晨悠北仑中学卢奕君姜山中学严李杰北仑中学徐敬镇海中学沈雪晶余姚中学钱城镇海中学孙寒光宁波中学陈汝彬慈溪中学陈可群象山中学俞奇宁波三中邵敏附件2：2007年宁波市高二物理竞赛学生获奖名单（非省一级重点中学组）一等奖（21名）育才中学王科柯象山三中钱耀育才中学朱余旭育才中学林觊蛟川书院吴玉超观城中学宓开拓蛟川书院朱天午育才中学周栋芝柔石中学王健育才中学沈碧峰蛟川书院王骁余姚五中沈蒙蒙育才中学宋开蛟川书院张可悦育才中学胡亮红余姚二中韩泽文蛟川书院周敏俐实验高中朱健泉蛟川书院仇翼露中兴中学杜往泽东方学校王志龙二等奖（35名）余姚高风中学朱立权浒山中学程佳亮实验高中戎宇阳实验高中许铁松实验高中王林杰柴桥中学陈之杰余姚二中严柯森实验高中吴旭烽余姚二中郑瀚实验高中潘伊莎余姚三中陈昶实验高中王佳云象山三中齐利朝育才中学严觊聃宁海三中阮北荣育才中学马诗铭余姚四中何沛华中兴中学陈慧明柴桥中学郑骏余姚高风中学胡旭蛟中兴中学叶耿帆实验高中吴思诗实验高中岑嘉忆育才中学吴盼盼柴桥中学朱李核中兴中学刘昊骥育才中学孙细拉余姚二中颜建辉余姚七中魏杭军育才中学余松春余姚二中韩佳男育才中学岑宏伟鄞州高级中学王颖中兴中学王佳韵同济中学郭盛磊三等奖（69名）象山三中丁宁育才中学罗辰午育才中学陈俊翮观城中学徐欢腾育才中学章达航柴桥中学刘骅育才中学柳孟开柔石中学吴挺挺中兴中学胡云波滨海学校虞先国余姚四中童秉寰实验高中周伟浒山中学戚核帅柴桥中学王颖杰五乡中学夏晋炎东方学校戴广达桃源书院应旭贝余姚二中张霖余姚二中李杰峰余姚四中姚科迪中兴中学林高峰大榭中学虞杰实验高中潘杰炣余姚二中李聪泰河中学李建波象山三中鲍练绮余姚五中赵海波观城中学蒋乃武实验高中徐文桔五乡中学杨健开中兴中学留君侠柴桥中学张海东余姚八中王兴兴奉化二中吴建望象山三中芦佳妮鄞州高级中学李修理浒山中学华聪立柔石中学陈柏聪浒山中学吴天佳余姚四中任泉庄鄞州高级中学王晖明港中学邱泽霖余姚高风中学陈贇东方学校裘锡伟象山三中石冬裕余姚二中马陈飞鄞州高级中学俞科柴桥中学蒋宗斌柴桥中学葛庆华中兴中学袁家帅慈湖中学胡午洋柔石中学王剑余姚四中张海斌五乡中学俞剑峰象山三中励辉大榭中学周芬鄞州高级中学张凯丽柴桥中学胡奇辉泰河中学张平中兴中学周辰迪柴桥中学乐佳瑜中兴中学谢修远桃源书院俞鑫柔石中学胡民东余姚高风中学诸汉涛余姚四中董濛迪余姚高风中学刘叶文余姚二中周雪峰五乡中学李旭东附件3：2007年宁波市高二物理竞赛城区获奖名单一等奖（9名）效实中学管耀宗宁波中学周默效实中学陈雨迪效实中学王一浩效实中学叶周侠效实中学苏文效实中学张航万里学校王天昊效实中学赵瀚杰二等奖（17名）宁波中学周颖效实中学薛昊洋效实中学曹洁效实中学黄光群效实中学叶劲松宁波中学夏至瑶效实中学郑旸宁波中学陆孝薇效实中学徐凌寒宁波中学陈佳宁波中学吴用宁波中学胡琼晶宁波中学陈迪效实中学周磊效实中学郑毅骏效实中学张之夏四明中学赵涛勇三等奖（26名）效实中学王绳冰慈湖中学郑魏魏华茂学校王璐婷联丰中学谌志华宁波三中陈敏至诚学校酆强胜万里学校程萍萍至诚学校程鑫万里学校茅泽鑫联丰中学黄剑雄万里学校徐錞联丰中学周灵万里学校周亦钊慈湖中学张旭东宁波三中邓金浩联丰中学魏莎李惠利中学胡旭强四明中学曹觊李惠利中学俞俊迪四明中学王琪李惠利中学邵东荣安中学毛丹丹联丰中学何素斌四明中学陈涛联丰中学夏念晓华茂学校张睿。

试题编制
的三重经 历
慈溪中学 苗孟义
一核四层四翼
报告
01 编制意图——目标导向 02 编制灵感——教学实践 03 编制手段——步步深入
01 编制意图——目标导向
PART
编制意图——目标导向
02 编制灵感——教学实践
PART
编制灵感——教学实践
03 编制手段——步步深入
PART
编制手段——步步深入
编制手段——步步深入
编制手段——步步深入
编制手段——步步深入
1 4
编制手段——步步深入
编制手段——步步深入
编制手段——步步深入
编制手段——步步深入
编制手段——步步深入
编制手段——步步深入
1
2
பைடு நூலகம்
6
步步 深入
3
5
4
没有 椭圆
有 椭圆
隐藏 椭圆
感谢聆听，斧正为感
Thank you for listening，ense of correction

所以采取了“消元”的思想．类似地，也可以消去ｅ狓 ，留
下ｌｎ狓．
思考三：注意到ｌｎ狓 与ｅ狓 也可以同时消去，故有
下面的方法．
因为ｅ狓 ≥狓 ＋１，所以 －ｅ狓 ≤－狓 －１， 又ｌｎ狓 ≤ 狓 －１，所 以 有ｌｎ狓 －ｅ狓 ≤ （狓 －１） ＋ （－狓 －１）＝－２，经检验等号取不到． 故 犿 ≥－２，即 犿 的最小整数值为 －２． 有了上面的铺垫以后，我们再来看题目２．
（２）若犳（狓）≥１，求犪 的取值范围．
分析：（１）略．
（２）本题仍是一 道 恒 成 立 的 问 题，最 直 接 的 想 法
就是：若犳（狓）≥１恒成立，只需要找到犳（狓）ｍｉｎ，则其
必满足犳（狓）ｍｉｎ ≥１．为寻找犳（狓）ｍｉｎ，做如下求解．
思考一：直 接 找 导 函 数 犳′（狓）的 零 点，然 后 通 过
题 目１：已知函数犳（狓）＝犿ｅ狓 －狓ｅ狓 （狓 ＞０），其中 犿 ∈ 犚，ｅ为自然对数的底数．
（１）讨论犳（狓）的单调性，并求极值； （２）当狓 ＞０时，犳（狓）＋狓ｅ狓 ≥ｅ狓ｌｎ狓－ｅ２狓 ，求犿 的最小整数值． 分析：（１）略． （２）本题实质上 是 一 种 恒 成 立 的 问 题，属 于 常 规 问题，但 恰 恰 是 在 这 种 常 见 问 题 上，却 体 现 了 方 法 的
７０ Copyrigh高t©中博看网 . All Rights Reserved.
教学
２０２１年３月 解法探究
参谋
题目２：已知函数犳（狓）＝犪ｅ狓－１ －ｌｎ狓 ＋ｌｎ犪． （１）当犪＝ｅ时，求曲线狔＝犳（狓）在点（１，犳（１））处 的切线与两坐标轴围成的三角形的面积；
灵活性． 多数学生会考虑到首先将犳（狓）代入，得到 犿ｅ狓

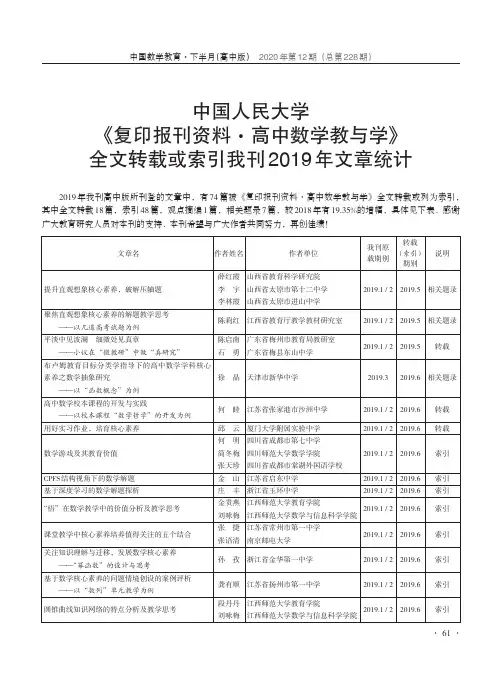
文章名提升直观想象核心素养，破解压轴题聚焦直观想象核心素养的解题教学思考——以几道高考试题为例平淡中见波澜细微处见真章——小议在“微教研”中做“真研究”布卢姆教育目标分类学指导下的高中数学学科核心素养之数学抽象研究——以“函数概念”为例高中数学校本课程的开发与实践——以校本课程“数学哲学”的开发为例用好实习作业，培育核心素养数学游戏及其教育价值CPFS结构视角下的数学解题基于深度学习的数学解题探析“悟”在数学教学中的价值分析及教学思考课堂教学中核心素养培养值得关注的五个结合关注知识理解与迁移，发展数学核心素养——“幂函数”的设计与思考基于数学核心素养的问题情境创设的案例评析——以“数列”单元教学为例圆锥曲线知识网络的特点分析及教学思考作者姓名薛红霞李宇李林霞陈莉红陈启南石勇徐晶何睦邱云何明简冬梅张天珍金山庄丰金贵燕刘咏梅张捷张语清孙孜龚有顺段丹丹刘咏梅作者单位山西省教育科学研究院山西省太原市第十二中学山西省太原市进山中学江西省教育厅教学教材研究室广东省梅州市教育局教研室广东省梅县东山中学天津市新华中学江苏省张家港市沙洲中学厦门大学附属实验中学四川省成都市第七中学四川师范大学数学学院四川省成都市棠湖外国语学校江苏省启东中学浙江省玉环中学江西师范大学教育学院江西师范大学数学与信息科学学院江苏省常州市第一中学南京邮电大学浙江省金华第一中学江苏省扬州市第一中学江西师范大学教育学院江西师范大学数学与信息科学学院我刊原载期别2019.1/22019.1/22019.1/22019.32019.1/22019.1/22019.1/22019.1/22019.1/22019.1/22019.1/22019.1/22019.1/22019.1/2转载（索引）期别2019.52019.52019.52019.62019.62019.62019.62019.62019.62019.62019.62019.62019.62019.6说明相关题录相关题录转载相关题录转载转载索引索引索引索引索引索引索引索引中国人民大学《复印报刊资料·高中数学教与学》全文转载或索引我刊2019年文章统计2019年我刊高中版所刊登的文章中，有74篇被《复印报刊资料·高中数学教与学》全文转载或列为索引，其中全文转载18篇，索引48篇，观点摘编1篇，相关题录7篇，较2018年有19.35%的增幅，具体见下表.感谢广大教育研究人员对本刊的支持.本刊希望与广大作者共同努力，再创佳绩！文章名布卢姆教育目标分类学指导下的高中数学学科核心素养之数学运算研究——以“对数运算”为例“概率的性质”教学设计布卢姆教育目标分类学指导下的高中数学学科核心素养融入课堂教学的策略研究布卢姆教育目标分类学指导下的高中数学学科核心素养之直观想象研究——以“椭圆及其标准方程”为例布卢姆教育目标分类学指导下的高中数学学科核心素养之数学抽象研究——以“函数概念”为例布卢姆教育目标分类学指导下的高中数学学科核心素养之数学建模研究——以“函数模型及其应用”为例布卢姆教育目标分类学指导下的高中数学学科核心素养之数据分析研究——以“统计图表与用样本估计总体”为例布卢姆教育目标分类学指导下的高中数学学科核心素养之逻辑推理研究——以“数列”为例“不等式的性质”教学设计立德树人与数学课程改革——暨“第九届高中青年数学教师优秀课展示与培训活动”总结“对数的概念与运算性质”教学设计与反思“概率的性质”教学设计“独立重复试验与二项分布”教学设计“导数的概念及其几何意义”教学设计“平面与平面垂直的判定”教学设计与评析“椭圆的几何性质”教学设计问题串引导下的“过程性”概念教学——“对数与对数运算”（第1课时）教学设计、实践及反思“二项式定理”教学设计“椭圆的简单几何性质”（第1课时）教学设计“导数的概念”（第1课时）教学设计“三角函数的单元复习”（第1课时）教学设计挖掘试题价值引领高考复习——解析几何复习起始课教学作者姓名曲全徐美松于川王成丽徐晶刘庆利邬楠朱小岩李磊章建跃张灿徐美松来洪臣马丽娜赵爽张晓斌张宏鹏段艳芳张立平李林霞刘志诚乔树华张传涛徐彬孙海琴蒋孟君作者单位天津市新华中学江苏省南京市金陵中学天津市新华中学天津市新华中学天津市新华中学天津市新华中学天津市新华中学天津市新华中学青海师范大学附属中学人民教育出版社课程教材研究所安徽省芜湖市第一中学江苏省南京市金陵中学东北育才学校天津市耀华中学重庆市南开中学校重庆市教育科学研究院江苏省丹阳高级中学山西省太原市实验中学山西省太原市教研科研中心山西省太原市进山中学河北省秦皇岛市第一中学天津市宁河区芦台第一中学河南省开封高级中学北京市中关村中学浙江省温岭中学广西桂林市中山中学我刊原载期别2019.32019.42019.32019.32019.32019.32019.32019.32019.42019.42019.42019.42019.42019.42019.42019.52019.52019.52019.52019.52019.52019.4转载（索引）期别2019.72019.72019.72019.72019.72019.72019.72019.82019.82019.82019.82019.82019.82019.82019.82019.82019.82019.82019.82019.82019.82019.8说明转载转载索引索引索引索引索引转载转载索引索引索引索引索引索引索引索引索引索引索引索引索引续表文章名立足教材发展素养——关于“独立重复试验与二项分布”一课的点评高效数学教学行为的案例研究基于核心素养的高中统计教学研究智能诊断下的精准教学——以三角变换为例注重素养导向开展精准教学——2019年全国各地高考数学试卷的特点及启示数学抽象、逻辑推理背景下的问题情境建构基于SOLO评价理论的数学解答题评分标准研究——以一道函数与导数解答题为例高中数学创新题编制的几个入手处2019年高考“选考内容”专题命题分析2019年高考“平面向量”专题命题分析2019年高考“函数与导数”专题命题分析2019年高考“算法与框图”专题解题分析2019年高考“数列”专题解题分析2019年高考“三角函数”专题解题分析2019年高考“集合、常用逻辑用语、复数”专题解题分析数学运算素养的理解与商榷深度学习案例：会意高中数学中的斐波那契数列“三角函数模型的简单应用”教学设计渗透唯物辩证法观点，落实立德树人理念基于数学运算素养培养的平面向量教学思考作者姓名龙正武陈利民高雪松郭方奇欧阳亚亚金佳琳陈延付朱恒元周德明顾晓骅曾辛金肖凌戆张金良姜思洋吴丽华张永成罗辉东薛红霞郭玉竹苗孟义张金良闫旭王恩波孙海琴郭玉峰段欣慰孙艳徐德均张翼周祝光池新回袁瑶刘咏梅作者单位人民教育出版社课程教材研究所浙江省杭州高级中学北京师范大学数学科学学院浙江省绍兴市第一中学浙江省景宁中学浙江省义乌中学江苏省太湖高级中学江苏省无锡市第三高级中学广东省广州市教育研究院广东省广州市黄埔区教育研究中心浙江省教育厅教研室黑龙江省哈尔滨市第三中学校黑龙江省教育学院天津市武清区教研室山西省实验中学山西省教育科学研究院广东省深圳中学浙江省慈溪中学浙江省教育厅教研室辽宁省大连市第二十三中学浙江省杭州学军中学北京师范大学附属中学江苏省南通中学四川省成都市第十二中学福建省三明市教育科学研究所江西师范大学数学与信息科学学院我刊原载期别2019.42019.52019.62019.62019.7/82019.62019.7/82019.92019.92019.7/82019.7/82019.7/82019.7/82019.7/82019.7/82019.102019.52019.102019.102019.10转载（索引）期别2019.82019.82019.92019.102019.112019.112019.122019.122019.122019.122019.122019.122019.122019.122019.122020.12020.12020.12020.12020.1说明索引索引转载转载转载转载转载索引索引索引索引索引索引索引索引转载相关题录转载索引索引续表北京师范大学第二附属中学北京师范大学数学科学学院文章名教学创新为落实核心素养而教——以江西省高中数学优秀课展示交流活动为例“三角函数模型的简单应用”教学设计基于核心素养的函数模型及其应用教学评析——以“几类不同增长的函数模型”一课为例通过“问题提出”培养学生的数学文化观念——以人教A版新高中数学教科书中阅材料的教学设计为例数学文化的六种常见高考题型及教学策略——以2018年高考试题为例依托网络平台，促进青年教师发展——张金良名师网络工作室建设的实践与思考在问题解决过程中提升学生的数学素养——“三角函数模型的简单应用”课例点评基于核心素养的函数模型及其应用教学评析——以“几类不同增长的函数模型”一课为例实验引探究融洽促成长——“均匀随机数的产生”课例点评在高中数学教学中开展项目学习的尝试——以“测量……”为例立足于“单元整体设计的研究性学习”课例——“椭圆的定义和方程”教学设计与实录基于ACODESA模式的数学任务设计——以“分形”为例数学抽象：从背景到概念再到结构——兼谈人教A版教材的数学问题创新设计问题背景及其创设基于核心素养视角的课堂教学建议——以“函数模型的应用实例”为例以退为进，曲径通幽——一道全国联赛试题的深度探究布卢姆教育目标分类学指导下的高中数学学科核心素养之数据分析研究——以“统计图表与用样本估计总体”为例落实“立德树人”根本任务下的HPM教学——以“椭圆及其标准方程”为例作者姓名江民杰张翼周祝光曲巍王洪军宋莉莉张金传张金良郭慧清曲巍王洪军陈昕薛红霞马胜利曹宗庆任燕巧张维忠章建跃李昌官丁明忠肖海东李世杰李盛邬楠沈金兴王华作者单位江西省九江第一中学四川省成都市第十二中学黑龙江省教育学院黑龙江省实验中学人民教育出版社课程教材研究所扎兰屯职业学院浙江省教育厅教研室广东省深圳中学黑龙江省教育学院黑龙江省实验中学海南省教育研究培训院山西省教育科学研究院山西省实验中学华中师范大学第一附属中学浙江师范大学教师教育学院人民教育出版社课程教材研究所浙江省台州市教育局教研室湖北省黄冈市教育科学研究院湖北省黄冈中学浙江省衢州市教育局教研室浙江省衢州第一中学天津市新华中学浙江省桐乡市凤鸣高级中学浙江省桐乡第二中学我刊原载期别2019.102019.102019.102019.122019.102019.112019.102019.102019.102019.102019.52019.122019.122019.122019.122019.122019.32019.11转载（索引）期别2020.12020.12020.22020.32020.32020.32020.32020.32020.32020.32020.42020.42020.42020.42020.42020.42020.82020.9说明索引索引转载转载相关题录转载索引索引索引索引相关题录转载索引索引索引索引观点摘编相关题录续表。

2018学年第一学期9+1高中联盟期中考高三年级数学学科 试题命题：长兴中学 常广胜 钱百花 慈溪中学 施斌 苗孟义考生须知：1．本卷满分150分，考试时间120分钟；2．答题前，在答题卷指定区域填写班级、姓名、考场、座位号及准考证号并核对条形码信息； 3．所有答案必须写在答题卷上，写在试卷上无效，考试结束后，只需上交答题卷； 4．参加联批学校的学生可登陆 查询个人分析报告。

选择题部分(共40分)一、选择题（本大题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1．已知集合{|A x y ==，{|12}B x x =-≤≤，则AB =（ ▲ ）A ．{|12}x x <≤B ．{|01}x x ≤≤ C ．{|12}x x ≤≤D ．{|02}x x ≤≤2．已知i 是虚数单位，若复数z 满足i 1i z =+，则2z =（ ▲ ）A ．2i -B ．2iC ．2-D ．23．已知双曲线C ：22218y x b-=(0)b > ▲ ） A ．2 B ． C ．4 D ．8 4．若x ，y 满足约束条件1020220x ,y ,x y ,+≥⎧⎪-≤⎨--≤⎪⎩则z x y =+的最大值是（ ▲ ）A ．5-B ．1C ．2D ．4 5．已知x ，y 都是实数，则“x y ≤”是“x y ≤”的（ ▲ ） A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件高三数学试题 第2页 （共4页）6．函数()ln ||x f x e x =⋅的大致图象为（ ▲ ）A. B. C. D.7．若cos 2(1sin )αα=+，22k παπ≠-，k ∈Z ，则tan α=（ ▲ ）A ．43-B ．34-C ．34D ．438．若正实数,x y 满足ln(2)ln ln x y x y +=+，则2x y +取最小值时，x =（ ▲ ）A ．5B ．3C ．2D ．19．若方程32242(2)4x ax a x a x-++=-有四个不相等的正根，则实数a 的取值范围是（ ▲ ）A．a >B．a >C．a < D．a -<10．设I 是含数π的有限实数集，()f x 是定义在I 上的函数．若()f x 的图象绕坐标原点逆时针旋转3π后与原图象重合，则在以下各项中，()f π的取值不可能是（ ▲ ） ABC ．π D非选择题部分(共110分)二、填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分。

附件1：2013年浙江省高中数学竞赛获宁波市奖名单（A组）宁波市一等奖（共28人）朱镕杰宁波中学杨津京镇海中学常锐宁波中学孙岵镇海中学陈奕宁效实中学吴昊镇海中学孙敏超鄞州中学刘韬北仑中学俞佳鸣鄞州中学汪雨晨奉化中学王芝琳鄞州中学葛志辉奉化中学陈钇佳慈溪中学王益奉化中学陈燕芳慈溪中学尤浩谕宁海中学陆科杰余姚中学赵泽龙宁海中学童凯凯余姚中学谢廷效实中学何钶宇余姚中学任航效实中学金鹏程余姚中学周士杰效实中学赵哲堃余姚中学徐科鑫慈溪中学黄颖锋余姚中学支音宁海中学宁波市二等奖（共57人）俞登科宁波中学方略余姚中学包振宁波中学包哲余姚中学徐珑迪效实中学李丰余姚中学吴翔效实中学沈锡聪余姚中学李浩然效实中学马一丹余姚中学吴贝妮鄞州中学陈之镇海中学毛慈伟慈溪中学张子祺镇海中学莫鸿茗慈溪中学贺祺润北仑中学陈璐瑶慈溪中学陈家赟宁波中学王嘉雯慈溪中学赵婷婷宁波中学马熞余姚中学邵彬鄞州中学章琦余姚中学岑盛楠慈溪中学史顺宇余姚中学祁吉锋慈溪中学黄少瑛余姚中学陈则衔慈溪中学徐宁喆镇海中学叶坚栋余姚中学周子策镇海中学毛晟伟余姚中学吴旺宇镇海中学黄笑添余姚中学张挺北仑中学陆雨婷镇海中学王琦琦北仑中学葛智超镇海中学杨金涛北仑中学王天君镇海中学国益宁海中学童心镇海中学朱乾麒效实中学林宁镇海中学张好雨鄞州中学蔡一凡镇海中学王宁鄞州中学李益镇海中学应浩鄞州中学史章斌北仑中学龚佳震鄞州中学李叔唐北仑中学董世村鄞州中学蒋晨书象山中学徐哲慈溪中学赵泽成宁海中学岑凌翔慈溪市浒山中学宁波市三等奖（共94人）杨晨杰宁波中学罗含笑慈溪中学石凯元效实中学成桢哲慈溪中学卓子超效实中学陈徐锞慈溪中学郑勇磊李惠利中学朱旭东余姚中学童柯烨鄞州中学陈晨余姚中学田宇鄞州中学楼思琦余姚中学王峥嵘鄞州中学鲁煜天余姚中学李莹鄞州中学叶烜超余姚中学徐贝贝慈溪中学王焜昱镇海中学胡巍慈溪中学王陈圆镇海中学王嘉欣慈溪中学留泽君镇海中学崔燕慈溪中学林毅涵镇海龙赛中学叶仲儿余姚中学罗浩翔镇海龙赛中学俞亦奇余姚中学周渊钧北仑中学苏航余姚中学顾茅象山中学丁言豪镇海中学邬微微奉化中学黄志涛镇海中学胡子航知恩中学张贤益镇海中学林豪宁波万里国际学校李晔镇海中学朱家荣鄞州中学周昉洵北仑中学胡家铭慈溪中学竺益辉奉化中学周子逸镇海中学严一振知恩中学张煜皓镇海中学胡珏伟宁波中学何俊豪镇海中学吴浩鄞州中学梅皓天北仑中学曹晨鄞州中学蔡星浦象山中学张远慈溪中学沈晨凯奉化中学岑程慈溪中学罗祺华宁海中学任鑫磊慈溪中学金升升鄞州中学华一楷慈溪中学李家磊鄞州中学梁益涛余姚中学韩雄鄞州中学姚泽祎镇海中学马佳茜慈溪中学张慧镇海中学沈婷慈溪中学赵越北仑中学严炜炜慈溪中学邬婷婷北仑中学张克兢余姚中学周驰象山中学许钶余姚中学陈钊象山中学孙鑫磊余姚中学王士风象山中学罗哲余姚中学俞臻威奉化中学罗烨钦余姚中学王宁宁波二中陈凯芳余姚中学鲁昶熙效实中学梅自涵镇海中学杨锦如效实中学陈申伦镇海中学项萧风宁波万里国际学校傅泓元北仑中学李立东鄞州中学贺增吉北仑中学张涛鄞州中学陈豪象山中学朱露鄞州中学陈思睿象山中学陈浩启鄞州中学竺方欢奉化中学邹文娇慈溪中学吴丹桐宁海中学附件2：2013年浙江省高中数学竞赛获宁波市奖名单（B组）宁波市一等奖（共32人）沈丹阳宁波外国语学校顾玲双慈溪育才中学陈科达鄞州五乡中学冯少卿慈溪育才中学赵展文慈溪市慈中书院胡华慈溪育才中学余盛文慈溪实验高级中学莫怡晨余姚二中张威迪慈溪实验高级中学闻人一磊余姚二中华晶靖慈溪育才中学张环欣余姚四中蔡熊熊余姚四中黄鹏程慈溪市三山高级中学毛培欣余姚四中邬焕腾慈溪实验高级中学邱豪磊北仑柴桥中学潘梦娇慈溪实验高级中学陈露慈溪育才中学胡乃丹慈溪实验高级中学葛良荣宁海桃源书院任森沾慈溪育才中学金经凯宁海柔石中学朱莹莹慈溪育才中学周镜茹惠贞书院沈豪泽慈溪育才中学孙一绮慈溪市慈中书院方佳男余姚七中高竞慈溪实验高级中学叶坚挺余姚高风中学高佳辉慈溪育才中学陆旭超余姚高风中学宁波市二等奖（共57人）倪绮雯宁波外国语学校施航圻余姚四中金楚凡镇海蛟川书院邵佳男余姚高风中学屠玮镇海蛟川书院骆贤立余姚高风中学王杰北仑柴桥中学吴昊镇海蛟川书院吴朝阳北仑柴桥中学严舟航北仑泰河中学叶俊峰宁海桃源书院应漪红宁海桃源书院黄兆琪惠贞书院刘若晖惠贞书院孙鑫慈溪市慈中书院张腾宁波外国语学校傅旭攀慈溪实验高级中学周士钧宁波外国语学校龚廷辉慈溪实验高级中学应元隆成兴宁中学苗佳瑶慈溪实验高级中学王芝霞鄞州高级中学祝炀炀慈溪育才中学陈佳瑶鄞州五乡中学陈梦逸慈溪育才中学岑钰霞慈溪实验高级中学童卓斌余姚二中姚罗炜慈溪育才中学唐镐锋余姚高风中学许谢洋慈溪育才中学刘凯镇海蛟川书院徐浓浓余姚四中翁峰峰象山三中陈基旺余姚四中杨袁旭奉化高级中学何京锴余姚高风中学张悟晅惠贞书院胡逍锴余姚高风中学洪振达余姚高风中学谈天羽惠贞书院周涛奉化武岭中学谷镭斌余姚二中司徒佐奉化武岭中学吕泽钦余姚四中叶俊杰宁海桃源书院魏天阳镇海蛟川书院何文韬宁波外国语学校项宁敏镇海蛟川书院葛鸿飞兴宁中学王秋雨北仑泰河中学岑天瑜慈溪实验高级中学江明晨奉化高级中学何安琪慈溪实验高级中学蒋坤奉化高级中学颜惠玲慈溪实验高级中学俞凯浩奉化二中鲁可锦慈溪育才中学宁波市三等奖（共89人）阙超然宁波外国语学校邹子尧宁波外国语学校任申林鄞州高级中学柯培霖兴宁中学吴庆永鄞州高级中学施力业鄞州高级中学童灵慈溪市慈中书院董佳升慈溪市慈中书院黄天皓慈溪市慈中书院徐鋆文慈溪育才中学何思远慈溪市慈中书院陈余凯慈溪育才中学陈璐瑶慈溪市慈中书院王晨余姚二中茅培培慈溪实验高级中学方煜茂余姚二中魏佳荧慈溪实验高级中学张聪海北仑柴桥中学胡麦依慈溪育才中学徐浩哲北仑柴桥中学王银萍余姚二中郑涵峰北仑泰河中学黄诗嘉余姚二中赖琳璐象山三中方宽余姚二中陈奎霖宁海桃源书院林明余姚三中朱含韬兴宁中学李莹涛余姚高风中学岑君辉慈溪市三山高级中学叶哲宇余姚高风中学周依莎慈溪育才中学于朋弘余姚高风中学黄旭晨余姚二中谢杰余姚高风中学吕金金余姚二中朱文磊奉化高级中学孙银堞余姚二中张子潮惠贞书院史明翰余姚高风中学陈旭慈溪市观城中学沈天杰余姚高风中学周铁铮余姚二中王嘉豪镇海蛟川书院黄烨翀惠贞书院姚凌浩北仑柴桥中学夏凌峰惠贞书院顾蒙恩北仑柴桥中学王翀鄞州高级中学方昶岳奉化高级中学黄斌慈溪市三山高级中学李嘉毅惠贞书院赵冠慈溪市三山高级中学董璐璐鄞州高级中学宋海霖慈溪市三山高级中学赵立鄞州五乡中学邵旻慈溪市慈中书院张炯慈溪市横河中学华铁慈溪实验高级中学余安慈溪市三山高级中学裘翼滔慈溪实验高级中学徐键慈溪市三山高级中学孙凌铄慈溪育才中学宋嘉盈慈溪市三山高级中学阮淑怡慈溪育才中学胡雨楠慈溪实验高级中学岑铭杰慈溪育才中学岑恩杰慈溪实验高级中学蒋苏旦余姚二中周潘霞慈溪育才中学吕金辉余姚四中周洋余姚二中赵忱余姚四中王振业余姚四中胡梦林余姚高风中学胡航嘉余姚高风中学余城滨余姚高风中学李平平余姚高风中学徐宏彬余姚高风中学胡鑫余姚高风中学余会全镇海蛟川书院吴玥余姚高风中学胡竞尹镇海蛟川书院郑城余姚高风中学贺寒潇北仑柴桥中学吴子城北仑泰河中学陈诗绮北仑泰河中学江凤娟奉化高级中学董玉姣奉化武岭中学附件3：2013年浙江省高中数学竞赛获宁波城区奖名单（A组）宁波城区一等奖（共6人）张琪蓉宁波中学陈昊哲效实中学任之初宁波中学潘道萌效实中学郑玉书效实中学杨智宇效实中学宁波城区二等奖（共13人）江珂宁宁波中学杨子晴宁波中学陈佳雯效实中学王楠效实中学叶昕欣效实中学刘畅宁波中学石守珂效实中学施放效实中学袁志航效实中学罗文菁效实中学张震祺效实中学周凌峰效实中学钱宇效实中学宁波城区三等奖（共17人）金丹宁宁波中学邬昕韵宁波中学王天韵效实中学印文杰宁波二中蒋之超效实中学陈澹宁效实中学郑榕效实中学孙颖李惠利中学翁炜竣效实中学何璇效实中学顾颖效实中学谢昂效实中学尹译斯超宁波中学张正东宁波二中屠若文效实中学景译辉效实中学刘沁园效实中学附件4：2013年浙江省高中数学竞赛获宁波城区奖名单（B组）宁波城区一等奖（共4人）袁帅宁波外国语学校沈斯琦惠贞书院李亚宁波慈湖中学张子泽惠贞书院宁波城区二等奖（共6人）毛小军宁波慈湖中学张亦然惠贞书院范裕铭惠贞书院陈婷婷兴宁中学何瑜宁波外国语学校吴柯炯兴宁中学宁波城区三等奖（共8人）张丁赟兴宁中学丁哲宁波外国语学校李蓁铭宁波外国语学校王俊旻宁波四明中学钱凯文惠贞书院梁思慧兴宁中学叶林哲惠贞书院张晓雯惠贞书院。

温馨提示 笑迎高考——2010年高考复习查漏补缺（续）数学4谢光亚（广西蒙山县第一中学） 汪显林（江苏省涟水中学）三角函数1．你能熟练利用同角三角函数关系式进行相关计算吗？例1（2009年高考数学辽宁卷文科第8题）已知tan θ=2,则sin 2θ+sin θcos θ-2cos 2θ=( ). A. 34-B.45 C. 43-D.542．你能熟练运用诱导公式计算三角函数值或化简三角函数式吗？ 例2（2009年高考数学全国卷Ⅰ文科第1题）sin585°的值为( ). A. 22-B.22 C. 23-D.233．你能利用三角函数线研究三角函数值的范围吗？ 例3若θ，则点P (sin θ+cos θ,sin θ－cos θ)在直角坐标系内位于（ ）.A.第一象限B.第二象限C.第三象限D.第四象限4．你熟悉三角函数图象的对称性吗？你能根据对称性的特征解决有关问题吗？ 例4（2009年高考数学全国卷Ⅰ理科第8题）如果函数y =3cos(2x +φ)的图象关于点中心对称，那么|φ|的最小值为（ ）.A . B. C. D.5．你能综合运用三角函数相关公式及其图象的平移规律（特别注意系数不是1的情况）解决三角函数图象平移问题吗？例5(2009年高考数学山东卷理科第3题)将函数y =sin2x 的图象向左平移个单位, 再向上平移1个单位,所得图象的函数解析式是( ).A.y=cos 2xB.y=2cos2xC.y=1+（sin2x+）D.y=2sin2x6．三角函数图象与周期性的关系你熟悉吗？你会求三角函数的单调区间吗？例6（2009年高考数学安徽卷理科第8题）已知函数f(x)=3sin ωx+cos ωx(ω＞0)，y=f(x)的图象与直线y=2的两个相邻交点的距离等于π，则f(x)的单调递增区间是( ).A.[kπ-,kπ+],k∈ZB.[kπ+,kπ+],k∈ZC.[kπ-,kπ+],k∈ZD.[kπ+,kπ+],k∈Z7．你能根据三角函数图象求三角函数解析式吗？例7(2009年高考数学陕西卷理科第17题) 已知函数f(x)=A sin(ωx+φ),x∈R（其中A＞0,ω＞0,0＜φ＜)的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为M（,-2）.(Ⅰ)求f(x)的解析式；（Ⅱ）当x∈[]时，求f(x)的值域.向量1．你熟悉向量的基本运算吗？你能利用向量共线的特征进行解题吗？例1（2009年高考数学北京卷文科第2题）已知向量a=(1,0),b=(0,1),c=k a+b(k∈R)，d=a-b.如果c∥d，那么( ).A．k=1且c与d同向B．k=1且c与d反向C ．k =-1且c 与d 同向D ．k =-1且c 与d 反向2．你能利用向量运算的平行四边形法则转化图形中的向量关系吗？例2（2009年高考数学湖南卷文科第4题）如图1， D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点，则（ ）.A. =0B.＝0C.=0D.=03．向量中平行、垂直是最重要的题型之一，你熟悉平行、垂直问题的处理方法吗？ 例3（2009年高考数学浙江卷文科第5题）已知向量a =(1,2)，b =(2,-3)．若向量c 满足(c +a )∥b ，c ⊥(a +b )，则c = （ ）. A ．(37,97) B ．(97,37--) C ．(97,37) D ．(37,97-- )4．向量中数量积是考查的重点，数量积的有关运算你熟悉吗？你能灵活运用数量积与夹角的关系进行解题吗？例4（2009年高考数学全国卷Ⅰ理科第6题）设a 、b 、c 是单位向量，且a·b ＝0，则(a -c )·（b -c ）的最小值为 ( ).A.-2B.2-2 C.-1 D.1-25．向量中两个用同一组基底表示的相等向量对应系数相等的性质你熟悉吗？你会把两个向量用同一组基底表示并用来解决问题吗？例5（2009年高考数学安徽卷文科第14题）在平行四边形ABCD 中，E 和F 分别是边CD 和BC 的中点，若，其中λ，μ∈R ，则λ+μ=______.三角恒等变换1．在和差角公式运用过程中经常涉及用变角的方法，你熟悉吗？在用同角三角函数关系式时你注意了角的范围对函数值的符号的影响了吗？ 例1设cos(α－2β)=97-,sin(2∂－β)=32,且2π<α<π,0<β<2π,求cos(α+β)的值.2．形如a sin α+b cos α=22b a +sin (α+φ)及a sin 2x +b cos 2x +c sin x cos x 用二倍角降次的方法是高考常考题型，你掌握了吗？例2（2008年高考数学北京卷文科第15题）已知函数f （x ）=sin 2ωx +3sin ωx sin(ωx +2π)(ω＞0)的最小正周期为π． （Ⅰ）求ω的值； （Ⅱ）求函数f (x )在区间⎥⎦⎤⎢⎣⎡32π,0上的取值范围． 3．三角函数中知值求值、知值求角的问题你会吗？例3（2008年高考数学江苏卷第15题）如图2，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α、β，它们的终边分别与单位圆相交于A 、B 两点，已知A 、B 的横坐标分别为552102、． （Ⅰ）求tan(α+β)的值； （Ⅱ）求α+２β的值．4．向量与三角函数结合是高考常考题型，你能灵活利用向量与三角函数有关性质或公式进行解题吗？例4（2009年高考数学湖南卷文科第16题）已知向量a =(sin θ,cos θ-2sin θ),b =(1,2). （Ⅰ）若a ∥b ，求tan θ的值； （Ⅱ）若|a |=|b |,0＜θ＜π,求θ的值.5．在三角形中考查三角函数的有关运用也是高考常考题型，你能用好三角形的有关条件以及三角公式进行解题吗？例5 （2008年高考数学全国卷Ⅱ理科第17题）在△ABC 中，cos B =135-,cos C =54．（Ⅰ）求sin A 的值； （Ⅱ）△ABC 的面积S △ABC =233，求BC 的长．6．三角函数的图象、性质及和差公式、倍角公式、半角公式的综合考查也是高考常考题型，你能灵活运用相关性质、公式解决有关问题吗？ 例6（2008年高考数学陕西卷理科第17题）已知函数f (x )=2sin 4x cos4x -32sin 24x +3．（Ⅰ）求函数f (x )的最小正周期及最值；（Ⅱ）令g (x )=)3π(+x f ，判断函数g (x )的奇偶性，并说明理由．数学5邓凯（广东省中山市坦洲实验中学） 解三角形1．你能依据题目中的已知条件,灵活选取正弦定理或余弦定理解三角形吗？例1(2009年高考数学广东卷文科第7题)已知△ABC 中，∠A 、∠B 、∠C 的对边分别为a 、b 、c ，若a =c =6+2，且∠A =75°，则b = （ ）. A.2B ．6-2C ．324- D ．324+2．你解三角形时有分类讨论和检验的习惯吗？例2 （2009年高考数学全国卷Ⅱ文科第18题）设△ABC 的内角A 、B 、C 的对边长分别为a 、b 、c ，cos(A －C )+cos B =23，b 2=ac ，求B .3．你能够利用三角形的相关知识确定角的范围或者边的范围吗？例3（2009年高考数学江西卷理科第19题）在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，tan C =BA B A cos cos sin sin ++，sin(B －A )=cos C .（Ⅰ）求A 、C ;(Ⅱ)若S △ABC =3+3,求a 、c .4．你能够将向量条件或者结论转化为含三角形的边和角的形式吗？例4(2009年高考数学湖南卷理科第16题)在△ABC 中，已知2==3，求角A 、B 、C 的大小．5．解答解三角形的应用题时，你能够根据题中的信息结合图形进行观察、比较、分析、加工、综合、抽象和概括吗？能够恰当地选择数学模型求解吗？例5（2009年高考数学辽宁卷理科第17题）如图3，A 、B 、C 、D 都在同一个与水平面垂直的平面内，B 、D 为两岛上的两座灯塔的塔顶．测量船于水面A 处测得B 点和D 点的仰角分别为75°、30°，于水面C 处测得B 点和D 点的仰角均为60°，AC=0.1km ．试探究图中B 、D 间距离与另外哪两点间距离相等，然后求B 、D 的距离（计算结果精确到0.01km ，2≈1.414，6≈2.449）. 数列1．对于数列的基本问题，你是否习惯运用基本量求解？例1（2009年高考数学广东卷文科第5题）已知等比数列｛a n ｝的公比为正数，且a 3·a 9=2a 25，a 2=1，则a 1=（ ）.A ．2B ．2C ．22 D ．22.你是否掌握等差数列、等比数列的对称性的公式，并能够变式运用？例2（2009年高考数学安徽卷文科第5题）已知{a n }为等差数列，a 1+a 3+a 5=105，a 2+a 4+a 6=99，则a 20等于（）.A ． -1B ． 1C ． 3D ．7 3．你能否解决数列之和与最值综合的问题？例3（2009年高考数学安徽卷理科第5题）已知｛a n ｝为等差数列，a 1+a 3+a 5=105，a 2+a 4+a 6=99，以S n 表示{a n }的前n 项和，则使得S n 达到最大值的n 是（ ）. A ．21 B ．20 C ．19 D ．184．你是否理解等差数列、等比数列的求和公式的本质，并能够变式运用？ 例4（2009年高考数学辽宁卷理科第6题）设等比数列｛a n ｝的前n 项和为S n ，若336 S S ，则69S S =（ ）.A ．2B ．37 C ．38 D ．35．你能否熟练地利用等差（或等比）中项公式判断等差（或等比）数列？例5（2009年高考数学湖北卷文科第9题）若x ∈R ，记不超过x 的最大整数为［x ］，令{x }=x -［x ］，则⎭⎬⎫⎩⎨⎧+215⎦⎤⎢⎣⎡+215，215+（ ）.A ．是等差数列但不是等比数列B ．是等比数列但不是等差数列C ．既是等差数列又是等比数列D ．既不是等差数列也不是等比数列6．你了解等差数列、等比数列的“分段和”的性质吗？你能够运用这些性质解题吗？ 例6（2009年高考数学浙江卷文科第16题）设等差数列｛a n ｝的前n 项和为S n ，则S 4，S 8-S 4，S 12-S 8，S 16-S 12成等差数列．类比以上结论有：设等比数列{b n }的前n 项积为T n ，则T 4， ， ，1216T T 成等比数列．7．对于一些有生活背景的“找规律”的数列问题，你能够根据已知的前几项求出该数列的通项公式吗？例7（2009年高考数学湖北卷文科第10题）古希腊人常用小石子在沙滩上摆成各种形状来研究数，比如：他们研究过图4中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数;类似地，称图5中的1，4，9，16…这样的数为正方形数．下列数中既是三角形数又是正方形数的是（）.A ．289B ．1024C ．1225D ．1378 8．你能够注意到数列的定义域吗？你习惯于对计算结果进行检验吗？例8（2009年高考数学宁夏/海南卷理科第16题）等差数列｛a n ｝的前n 项和为S n ，已知a m -1+a m+1-a 2m =0，S 2m -1=38，则m = . 9．你会解决“确定数列中的项”的问题吗？例9（2009年高考数学江苏卷第17题）设{ a n }是公差不为零的等差数列，S n 为其前n 项和，满足a 22+a 23=a 24+a 25,S 7=7.（Ⅰ）求数列{ a n }的通项公式及前n 项和S n ；（Ⅱ）试求所有的正整数m ，使得21++m m m a a a 为数列S n 中的项．不等式1．不等式的性质你是否熟练掌握？例1（2009年高考数学安徽卷文科第4题）“a +c ＞b +d ”是“a ＞b 且c ＞d ”的（ ）. A ．必要不充分条件 B ．充分不必要条件 C ．充分必要条件 D ．既不充分也不必要条件 2．你是否铭记均值不等式的使用条件？例2（2009年高考数学重庆卷文科第7题）已知a >0,b >0，则ab ba211++的最小值是（ ）.A ．2B ．22C ．4D ．5 3．你会利用函数的单调性解不等式吗？你会解一元二次不等式吗？例3（2009年高考数学天津卷理科第8题）已知函数f (x )= ⎪⎩⎪⎨⎧<-≥+.0,4,0,422x x x x x x 若f (2－a 2)>f (a ),则实数a 的取值范围是 （ ）.A ．(－∞,－1)∪(2,+∞)B ．(－1,2)C ．(－2,1)D ．(－∞,－2)∪(1,+∞) 4．你会解含绝对值的不等式吗？例4（2009年高考数学山东卷理科第13题）不等式0212<---x x 的解集为 ．5．你会解含参数的不等式吗？例5（2009年高考数学天津卷理科第10题）设0<b <1+a ，若关于x 的不等式(x －b )2＞(ax )2的解集中的整数恰有3个，则（ ）.A ．－1<a <0B ．0<a <1C ．1<a <3D ．3<a <6 6．你会解线性规划与基本不等式综合的问题吗？例6（2009年高考数学山东卷理科第12题）设x ，y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--,0,0,02,063y x y x y x若目标函数z =ax +by （a >0，b >0）的最大值为12，则ba32+的最小值为 （ ）.A ．625 B ．38 C ．311 D ． 4选修课程系列1王彬彬(江苏省涟水中学) 常用逻辑用语1．命题的四种形式的概念你熟悉吗？你会用互为逆否的两个命题同真假的性质解题吗？例1（2008年高考数学山东卷文科第4题）给出命题：若函数y =f (x )是幂函数，则函数y =f (x )的图象不过第四象限．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ ）.A ．3B ．2C ．1D ．02．充分条件、必要条件和充要条件的概念你理解了吗？你能判断条件的充要性吗？ 例2（2009年高考数学天津卷文科第3题）设x ∈R ,则“x =1”是“x 3=x ”的（ ）. A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件3.逻辑联结词“或”“且”“非”的含义你熟悉吗？你会用真值表判断复合命题的真假吗？ 例3（2008年高考数学广东卷理科第6题）已知命题p :所有有理数都是实数，命题q :正数的对数都是负数，则下列命题中为真命题的是（）. A.( ﹁p )∨q B. p ∧q C. (﹁p )∧(﹁q ) D. (﹁p )∨(﹁q )4.全称命题与存在性命题的真假你能判断吗？例4（2009年高考数学海南/宁夏卷文科第4题）有四个关于三角函数的命题： p 1： ∃x ∈R , sin 22x +cos 22x =21p 2: ∃x ,y ∈R , sin(x －y )=sin x －sin y p 3: ∀x ∈[0,π],22cos 1x-=sin xp 4: sin x =cos y ⇒x +y =2π其中的假命题是（ ）.A.p 1，p 4 B .p 2，p 4 C.p 1，p 3 D .p 2，p 3 圆锥曲线与方程1.椭圆、双曲线及抛物线的概念是高考的重点，你能应用定义解题吗？ 例1（2008年高考数学浙江卷文科第13题）已知F 1、F 2为椭圆192522=+yx的两个焦点，过F 1的直线交椭圆于A 、B 两点，若|F 2A |+|F 2B |=12，则|AB |= .2.求圆锥曲线的标准方程是圆锥曲线中的基本问题，也是高考的热点问题.求圆锥曲线的标准方程要根据圆锥曲线的几何性质进行分析，寻找等量关系，求出基本量，你掌握了吗？ 例2（2008年高考数学天津卷文科第7题）设椭圆12222=+ny mx (m >0,n >0)的右焦点与抛物线y 2=8x 的焦点相同，离心率为12，则此椭圆的方程为（ ）. A ．1161222=+yxB ．1121622=+yxC ．1644822=+yxD ．1486422=+yx3.椭圆、双曲线中的焦点三角形是高考经常考查的内容，你能利用定义及正弦定理、余弦定理建立方程组进行相关求解吗?例3（2008年高考数学四川卷文科第11题）已知双曲线C :116922=-yx的左、右焦点分别为F 1、F 2，P 为双曲线C 的右支上一点，且212F F PF =，则△PF 1F 2的面积等于( ). Ａ.24 Ｂ.36 Ｃ48 Ｄ.96 4.你能根据条件求椭圆、双曲线的离心率吗？你会转化与离心率有关的问题吗？ 例4（2009年高考数学江苏卷第13题）如图6，在平面直角坐标系xOy 中，A 1 、A 2 、B 1 、B 2 为椭圆12222=+ay bx (a >b >0)的四个顶点，F 为其右焦点，直线A 1B 2与直线B 1F 相交于点T ，线段OT 与椭圆的交点M 恰为线段OT 的中点，则该椭圆的离心率为 .5.你理解椭圆、双曲线、抛物线的统一定义吗？会运用它们进行解题吗? 例5（2009年高考数学全国卷Ⅰ文科第12题）已知椭圆C :1222=+yx的右焦点为F ,右准线为l ，点A ∈l ，线段AF 交C 于点B .若,则=（ ）.A. 2B. 2C. 3D.36.你能利用方程根与系数关系，设而不求解决有关问题吗？例6（2008年高考数学辽宁卷文科第21题）在平面直角坐标系xOy 中，点P 到两点(0，－3)、(0，3)的距离之和等于4，设点P 的轨迹为C ．（Ⅰ）写出C 的方程；（Ⅱ）设直线y = kx + 1与C 交于A 、B 两点．k 为何值时OA OB ⊥ ？此时A B的值是多少？7.在涉及弦中点问题时，你能利用代点相减法解决有关问题吗？ 例7（2009高考数学北京卷文科第19题）已知双曲线C :22221x y ab-=(a >0,b >0)的离心率为，右准线方程为x =. （Ⅰ）求双曲线C 的方程；（Ⅱ）已知直线x -y +m =0与双曲线C 交于不同的两点A 、B ，且线段AB 的中点在圆x 2+y 2=5上，求m 的值.导数及其应用1.你能利用导数求曲线的切线方程吗？例1（2009年高考数学海南/宁夏卷文科第13题）曲线y =x e x +2x +1在点（0,1）处的切线方程为 .2.由导数的几何意义研究曲线切线斜率与倾斜角的问题,你掌握了吗？例2（2009年高考数学福建卷文科第15题）若曲线f (x )=ax 2+ln x 存在垂直于y 轴的切线，则实数a 的取值范围是 .3.利用导数研究函数的单调区间,你掌握了吗？例3（2009年高考数学福建卷文科第21题）已知函数f(x)=x3+ax2+bx,且f ′(－1)=0.（Ⅰ）试用含a的代数式表示b；（Ⅱ）求f(x)的单调区间.4.你会运用导数解决恒成立问题吗？例4（2008年高考数学江苏卷文科第14题）f(x)=ax3－3x+1对于x∈［－1,1］总有f(x)0成立，则a= .数系的扩充与复数的引入1.复数的四则运算你熟练掌握了吗？例1已知复数z满足: z=1+3i－z,求()()221i34i2z++的值.推理与证明1.你理解合情推理的含义吗？能利用归纳和类比等进行简单的推理吗？例1已知：sin230°+sin290°+sin2150°=；sin25°+sin265°+sin2125°=.通过观察上述两等式的规律，请你写出一般性的命题：=. （*）并给出（*）式的证明.选修课程系列2苗孟义(浙江省慈溪市三山高级中学)常用逻辑用语1．如何判断一个语句是否是命题？你是否掌握命题的四种不同表达形式，是否会进行命题间的相互转化？例1(2009年高考数学重庆卷文科第2题)命题“若一个数是负数，则它的平方是正数”的逆命题是( ).A．“若一个数是负数，则它的平方不是正数”B．“若一个数的平方是正数，则它是负数”C．“若一个数不是负数，则它的平方不是正数”D ．“若一个数的平方不是正数，则它不是负数”2．如何正确认识四种命题间的相互关系？能否正确找出命题的条件与结论？能否根据条件与结论判断命题的真假？是否知道“否命题”与“命题的否定”之间的区别？例2(2008年高考数学山东卷文科第4题)给出命题：若函数y =f (x )是幂函数，则函数y =f (x )的图象不过第四象限．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是( ).A ．3B ．2C ．1D ．03．必要条件、充分条件与充要条件的概念记住了吗？如何判断？(利用定义法、集合间的关系、传递关系、等价关系)要正确区分“甲是乙的充分条件（甲乙）”与“甲的充分条件是乙（乙甲）”是两种不同形式的问题.例3 (2009年高考数学浙江卷理科第2题)已知a 、b 是实数，则“a >0且b >0”是“a +b >0且ab >0”的( ).A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件4．对逻辑联结词“或”“且”“非”的含义是否了解？它们的表示符号会正确使用吗？你是否熟悉含有逻辑联结词的命题的真假判断的准则？例4 (2008年高考数学广东卷理科第6题)已知命题p ：所有有理数都是实数；命题q ：正数的对数都是负数，则下列命题中为真命题的是( ).A.(⌝p )∨qB. p ∧qC. (⌝p )∧(⌝q )D. (⌝p )∨(⌝q )5．是否理解全称量词与存在量词的意义，如何判断含有一个量词的命题的真假？ 例5 (2009年高考数学辽宁卷文科第11题)下列4个命题： p 1： ∃x ∈(0,+∞)，12x⎛⎫ ⎪⎝⎭<13x⎛⎫ ⎪⎝⎭;p 2： ∃x ∈(0,1)，12log x >13log x ;p 3： ∀x ∈(0,+∞)，12x⎛⎫ ⎪⎝⎭>12log x ;p4：∀x∈1 0,3⎛⎫ ⎪⎝⎭，12x⎛⎫⎪⎝⎭<13log x.其中的真命题是( ).A．p1,p3B．p1,p4C．p2,p3D．p2,p46．如何正确理解含有一个量词的命题的否定？如何书写全称命题的否定？如何书写特称命题的否定？例6 (2009年高考数学天津卷理科第3题) 命题“存在x0∈R，02x≤0”的否定是( ).A．不存在x0∈R，02x>0B．存在x0∈R，02x≥0C．对任意的x∈R，2x≤0D．对任意的x∈R，2x>0圆锥曲线与方程1．圆锥曲线的定义是高考的重点，是否对椭圆和抛物线的定义熟练掌握，会应用吗？例1(2009年高考数学四川卷理科第9题)已知直线l1：4x－3y+6=0和直线l2：x=－1，抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( ).A．2 B．3 C．115D．37162．椭圆、双曲线的标准方程各有两种形式，抛物线的标准方程有四种形式，对各种标准方程你是否运用自如？例2 (2009年高考数学广东卷理科第11题)已知椭圆G的中心在坐标原点，长轴在x轴上，离心率为2，且G上一点到G的两个焦点的距离之和为12，则椭圆G的方程为．3．能否用坐标法解决简单的直线与椭圆、抛物线的位置关系等问题？要提醒自己：笔下留心，解答题两个问答有没有关联(即第(Ⅰ)问的结论是否要用在第(Ⅱ)问中，若需要的话，第(Ⅰ)问的结论必须是正确的，否则第（Ⅱ）问即使方法对，结果也是错的)．例3(2009年高考数学浙江卷理科第21题)如图7所示，已知椭圆C1：22221 y xa b+=(a>b>0)的右顶点为A(1,0)，过C1的焦点且垂直长轴的弦长为1．(Ⅰ)求椭圆C1的方程；(Ⅱ)设点P在抛物线C2：y=x2+h(h∈R)上，C2在点P处的切线与C1交于点M、N．当线段AP的中点与MN的中点的横坐标相等时，求h的最小值．空间向量与立体几何1．将空间向量的运算与向量的坐标表示结合起来，不仅可以解决立体几何中的共线、垂直的判断及夹角与距离的计算等有关问题，而且还可以使这些问题的解决变得更加简单，如何建立恰当的空间直角坐标系？(利用图形特征：垂直、中线、中点等)如何正确地写出相应点的坐标？例1(2009年高考数学浙江卷理科第20题)如图8，平面PAC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E、F、O分别为PA、PB、AC的中点，AC=16,P A=PC=10．(Ⅰ)设G是OC的中点，证明：FG∥平面BOE；(Ⅱ)证明：在△ABO内存在一点M，使FM⊥平面BOE，并求点M到OA、OB的距离．2．直线的方向向量、平面的法向量的概念清楚吗？空间向量的数量积及其坐标表示、向量的长度公式、两向量夹角公式、空间两点间的距离公式是否记住？能否熟练应用？能否用向量语言表述直线与直线、直线与平面、平面与平面的垂直和平行关系？能否用向量方法解决直线与直线、直线与平面、平面与平面夹角的计算问题？例2 (2009年高考数学北京卷理科第16题)如图9，在三棱锥P-ABC中，PA⊥底面ABC，PA=AB，∠ABC=60°，∠BCA=90°，点D、E分别在棱PB、PC上，且DE∥BC．(Ⅰ)求证：BC ⊥平面PAC ；(Ⅱ)当D 为PB 的中点时，求AD 与平面PAC 所成的角的大小； (Ⅲ)是否存在点E 使得二面角A -DE -P 为直二面角？并说明理由．导数及其应用1．是否理解导数的几何意义？怎样利用导数的几何意义解决有关的切线或最值问题？运用导数求解含切线的数学问题时，是否留意切线过切点，或者切线过不是切点的某点？例1 (2009年高考数学辽宁卷理科第7题) 曲线y =2x x -在点(1,－1)处的切线方程为（ ）.A ．y =x －2B ．y =－3x +2C ．y =2x －3D ．y =－2x +12．能根据导数定义，求函数y =C （C 为常数）,y =x ,y =x 2,y =x 3,y =1x,y 否根据常见基本初等函数的导数公式(8个)和导数运算公式(3个)求简单函数的导数？例2 (2009年高考数学安徽卷文科第9题)设函数f (x )=sin 3θx 32x 2+tan θ，其中θ∈5π0,12⎡⎤⎢⎥⎣⎦，则导数 f ′(1)的取值范围是( ). A ．［－2,2］ B ．［2,3］C ．［3,2］D ．［2,2］3．能求简单的复合函数(仅限于形如f (ax +b )的函数)的导数，这是正确应用导数的前提． 例3 (2009年高考数学陕西卷理科第20题第（Ⅰ）问) 已知函数f (x )=ln(ax +1)+ 11x x-+，x ≥0，其中a >0．若f (x )在x =1处取得极值，求a 的值.4．无论是求单调区间还是求极值，首先需要确定函数的定义域，你做到了吗？ 例4 (2009年高考数学安徽卷理科第19题) 已知函数f (x )=x －2x+a (2－ln x )，a >0.讨论f (x )的单调性．5．在应用导数研究函数的单调性时，往往需要解含有参数的二次不等式，在进行讨论时，能否考虑全面？能否注意到特殊情况？是否注意到二次项系数可能为零的情形？例5 (2009年高考数学辽宁卷理科第21题)已知函数f (x )= 12x 2－ax +(a －1)ln x ，a >1．(Ⅰ)讨论函数f (x )的单调性；(Ⅱ)证明：若a <5，则对任意x 1,x 2∈(0,+∞)，x 1≠x 2，有1212()()f x f x x x -->－1．6．对于可导函数，f ′(x 0)=0是f (x )在x =x 0处有极值的必要不充分条件．在解决问题时，是否注意到这一点？例6 (2008年高考数学陕西卷理科第21题)已知函数f (x )= 21kx x c++（c >0且c ≠1，k ∈R ）恰有一个极大值点和一个极小值点，其中一个是x =－c ．(Ⅰ)求函数f (x )的另一个极值点；(Ⅱ)求函数f (x )的极大值M 和极小值m ，并求M －m ≥1时k 的取值范围．7．在应用导数求参数的范围时，是否注意到端点的取舍？讨论时是否遗漏特殊情况？ 例7 (2009年高考数学山东卷文科第21题)已知函数f (x )= 13ax 3+bx 2+x +3，其中a ≠0．(Ⅰ)当a 、b 满足什么条件时，f (x )取得极值?(Ⅱ)已知a >0，且f (x )在区间(0,1］上单调递增，试用a 表示出b 的取值范围．推理与证明1．是否了解合情推理的含义？怎样利用归纳推理，通过观察个别情况发现某些相同本质？如何从已知的相同性质中推出一个明确的一般性命题？例1 (2009年高考数学浙江卷理科第15题) 观察下列等式：15C +55C =32－2, 19C +59C +99C =72+23, 113C +513C +913C +1313C =211－25, 117C +517C +917C +1317C +1717C =215+27,…由以上等式推测到一个一般的结论：对于n ∈N *, 141C n ++541C n ++941C n ++…+4141C n n ++= ． 2．平面几何与立体几何之间的类比，你知道多少？怎样通过观察、联想进行类比推理得出猜想？平面向量与空间向量呢？例2已知△ABC 的三边长为a 、b 、c ，内切圆半径为r (用S △ABC 表示△ABC 的面积)，则S △ABC =12(a +b +c )r ；类比这一结论有：若三棱锥A -BCD 的内切球半径为R ，则三棱锥的体积V A-BCD = ．3．是否了解直接证明的两种基本方法——分析法和综合法的思考过程、特点？是否了解间接证明的一种基本方法——反证法的思考过程、特点？能否用数学归纳法证明一些简单的数学命题？例3 (2009年高考数学山东卷理科第20题)等比数列{}n a 前n 项和为S n ，已知对任意的n ∈N *，点(n ,S n )均在函数y =b x +r （b >0且b ≠1，b 、r 均为常数）的图象上．(Ⅰ)求r 的值；(Ⅱ)当b =2时，记b n =2(log 2a n +1)(n ∈N *)，证明：对任意的n ∈N *，不等式111b b +·221b b +·…·1nnb b +数系的扩充与复数的引入1．理解复数的基本概念吗？例1 (2009年高考数学重庆卷理科第2题)已知复数z 的实部为－1，虚部为2，则5i z=（ ）.A ．2－iB ．2+iC ．－2－iD ．－2+i2．复数的模与共轭复数有哪些性质？例2 (2009年高考数学全国卷Ⅰ理科第2题) 已知1iz +=2+i ，则复数z =( ).A ．－1+3iB ．1－3iC ．3+ID ．3－i3．复数分别为实数、虚数、纯虚数的充要条件是什么？例3(2009年高考数学江西卷理科第1题)若z=(x2－1)2+(x－1)i为纯虚数，则实数x的值为（）.A．－1 B．0 C．1 D．－1或14．如何理解复数相等，是否已掌握复数相等的充要条件？例4(2009年高考数学安徽卷理科第1题) i是虚数单位，若17i2i+-=a+b i(a,b∈R)，则乘积ab的值是( ).A．－15 B．－3 C．3 D．15 5．是否熟练掌握复数的加、减、乘、除四则运算？例5(2009年高考数学海南/宁夏卷理科第2题)复数32i23i+-－32i23i-+=( ).A．0 B．2 C．－2i D．2i6．复数的代数表示法及其几何意义是什么？复数代数形式的加、减运算的几何意义是什么?是否会运用它们来解决复数的相关问题？例6 已知z∈C，且z－2－2i=1，i为虚数单位，则22iz+-的最小值是( ).A．2 B．3 C．4 D．5计数原理1．两个计数原理理解得怎样，在做题时会选择吗？例1(2009年高考数学北京卷理科第7题)用0到9这10个数字，可以组成没有重复数字的三位偶数的个数为（）.A．324 B．328 C．360 D．6482．解排列组合问题的依据是什么？(分类相加，分步相乘，有序排列，无序组合)例2 (2009年高考数学浙江卷理科第16题)甲、乙、丙3人站到共有7级的台阶上，若每级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法种数是（用数字作答）．3．解排列组合问题的规律是什么？(1)元素相邻，捆绑处理；元素间隔，插空处理.例3 (2009年高考数学四川卷理科第11题) 3位男生和3位女生共6位同学站成一排，若男生甲不站两端，3位女生中有且只有两位女生相邻，则不同排法的种数是( ).A ．360B ．288C ．216D ．96(2)多排问题单排法，定位问题优先法.例4 10名同学合影，站成了前排3人后排7人，现摄影师要从后排7人中抽2人站到前排，其他人的相对顺序不变，则不同调整方法的种数为( ).A ．2575C AB ．2272C AC ．2275C AD ．2375C A(3)选取问题先组合后排列，多元问题分类法.例5 (2009年高考数学广东卷理科第7题)2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作，若其中小张和小赵只能从事前两项工作，其余三人均能从事这四项工作，则不同的选派方案共有( ).Ａ．36种 Ｂ．12种 Ｃ．18种 Ｄ．48种 (4)分组和分配问题，分配有序，分组无序.例6 (2009年高考数学重庆卷理科第13题) 将4名大学生分配到3个乡镇去当村官，每个乡镇至少一名，则不同的分配方案有 种（用数字作答）．(5)至多至少问题间接法.例7 (2009年高考数学全国卷Ⅱ理科第10题)甲、乙两人从4门课程中各选修2门，则甲、乙所选的课程中至少有1门不相同的选法共有( ).A ．6种B ．12种C ．30种D ．36种4．二项式的展开式还记得吗？是否会用计数原理证明二项式定理？能否交换位置？展开式的通式是什么？能否利用通项公式解决二项式展开中的“特定项”问题？例8 (2009年高考数学浙江卷理科第4题) 在二项式521x x ⎛⎫- ⎪⎝⎭的展开式中，含x 4的项的系数是( ).A ．-10B ．10C ．-5D ．55．如何开展二项式定理的逆用？是否掌握二项式系数的性质(对称性，增减性，最大值)？二项式展开中的二项式系数和系数有何区别？如何正确求解(赋值法)？整除问题和求近似解是二项式定理中两类常见的应用问题，你会解决吗？例9 (2008年高考数学福建卷理科第13题) 若(x －2)5=a 5x 5+a 4x 4+a 3x 3+a 2x 2+a 1x +a 0，则。

人教社 教研网
学科网
http:/

二、汇报实践中所面临的若干问题 及应对策略和措施
㈠初高中教学中的衔接问题 ㈡模块化教学中的顺序问题 ㈢课时问题、教学难度 ㈣对教材例题、习题的开发和研究 ㈤根据学生实际，适当调整教学内容 ㈥资料问题(教学案) ㈦加强合作，互助互补，共同研究， 一起提高 ㈧关于平时练习和考试评价
㈣对教材例题、习题的开发和研究
二、汇报实践中所面临的若干问题 及应对策略和措施
㈠初高中教学中的衔接问题
㈡模块化教学中的顺序问题
㈢课时问题、教学难度
㈣对教材例题、习题的开发和研究
㈤根据学生实际，适当调整教学内容
二、汇报实践中所面临的若干问题 及应对策略和措施
㈠初高中教学中的衔接问题 ㈡模块化教学中的顺序问题 ㈢课时问题、教学难度 ㈣对教材例题、习题的开发和研究 ㈤根据学生实际，适当调整教学内容 ㈥资料问题(教学案) ㈦加强合作，互助互补，共同研究， 一起提高
慈溪市三山高级中学（315300）苗孟义
cx6390@
一、摆正“课标”、“意见”、 “教材”的 位置，逐渐体现课标理念
㈠不可忽视的“课标”，是课改的方向 ㈡日夜牵挂的“意见”，是课改的法宝 ㈢精益求精的“教材”，是课改的舞台
二、汇报实践中所面临的若干问题 及应对策略和措施
㈠初高中教学中的衔接问题
二、汇报实践中所面临的若干问题 及应对策略和措施
㈠初高中教学中的衔接问题
㈡模块化教学中的顺序问题
模块顺序百分比
其他 12% 12345 37%
14523 29% 12453 22%
二、汇报实践中所面临的若干问题 及应对策略和措施
㈠初高中教学中的衔接问题
㈡模块化教学中的顺序问题
㈢课时问题、教学难度

三山高级中学2010学年第一学期高三第一次月考数学卷（文科）（时间：120分钟 满分：150分 命题：苗孟义 审题:徐幼红)一、选择题(本大题共10小题，每小题5分,共50分，在每小题给出的四个选项中,只有一项是符合题目要求的,把答案写在答题卷中的相应位置）1.若将复数2i i +表示为(,,a bi a b R i +∈是虚数单位)的形式,则b a的值为 （ ）A.2- B 。

12- C 。

2 D.122。

函数()cos 4,f x x x R =∈是最小正周期为（ ） A.π的偶函数 B.π的奇函数 C. 2π的偶函数 D. 2π的奇函数3。

已知||||2==a b ,2⋅=-a b ,且()()t +⊥+a b a b ,则实数t 的值为 ( ）A.1- B 。

1 C 。

2- D 。

24。

如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，则在这几场比赛中甲得分的中位数与乙得分的众数分别是 （ ）A ．3,2B ．8，2C ．23，23D ．28，325.复数11212i i +--的虚部为（ ）A 。

15B 。

15i C.15- D.15i - 6.从数字1,2,3,4,5这五个数中，随机抽取2个不同的数,则这2个数的和为偶数的概率是 ( ） A.15 B.25 C.35 D.457。

已知11a -≤≤,11b -≤≤,则关于x 的方程220x ax b ++=有实根的概率是 （ ） A.12 B 。

14 C 。

18 D 。

1108.甲、乙两人各抛掷一次正方体骰子（六个面均标有数字1,2,3,4,5,6），设甲、乙所抛掷骰子朝上的面的点数分别为,x y ，则满足复数x yi +的实部大于虚部的概率是（ ）A 。

16B 。

512C 。

712D. 139。

在ABC ∆中，AB =2BC =，2A π∠=，如果不等式||||BA tBC AC -≥恒成立，则实数t 的取值范围是 （ ）A 。

运动觅本质变化提素养李学军;苗孟义;沈虎跃【摘要】在高三的复习中,老师会根据学生的不同需求,设计一些有针对性的专题复习课,通过专题复习课,引导学生用数学的思维去发现、思考和解决一类问题,结合2018年11月的一节示范课,探索数学课堂如何处理好三个“关注”即关注教材的潜力,关注专题的实效,关注考题的联系.【期刊名称】《中学数学教学》【年(卷),期】2019(000)003【总页数】5页(P38-42)【关键词】示范课;本质;教学启示【作者】李学军;苗孟义;沈虎跃【作者单位】浙江省平湖中学 314000;浙江省慈溪中学 315323;浙江省镇海中学315200【正文语种】中文源起 2018年11月26日，浙江省教育厅“百人千场”高中数学专家名师赴磐安县送教活动中，沈虎跃名师网络工作室学科带头人慈溪中学苗孟义老师在磐安二中开设了一节课题为《立体几何动态问题复习》高三一轮专题复习课，这节示范课使学生主动深入探究环境当中，在恰当的时机给学生创造自由飞翔的空间，有效地激发了学生的学习潜能，使得各种层次的学生都能够学有所获.苗老师的这节课设计朴实而有针对性，选题精炼而有代表性，在充分尊重学生的同时，又激发了学生对问题解决的热情，下面简要回顾课堂教学的部分环节以及自己的切身感受，谈一下自己对课堂教学的思考.1 教师主导——驾驭课堂真老师苗老师在知识复习阶段，回顾了余弦定理及余弦定理的变形，接下来从余弦定理出发，向平面向量过渡，通过平面向量公式的变形，逐步探究出本节课的主干知识，在这个探究的过程中，既要兼顾到教材概念、思想、方法的回顾，又要把相互关联的概念、思想和方法有机地串联起来，使学生能够达到真正意义的融汇贯通.课堂实录1对角线向量定理的探究师：余弦定理可以写成向量的形式吗？生：师：非常好，因此上式可以变形成师：如图在△ADC中，等于什么？生：师：两式相减，左边等于什么？生：左边师：右边等于什么？生：右边师：在四边形ABCD中，图1师：同学们发现这个公式中字母的规律了吗？生：由内及外再交叉相减.师：这个定理就叫做对角线向量定理，有些书上也叫做四点向量定理；对角线向量定理，表明四边形的两条对角线对应向量的数量积可用四条边的长度表示.图2师：今天我们研究的主要内容是立体几何中的动态问题，因此这个四边形要进行翻折，对不对？师：假如我们以BD为轴进行翻折，这样平面问题转换为空间问题，同学们思考一下，在空间中，对角线向量定理是否成立？生：在翻折的过程中，四条边的长度没有发生变化，因此在空间四边形中，对角线向量定理仍然成立；师：对上述定理进行进一步理解：(1)当时，有即对角线互相垂直时，四边形两组对边的平方和相等；即可以求平面或空间的角度问题，包括三种角(线线角，线面角，二面角)……感悟《普通高中数学课程标准(2017版)》中说“教师应理解不同数学学科素养水平的具体要求，不仅关注每节课的教学目标，更应关注主题、单元的教学目标，明晰这些目标对实现数学学科素养发展的贡献.”苗老师的这个环节从学生的最近发展区出发到知识理解，知识迁移，知识创新层层递进.真正体现了“整体设计必修和选择性必修课程的体系，处理好数学内容的层次性与数学学科核心素养水平发展的连续性”.在高三的一轮复习中从教材出发进行追本溯源，挖掘知识的本源，渗透必要的数学核心素养，这样的复习为后续的综合能力的提升奠定了非常扎实的基础.2 学生主体——课堂掌控真主人图3例1(2012年浙江高考)已知矩形将△ABD沿对角线BD所在直线进行翻折，在翻折的过程中( )A.存在某个位置，使得直线AC与直线BD垂直B.存在某个位置，使得直线AB与直线CD垂直C.存在某个位置，使得直线AD与直线BC垂直D.对于任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直课堂实录2对角线向量定理的理解师：请同学们用自己所带的纸折一下，然后猜猜看或者用我们刚刚探究过的对角线向量定理.(巡视和学生交流是猜的选项B，还是算出来的)师：对于选项A如何判断？生：因此选项A不正确.师：对于选项B呢？生：图4师：请问是确定的值吗？生：在一个范围内变化.师：最大值是多少呢？生：最大值是师：最小值如何求呢？生：当翻折后与A、B、D共面时最小.师：如何求此时的AC′的长度呢？翻折后AC′与BD有什么关系呢？生：翻折后AC′与BD平行，过A作AE⊥BD于点E，在Rt△ABD中，AB2=BE·BD，所以同理所以师：非常棒！那么所以就可以取到0，所以选项B正确.师：在平时的学习中，我们要对每一个选项进行深究一下，选项C如何判断呢？生：一定不能取到0，因此选项C不成立.师：如果这种方法，在平时你一直在用，那么在大型考试中遇到这样类型的小题你就可以进行秒杀了.感悟这个题目是2012年浙江高考数学理科的第10题，苗老师在课堂上引导学生动手折一折，实际上就是培养学生因地制宜，充分利用周围的环境解决问题，通过数学实验直观的发现答案.接下来苗老师“话风”一转，数学讲究严谨性，引导学生通过计算的方式进行严格推理论证.学生在苗老师的引导下，紧张有序的进行逐个选项的论证.虽然这是高三的一轮复习，但是苗老师在课堂上给学生留出足够的时间，让学生对所学习的知识进行去思，去悟，去用，真正实现了学以致用.3 课堂主场——渗透素养真领地图5例2(2016年浙江(文)14题)如图，已知平面四边形沿直线AC将△ACD翻折成△ACD′，直线AC与BD′所成角的余弦值的最大值是.课堂实录3对角线向量定理的内化师：因为如何求呢？生：师：那么在翻折的过程中，范围怎样呢？师：在Rt△ACD中，在△ABC中，由余弦定理得你有什么发现？图6生：∠ACD=∠BCD，师：请问，cos∠BCD等于多少？生：cos∠BCD=cos2∠ACD=师：在平面四边形ABCD中，你会求BD的长度吗？所以所以师：当点D在什么位置时，BD的长度最小？生：当点D′落在BC的三等分点E处时BD′=3-1=2最小.师：因此所以所以直线AC与BD′所成角的余弦值的最大值是感悟《普通高中数学课程标准(2017版)》中提出“数学学科素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.这些数学核心素养既相对独立、又相互交融，是一个有机的整体.”在标准中还给出了核心素养的水平划分的三个层次具体的要求，因此在课堂教学中，苗老师根据学生的现有的学习能力，引导学生主动地参与学习，培养学生用数学思维和习惯进行学习，通过较为复杂的数据运算，取值范围的求解，翻折过程中的动态变化，使得数学运算，逻辑推理，直观想象等数学核心素养有效扎实地落到实处.图74 问题主线——能力提升真效果例3(2015年浙江省普通高中学业水平考试数学试题18题)如图，在菱形ABCD 中，∠BAD=60o，线段AD、BD的中点分别为E、F，现将△ABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是( )图8课堂实录4一类问题的多种思维师：这是一个选择题，你有没有办法猜出答案呢？生：当平面ABD⊥平面BCD时，直线CF⊥平面ABD，因此CF⊥BE，当点E落在CD上时，直线BE与CF所成角为因此选C.师：通过特殊值法进行定性分析是有风险的，如果题目中有陷阱就比较麻烦，接下来，我们进行定量计算，不妨设菱形ABCD的边长为2.生：在菱形ABCD中，在△CDE中，由余弦定理得所以当点E在翻折过程中落在边CD上时，CE=1，所以所以所以异面直线BE与CF所成角的取值范围是师：非常棒！事实上当△ABD沿对角线BD翻折的过程中，点E的轨迹是是什么？生：是一个圆.师：线段BE在翻折的过程中的轨迹是什么？生：是圆锥的侧面.师：请同学们课后思考一下，你可以通过这样的思路解决这道题吗？感悟在这个学考题的探究过程中，苗老师非常巧妙地引导学生去思考动点的轨迹问题，选择题的答题策略问题，利用本节课所学知识进行严谨论证策略问题，课后思考题等，使得本节课的学习氛围达到了高潮.事实上这个题目还可以进行如下的解答：由题意知所以所以所以异面直线BE与CF所成角的取值范围是作为探究的题目，还可以从坐标系的视角，基底的视角，异面直线定义的视角等方向进行思考. 教学启示图9(1)关注教材的潜力数学选修2-1第106页例2如图，甲站在水库底面上的点A处，乙站在水坝斜面上的点B处.从A、B到直线l(库底与水坝的交线)的距离AC和BD分别为a和b，CD的长为c，AB的长为d.求库底与水坝所成二面角的余弦值.在解决这个问题我们可以从三个层次进行探究.第一层次：因为所以所以所以第二层次：再延伸一下所以所以第三层次：再推广一下当AC，BD与CD不垂直时，所以所以正如叶圣陶先生所说：“教材无非是个例子，它只能作为教课的依据.要教得好，使学生受益，还要靠教师善于运用.”事实上在我们的教材中，只要我们做个有心人，用心去挖掘这样的素材，一定可以从不同角度得出更多有意义的结论，使得我们课堂更加韵味无穷.(2)关注专题的实效对角线向量定理，可以快速解决一类关于向量数量积或向量夹角问题，但并不是一味追求高难度的解题技巧，恰恰相反，通过这种专题的探究，寻求一类问题的通解通法，进而形成一类问题的统一解法.事实上对于动点的轨迹问题苗老师的这节课完全可以设计动画演示，通过动画学生对动点的运动状态理解可能会更加深刻，尤其对空间想象能力不强的学生来说效果会更好.但是高三复习目的是让学生在考场上能够在有效的时间内对所考查的问题进行有效解决，因此在高三的复习课堂就应该为这样的目的进行设计和实施.(3)关注考题的联系考题1(2014年1月浙江省普通高中学业水平考试第25题)如图，在Rt△ABC中，AC=1,BC=x，D是斜边AB的中点，将△BCD沿直线CD翻折，若在翻折的过程中存在某一时刻，使得CB⊥AD，则x的取值范围是( )图10图11图12考题2(2009浙江高考理科第17题)如图，在长方形ABCD中，AB=2,BC=1，E 为DC的中点，F为线段EC(端点除外)上的一动点.现将△AFD沿AF折起，使平面ABD⊥平面ABC，在平面ABD内过点D作DK⊥AB，K为垂足.设AK=t，则t的取值范围是.这样背景的试题在高三的复习资料中会经常出现，在解决问题的过程中，我们也应该关注这些试题之间是否存在共性的东西，解决这类问题是否有行之有效的共性办法，这也就是数学中的合情推理和演绎推理的最好落实.正如波利亚曾形象地指出“好问题同某些蘑菇有些相似，它们大都成堆地生长，找到一个之后，你应当在周围再找一找，很可能就有几个”.总之，数学教学不仅要教授数学知识，数学方法，更要引导学生把握数学内容的本质，发展学生的数学核心素养，用数学的眼光看问题.张奠宙教授曾经说过：“数学教学的有效性关键在于对数学本质的把握、揭示和体验.”在教学中要想更好的驾驭时刻在变化的课堂，就需要老师在平时不断提升自身的数学素养，从而实现真正意义的教学相长.参考文献【相关文献】1 吴淑芳，朱万成. 1个公式 5类问题 14年高考[J].中学教研(数学)2017(8):36-402 中华人民共和国教育部. 普通高中数学课程标准(2017版)[S]. 北京：人民教育出版社，2018。

(
)
f（ － x） = － f（ x） ， f（ x + 2 π ） = f （ x ） ， 所以 f （ x ） 既是奇函数， 又是周期函数， 排除选项 D． 故选 C． 题型 4 例4 三角函数图像的变换 3cosx + sinx（ x∈Ｒ） 的图像向左平移 将函数 y = 槡 （ B． π 6 C． π 3 D． 5π 6 ）
点评 题型 6 例6 “一开 正确化简函数关系式是解题的关键， 警惕 三角函数的最值 3 3 sin2 ωx － sinωxcosωx （ ω ＞ 设函数 f （ x ） = 槡 － 槡 2 始算错， 接下来白做！ ”
2 ． 已知 a 是实数， 则函数 f（ x） = acosax 的图像可能是 （ ）
m=
m 取得最小值为 当 k = 0 时， 点评
本题主要考查三角恒等变换 、 三角函数图像的 π + kπ（ k∈Z） ； 若此函 2
平移及三角函数的对称 性 ． 另 外 对 于 函 数 y = Asin （ ωx + φ） ， 若此函数为偶函数， 则必有 φ =
数为奇函数， 则必有 φ = kπ （ k ∈ Z ） ． 掌握这些结论便可以 快速准确地解决类似的选择 、 填空题， 达到事半功倍的效 果． 题型 5 例5 三角函数的单调性 已知函数 f （ x ） = 4cosωx · sin ωx +
(
)
y0 ） ， 其中 x0 ≠4 ， 将向量坐标代入并化简得 设 P （ x0 ， m （ 4 x2 － 16 ） = 3 x3 0 0 － 12 x0 ． 3 2 2） ， x ， 所以 m = 而 x0 ∈ （ － 2 ， 因为 x0 ≠ 4 ， 故 m∈ 4 0 3 3 － ， ． 2 2 l 为椭圆在点 P 处的切线， （ 3 ） 证明 由题意可知， 由 x0 x + y0 y = 1 ， 从而 导数法可求得切线方程为 4 x0 k= － ． 4 y0 y0 y0 1 1 + ， ， k2 = 将 k1 = 得 代入 kk1 kk2 x +槡 3 x －槡 3

三角函数与平面向量的复习苗孟义;黄国员【期刊名称】《中学教研：数学版》【年(卷),期】2016(000)002【总页数】4页(P10-13)【作者】苗孟义;黄国员【作者单位】三山高级中学浙江慈溪 315300;慈溪市教育局教研室浙江慈溪315300【正文语种】中文回顾近几年浙江省数学高考试题中关于“三角函数与平面向量”的考题，给我们一种“题在书外、根在书中”的感觉(以2015年为例):文、理科第11题，与《数学(必修4)》第147页复习参考题类似;文科第13题呈现熟悉，理科第15题呈现新颖，理科第16题更关注通性通法，考查有价值的常规方法的应用，凸显学生运用数学思想方法，把数学的知识与技能转化为分析问题和解决问题的能力．全卷一般有3～4个三角函数与平面向量的试题，分值占15%～20%．三角函数主要考查:三角函数名称、角、关系式的变换;三角函数图像与性质，图像的变换，三角函数的单调性、奇偶性、周期性、对称性、最值等;简单的三角恒等变换，包括两角和与差的正弦、余弦和正切公式、二倍角公式等，合理运用三角公式是解决三角函数的图像与性质、三角恒等变换等问题的关键．解三角形主要考查:内角和定理与正弦(余弦)定理，解三角形的边、角、面积及判断三角形形状等．平面向量主要考查:平面向量的几何意义、基向量转化、坐标法．在高考试题中，三角函数试题的考查难度不大，容易得满分;平面向量试题往往短小精悍，内涵丰富，有挑战性．2015年浙江省数学高考理科试题对有关向量问题的考查，悄悄地由平面转向空间，值得关注．例11)设，则( )2)已知角α，β均为锐角，且，则tanβ=( )A．3 B C D3)设△ABC的内角A，B，C所对的边a，b，c成等比数列，则的取值范围是( ) 分析1)易得，从而因此故选C．2)易得，则故选A．3)因为b2=ac，即，由即得解得因此故选D．评析此题组考查同角三角函数关系、两角和与差的正弦(正切)公式．其解答过程集中体现在运算上，是突出对运算能力考查的一组试题，关键是对公式的选择和运算方向的把握．在选择公式、确定运算路径时，应本着从简的原则，尽量缩短运算路径，简化运算过程，提高运算的准确率，这些都是对运算能力的考查要求．例21)将函数y=sin2x的图像向右平移φ个单位后得到函数g(x)的图像，若对满足|f(x1)－g(x2)|=2成立的x1，x2，均有，则φ=( )ABCD2)已知函数f(x)=Asin(ωx+φ)(其中A，ω，φ均为正常数)的最小正周期为π，当时，函数f(x)取得最小值，则下列结论正确的是( )A．f(2)＜f(－2)＜f(0)B．f(0)＜f(2)＜f(－2)C．f(－2)＜f(0)＜f(2)D．f(2)＜f(0)＜f(－2)3)函数f(x)=cos(ωx+ φ)的部分图像如图1所示，则f(x)的单调递减区间为( ) A．B．C．D．分析1)向右平移φ个单位后，得到因为|f(x1)－g(x2)|=2，所以当|x1－x2|取最小值时，刚好是取2个函数相邻的最大值与最小值点．令，则解得故选D．2)依题意得f(x)在上单调递减，且直线是f(x)的图像的一条对称轴．又f(－2)=从而故选A．3)由五点作图法知解得，从而令，其中k∈Z，解得从而f(x)的单调递减区间为，其中k∈Z．故选D．评析三角函数作为重要的基本初等函数，是高考必考的内容之一．对函数图像与性质(如:定义域、值域、周期性、对称性、奇偶性、单调性、最值等)的掌握情况可以在三角函数中得到体现．公式运用及其变形能力、运算能力等可以在这些问题中进行考查，在复习时要注意基础知识的理解与落实．例31)已知平面向量a，b，且|b|=2，b· (2a－b)=0，则|tb+(1－2t)a|(其中t∈R)的最小值为_____.2)已知平面向量a，b满足|a|=5，|b|≤1，且，则a·b的最小值为_____.3)若平面向量a，b，e满足|e|=1，a·e=1，b·e=2，|a－b|=2，则a·b 的最小值为_____.分析1)方法1由|b|=2，b·(2a－b)=0知a·b=2，从而a在b方向上的投影为不妨设b=(2，0)，a=(1，y)，y任意，因为所以故所求的最小值为1，当且仅当y=0时取等号．方法2如图2，不妨设c=，则因为2t+(1－2t)=1，记2tc+点P在直线x=1上，所以|OP|min=1，即当且仅当点P在(1，0)处时，|OP|取到最小值．2)因为a·(a－4b)≤|a|·|a－4b|≤5×，所以即从而故a·b的最小值为3)因为(a+b)·e=3≤|a+b|·|e|，所以从而故a·b的最小值为评析平面向量与不等式结合的问题，解题的关键是利用向量知识将问题转化为不等式问题，通过解不等式、数形结合、极化恒等式来求最值或范围．向量与不等式的结合，既考查了学生的创新数学素养，又加强了对“双基”的考查，特别是向量的坐标表示及运算．这种命题形式符合考纲要求，从学科的整体高度和思维价值的高度考虑问题，在知识网络的交汇处设计试题，对数学基础知识的考查达到必要的深度．例4在△ABC中，点D在BC边上，AD=BD，求AD的长．方法1由余弦定理易得设 AD=BD=x，则在△ADC中，在△ABD中，又cos∠ADC=－cos∠ADB，得，故AD=方法2如图3，过点C作边AB所在直线的垂线，垂足为E，过点D作DF⊥AB，垂足为F．由得 AE=CE=3，则又AD=BD，在Rt△DFB中，因此DF=1，故评析方程思想是通过列方程，找到相关量的关系，通过方程关系的转化得到需要的量进而解决问题．列方程可以将逆向思维的算术问题转化为正向思维的代数问题，学生如果能牢固树立这一思想意识，可以减少很多不必要的思考．另外通过数形结合的思想，借助图形，甚至建立坐标系等，都可以比较快捷地解决此类问题．例5已知函数cos2x．1)求函数f(x)的单调递增区间;2)在锐角△ABC中，角A，B，C的对边分别为a，b，c，若，△ABC的面积为，求的取值范围．分析1)先利用诱导公式、二倍角公式、三角恒等变换化简解析式然后求单调递增区间为，其中k∈Z．2)由第1)小题化简，得在锐角△ABC中，结合面积公式得bc=1，从而因为△ABC为锐角三角形，所以由a2=b2+c2－1，知又bc=1，从而故的取值范围是评析正确化简函数关系式是解题的关键，要警惕“一开始算错，接下来白做!”审题时要注意△ABC是锐角三角形．1．在△ABC中，若，则( )A．2 B．4 C．6 D．82．已知函数f(x)=2cos(ωx+φ)的最小正周期为π，且其图像向右平移个单位后得到函数h(x)=2cosωx的图像，则函数f(x)的图像关于( )A．直线对称B．直线对称C．点对称D．点对称3．已知，⊙A是以A为圆心、半径为1的圆，⊙B是以B为圆心的圆．设点P，Q分别为⊙A，⊙B上的动点，且则的取值范围是( )A．［－1，11］B．［1，13］C．[ 5－D．[ 7－4．已知，则cosα=5．已知a⊥b，c=a+2b，若，则c与 a+b 夹角的余弦值的最小值等于______．6．设，且tanα=，则tanα的取值范围是______，α－β= ______．7．已知函数(其中0＜ω＜1)的图像关于点对称．1)求ω的值;2)若，求cosα的值．1．B2．D3．D4567．解1)，由已知当时，f(x)=0，即从而，其中k∈Z．又ω∈(0，1)，故2)由得由得，从而故。

重视基础，体现课改动向强调能力，昭示课改决心——2013
年浙江省数学高考试卷评析
沈新权;苗孟义
【期刊名称】《中学教研：数学版》
【年(卷),期】2013(000)008
【摘要】1试题特色2013年浙江省数学高考试卷深入贯彻“调结构、减总量、优方法、改评价、创条件”的课改精神，认真落实“降低考试难度，减轻学生负担”的命题要求，严格遵循《浙江省普通高中学科教学指导意见》和《浙江省普通高考考试说明》，着力体现“起点低、坡度缓、层次多、区分好”的命题特色，系统、全面地考查了高中数学的基础知识、基本技能、基本思想，在兼顾考查学生能力的同时，保持了命题的连续性、稳定性、创新性，其主要特色总结如下：
【总页数】4页(P1-4)
【作者】沈新权;苗孟义
【作者单位】
【正文语种】中文
【中图分类】G632
【相关文献】
1.重视基础联系课改呈现综合体现创新——2009年全国高考理综(全国卷Ⅰ)化学试题评析及启示 [J], 李俊生;王丽华;武永刚
2.基础与能力并举经典与创新共舞——2017年浙江省数学高考试卷评析 [J], 郑
日锋
3.体现新理念服务新课改——孝感市2004年中考数学试卷评析 [J], 喻俊鹏
4.体现课改理念,注重能力提升——2006年江苏南通市课改区海门中考语文试卷评析 [J], 张永林
5.能力立意呼唤教学回归——2015年浙江省数学高考试卷评析 [J], 郑日锋
因版权原因，仅展示原文概要，查看原文内容请购买。