下载文档原格式
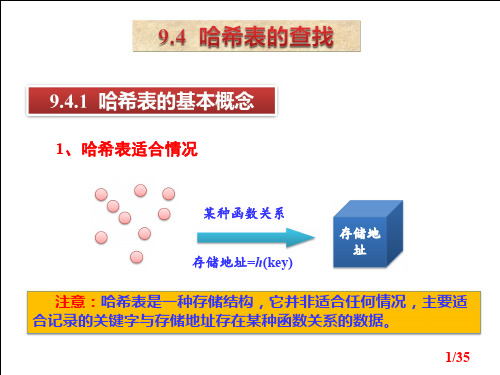
哈希表（Hash）的查找一、哈希表相关概念1、哈希函数的基本概念哈希表又称散列表。
哈希表存储的基本思想是：以数据表中的每个记录的关键字 k为自变量，通过一种函数H(k)计算出函数值。
把这个值解释为一块连续存储空间（即数组空间）的单元地址（即下标），将该记录存储到这个单元中。
在此称该函数H为哈希函数或散列函数。
按这种方法建立的表称为哈希表或散列表。
理想情况下，哈希函数在关键字和地址之间建立了一个一一对应关系，从而使得查找只需一次计算即可完成。
由于关键字值的某种随机性，使得这种一一对应关系难以发现或构造。
因而可能会出现不同的关键字对应一个存储地址。
即k1≠k2，但H(k1)=H(k2)，这种现象称为冲突。
把这种具有不同关键字值而具有相同哈希地址的对象称“同义词”。
在大多数情况下，冲突是不能完全避免的。
这是因为所有可能的关键字的集合可能比较大，而对应的地址数则可能比较少。
对于哈希技术，主要研究两个问题：（1）如何设计哈希函数以使冲突尽可能少地发生。
（2）发生冲突后如何解决。
2、哈希函数的构造方法常见的构造方法有很多种，如直接定址法，数字分析法，平方取中法等。
接下来，我们介绍其中的几种：（1）除留余数法取关键字k被某个不大于表长m的数p除后所得余数作为哈希函数地址的方法。
即：H（k）＝k mod ｐ这种方法的关键是选择好p。
使得数据集合中的每一个关键字通过该函数转化后映射到哈希表的任意地址上的概率相等。
理论研究表明，一般取p为小于ｍ的最大质数或不包含小于20的质因素的合数。
（2）平方取中法先将关键字平方，然后取其中间几位作为散列地址。
所取位数由地址空间范围决定。
若地址空间小于所取位数值决定的范围，可通过乘以一比例因子来解决。
（3）折叠法把关键字分割成位数相等（最后一部分的位数可以不同）的几部分，然后通过折叠后将几部分进行相加，丢掉进位位，所得值即为散列地址。
散列的位数由地址空间的位数而定。
分割方法：从右至左相加方法有两种：移位叠加：将分割后的各部分低位对齐相加。
详解哈希表的查找哈希表和哈希函数在记录的存储位置和它的关键字之间是建立一个确定的对应关系（映射函数），使每个关键字和一个存储位置能唯一对应。
这个映射函数称为哈希函数，根据这个原则建立的表称为哈希表(Hash Table)，也叫散列表。
以上描述，如果通过数学形式来描述就是：若查找关键字为key，则其值存放在f(key) 的存储位置上。
由此，不需比较便可直接取得所查记录。
注：哈希查找与线性表查找和树表查找最大的区别在于，不用数值比较。
冲突若key1 ≠ key2 ，而f(key1) = f(key2)，这种情况称为冲突(Collision)。
根据哈希函数f(key)和处理冲突的方法将一组关键字映射到一个有限的连续的地址集（区间）上，并以关键字在地址集中的“像”作为记录在表中的存储位置，这一映射过程称为构造哈希表。
构造哈希表这个场景就像汽车找停车位，如果车位被人占了，只能找空的地方停。
构造哈希表由以上内容可知，哈希查找本身其实不费吹灰之力，问题的关键在于如何构造哈希表和处理冲突。
常见的构造哈希表的方法有 5 种：（1）直接定址法说白了，就是小学时学过的一元一次方程。
即 f(key) = a * key + b。
其中，a和b 是常数。
（2）数字分析法假设关键字是R进制数（如十进制）。
并且哈希表中可能出现的关键字都是事先知道的，则可选取关键字的若干数位组成哈希地址。
选取的原则是使得到的哈希地址尽量避免冲突，即所选数位上的数字尽可能是随机的。
（3）平方取中法取关键字平方后的中间几位为哈希地址。
通常在选定哈希函数时不一定能知道关键字的全部情况，仅取其中的几位为地址不一定合适；而一个数平方后的中间几位数和数的每一位都相关，由此得到的哈希地址随机性更大。
取的位数由表长决定。
（4）除留余数法取关键字被某个不大于哈希表表长 m 的数 p 除后所得的余数为哈希地址。
即f(key) = key % p (p ≤ m)这是一种最简单、最常用的方法，它不仅可以对关键字直接取模，也可在折叠、平方取中等运算之后取模。
