气体动理论

气体动理论的基本假设气体动理论是研究气体行为和性质的学科，它基于一系列假设和原理，用于解释气体分子的运动和相互作用。

这些假设是对实际情况的简化和理想化，使得我们能够通过数学模型更好地理解气体的行为。

本文将就气体动理论的基本假设进行探讨。

1. 气体分子是微观粒子气体动理论的基本假设之一是将气体看作是由大量微观粒子组成的物质。

这些微观粒子可以是分子，也可以是原子。

根据这一假设，气体的物态特性可以通过对这些微观粒子的运动和相互作用进行研究来解释。

这种假设可以追溯到19世纪早期，由波尔特曼和马克斯韦尔等人提出。

2. 碰撞是气体分子的基本作用基于气体分子是微观粒子的假设，气体动理论认为气体分子之间的碰撞是其基本作用。

这些碰撞会导致分子的运动和相互作用，从而决定了气体的性质。

在碰撞中，气体分子之间会交换能量和动量，使得气体分子的速度和方向发生改变。

碰撞的频率和能量转移的大小会受到温度等因素的影响。

3. 气体分子运动是无规则的气体动理论假设气体分子的运动是无规则的。

这意味着在宏观层面上，气体分子的运动是随机的，无法准确预测。

每个气体分子根据自身能量和速度的微小差异，会呈现出不同的运动轨迹和行为。

尽管分子的总体行为是未知的，但是通过大量气体分子的统计平均，可以得到气体的宏观性质，如压强、温度和体积等。

4. 分子之间的相互作用力可以忽略不计气体动理论的另一个基本假设是忽略气体分子之间的相互作用力。

这意味着在描述气体分子的运动时，我们不考虑分子之间的引力或斥力等相互作用。

这一假设在许多情况下是合理的，尤其是当气体分子之间的距离足够远时，相互作用力可以忽略不计。

因此，气体动理论可以建立在这种简化的假设下，更好地解释气体的宏观性质。

总的来说，气体动理论基于一系列假设和原理，用于解释气体分子的运动和相互作用。

这些基本假设包括气体分子是微观粒子、碰撞是气体分子的基本作用、气体分子运动是无规则的以及分子之间的相互作用力可以忽略不计。

气体动理论公式总结气体动理论是研究气体分子的运动规律和性质的科学理论。

在研究气体动理论时，我们常常会用到一些重要的公式来描述气体的状态和性质。

下面我们将对一些常用的气体动理论公式进行总结和归纳，以便更好地理解和应用这些公式。

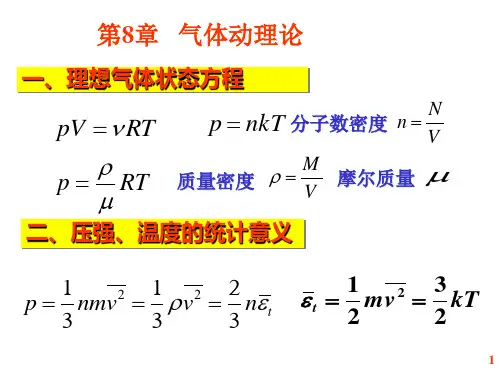
1. 理想气体状态方程。

理想气体状态方程是描述气体状态的重要公式之一，它表达了气体的压强、体积和温度之间的关系。

理想气体状态方程的数学表达式为：PV = nRT。

其中，P表示气体的压强，V表示气体的体积，n表示气体的物质量，R为气体常数，T表示气体的温度。

这个方程描述了理想气体在一定条件下的状态，对于理想气体的研究和应用具有重要意义。

2. 理想气体内能公式。

理想气体内能是气体分子的平均动能，它与气体的温度有直接的关系。

理想气体内能的数学表达式为：U = (3/2)nRT。

其中，U表示气体的内能，n表示气体的物质量，R为气体常数，T表示气体的温度。

这个公式表明了理想气体内能与温度的关系，对于研究气体的热力学性质和能量转化具有重要意义。

3. 理想气体压强公式。

理想气体的压强是描述气体状态的重要参数之一，它与气体的温度和体积有直接的关系。

理想气体压强的数学表达式为：P = (nRT)/V。

其中，P表示气体的压强，n表示气体的物质量，R为气体常数，T表示气体的温度，V表示气体的体积。

这个公式描述了理想气体的压强与温度、体积的关系，对于理想气体的状态和性质具有重要意义。

4. 理想气体密度公式。

理想气体的密度是描述气体物质分布的重要参数，它与气体的压强和温度有直接的关系。

理想气体密度的数学表达式为：ρ = (nM)/V。

其中，ρ表示气体的密度，n表示气体的物质量，M表示气体的摩尔质量，V 表示气体的体积。

这个公式描述了理想气体的密度与物质量、摩尔质量、体积的关系，对于理想气体的物质分布和性质具有重要意义。

5. 理想气体平均速度公式。

理想气体分子的平均速度是描述气体分子运动规律的重要参数，它与气体的温度和摩尔质量有直接的关系。

气体分子动理论气体分子动理论是物理学中研究气体行为的理论框架。

它基于原子和分子在气体中的微观运动，试图解释和预测气体的宏观性质。

本文将介绍气体分子动理论的基本原理和相关概念。

分子运动和气体行为气体由大量分子组成，这些分子在气体容器中不断运动，并与容器和其他分子发生碰撞。

气体的宏观性质，如温度、压力和体积，可以从分子的运动状态推导出来。

气体分子动理论通过研究分子之间的相互作用和运动规律，解释了气体的行为。

分子运动规律根据气体分子动理论，分子具有以下运动规律：1.分子无规则运动：分子在气体容器中呈现无规则、自由的运动状态。

它们在容器内沿不同方向高速运动，并不断改变运动方向和速度。

2.分子之间的弹性碰撞：分子之间发生弹性碰撞，碰撞后能量和动量守恒，但在碰撞中的分子可能会发生运动速度和方向的改变。

3.平均运动速度：分子的速度服从Maxwell-Boltzmann分布，即分子的速度呈现连续分布，平均速度与温度相关。

4.分子间距和碰撞：分子之间的距离很大，相对于分子的体积而言，分子之间的相互作用可以忽略不计。

然而，当分子靠近时，它们之间的碰撞会对气体的性质产生影响。

气体宏观性质的解释气体分子动理论通过分子的运动规律，解释了气体的一些宏观性质：1.压力：气体分子运动产生的碰撞力对容器壁施加压力，压力与分子速度和碰撞频率有关。

2.温度：气体分子的平均动能与其速度平方成正比，因此温度可以视为分子的平均运动速度的度量。

3.体积：气体分子之间的距离较大，在碰撞时每个分子所占的体积可以忽略不计，因此气体没有固定的形状和体积，可以完全填满容器。

气体状态方程气体状态方程描述了气体的状态和性质。

根据气体分子动理论，可以推导出理想气体状态方程：PV = nRT其中，P是气体的压力，V是气体的体积，n是气体的摩尔数，R是气体常数，T是气体的温度。

这个方程表明，在一定温度下，气体的压力和体积成正比，与摩尔数成正比。

该方程也可以用来推导气体的其他性质。

气体动理论公式总结气体动理论是研究气体分子在微观层面上的运动规律的一门学科。

它主要研究气体分子的速度、能量、碰撞等方面的性质。

气体动理论公式是描述气体分子运动规律的数学表达式，可以用来计算气体分子的平均速度、平均能量等参数。

下面将总结一些常见的气体动理论公式。

1. 理想气体状态方程理想气体状态方程描述了理想气体在一定温度、压力和体积下的状态关系。

它的数学表达式为：PV = nRT其中，P为气体的压力，V为气体的体积，n为气体的摩尔数，R为气体常数，T为气体的温度。

2. 平均动能公式平均动能公式描述了气体分子的平均动能与温度之间的关系。

它的数学表达式为：K = (3/2)kT其中，K为气体分子的平均动能，k为玻尔兹曼常数，T为气体的温度。

3. 动量-速度关系动量-速度关系描述了气体分子的动量与速度之间的关系。

它的数学表达式为：p = mv其中，p为气体分子的动量，m为气体分子的质量，v为气体分子的速度。

4. 均方根速度公式均方根速度公式描述了气体分子的速度分布规律。

它的数学表达式为：v = √(3kT/m)其中，v为气体分子的均方根速度，k为玻尔兹曼常数，T为气体的温度，m为气体分子的质量。

5. 平均自由程公式平均自由程公式描述了气体分子在运动过程中与其他分子或壁面碰撞的平均距离。

它的数学表达式为：λ = (1/√2πd^2n)其中，λ为气体分子的平均自由程，d为气体分子的直径，n 为气体分子的密度。

6. 分子碰撞频率公式分子碰撞频率公式描述了气体分子碰撞的频率与气体分子数密度之间的关系。

它的数学表达式为：Z = 4πn(d^2)v其中，Z为气体分子的碰撞频率，n为气体分子的数密度，d 为气体分子的直径，v为气体分子的速度。

以上是一些常见的气体动理论公式总结，它们可以用来描述气体分子的运动规律和性质。

利用这些公式，我们可以进行气体的热力学计算和分析，深入理解气体的特性和行为。

同时，这些公式也为相关实验提供了理论基础，促进了气体动理论的发展。

气体动理论（kinetic theory of gases）是19世纪中叶建立的以气体热现象为主要研究对象的经典微观统计理论。

气体由大量分子组成，分子作无规则的热运动，分子间存在作用力，分子的运动遵循经典的牛顿力学。

根据上述微观模型，采用统计平均的方法来考察大量分子的集体行为，为气体的宏观热学性质和规律，如压强、温度、状态方程、内能、比热以及输运过程（扩散、热传导、黏滞性）等提供定量的微观解释。

气体动理论揭示了气体宏观热学性质和过程的微观本质，推导出宏观规律，给出了宏观量与微观量平均值的关系。

它的成功印证了微观模型和统计方法的正确性，使人们对气体分子的集体运动和相互作用有了清晰的物理图像，标志着物理学的研究第一次达到了分子水平。

气体分子动理论气体是物质存在的其中一种形态，它的分子运动对于我们理解气体的性质至关重要。

气体分子动理论是一种描述气体性质的科学理论，它通过解释气体分子的运动行为和碰撞规律，为我们提供了对气体行为的深入认识。

1. 分子运动的基本规律气体分子的运动有其基本规律，其中最重要的是玻尔兹曼分布规律。

根据玻尔兹曼分布规律，气体分子的速度分布服从高斯分布，即呈现一个钟形曲线。

这意味着气体分子的速度有一定的平均值，同时也存在一定的速度分散。

这种分布规律的存在，决定了气体的宏观性质，如压强、温度等。

2. 碰撞与压强气体分子之间的碰撞是气体压强产生的主要原因。

当气体分子运动速度较慢，分子之间碰撞不频繁时，气体的压强较低。

相反，当气体分子运动速度较快，分子之间碰撞频繁时，气体的压强较高。

根据气体分子动理论，气体压强与温度呈正相关，其数学关系为压强和温度的乘积与分子间平均速度的平方成正比。

3. 温度与分子速度气体分子运动的速度与气体的温度有着密切的关系。

根据气体分子动理论，气体温度与分子平均动能成正比。

换句话说，温度越高，气体分子的平均动能越大，分子的平均速度也会增加。

这也解释了为什么在相同温度下，不同气体的分子速度可能不同的原因。

例如，氢气分子较轻，根据等温分子速度公式，它的速度较大；而氮气分子较重，其速度相对较低。

4. 分子扩散与扩散速率分子扩散是气体分子运动的另一个重要现象。

根据气体分子动理论，气体分子会自发地从高浓度区域向低浓度区域扩散。

扩散速率受到多种因素的影响，如温度、分子间相互作用力以及分子质量等。

高温下的气体分子动能较大，扩散速率较快；而分子间的相互作用力越大，扩散速率越慢。

5. 分子间相互作用力气体分子间存在一定的相互作用力，这种作用力对气体性质有着重要影响。

分子间相互作用力可以分为吸引力和斥力。

对于吸引力较大的气体分子，它们的运动速度相对较慢，而分子间距离较小。

这种相互作用力称为范德华力。

相反，当气体分子间的斥力较大时，其运动速度较快，分子间距离较大，这种相互作用力被称为排斥力。

气体动理论公式总结气体动理论是研究气体运动的基本理论，涉及到气体的压力、体积、温度等性质。

在研究气态物质的行为和性质时，气体动理论公式是非常重要的工具。

本文将对一些常用的气体动理论公式进行总结和解析。

1. 状态方程公式状态方程是描述气体状态的物理方程，常见的状态方程包括理想气体状态方程和范德华方程。

理想气体状态方程：PV = nRT其中，P表示气体的压力，V表示气体的体积，n表示气体的摩尔数，R为气体常数，T表示气体的绝对温度。

范德华方程：(P + an^2/V^2)(V - nb) = nRT其中，a和b为范德华常数，和实际气体分子之间的作用有关。

2. 理想气体状态方程的推导理想气体状态方程可以通过气体分子的平均动能推导得到。

根据气体分子的平均运动能量定理，可得到以下公式：KE = (3/2)kT其中，KE表示气体分子的平均动能，k为玻尔兹曼常数，T表示气体的绝对温度。

另外，气体分子的动能与气体分子的速度和质量有关：KE = (1/2)mv^2其中，m为气体分子的质量，v为气体分子的速度。

将上述两个公式相等，可以得到：(1/2)mv^2 = (3/2)kT由此，可以推导出理想气体状态方程：PV = (1/3)Nm<v^2>其中，N为气体分子的个数，<v^2>表示气体分子速度的平方的平均值。

3. 分子平均自由程公式分子平均自由程是指气体分子在碰撞间隔期间所飞过的平均距离。

分子平均自由程与气体分子的摩尔数、体积和气体分子直径有关。

分子平均自由程的公式为：λ = (1/√2) * (V/nπd^2)其中，λ表示分子平均自由程，V表示气体的体积，n表示气体的摩尔数，d表示气体分子的直径。

4. 均方根速度公式气体分子的运动速度可以用均方根速度来描述，均方根速度是指所有气体分子速度平方的平均值的平方根。

均方根速度的公式为：v(rms) = √(3kT/m)其中，v(rms)表示气体分子的均方根速度。

气体运动理论气体是物质的一种形态，其分子在空间中自由运动并具有一定的独立性。

气体的运动行为被广泛研究，形成了气体运动理论。

本文将从分子速度分布、气体扩散、气体压强和气体温度等几个方面探讨气体运动的基本原理和相关理论。

一、分子速度分布气体分子在运动过程中具有不同的速度。

根据气体分子的速度分布可以揭示气体内部的动力学特性。

根据麦克斯韦-波尔兹曼速度分布定律，气体分子的速度服从高斯分布。

高斯分布的曲线呈钟形，其峰值对应着最常见的分子速度，而曲线两侧的尾部则表示了高速和低速分子的相对少见性。

高速分子的出现频率低于中等速度分子，而低速分子的出现频率也较低。

这一分布规律揭示了气体运动中分子速度分布的统计特性。

二、气体扩散气体扩散是指气体分子沿其浓度梯度自发传播的过程。

根据弗里克定律，气体扩散速率与气体分子的平均速度成正比，与气体分子的自由程成反比。

气体分子的平均速度越大，扩散速率越快；气体分子的自由程越小，扩散速率越慢。

气体扩散的速率还受到温度、压强和介质粘度等因素的影响。

温度升高会增加气体分子的平均速度，进而加快扩散速率；而压强升高会使气体分子更加密集，扩散速率也会相应增加。

介质的粘度越小，气体分子的碰撞频率越低，扩散速率越大。

三、气体压强气体的压强是指气体分子对容器壁面单位面积所产生的压力。

根据动理学理论，气体压强与气体分子的碰撞频率和分子速度的平均平方值成正比。

气体分子的碰撞频率与分子浓度成正比，分子速度的平均平方值与温度成正比。

因此，气体的压强与气体的浓度、温度和分子质量有关。

四、气体温度气体的温度是指气体分子运动的热度程度。

根据运动理论，气体分子的速度与温度成正比。

气体温度的单位是开尔文（K），其与摄氏度（℃）的换算关系是K = ℃ + 273.15。

绝对零度为0K，即-273.15℃，在此温度下气体分子的速度趋近于零。

随着温度的升高，气体分子的速度和能量也相应增加。

结语气体运动理论是研究气体分子运动行为的重要理论体系。

气体分子动理论气体分子动理论是指根据分子动力学原理来描述气体分子的运动和行为的理论。

它的提出和发展对于解释气体的物理性质和行为具有重要的意义。

本文将就气体分子动理论的起源、基本假设和应用等方面进行探讨。

一、气体分子动理论的起源气体分子动理论的起源可以追溯到19世纪。

在那个时候，科学家们对气体的行为和性质提出了许多疑问。

为了解释这些现象，克劳修斯和麦克斯韦等科学家开始研究气体分子的运动规律，并提出了气体分子动理论。

二、气体分子动理论的基本假设气体分子动理论的基本假设有以下几点：1. 气体分子是微小的无质量的粒子，它们之间没有相互作用。

2. 气体分子的运动是完全混乱的，没有任何规律性。

3. 气体分子之间的碰撞是弹性碰撞，即在碰撞过程中能量守恒、动量守恒。

4. 气体分子之间的平均距离远大于分子本身的大小。

这些假设为描述气体的性质和行为提供了基础。

三、气体分子动理论的应用气体分子动理论在许多方面都有广泛的应用，下面将就几个重要的应用领域进行介绍。

1. 描述气体的物态变化：根据气体分子动理论，当气体受到加热时，分子的平均动能增加，分子之间的碰撞频率和力量都会增加，从而导致气体的压强增加。

当气体受到冷却时，则相反。

2. 热力学理论的基础：气体分子动理论为热力学的发展提供了理论基础。

根据理论的推导，可以得到诸如理想气体状态方程和分子平均动能与温度的关系等重要的热力学性质。

3. 涨落理论：根据气体分子动理论，气体分子的运动是混乱的，因此气体在微观尺度上会存在一定的涨落。

这种涨落现象不仅在气体中存在，在固体和液体中也同样适用。

4. 扩散和输运现象：气体分子动理论对于扩散和输运现象的研究有很大的帮助。

通过分析气体分子的速度和运动方式，可以更好地理解扩散和输运的原理和机制。

总结：气体分子动理论是对气体分子运动和行为进行描述的理论。

它的起源可以追溯到19世纪，科学家们根据气体的性质和行为提出了基本假设，并在许多领域中得到了应用。

气体动理论知识点总结气体动理论是研究气体的微观运动状态及宏观性质的一门物理学理论，是现代物理学中较为重要的分支之一。

气体动理论不仅对实际问题的探究有着重要的作用，它的理论体系及方法也为其他学科提供了有力的支持。

下面将围绕着气体运动状态、气体的性质以及气体的热力学定律三个方面，介绍气体动理论中的相关知识点。

一、气体运动状态气体动理论认为，气体分子的运动状态决定了气体的宏观控制状态。

因此，研究气体分子的运动状态对于了解气体的性质及可控性具有重要的意义。

1.分子移动气体分子无序地、自由地运动，并且分子的速度是高度非一致性的。

分子的速度与温度、分子的种类有关。

分子受温度影响，速度随温度的升高而增加。

2.分子运动轨迹气体分子在空间中做无规则运动，但可以将其平均运动速度视为直线运动。

分子的运动具有随机性，在时间、位置上无法精确定位。

3.分子碰撞气体分子之间存在碰撞，碰撞时能量和动量都会发生变化，同时碰撞前和碰撞后分子的速度方向也会发生改变。

二、气体的性质气体的性质不仅涉及气体的物理状态，还涉及气体的化学性质，气体与其他物质的相互作用，气体的电学性质等方面，其中，最为重要的性质包括以下几个方面：1.流动性：气体具有流动性，能够流动并具有一定的流动性质。

2.扩散性：气体分子具有无序运动状态，具有自由的运动方式。

在一定条件下，气体分子能够通过物质间的空隙扩散到其他区域。

3.压缩性：气体分子间的间隔较大，气体分子之间的相互作用力较弱，分子之间可以变形并发生相对位移，气体具有较好的压缩性。

4.热膨胀性：在一定温度下，气体分子具有较大的运动能，随着温度的升高，气体分子之间的反向作用力会减小，会引起体积的增加。

5.气体的状态方程：气体在不同温度下具有不同的压强、体积关系，可以利用理想气体状态方程（P V/ nRT）来描述气体的状态。

三、气体的热力学定律气体动理论依据物理实验，建立了气体的热力学学说体系，包括状态方程、热力学过程、热力学定律等。