九年级数学等腰梯形的性质和判定

初中数学等腰梯形的性质和定理学习技巧学习初中数学中关于等腰梯形的性质和定理时，以下是一些有效的学习技巧：1.理解定义：首先确保你清楚等腰梯形的定义：等腰梯形是一组对边平行，另一组对边不平行但相等的四边形。

理解这个定义是掌握等腰梯形性质的基础。

2.掌握基本性质：等腰梯形有一些基本的性质，如两腰相等、两底平行、对角线相等、同一底上的两个角相等。

深入理解和记忆这些性质，它们将是你解题的关键。

3.学习判定定理：等腰梯形的判定定理主要有两条对角线相等的梯形是等腰梯形，以及一组对边平行，另一组对边相等的四边形是等腰梯形等。

理解这些定理的条件和结论，并能够灵活应用它们。

4.大量练习：通过做大量的练习题来巩固对等腰梯形性质和定理的理解。

从简单的题目开始，逐步挑战更复杂的题目，提升解题能力。

5.图形直观：利用图形来辅助学习。

绘制等腰梯形并标记出重要的元素（如腰、底、对角线、角等），这样可以更直观地理解等腰梯形的性质和定理。

6.关联与对比：将等腰梯形的性质与矩形、平行四边形、菱形等其他四边形进行对比和关联，找出它们之间的异同点，加深对等腰梯形知识的理解。

7.总结归纳：将学习到的等腰梯形性质和定理进行归纳整理，形成自己的知识体系。

这样可以帮助你更好地记忆和应用这些知识。

8.参与讨论：与同学或老师讨论等腰梯形相关的问题，通过交流和分享来加深对等腰梯形性质和定理的理解。

9.持续复习：定期复习等腰梯形的性质和定理，确保你能够长期记忆和应用它们。

在复习过程中，可以不断回顾和巩固之前学过的知识，形成更加完整的知识体系。

遵循这些学习技巧，你将能够更好地掌握初中数学中等腰梯形的性质和定理，提高解题能力。

初中数学知识归纳梯形的性质与判定梯形是初中数学中一个重要的几何图形，它的性质与判定常常出现在数学考试中。

本文将对梯形的性质与判定进行归纳总结，帮助初中生们更好地理解和运用梯形。

梯形的定义：梯形是一个有四边的几何图形，其中两边是平行线段，另外两边则不一定平行。

这两个平行线段被称为梯形的上底和下底，两个非平行的边被称为梯形的斜边。

梯形上底和下底之间的垂直距离被称为梯形的高。

梯形的性质与定理：1. 梯形的对角线相等：梯形的两条对角线分别连接了梯形的非相邻顶点，而这两条对角线相等。

证明：画出梯形的对角线，然后利用平行线和同位角的性质，可以证明两条对角线相等。

2. 梯形的底角和顶角互补：梯形的底角和顶角之和为180度。

证明：利用平行线和同位角的性质，可以证明底角和顶角之和为180度。

3. 等腰梯形的性质：如果一个梯形的两个腰（斜边）相等，那么这个梯形就是等腰梯形。

证明：利用等腰三角形的性质，可以证明一个梯形的两个腰相等。

4. 等腰梯形的底角相等：如果一个梯形是等腰梯形，那么这个梯形的底角相等。

证明：利用等腰三角形的性质，可以证明一个梯形的底角相等。

5. 直角梯形的性质：如果一个梯形的一个内角是直角，那么这个梯形就是直角梯形。

证明：利用直角三角形的性质，可以证明一个梯形的一个内角是直角。

梯形的判定方法：在做题时，我们有时需要通过给定条件来判定一个四边形是否是梯形。

常用的判定方法有以下几种：1. 如果一个四边形的两条对角线相等，并且底角和顶角之和为180度，那么这个四边形是梯形。

2. 如果一个四边形的两条对边都平行，并且有一对对角线相等，那么这个四边形是梯形。

3. 如果一个四边形的两条对边都平行，并且有一条边平分了另一条边，那么这个四边形是梯形。

4. 如果一个四边形的两条对边都平行，并且有一条边垂直于另一条边，那么这个四边形是梯形。

通过以上性质与判定方法，我们可以更加准确地判断和运用梯形。

在解决几何问题时，我们可以根据题目给出的条件，应用相关的性质与判定方法，灵活运用，得出正确的结论。

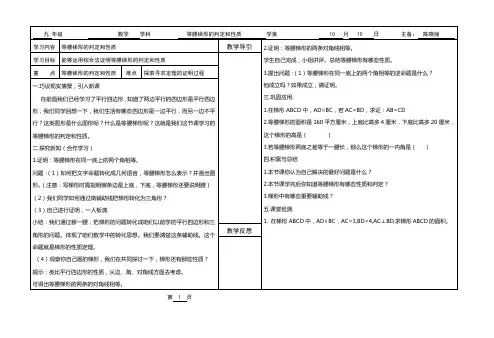
学习过程一.【预习指导】1.什么样的四边形叫梯形？2.什么样的梯形是直角梯形、等腰梯形？3.等腰梯形有哪些性质？等腰梯形有哪些判定方法？4.在研究解决梯形问题时的基本思想和方法是什么？常用的辅助线有哪几种？二.【效果检测】1. 证明定理：在同一底上的两个角相等的梯形是等腰梯形． 已知：求证：分析：本题可以从多个角度进行思考。

点拨：方法一，平移一腰，把梯形分成平行四边形和三角形，只需证AB=DE=DC 。

方法二，作梯形的两条高，证明两直角三角形全等，便可证得AB=DC 。

方法三，延长两腰，先证EB=EC,EA=ED,便可证得AB=DC 。

思考：这个定理用符号语言如何表示？感悟栏DC B A三.【小组检查】感悟栏小组内成员就上述习题进行讨论、修正。

四.【布置任务】师生互动探究问题1. “在同一底上的两个角相等的梯形是等腰梯形”的逆命题是什么？证明：等腰梯形同一底上的两底角相等。

思考：这个定理用符号语言如何表示？问题2. 等腰梯形的两条对角线相等。

思考：这个定理用符号语言如何表示？五.【小组交流】学生展示1.证明：等腰梯形同一底上的两底角相等。

2.证明：两条对角线相等的梯形是等腰梯形六.【课堂训练】拓展延伸问题3.如图等腰梯形ABCD 中，AD ∥BC ，AB=DC ,M 是AD 的中点， 求证：BM=CM思考：你能够用一个命题概括吗？拓展：（1）如图等腰梯形ABCD 中，AD ∥BC ，BM=CM 。

求证： M 是AD 的中点（2）如图梯形ABCD 中，AD ∥BC ，M 是AD 的中点，BM=CM 。

求证：四边形ABFE 是等腰梯形；七.【课堂小结】1.梯形性质和判定定理是什么？2.解决梯形问题的基本思想和方法有哪些？3.解决梯形问题时，常用的辅助线有哪几种？．4.你还有哪些困惑？B C A M D感悟栏八.【课堂反馈】 班级____________ 姓名________ 成绩____________1.四边形的四个内角的度数比是2∶3∶3∶4，则这个四边形是（ ）A.等腰梯形B.直角梯形C.平行四边形D.不能确定2.在等腰梯形ABCD 中，AD ∥BC ，AE ⊥BC 于E ，且AE=AD ，BC=3AD ，则∠B 等于（ ）A.30°B.45°C.60°D.135°3.梯形的上底长为6 cm ，将一腰平移到上底的另一端点位置后与另一腰和 下底所构成的三角形的周长为20 cm ，那么梯形的周长为_______.4.梯形ABCD 中，AD ∥BC ，∠B=50°,∠C=80°,AD=8，BC=11，则CD=____。

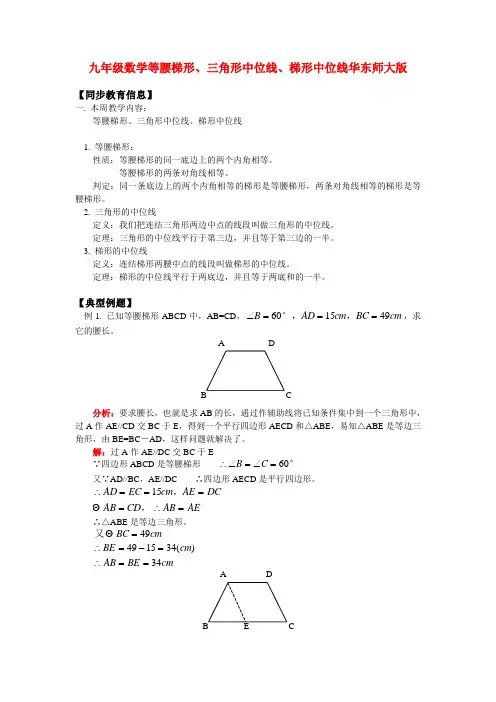
九年级数学等腰梯形、三角形中位线、梯形中位线华东师大版【同步教育信息】一. 本周教学内容：等腰梯形、三角形中位线、梯形中位线1. 等腰梯形：性质：等腰梯形的同一底边上的两个内角相等。

等腰梯形的两条对角线相等。

判定：同一条底边上的两个内角相等的梯形是等腰梯形，两条对角线相等的梯形是等腰梯形。

2. 三角形的中位线定义：我们把连结三角形两边中点的线段叫做三角形的中位线。

定理：三角形的中位线平行于第三边，并且等于第三边的一半。

3. 梯形的中位线定义：连结梯形两腰中点的线段叫做梯形的中位线。

定理：梯形的中位线平行于两底边，并且等于两底和的一半。

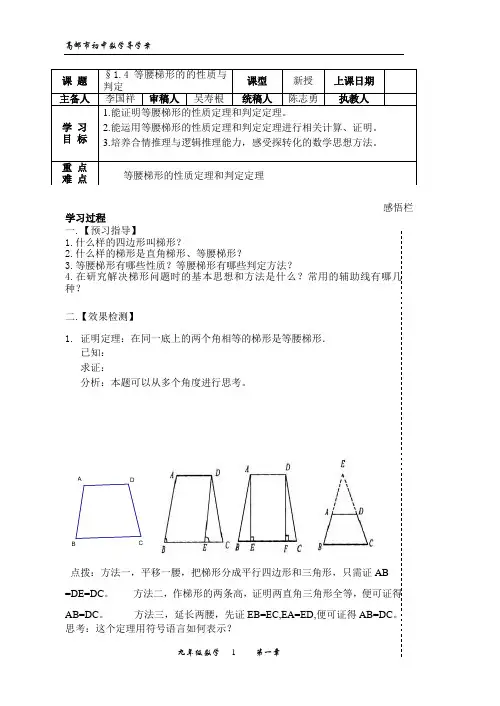
【典型例题】例1. 已知等腰梯形ABCD 中，AB=CD ，∠===B AD cm BC cm 601549°，，，求它的腰长。

A D分析：要求腰长，也就是求AB 的长，通过作辅助线将已知条件集中到一个三角形中，过A 作AE//CD 交BC 于E ，得到一个平行四边形AECD 和△ABE ，易知△ABE 是等边三角形，由BE=BC －AD ，这样问题就解决了。

解：过A 作AE//DC 交BC 于E∵四边形ABCD 是等腰梯形 ∴∠=∠=B C 60° 又∵AD//BC ，AE//DC ∴四边形AECD 是平行四边形。

∴====∴=AD EC cm AE DC AB CD AB AE15，，∴△ABE 是等边三角形。

又 BC cm =49∴=-=∴==BE cm AB BE cm49153434()A D例2. 已知：如图所示，在等腰梯形ABCD 中，对角线AC=BC+AD ，求∠DBC 的度数。

分析：由等腰梯形的性质得AC=BD ，又题设与对角线有关，考虑平移对角线BD 到AE 的位置，则∠=∠DBC E ，需求∠E ，猜想△ACE 是等边三角形。

解：过A 作AE//BD 交CB 的延长线于E ，则四边形AEBD 是平行四边形。

∴==∴=+=+=AE DB AD BECE BC BE BC AD AC，∵梯形ABCD 是等腰梯形。

中考数学专题复习第二十二讲梯形【基础知识回顾】一、 梯形的定义、分类、和面积：1、定义：一组对边平行，而另一组对边的四边形，叫做梯形。

其中，平行的两边叫做两底间的距离叫做梯形的2、分类：梯形3、梯形的面积：梯形= （上底+下底） X 高【赵老师提醒：要判定一个四边形是梯形，除了要注明它有一组对边外，还需注明另一组对边不平行或的这组对边不相等】二、等腰梯形的性质和判定：1、性质：⑴等腰梯形的两腰相等，相等⑵等腰梯形的对角线⑶等腰梯形是对称图形一般梯形特殊梯形等腰梯形：两腰 的梯形叫做等腰梯形直角梯形：一腰与底 的梯形叫做直角梯形2、判定：⑴用定义：先证明四边形是梯形，再证明其两腰相等⑵同一底上两个角的梯形是等腰梯形⑶对角线的梯形是等腰梯形【赵老师提醒：1、梯形的性质和判定中同一底上的两个角相等“不被成”两底角相等2、等腰梯形所有的判定方法都必须先证它是梯形3、解决梯形问题的基本思路是通过做辅助线将梯形转化为形式常见的辅助线作法有要注意根据题目的特点灵活选用辅助线】【重点考点例析】考点一：梯形的基本概念和性质例1 （2012•内江）如图，四边形ABCD是梯形，BD=AC且BD⊥AC，若AB=2，CD=4，则S梯形ABCD= 9．思路分析：过点B作BE∥AC交DC的延长线于点E，过点B 作BF⊥DC于点F，判断出△BDE是等腰直角三角形，求出BF，继而利用梯形的面积公式即可求解．解答：解：过点B作BE∥AC交DC的延长线于点E，过点B 作BF⊥DC于点F，则AC=BE，DE=DC+CE=DC+AB=6，又∵BD=AC 且BD⊥AC，∴△BDE是等腰直角三角形，∴BF=DE=3，故可得梯形ABCD的面积为（AB+CD）×BF=9．故答案为：9．点评：此题考查了梯形的知识，平移一条对角线是经常用到的一种辅助线的作法，同学们要注意掌握，解答本题也要熟练等腰直角三角形的性质，难度一般．对应训练1.（2012•无锡）如图，梯形ABCD中，AD∥BC，AD=3，AB=5，BC=9，CD的垂直平分线交BC于E，连接DE，则四边形ABED 的周长等于（）A．17B．18C．19D．201．考点：；．分析：由CD的垂直平分线交BC于E，根据线段垂直平分线的性质，即可得DE=CE，即可得四边形ABED的周长为AB+BC+AD，继而求得答案．解答：解：∵CD的垂直平分线交BC于E，∴DE=CE，∵AD=3，AB=5，BC=9，∴四边形ABED的周长为：AB+BE+DE+AD=AB+BE+EC+AD=AB+BC+AD=5+9+3=17．故选A．点评：此题考查了线段垂直平分线的性质．此题比较简单，注意掌握数形结合思想与转化思想的应用是解此题的关键．考点二：等腰梯形的性质例2 （2012•呼和浩特）已知：在等腰梯形ABCD中，AD∥BC，AC⊥BD，AD=3，BC=7，则梯形的面积是（）A．25B．50C．25 D．思路分析：过点D作DE∥AC交BC的延长线于点E，作DF⊥BC 于F，证平行四边形ADEC，推出AC=DE=BD，∠BDE=90°，根据等腰三角形性质推出BF=DF=EF= BE，求出DF，根据梯形的面积公式求出即可．解答：解：过点D作DE∥AC交BC的延长线于点E，∵AD∥BC （已知），即AD∥CE，∴四边形ACED是平行四边形，∴AD=CE=3，AC=DE，在等腰梯形ABCD中，AC=DB，∴DB=DE （等量代换），∵AC⊥BD，AC∥DE，∴DB⊥DE，∴△BDE是等腰直角三角形，作DF⊥BC于F，则DF=BE=5，S梯形ABCD=（AD+BC）•DF=（3+7）×5=25，故选A．点评：本题主要考查对等腰三角形性质，平行四边形的性质和判定，等腰梯形的性质，等腰直角三角形等知识点的理解和掌握，能求出高DF的长是解此题的关键．对应训练2．（2012•厦门）如图，在等腰梯形ABCD中，AD∥BC，对角线AC与BD相交于点O，若OB=3，则OC= 3．2．3考点：．分析：先根据梯形是等腰梯形可知，AB=CD，∠BCD=∠ABC，再由全等三角形的判定定理得出△ABC≌△DCB，由全等三角形的对应角相等即可得出∠DBC=∠ACB，由等角对等边即可得出OB=OC=3．解答：解：∵梯形ABCD是等腰梯形，∴AB=CD，∠BCD=∠ABC，在△ABC与△DCB中，∵,∴△ABC≌△DCB，∴∠DBC=∠ACB，∴OB=OC=3．故答案为：3．点评：本题考查的是等腰梯形的性质及全等三角形的判定与性质，熟知在三角形中，等角对等边是解答此题的关键．考点三：等腰梯形的判定例3 （2012•襄阳）如图，在梯形ABCD中，AD∥BC，E为BC的中点，BC=2AD，EA=ED=2，AC与ED相交于点F．（1）求证：梯形ABCD是等腰梯形；（2）当AB与AC具有什么位置关系时，四边形AECD是菱形？请说明理由，并求出此时菱形AECD的面积．考点：；；．分析：（1）由AD∥BC，由平行线的性质，可证得∠DEC=∠EDA，∠BEA=∠EAD，又由EA=ED，由等腰三角形的性质，可得∠EAD=∠EDA，则可得∠DEC=∠AEB，继而证得△DEC≌△AEB，即可得梯形ABCD是等腰梯形；（2）由AD∥BC，BE=EC=AD，可得四边形ABED和四边形AECD均为平行四边形，又由AB⊥AC，AE=BE=EC，易证得四边形AECD是菱形；过A作AG⊥BE 于点G，易得△ABE是等边三角形，即可求得答案AG的长，继而求得菱形AECD的面积．解答：（1）证明：∵AD∥BC，∴∠DEC=∠EDA，∠BEA=∠EAD，又∵EA=ED，∴∠EAD=∠EDA，∴∠DEC=∠AEB，又∵EB=EC，∴△DEC≌△AEB，∴AB=CD，∴梯形ABCD是等腰梯形．（2）当AB⊥AC时，四边形AECD是菱形．证明：∵AD∥BC，BE=EC=AD，∴四边形ABED和四边形AECD均为平行四边形．∴AB=ED，∵AB⊥AC，∴AE=BE=EC，∴四边形AECD是菱形．过A作AG⊥BE于点G，∵AE=BE=AB=2，∴△ABE是等边三角形，∴∠AEB=60°，∴AG=，∴S菱形AECD=EC•AG=2×=2。

1.4 等腰梯形的性质和判定学习目标1.会能证明等腰梯形的性质定理和判定定理。

2.逐步学会分析和综合的思考方法,发展思考能力。

知识详解1.性质性质定理1：等腰梯形在同一底上的两个角相等。

已知：如图，在梯形ABCD中，AD∥BC，AB＝DC。

求证：∠B＝∠C，∠A＝∠D。

证明：过点D作DE∥AB，交BC于点E，∴∠1＝∠B，∵AD∥BC，∴四边形ABED是平行四边形，∴AB＝DE，∵AB＝DC，∴DE＝DC，∴∠1＝∠C，∴∠B＝∠C，∵∠A＋∠B＝180°，∠ADC＋∠C＝180°，∴∠A＝∠ADC。

性质定理2：等腰梯形的两条对角线相等。

已知：在梯形ABCD中，AD∥BC，AB＝DC，AC、BD为梯形ABCD的对角线。

求证：AC＝DB。

证明：梯形ABCD中，AD∥BC，∵AB＝DC，∴∠ABC＝∠DCB，又∵BC ＝CB ，∴ΔABC ≌ΔDCB(SAS)，∴AC ＝DB 。

2.判定同一底上的两个角相等的梯形是等腰梯形。

已知：在梯形ABCD 中，AD ∥BC ，∠B ＝∠C 。

求证：AB ＝DC 。

证明：过点D 作DE ∥AB 交BC 于点E ，∴∠B ＝∠DEC ，∵AD ∥BC ，∴四边形ABED 是平行四边形，∴AB ＝DE ，又∵∠B ＝∠C ，∴∠DEC ＝∠C ，∴DE ＝DC ，∴AB ＝DC 。

【典型例题】例1. 如图，在等腰梯形ABCD 中，AD ∥BC ，对角线AC 、BD 相交于点O ，下列结论不一定正确的是（ ）A ．AC=BDB ．∠OBC=∠OCBC ．AOB DOC S S =△△D ．∠BCD=∠BDC【答案】D【解析】A 、∵四边形ABCD 是等腰梯形，∴AC=BD ，故本选项正确；B 、∵四边形ABCD 是等腰梯形，∴AB=DC ，∠ABC=∠DCB ，在△ABC 和△DCB 中，AB DC ABC BC CB DCB⎧⎪∠∠⎨⎪⎩＝＝＝∴△ABC ≌△DCB （SAS ），∴∠ACB=∠DBC ，∴OB=OC ，故本选项正确；C 、∵无法判定BC=BD ，∴∠BCD 与∠BDC 不一定相等，故本选项错误；D 、∵∠ABC=∠DCB ，∠ACB=∠DBC ，∴∠ABD=∠ACD ．故本选项正确．例2. 如图，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD 于点O ，AE ⊥BC ，DF ⊥BC，垂足分别为E、F，AD=4，BC=8，则AE+EF等于（）A．9B．10C．11D．12【答案】B【解析】作辅助线：延长BC至G，使DG∥AC，由AD∥BC，可知四边形ADGC为平行四边形，所以DG=AC，而等腰梯形中两对角线相等，所以DG=BD，而DF⊥BG，则△AEC为等腰直角三角形，从而得到FC=FG-AD=2，则EF=BC-2FC=8-2FC=4，所以AE+EF=6+4=10．例3. 如图，等腰梯形ABCD中，AD=5，AB=CD=7，BC=13，且CD之中垂线L交BC于P点，连接PD．求四边形ABPD的周长为何（）A．24B．25C．26D．27【答案】B【解析】∵L为中垂线，∴DP=CP，∴四边形ABPD的周长=AD+AB+BP+PD=AD+AB+BP+PC=5+7+13=25【误区警示】易错点1：理解等腰梯形判定1.如图，在等腰梯形ABCD中，AD∥BC，过C作CE∥AB，P为梯形ABCD内一点，连接BP并延长交CD于F，交CE于E，再连接PC，已知BP=PC，则下列结论中错误的是（）A．∠1=∠2B．∠2=∠EC．△PFC∽△PCED．△EFC∽△ECB【答案】D【解析】∵ABCD是等腰梯形，∴∠ABC=∠DCB，∵BP=CP，∴∠PBC=∠PCB，∴∠1=∠2（A 正确），∵CE∥AB，∴∠1=∠E，∴∠2=∠E（B正确），∵∠P=∠P，∠2=∠E，∴△PFC∽△PCE（C正确）．易错点2：理解等腰梯形性质2.如图所示，等腰梯形ABCD中，AD∥BC，BD⊥DC，点E是BC边的中点，ED∥AB，则∠BCD 等于（）A．30°B．70°C．75°D．60°【答案】D【解析】已知四边形ABCD为等腰梯形，故AB=DC．∵AD∥BC，ED∥AB，∴四边形ABED是平行四边形，∴DE=AB，∴DE=CD，∵BD⊥DC，点E是BC边的中点，∴DE=BE=CD，∴BE=ED=EC=DC，故△DCE为等边三角形，∴∠BCD=60°【综合提升】针对训练1. 如图是用若干个全等的等腰梯形拼成的图形，下列说法错误的是（）A．梯形的下底是上底的两倍B．梯形最大内角是120°C．梯形的腰与上底相等D．梯形的底角是60°2. 如图，小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形，则图中∠α的度数是（）A．60°B．55°C．50°D．45°3. 下列命题：①平行四边形对角线一定相等；②等腰梯形在同一底上的两个角相等；③四边形的内角和等于360°；④关于中心对称的两个图形是全等形．其中正确命题的个数有（）A．1个B．2个C．3个D．4个1.【答案】D【解析】由图可知，较小的底角的3倍=180°，从而可得到较小的底角为60度，则最大的角为120°（B正确），过上底顶点作下底上的高，则可证得，梯形的腰等于其上底（C正确），2.【答案】A【解析】观察可看出，菱形的边长和对角线都等于下底与腰的和，所以∠α=60°，故选A．3.【答案】C【解析】平行四边形对角线不一定相等，故此项错误；其它三个均可由等腰梯形的性质，多边形的内角公式及中心对角的性质得到，所以正确的是：②；③；④共三个，故选C．课外拓展商高定理这个定理在中国又称为"商高定理"，在外国称为"毕达哥拉斯定理"。

九年级数学等腰梯形的性质和判定教学反思本节课的教学目标是掌握梯形、等腰梯形、直角梯形的有关概念;逐步学会分析和综合的思考方法，发展合乎逻辑的思考能力;经历对操作活动的合理性进行证明的过程，不断感受证明的必要性、感受合情推理和演绎推理都是人们正确认识事物的重要途径;能够运用等腰梯形的性质和判定进行有关问题的论证和计算，进一步培养学生的分析能力和计算能力。

本节的教学重点等腰梯形的性质和判定。

教学难点是通过添加辅助线把梯形的问题转化成平行四边形或三角形问题，使学生体会图形变换的方法和转化的思想。

等腰梯形的性质与判定定理的证明仅止于合情推理，但学生对梯形的题型中辅助线的添加已有了初步的认识，因此在教学设计中通过探索并证明梯形的性质与判定这些重要结论，从学生已有的知识水平出发，通过在同一梯形中不同类型辅助线的添加，不仅让学生理解等腰梯形的性质与判定定理，又让学生感觉通过添加辅助线，将梯形的问题转化成平行四边形或三角形问题，体现所学知识与已学知识的密切联系。

同时也让学生体验一题多解的乐趣，开阔学生的视野，提高解题的能力。

本节课始终以学生为中心，教师作为教学活动的组织者，引导者，合作者，体会用类比的思想研究腰梯形的性质和判定，体验研究数学问题的常用方法：由特殊到一般，由简单到复杂，体现“动手实践，自主探索。

合作交流是学生学习数学的重要方式”这一思想，教学中为学生创造大量的操作。

思考和交流的机会，关注学生思考问题的过程，鼓励学生在探索规律的过程中从多个角度进行考虑，培养学生主动探索，敢于实践，善于发现的科学精神以及合作精神，树立创新意识，品尝成功的喜悦，激发学生应用数学的热情。

因此，本节课的教学任务进行的很顺利，学生的学习积极性与参与度极高。

本节课进行中，个别学生的思路较奇特，由于出乎我的意料，方法也不是较简单，故我只是肯定了他们的做法，课后感觉我太吝啬对学生评价了。

学生有些地方做得很好，不能“好”或者“这种方法也可以”简单带过，这样无形中扼杀了孩子的一些很有创造性的想法，也降低了孩子们思考的积极性。