直角三角形的边角关系知识点

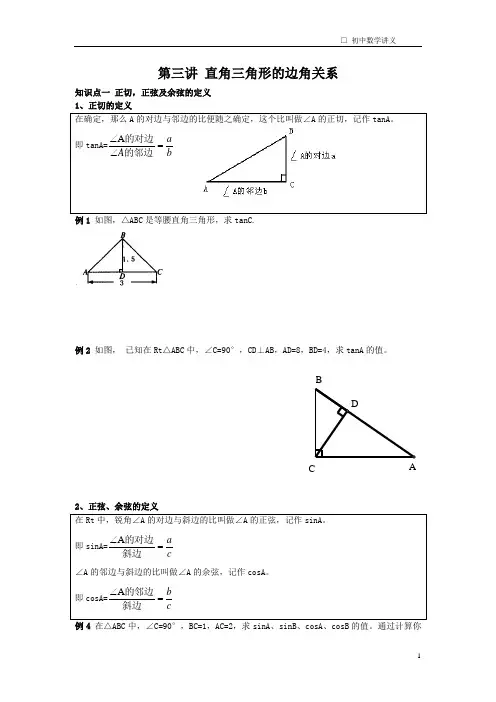
第三讲 直角三角形的边角关系知识点一 正切，正弦及余弦的定义1、正切的定义的对边与邻边的比便随之确定，这个比叫做∠A 的正切，记作例1 如图，△ABC 是等腰直角三角形，求tanC.例2 如图， 已知在Rt △ABC 中，∠C=90°，CD ⊥AB ，AD=8，BD=4，求tanA 的值。

C B A有什么发现？请加以证明。

3、三角函数的定义（重点）能判断谁的木棒更陡吗？说明理由。

同步练习：1、∠C=90°，点D 在BC 上，BD=6，AD=BC ，cos ∠ADC=53，求CD 的长。

2、P 是a 的边OA 上一点，且P 点的坐标为（3，4），求sina 、tana 的值。

3、在△ABC 中，D 是AB 的中点，DC ⊥AC ，且tan ∠BCD=31，求tanA 的值。

4、在Rt △ABC 中，∠C=90°，tanA=125，周长为30，求△ABC 的面积。

5、（2008·浙江中考）在Rt △ABC 中，CD 是斜边AB 上的中线，已知CD=2，AC=3，则sinB 的值是多少？知识点二 30°，45°，60°角的三角函数值例 求下列各式的值。

（1）︒︒-︒60tan 30sin 60sin ；（2）︒-+︒-︒45sin 22460tan 460tan 2。

同步练习：1、 求下列各式的值。

（1）︒+︒+︒45tan 30tan 330sin 2； （2）︒⋅︒+︒30cos 60tan 45cos 2。

(3) 6tan 2 30°－3sin 60°＋2tan45°(4)022)30tan 45(sin )60cos (160sin 260sin 60tan 245tan o o o o o oo-+-++----2、 已知a 为锐角，且tana=5，求aa aa sin cos 2cos 3sin +-的值。

直角三角形的边角关系知识点一、勾股定理勾股定理是指在直角三角形中，直角边的平方等于两个其他两边平方的和。

即a^2+b^2=c^2，其中c表示直角边，a和b分别表示斜边。

二、正弦定理正弦定理是指在任意三角形中，任意两边的比例等于它们所对的角的正弦值的比例。

在直角三角形中，不包含直角的两个角分别为A和B，直角所对的边为c，则正弦定理可以表示为sinA=a/c，sinB=b/c。

三、余弦定理余弦定理是指在任意三角形中，任意一边的平方等于另外两边的平方和减去它们的两倍乘以它们夹角的余弦。

在直角三角形中，不包含直角的两个角分别为A和B，直角边所对的边为c，则余弦定理可以表示为cosA=b/c，cosB=a/c。

四、正切定理正切定理是指在任意三角形中，两条边的比例等于它们所对的角的正切值的比例。

在直角三角形中，不包含直角的两个角分别为A和B，直角所对的边为c，则正切定理可以表示为tanA=a/b，tanB=b/a。

五、边角关系1.直角三角形中，一个角是90度，另外两个角的和是90度。

2.直角三角形中，直角边所对的角是90度，而另外两边所对的角是锐角。

3.直角三角形中，两个锐角的正弦、余弦、正切值彼此互为倒数。

4.直角三角形中，两个锐角的余弦值等于彼此的正弦值。

5.直角三角形中，一个锐角的正弦值等于另一个锐角的余弦值。

六、特殊三角形1.在直角三角形中，当两个直角边的长度相等时，该直角三角形为等腰直角三角形。

2.在等腰直角三角形中，两个锐角相等，且为45度。

3.在等腰直角三角形中，斜边的长度等于直角边的平方根的两倍。

以上是直角三角形的边角关系的主要知识点。

通过对直角三角形的边长和角度关系的了解，我们可以应用这些关系来解决与直角三角形相关的问题。

同时，直角三角形也是三角学中一个重要的基础概念，为后续学习提供了坚实的基础。

边角关系知识点总结1. 任意三角形的边角关系：（1）在任意三角形中，三个内角的和等于180°，即A + B + C = 180°。

（2）三角形的外角等于其不相邻的两个内角的和。

也就是说，三角形的一个内角加上其对边的外角等于180°。

（3）在任意三角形中，任意两边之和大于第三边。

即AB + BC > AC、AC + BC > AB、AB + AC > BC。

2. 直角三角形的边角关系：（1）直角三角形的三个内角中，一个为90°，一个为锐角，一个为钝角。

（2）直角三角形的斜边是其它两条边的平方和的平方根。

即c² = a² + b²。

（3）直角三角形的两个锐角互余，即一个角的余角是另一个角。

3. 等腰三角形的边角关系：（1）等腰三角形的底边相等，顶角相等。

（2）等腰三角形的底角相等，顶角相等。

（3）等腰三角形的底边上的高相等。

4. 等边三角形的边角关系：（1）等边三角形三个内角相等，每个角都是60°。

（2）等边三角形的三条边相等。

（3）等边三角形的高、中线、角平分线、垂径都是同一条线段。

5. 直角三角形、等腰三角形和等边三角形的区别：（1）直角三角形有一个角是90°，等腰三角形和等边三角形没有。

（2）等腰三角形有两条边相等，直角三角形和等边三角形没有。

（3）等边三角形的三条边都相等，直角三角形和等腰三角形没有。

6. 三角形的角平分线：（1）三角形的角平分线是指从三角形的一个角的顶点出发，把这个角平分成两个相等的角的线段。

（2）三角形的三个角都各有一条角平分线。

（3）角平分线和对边的比例关系：AB/BD = AC/CD。

7. 外接角和内切角：（1）外接角：指与三角形的外角相对应的一个角，外接角等于两个不相邻内角的和。

（2）内切角：指与三角形的内角相对应的一个角，内切角等于两个不相邻外角的和。

8. 三角形的全等条件：（1）两个三角形的三边全相等，则这两个三角形全等。

直角三角形边角关系专题复习一. 知识体系：1. 三种三角函数与直角三角形中边与角的关系，在Rt△中在此应注意的问题是无论是求哪一个角的三角函数，一定要先把这个角放在直角三角形中 2. 特殊角的三角函数值3. 三角函数的有关计算（对于一般角的三角函数值可利用计算器）41 2 3 4.三角函数的应用（）测山的高度（）测楼的高度（）测塔的高度（）其它⎧⎨⎪⎪⎩⎪⎪题型一：三角形内的计算问题（计算三角函数值、面积等） 例1．在ABC Rt ∆中，∠C=90° ，且21sin =A ，AB=3，求BC ，AC 及B ∠.例2．已知，四边形ABCD 中，∠ABC = ∠ADB =090，AB = 5，AD = 3，BC = 32，求四边形ABCD 的面积。

例3．如图，在Rt ABC ∆中，90BCA ∠=︒，CD 是中线，5,4BC CD ==，求AC 的长。

B变式训练：1、ABC Rt ∆中，∠C=90°，AC=4，BC=3，B cos 的值为…………………【 】 A 、51 B 、53 C 、 34 D 、 432、在菱形ABCD 中，∠ABC=60° ， AC=4，则BD 的长是…………………【 】 A 、 38 B 、34 C 、32 D 、83、在ABC Rt ∆中，∠C=90° ，A tan =3，AC=10，则S △ABC 等于………【 】 A 、 ３ B 、３00 C 、350D 、1５0 4、在Rt △ABC 中，如果各边长度都扩大为原来的2倍，那么锐角A 的正弦值（ ） A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化5、在ABC Rt ∆中，∠C=90°，∠A 、∠B 、∠C 的对边分别为a 、b 、c 三边，则下列式子一定成立的是………………………………………………………………【 】 A 、B c a sin ⋅= B 、B c a cos ⋅= C 、Bac tan =D 、A a c sin ⋅= 6、等腰三角形的腰长为10cm ，顶角为120，此三角形面积为 。

直角三角形的边角关系知识点1：锐角三角函数一、知识点讲解： 1．锐角三角函数的概念：锐角三角函数包括正弦函数，余弦函数，和正切函数，如图1－1－1，在Rt △ABC 中，∠C ＝90°，∠A 、∠B 、∠C 的对边分别为a 、b ，c ． ∠A 的正弦=A asin A=c∠的对边，即斜边；∠A 的余弦=A b cos A=c∠的邻边，即斜边,∠A 的正切=A a tan=A b∠的对边，即∠的邻边注：三角函数值是一个比值．2．特殊角是指0°，30°，45°，60°，90°的角． 3．特殊角的三角函数值．4．互为余角的三角函数关系．sin （90○－A ）=cosA ， cos （90○－A ）=sin A tan （90○－A ）= cotA cot （90○－A ）=tanA 5．同角的三角函数关系． ①平方关系：sin 2 A+cos 2A=l ②倒数关系：tanA ×cotA=1③商数关系：sin cos tan ,cot cos sin A AA A A A==④sin cos 12sin cos a a a a +=+ ⑤222tan cot (tan cot )2a a a a +=+- 二、经典例题讲解： 类型一、关于特殊的函数值 例题1、计算：()()013222sin 60-︒-+-+⋅（结果保留根号．．．．．．）中考典练1： 024cos 458(3)(1)π-+++-分值6分中考典练2：2(tan 301)____-= 中考典练3：13tan 60|2|22-+-+例题2、 2sin60°－cos30°·tan45°的结果为（ ） A 、 3 33. .22B C -D ．0 例题3、等腰直角三角形一个锐角的余弦为（ ） A 、12 32. .22B C D ．l 例4、点M(tan60°，－cos60°）关于x 轴的对称点M ′的坐标是（ ） 1111.(3,); .(3,); .(3,) .(3,)2222A B C D ----例5、在锐角△ABC 中，如果2sinC=sin90°，则∠C=__。

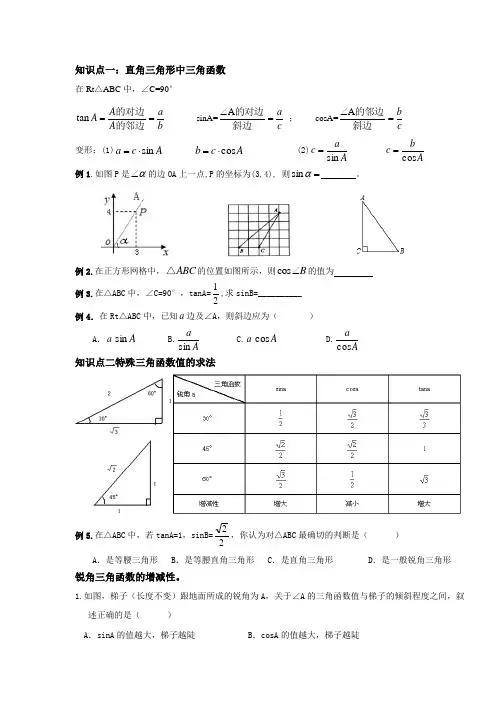
知识点一：直角三角形中三角函数在Rt △ABC 中，∠C=90°b a A A A ==的邻边的对边tan sinA=c a =∠斜边的对边A ； cosA=cb =∠斜边的邻边A 变形：(1)Ac a sin ⋅= A c b cos ⋅= (2)A a c sin = A b c cos = 例1.如图P 是α∠的边OA 上一点,P 的坐标为(3,4), 则=αsin 。

例2.在正方形网格中，ABC △的位置如图所示，则cos B ∠的值为例3.在△ABC 中，∠C=90°，tanA=21,求sinB=__________ 例4．在Rt △ABC 中，已知a 边及∠A ，则斜边应为（ ）A ．a A sin B.Aa sin C.a A cos D.A a cos 知识点二特殊三角函数值的求法例5.在△ABC 中，若tanA=1，sinB=22，你认为对△ABC 最确切的判断是（ ） A ．是等腰三角形 B ．是等腰直角三角形 C ．是直角三角形 D ．是一般锐角三角形 锐角三角函数的增减性。

1.如图，梯子（长度不变）跟地面所成的锐角为A ，关于∠A 的三角函数值与梯子的倾斜程度之间，叙述正确的是（ ）A ．sinA 的值越大，梯子越陡B ．cosA 的值越大，梯子越陡C ．tanA 的值越小，梯子越陡D ．陡缓程度与∠A 的函数值无关2.（2011•茂名）如图，已知45°＜A ＜90°，则下列各式成立的是（ ）A ．sinA=cosA B.sinA ＞cosA C.sinA ＞tanA D.sinA ＜cosA3.若23cos 0<<α，则锐角α的取值范围是( ) A.︒<<︒300α B. ︒>30α C. ︒<<︒6030α D. ︒<<︒9030α 解直角三角形：在直角三角形中，已知一些边、角，求出另一些边、角的过程Rt △ABC 中，∠C=90°，∠A 、∠B 、∠C 所对的边分别为c b a 、、。

DSE 金牌数学专题系列 经典专题系列直角三角形边角关系一、 导入二、 知识点回顾 （一）、基础知识1．锐角三角函数定义在直角三角形ABC 中，∠C=900，设BC=a ，CA=b ，AB=c ，锐角A 的四个三角函数是： (1) 正弦定义：∠A 的正弦=A a sin A=c∠的对边，即斜边； （2）余弦的定义：∠A 的余弦=A b cos A=c∠的邻边，即斜边 ,（3）正切的定义：∠A的正切=A a tan=A b∠的对边，即∠的邻边这种对锐角三角函数的定义方法，有两个前提条件：（1）锐角∠A 必须在直角三角形中，且∠C=900；（2）在直角三角形 ABC 中，每条边均用所对角的相应的小写字母表示。

否则，不存在上述关系 2、坡角与坡度:①坡面的铅直高度h 与水平宽度l 的比为坡度（或坡比），用字母i 表示，即i=hl，坡面与水平夹角α叫 坡角 ，即坡度等于坡角的正切（tan α= i ）。

②工程上斜坡的倾斜程度通常用坡度来表示，坡面的铅直高度h 与水平宽度l 的比为坡度（或坡比），坡度是坡角的正切，坡度越大，坡面越陡 3、锐角三角函数关系：(1) 互为余角的三角函数关系．若∠A+∠B=∠90，则sinA=cosB,cosA=sinB.即：sin （90○－A ）=cosA ， cos （90○－A ）=sin Atan （90○－A ）= cotA cot （90○－A ）=tanA (2) 同角的三角函数关系．①平方关系：sin 2 A+cos 2A=l ②倒数关系：tanA ×cotA=1③商数关系：sin cos tan ,cot cos sin A AA A A A==00 300 450 600sin A 0 2122 22 cos A 1 22 2221tan A331 3(1) 同名三角函数的大小比较①正弦、正切是增函数．三角函数值随角的增大而增大，随角的减小而减小． ②余弦、余切是减函数．三角函数值随角的增大而减小，随角的减小而增大。

直角三角形的边角关系知识点总结
嘿，宝子们！今天咱就来好好唠唠直角三角形的边角关系知识点，这可真是超级重要的呢！
咱先说说正弦吧。

正弦就是一个角的对边与斜边的比值哟！比如说，在
一个直角三角形里，那个角就像是我们努力的方向，对边就是我们朝着这个方向前进的距离，斜边呢就是总的路程。

就像你考试想拿高分，那高分就是你的“角”，你努力学习的成果就是对边，而整个学习的过程就是斜边呀！
还有余弦呢！余弦是邻边与斜边的比值。

可以把它想象成在一个团队里，邻边就是你身边一起努力的小伙伴，斜边依然是整个团队的力量。

是不是一下子就好理解啦？
正切就更有意思啦！正切是对边与邻边的比值。

就像是一场比赛中你的
速度和竞争对手速度的比较。

好比你和朋友一起跑步，你跑过的距离和你旁边朋友跑过的距离之比，这就是正切呀！
在直角三角形中，这些边角关系可太有用啦！知道这些，咱就能解决好
多实际问题呢！比如说，工程师盖房子的时候，就需要用这些知识来确保房子的结构稳定呀！
学习直角三角形的边角关系就像是打开了一扇通往数学奇妙世界的大门！能让我们更清楚地看到世界的规律和美好。

大家一定要好好掌握哟！我的观点就是，直角三角形的边角关系是数学中非常重要且有趣的一部分，我们一定要深入理解和运用它！。

第七讲 直角三角形的边角关系一、知识点快速归纳理解：考点一、直角三角形的性质 1、直角三角形的两个锐角互余可表示如下：∠C=90°⇒∠A+∠B=90°2、在直角三角形中，30°角所对的直角边等于斜边的一半。

∠A=30°可表示如下： ⇒BC=21AB ∠C=90°3、直角三角形斜边上的中线等于斜边的一半 ∠ACB=90°可表示如下： ⇒CD=21AB=BD=AD D 为AB 的中点 4、勾股定理直角三角形两直角边a ，b 的平方和等于斜边c 的平方，即222c b a =+ 5、射影定理在直角三角形中，斜边上的高线是两直角边在斜边上的摄影的比例中项，每条直角边是它们在斜边上的摄影和斜边的比例中项∠ACB=90° BD AD CD •=2⇒ AB AD AC •=2CD ⊥AB AB BD BC •=2 6、常用关系式由三角形面积公式可得：AB •CD=AC •BC考点二、直角三角形的判定1、有一个角是直角的三角形是直角三角形。

2、如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

3、勾股定理的逆定理如果三角形的三边长a ，b ，c 有关系222c b a =+，那么这个三角形是直角三角形。

考点三、锐角三角函数的概念 1、如图，在△ABC 中，∠C=90°①锐角A 的对边与斜边的比叫做∠A 的正弦，记为sinA ，即casin =∠=斜边的对边A A②锐角A 的邻边与斜边的比叫做∠A 的余弦，记为cosA ， 即cbcos =∠=斜边的邻边A A③锐角A 的对边与邻边的比叫做∠A 的正切，记为tanA ，即b atan =∠∠=的邻边的对边A A A④锐角A 的邻边与对边的比叫做∠A 的余切，记为cotA ，即abcot =∠∠=的对边的邻边A A A2、锐角三角函数的概念锐角A 的正弦、余弦、正切、余切都叫做∠A 的锐角三角函数 3、一些特殊角的三角函数值 三角函数 0° 30°45°60° 90° sinα21 22 23 1cos α 123 22 21 0tan α 0 33 13不存在cot α 不存在 3133 04、各锐角三角函数之间的关系（1）互余关系： sinA=cos(90°—A)，cosA=sin(90°—A)tanA=cot(90°—A)，cotA=tan(90°—A) （2）平方关系： 1cos sin 22=+A A （3）倒数关系： tanA •tan(90°—A)=1 （4）弦切关系： tanA=AAcos sin 5、锐角三角函数的增减性 当角度在0°~90°之间变化时， （1）正弦值随着角度的增大（或减小）而增大（或减小） （2）余弦值随着角度的增大（或减小）而减小（或增大） （3）正切值随着角度的增大（或减小）而增大（或减小） （4）余切值随着角度的增大（或减小）而减小（或增大） 考点四、解直角三角形 1、解直角三角形的概念2、解直角三角形的理论依据在Rt △ABC 中，∠C=90°，∠A ，∠B ，∠C 所对的边分别为a ，b ，c（1）三边之间的关系：222c b a =+（勾股定理） （2）锐角之间的关系：∠A+∠B=90° （3）边角之间的关系：ba B ab Bc a B c b B a b A b a A c b A c a A ========cot ,tan ,cos ,sin ;cot ,tan ,cos ,sin二、知识点练习题方式方法及技巧渗透1．如图，小颖利用有一个锐角是30°的三角板测量一棵树的高度，已知她与树之间的水平距离BE 为5m ，AB 为1.5m （即小颖的眼睛距地面的距离），那么这棵树高是（ ） A ．（53332+）m B ．（3532+）m C ． 533m D ．4m 2．如图，在等腰Rt △ABC 中，∠C =90o ，AC =6，D 是AC 上一点，若tan ∠DBA =51，则AD 的长为（ ） （A ） 2 （B ）3 （C ）2 （D ）13．已知在ABC △中，90C ∠=o，设sinB n =，当B ∠是最小的内角时，n 的取值范围是（ ）A ．202n <<B ．102n << C ．303n << D ．302n << 4．如图，小正方形的边长都为1，A 、B 、C 是小正方形的顶点，则∠ABC 的度数为（ ）A ．90°B ．60°C ．45°D ．30°5．如图，已知一商场自动扶梯的长z 为10米，该自动扶梯到达的高度h 为6米，自动扶梯与地面所成的角为θ，则tan θ的值等于( )6．如图，矩形ABCD 中，AB ＞AD ，AB =a ，AN 平分∠DAB ，DM ⊥AN 于点M ，CN ⊥AN 于点N ．则DM +CN 的值为（用含a 的代数式表示）( )A ．aB ．a 54C ．a 22D ． a 23 7．在△ABC 中，∠C ＝90°，sinA ＝45，则tanB ＝ （ ） A ．43 B ．34 C ．35 D ．458．在正方形网格中，ABC △的位置如图所示，则cos B ∠的值为（ ）A ．12B ．22C ．32D ．33aNM CDAB（第6题）BA ED C30°第1题第2题CA第4题图第5题图9．计算2sin 45°的结果等于（ ）A ．2B ．1C ．22 D ．21 10．在Rt △ABC 中,∠C=90°,若AC=2BC,则sin A 的值是( )A ．12B ．2C ．5D ．5 11．在Rt △ABC 中，∠C=90°，sinA=54，则cosB 的值等于（ ） A ．53 B. 54 C. 43D. 5512．在△ABC 中，∠C ＝90°，sinA ＝45，则tanB ＝（ ） A ．43 B ．34 C ．35 D ．4513．在7,35,90,==∠=∠∆AB B C ABC Rt οο中，则BC 的长为 （ ）（A ）ο35sin 7（B ）ο35cos 7（C ）ο35cos 7 （D ）．ο35tan 714．如上右第9题图，在梯形ABCD 中，AD//BC ，AC ⊥AB ，AD=CD 54cos =∠DCA ，BC=10，则AB 的值是（ ） A ．9 B ．8 C ．6 D ．315．如图，小明为了测量其所在位置A 点到河对岸B 点之间的距离，沿着与AB 垂直的方向走了m 米，到达点C ，测得∠ACB ＝α，那么AB 等于（ ）(A) m ·sin α米 (B) m ·tan α米 (C) m ·cos α米 (D) αtan m米16．如图，△ABC 的三个顶点分别在正方形网格的格点上，则A ∠tan 的值是 （ ）A ．56 B ．65 C ．3102 D ．1010317．sin30︒的值等于 （ ） （A ）12（B ）2 （C ）3 （D ）118．已知在Rt ABC △中，390sin 5C A ∠==°，，则tan B 的值为（ ） A ．43B ．45C ．54D ．3419．如图，为测量一幢大楼的高度，在地面上距离楼底O 点20 m 的点A 处，测得楼顶B 点的仰角∠OAB A BC m α(第15题图)D BC E ＝65°，则这幢大楼的高度为 （ ） （结果保留3个有效数字）． （A ）42.8 m（B ）42.80 m （C ）42.9 m （D ）42.90 m20．如图，在正方形ABCD 中，O 是CD 边上一点，以O 为圆心，OD 为半径的半圆恰好与以B 为圆心，BC 为半径的扇形的弧外切，则∠OBC 的正弦值为 ．21．如图，已知直线1l ∥2l ∥3l ∥4l ，相邻两条平行直线间的距离都是1，如果正方形ABCD 的四个顶点分别在四条直线上，则sin α= ．22．已知：如图，梯形ABCD 中，AB//CD ，∠A=600 ，AD=5cm ，DC=6cm ，AB=10cm 。