串联电路的等效电阻

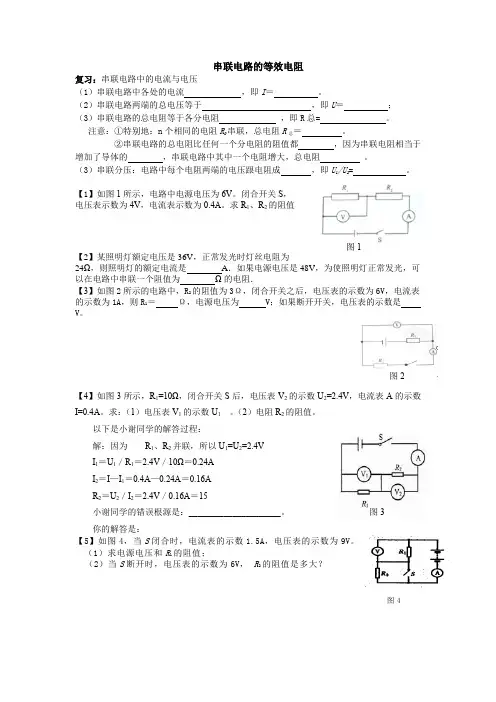
串联电路的等效电阻复习：串联电路中的电流与电压（1）串联电路中各处的电流 ，即I ＝ 。

（2）串联电路两端的总电压等于 ，即U ＝ ；（3）串联电路的总电阻等于各分电阻 ，即R 总= 。

注意：①特别地：n 个相同的电阻R 0串联，总电阻R 总＝ 。

②串联电路的总电阻比任何一个分电阻的阻值都 ，因为串联电阻相当于增加了导体的 ，串联电路中其中一个电阻增大，总电阻 。

（3）串联分压：电路中每个电阻两端的电压跟电阻成 ，即U 1/U 2= 。

【1】如图1所示，电路中电源电压为6V 。

闭合开关S ，电压表示数为4V ，电流表示数为0.4A 。

求R 1、R 2的阻值【2】某照明灯额定电压是36V ，正常发光时灯丝电阻为24Ω，则照明灯的额定电流是 A ．如果电源电压是48V ，为使照明灯正常发光，可以在电路中串联一个阻值为 Ω的电阻．【3】如图2所示的电路中，R 2的阻值为3Ω，闭合开关之后，电压表的示数为6V ，电流表的示数为1A ，则R 1＝ Ω，电源电压为 V ；如果断开开关，电压表的示数是 V 。

【4】如图3所示，R 1=10Ω，闭合开关S 后，电压表V 2的示数U 2=2.4V ，电流表A 的示数I=0.4A 。

求：（1）电压表V 1的示数U 1 。

（2）电阻R 2的阻值。

以下是小谢同学的解答过程：解：因为 R 1、R 2并联，所以U 1=U 2=2.4VI 1＝U 1／R 1＝2.4V ／10Ω＝0.24AI 2＝I —I 1＝0.4A —0.24A ＝0.16AR 2＝U 2／I 2＝2.4V ／0.16A ＝15小谢同学的错误根源是：_____________________。

你的解答是：【5】如图4，当S 闭合时，电流表的示数1.5A ，电压表的示数为9V 。

（1）求电源电压和R 1的阻值；（2）当S 断开时，电压表的示数为6V ， R 2的阻值是多大？图2图1图3 图4。

串并联电路中的等效电阻计算公式串联电路中的等效电阻计算公式：在串联电路中，多个电阻连在一起，电流依次通过每个电阻。

电阻的总和即为等效电阻，用来表示整个电路的总阻力。

在串联电路中，电流恒定，即通过每个电阻的电流相等。

根据欧姆定律，电阻的电压与电流成正比。

因此，可以通过串联电阻的电压和电流来计算等效电阻。

设有 n 个串联电阻，每个电阻的阻值分别为 R₁, R₂, ..., Rₙ，则串联电路的等效电阻 R_eq 的计算公式为：R_eq = R₁ + R₂ + ... + Rₙ并联电路中的等效电阻计算公式：在并联电路中，多个电阻分别连接在电路的不同分支上，电压相同，电流分成多个支路。

并联电路的等效电阻用来表示整个电路的总阻力。

在并联电路中，电压恒定，即每个电路分支的电压相等。

根据欧姆定律，电流与电阻成反比。

因此，可以通过并联电阻的电流和电压来计算等效电阻。

设有 n 个并联电阻，每个电阻的阻值分别为 R₁, R₂, ..., Rₙ，则并联电路的等效电阻 R_eq 的计算公式为：1/R_eq = 1/R₁ + 1/R₂ + ... + 1/Rₙ等效电阻的实际应用：1.简化复杂电路：等效电阻可以将复杂的电路简化为一个电阻，方便计算和分析整个电路的特性。

2.增加电路的性能：通过调整等效电阻的值，可以改变电路的总阻力，从而实现对电路性能的控制。

3.电阻的替代：等效电阻可以用来替代一组电阻，使得电路更为简单且易于设计。

4.电阻的合并：等效电阻可以将多个电阻合并为一个，减少电路元件的数量和占用空间。

总结：串联电路的等效电阻可通过将每个电阻的阻值相加得到，而并联电路的等效电阻可通过将每个电阻的倒数相加，再取倒数得到。

等效电阻的计算公式是在电路分析和计算中的基础，能够简化复杂电路的分析和设计过程，同时也能够优化电路的性能。

电阻电路中的等效电阻与等效电源计算1. 引言电阻电路是电子电路中最基本的部分之一，对于理解电路的行为和性能起着关键作用。

在分析电阻电路时，常常需要计算等效电阻和等效电源，以简化电路的复杂性。

本文将介绍电阻电路中的等效电阻与等效电源的计算方法。

2. 等效电阻的计算等效电阻是指将一个复杂的电路替换为一个简单的电路，使得两个电路在任何外部测量或连接条件下都有相同的电流-电压特性。

计算等效电阻的方法有以下几种：（1）串联电阻的等效电阻：在电路中，若存在多个串联的电阻，则它们的等效电阻可以简单地通过相加来计算。

即等效电阻 Requ = R1 + R2 + ... + Rn。

其中，R1, R2, ..., Rn 为串联电阻的阻值。

（2）并联电阻的等效电阻：在电路中，若存在多个并联的电阻，则它们的等效电阻可以通过公式 1/Requ = 1/R1 + 1/R2 + ... + 1/Rn 来计算。

即等效电阻 Requ = 1 / (1/R1 + 1/R2 + ... + 1/Rn)。

其中，R1, R2, ..., Rn 为并联电阻的阻值。

（3）复杂电路中的等效电阻：对于复杂的电路，可以根据网络分析方法，使用基尔霍夫定律、戴维南定理等进行分析和计算，以得到等效电阻。

3. 等效电源的计算等效电源是指将一个复杂的电路替换为一个简单的电源，使得两个电路在任何外部测量或连接条件下都有相同的电流-电压特性。

计算等效电源的方法有以下几种：（1）串联电源的等效电源：在电路中，若存在多个串联的电源，则它们的等效电源可以简单地通过相加来计算。

即等效电源 Veq = V1 + V2 + ... + Vn。

其中，V1,V2, ..., Vn 为串联电源的电压值。

（2）并联电源的等效电源：在电路中，若存在多个并联的电源，则它们的等效电源可以简单地通过相加来计算。

即等效电源 Veq = V1 = V2 = ... = Vn。

其中，V1,V2, ..., Vn 为并联电源的电压值。

电路等效电阻的求法
要求电路的等效电阻，可以通过以下三种方法进行计算：
1.串/并联电阻公式：对于串联电路，各个电阻之间是顺序连接，因此串联电路的等效电阻等于各个电阻的总和。

即R_eq
= R1 + R2 + R3 + ...。

对于并联电路，各个电阻之间是并列连接，因此并联电路的等效电阻按照倒数的方式计算。

即
1/R_eq = 1/R1 + 1/R2 + 1/R3 + ...
2.电路简化：对于复杂的电路，可以通过简化电路的方法计算
等效电阻。

根据电路中的对称性和平行性，可以将一些电阻合并为等效电阻，从而简化电路，最终求得等效电阻。

这种方法适用于对电路结构和特性较为了解的情况。

3.基尔霍夫定律：基尔霍夫定律是电路分析中的重要定律之一。

根据基尔霍夫定律，电路中的电流和电压之间满足一些方程。

通过建立方程组，可以求解电路的电流分布和电压分布，从而得到等效电阻。

这种方法适用于对电路分析较为熟悉的情况。

电阻连接的等效变换公式电阻是电路中常见的元件之一，它可以对电流的流动产生阻碍作用。

在实际的电路中，我们经常需要对电阻进行等效变换，以便更好地分析和设计电路。

本文将介绍电阻连接的等效变换公式，帮助读者更好地理解和运用这些公式。

1. 串联电阻的等效电阻当多个电阻依次连接在一起，形成串联电路时，它们的等效电阻可以通过简单相加得到。

假设有两个电阻R1和R2串联连接在一起，它们的等效电阻可以表示为：Req = R1 + R2如果有更多的电阻串联连接在一起，可以依次相加得到总的等效电阻。

2. 并联电阻的等效电阻当多个电阻同时连接在电路中，形成并联电路时，它们的等效电阻可以通过倒数相加后再取倒数得到。

假设有两个电阻R1和R2并联连接在一起，它们的等效电阻可以表示为：1/Req = 1/R1 + 1/R2如果有更多的电阻并联连接在一起，可以依次倒数相加后再取倒数得到总的等效电阻。

3. 三角形电阻网络的等效电阻在一些特殊情况下，电路中的电阻可以组成一个三角形网络。

对于三角形电阻网络，我们可以通过等效变换将其转化为星形电阻网络，以便更好地分析和设计电路。

三角形电阻网络的等效电阻可以通过下式得到：Req = R1 * R2 / (R1 + R2 + R3)其中，R1、R2和R3分别表示三角形电阻网络中的三个电阻。

4. 星形电阻网络的等效电阻与三角形电阻网络相对应的是星形电阻网络。

对于星形电阻网络，我们可以通过等效变换将其转化为三角形电阻网络。

星形电阻网络的等效电阻可以通过下式得到：1/Req = 1/R1 + 1/R2 + 1/R3其中，R1、R2和R3分别表示星形电阻网络中的三个电阻。

5. 电阻的温度系数电阻的阻值是随温度的变化而变化的，这是由于电阻材料的特性所决定的。

电阻的温度系数是描述电阻阻值随温度变化的程度的指标，通常用符号α表示。

电阻的阻值与温度的关系可以用下式表示：Rt = R0 * (1 + α * (T - T0))其中，Rt表示温度为T时的电阻阻值，R0表示参考温度T0时的电阻阻值，α表示电阻的温度系数。

电阻网络中的等效电路计算方法电阻网络是电子电路中常见的一种电路结构，它由多个电阻组成，通过合理地计算和分析电阻网络，可以得到等效电路，简化电路结构，提高电路设计的效率。

本文将介绍电阻网络中的等效电路计算方法。

一、串联电阻的等效电路计算串联电阻是指多个电阻依次连接在电路中，电流依次流过各个电阻。

为了简化串联电阻的计算，我们可以将其视为一个等效电阻。

计算等效电阻的方法是将串联电阻的阻值相加。

假设有两个串联电阻R1和R2，则它们的等效电阻Re系列为：Re = R1 + R2同理，如果有多个串联电阻R1，R2，R3...Rn，它们的等效电阻Re可以表示为：Re = R1 + R2 + R3 + ... + Rn这样，通过简单的相加运算，我们就可以得到串联电阻的等效电路。

二、并联电阻的等效电路计算并联电阻是指多个电阻同时连接在电路中，电流分流通过各个电阻。

为了简化并联电阻的计算，我们可以将其视为一个等效电阻。

计算等效电阻的方法是将并联电阻的阻值取倒数后再相加，再将结果取倒数。

假设有两个并联电阻R1和R2，则它们的等效电阻Re并联为：1/Re = 1/R1 + 1/R2同理，如果有多个并联电阻R1，R2，R3...Rn，它们的等效电阻Re 可以表示为：1/Re = 1/R1 + 1/R2 + 1/R3 + ... + 1/Rn最后再将结果取倒数，即可得到并联电阻的等效电路。

三、混合电阻的等效电路计算混合电阻是指同时包含串联电阻和并联电阻的电路。

为了简化混合电阻的计算，我们可以分步骤进行。

首先，将串联电阻的阻值相加，得到等效串联电阻Re1。

其次，将并联电阻的阻值取倒数后再相加，再将结果取倒数，得到等效并联电阻Re2。

最后，将等效串联电阻Re1和等效并联电阻Re2按照并联电阻的计算方法相加，得到混合电阻的等效电路。

四、图解法计算等效电路除了上述的计算方法，我们还可以通过图解法来计算等效电路。

图解法通过绘制电路示意图，根据电阻之间的连接关系和电流的分布情况，快速地得到电阻网络的等效电路。

初中物理电学串联和并联电路的等效电阻在物理学中，电学是一个很重要的研究领域。

在电学中，串联和并联电路是两个基本的电路连接方式，我们经常使用它们来构建各种电子设备。

而在电路中，等效电阻是一个重要的概念，它表示了电路在电阻方面的性质。

本文将主要介绍初中物理中电学串联和并联电路的等效电阻的概念和计算方法。

1. 串联电路的等效电阻在串联电路中，电阻按照一定的顺序连接在一起，电流在每个电阻中是依次流过的。

串联电路的等效电阻是指将这些电阻替换为一个等效电阻，使得串联电路中的总电流等于等效电阻分压下的电流。

计算串联电路的等效电阻的方法为将各个电阻相加。

例如，假设我们有两个电阻R1和R2串联连接在一个电源上，我们需要计算它们的等效电阻。

根据串联电路的特点，电流依次通过R1和R2，所以它们的电流相等。

根据欧姆定律，电压V1和V2等于它们对应电阻的电流乘以电阻值，即V1=I*R1，V2=I*R2。

因此，总电压等于各个电阻电压的和，即V = V1 + V2 = I*R1 + I*R2 = I*(R1 + R2)。

根据欧姆定律，总电压等于总电流乘以等效电阻，即V = I*Req。

所以，我们可以得到等效电阻的计算公式为Req = R1 + R2。

在更复杂的串联电路中，我们可以按照这个方法依次计算各个电阻的电压并相加，最后求得等效电阻。

2. 并联电路的等效电阻在并联电路中，电阻的两端被平行地连接在一起，电流在各个电阻中是分流的。

与串联电路不同，电阻的电流并不相等，总电流等于各个分支电流的和。

并联电路的等效电阻是指将这些电阻替换为一个等效电阻，使得并联电路中的总电流等于等效电阻并流下的电流。

计算并联电路的等效电阻的方法为将各个电阻的倒数相加再取倒数。

例如，假设我们有两个电阻R1和R2并联连接在一个电源上，我们需要计算它们的等效电阻。

根据并联电路的特点，总电压相等于各个电阻的电压，即V = V1 = V2。

而根据欧姆定律，电流I等于总电压除以电阻，即I = V/R，所以I1 = V/R1，I2 = V/R2。

电路等效电阻的求法在电路分析以及电路设计过程中，求解电路中的等效电阻是一个非常重要的任务。

准确地求解电路等效电阻可以帮助我们理解电路的特性，优化电路设计，提高电路性能。

本文将介绍一些常用的方法来求解电路的等效电阻。

一、串联电阻的等效电阻求解串联电阻是指多个电阻依次连接在电路中，电流按顺序依次流过每个电阻的电路。

求解串联电阻的等效电阻可以使用以下公式：R等效 = R1 + R2 + R3 + ... + Rn其中，R1、R2、R3......Rn分别表示电路中每个串联电阻的电阻值。

通过按照电阻的顺序将各个电阻的电阻值相加，即可得到串联电阻的等效电阻。

二、并联电阻的等效电阻求解并联电阻是指多个电阻同时连接在电路中，电流在分支中按并联电阻的比例流过各个电阻的电路。

求解并联电阻的等效电阻可以使用以下公式：1/Requ = 1/R1 + 1/R2 + 1/R3 + ... + 1/Rn其中，R1、R2、R3......Rn分别表示电路中每个并联电阻的电阻值。

通过将每个并联电阻的倒数相加，然后再取倒数，即可得到并联电阻的等效电阻。

三、复杂电路的等效电阻求解对于复杂的电路，可以通过将其划分成简单的串并联电路来求解等效电阻。

首先，将电路按照串并联的结构进行分解，将电路简化为串并联电路组合。

然后，分别求解每个子电路的等效电阻。

最后，将各个子电路的等效电阻按照串并联的方式进行组合，得到整个电路的等效电阻。

四、其他方法的等效电阻求解除了上述的串并联求解方法，还有一些其他方法可以用来求解电路的等效电阻。

例如，可以使用电路的节点分析或者网孔分析等方法来建立方程，进而求解电路的等效电阻。

此外，还可以借助软件工具进行电路分析，得到电路的等效电阻。

求解电路的等效电阻是电路分析中的重要任务，可以帮助我们理解电路特性，优化电路设计。

通过串并联的方法以及其他分析方法，我们可以准确地求解电路的等效电阻。

在实际应用中，我们可以根据具体情况选择合适的方法，灵活运用，以满足电路分析的需要。

串联电阻与并联电阻的等效电阻电阻是电路中常见的元件之一，它具有阻碍电流流动的作用。

在电路中，常常会遇到串联电阻和并联电阻这两种情况。

本文将探讨串联电阻和并联电阻的等效电阻概念及其计算方法。

一、串联电阻的等效电阻串联电阻指的是将多个电阻依次连接在一起，电流按顺序通过每个电阻。

串联电阻的等效电阻是指将这些串联电阻简化为一个等效电阻，与串联电阻组合相连的电路的性质相同。

计算串联电阻的等效电阻需要使用串联电阻的计算公式，即等效电阻为各个电阻之和，即R_eq = R₁ + R₂ + ... + Rₙ，其中R_eq为等效电阻，R₁、R₂、...、Rₙ分别为串联电阻的各个电阻值。

例如，有三个串联电阻，分别为10欧姆、20欧姆和30欧姆，求它们的等效电阻。

根据串联电阻的计算公式可知，等效电阻R_eq = 10欧姆 + 20欧姆 + 30欧姆 = 60欧姆。

二、并联电阻的等效电阻并联电阻指的是将多个电阻同时连接在电路中，电流可以分别通过每个电阻。

并联电阻的等效电阻是指将这些并联电阻简化为一个等效电阻，与并联电阻组合相连的电路的性质相同。

计算并联电阻的等效电阻需要使用并联电阻的计算公式，即等效电阻为各个电阻的倒数之和的倒数，即1/R_eq = 1/R₁ + 1/R₂ + ... + 1/Rₙ，然后取其倒数。

例如，有三个并联电阻，分别为10欧姆、20欧姆和30欧姆，求它们的等效电阻。

根据并联电阻的计算公式可知，1/R_eq = 1/10欧姆 +1/20欧姆 + 1/30欧姆= 0.1 + 0.05 + 0.033 ≈ 0.183，再将其倒数，即R_eq = 1 / 0.183 ≈ 5.46欧姆。

三、串联电阻和并联电阻的等效电阻应用串联电阻和并联电阻的等效电阻概念在电路设计和分析中具有广泛的应用。

通过求解等效电阻，可以简化电路，方便后续计算和分析。

在实际应用中，我们经常需要根据电路的需求来选择串联电阻和并联电阻的数值，以达到所期望的电路性能。

电阻电路的等效变换电阻电路的等效变换是指将一个电阻电路转化为另一个等效的电阻电路，使得两个电路在电学性质上完全相同。

等效变换在电路分析和设计中起着重要的作用，能够简化电路分析过程，提高计算效率。

一、串联电阻的等效变换串联电阻是指多个电阻按顺序连接在一起，电流依次通过每个电阻。

当电路中有多个串联电阻时，可以通过等效变换将其转化为一个等效电阻。

假设有两个串联电阻R1和R2，其等效电阻为Req。

根据欧姆定律可知，串联电阻中的电流相同。

根据电阻的定义可知，电阻与电流和电压之间存在线性关系，即R = U / I。

因此，R1和R2的电阻值可以表示为R1 = U / I1，R2 = U / I2。

在串联电路中，电流I1通过R1，电流I2通过R2，由于串联电路中电流只有一个路径，所以I1 = I2。

将上述两个等式相等，可得到R1 / I1 = R2 / I2，即R1 / R2 = I1 / I2。

由此可推导出串联电阻的等效电阻为Req = R1 + R2。

二、并联电阻的等效变换并联电阻是指多个电阻同时连接在一起，电流分别通过每个电阻。

当电路中有多个并联电阻时，可以通过等效变换将其转化为一个等效电阻。

假设有两个并联电阻R1和R2，其等效电阻为Req。

根据欧姆定律可知，电压在并联电路中相同。

根据电阻的定义可知，电阻与电流和电压之间存在线性关系，即R = U / I。

因此，R1和R2的电阻值可以表示为R1 = U1 / I，R2 = U2 / I。

在并联电路中，电压U1作用在R1上，电压U2作用在R2上，由于并联电路中电压相同，所以U1 = U2。

将上述两个等式相等，可得到R1 / U1 = R2 / U2，即R1 / R2 = U1 / U2。

由此可推导出并联电阻的等效电阻为1 / Req = 1 / R1 + 1 / R2。

三、星型-三角形转换星型电阻网络和三角形电阻网络是常见的电阻网络拓扑结构。

在电路分析中，有时需要将星型电阻网络转换为三角形电阻网络，或将三角形电阻网络转换为星型电阻网络，以便于进行电路分析。

第十讲等效电阻知识要点知识点l 串联电路的等效电阻(1)等效电阻的定义：几个连接起来的电阻所起的作用，可以用一个电阻来代替，这个电阻就是那些电阻的电阻。

(2)串联电路的等效电阻①规律： 串联电路的等效电阻等于。

②表达式：。

注：对于两个电阻串联，有R=。

(3)知识拓展： ．①把几个电阻串联起来，相当于增大了导体的，其等效电阻一定比任何一个串联电阻都(选填‘‘大”或“小”)。

②n 个阻值均为R 。

的电阻串联，其等效电阻R=。

③把几个电阻串联起来，若其中一个电阻增大(或减小)，则等效电阻也随着。

④要使电路中的等效电阻变大，可以采取电阻串联的方法。

⑤串联分压公式：。

(说明在串联电路中各分电阻两端的电压与其电阻的阻值成正比，即一个电阻是另一个电阻的多少倍，其两端的电压就是另一个电阻两端电压的多少倍。

这说明串联电路中的各电阻有分压作用)【例1】 将10 Ω和20 Ω两个电阻串联，总电阻是Ω。

若通过它们的电流是0.3A ，则两电阻两端的总电压是V 。

【例2】 一只小灯泡上标有“2．5 V ，o ．3 A ”字样，即该灯泡在2．5 V 的电压下正常发光时的电流为0．3 A 。

现在只有一个电压为4 V 的电源，为了使小灯泡正常发光，就需要联一个Ω的电阻。

方法点拨：若电路中总电压大于用电器正常工作时允许加的最大电压时，可在电路中串联一个电阻分去多余的电压，以保护电路。

变式训练1如图所示的电路中，R2的阻值为3Ω。

闭合开关之后，电压表的示数为6 V ，电流表的示数为1 A ，则R1=Ω，电源的电压为V ；如果断开开关，电压表的读数是V 。

变式训练2如图甲所示，闭合开关S 后，两相同电压表的指针偏转都如图乙所示，则L1和L2两灯的电阻之比为( )A ． 1： 4B 。

4： 1C 。

1： 5D 。

5： 1变式训练3如图所示，虚线框内有两个阻值分别为5 Ω、10 Ω的电阻，小明同学想了解其连接方式，于是用3 v 的电源、电流表和开关进行了检测，闭合开关后，测得电流表的读数为0．2 A 。

电阻连接的等效变换公式在电路中，电阻是一种常见的元件，用于控制电流的流动。

在实际的电路中，常常需要对电阻的连接方式进行变换和等效处理。

通过合理的变换和等效处理，可以简化电路，使其更易于分析和计算。

本文将介绍几种常见的电阻连接方式的等效变换公式，并给出详细的说明。

1. 串联电阻的等效电阻当若干个电阻按照串联的方式连接在一起时，它们的等效电阻可以通过求和的方式计算。

假设有两个串联电阻R1和R2，则它们的等效电阻R等可以表示为：R等 = R1 + R2当有多个电阻串联时，可以逐个将它们的阻值相加，得到它们的等效电阻。

2. 并联电阻的等效电阻当若干个电阻按照并联的方式连接在一起时，它们的等效电阻可以通过倒数和求和的方式计算。

假设有两个并联电阻R1和R2，则它们的等效电阻R等可以表示为：1/R等 = 1/R1 + 1/R2当有多个电阻并联时，可以逐个将它们的阻值的倒数相加，再取倒数得到它们的等效电阻。

3. 三角形连接电阻的等效电阻在某些电路中，电阻可能按照三角形连接的方式进行连接。

对于三角形连接的电阻，其等效电阻可以通过求和和平均值的方式计算。

假设有三个三角形连接的电阻R1、R2和R3，则它们的等效电阻R 等可以表示为：R等 = (R1 + R2 + R3)/3即将三个电阻的阻值相加，再除以3得到它们的等效电阻。

4. 星形连接电阻的等效电阻在某些电路中，电阻可能按照星形连接的方式进行连接。

对于星形连接的电阻，其等效电阻可以通过求和和平方根的方式计算。

假设有三个星形连接的电阻R1、R2和R3，则它们的等效电阻R等可以表示为：1/R等 = 1/R1 + 1/R2 + 1/R3即将三个电阻的阻值的倒数相加，再取倒数得到它们的等效电阻。

除了上述的几种常见的电阻连接方式的等效变换公式外，还有一些特殊的情况需要特别注意。

比如在电路中存在有限电源电阻和无限电源电阻的情况下，等效电阻的计算方式会有所不同。

此外，在某些复杂的电路中，可能需要进行更复杂的等效变换计算，涉及到网络理论和电路分析方法。

串联电阻的等效电阻计算串联电阻网络是电路中常见的连接方式之一，它由多个电阻依次连接而成。

在实际电路中，我们经常需要计算串联电阻的等效电阻，以便分析电路的性质和工作情况。

本文将详细介绍串联电阻的等效电阻计算方法，并给出一些实际例子来帮助读者理解。

首先，我们来看一下两个电阻串联时等效电阻的计算方法。

设两个串联电阻分别为R1和R2，它们依次相连，形成一个电路。

那么，整个电路的等效电阻记为Req。

根据欧姆定律，我们知道电路中的电流是由电压和电阻共同决定的。

因此，我们可以通过电流来计算等效电阻。

根据串联电路的特点，整个电路中的电流是相同的。

假设这个电流为I，则从电路中的电压分布可以得到以下等式：U = UR1 + UR2其中，U为整个电路的电压，UR1和UR2分别为两个电阻上的电压。

根据欧姆定律，我们可以得到以下关系式：UR1 = R1 * IUR2 = R2 * I将以上两个等式代入第一个等式中，我们可以得到一个关于电流I的方程：U = R1 * I + R2 * I我们可以将这个方程进一步化简为：I = U / (R1 + R2)现在我们可以得到电流I与电压U之间的关系。

根据欧姆定律，电阻的等效电阻可以定义为电压和电流的比值，即：Req = U / I将上面的表达式代入，我们可以得到串联电阻的等效电阻计算公式：Req = (R1 * R2) / (R1 + R2)> 例如，假设有两个串联电阻，电阻值分别为R1=10欧姆和R2=20欧姆。

通过上述计算公式，我们可以得到串联电阻的等效电阻：> Req = (10 * 20) / (10 + 20) = 200 / 30 = 6.67欧姆通过这个例子，我们可以看到，当两个电阻串联时，等效电阻小于任何一个电阻的电阻值。

这是因为电阻串联后，电流要经过两个电阻，总体来说电路的阻力增加了，导致等效电阻较小。

除了计算两个电阻串联时的等效电阻，我们还可以推广到多个电阻的情况。

电阻的串联与并联电路的等效电阻电阻是电流在电路中的阻碍物，用来限制电流通过的能力。

在实际电路中，电阻经常被串联或并联连接以满足电流和电压的需求。

这篇文章将探讨电阻的串联与并联电路，并介绍它们的等效电阻。

1. 串联电路串联电路是指将多个电阻依次连接在一起，电流只能依次通过每个电阻。

在串联电路中，总电阻等于每个电阻的阻值之和。

假设有三个电阻R1、R2和R3，它们串联连接在一起，电流依次通过它们。

则串联电路的总电阻（ Rt ）可以由以下公式计算：1/Rt = 1/R1 + 1/R2 + 1/R3通过这个公式，可以得到串联电路的总电阻。

串联电路中的电流是相同的，而电压则根据每个电阻的阻值进行分配。

2. 并联电路并联电路是指将多个电阻同时连接在一起，电流可以选择流经其中的任意一个电阻。

在并联电路中，总电阻的倒数等于每个电阻倒数的和的倒数。

假设有三个电阻R1、R2和R3，它们并联连接在一起，电流可以选择通过其中任意一个电阻。

则并联电路的总电阻（ Rt ）可以由以下公式计算：1/Rt = 1/R1 + 1/R2 + 1/R3通过这个公式，可以得到并联电路的总电阻。

并联电路中的电压是相同的，而电流则根据电阻的阻值进行分配。

3. 串联与并联的等效电阻有时候，我们需要知道串联或并联连接的电路的等效电阻，以方便我们在实际应用中进行计算。

对于串联电路，等效电阻等于各个电阻的阻值之和，即 Rt = R1 + R2 + R3。

对于并联电路，等效电阻等于各个电阻阻值的倒数之和的倒数，即 Rt = 1/(1/R1 + 1/R2 + 1/R3)。

通过计算等效电阻，我们可以简化电路的分析和计算过程。

这对于设计和排版电路来说非常有用。

4. 应用举例假设有一个电路，其中有三个串联连接的电阻R1、R2和R3，分别为10Ω、20Ω和30Ω。

我们可以使用以下公式计算总电阻：Rt = R1 + R2 + R3 = 10Ω + 20Ω + 30Ω = 60Ω因此，这个串联电路的等效电阻为60Ω。

电阻电路的串并联等效电阻计算电阻电路是电子电路中常见的一种电路形式。

在实际的电路中，电阻器经常会被串联或并联起来，形成串联电路或并联电路。

了解如何计算串并联电路的等效电阻对于解决实际问题以及设计电路非常重要。

一、串联电路的等效电阻计算串联电路是指将电阻器顺序连接在一起，电流从一个电阻器流过，再流向下一个电阻器。

在串联电路中，电阻器的总电阻等于各个电阻器的电阻之和。

设有n个串联的电阻器R1，R2，…，Rn，它们的电阻分别为R1，R2，…，Rn，则电阻器的总电阻R为：R = R1 + R2 + … + Rn二、并联电路的等效电阻计算并联电路是指将电阻器的一个端头连接在一起，另一个端头连接在一起。

在并联电路中，电阻器的总电阻等于各个电阻器电阻倒数之和的倒数。

设有n个并联的电阻器R1，R2，…，Rn，它们的电阻分别为R1，R2，…，Rn，则电阻器的总电阻R为：1/R = 1/R1 + 1/R2 + … + 1/Rn三、串并联电路的等效电阻计算有时候电路中既存在串联电路，又存在并联电路，此时需要根据具体情况进行计算。

1. 若电路先进行串联，再进行并联，计算步骤如下：- 首先，将串联电路的电阻器计算出总电阻R1；- 然后，将并联电路的电阻器计算出总电阻R2；- 最后，总电阻R等于R2。

2. 若电路先进行并联，再进行串联，计算步骤如下：- 首先，将并联电路的电阻器计算出总电阻R1；- 然后，将串联电路的电阻器计算出总电阻R2；- 最后，总电阻R等于R2。

请注意，以上的计算方法适用于只包含电阻器的简单电路。

在实际情况中，电路可能还包含电感、电容等元件，此时计算方法会更加复杂。

总结：了解如何计算串并联电路的等效电阻对于理解电路的性质和设计电路非常重要。

在串联电路中，电阻器的总电阻等于各个电阻器的电阻之和；在并联电路中，电阻器的总电阻等于各个电阻器电阻倒数之和的倒数。

根据具体情况，可以通过不同的计算步骤来计算串并联电路的等效电阻。

串并联电路中等效电阻计算公式在串并联电路中，我们需要确定电路中的等效电阻。

等效电阻是指将整个电路简化到一个等效电阻上，使得通过该等效电阻的电流与原始电路中的电流相同，通过该等效电阻的电压与原始电路中的电压相同。

对于串联电路，串联电阻等效值的计算公式为：R_eq = R1 + R2 + R3 + ... + Rn其中R_eq是等效电阻值，R1, R2, R3, ... Rn 是串联电路中各个电阻的阻值。

对于并联电路，并联电阻等效值的计算公式为：1/R_eq = 1/R1 +1/R2 + 1/R3 + ... + 1/Rn其中R_eq是等效电阻值，R1, R2, R3, ... Rn 是并联电路中各个电阻的阻值。

下面，我们将详细探讨串并联电路中等效电阻的计算公式。

1.串联电路中等效电阻：串联电路是指多个电阻依次连接在一起，形成一个单一路径的电路。

在串联电路中，电流在各个电阻中是相等的，而电压则是依次分配给每个电阻的。

因此，将整个电路简化到一个等效电阻上，使得通过该等效电阻的电流与原始电路中的电流相同，通过该等效电阻的电压与原始电路中的电压相同。

计算串联电路中的等效电阻的公式很简单，只需将各个电阻的阻值相加即可。

即：R_eq = R1 + R2 + R3 + ... + Rn例如，对于一个有三个电阻（R1=10Ω,R2=20Ω,R3=30Ω）的串联电路，其等效电阻为：R_eq = 10Ω + 20Ω + 30Ω = 60Ω2.并联电路中等效电阻：并联电路是指多个电阻并联在一起，形成多个并行路径的电路。

在并联电路中，电流会分流通过各个电阻，而电压则是各个电阻所在路径上的电压相等。

因此，将整个电路简化到一个等效电阻上，使得通过该等效电阻的电流与原始电路中的电流相同，通过该等效电阻的电压与原始电路中的电压相同。

计算并联电路中的等效电阻的公式需要注意，因为电阻是倒数关系，所以计算的时候需要将每个电阻的倒数相加，并将结果再次取倒数。