三角形专题复习课件资料讲解
- 格式：ppt
- 大小：53.00 KB
- 文档页数：8
下载文档原格式
合集下载
三角形的认识复习与整理ppt
而判断出三角形ABC的
形状。
解答技巧：在解答此类 问题时，首先要明确题 目所给的条件和需要判 断的结论，然后结合相 关的性质定理进行推导。 在推导过程中，要注意 灵活运用所学的知识点， 并结合实际情况进行判 断。
易错知识点归纳及纠正方法
01
02
03
04
易错知识点1
对三角形的基本性质理解不透 彻，导致在解题过程中出现错
应用举例
利用全等三角形解决与边 长、角度、面积相关的问 题，如证明线段相等、角 相等或者面积相等。
03 三角形面积计算方法
海伦公式求解任意三角形面积
海伦公式定义
海伦公式是用于求解任意三角形面积的一种公式，其基本 形式为S=√[p(p-a)(p-b)(p-c)]，其中a、b、c分别为三角 形的三边长，p为半周长，即p=(a+b+c)/2。
该公式适用于任何类型的三角形，只要已知三边长即可求解面积。需要
注意的是，在使用该公式时，需要先计算出半周长p。
04 三角形在生活中的应用
建筑结构中稳定性应用
三角形框架
在建筑结构中，三角形框架常被用于增强稳定性，如桥梁、 塔楼和屋顶等。由于三角形的形状特性，它能够有效地分散 和承受重力、风力和地震等外力。
在解题过程中，注意步骤的严谨性和 逻辑性，避免出现计算错误或逻辑混 乱的情况。
多做相关练习题，加强对知识点的理 解和记忆。
对于复杂的题目，可以尝试使用多种 方法进行求解，比较不同方法的优劣 性，选择最适合自己的方法进行求解。
06 总结回顾与拓展延伸
关键知识点总结回顾
三角形的定义和性质
三角形是由三条不在同一直线上的线段首尾顺次连接所组成的封闭图形。三角形的内角和为180度，且任意两边之和 大于第三边，任意一边都小于另外两边之和。
全等三角形的基本模型复习(正式经典)PPT课件
2021
10
模型四 一线三垂直型 模型解读：基本图形如下：此类图形 通常告诉 BD⊥DE，AB⊥AC， CE⊥DE，那么一定有∠B＝∠CAE.（常用到同（等）角的余角相等）
2021
11
4．如图，AD⊥AB于A，BE⊥AB于B，点C在AB上，且CD⊥CE，CD＝CE. 求证：AB＝AD＋BE.
2021
2021
3
1．如图，AB∥DE，AC∥DF，BE＝CF，求证：AB＝DE.
2021
4
解：∵BE＝CF，∴BE＋EC＝CF＋EC，即 BC＝EF， ∵AB∥DE，AC∥DF，∴∠B＝∠DEF，∠ACB＝∠F， 在△ABC 与△DEF 中 ∠B＝∠DEF， BC＝EF， ∠ACB＝∠F， ∴△ABC≌△DEF(ASA) ∴AB＝DE
2021
8
3．如图，AB⊥CD于B，CF交AB于E，CE＝AD，BE＝BD.求证：CF⊥AD.
2021
9
解：∵AB⊥CD，∴∠EBC＝∠DBA＝90°.在 Rt△CEB 与 Rt△ADB 中 CBEE＝ ＝ABDD，，∴Rt△CEB≌Rt△ADB(HL)，∴∠C＝∠A，又∵∠C＋∠CEB＝ 90°，∠CEB＝∠AEF，∴∠A＋∠AEF＝90°，∴CF⊥AD
12
解：∵AD⊥AB，BE⊥AB，CD⊥CE，∴∠DAC＝∠CBE＝∠DCE＝90 °，又∵∠DCB＝∠D＋∠DAC＝∠DCE＋∠ECB，∴∠D＝∠ECB.在△ACD
与△BEC 中，∠∠AD＝＝∠∠BEC，B，∴△ACD≌△BEC(AAS)，∴AC＝BE，CB＝ DC＝CE，
AD，∴AB＝AC＋CB＝AD＋BE
2021
5
模型二 翻折型 模型解读：将原图形沿着某一条直线折叠后，直线两边的部分能够完全重 合，这两个三角形称之为翻折型全等三角形．此类图形中要注意其隐含条件， 即公共边或公共角相等．
完整版-全等三角形总复习教学课件
判定 到角的两边的距离相等的点在角平分线上 2
全等三角形的判定方法
三角形全等判定方法1
三边对应相等的两个三角形全等（可以简写
为“边边边”或“SSS”）。
A
用符号语言表达为:
在△ABC和△ DEF中
B
C
AB=DE
D
BC=EF
CA=FD
∴ △ABC ≌△ DEF（SSS） E
F
2024/9/30
3
三角形全等判定方法2
∴ △ABC≌△DEF（AAS）
2024/9/30
6
三角形全等判定方法5
有一条斜边和一条直角边对应相等的两个直角 三角形全等(HL）。
在Rt△ABC和Rt△DEF中
A
D
AB=DE （已知 ） AC=DF（已知 ）
C ∴ △ABC≌△DEF（HL）
2024/9/30
B
F
E
7
知识点
1.全等三角形的性质: 对应边、对应角、对应线段相等, 周长、面积也相等。
A．1对 B．2对 C．3对 D．4对
2024/9/30
17
例3. 已知： AC⊥BC，BD⊥AD，AC=BD. 求证：BC=AD.
D
C
A
B
2024/9/30
18
▪例4:下面条件中, 不能证出Rt△ABC≌Rt△A' B'C'的是[ C] (A.)AC=A'C' , BC=B'C' (B.)AB=A'B' , AC=A'C' (C.) AB=B'C' , AC=A'C' (D.)∠B=∠B' , AB=A'B'
解三角形复习课课件
2. 已知一个三角形的两边长分别为a和b，它们的 02 夹角为θ，且满足a>b，求证：
cosθ=(a²+b²)/(2ab)。
3. 已知一个三角形的三条边长分别为a、b和c， 03 且满足a²=b²+c²，求证：该三角形为直角三角形
。
THANKS
感谢观看
详细描述
三角形的分类是根据其角度和边长进行的，常见的分类包括锐角三角形、直角三 角形、钝角三角形、等边三角形和等腰三角形等。这些分类在解三角形的过程中 具有重要的应用价值，可以帮助我们更好地理解和解决问题。
02
解三角形的主要方法
正弦定理
总结词
利用正弦定理可以解决与三角形边和角 有关的问题，特别是当已知两边及其夹 角时。
解三角形时常见的错误
忽视角度范围
在解题过程中，由于忽视角度的范围 ，导致得出的答案不符合实际情况。
使用错误的公式
在解题过程中，使用了不合适的三角 恒等式或解三角形公式，导致答案错
误。
混淆相似与全等三角形
在解题过程中，将相似与全等三角形 混淆，导致解题思路和答案错误。
计算错误
由于计算失误，导致得出的答案与正 确答案不符。
几何图形制作中的应用
01
制作几何图形
通过解三角形的方法，可以制作各种几何图形， 如三角形、四边形等。
02
制作立体几何模型
通过解三角形的方法，可以制作各种立体几何模 型，如立方体、球体等。
建筑设计中的应用
设计建筑结构
通过解三角形的方法，可以设计出建筑的支撑结 构，以确保建筑的稳定性。
设计建筑外观
通过解三角形的方法，可以设计出建筑的外观线 条和造型，以达到美观和实用的效果。
解三角形复习课课件
cosθ=(a²+b²)/(2ab)。
3. 已知一个三角形的三条边长分别为a、b和c， 03 且满足a²=b²+c²，求证：该三角形为直角三角形
。
THANKS
感谢观看
详细描述
三角形的分类是根据其角度和边长进行的，常见的分类包括锐角三角形、直角三 角形、钝角三角形、等边三角形和等腰三角形等。这些分类在解三角形的过程中 具有重要的应用价值，可以帮助我们更好地理解和解决问题。
02
解三角形的主要方法
正弦定理
总结词
利用正弦定理可以解决与三角形边和角 有关的问题，特别是当已知两边及其夹 角时。
解三角形时常见的错误
忽视角度范围
在解题过程中，由于忽视角度的范围 ，导致得出的答案不符合实际情况。
使用错误的公式
在解题过程中，使用了不合适的三角 恒等式或解三角形公式，导致答案错
误。
混淆相似与全等三角形
在解题过程中，将相似与全等三角形 混淆，导致解题思路和答案错误。
计算错误
由于计算失误，导致得出的答案与正 确答案不符。
几何图形制作中的应用
01
制作几何图形
通过解三角形的方法，可以制作各种几何图形， 如三角形、四边形等。
02
制作立体几何模型
通过解三角形的方法，可以制作各种立体几何模 型，如立方体、球体等。
建筑设计中的应用
设计建筑结构
通过解三角形的方法，可以设计出建筑的支撑结 构，以确保建筑的稳定性。
设计建筑外观
通过解三角形的方法，可以设计出建筑的外观线 条和造型，以达到美观和实用的效果。
解三角形复习课课件
《三角形复习课》PPT教学课件
11. 三角形外角和定理 三角形的外角和等于3600
7
12. 三角形的外角与内角的关系 三角形的一个外角等于与它不相邻的
两个内角的和。 三角形的一个外角大于与它不相邻的
任何一个内角。
8
13、n边形的内角和等于(n－2)·180 多边形的外角和都等于360°.
我们通过把多边形划分为若干个三
角形，用三角形内角和去求多边形内角
20
例3、如图所示，∠B＝45°， ∠A=30°,∠C＝25°， 求∠ADC的度数
A
D
B
C
21
析：利用转化思想，把四边形转化成 几个三角形，再利用三角形内角和定 理来解答。
A
A
D
D
B
C
B
A
C
D
22
例4、如图所示：
求∠A＋∠B＋∠C＋∠D＋ ∠E＋∠F＋∠G的度数
C
F
G
D
B
A
分析
E
C
：
B
F
G
D
A
B
DC
27
2、有一六边形，截去一三角形，内角和会发生 怎样变化？请画图说明。
内角和减少180O 内角和不变 内角和增加180O
28
29
16
3.如图，已知：AD是△ABC 的中线，△ABC的面积为 60cm2 ,求
△ABD的面积
A
解:作AE BC,垂足为E, AD是 ABC的中线,
BD CD,
B
DE
C
又 S ABC 60cm2
S
ABD
1 BD AE, 2
S
ADC
1 CD AE, 2
7
12. 三角形的外角与内角的关系 三角形的一个外角等于与它不相邻的
两个内角的和。 三角形的一个外角大于与它不相邻的
任何一个内角。
8
13、n边形的内角和等于(n－2)·180 多边形的外角和都等于360°.
我们通过把多边形划分为若干个三
角形，用三角形内角和去求多边形内角
20
例3、如图所示，∠B＝45°， ∠A=30°,∠C＝25°， 求∠ADC的度数
A
D
B
C
21
析：利用转化思想，把四边形转化成 几个三角形，再利用三角形内角和定 理来解答。
A
A
D
D
B
C
B
A
C
D
22
例4、如图所示：
求∠A＋∠B＋∠C＋∠D＋ ∠E＋∠F＋∠G的度数
C
F
G
D
B
A
分析
E
C
：
B
F
G
D
A
B
DC
27
2、有一六边形，截去一三角形，内角和会发生 怎样变化？请画图说明。
内角和减少180O 内角和不变 内角和增加180O
28
29
16
3.如图，已知：AD是△ABC 的中线，△ABC的面积为 60cm2 ,求
△ABD的面积
A
解:作AE BC,垂足为E, AD是 ABC的中线,
BD CD,
B
DE
C
又 S ABC 60cm2
S
ABD
1 BD AE, 2
S
ADC
1 CD AE, 2
解三角形复习课课件
余弦定理
总结词
余弦定理是解三角形的另一种重要方法，它通过已知的两边和夹角来求解第三 边。
详细描述
余弦定理是指在一个三角形中，任意两边及其夹角的余弦值的乘积等于第三边 的平方减去另两边的平方与这两边夹角的余弦值的乘积，即 $c^2 = a^2 + b^2 - 2abcos C$。
勾股定理
总结词
勾股定理是解三角形的基础定理之一 ，它描述了直角三角形中两直角边的 平方和等于斜边的平方。
03
总结词
在应用正弦定理或余弦定理时，要注意等式 或不等式的成立条件，避免出现错误的结果
。
05
02
总结词
在解题过程中，要特别注意边长和角度的取 值范围，避免出现无解或多解的情况。
04
问题二
等式或不等式的成立条件
06
详细描述
正弦定理适用于任何三角形，但余弦定理只适 用于非钝角三角形。在解题时，要确保所使用 的定理适用于给定的三角形。
解三角形的步骤和方法
步骤二
应用正弦定理或余弦定理
总结词
正弦定理和余弦定理是解三角形的重要工具，通过它们可以建立边 长或角度之间的关系。
详细描述
根据题目条件，选择适当定理进行推导。正弦定理用于求解边长或 角度，余弦定理用于证明角度和边长的关系。
解三角形的步骤和方法
步骤三
01
解方程或不等式
总结词
02
详细描述
回顾解题过程，分析自己在解题中遇到的 困难和错误。找出问题的根源，并采取措 施避免类似错误再次发生。
感谢您的观看
THANKS
在得到边长或角度之间的关系后，需要解方程或不等式来找到
具体的数值。
详细描述
解三角形复习课课件
03
余弦定理及其应用
余弦定理的推导与证明
80%
向量法推导余弦定理
通过向量的点积和模长关系，推 导出余弦定理的表达式。
100%
几何法证明余弦定理
利用三角形的面积和边长关系， 通过几何图形证明余弦定理。
80%
解析法证明余弦定理
通过三角形的坐标表示和距离公 式，解析地证明余弦定理。
余弦定理在解三角形中的应用
这两边所夹的角。
推导过程
通过作高将三角形分为两个直角三 角形，利用直角三角形的面积公式 和三角函数的性质推导出三角形面 积公式。
证明方法
可以采用向量的方法或者几何的方 法证明三角形面积公式的正确性。
三角形面积公式在解三角形中的应用
已知三边求面积
直接应用三角形面积公式计算面积。
已知两边及夹角求面积
同样应用三角形面积公式计算面积，需要先求出夹角。
1 2
已知两边及夹角求第三边
利用余弦定理求解三角形中已知两边及夹角时的 第三边长度。
已知三边求角度
通过余弦定理求解三角形中已知三边长度时的角 度大小。
3
判断三角形的形状
根据余弦定理判断三角形的形状，如等边、等腰、 直角等。
特殊情况下余弦定理的应用
在直角三角形中的应用
在直角三角形中，余弦定理可 简化为勾股定理，用于求解直 角三角形的边长和角度。
c² = a² + b² - 2ab*cos(C)
判断三角形形状
根据c²与a² + b²的关系，判断三角形是锐角、直角还是钝角三角形
求解其他角度
利用正弦定理a/sin(A) = b/sin(B) = c/sin(C)求解角A和角B
已知两角及夹边求解三角形问题
三角形-ppt课件
图9
14.如图9， 是 的外角， 平分 ，若 ， ，则 _ ___.
15.已知 为正整数，若一个三角形的三边长分别是 ， ， ，则满足条件的 值有___个.
7
图10
16.将三角尺按如图10所示放置在一张矩形纸片上， ， ， ，则 的度数为_ _____.
三、解答题
C
A. B. C. D.
图4
7.如图4，已知直线 ， ， ，则 的度数为( ) .
B
A. B. C. D.
图5
8.将一副三角尺按图5所示位置摆放，点 在 上，其中 ， ， ， ， ，则 的度数是( ) .
A
A. B. C. D.
图6
9.如图6， ， 是 的高， 与 相交于点 ，则 与 之间的数量关系是( ) .
C
A. B. C. D.不能确定
图7
10.如图7，将 沿着 减去一个角后得到四边形 ，若 和 的平分线交于点 ， ，则 的度数是( ) .
B
A. B. C. D.
图11
17.如图11，在 中， 分别是 的高和角平分线.
（1）若 ， ，求 的度数.
[答案]
（2）写出 与 的数量关系,并证明你的结论.
[答案]
图12
18.如图12，在 中， ， 于点 .
（1）求证 .
证明： ， ， ，
（2）若 平分 分别交 于点 求证 .
第十一章 三角形
知识梳理、真题剖析
单元练习
知识梳理1
三角形
与三角形有关的边
（1）三角形的定义：由__________________的三条线段______________所组成的图形.（2）三边关系：三角形两边的和______第三边，两边的差______第三边.（3）三角形的高：从三角形的一个顶点向它所对的边所在直线________所得线段.（4）三角形的中线：在三角形中，连接一个顶点和它对边______的线段.（5）三角形的重心：三角形三条______的交点.
直角三角形的边角关系专题复习ppt课件
6 3 6 6,渔船不改变航向有触礁 危险。
分组讨论 ,合作交流
3、如图，山上有一座铁塔，山脚下有一矩形建筑物ABCD，且 建筑物周围没有开阔平整地带．该建筑物顶端宽度AD和高度 DC都可直接测得，从A、D、C三点可看到塔顶端H．可供使 用的测量工具有皮尺、测倾器．
请你根据现有条件，充分利用矩形建筑物，设计一个测量塔顶 端到地面高度HG的方案．具体要求如下：
4．（2010湖北省咸宁市）如图，已知直l1‖l2‖l3‖l4相邻 两条平行直线间的距离都是1，如果正方形ABCD
5
的四个顶点分别在四条直线上，则sinα=____5_。
分析：分别作BE⊥l1，DF⊥l1，垂足分别为E、F
E
F
易证：△DFA≌△AEB
∴AF=BE=2
在Rt△DFA中由勾股定理得：
AD AF2 DF2 22 12 5
E、F分别是AB、AD的中点，若EF=2，BC=5，
CD=3，则tanC等于（ B ）
A.
B.
C.
D.
解：连接BD，∵E、F分别为AB、AD中点，∴BD=2EF=2×2=4
BD 2 CD2 42 32 25 BC 2
BDC 90; tan C BD 4 CD 3
3、在△ABC中，∠C＝90°，则sinA+cosA的（ B ）
sin（__9_0_°__- A_）=cosA
cos（__9_0°__-_A_）=sinA
4、锐角三角函数的范围：_0__＜sinA＜_1__；
_0__＜cosA＜__1__； tanA＞__0__，
当堂训练,巩固提高
考法一：注重对锐角三角函数定义的考查
1、（2010年怀化市）在Rt△ABC中∠C=90°sinA=
《三角形》复习课件
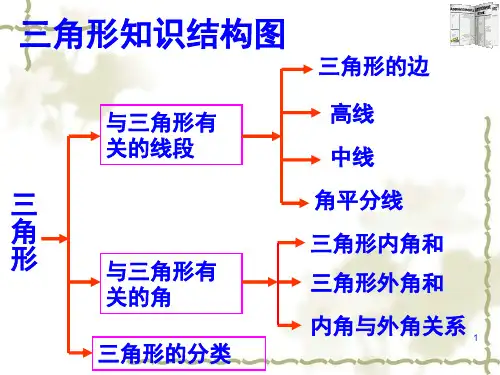
《三角形》复习课件一、三角形的定义和基本要素三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形。
这三条线段就是三角形的边，它们相交的点称为三角形的顶点，相邻两边组成的角叫做三角形的内角。
三角形有三个顶点、三条边和三个内角。
需要注意的是，三角形的三条边必须满足任意两边之和大于第三边，任意两边之差小于第三边。
这是判断三条线段能否组成三角形的重要依据。
例如，有三条线段长度分别为 3、4、5，因为 3 ＋ 4 ＞ 5，4 3 ＜ 5，所以这三条线段可以组成三角形。
二、三角形的分类1、按角分类（1）锐角三角形：三个内角都小于 90 度的三角形。
（2）直角三角形：有一个内角等于 90 度的三角形。
（3）钝角三角形：有一个内角大于 90 度小于 180 度的三角形。
判断一个三角形属于哪种类型，只需看其最大内角的度数。
2、按边分类（1）等边三角形：三条边长度都相等的三角形，其三个内角也都相等，均为 60 度。
（2）等腰三角形：至少有两条边长度相等的三角形。
相等的两条边称为腰，另一条边称为底边。
等腰三角形的两个底角相等。
（3）不等边三角形：三条边长度都不相等的三角形。
三、三角形的内角和三角形的内角和是 180 度。
这是三角形的一个重要性质，可以通过多种方法来证明。
比如，我们可以将三角形的三个内角剪下来，拼在一起，会发现它们刚好组成一个平角，也就是 180 度。
在求解三角形内角的度数问题时，常常会用到这个性质。
例如，在一个三角形中，已知其中两个角分别为 50 度和 70 度，那么第三个角的度数就是 180 50 70 ＝ 60 度。
四、三角形的外角三角形的一边与另一边的延长线组成的角，叫做三角形的外角。
三角形的一个外角等于与它不相邻的两个内角的和。
例如，在三角形 ABC 中，∠ACD 是∠A 的外角，那么∠ACD ＝∠A ＋∠B。
利用这个性质，可以很方便地求解与外角有关的问题。
五、三角形的稳定性三角形具有稳定性，这是三角形的一个重要特性。
第四章《 三角形 》复习总结 ppt课件
本章总结提升
[点析]本题以构成三角形三边关系为载体，主要考查了整式 计算与三角形的有关边知识的理解与运用，在探究等腰三角形的 形状时要注意分类讨论，构建方程分析与解决实际问题．
本章总结提升
► 类型二 等腰三角形
例3 一个三角形的两条边相等，周长为18 cm，三角形一边 长为4 cm，求其他两边长．
本章总结提升
例10 如图4－T－8，AB＝AE，∠B＝∠E，BC＝ED，F是CD的
中点，则AF⊥CD吗？试说明理由．
图4－T－8
本章总结提升
解：连接AC，AD，由AB＝AE，∠B＝∠E，BC＝DE，根据 “SAS”可知△ABC≌△AED，
根据全等三角形的对应边相等可知AC＝AD. 由AC＝AD，CF＝DF，AF＝AF(公共边)， 根据“SSS”可知△ACF≌△ADF. 根据全等三角形的对应角相等可知∠AFC＝∠AFD. 又由于F在直线CD上，可得∠AFC＝90°， 即AF⊥CD.
[解析] 本题分两种情况：①腰长为4 cm，②底边长为4 cm. 解答时要注意求出的边长要符合“三角形两边之和大于第三边” ．
本章总结提升
解：①当腰长为 4 cm 时，则底边长为 18－4×2＝10(cm)，此 时，三角形三边长为 4 cm，4 cm，10 cm，因为 4＋4＜10，不符合 三角形三边关系，所以当三角形的腰长为 4 cm 时不合题意，舍去； ②当底边长为 4 cm 时，则腰长为182－4＝7(cm)，此时三角形的三 边长为 4 cm，7 cm，7 cm，4＋7＞7，符合三角形三边关系，所以， 该三角形其他两边长为 7 cm，7 cm.
图4－T－4
本章总结提升
解：如图4－T－5所示．①先画射线BC；
图4－T－5
三角形及其性质ppt
A．50。
B. 60。
C. 30。 D. 40。
• 例2．如图1，∠A=65°，∠B=75°，将纸片 的一角折叠，使点C落在△ABC内，若 ∠1=20°，则∠2的度数为（ A ）． A．60 B．80 C．90 D．100
C` 图1
变式练习
变式1.如图2所示，将△ABC沿着DE翻折，若 ∠1+∠2=
2．小华在电话中问小明：“已知一个三角形三边长分别是4，9，12， 如何求这个三角形的面积”？小明提示说：“可通过作最长边上的 高来求解”．小华根据小明的提示作出下列图形，其中正确的是
( C)
3.已知四组线段的长分别如下，以各组线段为边，能
组成三角形的是( C )
• A．1，2，3
B．2，5，8
• C．3，4，5
• 3．以三条线段3、4、x－5为这组成三角形，则x的取 值为（6<x<12）。
4.将一个正三角形纸片剪成四个全等的小正
三角形，再将其中的一个按同样的方法剪成
四个更小的正三角形，……如此继续下去，
结果如下表：
则an= 3n+1
（用含n的代数式表示）.
所剪次数 1 2 3
4
…
n
正 三 角 形 个 4 7 10 13 …
• A．14 B．15 C．16 D．17
[解析] 设第三边的长为x，则7－3＜x＜7＋3，所以4 ＜x＜10.又x为整数，所以x可取5,6,7,8，所以这个三 角形的周长的最小值为15.
考点2：三角形的内角和及其推论
• 例1．如图，在△ABC中，C 90。EF//AB,1 50。,
则 B 的度数为（D ）
三角形的中位线），这也是一种常见的作辅助线的方法。
课件解直角三角形的应用专题复习
03
锐角三角函数的运用
在解直角三角形的过程中，可以通过锐角三角函数来求解相应的角度或
边长。
测量问题
01
02
03
定义
测量问题是指通过解直角 三角形的方法来解决实际 生活中与长度、高度、角 度等有关的测量问题。
常见类型
常见的测量问题包括测建 筑物的高度、测不可直接 测量的距离等。
解决策略
解决测量问题的关键是将 实际问题转化为数学模型 ，通过解直角三角形来得 到所需的结果。
综合应用
总结词
综合应用是指将解直角三角形的知识与其他的数学知识结合起来解决问题。
详细描述
在综合应用中，需要将解直角三角形的知识与其他的数学知识结合起来，例如 代数、几何等，以解决更复杂的问题。这需要学生具备较高的思维能力和解题 技巧。
03
解题策略
直接解直角三角形
定义法
根据直角三角形的定义，利用勾股定理直接求解。
02
例题解析
直接应用
总结词
直接应用是指直接利用解直角三 角形的知识求解问题。
ห้องสมุดไป่ตู้详细描述
通过使用正切、余切、正弦和余 弦等三角函数的知识，可以解决 与直角三角形相关的问题，例如 求角度、长度等。
间接应用
总结词
间接应用是指通过解直角三角形来求 解其他问题。
详细描述
解直角三角形的知识可以用于解决一 些间接的问题，例如通过测量和计算 来求解实际问题，如建筑测量、航海 等。
模型法
将实际问题抽象成数学模型，利用解 直角三角形的知识求解模型，从而得 到实际问题的解。
04
专题练习
基础练习
直角三角形中的勾股定理
勾股定理是解直角三角形的基础，通过基础练习可以加深对勾股定理的理解和掌握。
全等三角形总复习课件
解题关键
理解面积的概念和计算方法，找出全等三角形，并利用全等三角形的 性质进行计算。
常见考点
全等三角形的判定和性质、面积的计算和比较、几何图形的面积公式 等。
05
全等三角形的易错点分析
判定定理的混淆
总结词
判定定理的混淆是学生在学习全等三角形时常见的问题，主要表现在不能正确理解和区 分SSS、SAS、ASA、AAS和HL等判定定理。
03
全等三角形的解题策略
构造法
总结词
通过添加辅助线构造新的三角形，利用已知条件证明新构造的三角形与原三角形全等，从而解决问题 。
详细描述
构造法是解决全等三角形问题的一种常用策略。通过作平行线、垂线或延长线等辅助线，构造出新的 三角形，利用已知条件证明新构造的三角形与原三角形全等，从而得出所需结论。在运用构造法时， 需要充分理解题意，寻找合适的构造方式。
详细描述
计算题通常会涉及角度、边长等几何量的计算。在解题过程中，学生需要利用 全等三角形的性质和定理，找到与所求量相关的已知量，通过计算得出结果。
作图题
总结词
作图题是全等三角形应用中较为特殊的一种题型，主要考察学生的空间想象能力 和作图技能。
详细描述
作图题通常会要求学生根据已知条件，画出两个全等的三角形。在解题过程中， 学生需要理解全等三角形的性质和判定定理，并能够根据题目要求进行准确的作 图。
推论
全等三角形的周长、面积 相等。
判定定理
SSS定理
SAS定理
如果两个三角形的三边分别相等，则这两 个三角形全等。
如果两个三角形的两边及其夹角分别相等 ，则这两个三角形全等。
ASA定理
HL定理
如果两个三角形的两角及其夹边分别相等 ，则这两个三角形全等。
理解面积的概念和计算方法，找出全等三角形，并利用全等三角形的 性质进行计算。
常见考点
全等三角形的判定和性质、面积的计算和比较、几何图形的面积公式 等。
05
全等三角形的易错点分析
判定定理的混淆
总结词
判定定理的混淆是学生在学习全等三角形时常见的问题，主要表现在不能正确理解和区 分SSS、SAS、ASA、AAS和HL等判定定理。
03
全等三角形的解题策略
构造法
总结词
通过添加辅助线构造新的三角形，利用已知条件证明新构造的三角形与原三角形全等，从而解决问题 。
详细描述
构造法是解决全等三角形问题的一种常用策略。通过作平行线、垂线或延长线等辅助线，构造出新的 三角形，利用已知条件证明新构造的三角形与原三角形全等，从而得出所需结论。在运用构造法时， 需要充分理解题意，寻找合适的构造方式。
详细描述
计算题通常会涉及角度、边长等几何量的计算。在解题过程中，学生需要利用 全等三角形的性质和定理，找到与所求量相关的已知量，通过计算得出结果。
作图题
总结词
作图题是全等三角形应用中较为特殊的一种题型，主要考察学生的空间想象能力 和作图技能。
详细描述
作图题通常会要求学生根据已知条件，画出两个全等的三角形。在解题过程中， 学生需要理解全等三角形的性质和判定定理，并能够根据题目要求进行准确的作 图。
推论
全等三角形的周长、面积 相等。
判定定理
SSS定理
SAS定理
如果两个三角形的三边分别相等，则这两 个三角形全等。
如果两个三角形的两边及其夹角分别相等 ，则这两个三角形全等。
ASA定理
HL定理
如果两个三角形的两角及其夹边分别相等 ，则这两个三角形全等。
三角形的初步知识复习ppt课件
改变条件：
1、如图，BE、CF是△ABC 的外角平分线，
∠A=40°求∠BOC度数． 700
2、如图，BE、CF分别是△ABC 的内角与外角平
20 分线，∠A=40°求∠BOC度数． 0
A
A
B
C
F
O
E
O
F
E
B
C
D
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
例1、已知如图，AB＝AC，AO平分∠BAC，请说明
(1)△ABO≌△ACO；（2）DO＝EO的理由.
A 解（1）∵ AO平分∠BAC（已知）
12
D
E
34 O
∴∠1=∠2 （角平分线定义）
在△ABO和△ACO中 AB=AC （已知）
∠1=∠2
B
AO=AO （公共边）
C ∴ △ABO≌△ACO（SAS）
BC=CD 或∠B=∠D
A
或∠BAC=∠DAC
C
5、如图，在△ABC中，AB=AC，E、F分 别为AB、AC上的点，且AE=AF，BF与CE
A D
相交于点O。
（1）图中有哪些全等的三角形？
E
F
△EBC≌△FCB（SSS）△EBO≌△FCO（AAS）
（2）图中有哪些相等的线段？
（3）图中有哪些相等的角？
A
ΔCBD≌ΔABE
E
S
A
S
B
C CB = AB ∠CBD = ∠ABE BD=BE
D
∠EBD -∠EBC = ∠ABC -∠EBC
∠EBD = ∠ABC = 60°
1、如图，BE、CF是△ABC 的外角平分线，
∠A=40°求∠BOC度数． 700
2、如图，BE、CF分别是△ABC 的内角与外角平
20 分线，∠A=40°求∠BOC度数． 0
A
A
B
C
F
O
E
O
F
E
B
C
D
为了规范事业单位聘用关系，建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ，保障 用人单 位和职 工的合 法权益
例1、已知如图，AB＝AC，AO平分∠BAC，请说明
(1)△ABO≌△ACO；（2）DO＝EO的理由.
A 解（1）∵ AO平分∠BAC（已知）
12
D
E
34 O
∴∠1=∠2 （角平分线定义）
在△ABO和△ACO中 AB=AC （已知）
∠1=∠2
B
AO=AO （公共边）
C ∴ △ABO≌△ACO（SAS）
BC=CD 或∠B=∠D
A
或∠BAC=∠DAC
C
5、如图，在△ABC中，AB=AC，E、F分 别为AB、AC上的点，且AE=AF，BF与CE
A D
相交于点O。
（1）图中有哪些全等的三角形？
E
F
△EBC≌△FCB（SSS）△EBO≌△FCO（AAS）
（2）图中有哪些相等的线段？
（3）图中有哪些相等的角？
A
ΔCBD≌ΔABE
E
S
A
S
B
C CB = AB ∠CBD = ∠ABE BD=BE
D
∠EBD -∠EBC = ∠ABC -∠EBC
∠EBD = ∠ABC = 60°
人教版11章《三角形》全章复习(共25张PPT)
例5 如图，在锐角△ABC中，CD、BE 分别是AB、AC边上的高，且CD、BE 交于一点P，若∠A=50°，则∠BPC的 度数是（B）
A.150° B.130° C.120° D.100°
例6 如图所示，BE与CD相交于点A，CF为∠BCD 的平分线，EF为∠BED的平分线。 （1）试探求∠F与∠B、∠D间有何等量关系。
（2）根据你的猜想，当n=4时说明∠BO3C的 度数成立.
解：当n=4时，代入所猜想的公式得 ∠BO3C=(1/4)×180°+(3/4)×∠A。
另外，在△BO3C中由三角形内角和定理 得：
∠BO[3]C=180°-（∠O3BC+∠O3CB） =180°-(3/4)（∠ABC+∠ACB） =180°-(3/4)（180°-∠A） =(1/4)×180°+(3/4)∠A
解：（1）∠D+∠B=2∠F ∵EF平分∠BED，CF平分∠BCD ∴∠DEF=(1/2)DEB，∠FCD=(1/2)∠BCD 而∠EMC=∠D+(1/2)∠BED，
∠EMC=∠F+(1/2)∠BCD ∴∠D+(1/2)∠BED=∠F+(1/2)∠BCD ① 同理可得： ∠B+(1/2)∠BCD=∠F+(1/2)∠BED ②
11章《三角形》 章末复习
R·八年级上册
知识框架
回顾思考
1.本章的主要内容是： 三角形的概念， 三角形的三边关系定理， 三角形的三条重要线段（高、中线和角平分线）， 三角形内角和定理。
三角形的外角，多边形的内、外角和定理，简单 的平面镶嵌。
三角形的稳定性和四边形的不稳定性。
2.经历三角形内角和等于180°的验证与证明过 程，初步体验对一个规律的发展到发现确认艰 辛历程。体会证明的重要性，初步接触辅助线 在几何研究中不 可或缺的作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 3、如图，在直角梯形ABCD中，BC⊥AB， BD⊥AD，CD∥AB，且BD=3，CD=2，则下底 AB的长是 。
D
C
A
B
（第3题图）
此课件下载可自行编辑修改，仅供参考！ 感谢您的支持，我们努力做得更好！谢谢
C
B
B
C
A
D 图2
达标训练
• （一）选择题 第1题图
•
1．（2010湖北武汉）如图，△ABC内有一点D， 且DA=DB=DC，若∠D AB=20°，∠DAC=30°，则∠BDC的大小是（ ） A.100 ° B.80° C.70° D.50°
A
D
B
C
• 2、如图，在ΔABC中，∠C=90°∠ABC的平分线 BD交AC于点D,若BD=10厘米，BC=8厘米，则 点D到直线AB的距离是__________厘米。
• (A)-6<a<-3 (B)-5<a<-2 (C)2<a<5 (D)a<-5 或a>-2
• 2．（2010四川 巴中）如图2 所示，AB = AC ， 要说明△ADC≌△AEB，需添加的条件
• 不能是（
) A．∠B ＝∠C B. AD = AE
C．∠ADC＝∠AEB D. DC = BE F
•
• 3.已知如图，在△ABC中，∠B＝90°，AB＝BC， BD ＝CE，M是AC的中点，
• 求证：△DEM是等腰三角形
典例剖析
• 例1.（1）如图1，点O是线段AD的中点，分别以AO和 DO为边在线段AD的同侧作等边三角形OAB和等边三 角形OCD，连结AC和BD，相交于点E，连结BC． 求 ∠AEB的大小；
（2）如图2，ΔOAB固定不动，保持ΔOCD的形状 和大小不变，将ΔOCD绕着点O旋转（ΔOAB和ΔOCD 不能重叠），求∠AEB的大小.
三角形专题复习课件
知识要点：
• 1、三角形的三边间的不等关系，三角形的内角 和，三角形的分类，全等三角形及其性质，三角 形全等判定。
• 2、等腰三角形、等腰三角形的性质和判定；等 边三角形、等边三角形的性质和判定；直角三角 形全等，轴对称、轴对称图形
考点再现
• 1．三角形的三边分别为3，1-2a,8,则a的取值范 围是（ ）
D
C
A
B
（第3题图）
此课件下载可自行编辑修改，仅供参考！ 感谢您的支持，我们努力做得更好！谢谢
C
B
B
C
A
D 图2
达标训练
• （一）选择题 第1题图
•
1．（2010湖北武汉）如图，△ABC内有一点D， 且DA=DB=DC，若∠D AB=20°，∠DAC=30°，则∠BDC的大小是（ ） A.100 ° B.80° C.70° D.50°
A
D
B
C
• 2、如图，在ΔABC中，∠C=90°∠ABC的平分线 BD交AC于点D,若BD=10厘米，BC=8厘米，则 点D到直线AB的距离是__________厘米。
• (A)-6<a<-3 (B)-5<a<-2 (C)2<a<5 (D)a<-5 或a>-2
• 2．（2010四川 巴中）如图2 所示，AB = AC ， 要说明△ADC≌△AEB，需添加的条件
• 不能是（
) A．∠B ＝∠C B. AD = AE
C．∠ADC＝∠AEB D. DC = BE F
•
• 3.已知如图，在△ABC中，∠B＝90°，AB＝BC， BD ＝CE，M是AC的中点，
• 求证：△DEM是等腰三角形
典例剖析
• 例1.（1）如图1，点O是线段AD的中点，分别以AO和 DO为边在线段AD的同侧作等边三角形OAB和等边三 角形OCD，连结AC和BD，相交于点E，连结BC． 求 ∠AEB的大小；
（2）如图2，ΔOAB固定不动，保持ΔOCD的形状 和大小不变，将ΔOCD绕着点O旋转（ΔOAB和ΔOCD 不能重叠），求∠AEB的大小.
三角形专题复习课件
知识要点：
• 1、三角形的三边间的不等关系，三角形的内角 和，三角形的分类，全等三角形及其性质，三角 形全等判定。
• 2、等腰三角形、等腰三角形的性质和判定；等 边三角形、等边三角形的性质和判定；直角三角 形全等，轴对称、轴对称图形
考点再现
• 1．三角形的三边分别为3，1-2a,8,则a的取值范 围是（ ）