逐步回归matlab程序
- 格式：doc
- 大小：18.00 KB
- 文档页数：3
下载文档原格式
合集下载
matlab回归建模过程
matlab回归建模过程摘要：一、回归建模概述- 回归分析的定义- 回归建模的目的和意义二、MATLAB 回归建模过程- 一元线性回归- 数学模型定义- 模型参数估计- 检验、预测及控制- 多元线性回归- 数学模型定义- 模型参数估计- 多元线性回归中检验与预测- 逐步回归分析三、MATLAB 回归建模应用案例- 案例一：一元线性回归分析- 案例二：多元线性回归分析- 案例三：逐步回归分析正文：一、回归建模概述回归分析是一种研究变量之间关系的统计方法，通过建立一个数学模型，描述自变量与因变量之间的线性关系。
回归建模在实际应用中有着广泛的应用，如经济学、生物学、社会学等学科的研究中，可以帮助我们更好地理解变量之间的关系，并对未来趋势进行预测和控制。
MATLAB 是一种广泛应用于科学计算和数据分析的编程语言，提供了丰富的回归建模工具箱，可以帮助我们快速、高效地进行回归建模分析。
二、MATLAB 回归建模过程1.一元线性回归一元线性回归是最简单的回归分析方法，适用于只有一个自变量和一个因变量的情况。
在MATLAB 中，我们可以使用回归分析工具箱中的`regress`函数进行一元线性回归建模。
（1）数学模型定义一元线性回归的数学模型可以表示为：y = a + bx其中，y 表示因变量，x 表示自变量，a 和b 分别表示回归系数。
（2）模型参数估计在MATLAB 中，我们可以使用`regress`函数对模型参数进行估计。
函数的原型为：b = regress(y, x)其中，y 表示因变量向量，x 表示自变量向量，b 表示回归系数向量。
（3）检验、预测及控制在得到回归系数向量b 后，我们可以进行回归检验、预测以及控制。
2.多元线性回归多元线性回归适用于有多个自变量和因变量的情况。
在MATLAB 中，我们可以使用回归分析工具箱中的`polyfit`函数进行多元线性回归建模。
（1）数学模型定义多元线性回归的数学模型可以表示为：y = a0 + a1x1 + a2x2 + ...+ anxn其中，y 表示因变量，x1、x2、...、xn 表示自变量，a0、a1、a2、...、an 分别表示回归系数。
matlab多元线性回归与逐步回归实验1
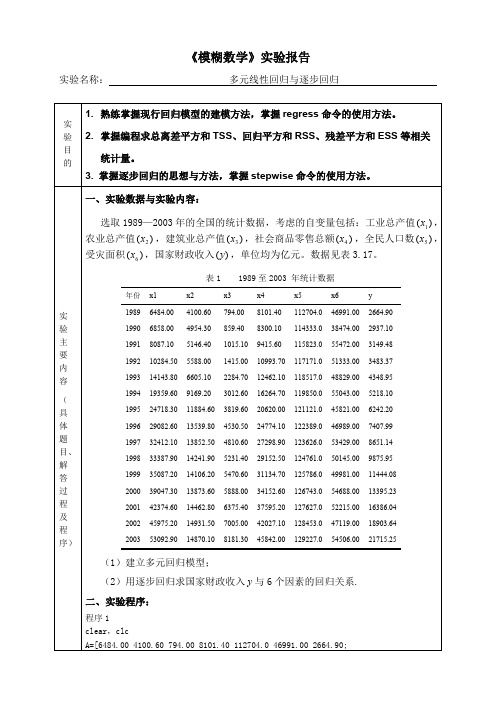
《模糊数学》实验报告实验名称：多元线性回归与逐步回归实验目的1.熟练掌握现行回归模型的建模方法，掌握regress命令的使用方法。
2.掌握编程求总离差平方和TSS、回归平方和RSS、残差平方和ESS等相关统计量。
3. 掌握逐步回归的思想与方法，掌握stepwise命令的使用方法。
实验主要内容（具体题目、解答过程及程序）一、实验数据与实验内容：选取1989—2003年的全国的统计数据，考虑的自变量包括：工业总产值，)(1x农业总产值，建筑业总产值，社会商品零售总额，全民人口数，)(2x)(3x)(4x)(5x受灾面积，国家财政收入，单位均为亿元。
数据见表3.17。
)(6x)(y表1 1989至2003 年统计数据年份x1x2x3x4x5x6y19896484.004100.60794.008101.40112704.046991.002664.9019906858.004954.30859.408300.10114333.038474.002937.1019918087.105146.401015.109415.60115823.055472.003149.48199210284.505588.001415.0010993.70117171.051333.003483.37199314143.806605.102284.7012462.10118517.048829.004348.95199419359.609169.203012.6016264.70119850.055043.005218.10199524718.3011884.603819.6020620.00121121.045821.006242.20199629082.6013539.804530.5024774.10122389.046989.007407.99199732412.1013852.504810.6027298.90123626.053429.008651.14199833387.9014241.905231.4029152.50124761.050145.009875.95199935087.2014106.205470.6031134.70125786.049981.0011444.08200039047.3013873.605888.0034152.60126743.054688.0013395.23200142374.6014462.806375.4037595.20127627.052215.0016386.04200245975.2014931.507005.0042027.10128453.047119.0018903.64200353092.9014870.108181.3045842.00129227.054506.0021715.25（1）建立多元回归模型；（2）用逐步回归求国家财政收入与6个因素的回归关系.y二、实验程序：程序1clear，clcA=[6484.00 4100.60 794.00 8101.40 112704.0 46991.00 2664.90;6858.00 4954.30859.40 8300.10 114333.038474.00 2937.10;8087.105146.401015.109415.60115823.055472.003149.48;10284.505588.001415.0010993.70117171.051333.003483.37; 14143.806605.102284.7012462.10118517.048829.004348.95; 19359.609169.203012.6016264.70119850.055043.005218.10; 24718.3011884.603819.6020620.00121121.045821.006242.20; 29082.6013539.804530.5024774.10122389.046989.007407.99; 32412.1013852.504810.6027298.90123626.053429.008651.14; 33387.9014241.905231.4029152.50124761.050145.009875.95; 35087.2014106.205470.6031134.70125786.049981.0011444.08; 39047.3013873.605888.0034152.60126743.054688.0013395.23; 42374.6014462.806375.4037595.20127627.052215.0016386.04; 45975.2014931.507005.0042027.10128453.047119.0018903.64; 53092.9014870.108181.3045842.00129227.054506.0021715.25];%自变量数据[m,n]=size(A);subplot(3,2,1),plot(A(:,1),A(:,7),'+')xlabel('x1(工业总产值)')ylabel('y(国家财政收入)')subplot(3,2,2),plot(A(:,2),A(:,7),'*')xlabel('x2(农业总产值)')ylabel('y(国家财政收入)')subplot(3,2,3),plot(A(:,3),A(:,7),'o')xlabel('x3(建筑业总产值)')ylabel('y(国家财政收入)')subplot(3,2,4),plot(A(:,4),A(:,7),'+')xlabel('x4(社会商品零售总额)')ylabel('y(国家财政收入)')subplot(3,2,5),plot(A(:,5),A(:,7),'*')xlabel('x5(全民人口数)')ylabel('y(国家财政收入)')subplot(3,2,6),plot(A(:,6),A(:,7),'o')xlabel('x6(受灾面积)')ylabel('y(国家财政收入)')x=[ones(m,1),A(:,1),A(:,2),A(:,3),A(:,4),A(:,5),A(:,6)];%构造设计矩阵y=A(:,7);[n,p]=size(x);%矩阵x0的行数即样本容量[db,dbint,dr,drint,dstats]=regress(y,x)%调用多元回归分析命令TSS=y'*(eye(n)-1/n*ones(n,n))*y%计算TSSH=x*inv((x'*x))*x';%计算对称幂等矩阵ESS=y'*(eye(n)-H)*y%计算ESSRSS=y'*(H-1/n*ones(n,n))*y%计算RSSMRS=RSS/p%计算MRSMSE=ESS/(n-p-1)%计算MSE%F检验F0=(RSS/p)/(ESS/(n-p-1))%计算F0。
MATLAB统计工具箱中的回归分析命令
解 设国民收入、工业总产值、农业总产值、总人口、就业 人口、固定资产投资分别为x1、x2、x3、x4、x5、x6，财政收 入为y，设变量之间的关系为： y= ax1+bx2+cx3+dx4+ex5+fx6 使用非线性回归方法求解.
1． 对回归模型建立M文件model.m如下: function yy=model(beta0,X) a=beta0(1); b=beta0(2); c=beta0(3); d=beta0(4); e=beta0(5); f=beta0(6); x1=X(:,1); x2=X(:,2); x3=X(:,3); x4=X(:,4); x5=X(:,5); x6=X(:,6); yy=a*x1+b*x2+c*x3+d*x4+e*x5+f*x6;
回 归 系
残 差
置 信 区
数
间
显著性水平 （缺省时为0.05）
的
用于检验回归模型的统计量，
区
有三个数值：相关系数r 2、
间 估
F值、与F 对应的概率p
计
相关系数 r2 越接近 1，说明回归方程越显著；
F > F1-α （k，n-k-1）时拒绝 H0，F 越大，说明回归方程越显著；
与 F 对应的概率 p 时拒绝 H0，回归模型成立.
例3 设某商品的需求量与消费者的平均收入、商品价格的统计数 据如下，建立回归模型，预测平均收入为1000、价格为6时 的商品需求量.
需求量 100 75
80
70
50
65
90
100 110 60
收入 1000 600 1200 500 300 400 1300 1100 1300 300
1． 对回归模型建立M文件model.m如下: function yy=model(beta0,X) a=beta0(1); b=beta0(2); c=beta0(3); d=beta0(4); e=beta0(5); f=beta0(6); x1=X(:,1); x2=X(:,2); x3=X(:,3); x4=X(:,4); x5=X(:,5); x6=X(:,6); yy=a*x1+b*x2+c*x3+d*x4+e*x5+f*x6;
回 归 系
残 差
置 信 区
数
间
显著性水平 （缺省时为0.05）
的
用于检验回归模型的统计量，
区
有三个数值：相关系数r 2、
间 估
F值、与F 对应的概率p
计
相关系数 r2 越接近 1，说明回归方程越显著；
F > F1-α （k，n-k-1）时拒绝 H0，F 越大，说明回归方程越显著；
与 F 对应的概率 p 时拒绝 H0，回归模型成立.
例3 设某商品的需求量与消费者的平均收入、商品价格的统计数 据如下，建立回归模型，预测平均收入为1000、价格为6时 的商品需求量.
需求量 100 75
80
70
50
65
90
100 110 60
收入 1000 600 1200 500 300 400 1300 1100 1300 300
利用MATLAB进行回归分析
利用MATLAB进行回归分析一、实验目的：1．了解回归分析的基本原理，掌握MATLAB实现的方法；2. 练习用回归分析解决实际问题。
二、实验内容：题目1社会学家认为犯罪与收入低、失业及人口规模有关，对20个城市的犯罪率y（每10万人中犯罪的人数）与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数3x（千人）进行了调查，结果如下表。
（1）若1x~3x中至多只许选择2个变量，最好的模型是什么？（2）包含3个自变量的模型比上面的模型好吗？确定最终模型。
（3）对最终模型观察残差，有无异常点，若有，剔除后如何。
理论分析与程序设计：为了能够有一个较直观的认识，我们可以先分别作出犯罪率y与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数x（千人）之间关系的散点图，根据大致分布粗略估计各因素造3成的影响大小，再通过逐步回归法确定应该选择哪几个自变量作为模型。
编写程序如下：clc;clear all;y=[11.2 13.4 40.7 5.3 24.8 12.7 20.9 35.7 8.7 9.6 14.5 26.9 15.736.2 18.1 28.9 14.9 25.8 21.7 25.7];%犯罪率（人/十万人）x1=[16.5 20.5 26.3 16.5 19.2 16.5 20.2 21.3 17.2 14.3 18.1 23.1 19.124.7 18.6 24.9 17.9 22.4 20.2 16.9];%低收入家庭百分比x2=[6.2 6.4 9.3 5.3 7.3 5.9 6.4 7.6 4.9 6.4 6.0 7.4 5.8 8.6 6.5 8.36.7 8.6 8.4 6.7];%失业率x3=[587 643 635 692 1248 643 1964 1531 713 749 7895 762 2793 741 625 854 716 921 595 3353];%总人口数（千人）figure(1),plot(x1,y,'*');figure(2),plot(x2,y,'*');figure(3),plot(x3,y,'*');X1=[x1',x2',x3'];stepwise(X1,y)运行结果与结论：犯罪率与低收入散点图犯罪率与失业率散点图犯罪率与人口总数散点图低收入与失业率作为自变量低收入与人口总数作为自变量失业率与人口总数作为自变量在图中可以明显看出前两图的线性程度很好，而第三个图的线性程度较差，从这个角度来说我们应该以失业率和低收入为自变量建立模型。
matlab数据拟合回归分析
返回
二、模型参数估计
1、回归系数的最小二乘估计
有 n 组独立观测值， 1，y1）（x2，y2） （x ， ，„， n，yn） （x
yi 0 1 x i i , i 1,2,..., n 设 E i 0, D i 2 且 1 2， n 相 互 独 立 ...,
y与x2的散点图
y 0 1 x1 2 x2 3 x3
回归系数0, 1, 2, 3 由数据估计, 是随机误差
MATLAB 统计工具箱常用命令(1)
多元线性回归 y 0 1 x1 ... p x p
1、确定回归系数的点估计值：
b=regress( Y, X )
固定的未知参数 0 、 1 称为回归系数，自变量 x 也称为回归变量.
Y 0 1 x ，称为 y 对 x 的回归直线方程.
一元线性回归分析的主要任务是：
1、用试验值（样本值）对 0 、 1 和 作点估计； 2、对回归系数 0 、 1 作假设检验； 3、在 x= x0 处对 y 作预测，对 y 作区间估计.
1 n 2 1 n xi , xy xi yi . n i 1 n i 1
（经验）回归方程为:
ˆ ˆ ˆ ˆ y 0 1 x y 1 ( x x )
2 的无偏估计 2、
ˆ ˆ 记 Qe Q( 0 , 1 ) ˆ y
n i 1 i 0
默认值是
0.05
[b, bint, r, rint, stats] = regress(Y, X, alpha)
1 x11 x1m 相关系数R2，F-统计量和与F(1,n-2) 分布大于 回归系数beta以及它们的置信区间 y1 残差向量r=Y-Y及它们的置信区间 X , Y F值的概率p，p<时回归模型有效. 1 x n1 x nm yn
天大matlab大作业逐步回归方法分析
逐步回归分析方法在实际中，影响Y的因素很多，这些因素可能存在多重共线性（相关性），这就对系数的估计带来不合理的解释，从而影响对Y的分析和预测。
“最优”的回归方程就是包含所有对Y有影响的变量, 而不包含对Y 影响不显著的变量回归方程。
选择“最优”的回归方程有以下几种方法：（1）从所有可能的因子（变量）组合的回归方程中选择最优者；（2）从包含全部变量的回归方程中逐次剔除不显著因子；（3）从一个变量开始，把变量逐个引入方程；（4）“有进有出”的逐步回归分析。
以第四种方法，即逐步回归分析法在筛选变量方面较为理想.逐步回归分析法的思想：从一个自变量开始，视自变量Y作用的显著程度，从大到小地依次逐个引入回归方程。
当引入的自变量由于后面变量的引入而变得不显著时，要将其剔除掉。
引入一个自变量或从回归方程中剔除一个自变量，为逐步回归的一步。
对于每一步都要进行Y值检验，以确保每次引入新的显著性变量前回归方程中只包含对Y作用显著的变量。
这个过程反复进行，直至既无不显著的变量从回归方程中剔除，又无显著变量可引入回归方程时为止。
原理：1、最优选择的标准设n 为观测样本数，},,,{21m x x x X为所有自变量构成的集合，li i i x x x A ,,,21 为X 的子集。
（1）均方误差s2最小达到最小（2）预测均方误差最小A S l n l n A J E 11)(达到最小（3）统计量最小准则nl m n S A S A C EE p21达到最小（4）AIC 或BIC 准则n lA S A AIC E 2ln )(或n n l A S A BIC E ln ln )( 达到最小 （5）修正R 2准则)1(122R l n in R 达到最大2、选择最优回归子集的方法（1）选择最优子集的简便方法：逐步筛选法（STEPWISE）向前引入法或前进法（FORWARD）向后剔除法或后退法（BACKWARD）（2）计算量最大的全子集法：R2选择法（RSQUARE）Cp选择法（CP）修正R2选择法（ADJRSQ）。
MATLAB程序设计之算法回归分析54页PPT
15.08.2021
故 T t 1 ( n 2 ) ， 拒 绝 H 0 ， 否 则 就 接 受 H 0 .
2 n
n
其 L x 中 x (x i x )2x i2 n x 2
i 1
i 1
11
（Ⅲ）r检验法
n
( x i x ) y i ( y )
记 r i 1
n
n
( x i x ) 2( y i y ) 2
n
n
记Q Q (0,1) i2 yi01xi2
i 1
i 1
最 小 二 乘 法 就 是 选 择 0和 1的 估 计 ˆ0， ˆ1 使 得
Q (ˆ0,ˆ1)m 0,1Q i(n0, 1)
15.08.2021
7
ˆ
0
y
ˆ1x
ˆ1
xy x2
xy x2
n x i x y i y
8
2 2
n
记 Qe Q(ˆ0,ˆ1)
yi ˆ0 ˆ1xi 2 n (yi yˆi )2
i1
i1
称Qe为残差平方和或剩余平方和.
2 的无偏估计为 ˆe2 Qe (n2)
称ˆe2
为剩余方差（残差的方差），ˆ
2 e
分别与ˆ0ˆ1、 独立。
ˆe 称为剩余标准差.
15.08.2021
返回
9
三、检验、预测与控制
和 ˆ 1 t 1 2 ( n 2 ) ˆ e /L x ,ˆ x 1 t 1 2 ( n 2 ) ˆ e /L x x
2 的 置 信 水 平 为 1 - 的 置 信 区 间 为 1 2 2 Q ( n e 2 ) , 2 2 ( Q n e 2 )
i 1
i 1
用MATLAB求解回归分析
（2）非线性回归命令：nlintool（x，y，’model’, beta0，alpha） ） 2、预测和预测误差估计： 、预测和预测误差估计： [Y，DELTA]=nlpredci（’model’, x，beta，r，J） 求nlinfit 或nlintool所得的回归函数在x处的预测值Y及预测值的显 著性为1-alpha的置信区间Y ± DELTA.
4、预测及作图： [;,x',beta,r ,J)； plot(x,y,'k+',x,YY,'r')
例5 财政收入预测问题：财政收入与国民收入、工业总产值、 农业总产值、总人口、就业人口、固定资产投资等因素有关。 下表列出了1952-1981年的原始数据，试构造预测模型。
得结果：b = -16.0730 0.7194 stats = 0.9282 180.9531 0.0000 bint = -33.7071 0.6047 1.5612 0.8340
ˆ ˆ ˆ ˆ 即 β 0 = −16.073, β 1 = 0.7194 ； β 0 的置信区间为[-33.7017，1.5612], β 1 的置信区间为[0.6047,0.834];
回 归 系 数 的 区 间 估 计 F 检验回归模型的 计 数 ： 系数r2、 、 F 的 p 差 区 间 时 为 水 0 平 05 ） . 性 残 信 省 著 置 （缺 显
系数 r2 F > F1F k 的 n-k-1
1
回归 H0 F H0 回归模型 回归 .
p< α
3、 、
区间： 区间：
rcoplot
r2=0.9282, F=180.9531, p=0.0000 p<0.05, 可知回归模型 y=-16.073+0.7194x 成立.
3.3 逐步回归
方法2：逐步引入法—只进不出
3.3.1最优回归方程的选择
•思想：所有可能自变量集合{X1,
X2,…,XM},从一个变量开始 ，按重要性把变量逐个引入回归方程 .
计算M个变量Xi与Y的相关系数，将绝对值最大的变量Xi1引入 方程，并对{Y,Xi1}回归模型进行显著性检验,若显著则引入; 找出余下M-1个自变量中与Y偏相关系数最大变量Xi2引入方程 ,检验{Y,Xi1,Xi2}回归显著性,显著则引入,否则停止,不引入; 剩下的M-2个变量中选择与Y偏相关系数最大变量Xi3 ,检验 {Y,Xi1,Xi2,Xi3}显著性，...,直至得到“最优”回归方程为止 .
3.3 逐步回归分析
Y f ( X1 , X 2 ,, X p )
因变量 确定函数关系 自变量，回归变量
随机误差项
Y 0 1 X1 2 X 2 p X p
0 , 1 , p ----待定常数，回归系数
3.3 逐步回归
1 最优回归方程选择 逐步回归Matlab方法
程序执行后得到下列逐步回归的窗口(如图3.23所示)：
图3.23 逐步回归窗口
图中蓝色行显示变量x1、x2、x3、x4均保留在模型中,窗口 右侧按钮上方提示:将变量x3剔除回归方程(Move x3 out).
1.点击Next Step进行下一步运算,将第3列数据对应变量x3剔除回 归方程;点击Next Step,剔除的变量x3对应行用红色表示,同时又得 到提示:将变量x4剔除回归方程(Move x4 out)；
~ ~ ~ 剔除X k 后模型 Y 0 1 X1 2 X 2 l X l (*) 变为集A,SSE(A)
绝对贡献
SSR( X k | A) SSE( A) SSE( A, X k ) - -剔除后残差增加量
(完整)逐步回归matlab程序
function stepregress（x，y,F)x=zscore（x，1）；％数列标准化y=zscore（y,1)；％数列标准化r=corrcoef（[x，y]）;l=0; %消去的次数L=0; %引入变量的个数［n,m］=size(x）; %m为变量的个数，n为观测的次数k=ones(m)；q=1; ％判断逐步回归是否继续while（q==1）q=0;for i=1：mv(i）=r（i，m+1)^2/r(i,i）； %计算各因子的方差贡献endmax=1；min=1;for i=1:mif（(max==1)&＆(k(i）==1)&&(k（1）==0))|｜((v(i）>v（max））&＆（k（i）==1)） max=i；endif(（min==1）&&(k(i）==0）&＆（k(1)==1)）｜|(（v(i）〈v(min)）＆＆（k(i)==0)) min=i；endendif(l〈3)＆&(L+1<=m)F1=v（max）/（(r（m+1,m+1)—v（max）)/（n—l—2)）;if（F1>F）disp( ［ '引入第'， num2str（max)，’个变量'］）;k(max)=0;L=L+1；l=l+1;r=matdel（max,m+1，r); %matdel为消去变换程序q=1；endelseF2=v（min）/(r(m+1,m+1)/(n-l—1）);if（(F2<F)＆&（k（min)==0))disp( [ '剔除第’， num2str(min）, ’个变量']）；k(min)=1；L=L-1；l=l+1；r=matdel（min，m+1，r)；q=1；elseF1=v(max）/（（r(m+1，m+1）—v（max)）/(n—l—2));if（F1>F）disp（ [ ’引入第', num2str（max）, ’个变量’］);k(max)=0; ％如果变量i引入,则对应的k变为0L=L+1;l=l+1;r=matdel（max,m+1,r）;q=1;endendendenddisp（'没有可剔除或引入的变量,逐步回归结束’);a=zeros(L);j=1；for i=1:mif (k(i）==0）a(j)=i;j=j+1；end;end；xx=x(：，a(1));for i=2：Lxx=［xx x(:，a(i)）];end;b=regress（y,xx)；％回归系数R=sqrt(1-r(m+1,m+1））；％复相关系数yyy=xx*b; %y的估计值ymean=mean(y)； %y平均值Q=（y—yyy）'*(y—yyy); ％剩余平方和U=(yyy-ymean)’＊（yyy-ymean)； %回归平方和rs=Q/（n—L-1）; ％剩余方差f=U/L/（Q/(n—L—1）)； %F统计量fid=fopen（’result'，’w')；ss=['引入第’，num2str（a（1)）];for i=2：Lss=[ss，’,’,num2str（a(i))］;endss=［ss,'个变量’］;ss1=[’y=(',num2str(b(1))，'x’，num2str(a(1）)，'）']；for i=2：Lss1=［ss1，’+(',num2str（b（i)）,'x’,num2str（a(i）)，’)'］；end；ss2=[’复相关系数=’，num2str（R)］；ss3=[’剩余方差='，num2str(rs）］;ss4=［’F统计量=',num2str(f)];ss5=［’剩余平方和=’，num2str(Q）］;fprintf(fid,'％s\n’,ss）；fprintf(fid,’%s\n’，ss1）;fprintf（fid,’%s\n'，ss2）;fprintf(fid，’％s\n’，ss3)；fprintf（fid,'%s\n',ss4）; fprintf（fid，’％s’，ss5）；fclose(fid）;end。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
~
function stepregress(x,y,F)
x=zscore(x,1); %数列标准化
y=zscore(y,1); %数列标准化
r=corrcoef([x,y]);
l=0; %消去的次数
L=0; %引入变量的个数
[n,m]=size(x); %m为变量的个数，n为观测的次数
k=ones(m);
?
q=1; %判断逐步回归是否继续
while(q==1)
q=0;
for i=1:m
v(i)=r(i,m+1)^2/r(i,i); %计算各因子的方差贡献
end
max=1;
min=1;
>
for i=1:m
if((max==1)&&(k(i)==1)&&(k(1)==0))||((v(i)>v(max))&&(k(i)==1)) max=i;
end
if((min==1)&&(k(i)==0)&&(k(1)==1))||((v(i)<v(min))&&(k(i)==0)) min=i;
end
end
《
if(l<3)&&(L+1<=m)
F1=v(max)/((r(m+1,m+1)-v(max))/(n-l-2));
if(F1>F)
disp( [ '引入第', num2str(max), '个变量']);
k(max)=0;
L=L+1;
l=l+1;
￥
r=matdel(max,m+1,r); %matdel为消去变换程序
q=1;
end
else
F2=v(min)/(r(m+1,m+1)/(n-l-1));
if((F2<F)&&(k(min)==0))
disp( [ '剔除第', num2str(min), '个变量']);
k(min)=1;
…
L=L-1;
l=l+1;
r=matdel(min,m+1,r);
q=1;
else
F1=v(max)/((r(m+1,m+1)-v(max))/(n-l-2));
if(F1>F)
disp( [ '引入第', num2str(max), '个变量']); /
k(max)=0; %如果变量i引入，则对应的k变为0 L=L+1;
l=l+1;
r=matdel(max,m+1,r);
q=1;
end
end
end
…
end
disp('没有可剔除或引入的变量，逐步回归结束');
a=zeros(L);
j=1;
for i=1:m
if (k(i)==0)
a(j)=i;
、
j=j+1;
end;
end;
xx=x(:,a(1));
for i=2:L
xx=[xx x(:,a(i))];
end;
b=regress(y,xx); %回归系数
!
R=sqrt(1-r(m+1,m+1)); %复相关系数
yyy=xx*b; %y的估计值
ymean=mean(y); %y平均值
Q=(y-yyy)'*(y-yyy); %剩余平方和
U=(yyy-ymean)'*(yyy-ymean); %回归平方和
rs=Q/(n-L-1); %剩余方差
f=U/L/(Q/(n-L-1)); %F统计量
fid=fopen('result','w');
/
ss=['引入第',num2str(a(1))];
for i=2:L
ss=[ss,',',num2str(a(i))];
end
ss=[ss,'个变量'];
ss1=['y=（',num2str(b(1)),'x',num2str(a(1)),')'];
for i=2:L
ss1=[ss1,'+(',num2str(b(i)),'x',num2str(a(i)),')']; }
end;
ss2=['复相关系数=',num2str(R)];
ss3=['剩余方差=',num2str(rs)];
ss4=['F统计量=',num2str(f)];
ss5=['剩余平方和=',num2str(Q)];
fprintf(fid,'%s\n',ss);
fprintf(fid,'%s\n',ss1);
fprintf(fid,'%s\n',ss2);
<
fprintf(fid,'%s\n',ss3);
fprintf(fid,'%s\n',ss4);
fprintf(fid,'%s',ss5);
fclose(fid);
end。