第6章 时变电磁场(6).

第六章时变电磁场有一导体滑片在两根平行的轨道上滑动，整个装置位于正弦时变磁场之中，如题图所示。

滑片的位置由确定，轨道终端接有电阻，试求电流i.解穿过导体回路abcda的磁通为故感应电流为一根半径为a的长圆柱形介质棒放入均匀磁场中与z轴平行。

设棒以角速度绕轴作等速旋转，求介质内的极化强度、体积内和表面上单位长度的极化电荷。

解介质棒内距轴线距离为r处的感应电场为故介质棒内的极化强度为极化电荷体密度为极化电荷面密度为则介质体积内和表面上同单位长度的极化电荷分别为平行双线传输线与一矩形回路共面，如题图所示。

设、、，求回路中的感应电动势。

解由题给定的电流方向可知，双线中的电流产生的磁感应强度的方向，在回路中都是垂直于纸面向内的。

故回路中的感应电动势为式中故则有一个环形线圈，导线的长度为l，分别通过以直流电源供应电压U0和时变电源供应电压U（t）。

讨论这两种情况下导线内的电场强度E。

解设导线材料的电导率为，横截面积为S，则导线的电阻为而环形线圈的电感为L，故电压方程为当U=U0时，电流i也为直流，。

故此时导线内的切向电场为当U=U（t）时，，故即求解此微分方程就可得到。

一圆柱形电容器，内导体半径为a，外导体内半径为b，长为l。

设外加电压为，试计算电容器极板间的总位移电流，证明它等于电容器的传导电流。

解当外加电压的频率不是很高时，圆柱形电容器两极板间的电场分布与外加直流电压时的电场分布可视为相同（准静态电场），即故电容器两极板间的位移电流密度为则式中，是长为l的圆柱形电容器的电容。

流过电容器的传导电流为可见由麦克斯韦方程组出发，导出点电荷的电场强度公式和泊松方程。

解点电荷q产生的电场满足麦克斯韦方程和由得据散度定理，上式即为利用球对称性，得故得点电荷的电场表示式由于，可取，则得即得泊松方程试将麦克斯方程的微分形式写成八个标量方程：（1）在直角坐标中；（2）在圆柱坐标中；（3）在球坐标中。

解（1）在直角坐标中（2）在圆柱坐标中（3）在球坐标系中已知在空气中，求和。

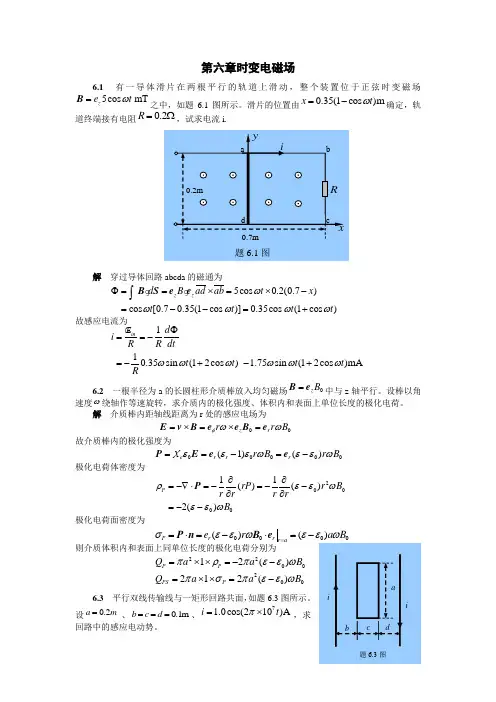
第六章时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动，整个装置位于正弦时变磁场5cos mT z e t ω=B 之中，如题6.1图所示。

滑片的位置由0.35(1cos )m x t ω=-确定，轨道终端接有电阻0.2R =Ω，试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰ B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。

设棒以角速度ω绕轴作等速旋转，求介质内的极化强度、体积内和表面上单位长度的极化电荷。

解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面，如题6.3图所示。

设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯，求回路中的感应电动势。

第5章 恒定电流的磁场欧阳光明（2021.03.07）5.1简述安培力定理答：在真空中有两个通有恒定电流I 1和I 2的细导线回路，它们的长度分别是l 1和l 2。

通有电流I 1的回路对通有电流I 2 的回路的作用力F 12是5.2一个半径为a 的圆线圈，通有电流I ，求圆线圈轴线上任一点的磁感应强度B 。

解：根据电流的对称性，采用圆柱坐标系，坐标原点设在圆形线圈的圆心，Z 轴与线圈轴线重合，场点P 的坐标为),,0(z α ，取一个电流元＇αIad ，源点坐标为),,(０＇αa ,如题5-2图所示，则r z ae Ze -Ｒ＝，当z=0时，Zea I a U B 23220)(2=5.3简述洛仑兹力答：电荷以某一速度v 在磁场运动，磁场对运动电荷有作用力，这种作用力称为洛仑兹力，洛仑兹力与运动电荷垂直。

所以，他不作功，只改变运动电荷的方向，不改变运动电荷的速度。

5.4 矢量磁位与磁感应强度的关系是什么？ 答：矢量磁位的旋度是磁感应强度5.5已知某一电流在空间产生的矢量磁位A ，求磁感应强度B 。

（xyz e xy e y xe A z y x422-+=）解： )4()(22z y x z y xxyze e xy ye x e ze y exA B -+⨯∂∂+∂∂+∂∂=⨯∇= =z y x x z y ze x y yze xze xze e x yze ey )(44442222-++-=--+5.6 有一根长位2L 的细直导线与柱坐标的z 轴重合，导线的中心在坐标原点。

设导线中通有电流I ，方向沿z 轴的方向。

1）求空间任一点()z p ,,ϕρ 的矢量磁位A ；2）求在z=0的平面上任一点()z p ,,ϕρ的矢量磁位A 。

当ρ<<2L 和ρ>>2L 时，结果又如何？解：1）由于对称性，可以只讨论Z ≥0的情况由矢量磁位方程得：ze RIdz dA πμ40=θsin r R =θrctg Z Z-=＇θθd r dZ2sin =＇θθπμπμd Ie e RdZd zz sin 44I A 00==＇在整条线段上积分得 由 C ctg d +-=⎰)sin 1ln(sin θθθθ 得)cos 1(sin )cos 1(sin ln4sin cos sin 1sin cos sin 1ln 4122101112220θθθθπμθθθθθθπμ--=--=z z Ie e Ie A 由图可知 221)(sin l z r r ++=θ 222)(sin l z r r -+=θ（1）z e l z l z r l z l z r I A )()()()(ln422220+-++---+=πμ（2）在Z=0时，r ll r I r l l r I e l l r l l r l l r l l r I e l l r ll r I A zz ++++=++-+++++=-+++=2202222022222222022220ln 2)(ln 4))(())((ln 4ln 4πμπμπμπμ5.7什么是磁偶极子？答：如果观察距离R 远远大于一个小圆形电流线圈的半径（半径为r ），即R>>r 。

第六章 层状媒质中偶极子源的电磁场6-1 利用磁场边界条件，证明位于无限大理想导电平面附近的垂直电流元及磁流元的镜像关系。

6-2 一个平行电流元I l 位于无限大的理想导电平面附近，距离为d ，如习题6-2图所示。

试求空间辐射场。

y习题6-2图解：假定电流源元a a I l 在空间某点可以产生的电场强度a E 。

在该点放置另一个点电流元b b I l ，且令b l 和a E 的方向一致。

已知理想导体表面仅可以存在电场强度的垂直分量，所以电流源b b I l 在电流元a a I l 附近产生的电场强度b E 必须垂直于理想导体表面，因而同时也垂直于电流元a a I l 。

对于该两组源a a I l 、b b I l 及其产生的电场强度a E 、b E ，应用Carson 互易原理，并考虑到电流元()I ds l dV ==l J J 及a b b a b b I I ⋅=E l E l ，求得b a a a b b I I ⋅=E l E l 。

由于b a ⊥E l ，所以上式左端为零，即0a b b E I L =。

但0b b I L ≠，因此只能0a E =，即位于理想导体表面附近的平行电流元不可能在空间产生任何电磁场。

6-3 谐变频率为ω、磁偶极距为i 0etω=m m 的谐变磁偶极子垂直放置于两媒质的分界面上方，如习题6-3图所示。

求媒质1和媒质2中反射波及透射波。

习题6-3图解：易知磁偶极子垂直于分界面，故其激发TE 波，由图形可知z m m =e ，z d =一次场的矢量位仅有z 分量且满足标量波动方程22()()()m m A k A i m x y z d ωεμδδδ∇+=-在0z d ≤≤的区域内，一次场的平面波分量为1102d zm i m A e e εεϖεμε--=则反射波和透射波的矢量位分别为1111102d z m TEi m A R e e εεϖεμε--=，2211202d zm i m A e e εεϖεμε--= 其中反射系数1212TE R ξξξξ-=+，透射系数1122TE T ξξξ=+对以上两式进行傅里叶反变换得1111()111010(,)()4z d m TE k i m A z R e J k dk ρξρρωεμρρπξ∞-+=⎰ 2()112202220(,)()4z d m TE i m k A z T e J k dk ξωεμρρρρρπξ∞-=⎰ 由公式1m m ξ=-∇⨯E A ，1m m m i i σωεεωεμ+=-+∇∇H A A 可得垂直磁偶极子的反射波电磁场分量为1111()21211120()4z d m m H e k J k dk ξρρρρξξρπξξ∞-+-=-+⎰ 11113()12101210()4z d mz k m H e J k dk ρξρρξξρπξξε∞-+-=+⎰ 11113()112111210()4z d m k i m E e J k dk ρξϕρρωμξξρπξξε∞-+-=-+⎰ 1110m m mz H E E ϕρ===透射波电磁场分量为2222()211121221202()4z d m m H e k J k dk ξρρρρεμξρπεμξξ∞-=-+⎰ 22223()111202212102()4z d mz k m H e J k dk ρξρρεμξρπεμξξε∞-=+⎰22222()11121212102()4z d m k i m E e J k dk ρξϕρρωεμξρπεξξε∞-=-+⎰2220m m mz H E E ϕρ===6-4 谐变频率为ω的电偶极子水平放置于两媒质的分界面上方，如习题6-4图所示。