1.4.1正弦函数、余弦函数的图象知识点归纳与练习(含详细答案)
- 格式:doc
- 大小:268.50 KB
- 文档页数:6
1.4.1 正弦函数、余弦函数的图象1.4.2 正弦函数、余弦函数的性质考试标准知识导图学法指导1.本节内容以三角函数的图象及其性质为主,因此在学习过程中应先学会作图,然后利用图象研究函数的性质.2.深刻理解五点的取法,特别是非正常周期的五点.3.注意所有的变换是图象上的点在移动,是x 或y 在变化而非ωx .4.运用整体代换的思想,令ωx +φ=t ,借助y =sin t ,y =cos t 的图象和性质研究函数y =sin(ωx +φ),y =cos(ωx +φ)的图象和性质.第1课时 正弦函数、余弦函数的图象正弦曲线与余弦曲线及其画法状元随笔 1.关于正弦函数y =sin x 的图象(1)正弦函数y =sin x ,x∈[2k π,2(k +1)π],k∈Z 的图象与x ∈[0,2π]上的图形一致,因为终边相同角的同名三角函数值相等.(2)正弦函数的图象向左、右无限延伸,可以由y =sin x ,x ∈[0,2π]图象向左右平移得到(每次平移2π个单位).2.“几何法”和“五点法”画正、余弦函数的比较(1)“几何法”就是利用单位圆中正弦线和余弦线作出正、余弦函数图象的方法. 该方法作图较精确,但较为烦琐.(2)“五点法”是画三角函数图象的基本方法,在要求精度不高的情况下常用此法. 提醒:作图象时,函数自变量要用弧度制,自变量与函数值均为实数,因此在x 轴、y 轴上可以统一单位,这样作出的图象正规便于应用.[小试身手]1.判断下列命题是否正确. (正确的打“√”,错误的打“×”)(1)“五点法”作正、余弦函数的图象时的“五点”是指图象上的任意五点.( )(2)正弦函数在⎣⎢⎡⎦⎥⎤-3π2,π2和⎣⎢⎡⎦⎥⎤π2,5π2上的图象相同.( )(3)正弦函数、余弦函数的图象分别向左、右无限延伸.( ) 答案:(1)× (2)√ (3)√2.以下对正弦函数y =sin x 的图象描述不正确的是( )A .在x ∈[2k π,2(k +1)π](k ∈Z )上的图象形状相同,只是位置不同B .介于直线y =1与直线y =-1之间C .关于x 轴对称D .与y 轴仅有一个交点解析:画出y =sin x 的图象,根据图象可知A ,B ,D 三项都正确. 答案:C3.下列图象中,是y =-sin x 在[0,2π]上的图象的是( )解析:函数y =-sin x 的图象与函数y =sin x 的图象关于x 轴对称,故选D. 答案:D4.用“五点法”作函数y =cos 2x ,x ∈R 的图象时,首先应描出的五个点的横坐标是________________.解析:令2x =0,π2,π,3π2和2π,得x =0,π4,π2,34π,π.答案:0,π4,π2,34π,π类型一 用“五点法”作三角函数的图象例1 用“五点法”作出下列函数的简图: (1)y =sin x +12,x ∈[0,2π];(2)y =1-cos x ,x ∈[0,2π]. 【解析】 (1)按五个关键点列表:(2)列表:作函数图象需要先列表再描点,最后用平滑曲线连线. 方法归纳作形如y =a sin x +b (或y =a cos x +b ),x ∈[0,2π]的图象的三个步骤跟踪训练1 画出函数y =3+2cos x 的简图. 解析:(1)列表,如下表所示(2)利用五点作图法画简图.类型二 正、余弦函数曲线的简单应用 例2 根据正弦曲线求满足sin x ≥-32在[0,2π]上的x 的取值范围. 【解析】 在同一坐标系内作出函数y =sin x 与y =-32的图象,如图所示.观察在一个闭区间[0,2π]内的情形,满足sin x ≥-32的x ∈⎣⎢⎡⎦⎥⎤0,43π∪⎣⎢⎡⎦⎥⎤53π,2π,所以满足sin x ≥-32在[0,2π]上的x 的范围是{x 0≤x ≤43π或5π3≤x ≤2π}.或⎣⎢⎡⎦⎥⎤0,43π∪⎣⎢⎡⎦⎥⎤53π,2π在同一坐标系内作y =sin x 与y =-32的图象,利用图象求x 的范围. 方法归纳利用三角函数图象解sin x >a (或cos x >a )的三个步骤 (1)作出直线y =a ,y =sin x (或y =cos x )的图象. (2)确定sin x =a (或cos x =a )的x 值. (3)确定sin x >a (或cos x >a )的解集.[注意] 解三角不等式sin x >a ,如果不限定范围时,一般先利用图象求出x ∈[0,2π]范围内x 的取值范围,然后根据终边相同角的同名三角函数值相等,写出原不等式的解集.跟踪训练2 根据余弦曲线求满足cos x ≤12的x 的取值范围.解析:作出余弦函数y =cos x ,x ∈[0,2π]的图象,如图所示,由图象可以得到满足条件的x 的集合为[π3+2k π,5π3+2k π],k ∈Z .在同一坐标内作y =cos x 与y =12的图象,利用图象求x 的范围.1.4.1-2.1[基础巩固](25分钟,60分)一、选择题(每小题5分,共25分)1.下列对函数y =cos x 的图象描述错误的是( ) A .在[0,2π]和[4π,6π]上的图象形状相同,只是位置不同 B .介于直线y =1与直线y =-1之间 C .关于x 轴对称 D .与y 轴只有一个交点解析:观察余弦函数的图象知:y =cos x 关于y 轴对称,故C 错误. 答案:C2.下列各点中,不在y =sin x 图象上的是( ) A .(0,0) B.⎝ ⎛⎭⎪⎫π2,1C.⎝⎛⎭⎪⎫3π2,-1 D .(π,1) 解析:y =sin x 图象上的点是(π,0),而不是(π,1). 答案:D3.不等式sin x >0,x ∈[0,2π]的解集为( ) A .[0,π] B .(0,π)C.⎣⎢⎡⎦⎥⎤π2,3π2D.⎝ ⎛⎭⎪⎫π2,3π2解析:由y =sin x 在[0,2π]的图象可得. 答案:B 4.点M ⎝⎛⎭⎪⎫π2,-m 在函数y =sin x 的图象上,则m 等于( )A .0B .1C .-1D .2解析:点M 在y =sin x 的图象上,代入得-m =sin π2=1,∴m =-1.答案:C5.在同一平面直角坐标系内,函数y =sin x ,x ∈[0,2π]与y =sin x ,x ∈[2π,4π]的图象( )A .重合B .形状相同,位置不同C .关于y 轴对称D .形状不同,位置不同解析:根据正弦曲线的作法过程,可知函数y =sin x ,x ∈[0,2π]与y =sin x ,x ∈[2π,4π]的图象位置不同,但形状相同.答案:B二、填空题(每小题5分,共15分) 6.下列叙述正确的有________.(1)y =sin x ,x ∈[0,2π]的图象关于点P (π,0)成中心对称; (2)y =cos x ,x ∈[0,2π]的图象关于直线x =π成轴对称; (3)正弦、余弦函数的图象不超过直线y =1和y =-1所夹的范围.解析:分别画出函数y =sin x ,x ∈[0,2π]和y =cos x ,x ∈[0,2π]的图象,由图象观察可知(1)(2)(3)均正确.答案:(1)(2)(3)7.关于三角函数的图象,有下列说法: (1)y =sin|x |与y =sin x 的图象关于y 轴对称; (2)y =cos(-x )与y =cos|x |的图象相同;(3)y =|sin x |与y =sin(-x )的图象关于x 轴对称; (4)y =cos x 与y =cos(-x )的图象关于y 轴对称. 其中正确的序号是________.解析:对(2),y =cos(-x )=cos x ,y =cos|x |=cos x ,故其图象相同; 对(4),y =cos(-x )=cos x ,故其图象关于y 轴对称,由作图可知(1)(3)均不正确. 答案:(2)(4)8.直线y =12与函数y =sin x ,x ∈[0,2π]的交点坐标是________.解析:令sin x =12,则x =2k π+π6或x =2k π+56π,又∵x ∈[0,2π],故x =π6或56π.答案:⎝ ⎛⎭⎪⎫π6,12,⎝ ⎛⎭⎪⎫56π,12三、解答题(每小题10分,共20分)9.利用“五点法”作出函数y =1-sin x (0≤x ≤2π)的简图. 解析:(1)取值列表:(2)10.根据y =cos x 的图象解不等式:-32≤cos x ≤12,x ∈[0,2π]. 解析:函数y =cos x ,x ∈[0,2π]的图象如图所示:根据图象可得不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪π3≤x ≤5π6或7π6≤x ≤5π3. [能力提升](20分钟,40分)11.已知函数y =2cos x (0≤x ≤2π)的图象和直线y =2围成一个封闭的平面图形,则这个封闭图形的面积为( )A .4B .8C .2πD .4π解析:依题意,由余弦函数图象关于点⎝ ⎛⎭⎪⎫π2,0和点⎝ ⎛⎭⎪⎫3π2,0成中心对称,可得y =2cosx (0≤x ≤2π)的图象和直线y =2围成的封闭图形的面积为2π×2=4π.答案:D12.函数y =2cos x -2的定义域是________. 解析:要使函数有意义,只需2cos x -2≥0,即cos x ≥22.由余弦函数图象知(如图),所求定义域为⎣⎢⎡⎦⎥⎤-π4+2k π,π4+2k π,k ∈Z .答案:⎣⎢⎡⎦⎥⎤-π4+2k π,π4+2k π,k ∈Z 13.利用“五点法”作出y =sin ⎝⎛⎭⎪⎫x -π2⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤π2,52π的图象.解析:列表如下:14.利用图象变换作出下列函数的简图:(1)y=1-cos x,x∈[0,2π];(2)y=|sin x|,x∈[0,4π].解析:(1)首先用“五点法”作出函数y=cos x,x∈[0,2π]的简图,再作出y=cos x,x∈[0,2π]的简图关于x轴对称的简图,即y=-cos x,x∈[0,2π]的简图,将y=-cos x,x∈[0,2π]的简图向上平移1个单位即可得到y=1-cos x,x∈[0,2π]的简图,如图所示.(2)首先用“五点法”作出函数y=sin x,x∈[0,4π]的简图,再将该简图在x轴下方的部分翻折到x轴的上方,即得到y=|sin x|,x∈[0,4π]的简图,如图所示.。



《正弦函数、余弦函数的图象》知识清单知识点1正弦函数、余弦函数的图象 正弦函数y =sin x余弦函数y =cos x①______知识点2周期函数 1.周期函数设函数()f x 的定义域为D ,如果存在一个⑭________常数T ,使得对每一个x D ∈都有x T D +∈,且⑮________,那么函数()f x 就叫做周期函数,⑯________叫做这个函数的周期. 2.最小正周期如果在周期函数()f x 的所有周期中存在一个⑰________的正数,那么这个⑱________正数就叫做()f x 的最小正周期. 知识点3正弦函数、余弦函数的性质y =sin xy =cos x⑲________【答案】①R ②(0,0)③,12π⎛⎫ ⎪⎝⎭④(,0)π⑤3,12π⎛⎫- ⎪⎝⎭⑥(2,0)π⑦(0,1)⑧,02π⎛⎫⎪⎝⎭⑨(,1)π-⑩3,02π⎛⎫⎪⎝⎭⑪(2,1)π⑫左(或右)⑬(2π或3)2π⑭非零⑮()()f x T f x +=⑯非零常数T ⑰最小⑱最小⑲R ⑳2π○21 [1,1]-○2222k ππ+○23322k ππ+○242k π○252k ππ+○26奇○27偶○282x k ππ=+○29x k π=○302,222k k ππππ-+⎡⎤⎢⎥⎣⎦○3132,222k k ππππ⎡⎤++⎢⎥⎣⎦○32[2,2]k k πππ-○33[2,2]k k πππ+ 【知识辨析】判断正误,正确的画“√”,错误的画“⨯”. 1.正、余弦函数的图象形状相同,位置不同.( ) 2.正、余弦函数的图象向左、右和上、下无限伸展.( ) 3.函数sin y x =的图象向右平移2π个单位长度得到函数cos y x =的图象.( )4.直线12y =与函数sin ,[0,2]y x x π=∈的图象有两个交点.( ) 5.周期函数()y f x =的周期可能只有一个.( ) 6.任何周期函数都有最小正周期.( )7.若存在正数T ,使()()f x T f x +=-,则2T 为函数()f x 的周期.( )8.sin y x =的图象与cos y x =的图象既是中心对称图形又是轴对称图形.( ) 9.正弦函数、余弦函数在定义域内是单调函数.( )10.存在实数x ,使得sin x =【答案】 1.√2.×正、余弦函数的图象向左、右无限伸展,但上、下限定在直线y =1和y =-1之间.3.×函数y =sin x 的图象向左(或右)平移2π(或32π)个单位长度得到函数y =cos x 的图象. 4.√5.×周期函数的周期一定有无限个,如T 是它的周期,则nT (n ∈Z ,n ≠0)也是它的周期.6.×对于常数函数f (x )=c ,任意一个正实数都是其周期,因而不存在最小正周期.7.√8.√9.×正弦函数、余弦函数在定义域内呈周期性变化,增减交替,不是单调函数. 10.×正弦函数的最大值为1.。

余弦函数图象和性质一、知识点梳理:1.正、余弦函数图象和性质表函数 正弦函数R x x y ∈=,sin余弦函数R x x y ∈=,cos定义域),(+∞-∞),(+∞-∞值域]1,1[-当=x时,1max =y 当=x时,1min -=y]1,1[-当=x 时,1max =y 当=x时,1min -=y周期性 是周期函数,最小正周期=T 是周期函数,最小正周期=T奇偶性奇函数,图象关于 对称 偶函数,图象关于 对称 单调性在)(],[Z k ∈上是增函数 在)(],[Z k ∈上是减函数 在)(], [Z k ∈上是增函数 在)(],[Z k ∈上是减函数 对称轴 )(,Z k x ∈=)(,Z k x ∈=对称 中心)( ),(Z k ∈)( ),(Z k ∈2.利用“五点法”作函数R x x A y ∈+=),sin(ϕω(其中0,0>>ωA )的简图,是将ϕω+x 看着一个整体,先令ππππϕω2,23,,2,0=+x 列表求出对应的x 的值与y 的值,用平滑曲线连结各点,即可得到其在一个周期内的图象。
3.研究函数R x x A y ∈+=),sin(ϕω(其中0,0>>ωA )的单调性、对称轴、对称中心仍然是将ϕω+x 看着整体并与基本正弦函数加以对照而得出。
它的最小正周期||2ωπ=T 4.图象变换 (1)振幅变换 Rx x y ∈=,sin −−−−−−−−−−−−−−→−<<>倍到原来的或缩短所有点的纵坐标伸长A 1)A (01)(A R x x y ∈=,sin A(2)周期变换Rx x y ∈=,sin −−−−−−−−−−−−−−→−<<>倍到原来的或伸长所有点的横坐标缩短ωωω11)(01)(R x x y ∈=,sin ω(3)相位变换 Rx x y ∈=,sin −−−−−−−−−−−−→−<>个单位长度平移或向右所有点向左||0)(0)(ϕϕϕR x x y ∈+=,)(sin ϕ二、习题训练1、要得到函数x x y 2cos 2sin -=的图象,只要将函数x x y 2cos 2sin +=的图象沿x 轴( )个单位 A .向右平移4πB .向左平移4πC .向右平移2πD .向左平移2π2、已知的定义域是函数x x y o x cos sin ),2,(-+=∈π ( )A.][0,πB.]23,2[ππC. ],2[ππD. ],223[ππ3、如果mm x 44cos +=有意义,则m 的取值范围是( )A .4≤mB .4≥m C. 4=m D .4≠m4、若x x f sin )(是周期为π的奇函数,则)(x f 可以是 ( )A .x sinB .x cos C. x 2sin D .x 2cos5、对于函数)0,(A, )sin(的常数均为不等于,ϕωϕω+=x A y ,有下列说法: ①最大值为A ; ②最小正周期为|2|ωπ; ③在],0[π至少有一个x ,使得0=y ;④由)( 2222Z k k x k ∈+≤+≤-ππϕωππ解得x 的区间即为原函数的递增区间。


§1.4三角函数的图象与性质1.4.1正弦函数、余弦函数的图象学习目标1.了解利用单位圆中的正弦线画正弦曲线的方法.2.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.3.理解正弦曲线与余弦曲线之间的联系.知识点一 正弦函数、余弦函数的概念实数集与角的集合之间可以建立一一对应关系,而一个确定的角又对应着唯一确定的正弦(或余弦)值.这样,任意给定一个实数x ,有唯一确定的值sin x (或cos x )与之对应.由这个对应法则所确定的函数y =sin x (或y =cos x )叫做正弦函数(或余弦函数),其定义域是R . 知识点二 几何法作正弦函数、余弦函数的图象利用正弦线,这种作图方法称为“几何法”,其基本步骤如下:①作出单位圆:作平面直角坐标系,并在直角坐标系中y 轴左侧的x 轴上取一点O 1,作出以O 1为圆心的单位圆;②等分单位圆,作正弦线:从⊙O 1与x 轴的交点A 起,把⊙O 1分成12等份.过⊙O 1上各分点作x 轴的垂线,得到对应于0,π6,π3,π2,…,2π等角的正弦线;③找横坐标:把x 轴上从0到2π这一段分成12等份;④找纵坐标:把角x 的正弦线向右平移,使它的起点与x 轴上对应的点x 重合,从而得到12条正弦线的12个终点;⑤连线:用光滑的曲线将12个终点依次从左至右连接起来,即得到函数y =sin x ,x ∈[0,2π]的图象,如图.因为终边相同的角有相同的三角函数值,所以函数y =sin x ,x ∈[2k π,2(k +1)π),k ∈Z 且k ≠0的图象与函数y =sin x ,x ∈[0,2π)的图象的形状完全一致.于是只要将函数y =sin x ,x ∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度),就可以得到正弦函数y =sin x ,x ∈R 的图象,如图.把y =sin x ,x ∈R 的图象向左平移π2个单位长度,即可得到y =cos x ,x ∈R 的图象.正弦函数的图象和余弦函数的图象分别叫做正弦曲线和余弦曲线. 知识点三 “五点法”作正弦函数、余弦函数的图象“五点法”作正弦函数y =sin x (x ∈[0,2π])、余弦函数y =cos x ,x ∈[0,2π]图象的步骤 1.列表2.描点画正弦函数y =sin x ,x ∈[0,2π]的图象,五个关键点是 (0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0); 画余弦函数y =cos x ,x ∈[0,2π]的图象,五个关键点是 (0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1). 3.用光滑曲线顺次连接这五个点,得到正弦函数y =sin x (x ∈[0,2π])、余弦函数y =cos x (x ∈[0,2π])的简图.1.正弦函数y =sin x 的图象向左、右和上、下无限伸展.( × )提示 正弦函数y =sin x 的图象向左、右无限伸展,但上、下限定在直线y =1和y =-1之间.2.函数y =sin x 与y =sin(-x )的图象完全相同.( × ) 提示 二者图象不同,而是关于x 轴对称.3.余弦函数y =cos x 的图象与x 轴有无数个交点.( √ )4.余弦函数y =cos x 的图象与y =sin x 的图象形状和位置都不一样.( × ) 提示 函数y =cos x 的图象与y =sin x 的图象形状一样,只是位置不同.题型一“五点法”作图的应用例1利用“五点法”作出函数y=1-sin x(0≤x≤2π)的简图.考点正弦函数图象题点正弦函数图象解(1)取值列表:(2)描点连线,如图所示.反思感悟作正弦曲线要理解几何法作图,掌握五点法作图.“五点”即y=sin x或y=cos x 的图象在[0,2π]内的最高点、最低点和与x轴的交点.“五点法”是作简图的常用方法.跟踪训练1 利用“五点法”作出函数y =-1-cos x (0≤x ≤2π)的简图. 解 (1)取值列表如下:(2)描点连线,如图所示.题型二 利用正弦、余弦函数图象求定义域 例2 求函数f (x )=lg sin x +16-x 2的定义域. 考点 正弦函数图象 题点 正弦函数图象的应用解 由题意,得x 满足不等式组⎩⎪⎨⎪⎧sin x >0,16-x 2≥0,即⎩⎪⎨⎪⎧sin x >0,-4≤x ≤4,作出y =sin x 的图象,如图所示.结合图象可得x ∈[-4,-π)∪(0,π).反思感悟 一些三角函数的定义域可以借助函数图象直观地观察得到,同时要注意区间端点的取舍.跟踪训练2 求函数y = log 21sin x-1的定义域. 考点 正弦函数图象 题点 正弦函数图象的应用解 为使函数有意义,需满足⎩⎪⎨⎪⎧log 21sin x -1≥0,sin x >0,即0<sin x ≤12.由正弦函数的图象或单位圆(如图所示),可得函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π<x ≤2k π+π6或2k π+5π6≤x <2k π+π,k ∈Z .正弦、余弦函数图象的应用典例 利用正弦曲线,求满足12<sin x ≤32的x 的集合.考点 正弦函数的图象 题点 正弦函数图象的应用解 首先作出y =sin x 在[0,2π]上的图象,如图所示,作直线y =12,根据特殊角的正弦值,可知该直线与y =sin x ,x ∈[0,2π]的交点横坐标为π6和5π6.作直线y =32,该直线与y =sin x ,x ∈[0,2π]的交点横坐标为π3和2π3. 观察图象可知,在[0,2π]上,当π6<x ≤π3或2π3≤x <5π6时,不等式12<sin x ≤32成立.所以12<sin x ≤32的解集为⎩⎨⎧ x ⎪⎪ π6+2k π<x ≤π3+2k π,⎭⎬⎫或2π3+2k π≤x <5π6+2k π,k ∈Z . [素养评析] 作出相应正弦、余弦函数的图象,借助三角函数图象使问题得解,这正是数学核心素养直观想象的具体体现.1.用“五点法”作y =2sin 2x 的图象时,首先描出的五个点的横坐标是( ) A .0,π2,π,3π2,2πB .0,π4,π2,3π4,πC .0,π,2π,3π,4πD .0,π6,π3,π2,2π3考点 正弦函数图象 题点 正弦函数图象 答案 B解析 “五点法”作图是当2x =0,π2,π,3π2,2π时的x 的值,此时x =0,π4,π2,3π4,π,故选B.2.函数y =-sin x ,x ∈⎣⎡⎦⎤-π2,3π2的简图是( )考点 正弦函数图象 题点 正弦函数图象 答案 D解析 方法一 由y =sin x ,x ∈⎣⎡⎦⎤-π2,3π2的图象,作关于x 轴的对称图象,就可以得到函数y =-sin x ,x ∈⎣⎡⎦⎤-π2,3π2的简图. 方法二 可以用特殊点来验证. x =0时,y =-sin 0=0,排除A ,C. 当x =3π2时,y =-sin 3π2=1,排除B.3.在[0,2π]内,不等式sin x <-32的解集是( ) A .(0,π) B.⎝⎛⎭⎫π3,4π3 C.⎝⎛⎭⎫4π3,5π3 D.⎝⎛⎭⎫5π3,2π考点 正弦函数图象 题点 正弦函数图象的应用 答案 C解析 画出y =sin x ,x ∈[0,2π]的草图如下:因为sin π3=32,所以sin ⎝⎛⎭⎫π+π3=-32,sin ⎝⎛⎭⎫2π-π3=-32. 即在[0,2π]内,满足sin x =-32的是x =4π3或x =5π3. 可知不等式sin x <-32的解集是⎝⎛⎭⎫4π3,5π3. 4.点M ⎝⎛⎭⎫π2,-m 在函数y =sin x 的图象上,则m =________. 考点 正弦函数图象 题点 正弦函数图象的应用 答案 -1解析 点M 在y =sin x 的图象上, 代入坐标得-m =sin π2=1,所以m =-1.5.函数y =cos x ,x ∈[0,2π]的图象与直线y =-12的交点有________个.答案 2解析 画图可知(图略).1.对“五点法”画正弦函数图象的理解(1)与前面学习函数图象的画法类似,在用描点法探究函数图象特征的前提下,若要求精度不高,只要描出函数图象的“关键点”,就可以根据函数图象的变化趋势画出函数图象的草图.(2)正弦型函数图象的关键点是函数图象中最高点、最低点以及与x轴的交点.2.作函数y=a sin x+b的图象的步骤3.用“五点法”画的正弦型函数在一个周期[0,2π]内的图象,如果要画出在其他区间上的图象,可依据图象的变化趋势和周期性画出.一、选择题1.以下对正弦函数y =sin x 的图象描述不正确的是( ) A .在x ∈[2k π,2(k +1)π](k ∈Z )上的图象形状相同,只是位置不同 B .介于直线y =1与直线y =-1之间 C .关于x 轴对称 D .与y 轴仅有一个交点 考点 正弦函数的图象 题点 正弦函数图象的应用 答案 C解析 画出y =sin x 的图象(图略),根据图象可知A ,B ,D 三项都正确.2.用“五点法”作函数y =2sin x -1的图象时,首先应描出的五点的横坐标可以是( ) A .0,π2,π,3π2,2πB .0,π4,π2,3π4,πC .0,π,2π,3π,4πD .0,π6,π3,π2,2π3考点 正弦函数图象 题点 正弦函数图象 答案 A解析 由“五点法”可知选A.3.(2018·山西孝义高二期末)对于余弦函数y =cos x 的图象,有以下描述: ①将[0,2π]内的图象向左、向右平移2k π(k ∈Z )个单位长度;②与y=sin x图象形状完全一样,只是位置不同;③与x轴有无数个交点;④关于y轴对称.其中正确的描述有()A.1个B.2个C.3个D.4个考点余弦函数的图象题点余弦函数图象的应用答案 D解析根据余弦函数的图象可以判断都正确.4.(2018·安徽滁州高二期末)函数y=1-sin x,x∈[0,2π]的大致图象是()考点正弦函数的图象题点正弦函数图象答案 B解析 当x =π2时,y =0;当x =0时,y =1; 当x =2π时,y =1;结合正弦函数的图象可知B 正确. 5.下列各组函数中图象相同的是( ) ①y =cos x 与y =cos(π+x ); ②y =sin ⎝⎛⎭⎫x -π2与y =sin ⎝⎛⎭⎫x +π2; ③y =sin x 与y =sin(-x ); ④y =sin(2π+x )与y =sin x .A .①③B .①②C .③④D .④ 考点 正弦、余弦函数图象的综合应用 题点 正弦、余弦函数图象的综合应用 答案 D解析 由诱导公式知,只有④中,y =sin(2π+x )=sin x . 6.方程|x |=cos x 在(-∞,+∞)内( ) A .没有根 B .有且仅有一个根 C .有且仅有两个根 D .有无穷多个根考点 余弦函数的图象 题点 余弦函数图象的应用 答案 C解析 在同一坐标系中作出函数y =|x |及函数y =cos x 的图象,如图所示.由图知两函数的图象有两个交点,所以方程|x |=cos x 有两个根. 7.(2018·广西贺州高二期末)在[0,2π]上,满足sin x ≥22的x 的取值范围是( ) A.⎣⎡⎦⎤0,π6 B.⎣⎡⎦⎤π4,5π4 C.⎣⎡⎦⎤π4,3π4 D.⎣⎡⎦⎤3π4,π考点 正弦函数图象 题点 正弦函数图象的应用 答案 C解析 如图所示,在同一坐标系内作出y =sin x 在[0,2π]上的图象和y =22的图象.由图可知,满足sin x ≥22的x 的取值范围是⎣⎡⎦⎤π4,3π4. 8.函数y =cos x +|cos x |,x ∈[0,2π]的大致图象为( )答案 D解析 y =cos x +|cos x |=⎩⎨⎧2cos x ,x ∈⎣⎡⎦⎤0,π2∪⎣⎡⎦⎤3π2,2π,0,x ∈⎝⎛⎭⎫π2,3π2,故选D.二、填空题9.若sin x =2m +1且x ∈R ,则m 的取值范围是________. 答案 [-1,0]解析 ∵2m +1=sin x ∈[-1,1], 即-1≤2m +1≤1, ∴-1≤m ≤0.10.不等式sin x <-12,x ∈[0,2π]的解集为________.答案 ⎝⎛⎭⎫7π6,11π611.已知函数f (x )=⎩⎪⎨⎪⎧sin x ,x ≥0,x +2,x <0,则不等式f (x )>12的解集是____________.考点 正弦函数图象 题点 正弦函数图象的应用答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪-32<x <0或π6+2k π<x <5π6+2k π,k ∈N 解析 在同一平面直角坐标系中画出函数f (x )和函数y =12的图象,如图所示.当f (x )>12时,函数f (x )的图象位于函数y =12的图象的上方,此时-32<x <0或π6+2k π<x <5π6+2k π(k ∈N ).三、解答题12.求函数y =1-2cos x +lg(2sin x -1)的定义域. 考点 正弦、余弦函数图象的综合应用 题点 正弦、余弦函数图象的综合应用 解 要使函数有意义,只要⎩⎪⎨⎪⎧1-2cos x ≥0,2sin x -1>0,即⎩⎨⎧cos x ≤12,sin x >12.如图所示.cos x ≤12的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π3+2k π≤x ≤53π+2k π,k ∈Z .sin x >12的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π6+2k π<x <5π6+2k π,k ∈Z ,它们的交集为⎩⎨⎧⎭⎬⎫x ⎪⎪π3+2k π≤x <5π6+2k π,k ∈Z ,即为函数的定义域.13.用“五点法”作出函数y =1-2sin x ,x ∈[-π,π]的简图,并回答下列问题: (1)观察函数图象,写出满足下列条件的x 的区间.①y>1;②y<1.(2)若直线y=a与y=1-2sin x,x∈[-π,π]的图象有两个交点,求a的取值范围.考点正弦函数图象题点正弦函数图象的应用解列表如下:描点并将它们用光滑的曲线连接起来,如图:(1)由图象可知,图象在直线y=1上方部分时y>1,在直线y=1下方部分时y<1,所以①当x∈(-π,0)时,y>1;②当x∈(0,π)时,y<1.(2)由图可知,当直线y=a与y=1-2sin x,x∈[-π,π]的图象有两个交点时,1<a<3或-1<a<1,所以a的取值范围是(-1,1)∪(1,3).14.(2018·广西钦州高二期末)已知函数y =sin x ,x ∈⎣⎡⎦⎤π2,5π2的图象与直线y =1围成一个平面图形,则这个封闭图形的面积是( ) A .2 B .4 C .2π D .4π 考点 正弦函数图象 题点 正弦函图图象的应用 答案 C解析 如图,由正弦函数图象的对称性知,所围成平面图形的面积是长为5π2-π2=2π,宽为1的矩形的面积, ∴S =2π.15.函数f (x )=sin x +2|sin x |,x ∈[0,2π]的图象与直线y =k 有且仅有两个不同的交点,求k 的取值范围.考点 正弦函数图象 题点 正弦函数图象的应用解 f (x )=sin x +2|sin x |=⎩⎪⎨⎪⎧3sin x ,x ∈[0,π],-sin x ,x ∈(π,2π].图象如图所示,若使f (x )的图象与直线y =k 有且仅有两个不同的交点,根据图象可得k 的取值范围是(1,3).。

余弦函数与正切函数的图象和性质【学习目标】1.能借助正弦线画出正弦函数的图象,并在此基础上由诱导公式画出余弦函数的图象.2.借助图象理解余弦函数的性质.3.借助正切线画出正切函数的图象,并通过该图象理解正切函数的性质. 【要点梳理】要点一:余弦函数图象的画法 1.描点法:按照列表、描点、连线三步法作出余弦函数图象的方法. 2.几何法利用三角函数线作出余弦函数在]2,0[π内的图象,再通过平移得到cos y x =的图象. 3.五点法先描出余弦曲线的波峰、波谷和三个平衡位置这五个点,再利用光滑曲线把这五点连接起来,就得到余弦曲线在一个周期内的图象.在确定余弦函数cos y x =在]2,0[π上的图象形状时,起关键作用的五个点是3(0,1),(,0),(,1),(,0),(2,1)22ππππ-要点诠释:(1)熟记余弦函数图象起关键作用的五点.(2)若x R ∈,可先作出余弦函数在]2,0[π上的图象,然后通过左、右平移可得到cos y x =的图象.(3)由诱导公式cos sin()2y x x π==+,故cos y x =的图象也可以将x y sin =的图象上所有点向左平移2π个单位长度得到.要点二:余弦曲线(1)定义:余弦函数cos ()y x x R =∈的图象分别叫做余弦曲线. (2)图象要点诠释:(1)由余弦曲线可以研究余弦函数的性质.(2)运用数形结合的思想研究与余弦函数有关的问题. 要点三:余弦函数的性质函数 余弦函数y=cosx定义域 R 值域 [-1,1] 奇偶性 偶函数 周期性最小正周期2π 单调区间(k ∈Z )增区间[]22k k πππ-,减区间[]22k k πππ+, 最值点(k ∈Z )最大值点()21k π,最小值点()2,1k ππ+-对称中心(k ∈Z ) (,0)2k ππ+对称轴(k ∈Z ) x k π=要点诠释:(1)余弦函数的值域为[]1,1-,是指整个余弦函数或一个周期内的余弦曲线,如果定义域不是全体实数,那么余弦函数的值域就可能不是[]1,1-,因而求余弦函数的值域时,要特别注意其定义域。
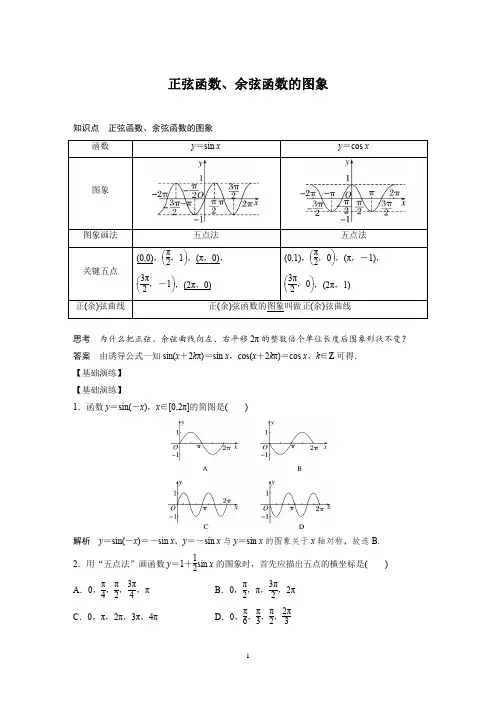
正弦函数、余弦函数的图象知识点正弦函数、余弦函数的图象五点法五点法思考为什么把正弦、余弦曲线向左、右平移2π的整数倍个单位长度后图象形状不变?答案由诱导公式一知sin(x+2kπ)=sin x,cos(x+2kπ)=cos x,k∈Z可得.【基础演练】【基础演练】1.函数y=sin(-x),x∈[0,2π]的简图是()解析y=sin(-x)=-sin x,y=-sin x与y=sin x的图象关于x轴对称,故选B.2.用“五点法”画函数y=1+12sin x的图象时,首先应描出五点的横坐标是() A.0,π4,π2,3π4,π B.0,π2,π,3π2,2πC.0,π,2π,3π,4π D.0,π6,π3,π2,2π3解析 所描出的五点的横坐标与函数y =sin x 的五点的横坐标相同,即0,π2,π,3π2,2π,故选B.3.在同一平面直角坐标系内,函数y =sin x ,x ∈[0,2π]与y =sin x ,x ∈[2π,4π]的图象( ) A .重合 B .形状相同,位置不同 C .关于y 轴对称 D .形状不同,位置不同答案 B解析 根据正弦曲线的作法可知函数y =sin x ,x ∈[0,2π]与y =sin x ,x ∈[2π,4π]的图象只是位置不同,形状相同. 4.在[0,2π]内,不等式sin x <-32的解集是( ) A .(0,π) B.⎝⎛⎭⎫π3,4π3 C.⎝⎛⎭⎫4π3,5π3 D.⎝⎛⎭⎫5π3,2π 解析 画出y =sin x ,x ∈[0,2π]的草图如下.当sin x =-32时,x =4π3或x =5π3, 可知不等式sin x <-32在[0,2π]上的解集是⎝⎛⎭⎫4π3,5π3.故选C. 5.函数y =cos x +4,x ∈[0,2π]的图象与直线y =4的交点的坐标为________.解析 由⎩⎪⎨⎪⎧y =cos x +4,y =4得cos x =0,当x ∈[0,2π]时,x =π2或3π2,∴交点坐标为⎝⎛⎭⎫π2,4,⎝⎛⎭⎫3π2,4.【典型例题】考点一:正弦函数、余弦函数图象的初步认识 例1 (1)下列叙述正确的个数为( )①y =sin x ,x ∈[0,2π]的图象关于点P (π,0)成中心对称; ②y =cos x ,x ∈[0,2π]的图象关于直线x =π成轴对称;③正弦、余弦函数的图象不超过直线y =1和y =-1所夹的范围. A .0 B .1 C .2 D .3解析 分别画出函数y =sin x ,x ∈[0,2π]和y =cos x ,x ∈[0,2π]的图象,由图象(略)观察可知①②③均正确.答案 D(2)函数y =sin |x |的图象是( )答案 B解析 y =sin |x |=⎩⎪⎨⎪⎧sin x ,x ≥0,-sin x ,x <0,结合选项可知选B.反思感悟 解决正弦、余弦函数图象的注意点对于正弦、余弦函数的图象问题,要画出正确的正弦曲线、余弦曲线,掌握两者的形状相同,只是在坐标系中的位置不同,可以通过相互平移得到.跟踪训练1 下列关于正弦函数、余弦函数的图象的描述,不正确的是( ) A .都可由[0,2π]内的图象向上、向下无限延展得到 B .都是对称图形 C .都与x 轴有无数个交点D .y =sin(-x )的图象与y =sin x 的图象关于x 轴对称 答案 A解析 由正弦、余弦函数图象知,B ,C ,D 正确.考点二:用“五点法”作三角函数的图象 例2 用“五点法”作出下列函数的简图: (1)y =sin x -1,x ∈[0,2π]; (2)y =-2cos x +3,x ∈[0,2π]. 解 (1)列表:描点并将它们用光滑的曲线连接起来,如图.(2)列表:描点、连线得出函数y=-2cos x+3,x∈[0,2π]的图象.反思感悟作形如y=a sin x+b(或y=a cos x+b),x∈[0,2π]的图象的三个步骤跟踪训练2利用“五点法”作出函数y=2+cos x(0≤x≤2π)的简图.解列表:描点并将它们用光滑的曲线连接起来,如图.考点三:正弦函数、余弦函数图象的应用 例3 不等式2sin x -1≥0,x ∈[0,2π]解集为( ) A.⎣⎡⎦⎤0,π6 B.⎣⎡⎦⎤0,π4 C.⎣⎡⎦⎤π6,π D.⎣⎡⎦⎤π6,5π6答案 D解析 因为2sin x -1≥0,所以sin x ≥12.在同一直角坐标系下,作函数y =sin x ,x ∈[0,2π]以及直线y =12的图象.由函数的图象知,sin π6=sin 5π6=12.所以根据图象可知,sin x ≥12的解集为⎣⎡⎦⎤π6,5π6. 延伸探究1.在本例中把“x ∈[0,2π]”改为“x ∈R ”,求不等式2sin x -1≥0的解集. 解 在x ∈[0,2π]上的解集为⎣⎡⎦⎤π6,5π6.所以x ∈R 时,不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π6+2k π≤x ≤5π6+2k π,k ∈Z . 2.试求关于x 的不等式12<sin x ≤32.解 作出正弦函数y =sin x 在[0,2π]上的图象,作出直线y =12和y =32,如图所示.由图可知,在[0,2π]上当π6<x ≤π3或2π3≤x <5π6时,不等式12<sin x ≤32成立,所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π6+2k π<x ≤π3+2k π或2π3+2k π≤x <5π6+2k π,k ∈Z . 反思感悟 利用三角函数图象解三角不等式sin x >a (cos x >a )的步骤 (1)作出相应的正弦函数或余弦函数在[0,2π]上的图象. (2)确定在[0,2π]上sin x =a (cos x =a )的x 值. (3)写出不等式在区间[0,2π]上的解集. (4)根据公式一写出定义域内的解集.跟踪训练3 求函数y =1-2cos x 的定义域. 解 依题意有1-2cos x ≥0,即cos x ≤12.作出余弦函数y =cos x ,x ∈[0,2π]以及直线y =12的图象,如图所示,由图象可以得到满足条件的x 的集合为⎩⎨⎧⎭⎬⎫x ⎪⎪π3+2k π≤x ≤5π3+2k π,k ∈Z .根据函数图象求范围典例 函数f (x )=sin x +2|sin x |,x ∈[0,2π]的图象与直线y =k 有且仅有两个不同的交点,则k 的取值范围是________. 答案 (1,3)解析 f (x )=⎩⎪⎨⎪⎧3sin x ,0≤x ≤π,-sin x ,π<x ≤2π.图象如图所示.结合图象可知1<k <3.[素养提升] 关于方程根的个数问题,往往运用数形结合的方法构造函数,转化为函数图象交点的个数问题来解决,体现了直观想象的核心素养.1.(多选)用五点法画y =3sin x ,x ∈[0,2π]的图象时,下列哪个点不是关键点( ) A.⎝⎛⎭⎫π6,32 B.⎝⎛⎭⎫π2,3 C .(π,0) D .(2π,3) 答案 AD解析 五个关键点的横坐标依次是0,π2,π,3π2,2π.代入计算得B ,C 是关键点.2.已知函数f (x )=sin ⎝⎛⎭⎫x +π2,g (x )=cos ⎝⎛⎭⎫x -π2,则f (x )的图象( ) A .与g (x )的图象相同 B .与g (x )的图象关于y 轴对称C .向左平移π2个单位长度,得g (x )的图象D .向右平移π2个单位长度,得g (x )的图象答案 D解析 f (x )=sin ⎝⎛⎭⎫x +π2,g (x )=cos ⎝⎛⎭⎫x -π2=cos ⎝⎛⎭⎫π2-x =sin x , f (x )的图象向右平移π2个单位长度得到g (x )的图象.3.在[0,2π]上,函数y =2sin x -2的定义域是( ) A.⎣⎡⎦⎤0,π4 B.⎣⎡⎦⎤π4,3π4 C.⎣⎡⎦⎤π4,π2D.⎣⎡⎦⎤3π4,π解析 依题意得2sin x -2≥0,即sin x ≥22.作出y =sin x 在[0,2π]上的图象及直线y =22,如图所示.由图象可知,满足sin x ≥22的x 的取值范围是⎣⎡⎦⎤π4,3π4,故选B. 4.函数y =1+sin x ,x ∈[0,2π]的图象与直线y =12交点的个数是( )A .0B .1C .2D .3 答案 C解析 由函数y =1+sin x ,x ∈[0,2π]的图象(如图所示),可知其与直线y =12有2个交点.5.函数f (x )=sin x -1,x ∈[0,2π]的零点为________. 答案 π2解析 令f (x )=0,∴sin x =1,∴又x ∈[0,2π],∴x =π2.6.已知函数f (x )=2cos x +1,若f (x )的图象过点⎝⎛⎭⎫π2,m ,则m =________;若f (x )<0,则x 的取值集合为________.答案 1 ⎩⎨⎧⎭⎬⎫x ⎪⎪2π3+2k π<x <4π3+2k π,k ∈Z 解析 当x =π2时,f (x )=2cos π2+1=1,∴m =1.f (x )<0,即cos x <-12,作出y =cos x 在x ∈[0,2π]上的图象,如图所示.由图知x 的取值集合为⎩⎨⎧⎭⎬⎫x ⎪⎪2π3+2k π<x <4π3+2k π,k ∈Z . 7.根据y =cos x 的图象解不等式:-32≤cos x ≤12,x ∈[0,2π]. 解 函数y =cos x ,x ∈[0,2π]的图象如图所示:根据图象可得不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π3≤x ≤5π6或7π6≤x ≤5π3.8.(多选)函数y =sin x -1,x ∈[0,2π]与y =a 有一个交点,则a 的值为( ) A .-1 B .0 C .1 D .-2 答案 BD解析 画出y =sin x -1的图象.如图.依题意a =0或a =-2.9.函数y =cos x +|cos x |,x ∈[0,2π]的大致图象为( )答案 D解析 由题意得y =⎩⎨⎧2cos x ,0≤x ≤π2或3π2≤x ≤2π,0,π2<x <3π2.10.函数f (x )=lg cos x +25-x 2的定义域为________________. 答案 ⎣⎡⎭⎫-5,-3π2∪⎝⎛⎭⎫-π2,π2∪⎝⎛⎦⎤3π2,5 解析 由题意,得x 满足不等式组⎩⎪⎨⎪⎧ cos x >0,25-x 2≥0,即⎩⎪⎨⎪⎧cos x >0,-5≤x ≤5,作出y =cos x 的图象,如图所示.结合图象可得x ∈⎣⎡⎭⎫-5,-3π2∪⎝⎛⎭⎫-π2,π2∪⎝⎛⎦⎤3π2,5.11.函数y =2cos x ,x ∈[0,2π]的图象和直线y =2围成的一个封闭的平面图形的面积是________. 答案 4π解析 如图所示,将余弦函数的图象在x 轴下方的部分补到x 轴的上方,可得一个矩形,其面积为2π×2=4π.12.若方程sin x =1-a 2在x ∈⎣⎡⎦⎤π3,π上有两个实数根,求a 的取值范围. 解 在同一直角坐标系中作出y =sin x ,x ∈⎣⎡⎦⎤π3,π的图象,y =1-a2的图象,由图象可知,当32≤1-a2<1,即当-1<a ≤1-3时,y =sin x ,x ∈⎣⎡⎦⎤π3,π的图象与y =1-a 2的图象有两个交点,即方程sin x =1-a 2在x ∈⎣⎡⎦⎤π3,π上有两个实数根.。


5.4.1 正弦函数、余弦函数的图像(基础知识+基本题型)知识点一 正弦函数的图象 1.正弦曲线的几何作法正弦函数sin ,y x x R 的图象如图,我们把正弦函数的图象叫做正弦曲线.如图,在直角坐标系的x 轴上取一点1O ,以1O 为圆心,单位长为半径作圆,从圆1O 与x 轴的交点A 起,把圆1O 分成12等份(份数越多,画出的图象越精确).过圆1O 上各分点作x 轴的垂线,得到对应于0,,,,,2632等角的正弦线,相应地,再把x 轴上从0到2这一段分成12等份,把角x 的正弦线向右平移,使它的起点与x 轴上的点x 重合,再把这些正弦线的终点用光滑曲线连接起来,即得sin ,[0,2]y x x 的图象.2.用“五点法”作sin ,[0,2]y x x 的简图在函数sin ,[0,2]y x x 的图象上,起关键作用的点有五个:(0,0),(,1)2,(,0),3(,1)2,(2,0). 一般地,在精确度要求不高时,我们常常先找出这五个关键点,再用光滑的曲线将它们连接起来,就得到正弦函数在[0,2]上的简图.这种方法叫“五点法”.【提示】(1)“五点法”作三角函数图象的实质是分别找到函数图象的最高点、最低点及三个平衡点,这五个点大致确定了函数图象的位置与形状.(2)用“五点法”作sin ,[0,2]y x x 的图象后,将其向左右平移(每次2个单位长度),可得出sin ,y x x R 的图象.知识点二 余弦函数的图象 1.利用图象变换作余弦函数的图象 由诱导公式六,有cos sin()2y x x .因此,将正弦函数sin ,y x x R 的图象向右平移2个单位长度,就得到函数sin()cos ,2y x x x R 的图象. 我们把余弦函数cos ,y x x R 的图象叫做余弦曲线,如图所示.2.用“五点法”作cos ,[0,2]y x x 的简图在函数cos ,[0,2]y x x 的图象上,起关键作用的点是它与x 轴的交点、函数图象的最高点和最低点,它们的坐标依次为:(0,1),(,0)2,(,1),3(,0)2,(2,1).用光滑的曲线将它们连接起来,就得到余弦函数在[0,2]上的简图.【提示】(1)作余弦函数图象时,可通过正弦函数的图象平移得到,但要注意平移的单位长度. (2)作x R 的余弦函数图象,可由cos ,[0,2]y x x 的图象左右平移得到,也可由 sin ,y x x R 的图象向左平移2个单位长度得到.考点一 通过图象变换作函数的图象 【例1】作函数32sin y x π⎛⎫=+⎪⎝⎭的图象. 解:3sin |cos |2y x x π⎛⎫=+= ⎪⎝⎭cos 22,Z 22,3cos 22,Z .22x k x k k x k x k k ππππππππ⎧⎛⎫-+≤≤+∈ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+<<+∈ ⎪⎪⎝⎭⎩故|cos |y x =的图象实际就是cos y x =的图象在x 轴下方的部分翻折到x 轴上方后得到的图象,如图由于余弦函数的图象是利用诱导公式依据图象变换画出的,故掌握利用诱导公式化简三角函数式也是画三角函数图象的切入点。
第一章三角函数1.4三角函数的图象与性质1.4.1正弦函数、余弦函数的图象学习目标1.能借助正弦线画出正弦函数的图象,并在此基础上由诱导公式画出余弦函数的图象.2.能熟练运用“五点法”作图.学习过程一、课前准备(预习课本P30~P33,找出疑惑之处)遇到一个新的函数,画出它的图象,通过观察图象获得对它的性质的直观认识是研究函数的基本方法,那么,一般采用什么方法画图象?二、新课导学问题1:在直角坐标系内把单位圆十二等分,分别画出对应角的正弦线.问题2:在相应坐标系内,在x轴上标出12个角(实数表示),把单位圆中12个角的正弦线进行右移.问题3:通过刚才描点(x0,sin x0),把一系列点用光滑曲线连结起来,你能得到什么?问题4:观察所得函数的图象,有五个点在确定形状中起着关键作用,哪五个点?问题5:如何作y=sin x,x∈R的图象?问题6:用以前学过的诱导公式cos x=(用正弦式表示),那么y=cos x的图象怎样作?三、典型例题【例题】作下列函数的简图.(1)y=1+sin x,x∈[0,2π];(2)y=-cos x.探究1:如何利用y=sin x,x∈(0,2π)的图象,通过图形变换(平移、翻转等)来得到:(1)y=1+sin x,x∈(0,2π)的图象?(2)y=sin(x-)的图象?探究2:如何利用y=cos x,x∈(0,2π)的图象,通过图形变换(平移、翻转等)来得到y=-cos x,x ∈(0,2π)的图象?探究3:如何利用y=cos x,x∈(0,2π)的图象,通过图形变换(平移、翻转等)来得到y=2-cos x,x ∈(0,2π)的图象?探究4:不用作图,你能判断函数y=sin(x-)和y=cos x的图象有何关系吗?请在同一坐标系中画出它们的简图,以验证你的猜想.四、课堂练习1.函数y=sin(a≠0)的定义域为()A.RB.[-1,1]C.[-]D.[-3,3]2.在[0,2π]上,满足sin x≥的x的取值范围是()A.[0,]B.[]C.[]D.[,π]3.用“五点法”作y=2sin x+1,x∈[0,2π]的图象.4.结合图象,判断方程sin x=x的实数解的个数.五、小结反思六、达标检测1.用“五点法”作函数y=2sin2x的图象时,首先应描出的五点横坐标可以是()A.0,,π,,2πB.0,,πC.0,π,2π,3π,4πD.0,2.在[0,2π]内,不等式sin x<-的解集是()A.(0,π)B.()C.()D.(,2π)3.方程sin x=的根的个数是()A.7B.8C.9D.104.用“五点法”画出y=2sin x在[0,2π]内的图象时,应取的五个点为.5.函数y=sin x,x∈[0,2π]的图象与直线y=-的交点有个.6.若sin x=2m+1且x∈R,则m的取值范围是.参考★答案★一、课前准备一般采用列表、描点、连线的方式作图.二、新课导学问题1:在直角坐标系的x轴上任取一点O1,以O1为圆心作单位圆,从这个圆与x轴的交点A起把圆分成n(这里n=12)等份.把x轴上从0到2π这一段分成n(这里n=12)等份.问题2:在单位圆中画出对应于角0,,…,2π的正弦线(等价于“列表”).把角x的正弦线向右平行移动,使得正弦线的起点与x轴上相应的点x重合,则正弦线的终点就是正弦函数图象上的点(等价于“描点”).问题3:用光滑曲线把这些正弦线的终点连接起来,就得到正弦函数y=sin x,x∈[0,2π]的图象.问题4:五个关键点是:(0,0),(,1),(π,0),(,-1),(2π,0).问题5:根据终边相同的同名三角函数值相等,所以函数y=sin x,x∈[2kπ,2(k+1)π,k∈Z且k≠0)的图象与函数y=sin x,x∈[0,2π)的图象的形状完全一致.于是我们只要将y=sin x,x∈[0,2π)的图象沿着x轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=sin x,x∈R的图象.用几何画板软件演示:把角x(x∈R)的正弦线平行移动,使得正弦线的起点与x轴上相应的点x重合,则正弦线的终点的轨迹就是正弦函数y=sin x的图象.问题6:根据诱导公式cos x=sin(x+),可以把正弦函数y=sin x的图象向左平移单位长度即得余弦函数y=cos x的图象.三、典型例题【例题】解:(1)列表得x0 π2πsin x0 1 0 -1 0y 1 2 1 0 1简图为(2)列表得x0 π2πcos x 1 0 -1 0 1y-1 0 1 0 -1简图为探究1:解:(1)将图象y=sin x上的点向上平移1个单位长度,即可得到y=1+sin x的图象;(2)将图象y=sin x上的点向右平移个单位长度,即可得到y=sin(x-)的图象.探究2:解:作y=cos x,x∈(0,2π)的图象关于x轴的对称图形即可得到y=-cos x,x∈(0,2π)的图象.探究3:解:先作y=cos x,x∈(0,2π)的图象关于x轴对称的图象即可得到y=-cos x,x∈(0,2π)的图象,再将得到的图象向上平移2个单位长度,即可得到y=2-cos x,x∈(0,2π)的图象.探究4:解:y=sin(x-)=cos x,这两个函数相等,图象重合.四、课堂练习1.A2.B3.解:列表得x0 π2πsin x0 1 0 -1 0y 1 3 1 -1 1简图为4.解:在同一坐标系中作出y=x和y=sin x的图象,如图由图象知y=x和y=sin x的图象只有一个交点,即方程x=sin x只有一个根.五、小结反思在区间[0,2π]上正、余弦函数图象上起关键作用的五个点分别是它的最值点及其与坐标轴的交点(平衡点).函数的图象可通过描点、平移、伸缩、对称等手段得到.六、达标检测1.B2.C3.A4.(0,0),(,2),(π,0),(π,-2),(2π,0)5.26.[-1,0]。
第一章 三角函数1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象[A 组 学业达标]1.函数y =-cos x (x >0)的图象中与y 轴最近的最高点的坐标为 ( )A.⎝ ⎛⎭⎪⎫π2,1 B .(π,1) C .(0,1)D .(2π,1)解析:用五点作图法作出函数y =-cos x (x >0)的一个周期的图象如图所示,由图易知与y 轴最近的最高点的坐标为(π,1).答案:B2.用“五点法”作函数y =cos ⎝ ⎛⎭⎪⎫4x -π6在一个周期内的图象时,第四个关键点的坐标是( )A.⎝ ⎛⎭⎪⎫5π12,0 B.⎝ ⎛⎭⎪⎫-5π12,1 C.⎝ ⎛⎭⎪⎫5π12,1 D.⎝ ⎛⎭⎪⎫-5π12,0 解析:令4x -π6=3π2,得x =5π12,∴该点坐标为⎝ ⎛⎭⎪⎫5π12,0.答案:A3.以下对正弦函数y =sin x 的图象描述不正确的是( )A .在x ∈[2k π,2k π+2π](k ∈Z )时的图象形状相同,只是位置不同B .介于直线y =1与直线y =-1之间C .关于x 轴对称D .与y 轴仅有一个交点解析:由正弦函数y =sin x 在x ∈[2k π,2k π+2π](k ∈Z )时的图象可知C 项不正确. 答案:C4.函数y =-sin x ,x ∈⎣⎢⎡⎦⎥⎤-π2,3π2的简图是( )解析:当x =-π2时,y =-sin x 取得最大值1,当x =3π2时,y =-sin x 取得最大值1,故选D. 答案:D5.与图中曲线(部分)对应的函数解析式是( )A .y =|sin x |B .y =sin |x |C .y =-sin |x |D .y =-|sin x |解析:注意图象所对的函数值的正负,可排除选项A ,D.当x ∈(0,π)时,sin |x |>0,而图中显然小于零,因此排除选项B.故选C. 答案:C6.方程x +sin x =0的根有________个.解析:作y =sin x 与y =-x 的图象交点为(0,0). 答案:17.函数y =cos x +4,x ∈[0,2π]的图象与直线y =4的交点坐标为________. 解析:作出函数y =cos x +4,x ∈[0,2π]的图象(图略),容易发现它与直线y =4的交点坐标为⎝ ⎛⎭⎪⎫π2,4,⎝ ⎛⎭⎪⎫3π2,4.答案:⎝ ⎛⎭⎪⎫π2,4,⎝ ⎛⎭⎪⎫3π2,48.在[0,2π]内,不等式sin x <-32的解集是________. 解析:画出y =sin x ,x ∈[0,2π]的图象如图:因为sin π3=32,所以sin ⎝ ⎛⎭⎪⎫π+π3=-32, sin ⎝ ⎛⎭⎪⎫2π-π3=-32. 即在[0,2π]内,满足sin x =-32的是x =4π3或x =5π3. 由图可知不等式sin x <-32的解集是⎝ ⎛⎭⎪⎫4π3,5π3.答案:⎝ ⎛⎭⎪⎫43π,53π9.用“五点法”作出函数y =cos ⎝ ⎛⎭⎪⎫x +π6,x ∈⎣⎢⎡⎦⎥⎤-π6,11π6的图象.解析:找出五个关键点,列表如下:u =x +π6π2π3π22πx -π6 π3 5π6 4π3 11π6 y =cos u1-11描点并将它们用光滑的曲线连接起来.10.根据y =cos x 的图象解不等式:-32≤cos x ≤12,x ∈[0,2π]. 解析:函数y =cos x ,x ∈[0,2π]的图象如图所示:根据图象可得不等式的解集为⎩⎨⎧x ⎪⎪⎪π3≤x ≤5π6或7π6≤⎭⎪⎬⎪⎫x ≤5π3.[B 组 能力提升]11.方程|x |=cos x 在(-∞,+∞)内 ( )A .没有根B .有且仅有一个根C .有且仅有两个根D .有无穷多个根解析:在同一坐标系中作出函数y =|x |及函数y =cos x 的图象,如图所示.由图知两函数的图象有两个交点,所以方程|x |=cos x 有两个根. 答案:C12.函数y =cos x +|cos x |,x ∈[0,2π]的大致图象为( )解析:y =cos x +|cos x |=⎩⎪⎨⎪⎧2cos x ,x ∈⎣⎢⎡⎦⎥⎤0,π2∪⎣⎢⎡⎦⎥⎤3π2,2π,0,x ∈⎣⎢⎡⎦⎥⎤π2,3π2,故选D. 答案:D13.函数f (x )=⎩⎨⎧sin x ,x ≥0,x +2,x <0,则不等式f (x )>12的解集是________.解析:在同一平面直角坐标系中画出函数f (x )和函数y =12的图象,如图所示.当f (x )>12时,函数f (x )的图象位于函数y =12的图象的上方,此时-32<x <0或π6+2k π<x <5π6+2k π(k ∈N ).答案:⎩⎨⎧⎭⎬⎫x ⎪⎪⎪-32<x <0或π6+2k π<x <5π6+2k π(k ∈N ) 14.在(0,2π)内,使sin x >cos x 成立的x 的取值范围为________.解析:分别作出y =sin x 、y =cos x 的图象x ∈(0,2π)(图略),使y =sin x 位于y =cos x 上方的部分为⎝ ⎛⎭⎪⎫π4,54π.答案:⎝ ⎛⎭⎪⎫π4,54π15.方程sin x =1-a 2在x ∈⎣⎢⎡⎦⎥⎤π3,π时有两个不相等的实数根,求a 的取值范围.解析:首先作出y =sin x ,x ∈⎣⎢⎡⎦⎥⎤π3,π的图象,然后再作出y =1-a 2的图象,如图所示.由图象知,如果y =sin x ,x ∈⎣⎢⎡⎦⎥⎤π3,π与y =1-a 2的图象有两个交点,那么方程sin x =1-a 2,x ∈⎣⎢⎡⎦⎥⎤π3,π就有两个不相等的实数根.由图象可知,当32≤1-a 2<1,即-1<a ≤1-3时,y =sin x ,x ∈⎣⎢⎡⎦⎥⎤π3,π的图象与y =1-a 2的图象有两个交点,即方程sin x =1-a 2在x ∈⎣⎢⎡⎦⎥⎤π3,π时有两个不相等的实数根.16.用“五点法”作出函数y =1-2sin x ,x ∈[-π,π]的简图,并回答下列问题:(1)观察函数图象,写出满足下列条件的x的区间.①y>1;②y<1.(2)若直线y=a与y=1-2sin x,x∈[-π,π]的图象有两个交点,求a的取值范围.解析:列表如下:x -π-π20π2πsin x 0-10101-2sin x 131-1 1(1)①由图象可知,当y>1时,-π<x<0,即(-π,0).②当y<1时,区间为(0,π).(2)当1<a<3或-1<a<1时y=a与y=1-2sin x,x∈[-π,π]有两个交点.。
第26讲 正弦函数、余弦函数的图象模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.理解正弦曲线和余弦曲线间的关系,会用“五点(画图)法”画给定区间上的正弦函数、余弦函数的图象;2.掌握正弦函数与余弦函数图象间的关系以及图象的变换,能通过函数图象解决简单的问题.知识点 1 正弦曲线与余弦曲线1、正弦曲线:正弦函数sin ,y x x R =∈的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线,如下图.【要点诠释】(1)由正弦曲线可以研究正弦函数的性质;(2)运用数形结合的思想研究与正弦函数有关的问题.2、余弦曲线:余弦函数cos ,y x x R =∈的图象叫做余弦曲线,它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线,如下图.3、将正弦曲线向左平移2π个单位长度即能得到余弦曲线.知识点 2 正(余)弦函数的图象1、正(余)弦函数的图象函数y =sin xy =cos x图象图象画法五点法五点法关键五点(0,0),π(,1)2,(,0)π,3π(,1)2-,(2,0)π(0,1),π(,0)2,(,1)π-,3π(,0)2,(2,1)π2、用“五点法”作正(余)弦函数的简图步骤(1)确定五个关键点:最高点、最低点、与x 轴的三个交点(三个平衡点);(2)列表:将五个关键点列成表格形式;(3)描点:在平面直角坐标系中描出五个关键点;(4)连线:用光滑的曲线连接五个关键点,注意连线时,必须符合三角函数的图象特征;(5)平移:将所作的[0,2]π上的曲线向左、向右平行移动(每次平移2π个单位长度),得到的图象即为所求正弦曲线、余弦曲线。
知识点 3 用三角函数图象解三角不等式的方法1、作出相应正弦函数或余弦函数在[0,2π]上的图象;2、写出适合不等式在区间[0,2π]上的解集;3、根据公式一写出不等式的解集.考点一:“五点法”画正(余)弦函数的图象例1.用“五点法”作出下列函数sin 1y x =-,[0,2π]x ∈的简图:【变式1-1】(22-23高一下·河南·月考)用五点法作出函数π2sin 6y x ⎛⎫=- ⎪⎝⎭在一个周期内的图象【变式1-2】(23-24高一上·陕西西安·期末)用五点作图法画出cos 2y x =的图象.【变式1-3】用“五点法”作出下列函数的简图.(1)2sin y x =-,[]0,2πx ∈;(2)πcos 6y x ⎛⎫=+ ⎪⎝⎭,π11,π66x ⎡⎤∈-⎢⎥⎣⎦.(3)πcos 3y x ⎛⎫=+ ⎪⎝⎭,π5π,33x ⎡⎤∈-⎢⎣⎦考点二:含绝对值的三角函数图象例2. 当[]2π,2πx ∈-时,作出下列函数的图象,把这些图象与sin y x =的图象进行比较,你能发现图象变换的什么规律?(1)sin y x =;(2)sin y x =.【变式2-1】(23-24高一上·四川绵阳·期末)函数()sin f x x =-在区间[]π,π-上的图象大致是( )A .B .C .D .【变式2-2】作出函数2sin sin y x x =+,[],x ππ∈-的大致图像.【变式2-3】(23-24高一上·云南昆明·期末)函数1(cos cos ),[0,2π]2y x x x =-∈的大致图象为( )A .B .C .D .考点三:用正(余)弦函数的图象解不等式例3. (22-23高一下·四川南充·月考)不等式1si n ,2x <-[0,2]x πÎ的解集是( )A .711,66ππ()B .45,33ππ⎡⎤⎢⎥⎣⎦C .57,66ππ()D .25,33ππ()【变式3-1】(22-23高一下·上海嘉定·期中)不等式[]()1cos π,π2x x ≥∈-的解集为 .【变式3-2】(23-24高一下·广东江门·月考)在()0,2π内,使sin cos x x >成立的x 的取值范围为( )A .π,π4⎛⎫⎪⎝⎭B .ππ5π,π,424⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭C .π5π,44⎛⎫ ⎪⎝⎭D .ππ3π5π4244⎛⎫⎛⎫⋃ ⎪ ⎪⎝⎭⎝⎭,,【变式3-3】(23-24高一上·江苏淮安·月考)在[]0,2π内函数()ln sin x f x ⎛= ⎝⎭的定义域是( )A .ππ,43⎛⎤ ⎥⎝⎦B .3π5π,43⎛⎤ ⎥⎝⎦C .π3π,34⎡⎫⎪⎢⎣⎭D .π,3π4⎡⎫⎪⎢⎣⎭考点四:正(余)弦函数的图象辨识例4. (23-24高一下·北京·期中)设a 是实数,则函数()sin 1axf x a=+的图象可能是( )A .B .C .D .【变式4-1】(22-23高一下·辽宁·月考)华罗庚说:“数缺形时少直观,形少数时难入微,数形结合百般好,隔离分家万事休.”所以研究函数时往往要作图,那么函数()sin cos 2f x x x=+的部分图像可能是()A.B.C.D.【变式4-2】(23-24高一下·重庆·月考)函数()3sin 2x x xf x-=的图象大致为()A.B.C.D.【变式4-3】(22-23高一下·湖南长沙·期末)函数()1 sin ln1xf x xx -=⋅+的大致图象为()A.B.C.D.考点五:与正(余)弦函数有关的交点例5. (23-24高一下·陕西·月考)(多选)函数πsin2π3y x x⎛⎫=<<⎪⎝⎭图象与直线y t=(t为常数)公共点的个数可能是()A.0B.1C.2D.3【变式5-1】(23-24高一上·江苏扬州·月考)函数()sin f x x =与()cos g x x =的图象在区间[]2π,π-的交点个数为.【变式5-2】(23-24高一下·辽宁盘锦·月考)若函数()sin 3sin f x x x =+在[]0,2πx ∈的图象与直线2y a =有两个交点,则实数a 的取值范围是.【变式5-3】(23-24高一上·广东江门·期末复习)在同一坐标系中,作函数sin y x =和lg y x =的图像,根据图像判断出方程sin lg x x =的解的个数为.一、单选题1.用“五点法”作2cos 2y x =的图象,首先描出的五个点的横坐标是( )A .π3π0,,π,,2π22B .ππ3π0,,,,π424C .0,π,2π,3π,4πD .πππ2π0,,,,63232.(23-24高二上·福建福州·月考)函数()cos 0y x x =-≥ 的图象中与y 轴最近的最高点的坐标为( )A .π,12⎛⎫ ⎪⎝⎭B .()π,1C .()0,1D .()2π,13.(22-23高一下·山西朔州·期中)函数()cos f x x =,ππ,36x ⎡⎤∈-⎢⎥⎣⎦的最小值为( )A .BC .12-D .124.(23-24高一上·浙江温州·月考)设a 为常数,且满足sin 1a x =+,且[]π,πx ∈-的x 的值只有一个,则实数a 的值为( )A .0B .1C .1或2D .0或25.(23-24高一上·山东青岛·期末)当(0,2π)x ∈时,函数()sin f x x =与()|cos |g x x =的图象所有交点横坐标之和为( )A .πB .2πC .3πD .4π6.(22-23高一上·江苏淮安·期末)我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔离分家万事休.”在数学学习和研究中,常用函数的图象来研究函数性质,也常用函数解析式来琢磨函数的图象特征,函数cos ()2sin ||x xf x x =+的部分图象大致为( )A .B .C .D .二、多选题7.函数()sin 2sin f x x x =+,[]0,2πx ∈的图象与直线y k =的交点个数可能是( )A .1B .2C .4D .68.(22-23高一下·江西抚州·期中)函数cos y x =,π4π,33x ⎛⎫∈ ⎪⎝⎭的图像与直线y t =(t 为常数,R t ∈)的交点可能有( )A .0个B .1个C .2个D .3个三、填空题9.已知函数()32cos f x x =-+的图象经过点π,3b ⎛⎫⎪⎝⎭,则b =.10.(23-24高一下·山东威海·月考)方程sin tan x x =在区间3π3π,22⎛⎫- ⎪⎝⎭上解的个数是.11.(23-24高一上·湖南长沙·月考)若()5533cos sin 3sin cos θθθθ-<-且[)0,2πθ∈,则θ的取值范围为 .四、解答题12.用“五点法”作出下列函数的简图.(1)2sin y x =,[]0,2πx ∈;(2)πsin 3⎛⎫=+ ⎪⎝⎭y x ,π5π[,33x ∈-.(3)1πsin()23y x =-在一个周期(4πT =)内的图像.13.(23-24高一上·福建厦门·月考)已知函数()sin y x α=+,其中α为三角形的内角且满足1cos 2α=.(1)求出角α.(用弧度制表示)(2)利用“五点法”,先完成列表,然后作出函数()sin y x α=+,在长度为一个周期的闭区间上的简图.(图中x 轴上每格的长度为π,6y 轴上每格的长度为1)x α+02πxy第26讲 正弦函数、余弦函数的图象模块一 思维导图串知识模块二 基础知识全梳理(吃透教材)模块三 核心考点举一反三模块四 小试牛刀过关测1.理解正弦曲线和余弦曲线间的关系,会用“五点(画图)法”画给定区间上的正弦函数、余弦函数的图象;2.掌握正弦函数与余弦函数图象间的关系以及图象的变换,能通过函数图象解决简单的问题.知识点 1 正弦曲线与余弦曲线1、正弦曲线:正弦函数sin ,y x x R =∈的图象叫做正弦曲线,是一条“波浪起伏”的连续光滑曲线,如下图.【要点诠释】(1)由正弦曲线可以研究正弦函数的性质;(2)运用数形结合的思想研究与正弦函数有关的问题.2、余弦曲线:余弦函数cos ,y x x R =∈的图象叫做余弦曲线,它是与正弦曲线具有相同形状的“波浪起伏”的连续光滑曲线,如下图.3、将正弦曲线向左平移2π个单位长度即能得到余弦曲线.知识点 2 正(余)弦函数的图象1、正(余)弦函数的图象函数y =sin xy =cos x图象图象画法五点法五点法关键五点(0,0),π(,1)2,(,0)π,3π(,1)2-,(2,0)π(0,1),π(,0)2,(,1)π-,3π(,0)2,(2,1)π2、用“五点法”作正(余)弦函数的简图步骤(1)确定五个关键点:最高点、最低点、与x 轴的三个交点(三个平衡点);(2)列表:将五个关键点列成表格形式;(3)描点:在平面直角坐标系中描出五个关键点;(4)连线:用光滑的曲线连接五个关键点,注意连线时,必须符合三角函数的图象特征;(5)平移:将所作的[0,2]π上的曲线向左、向右平行移动(每次平移2π个单位长度),得到的图象即为所求正弦曲线、余弦曲线。
第一章 三角函数 §1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象
课时目标 1.了解正弦函数、余弦函数的图象.2.会用“五点法”画出正弦函数、余弦函数
的图象.
1.正弦曲线、余弦曲线
2.“五点法”画图
画正弦函数y =sin x ,x ∈[0,2π]的图象,五个关键点是_________________________; 画余弦函数y =cos x ,x ∈[0,2π]的图象,五个关键点是__________________________. 3.正、余弦曲线的联系
依据诱导公式cos x =sin ⎝⎛⎭⎫x +π2,要得到y =cos x 的图象,
只需把y =sin x 的图象向________平移π
2个单位长度即可.
知识点归纳:
1.正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础.
2.五点法是画三角函数图象的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一.
一、选择题
1.函数y =sin x (x ∈R )图象的一条对称轴是( ) A .x 轴 B .y 轴
C .直线y =x
D .直线x =π
2
2.函数y =cos x (x ∈R )的图象向右平移π
2
个单位后,得到函数y =g (x )的图象,则g (x )的解析
式为( )
A .-sin x
B .sin x
C .-cos x
D .cos x
3.函数y =-sin x ,x ∈[-π2,3π
2
]的简图是( )
4.在(0,2π)内使sin x >|cos x |的x 的取值范围是( ) A.⎝⎛⎭⎫π4,3π4 B.⎝⎛⎦⎤π4,π2∪⎝⎛⎦⎤5π4,3π2 C.⎝⎛⎭⎫π4,π2 D.⎝⎛⎭
⎫5π4,7π4 5.若函数y =2cos x (0≤x ≤2π)的图象和直线y =2围成一个封闭的平面图形,则这个封闭图形的面积是( )
A .4
B .8
C .2π
D .4π 6.方程sin x =lg x 的解的个数是( )
A .1
B .2
C .3
D .4 题 号 1 2 3 4 5 6 答 案 7.函数y =sin x ,x ∈R 的图象向右平移π
2
个单位后所得图象对应的函数解析式是__________.
8.函数y =2cos x +1的定义域是________________. 9.方程x 2-cos x =0的实数解的个数是________.
10.设0≤x ≤2π,且|cos x -sin x |=sin x -cos x ,则x 的取值范围为________. 三、解答题
11.利用“五点法”作出下列函数的简图: (1)y =1-sin x (0≤x ≤2π); (2)y =-1-cos x (0≤x ≤2π).
12.分别作出下列函数的图象.
(1)y=|sin x|,x∈R;
(2)y=sin|x|,x∈R.
能力提升
13.求函数f(x)=lg sin x+16-x2的定义域.
14.函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,求k 的取值范围.
§1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象
答案
知识梳理
2.(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫32π,-1,(2π,0) (0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭
⎫3
2π,0,(2π,1) 3.左 作业设计
1.D 2.B 3.D 4.A [
∵sin x >|cos x |,
∴sin x >0,∴x ∈(0,π),在同一坐标系中画出y =sin x ,x ∈(0,π)与y =|cos x |,x ∈(0,π)
的图象,观察图象易得x ∈⎝⎛⎭⎫
π4,34π.] 5.D [
作出函数y =2cos x ,x ∈[0,2π]的图象,函数y =2cos x ,x ∈[0,2π]的图象与直线y =2围成的平面图形,如图所示的阴影部分.
利用图象的对称性可知该平面图形的面积等于矩形OABC 的面积,又∵|OA |=2,|OC |=2π, ∴S 平面图形=S 矩形OABC =2×2π=4π.]
6.C [用五点法画出函数y =sin x ,x ∈[0,2π]的图象,再依次向左、右连续平移2π个单位,得到y =sin x 的图象.
描出点⎝⎛⎭⎫110,-1,(1,0),(10,1)并用光滑曲线连接得到y =lg x 的图象,如图所示.
由图象可知方程sin x =lg x 的解有3个.]
7.y =-cos x
解析 y =sin x 2
π
−−−−−−→向右平移个单位
y =sin ⎝⎛⎭
⎫x -π2 ∵sin ⎝⎛⎭⎫x -π2=-sin ⎝⎛⎭⎫π
2-x =-cos x ,∴y =-cos x . 8.⎣
⎡⎦⎤2k π-23π,2k π+2
3π,k ∈Z 解析 2cos x +1≥0,cos x ≥-1
2
,结合图象知x ∈⎣⎡⎦⎤2k π-23π,2k π+2π3,k ∈Z . 9.2
解析 作函数y =cos x 与y =x 2的图象,如图所示, 由图象,可知原方程有两个实数解.
10.⎣⎡⎦⎤π4,5π4
解析 由题意知sin x -cos x ≥0,即cos x ≤sin x ,在同一坐标系画出y =sin x ,x ∈[0,2π]与 y =cos x ,x ∈[0,2π]的图象,如图所示:
观察图象知x ∈[π4,5
4
π].
11.解 利用“五点法”作图 (1)列表:
X 0 π2 π 3π2 2π sin x 0 1 0 -1 0 1-sin x
1
1
2
1
描点作图,如图所示.
(2)列表:
X
0 π2 π 3π2 2π cos x 1 0 -1 0 1 -1-cos x
-2
-1
-1
-2
描点作图,如图所示.
12.解 (1)y =|sin x |=⎩
⎪⎨⎪⎧
sin x (2k π≤x ≤2k π+π)
-sin x (2k π+π<x ≤2k π+2π) (k ∈Z ).
其图象如图所示,
(2)y =sin|x |=⎩
⎪⎨⎪
⎧
sin x (x ≥0)-sin x (x <0),其图象如图所示,
13.解 由题意,x 满足不等式组⎩⎪⎨⎪⎧ sin x >016-x 2≥0,即⎩
⎪⎨⎪
⎧
-4≤x ≤4sin x >0,作出y =sin x 的图象,如
图所示.
结合图象可得:x ∈[-4,-π)∪(0,π).
14.解 f (x )=sin x +2|sin x |=⎩
⎪⎨⎪⎧
3sin x x ∈[0,π],
-sin x x ∈(π,2π].
图象如图,
若使f (x )的图象与直线y =k 有且仅有两个不同的交点,根据上图可得k 的取值范围是(1,3).。