曲柄摇杆机构的运动分析

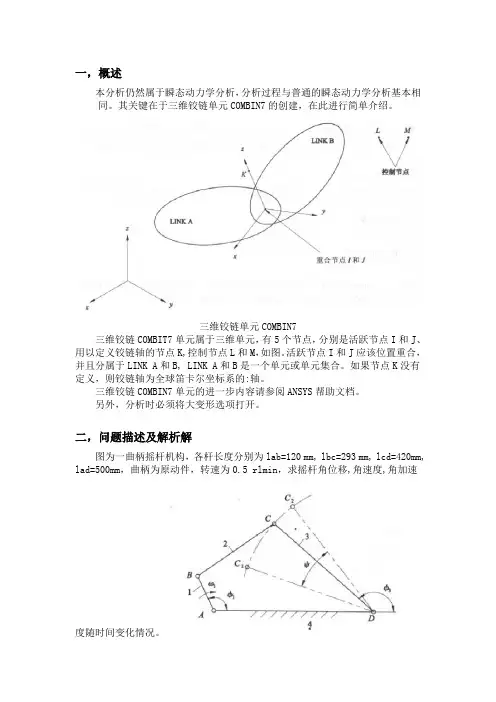
一，概述本分析仍然属于瞬态动力学分析，分析过程与普通的瞬态动力学分析基本相同。

其关键在于三维铰链单元COMBIN7的创建，在此进行简单介绍。

三维铰链单元COMBIN7三维铰链COMBIT7单元属于三维单元，有5个节点，分别是活跃节点I和J、用以定义铰链轴的节点K,控制节点L和M，如图。

活跃节点I和J应该位置重合，并且分属于LINK A和B, LINK A和B是一个单元或单元集合。

如果节点K没有定义，则铰链轴为全球笛卡尔坐标系的:轴。

三维铰链COMBIN7单元的进一步内容请参阅ANSYS帮助文档。

另外，分析时必须将大变形选项打开。

二，问题描述及解析解图为一曲柄摇杆机构，各杆长度分别为lab=120 mm, lbc=293 mm, lcd=420mm, lad=500mm，曲柄为原动件，转速为0.5 rlmin，求摇杆角位移,角速度,角加速度随时间变化情况。

根据机械原理的知识，该问题的解析解十分复杂，使用不太方便。

本例用图解法解决问题，由于过程比较烦琐，而且只是为了验证有限元解的正确性，所以，关于摇杆角位移、角速度、角加速度随时间1变化情况的图形没有必要给出。

在这里只求解了以下数据:摇杆的摆角=33.206°曲柄角度为115.443°时，摇杆角位移138.311°,角速度1.508*10﹣²rad/s三，分析步骤3.1改变工作名拾取菜单Utility Menu-File---Change Jflbnameo弹出如图所示的对话框，在" [IFILNAM]”文本框中输入EXAMPLE 12，单击“OK”按钮。

改变工作名对话框3.2定义参量拾取菜单Utility Menu-Parameters-Scalar Parameterso弹出如图所示的对话框，在“Selection”文本框中输入PI=3.1415926，单击“Accept",依次输入AX=0, AY=0(铰链A坐标),BX=0.07094,BY=0.09678(曲柄转速),CX=0.24417,CY=0.33309(铰链C坐标),DX=0.5,DY=0(铰链D坐标),OMGA1=0.5,T=601OMGA 1(曲柄转动一周所需时间，单位:s)，同时单击“Accept”按钮:最后，单击如图所示的对话框的“Close”按钮。

曲柄摇杆机构设计方法曲柄摇杆机构设计方法文档范本一、引言在机械设计领域中，曲柄摇杆机构是一种常见且重要的机构，它能够将旋转运动转换为往复运动。

本文档旨在提供一种详细的曲柄摇杆机构设计方法，以帮助工程师们更好地理解和应用该机构。

二、机构构成与功能1：曲柄：曲柄是机构的旋转部分，它通过旋转运动带动摇杆的往复运动。

2：摇杆：摇杆是机构的往复部分，其运动轨迹由曲柄的旋转和摇杆长度决定。

3：小端杆：小端杆连接曲柄与摇杆，使二者能够实现相对运动。

4：大端杆：大端杆连接摇杆与其他部件，传递摇杆的运动到所需位置。

三、设计步骤和考虑因素1：确定工作要求：根据实际应用，确定曲柄摇杆机构所需完成的工作和要求。

2：设计曲柄和摇杆的运动路径：根据工作要求和机构构型，确定曲柄和摇杆的运动路径，并绘制相应的示意图。

3：计算曲柄和摇杆的长度：根据运动路径以及机构的几何结构，计算曲柄和摇杆的长度，确保其能够满足工作要求。

4：确定杆长度：根据曲柄和摇杆的长度，确定小端杆和大端杆的长度，保证牢固可靠。

5：进行材料选择：根据机构的工作环境和所需承受的载荷，选择合适的材料以确保机构的强度和耐久性。

6：进行摩擦和润滑剂的选择：考虑摇杆与杆以及曲柄的接触情况，选择适当的润滑剂以减小摩擦，提高机构的效率和寿命。

7：进行强度计算：对机构的各个关键部位进行强度计算，以确保其在工作过程中不会发生破坏或变形。

8：进行运动分析和优化：利用运动学原理和模拟软件对机构的运动过程进行分析和优化，以确保其满足工作要求。

四、附件1：设计图纸：附上设计过程中所绘制的曲柄摇杆机构的设计图纸。

2：强度计算报告：附上对机构各个部件进行强度计算的报告。

五、法律名词及注释1：版权：指对于创作出来的文学、艺术和科学作品的拥有权，包括复制、分发、翻译等权利。

2：专利：指为新的技术、产品或产品的制造方法等发明所授予的专有权。

3：商标：指用于区别某个商品或服务来源的标识，具有独立性、显著性和可辨识性等特点。

栏杆机四杆机构运动学分析1 四杆机构运动学分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构，它可以用来实现转动和摆动之间运动形式的转换或传递动力。

对四杆机构进行运动分析的意义是：在机构尺寸参数已知的情况下，假定主动件（曲柄）做匀速转动，撇开力的作用，仅从运动几何关系上分析从动件（连杆、摇杆）的角位移、角速度、角加速度等运动参数的变化情况。

还可以根据机构闭环矢量方程计算从动件的位移偏差。

上述这些内容，无论是设计新的机械，还是为了了解现有机械的运动性能，都是十分必要的，而且它还是研究机械运动性能和动力性能提供必要的依据。

机构运动分析的方法很多，主要有图解法和解析法。

当需要简捷直观地了解机构的某个或某几个位置的运动特性时，采用图解法比较方便，而且精度也能满足实际问题的要求。

而当需要精确地知道或要了解机构在整个运动循环过程中的运动特性时，采用解析法并借助计算机，不仅可获得很高的计算精度及一系列位置的分析结果，并能绘制机构相应的运动线图，同时还可以把机构分析和机构综合问题联系起来，以便于机构的优化设计。

1.2 机构的工作原理在平面四杆机构中，其具有曲柄的条件为：a.各杆的长度应满足杆长条件，即：最短杆长度+最长杆长度≤其余两杆长度之和。

b.组成该周转副的两杆中必有一杆为最短杆，且其最短杆为连架杆或机架（当最短杆为连架杆时，四杆机构为曲柄摇杆机构；当最短杆为机架时，则为双曲柄机构）。

三台设备测绘数据分别如下：第一组(2代一套)四杆机构L1=125.36mm，L2=73.4mm， L3=103.4mm，L4=103.52mm最短杆长度+最长杆长度(125.36+73.4) <其余两杆长度之和(103.4+103.52)最短杆为连架杆，四杆机构为曲柄摇杆机构图1-1 II-1型栏杆机机构测绘及其运动位置图第二组(2代二套)四杆机构L1=125.36mm，L2=50.1mm，L3=109.8mm，L4=72.85mm最短杆长度+最长杆长度(125.36+50.1) <其余两杆长度之和(109.8+72.85)最短杆为连架杆，四杆机构为曲柄摇杆机构图1-2 II-2型栏杆机机构测绘及其运动位置图第三组(3代)四杆机构L1=163.2mm，L2=64.25mm，L3=150mm，L4=90.1mm最短杆长度+最长杆长度(163.2+64.25) <其余两杆长度之和(150+90.1)最短杆为连架杆，四杆机构为曲柄摇杆机构图1-3 III型栏杆机机构测绘及其运动位置图在如下图1所示的曲柄摇杆机构中，构件AB为曲柄，则B点应能通过曲柄与连杆两次共线的位置。

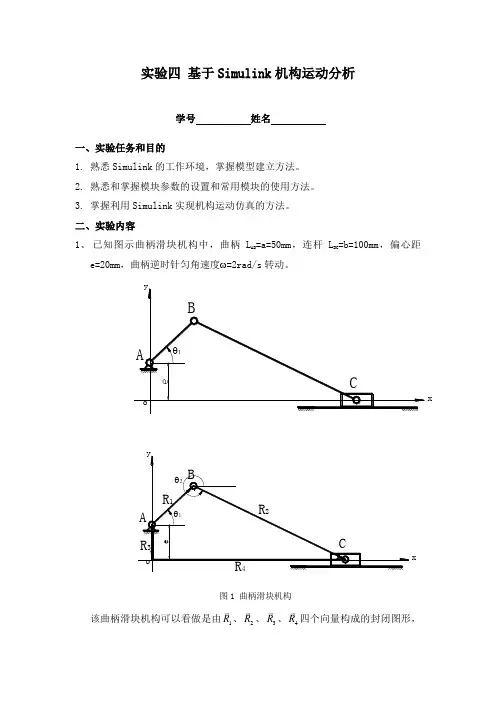
实验四 基于Simulink 机构运动分析学号 姓名一、实验任务和目的1. 熟悉Simulink 的工作环境，掌握模型建立方法。

2. 熟悉和掌握模块参数的设置和常用模块的使用方法。

3. 掌握利用Simulink 实现机构运动仿真的方法。

二、实验内容1、 已知图示曲柄滑块机构中，曲柄L AB =a=50mm ，连杆L BC =b=100mm ，偏心距e=20mm ，曲柄逆时针匀角速度ω=2rad/s 转动。

xx图1 曲柄滑块机构该曲柄滑块机构可以看做是由1R 、2R 、3R 、4R 四个向量构成的封闭图形，方向如图所示。

该机构的闭环位移矢量方程1234R R R R +=+上述矢量方程在x 和y 方向的投影方程1212cos cos (1)sin sin (2)c a b x a b eθθθθ+=⎧⎨+=-⎩ 对位移方程两边求一阶导数⎩⎨⎧=+=--)4(0cos cos )3(sin sin a 22112211θωθωθωθωb a v b C 上式可用于求解连杆角速度2ω和滑块速度C v⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--1111222cos sin 0cos 1sin θωθωωθθa a v b b C依此建立simulink 模型图2曲柄滑块机构Simulin 仿真模型其中（1） 计算连杆角速度和滑块速度的函数模块自定义函数模块vcslider.m源代码（2）计算连杆和滑块初始位置的函数模块自定义函数模块vcslider.m 源代码对上述曲柄滑块模型进行仿真。

2、 仿照上述曲柄滑块机构仿真方法，对图示曲柄摇杆机构进行建模仿真，要求用示波器显示CD 杆角位移4θ，角速度4ω和角加速度4α随曲柄转角（0~360°）变化曲线。

已知机构各构件尺寸100AB l mm =，200BC l mm =，200AD l mm =，150CD l mm =，原动件AB 以等角速度ω=10rad/s 逆时针方向转动，1θ初始位置为0。

Science &Technology Vision 科技视界0前言曲柄摇杆机构是一种典型的四杆机构之一,由曲柄、摇杆、连杆、机架组成的。

曲柄或摇杆通过直接接触将预定的运动传给从动件。

由于曲柄摇杆机构可以实现各种复杂的运动要求,而且具有结构简单紧凑的特点,所以广泛应用于各种自动化机器、仪器和装配线,例如在纺织机械、印刷机械以及一些控制系统等装置中,广泛应用着各种类型的曲柄摇杆机构。

具有急回特性的曲柄摇杆机构是常用的曲柄摇杆机构,曲柄的转动使从动件按预定的运动规律摆动。

由于曲柄摇杆机构的运动特征依赖于曲柄、摇杆、连杆的长度和行程速比的类型,在常规设计中,为了获得从动件的预定输出运动(位移、速度和加速度),必须合理选择从动件的类型和机构参数后精确地设计曲柄摇杆的数值参数。

1平面连杆机构运动分析杆组法简介平面连杆机构的运动分析,早已有成熟的算法,其中阿氏杆组法最为简单有效。

大部分连杆机构都是在基本机构上增加一个或多个常用的阿氏杆组构成的。

由于阿氏杆组的自由度为零,阿氏杆组具有运动的确定性。

就是说,当外部运动副的运动已知时,阿氏杆组中所有构件的运动就可以确定。

因此可以预先编写一些常用阿氏杆组子程序,通过调用少数几个杆组子程序,就可以完成各种各样连杆机构的运动分析,因而被广泛接受和应用。

为了论述的完整,这里对杆组法作一简要介绍。

用杆组法对平面连杆机构进行运动分析的思路是:先将机构拆成自由度为零的基本杆组和与机架相连的原动件,然后从原动件开始,逐个进行杆组的运动分析,直到完成预定的运动分析任务。

对某个杆组作运动分析,是由其外部运动副的运动状态(位置、速度、加速度)求解内部运动副及组成构件的运动状态。

一个构件的运动状态由其上一点和一直线的运动状态决定,由此可求出构件上任意其它点的运动。

由于本文所求机构的转换机构均为Ⅱ级杆组,因此我们只对平面Ⅱ级杆组进行运动分析。

平面Ⅱ级杆组由两个构件三个低副组成,低副可以是转动副或移动副。

实验三——用ADAMS 验证曲柄连杆机构如图3-1所示的铰链四杆机构（曲柄摇杆机构），AB 杆为原动件，逆时针匀速转动，其角速度为=/rad s ωπ2040602/3/3AB cm CD cm DA cm BAD ADC ππ===∠=∠=，，，，；对该机构进行验证，是否为曲柄摇杆机构；同时进行运动分析和动力分析。

图3-1 铰链四杆机构【实验目的】1、 了解ADAMS 软件；认识ADAMS 工作界面。

2、 掌握ADMAS 的建模与仿真；3、 验证铰链四杆机构中曲柄存在的条件。

【实验原理】1、 铰链四杆机构是指将4个杆件全部用转动副联接起来的机构。

2、 铰链四杆机构中曲柄存在的条件为以下两点：（1） 曲柄为最短杆件或最短的相邻杆件，此条件称为最短构件条件。

（2） 最短杆件与最长杆件的长度之和必须小于或等于其他两杆件的长度之和，即：'''min max l l l l +≤+此条件简称为构件长度和条件。

【实验仪器和设备】1、计算机。

2、机械系统动力学分析软件ADAMS 2013。

3、《机械设计基础》教材；实验指导书；实验报告。

【实验步骤】1、启动ADAMS。

双击桌面上ADAMS/View的快捷图标“”，打开ADAMS/View。

在欢迎对话框如图3-2中选择“新建模型”（Create a new model），弹出如图3-3所示“创建新模型”（Create a new model）对话框。

图3-2 欢迎对话框图3-3 “创建新模型”对话框在“模型名称”（Modelname）栏中输入：sparkplug；在“重力（Gravity）”栏中选择“正常重力（-全局Y轴）”；在“单位（Units）”栏中选择“MMKS –mm，kg，N，s，deg”；在“工作路径”栏中选择“C:\sparkplug”。

2、设置工作环境。

2.1 对于这个模型，网格间距需要设置成更高的精度以满足要求。

在ADAMS/View菜单栏中，选择设置（Setting）下拉菜单中的工作网格（Working Grid）命令。

曲柄摇杆机构在搅拌机上应用的受力分析与强度计算曲柄摇杆机构在搅拌机上的应用主要是通过曲柄摇杆的运动来驱动搅拌器进行搅拌操作。

下面是对曲柄摇杆机构在搅拌机上的受力分析与强度计算的简要介绍。

受力分析：
1.曲柄摇杆机构中，曲柄的一端连接到搅拌器，另一端连接到电机或其他动力源。

2.在运行过程中，曲柄摇杆机构会受到来自电机或其他动力源的旋转力矩作用，该力矩通过曲柄传递到搅拌器上。

3.曲柄的运动将会引起搅拌器的摆动，产生搅拌力和惯性力。

4.搅拌力和惯性力的大小取决于搅拌器的设计和工作条件，需要根据实际情况进行具体分析。

强度计算：
1.曲柄摇杆机构的强度计算主要包括曲柄和摇杆的强度计算。

2.曲柄的强度计算一般采用静态强度计算方法，考虑到受力情况和材料的强度特性。

3.摇杆的强度计算一般采用静态强度计算方法，考虑到受力情况和材料的强度特性。

4.强度计算需要考虑到曲柄和摇杆的材料、尺寸、受力情况等因素，可以通过有限元分析等方法进行具体计算。

曲柄摇杆机构的受力分析与强度计算是一个较为复杂的工程问
题，需要根据具体的搅拌机设计和工作条件进行详细的分析。

在实际应用中，建议寻求专业工程师的帮助，以确保曲柄摇杆机构的可靠性和安全性。

定出杆长的曲柄摇杆机构运动的分析作者：张楗来源：《科技视界》2019年第04期【摘要】简化平面四杆机构数学模型的基础上进行优化设计，并利用优化数据进行模拟仿真处理，对得出的仿真数据进行分析，最后达到优化设计的目的。

【关键词】曲柄摇杆机构;运动分析;计算模型中图分类号： TH112 文献标识码： A 文章编号： 2095-2457（2019）04-0149-004DOI：10.19694/ki.issn2095-2457.2019.04.0591 设计目的平面四杆机构是连杆机构中最常见的机构组成，由于其结构简单，可承受载荷大，连杆曲线具有多样性等特性，它在众多领域都有着广泛的运用。

常用的平面四杆机构设计方法有：解析法、作图法和实验法。

但这些方法设计精度不高，都在解决一些约束条件时存在较大困难。

而在机械优化设计的基础上，运用适当的优化算法，通过计算机编程可以方便快捷地达到优化设计的目的，且能很好地解决约束条件问题。

运动仿真可以很好地验证设计方案的优劣，找出设计缺陷，改进设计方案。

SolidWorks是专门的机械仿真模块，且能够得出最后的仿真数据。

本文正是在简化了平面四杆机构数学模型的基础上进行优化设计，并利用优化数据进行模拟仿真处理，对得出的仿真数据进行分析，最后达到优化设计的目的。

2 设计过程2.1 曲柄摇杆机构分析2.1.1 理论分析2.1.2 计算模型因此，应用公式（2）及图1的几何关系可以设计两两连架曲柄摇杆机构，机构设计计算步骤如下：2.2 特定杆长的曲柄摇杆机构运动分析在一些实际应用曲柄摇杆实例中，若建设通过建立坐标系可知机构两连架杆三组对应角位置（φ1，ψ1），（φ2，ψ2），（φ3，ψ3），（φ0，ψ0）——可选择及机构的任意一杆长，设计的曲柄摇杆机构。

如图1所示，φ1、φ2、φ3为连接杆AB的三个位置角，ψ1、ψ2、ψ3为连架杆CD的三个角位置，φ0和ψ0分别是φi与ψi的起始计量角，默认值为0。