高中数学第二章基本初等函数Ⅰ对数函数的图象及性质课后提升训练新人教A版必修0

习题课——对数函数及其性质(45分钟70分)一、选择题(每小题5分,共40分)1.下列不等式正确的是( )A.log0.47>log0.46B.log47<log46C.log37>log47D.log5>log52【解析】选C.由对数函数的单调性显然A、B、D均不正确,而===log34>1,故C正确.2.(2017·杭州高一检测)以下四个数中最大的是( )A.(ln2)2B.ln(ln2)C.lnD.ln2【解析】选D.因为0<ln2<1,所以ln(ln2)<0,(ln2)2<ln2,ln=ln2<ln2,故ln2最大.3.(2017·贵阳高一检测)已知函数f(x)是函数y=log a x(a>0且a≠1)的反函数,则函数y=f(x)+2图象恒过点的坐标为( )A.(1,0)B.(0,1)C.(1,2)D.(0,3)【解析】选D.因为y=log a x(a>0且a≠1)的图象过定点(1,0),所以f(x)的图象过定点(0,1),从而y=f(x)+2的图象过(0,3).4.函数f(x)=log2(3x+3-x)是( )A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数【解析】选B.因为3x+3-x>0恒成立,所以f(x)的定义域为R.又因为f(-x)=log2(3-x+3x)=f(x),所以f(x)为偶函数.5.(2017·大连高一检测)若log a>1(a>0且a≠1),则实数a的取值范围是( )A. B.C.∪D.(0,1)∪(1,+∞)【解析】选A.log a>1⇒log a>log a a⇒或⇒<a<1.6.已知lo b<lo a<lo c,则( )A.2b>2a>2cB.2a>2b>2cC.2c>2b>2aD.2c>2a>2b【解析】选A.由已知得b>a>c,因为y=2x在定义域内是单调递增的,所以2b>2a>2c.【延伸探究】若本题条件“lo b<lo a<lo c”换为“lo b>lo a>lo c”,其结论又如何呢?【解析】由已知得b<a<c,所以2b<2a<2c.7.(2017·汉口高一检测)设a=log54,b=(log53)2,c=log45,则( )A.a<c<bB.b<c<aC.a<b<cD.b<a<c【解析】选D.因为log45>log44=1,1=log55>log54>log53>(log53)2,所以b<a<c.8.(2017·杭州高一检测)若a∈R,且log a(2a+1)<log a(3a)<0,则a的取值范围是( )A. B.C. D.【解析】选D.原不等式等价于或解得a∈ 或<a<1,故a的取值范围是.二、填空题(每小题5分,共10分)9.(2017·大连高一检测)若指数函数f(x)=a x(x∈R)的部分对应值如表:则不等式log a(x-1)>0的解集为__________.【解析】因为f(-2)=4,所以a-2=4,故a=,故lo(x-1)>0⇒即1<x<2.答案:(1,2)10.(2017·宝鸡高一检测)函数f(x)=log a x(a>0且a≠1)在区间[2,8]上的最大值为6,则a=__________.【解析】当a>1时,log a8=6即a==.当0<a<1时,log a2=6,即a=.答案:或三、解答题(每小题10分,共20分)11.(2017·石家庄高一检测)已知函数y=f(x)的图象与g(x)=log a x(a>0,且a≠1)的图象关于x轴对称,且g(x)的图象过点(9,2).(1)求函数f(x)的解析式.(2)若f(3x-1)>f(-x+5)成立,求x的取值范围.【解析】(1)因为g(x)=log a x(a>0,且a≠1)的图象过点(9,2),所以log a9=2,解得a=3,所以g(x)=log3x.又因为函数y=f(x)的图象与g(x)=log 3x的图象关于x轴对称,所以f(x)=lo x.(2)因为f(3x-1)>f(-x+5),即lo(3x-1)>lo(-x+5),则解得<x<,所以x的取值范围为.12.已知函数f(x)=log a(1-x)+log a(x+3),其中0<a<1.(1)求函数f(x)的定义域.(2)若函数f(x)的最小值为-4,求a的值.【解题指南】(1)要使函数有意义,需每一个真数都大于零.(2)将函数式化简,转化成复合函数,利用其单调性求解. 【解析】(1)要使函数有意义,则有解得-3<x<1,所以函数的定义域为(-3,1).(2)函数可化为:f(x)=log a(1-x)(x+3)=log a(-x2-2x+3)=log a[-(x+1)2+4],因为-3<x<1,所以0<-(x+1)2+4≤4,因为0<a<1,所以log a[-(x+1)2+4]≥log a4,即f(x)min=log a4,由log a4=-4,得a-4=4,所以a==.【能力挑战题】已知函数f(x)=log a(x2-2),f(2)=1.(1)求a的值.(2)求f(3)的值.(3)解不等式f(x)<f(x+2).【解析】(1)因为f(2)=1,所以log a(22-2)=1,即log a2=1,解得a=2.(2)由(1)得函数f(x)=log2(x2-2),则f(3)=log2[(3)2-2]=log216=4.(3)不等式f(x)<f(x+2),即log2(x2-2)<log2[(x+2)2-2],化简不等式得log2(x2-2)<log2(x2+4x+2).因为函数y=log2x在(0,+∞)上为增函数,所以解得x>,所以原不等式的解集为(,+∞).敬请批评指正。

2.2.2 对数函数及其性质一、A组1.y=2x与y=log2x的图象关于()A.x轴对称B.直线y=x对称C.原点对称D.y轴对称解析:函数y=2x与y=log2x互为反函数,故函数图象关于直线y=x对称.答案:B2.函数y=ln(1-x)的图象大致为()解析:函数的定义域为(-∞,1),且函数在定义域上单调递减,故选C.答案:C3.函数f(x)=lo(5-4x-x2)的值域为()A.[2,+∞)B.(-∞,-2]C.[-2,+∞)D.(-∞,2]解析:令u=5-4x-x2=-(x+2)2+9,由题意知u∈(0,9],而y=lo u在(0,9]上为减函数,∴y≥lo9=-2.答案:C4.(2016·广东汕尾高二期末)函数y=的定义域为.解析:要使函数y=有意义,须解得x>0,且x≠1,所以函数y=的定义域为(0,1)∪(1,+∞).答案:(0,1)∪(1,+∞)5.若对数函数f(x)的图象经过点P(8,3),则f=.解析:设f(x)=log a x(a>0,a≠1),则log a8=3,∴a3=8,∴a=2.∴f(x)=log2x,故f=log2=-1.答案:-16.若函数f(x)=f·lg x+1,则f(10)=.解析:令x=10,得f(10)=f+1; ①令x=,得f=f(10)·(-1)+1.②由①②,得f(10)=1.答案:17.若函数f(x)=log a(x+1)在区间[0,1]上的最大值与最小值之和为-1,则a=.解析:当a>1时,f(x)单调递增;当0<a<1时,f(x)单调递减,所以最大值与最小值的和均为f(0)+f(1)=log a1+log a2=log a2.所以log a2=-1,即a=.答案:8.已知函数f(x)=lg(x-1).(1)求函数f(x)的定义域和值域;(2)证明f(x)在定义域上是增函数.(1)解:要使函数有意义,则x-1>0,解得x>1,即函数f(x)的定义域是(1,+∞).由于函数f(x)的定义域是(1,+∞),则有u=x-1的值域是(0,+∞),则函数f(x)的值域是R.(2)证明:设x1,x2为(1,+∞)上的任意两个实数,且x1<x2,则有f(x1)-f(x2)=lg(x1-1)-lg(x2-1)=lg.∵1<x1<x2,∴0<x1-1<x2-1.∴0<<1.又当0<x<1时,y=lg x<0,∴lg<0.∴f(x1)<f(x2).∴f(x)在定义域上是增函数.9y=|log2x|+2的图象,并根据图象写出函数的单调区间及值域.解:先作出函数y=log2x的图象,如图甲.再将y=log2x在x轴下方的图象关于x轴对称翻折到x轴上方(原来在x轴上方的图象不变),得函数y=|log2x|的图象,如图乙;然后将y=|log2x|的图象向上平移2个单位长度,得函数y=|log2x|+2的图象,如图丙.由图丙得函数y=|log2x|+2的单调递增区间是[1,+∞),单调递减区间是(0,1),值域是[2,+∞).二、B组1.函数y=log a(x+2)+1(a>0,且a≠1)的图象过定点()A.(1,2)B.(2,1)C.(-2,1)D.(-1,1)解析:令x+2=1,得x=-1,此时y=1.答案:D2.若函数f(x)=log2x的反函数为y=g(x),且g(a)=,则a=()A.2B.-2C.D.-解析:由题意,得g(x)=2x.∵g(a)=,∴2a=,∴a=-2.答案:B3.(2016·山东高唐高一期末)已知ab=1,函数f(x)=a x(a>0,且a≠1)与函数g(x)=-log b x(b>0,且b≠1)的图象可能是()解析:∵ab=1,∴g(x)=-log b x=log a x,∴函数f(x)=a x(a>0,且a≠1)与g(x)=-log b x(b>0,且b≠1)互为反函数.∴函数f(x)=a x(a>0,且a≠1)与g(x)=-log b x(b>0,且b≠1)的图象关于直线y=x对称,故选B.答案:B4.(2016·湖南长沙一中高一期中)函数f(x)=+log3(x+2)的定义域是.解析:由题意得解得-2<x≤3,且x≠-1.答案:(-2,-1)∪(-1,3]5.已知函数f(x)是定义在R上的奇函数,若当x∈(0,+∞)时,f(x)=lg x,则满足f(x)>0的x的取值范围是.解析:由已知条件可得函数f(x)的解析式为f(x)=其图象如图所示.由函数图象可得不等式f(x)>0时,x的取值范围为(-1,0)∪(1,+∞).答案:(-1,0)∪(1,+∞)6.已知函数f(x)=log2(1+x2).求证:(1)函数f(x)是偶函数;(2)函数f(x)在区间(0,+∞)上是增函数.证明:(1)函数f(x)的定义域是R,f(-x)=log2[1+(-x)2]=log2(1+x2)=f(x),所以函数f(x)是偶函数.(2)设x1,x2为(0,+∞)上的任意两个实数,且x1<x2,则f(x1)-f(x2)=log2(1+)-log2(1+)=log2.由于0<x1<x2,则0<,0<1+<1+,所以0<<1.又函数y=log2x在(0,+∞)上是增函数,所以log2<0.所以f(x1)<f(x2).所以函数f(x)在区间(0,+∞)上是增函数.7.已知函数f(x)=ln(ax2+2x+1),g(x)=lo(x2-4x-5).(1)若f(x)的定义域为R,求实数a的取值范围;(2)若f(x)的值域为R,求实数a的取值范围;(3)求函数g(x)的递减区间.解:(1)若f(x)的定义域为R,则y=ax2+2x+1的图象恒在x轴的上方,∴∴a>1.(2)若f(x)的值域为R,则y=ax2+2x+1的图象一定要与x轴有交点,∴a=0或∴0≤a≤1.(3)由x2-4x-5>0,得x>5或x<-1,∴函数g(x)的定义域为{x|x<-1,或x>5}.令u=x2-4x-5,则它在(5,+∞)上单调递增,在(-∞,-1)上单调递减,又y=lo u在u>0时单调递减,由复合函数单调性的“同增异减”法则可知函数g(x)的单调递减区间为(5,+∞).。

对数的运算(30分钟60分)一、选择题(每小题5分,共40分)1.(2017·大同高一检测)2log32-log3+log38的值为( )A. B.2 C.3 D.【解析】选B.原式=log322-log332+log39+log38=log34+log38- log332+2=log332-log332+2=2. 【补偿训练】(2017·杭州高一检测)2log510+log50.25= ( )A.0B.1C.2D.4【解析】选C.2log510+log50.25=log5100+log50.25=log525=2.2.下列各式中正确的个数是( )①log a(b2-c2)=2log a b-2log a c;②(log a3)2=2log a3;③=lg5.A.0B.1C.2D.3【解析】选A.由对数的运算性质和换底公式知,它们均不正确.3.(2017·黑龙江高一检测)已知lg2=a,lg3=b,则log36等于( )A. B. C. D.【解析】选B.log36===.4.若log5·log36·log6x=2,则x等于( )A.9B.C.25D.【解题指南】利用对数的换底公式将原式中的对数转化为常用对数,再计算.【解析】选D.由换底公式,得··=2,所以-=2.所以lgx=-2lg5=lg.所以x=.5.声强级L I(单位:dB)由公式L I=10lg给出,其中I为声音强度(单位:W/m2).交响音乐会坐在铜管乐前的声音强度约为 5.01×10-2W/m2,则其声强级为(其中lg5.01≈0.7) ( )A.99dBB.100dBC.107dBD.109dB【解析】选 C.当I=5.01×10-2时,其声强级为L I=10lg=10lg(5.01×1010)=10(lg5.01+10)≈107(dB).6.(2017·大连高一检测)若lna,lnb是方程3x2-6x+2=0的两个根,则的值等于( )A. B. C.4 D.【解析】选 A.由根与系数的关系,得lna+lnb=2,lna·lnb=,所以=(lna-lnb)2=(lna+lnb)2-4lna·lnb=22-4×=.7.(2017·北京高一检测)函数f(x)=log a x(a>0且a≠1),若f(x1x2…x n)=16,则f()+f()+…+f()的值等于( )A.2log216B.32C.16D.8【解析】选B.f(x)=log a x,f(x1x2…x n)=16,所以log a(x1x2…x n)=16,所以f()+f()+…+f()=log a+log a+…+log a=2(log a x1+log a x2+…+log a x n)=2log a(x1x2…x n)=32.8.(2017·武汉高一检测)已知2m=5n=10,则+= ( )A.0B.1C.2D.3【解析】选B.因为2m=5n=10,所以m=log210,n=log510,即=lg2,=lg5,故+=lg2+lg5=1.二、填空题(每小题5分,共10分)9.已知f(x)=lgx,若f(ab)=1,则f(a2)+f(b2)=________.【解析】因为f(ab)=1,所以lg(ab)=1,即lga+lgb=1,所以f(a2)+f(b2)=lga2+lgb2=2(lga+lgb)=2.答案:210.若lg3=a,lg5=b,那么lg=________.【解析】lg=lg4.5=lg=lg=(lg5+lg9-1)=(2a+b-1). 答案:三、解答题11.(10分)(2017·兰州高一检测)计算下列各式的值:(1)log535+2lo-log5-log514.(2)[(1-log63)2+log62·log618]÷log64.【解析】(1)原式=log535+log550-log514+2lo=log 5+lo2=log553-1=2.(2)原式=[(log66-log63)2+log62·log6(2×32)]÷log64=÷log622=[(log62)2+(log62)2+2log62·log63]÷2log62=log62+log63=log6(2×3)=1.【能力挑战题】已知2lg(x+y)=lg2x+lg2y,则log2=________.【解析】因为2lg(x+y)=lg2x+lg2y,所以lg(x+y)2=lg(4xy),所以(x+y)2=4xy,所以(x-y)2=0,所以x=y,所以=1,所以log2=log21=0. 答案:0。

2021年高中数学第二章基本初等函数Ⅰ2.2对数函数习题课课后习题新人教A版必修1.已知函数y=log a(x+c)(a,c为常数,且a>0,a≠1)的图象如图所示,则下列结论成立的是()A.a>1,c>1B.a>1,0<c<1C.0<a<1,c>1D.0<a<1,0<c<1解析:由题意可知y=log a(x+c)的图象是由y=log a x的图象向左平移c个单位长度得到的,结合题图知0<c<1.根据单调性易知0<a<1.答案:D2.已知a=,b=log2,c=lo,则()A.a>b>cB.a>c>bC.c>b>aD.c>a>b解析:∵0<a=<20=1,b=log2<log21=0,c=lo>lo=1,∴c>a>b.故选D.答案:D3.函数f(x)=的定义域为()A.(3,5]B.[-3,5]C.[-5,3)D.[-5,-3]解析:要使函数有意义,则3-log2(3-x)≥0,即log2(3-x)≤3,∴0<3-x≤8,∴-5≤x<3.答案:C4.函数f(x)=lo(x2-4)的单调递增区间为()A.(0,+∞)B.(-∞,0)C.(2,+∞)D.(-∞,-2)解析:令t=x2-4>0,可得x>2或x<-2.故函数f(x)的定义域为(-∞,-2)∪(2,+∞),当x∈(-∞,-2)时,t随x的增大而减小,y=lo t随t的减小而增大,所以y=lo(x2-4)随x的增大而增大,即f(x)在(-∞,-2)上单调递增.故选D.答案:D5.已知y=log a(2-ax)在区间[0,1]上为减函数,则a的取值范围为()A.(0,1)B.(1,2)C.(0,2)D.[2,+∞)解析:由题设知a>0,则t=2-ax在区间[0,1]上是减函数.因为y=log a(2-ax)在区间[0,1]上是减函数,所以y=log a t在定义域内是增函数,且t min>0.因此故1<a<2.答案:B6.已知函数f(x)=直线y=a与函数f(x)的图象恒有两个不同的交点,则a的取值范围是.解析:函数f(x)的图象如图所示,要使直线y=a与f(x)的图象有两个不同的交点,则0<a≤1.答案:(0,1]7.已知定义域为R的偶函数f(x)在区间[0,+∞)上是增函数,且f=0,则不等式f(log4x)<0的解集是.解析:由题意可知,f(log4x)<0⇔-<log4x<⇔log4<log4x<log4<x<2.答案:8.已知函数f(x)=log a(x+1)(a>0,且a≠1),g(x)=log a(4-2x).(1)求函数f(x)-g(x)的定义域;(2)求使函数f(x)-g(x)的值为正数时x的取值范围.解:(1)由题意可知,f(x)-g(x)=log a(x+1)-log a(4-2x),要使函数f(x)-g(x)有意义, 则解得-1<x<2.故函数f(x)-g(x)的定义域是(-1,2).(2)令f(x)-g(x)>0,得f(x)>g(x),即log a(x+1)>log a(4-2x).当a>1时,可得x+1>4-2x,解得x>1.由(1)知-1<x<2,所以1<x<2;当0<a<1时,可得x+1<4-2x,解得x<1,由(1)知-1<x<2,所以-1<x<1.综上所述,当a>1时,x的取值范围是(1,2);当0<a<1时,x的取值范围是(-1,1).9.若-3≤lo x≤-,求f(x)=的最值.解:f(x)==(log2x-1)(log2x-2)=(log2x)2-3log2x+2.令log2x=t,∵-3≤lo x≤-,∴-3≤-log2x≤-,∴≤log2x≤3.∴t∈.∴f(x)=g(t)=t2-3t+2=.∴当t=时,g(t)取最小值-;此时,log2x=,x=2;当t=3时,g(t)取最大值2,此时,log2x=3,x=8.综上,当x=2时,f(x)取最小值-;当x=8时,f(x)取最大值2.二、B组1.(xx·江西南昌二中高一期中)函数y=x·ln |x|的大致图象是()解析:函数f(x)=x·ln |x|的定义域(-∞,0)∪(0,+∞)关于原点对称,且f(-x)=-x·ln |-x|=-x·ln |x|=-f(x),所以f(x)是奇函数,排除选项B;当0<x<1时,f(x)<0,排除选项A,C.故选D.答案:D2.(xx·河南许昌四校高一联考)若函数f(x)=log2(x2-ax+3a)在区间[2,+∞)上是增函数,则实数a 的取值范围是()A.a≤4B.a≤2C.-4<a≤4D.-2≤a≤4解析:∵函数f(x)=log2(x2-ax+3a)在区间[2,+∞)上是增函数,∴y=x2-ax+3a在[2,+∞)上大于零且单调递增,故有解得-4<a≤4,故选C.答案:C3.已知函数f(x)在区间[0,+∞)上是增函数,g(x)=-f(|x|),若g(lg x)>g(1),则x的取值范围是()A.B.(0,10)C.(10,+∞)D.∪(10,+∞)解析:因为g(lg x)>g(1),所以f(|lg x|)<f(1).又f(x)在区间[0,+∞)上单调递增,所以0≤|lg x|<1,解得<x<10.答案:A4.已知a=log23.6,b=log43.2,c=log43.6,则a,b,c的大小关系为.解析:∵b=log23.2=log2,c=log23.6=log2,又函数y=log2x在区间(0,+∞)上是增函数,3.6>,∴log23.6>log2>log2,∴a>c>b.答案:a>c>b5.已知函数y=log a x,当x>2时恒有|y|≥1,则a的取值范围是.解析:当a>1时,y=log a x在区间(2,+∞)上是增函数,由log a2≥1,得1<a≤2;当0<a<1时,y=log a x在区间(2,+∞)上是减函数,且log a2≤-1,得≤a<1.故a的取值范围是∪(1,2].答案:∪(1,2]6.若函数f(x)=log a x(a>0,且a≠1)在区间[a,2a]上的最大值是最小值的3倍,则a的值为.解析:当0<a<1时,f(x)在区间(0,+∞)上是减函数,∴f(x)在区间[a,2a]上的最小值为log a(2a),最大值为log a a,∴log a a=3log a(2a),∴log a(2a)=, 即=2a,a=8a3,∴a2=,a=.当a>1时,f(x)在区间(0,+∞)上是增函数,∴f(x)在区间[a,2a]上的最小值为log a a,最大值为log a(2a),∴log a(2a)=3log a a,∴log a(2a)=3,即a3=2a,∴a2=2,a=.故a的值为.答案:7.已知函数f(x)=lg(3x-3).(1)求函数f(x)的定义域和值域;(2)设函数h(x)=f(x)-lg(3x+3),若不等式h(x)>t无实数解,求实数t的取值范围.解:(1)由3x-3>0,得x>1,所以f(x)的定义域为(1,+∞).因为(3x-3)∈(0,+∞),所以函数f(x)的值域为R.(2)因为h(x)=lg(3x-3)-lg(3x+3)=lg=lg的定义域为(1,+∞),且h(x)在区间(1,+∞)上是增函数,所以函数h(x)的值域为(-∞,0).若不等式h(x)>t无实数解,则t的取值范围为t≥0.8.已知函数f(x-1)=lg.(1)求函数f(x)的解析式;(2)解关于x的不等式f(x)≥lg(3x+1).解:(1)令t=x-1,则x=t+1.由题意知>0,即0<x<2,则-1<t<1.所以f(t)=lg=lg.故f(x)=lg(-1<x<1).(2)lg≥lg(3x+1)⇔≥3x+1>0.由3x+1>0,得x>-.因为-1<x<1,所以1-x>0.由≥3x+1,得x+1≥(3x+1)(1-x), 即3x2-x≥0,x(3x-1)≥0,解得x≥或x≤0.又x>-,-1<x<1,所以-<x≤0或≤x<1.故不等式的解集为.。

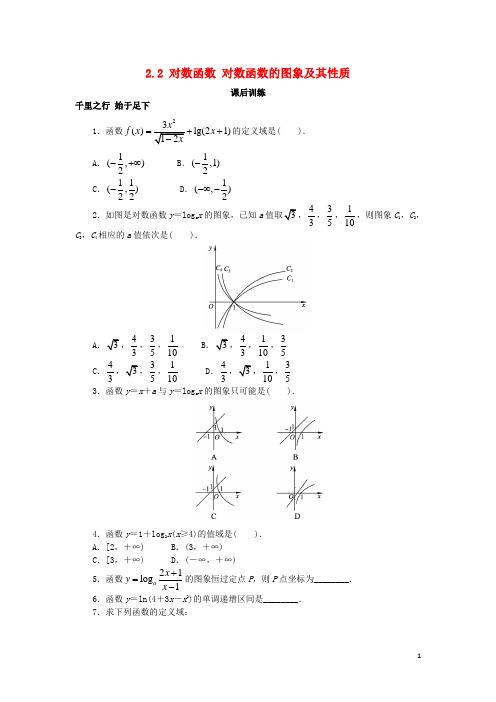
2.2 对数函数 对数函数的图象及其性质课后训练千里之行 始于足下1．函数2()lg(21)f x x =++的定义域是( )． A ．1(,)2-+∞ B ．1(,1)2- C ．11(,)22- D ．1(,)2-∞-2．如图是对数函数y ＝log a x 的图象，已知a 43，35，110，则图象C 1，C 2，C 3，C 4相应的a 值依次是( )．A 43，35，110B 43，110，35C ．43，35，110D ．43110，35 3．函数y ＝x ＋a 与y ＝log a x 的图象只可能是( )．4．函数y ＝1＋log 2x (x ≥4)的值域是( )．A ．[2，＋∞)B ．(3，＋∞)C ．[3，＋∞)D ．(－∞，＋∞)5．函数21log 1a x y x +=-的图象恒过定点P ，则P 点坐标为________． 6．函数y ＝ln(4＋3x －x 2)的单调递增区间是________．7．求下列函数的定义域：(1) 33log 34y x =+； (2)y ＝log (x －1)(3－x )．8．(1)求函数y =的定义域；(2)求函数212log (23)y x x =-++的值域．百尺竿头 更进一步已知函数f (x )＝log a (3－ax )，(1)当x ∈[0,2]时，函数f (x )恒有意义，求实数a 的取值范围．(2)是否存在实数a ，使得函数f (x )在区间[1,2]上为减函数，并且最大值为1？如果存在，试求出a 的值；如果不存在，请说明理由．答案与解析1.答案：C解析：由1201121022x x x ->⎧⇒-<<⎨+>⎩ 2.答案：A解析：∵当a >1时，图象上升；当0<a <1，图象下降．又当a >1时，a 越大，图象向右越靠近x 轴；当0<a <1时，a 越小，图象向右越靠近x 轴．故选A.3.答案：C解析：当a >1时，y ＝log a x 为增函数，且y ＝x ＋a 与y 轴交点的纵坐标a 应大于1，故排除B 、D.当0<a <1时，y ＝log a x 为减函数，且y ＝x ＋a 与y 轴交点的纵坐标a 应在(0,1)之间，故选C.4.答案：C解析：∵x ≥4，∴log 2x ≥2，即y ≥3.∴函数y ＝1＋log 2x (x ≥4)的值域是[3，＋∞)．5.答案：(－2,0)解析：对一切a ∈(0,1)∪(1，＋∞)，当x ＝－2时，2(2)1log 0(2)1a-+=--. ∴P 点坐标为(－2,0)．6.答案：31,2⎛⎤- ⎥⎝⎦解析：解不等式4＋3x －x 2>0得定义域(－1,4)．设2232543()24u x x x =+-=--+.函数u 在区间31,2⎛⎤- ⎥⎝⎦上为增函数，在区间3(,4)2上为减函数．而函数y ＝ln u 在区间(0，＋∞)上为增函数，所以函数y ＝ln(4＋3x －x 2)在区间31,2⎛⎤- ⎥⎝⎦上为增函数，在区间3(,4)2上为减函数．7.解：(1)∵3034x >+，∴43x >-， ∴函数33log 34y x =+的定义域为4(,)3-+∞．(2)∵30,10,11,x x x ->⎧⎪->⎨⎪-≠⎩∴13,2.x x <<⎧⎨≠⎩∴函数的定义域为(1,2)∪(2,3)．8.解：(1)要使函数式有意义，则0.5430,log (43)0,x x ->⎧⎨-≥⎩即430,431,x x ->⎧⎨-≤⎩解得314x <≤. ∴函数的定义域为3,14⎛⎤⎥⎝⎦．(2)设u ＝－x 2＋2x ＋3＝－(x －1)2＋4≤4， ∵12log y u =在(0，＋∞)上是减函数， ∴21122log (23)log 42x x -++≥=-.∴函数的值域为[－2，＋∞)．百尺竿头 更进一步解：(1)由题设，3－ax >0对x ∈[0,2]恒成立，且a >0，a ≠1. 设g (x )＝3－ax ，则g (x )在[0,2]上为减函数，∴g (x )min ＝g (2)＝3－2a >0， ∴32a <.∴a 的取值范围是(0,1)∪(1，32)．(2)假设存在这样的实数a ，则由题设知f (1)＝1， 即log a (3－a )＝1，∴32a =. 此时323()log (3)2f x x =-．但x ＝2时，32()log 0f x =无意义．故这样的实数不存在．。

2.2 对数函数习题课——对数函数及其性质的应用一、A组1.已知函数y=log a(x+c)(a,c为常数,且a>0,a≠1)的图象如图所示,则下列结论成立的是()A.a>1,c>1B.a>1,0<c<1C.0<a<1,c>1D.0<a<1,0<c<1解析:由题意可知y=log a(x+c)的图象是由y=log a x的图象向左平移c个单位长度得到的,结合题图知0<c<1.根据单调性易知0<a<1.答案:D2.已知a=,b=log2,c=lo,则()A.a>b>cB.a>c>bC.c>b>aD.c>a>b解析:∵0<a=<20=1,b=log2<log21=0,c=lo>lo=1,∴c>a>b.故选D.答案:D3.函数f(x)=的定义域为()A.(3,5]B.[-3,5]C.[-5,3)D.[-5,-3]解析:要使函数有意义,则3-log2(3-x)≥0,即log2(3-x)≤3,∴0<3-x≤8,∴-5≤x<3.答案:C4.函数f(x)=lo(x2-4)的单调递增区间为()A.(0,+∞)B.(-∞,0)C.(2,+∞)D.(-∞,-2)解析:令t=x2-4>0,可得x>2或x<-2.故函数f(x)的定义域为(-∞,-2)∪(2,+∞),当x∈(-∞,-2)时,t随x的增大而减小,y=lo t随t的减小而增大,所以y=lo(x2-4)随x的增大而增大,即f(x)在(-∞,-2)上单调递增.故选D.答案:D5.已知y=log a(2-ax)在区间[0,1]上为减函数,则a的取值范围为()A.(0,1)B.(1,2)C.(0,2)D.[2,+∞)解析:由题设知a>0,则t=2-ax在区间[0,1]上是减函数.因为y=log a(2-ax)在区间[0,1]上是减函数,所以y=log a t在定义域内是增函数,且t min>0.因此故1<a<2.答案:B6.已知函数f(x)=直线y=a与函数f(x)的图象恒有两个不同的交点,则a的取值范围是.解析:函数f(x)的图象如图所示,要使直线y=a与f(x)的图象有两个不同的交点,则0<a≤1.答案:(0,1]7.已知定义域为R的偶函数f(x)在区间[0,+∞)上是增函数,且f=0,则不等式f(log4x)<0的解集是.解析:由题意可知,f(log4x)<0⇔-<log4x<⇔log4<log4x<log4<x<2.答案:8.已知函数f(x)=log a(x+1)(a>0,且a≠1),g(x)=log a(4-2x).(1)求函数f(x)-g(x)的定义域;(2)求使函数f(x)-g(x)的值为正数时x的取值范围.解:(1)由题意可知,f(x)-g(x)=log a(x+1)-log a(4-2x),要使函数f(x)-g(x)有意义,则解得-1<x<2.故函数f(x)-g(x)的定义域是(-1,2).(2)令f(x)-g(x)>0,得f(x)>g(x),即log a(x+1)>log a(4-2x).当a>1时,可得x+1>4-2x,解得x>1.由(1)知-1<x<2,所以1<x<2;当0<a<1时,可得x+1<4-2x,解得x<1,由(1)知-1<x<2,所以-1<x<1.综上所述,当a>1时,x的取值范围是(1,2);当0<a<1时,x的取值范围是(-1,1).9.若-3≤lo x≤-,求f(x)=的最值.解:f(x)==(log2x-1)(log2x-2)=(log2x)2-3log2x+2.令log2x=t,∵-3≤lo x≤-,∴-3≤-log2x≤-,∴≤log2x≤3.∴t∈.∴f(x)=g(t)=t2-3t+2=.∴当t=时,g(t)取最小值-;此时,log2x=,x=2;当t=3时,g(t)取最大值2,此时,log2x=3,x=8.综上,当x=2时,f(x)取最小值-;当x=8时,f(x)取最大值2.二、B组1.(2016·江西南昌二中高一期中)函数y=x·ln |x|的大致图象是()解析:函数f(x)=x·ln |x|的定义域(-∞,0)∪(0,+∞)关于原点对称,且f(-x)=-x·ln |-x|=-x·ln |x|=-f(x),所以f(x)是奇函数,排除选项B;当0<x<1时,f(x)<0,排除选项A,C.故选D.答案:D2.(2016·河南许昌四校高一联考)若函数f(x)=log2(x2-ax+3a)在区间[2,+∞)上是增函数,则实数a的取值范围是()A.a≤4B.a≤2C.-4<a≤4D.-2≤a≤4解析:∵函数f(x)=log2(x2-ax+3a)在区间[2,+∞)上是增函数,∴y=x2-ax+3a在[2,+∞)上大于零且单调递增,故有解得-4<a≤4,故选C.答案:C3.已知函数f(x)在区间[0,+∞)上是增函数,g(x)=-f(|x|),若g(lg x)>g(1),则x的取值范围是()A.B.(0,10)C.(10,+∞)D.∪(10,+∞)解析:因为g(lg x)>g(1),所以f(|lg x|)<f(1).又f(x)在区间[0,+∞)上单调递增,所以0≤|lg x|<1,解得<x<10.答案:A4.已知a=log23.6,b=log43.2,c=log43.6,则a,b,c的大小关系为.解析:∵b=log23.2=log2,c=log23.6=log2,又函数y=log2x在区间(0,+∞)上是增函数,3.6>,∴log23.6>log2>log2,∴a>c>b.答案:a>c>b5.已知函数y=log a x,当x>2时恒有|y|≥1,则a的取值范围是. 解析:当a>1时,y=log a x在区间(2,+∞)上是增函数,由log a2≥1,得1<a≤2;当0<a<1时,y=log a x在区间(2,+∞)上是减函数,且log a2≤-1,得≤a<1.故a的取值范围是∪(1,2].答案:∪(1,2]6.若函数f(x)=log a x(a>0,且a≠1)在区间[a,2a]上的最大值是最小值的3倍,则a的值为.解析:当0<a<1时,f(x)在区间(0,+∞)上是减函数,∴f(x)在区间[a,2a]上的最小值为log a(2a),最大值为log a a,∴log a a=3log a(2a),∴log a(2a)=,即=2a,a=8a3,∴a2=,a=.当a>1时,f(x)在区间(0,+∞)上是增函数,∴f(x)在区间[a,2a]上的最小值为log a a,最大值为log a(2a),∴log a(2a)=3log a a,∴log a(2a)=3,即a3=2a,∴a2=2,a=.故a的值为.答案:7.已知函数f(x)=lg(3x-3).(1)求函数f(x)的定义域和值域;(2)设函数h(x)=f(x)-lg(3x+3),若不等式h(x)>t无实数解,求实数t的取值范围.解:(1)由3x-3>0,得x>1,所以f(x)的定义域为(1,+∞).因为(3x-3)∈(0,+∞),所以函数f(x)的值域为R.(2)因为h(x)=lg(3x-3)-lg(3x+3)=lg=lg的定义域为(1,+∞),且h(x)在区间(1,+∞)上是增函数, 所以函数h(x)的值域为(-∞,0).若不等式h(x)>t无实数解,则t的取值范围为t≥0.8.已知函数f(x-1)=lg.(1)求函数f(x)的解析式;(2)解关于x的不等式f(x)≥lg(3x+1).解:(1)令t=x-1,则x=t+1.由题意知>0,即0<x<2,则-1<t<1.所以f(t)=lg=lg.故f(x)=lg(-1<x<1).(2)lg≥lg(3x+1)⇔≥3x+1>0.由3x+1>0,得x>-.因为-1<x<1,所以1-x>0.由≥3x+1,得x+1≥(3x+1)(1-x),即3x2-x≥0,x(3x-1)≥0,解得x≥或x≤0.又x>-,-1<x<1,所以-<x≤0或≤x<1.故不等式的解集为.。

2018年秋高中数学第二章基本初等函数（Ⅰ）2.2 对数函数2.2.2 第1课时对数函数的图象及其性质练习新人教A版必修1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018年秋高中数学第二章基本初等函数（Ⅰ）2.2 对数函数2.2.2 第1课时对数函数的图象及其性质练习新人教A版必修1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018年秋高中数学第二章基本初等函数（Ⅰ）2.2 对数函数2.2.2 第1课时对数函数的图象及其性质练习新人教A版必修1的全部内容。

第1课时对数函数的图象及其性质A级基础巩固一、选择题1．已知集合A＝{y｜y＝log2x,x〉1｝，B＝错误!，则A∩B＝( ）A．｛y｜0<y〈1} B．{y｜y>1｝C.错误!D．∅解析:因为A＝｛y｜y>0}，B＝{y|y〉1}．所以A∩B＝｛y|y〉1｝．答案：B2．已知a＝21。

2，b＝错误!错误!,c＝2log52，则a，b，c的大小关系为( )A．c＜b＜a B．c＜a＜bC．b＜a＜c D．b＜c＜a解析：a＝21.2＞20＝1，b＝错误!错误!＝2错误!＞20＝1，又因为a＝21。

2＝2错误!＞2错误!＝b,所以a＞b.c＝2log52＝log54＜1,所以a＞b＞c.答案：A3．若f(x)＝错误!，则f(x）的定义域为( ）A。

错误!B。

错误!C。

错误!D．（0,＋∞)解析：由题意应有错误!解得错误!所以－错误!＜x＜0.故选A.答案：A4．已知f(x)为R上的增函数，且f（log2x)〉f(1)，则x的取值范围为（）A。

错误! B.错误!∪（2,＋∞)C．(2，＋∞) D．(0，1）∪（2，＋∞）解析：依题意有log2x>1,所以x〉2。

课后提升训练二十对数函数的图象及性质(45分钟70分)一、选择题(每小题5分,共40分)1.下列函数是对数函数的是( )A.y=log(-2)xB.y=log2x2C.y=log2xD.y=log2(x+2)【解析】选C.由对数函数定义知y=log2x=log4x是对数函数.2.函数f(x)=log0.25(2x-1)的定义域为( )A. B.C. D.【解析】选A.由题意知2x-1>0,即x>.3.(2017·德州高一检测)已知函数f(x)=a x(a>0,a≠1),且其图象过点(3,27),f(x)的反函数记为y=g(x),则g(x)的解析式是( ) A.g(x)=log3x B.g(x)=log2xC.g(x)=lo xD.g(x)=lo x【解析】选A.因为f(3)=27,所以a3=27,即a=3,又因为指数函数y=a x与y=log a x互为反函数,所以g(x)=log3x.4.(2017·长沙高一检测)已知f(x)=a-x,g(x)=log a x,且f(2)·g(2)>0,则函数f(x)与g(x)的图象是( )【解析】选D.因为f(2)·g(2)>0,所以a>1,所以f(x)=a-x与g(x)=log a x在其定义域上分别是减函数与增函数.5.(2017·开封高一检测)函数y=log a(x+2)+1的图象过定点( )A.(1,2)B.(2,1)C.(-2,1)D.(-1,1)【解题指南】借助对数函数图象过定点(1,0)这一性质,利用整体代换思想,令x+2=1,求出图象所过定点.【解析】选 D.令x+2=1,即x=-1,得y=log a1+1=1,故函数y=log a(x+2)+1的图象过定点(-1,1).6.若点(a,b)在y=lgx的图象上,a>0且a≠1,则下列点也在此图象上的是( )A. B.(10a,1-b)C. D.(a2,2b)【解析】选 D.若点(a,b)在y=lgx的图象上,则b=lga,所以2b=2lga=lga2,即(a2,2b)也在函数y=lgx的图象上.【延伸探究】本题条件不变,若, (100a,y2)也在函数y=lgx的图象上,试用b表示y1,y2.【解析】因为lg=2-lga=2-b,所以y1=2-b,因为lg(100a)=2+lga=2+b,所以y2=2+b.7.(2017·衡水高一检测)已知函数f(x)=a x+log a x(a>0,且a≠1)在[1,2]上的最大值与最小值之和为log a2+6,则a的值为( ) A. B. C.2 D.4【解题指南】对a分a>1和0<a<1两种情况分别求函数f(x)的最大值与最小值,然后根据题意列出关于a的方程即可.【解析】选C.①当a>1时,a2+log a2+a+log a1=log a2+6,解得a=-3(舍)或a=2.②当0<a<1时,a+log a1+a2+log a2=log a2+6,解得a=2(舍)或a=-3(舍).8.已知函数f(x)=若f(a)=,则实数a= ( )A.-1B.C.1或-D.-1或【解析】选D.f(a)=⇔或⇔a=或a=-1.二、填空题(每小题5分,共10分)9.(2017·临沂高一检测)图中的曲线是y=log a x的图象,已知a的值分别为,,,,相应曲线C1,C2,C3,C4中的a依次为a1,a2,a3,a4,则它们的值分别为__________.【解析】在x轴上方,由对数函数的“底大图右”的性质得到a2>a1>1>a4>a3,所以a1,a2,a3,a4的值分别为,,,.答案:,,,10.(2017·武汉高一检测)若f(x)是对数函数且f(9)=2,当x∈[1,3]时,f(x)的值域是________.【解析】设f(x)=log a x,因为log a9=2,所以a=3,即f(x)=lo x,又因为x∈[1,3],所以0≤f(x)≤1.答案:[0,1]三、解答题(每小题10分,共20分)11.求下列函数的定义域与值域.(1)y=log2(x-1).(2)y=log4(x2+4).【解析】(1)由x-1>0,得x>1,所以函数y=log2(x-1)的定义域是(1,+∞),值域是R.(2)因为对任意实数x,log4(x2+4)都有意义,所以函数y=log4(x2+4)的定义域是R.又因为x2+4≥4,所以log4(x2+4)≥log44=1,即函数y=log4(x2+4)的值域是[1,+∞).12.(2017·沈阳高一检测)已知函数f(x)=log a(ax-)(a>0,a≠1为常数).(1)求函数f(x)的定义域.(2)若a=2,x∈[1,9],求函数f(x)的值域.【解析】(1)ax->0⇒(a-1)>0,因为>0,所以a-1>0,因为a>0,所以>.所以x>,所以函数f(x)的定义域为.(2)a=2时,f(x)=log 2(2x-),令2x-=t,则t=2x-=2-,因为x∈[1,9],所以t∈[1,15],所以log 21≤log2(2x-)≤log215,即0≤f(x)≤log215,所以函数f(x)的值域为[0,log215].【能力挑战题】已知函数f(x)=x2-x+k,且log2f(a)=2,f(log2a)=k,a>0,且a≠1.(1)求a,k的值.(2)当x为何值时,f(log a x)有最小值?求出该最小值.【解析】(1)因为所以即又a>0且a≠1,所以(2)f(log a x)=f(log2x)=(log2x)2-log2x+2=+,所以当log 2x=,即x=时,f(log a x)有最小值.关闭Word文档返回原板块。

2021年高中数学第二章基本初等函数Ⅰ2.2对数函数2.2.1对数与对数运算课后训练新人教A版必修基础巩固1．下列说法中，错误的是( )A．零和负数没有对数B．任何一个指数式都可化为对数式C．以10为底的对数叫做常用对数D．以e为底的对数叫做自然对数2．已知log x16＝2，则x等于( )A．±4 B．4C．256 D．23．有以下四个结论：①lg(lg 10)＝0；②ln(ln e)＝0；③若10＝lg x，则x＝10；④若e＝ln x，则x＝e2．其中正确的是( )A．①③ B．②④C．①② D．③④4．的值是( )A． B．1C． D．25．在b＝log(a－2)(5－a)中，实数a的取值范围是( )A．a＞5或a＜2 B．2＜a＜3或3＜a＜5C．2＜a＜5 D．3＜a＜46．若2.5x＝1 000,0.25y＝1 000，则＝( )A． B．3 C． D．－37．log56·log67·log78·log89·log910＝( )A．1 B．lg 5C． D．1＋lg 28．方程log3(x2－10)＝1＋log3x的解是__________．9．lg2lg5lg112lg lg82+-+×(lg 32－lg 2)＝__________．10．已知log23＝a，log37＝b，则log1456＝__________(用a，b表示)．11．计算51－log0.23的值．能力提升12．已知a＝log32，则log38－2log36的值是( )A．a－2 B．5a－2C．3a－(1＋a)2 D．3a－a2－113．如果方程(lg x)2＋(lg 2＋lg 3)lg x＋lg 2·lg 3＝0的两根为x1，x2，则x1x2的值为__________．14．设x，y，z均为正数，且3x＝4y＝6z，求证：．15．(学科综合)根据规划，我国工农业生产总值从xx年到2020年经过20年将要翻两番，问年平均增长率至少应为多少？(lg 2＝0.301 0，lg 3＝0.477 1，lg 1.072＝0.030 1) 错题记录参考答案1．B 点拨：A 是对数的性质，C 是常用对数定义，D 是自然对数定义，显然正确．对于B ，任何一个底大于零且不等于1的指数式都可化为对数式，这是对数的定义，但整数指数幂和分数指数幂可以扩大底数的范围，如(－5)2＝25就不能写成log (－5)25＝2．2．B 点拨：由log x 16＝2得x 2＝16，又∵x ＞0，∴x ＝4．3．C 点拨：∵lg 10＝1，ln e ＝1，∴①②正确．由10＝lg x 得x ＝1010，故③错；由e ＝ln x 得x ＝e e ，故④错．4．A 点拨：322822222log 3log 3log 923log 3log 3log 33===． 5．B 点拨：由对数的定义知502021a a a ->⎧⎪->⎨⎪-≠⎩，，，即523.a a a <⎧⎪>⎨⎪≠⎩，，故2＜a ＜3或3＜a ＜5．6．A 点拨：∵x ＝log 2.51 000，y ＝log 0.251 000， ∴ 1 0002.5 1 000111log 1 000log 1000log 2.5x ==＝log 1 0002.5． 同理＝log 1 0000.25，∴＝log 1 0002.5－log 1 0000.25＝log 1 00010＝．7．C 点拨：原式＝lg 6lg 7lg8lg9lg10lg101lg5lg 6lg 7lg8lg9lg5lg5⋅⋅⋅⋅==． 8．x ＝5 点拨：原方程可化为log 3(x 2－10)＝log 3(3x )，所以x 2－10＝3x ，解得x ＝－2，或x ＝5．经检验知x ＝5．9．4 点拨：原式＝2lg(25)032lg 21lg 82⨯-⨯⎡⎤⎛⎫⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦＝×lg 24＝4．10． 点拨：由log 23＝a ，log 37＝b ，得log 27＝ab ， 则log 1456＝22222222log 56log 8log 73log 73log 14log 2log 71log 71ab ab+++===+++． 11．解：51－log 0.23＝0.25511log 3log 3log 3log 5355555155553-====＝15． 12．A 点拨：log 38－2log 36＝3log 32－2(log 32＋log 33)＝3a －2(a ＋1)＝a －2．13． 点拨：可将原方程看作关于lg x 的二次方程，则其根为lg x 1，lg x 2．由根与系数的关系，知lg x 1＋lg x 2＝－(lg 2＋lg 3)＝－lg 6＝，所以x 1x 2＝．14．证明：设3x ＝4y ＝6z ＝t ，由x ，y ，z 均为正数知t ＞1，在上式中取以t 为底的对数，可得x log t 3＝y log t 4＝z log t 6＝1，于是，，．因此＝log t 6－log t 3＝log t 2．∵＝log t2，∴．15．解：设xx年总产值为a，年平均增长率为x，由题意，得a(1＋x)20＝4a，即(1＋x)20＝4．∵将上式化为对数式得lg(1＋x)20＝lg 4，即20lg(1＋x)＝2lg 2＝0.602 0，∴lg(1＋x)＝0.030 1＝lg 1.072．∴1＋x＝1.072，即x＝0.072．故年平均增长率至少应为7.2%．。