高中数学函数常用函数图形及其基本性质

一次函数一、定义与定义式：自变量x和因变量y有如下关系：y=kx+b则此时称y是x的一次函数。

特别地，当b=0时，y是x的正比例函数。

即：y=kx （k为常数，k≠0）二、一次函数的性质：的变化值与对应的x的变化值成正比例，比值为k即：y=kx+b （k为任意不为零的实数 b取任何实数）2.当x=0时，b为函数在y轴上的截距。

三、一次函数的图像及性质：1．作法与图形：通过如下3个步骤（1）列表；（2）描点；（3）连线，可以作出一次函数的图像——一条直线。

因此，作一次函数的图像只需知道2点，并连成直线即可。

（通常找函数图像与x轴和y轴的交点）2．性质：（1）在一次函数上的任意一点P（x，y），都满足等式：y=kx+b。

（2）一次函数与y轴交点的坐标总是（0，b)，与x轴总是交于（-b/k，0）正比例函数的图像总是过原点。

3．k，b与函数图像所在象限：当k＞0时，直线必通过一、三象限，y随x的增大而增大；当k＜0时，直线必通过二、四象限，y随x的增大而减小。

当b＞0时，直线必通过一、二象限；当b=0时，直线通过原点当b＜0时，直线必通过三、四象限。

特别地，当b=O时，直线通过原点O（0，0）表示的是正比例函数的图像。

这时，当k＞0时，直线只通过一、三象限；当k＜0时，直线只通过二、四象限。

四、确定一次函数的表达式：已知点A（x1，y1）；B（x2，y2），请确定过点A、B的一次函数的表达式。

（1）设一次函数的表达式（也叫解析式）为y=kx+b。

（2）因为在一次函数上的任意一点P（x，y），都满足等式y=kx+b。

所以可以列出2个方程：y1=kx1+b …… ①和y2=kx2+b …… ②（3）解这个二元一次方程，得到k，b的值。

（4）最后得到一次函数的表达式。

五、一次函数在生活中的应用：1.当时间t一定，距离s是速度v的一次函数。

s=vt。

2.当水池抽水速度f一定，水池中水量g是抽水时间t的一次函数。

高中阶段常见函数性质汇总函 数 名 称:常数函数解析式 形 式:f (x )＝b (b ∈R) 图象及其性质:函数f (ｘ)得图象就是平行于x 轴或与x 轴重合(垂直于y 轴)得直线定 义 域:R值 域:{b} 单 调 性:没有单调性奇 偶 性:均为偶函数[当ｂ=0时,函数既就是奇函数又就是偶函数］反 函 数:无反函数周 期 性:无周期性函 数 名 称:一次函数解析式 形 式:ｆ(x )=kx +ｂ (k ≠0,ｂ∈Ｒ) 图象及其性质:直线型图象、｜k ｜越大,图象越陡;|k ｜越小,图象越平缓;当b =0时,函数ｆ(ｘ)得图象过原点;当b =０且k ＝１时,函数ｆ(x )得图象为一、三象限角平分线;当ｂ=0且k =－1时,函数f (x )得图象为二、四象限角平分线;定 义 域:Ｒ值 域:R单 调 性:当k ＞0时,函数f (x )为Ｒ上得增函数;当k<0时,函数f (ｘ)为Ｒ上得减函数;奇 偶 性:当ｂ＝0时,函数ｆ(x )为奇函数;当b ≠0时,函数f (ｘ)没有奇偶性;反 函 数:有反函数。

［特殊地,当ｋ＝－1或b ＝０且ｋ=1时,函数f (ｘ)得反函数为原函数f (x )本身]周 期 性:无函 数 名 称:反比例函数解析式 形 式:f (x )= (k ≠０)图象及其性质:图象分为两部分,均不与坐标轴相交,当k 〉０时,函数f (x )得图象分别在第一、第三象限;当ｋ<０时,函数ｆ(x )得图象分别在第二、第四象限;双曲线型曲线,x 轴与y 轴分别就是曲线得两条渐近线;图象成中心对称图形,对称中心为原点;图象成轴对称图形,对称轴有两条,分别为y =x 、y =-x ;定 义 域:值 域:单 调 性:当ｋ〉0时,函数f (x )为与上得减函数;当k 〈0时,函数ｆ(x )为与上得增函数;奇 偶 性:奇函数反 函 数:原函数本身 周 期 性:无函 数 名 称:变式型反比例函数解析式 形 式:f (ｘ)= (c ≠0且 d ≠0)图象及其性质:图象分为两部分,均不与直线、直线相交,当ｋ〉0时,函数f (x )得图象分别在直线与直线形成得左下与右上部分;当k<０时,函数f (ｘ)得图象分别在直线与直线形成得左上与b右下部分;双曲线型曲线,直线与直线分别就是曲线得两条渐近线;图象成中心对称图形,对称中心为点;图象成轴对称图形,对称轴有两条,分别为、;反 函 数:周 期 性:无函 数 名 称:二次函数 解析式 形 式:一般式: 顶点式:两根式:图象及其性质:①图形为抛物线,对称轴为,顶点坐标为或,与轴得交点为;②当时,抛物线得开口向上,此时函数图象有最低点;当时,抛物线得开口向下,此时函数图象有最高点; ③当时,函数图象与轴有两个交点,当时,函数图象与轴有一个交点,当时,函数图象与轴没有交点; ④横坐标关于对称轴对称时,纵坐标相等;当时,横坐标距对称轴近则函数值小,当时,横坐标距对称轴近则函数值大;⑤函数均可由函数平移得到;定 义 域:R值 域:当时,值域为;当时,值域为单 调 性:当时,上为减函数,上为增函数;当时,上为减函数,上为增函数;奇 偶 性:当时,函数为偶函数;当时,函数为非奇非偶函数反 函 数:定义域范围内无反函数,在单调区间内有反函数周 期 性:无函 数 名 称:指数函数 解析式 形 式:图象及其性质:①函数图象恒过点,与 轴不相交,只就是无限靠近;②函数与得图象关于轴对称;③当时,轴以左得图象夹在在直线与轴之间,轴以右得图象在直线以上;当时,轴以左得图象在直线以上,轴以右得图象夹在在直线与轴之间;f (x )=④第一象限内,底数大,图象在上方;定 义 域:R值 域:单 调 性:当时,函数为增函数;当时,函数为减函数;奇 偶 性:无反 函 数:对数函数周 期 性:无 函 数 名 称:对数函数解析式 形 式: 图象及其性质:①函数图象恒过点,与轴不相交,只就是无限靠近;②函数与得图象关于轴对称;③当时,轴以下得图象夹在在直线与轴之间,轴以上得图象在直线以右;当时,轴以下得图象在直线以右,轴以上得图象夹在在直线与轴之间;④第一象限内,底数大,图象在右方;定 义 域:R值 域:单 调 性:当时,函数为增函数;当时,函数为减函数;［与系数函数得单调性类似,因为两函数互为反函数]奇 偶 性:无 反 函 数:指数函数周 期 性:无函 数 名 称:对钩函数解析式 形 式:图象及其性质:①函数图象与轴及直线不相交,只就是无限靠近;②当时,函数有最低点,即当时函数取得最小值;③当时,函数有最高点,即当时函数取得最大值;定 义 域:值 域:单 调 性:在与上函数为增函数;在与上函数为减函数;奇 偶 性:奇函数反 函 数:定义域内无反函数周 期 性:无 2、3函数单调性(考点疏理+典型例题+练习题与解析)2.３函数单调性【典型例题】例1、(１)则a 得范围为( D)A 。

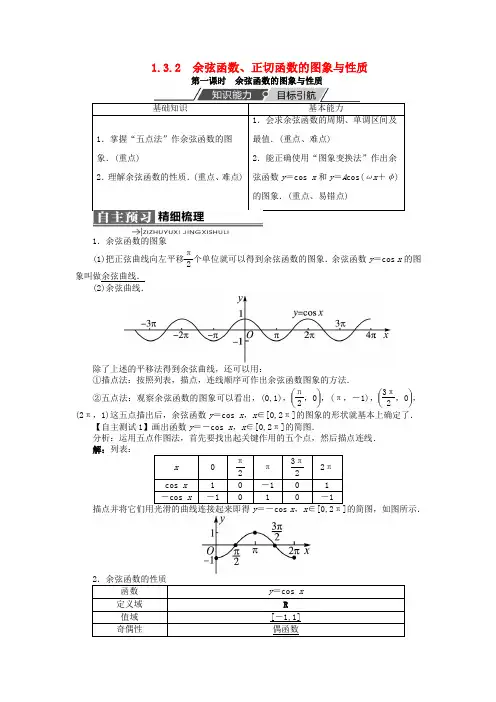
1.3.2 余弦函数、正切函数的图象与性质第一课时 余弦函数的图象与性质1．余弦函数的图象(1)把正弦曲线向左平移π2个单位就可以得到余弦函数的图象．余弦函数y ＝cos x 的图象叫做余弦曲线．(2)余弦曲线．除了上述的平移法得到余弦曲线，还可以用：①描点法：按照列表，描点，连线顺序可作出余弦函数图象的方法．②五点法：观察余弦函数的图象可以看出，(0,1)，⎝ ⎛⎭⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎫3π2，0，(2π，1)这五点描出后，余弦函数y ＝cos x ，x ∈[0,2π]的图象的形状就基本上确定了．【自主测试1】画出函数y ＝－cos x ，x ∈[0,2π]的简图．分析：运用五点作图法，首先要找出起关键作用的五个点，然后描点连线． 解：列表：ω＞0)的周期为T ＝2πω.今后，可以使用这个公式直接求这类函数的周期．【自主测试2－1】函数y ＝2cos x ＋1的最大值和最小值分别是( ) A ．2，－2 B ．3，－1 C ．1，－1 D ．2，－1 答案：B【自主测试2－2】已知函数f (x )＝sin ⎝⎛⎭⎪⎫x －π2(x ∈R )，下列结论错误的是( )A ．函数f (x )的最小正周期为2πB ．函数f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上是增函数C ．函数f (x )的图象关于直线x ＝0对称D ．函数f (x )是奇函数解析：∵f (x )＝sin ⎝⎛⎭⎪⎫x －π2＝－cos x (x ∈R )，f (－x )＝f (x )，∴函数f (x )是偶函数． 答案：D正弦函数与余弦函数的图象和性质的区别与联系(4)sin x ＋cos x ＝1题型一 用“五点法”作函数y ＝A cos(ωx ＋φ)的图象 【例题1】用“五点法”画出函数y ＝2cos 2x 的简图．分析：先找出此函数图象上的五个关键点，画出其在一个周期上的函数图象，再进行扩展得到在整个定义域内的简图．解：因为y ＝2cos 2x 的周期T ＝2π2＝π，所以先在区间[0，π]上按五个关键点列表如下．然后把y ＝2cos 2x 在[0，π]上的图象向左、右平移，每次平移π个单位长度，则得到y ＝2cos 2x 在R 上的简图如下．反思在用“五点法”画出函数y ＝A cos(ωx ＋φ)的图象时，所取的五点应由ωx ＋φ＝0，π2，π，3π2，2π来确定，而不是令x ＝0，π2，π，3π2，2π.题型二 三角函数的图象变换【例题2】函数y ＝sin 2x 的图象可由y ＝cos ⎝⎛⎭⎪⎫2x －π4的图象平移得到，若使平移的距离最短，则应( )A ．向左平移π8个单位长度B ．向右平移7π8个单位长度C ．向左平移π4个单位长度D ．向右平移π8个单位长度解析：y ＝cos ⎝ ⎛⎭⎪⎫2x －π4＝sin ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫2x －π4 ＝sin ⎝ ⎛⎭⎪⎫3π4－2x ＝－sin ⎝⎛⎭⎪⎫2x －3π4 ＝sin ⎝ ⎛⎭⎪⎫2x －3π4＋π＝sin ⎝ ⎛⎭⎪⎫2x ＋π4 ＝sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x ＋π8，故函数y ＝sin 2x 的图象可由y ＝cos ⎝⎛⎭⎪⎫2x －π4的图象向右平移π8个单位长度得到．故选D ．答案：D反思一定要注意看清变换的顺序，即看清是以哪个函数图象作为基准． 题型三 函数的定义域问题【例题3】求函数y ＝36－x 2＋lg cos x 的定义域．分析：首先根据函数解析式列出使函数有意义的条件不等式组，然后分别求解，最后求交集即可．解：要使函数有意义，只需⎩⎪⎨⎪⎧36－x 2≥0，cos x >0，即⎩⎪⎨⎪⎧－6≤x ≤6，2k π－π2<x <2k π＋π2k ∈Z .利用数轴求解，如图所示：所以函数的定义域为⎣⎢⎡⎭⎪⎫－6，－3π2∪⎝ ⎛⎭⎪⎫－π2，π2∪⎝ ⎛⎦⎥⎤3π2，6. 反思利用数轴或者单位圆取解集的交集或并集非常简捷、清晰，但要注意区间的开闭情况．题型四 余弦函数的最值或值域【例题4】(1)求函数y ＝cos x ，x ∈⎣⎢⎡⎦⎥⎤－π3，2π3的值域；(2)求函数y ＝2＋cos x2－cos x的最值；(3)求函数y ＝3cos 2x －4cos x ＋1，x ∈⎣⎢⎡⎦⎥⎤π3，2π3的值域．分析：(1)结合y ＝cos x 的图象在区间⎣⎢⎡⎦⎥⎤－π3，2π3上先增后减即可求解；(2)利用|cos x |≤1这一性质；(3)利用配方法，结合二次函数的性质求解．解：(1)∵y ＝cos x 在区间⎣⎢⎡⎦⎥⎤－π3，0上单调递增，在区间⎣⎢⎡⎦⎥⎤0，2π3上单调递减，∴y ma x ＝cos 0＝1，y min ＝cos 2π3＝－12，∴y ＝cos x 的值域为⎣⎢⎡⎦⎥⎤－12，1. (2)由y ＝2＋cos x 2－cos x ，求得cos x ＝2y －1y ＋1.∵|cos x |≤1，∴⎪⎪⎪⎪⎪⎪2y －1y ＋1≤1，∴[2(y －1)]2≤(y ＋1)2.解得13≤y ≤3，∴y ma x ＝3，y min ＝13.(3)y ＝3cos 2x －4cos x ＋1＝3⎝⎛⎭⎪⎫cos x －232－13，∵x ∈⎣⎢⎡⎦⎥⎤π3，2π3，∴cos x ∈⎣⎢⎡⎦⎥⎤－12，12， 从而当cos x ＝－12，即x ＝2π3时，y ma x ＝154.当cos x ＝12，即x ＝π3时，y min ＝－14.∴函数y ＝3cos 2x －4cos x ＋1的值域为⎣⎢⎡⎦⎥⎤－14，154.反思求函数的最值的方法有以下几种：(1)直接法．根据函数值域的定义，由自变量的取值范围求出函数值的取值范围． (2)利用函数的单调性．(3)利用函数的图象，转化为求函数图象上最高点和最低点的纵坐标的问题．(4)利用换元法，转化为一次函数、二次函数、指数函数、对数函数等基本初等函数问题．题型五 余弦函数图象的应用【例题5】求函数y ＝cos ⎝⎛⎭⎪⎫2x ＋π4的对称中心、对称轴方程、单调递减区间和最小正周期．分析：利用整体换元，设t ＝2x ＋π4，则问题转化为考查函数y ＝cos t 的相关性质．解：设t ＝2x ＋π4，则函数y ＝cos t 的图象如图所示．令t ＝k π(k ∈Z )，则2x ＋π4＝k π(k ∈Z )．故x ＝k ·π2－π8(k ∈Z )即为所求的对称轴方程．令t ＝k π＋π2(k ∈Z )，则2x ＋π4＝k π＋π2(k ∈Z )，则x ＝k ·π2＋π8(k ∈Z )．故⎝ ⎛⎭⎪⎫k ·π2＋π8，0(k ∈Z )即为所求的对称中心．当t ∈[2k π，2k π＋π](k ∈Z )时，2x ＋π4∈[2k π，2k π＋π](k ∈Z )，则x ∈⎣⎢⎡⎦⎥⎤k π－π8，k π＋3π8(k ∈Z )． 故其单调递减区间为⎣⎢⎡⎦⎥⎤k π－π8，k π＋3π8(k ∈Z )． ∵cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫2x ＋π4＋2π＝cos ⎣⎢⎡⎦⎥⎤2x ＋π＋π4， ∴最小正周期T ＝π.反思整体换元思想是解决较复杂三角函数问题常用的一种方法，它能将问题化归为对基本三角函数的考查．〖互动探究〗若将本例中的函数改为“y ＝⎪⎪⎪⎪⎪⎪cos ⎝⎛⎭⎪⎫2x ＋π4”呢？ 解：设t ＝2x ＋π4，则问题转化为考查函数y ＝|cos t |，如图所示：解答过程同例题，可得无对称中心．令t ＝k ·π2(k ∈Z )，则2x ＋π4＝k ·π2(k ∈Z )，∴对称轴为x ＝k ·π4－π8(k ∈Z )；令t ∈⎣⎢⎡⎦⎥⎤k π，k π＋π2(k ∈Z )， ∴2x ＋π4∈⎣⎢⎡⎦⎥⎤k π，k π＋π2(k ∈Z )，则x ∈⎣⎢⎡⎦⎥⎤k ·π2－π8，k ·π2＋π8故其单调递减区间为⎣⎢⎡⎦⎥⎤k ·π2－π8，k ·π2＋π8(k ∈Z )．最小正周期T ＝π2.反思(1)若三角函数式子中带绝对值号，则通常通过观察图象得到周期和单调区间． (2)正弦函数y ＝sin x 和余弦函数y ＝cos x 取绝对值后，周期缩为原来的一半，即 ①y ＝|sin x |的周期为π； ②y ＝|cos x |的周期为π.1．下列说法不正确的是( )A ．正弦函数、余弦函数的定义域是R ，值域是[－1,1]B ．余弦函数当且仅当x ＝2k π(k ∈Z )时取得最大值1，当且仅当x ＝(2k ＋1)π(k ∈Z )时取得最小值－1C ．正弦函数在每个区间⎣⎢⎡⎦⎥⎤π2＋2k π，3π2＋2k π(k ∈Z )上都是减函数 D ．余弦函数在每个区间[2k π－π，2k π](k ∈Z )上都是减函数 答案：D2．下列函数中，周期为π，且在⎣⎢⎡⎦⎥⎤π4，π2上为减函数的是( ) A ．y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π2 B ．y ＝cos ⎝ ⎛⎭⎪⎫2x ＋π2 C ．y ＝sin ⎝ ⎛⎭⎪⎫x ＋π2 D ．y ＝cos ⎝⎛⎭⎪⎫x ＋π2答案：A3．(2012·重庆期末)把函数y ＝cos ⎝⎛⎭⎪⎫2x ＋π3图象上所有点的横坐标缩短为原来的12倍(纵坐标不变)，得到图象的解析式为( )A ．y ＝cos ⎝ ⎛⎭⎪⎫x ＋π6B ．y ＝cos ⎝ ⎛⎭⎪⎫x ＋π3C ．y ＝cos ⎝ ⎛⎭⎪⎫4x ＋2π3D ．y ＝cos ⎝⎛⎭⎪⎫4x ＋π3 答案：D4．若函数y ＝a cos x ＋b 的最小值为－12，最大值为32，则a ＝__________，b ＝__________.解析：由于y ma x ＝32，y min ＝－12，且－1≤cos x ≤1，则当a ＞0时，有⎩⎪⎨⎪⎧a ＋b ＝32，－a ＋b ＝－12，解得⎩⎪⎨⎪⎧a ＝1，b ＝12.当a ＜0时，有⎩⎪⎨⎪⎧－a ＋b ＝32，a ＋b ＝－12，解得⎩⎪⎨⎪⎧a ＝－1，b ＝12.综上，a ＝±1，b ＝12.答案：±1 125．函数y ＝|cos x |的单调增区间为________，单调减区间为________，最小正周期为________．解析：函数y ＝|cos x |的图象，如图所示．由图可知它的最小正周期为π.又因为在一个周期⎣⎢⎡⎦⎥⎤－π2，π2上，函数的增区间是⎣⎢⎡⎦⎥⎤－π2，0，减区间是⎣⎢⎡⎦⎥⎤0，π2.而函数的周期是k π(k ∈Z )，因此函数y ＝|cos x |的增区间是⎣⎢⎡⎦⎥⎤k π－π2，k π(k ∈Z )，减区间是⎣⎢⎡⎦⎥⎤k π，k π＋π2(k ∈Z )． 答案：⎣⎢⎡⎦⎥⎤k π－π2，k π(k ∈Z ) ⎣⎢⎡⎦⎥⎤k π，k π＋π2(k ∈Z ) π 6．函数f (x )的定义域为[0,1]，则f (cos x )的定义域是__________．解析：由已知0≤cos x ≤1，得2k π－π2≤x ≤2k π＋π2(k ∈Z )．答案：⎣⎢⎡⎦⎥⎤2k π－π2，2k π＋π2(k ∈Z ) 7．已知函数f (x )＝3cos ⎝⎛⎭⎪⎫2x －π4，x ∈R . (1)用“五点法”画出函数f (x )在长度为一个周期的闭区间上的简图； (2)求函数f (x )的最大值，并求出取得最大值时自变量x 的取值集合； (3)求函数f (x )的单调增区间． 解：(1)列表：(2)当2x －π4＝2k π(k ∈Z )，即x ＝k π＋π8(k ∈Z )时，y ma x ＝3，此时x 取值的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝k π＋π8，k ∈Z. (3)当2k π－π≤2x －π4≤2k π(k ∈Z )时，k π－3π8≤x ≤k π＋π8，k ∈Z ，故函数f (x )的单调增区间为⎣⎢⎡⎦⎥⎤k π－3π8，k π＋π8(k ∈Z )．。

数函数对数函数的一般形式为，它实际上就是指数函数的反函数。

因此指数函数里对于a的规定，同样适用于对数函数。

右图给出对于不同大小a所表示的函数图形：可以看到对数函数的图形只不过的指数函数的图形的关于直线y=x 的对称图形，因为它们互为反函数。

（1）对数函数的定义域为大于0的实数集合。

（2）对数函数的值域为全部实数集合。

（3）函数总是通过（1，0）这点。

（4）a大于1时，为单调递增函数，并且上凸；a小于1大于0时，函数为单调递减函数，并且下凹。

（5）显然对数函数无界。

指数函数指数函数的一般形式为，从上面我们对于幂函数的讨论就可以知道，要想使得x能够取整个实数集合为定义域，则只有使得如图所示为a的不同大小影响函数图形的情况。

可以看到：（1）指数函数的定义域为所有实数的集合，这里的前提是a大于0，对于a不大于0的情况，则必然使得函数的定义域不存在连续的区间，因此我们不予考虑。

（2）指数函数的值域为大于0的实数集合。

（3）函数图形都是下凹的。

（4）a大于1，则指数函数单调递增；a小于1大于0，则为单调递减的。

（5）可以看到一个显然的规律，就是当a从0趋向于无穷大的过程中（当然不能等于0），函数的曲线从分别接近于Y轴与X轴的正半轴的单调递减函数的位置，趋向分别接近于Y轴的正半轴与X轴的负半轴的单调递增函数的位置。

其中水平直线y=1是从递减到递增的一个过渡位置。

（6）函数总是在某一个方向上无限趋向于X轴,永不相交。

（7）函数总是通过（0，1）这点。

（8）显然指数函数无界。

奇偶性注图：（1）为奇函数（2）为偶函数1．定义一般地，对于函数f(x)（1）如果对于函数定义域内的任意一个x，都有f(-x)=－f(x)，那么函数f(x)就叫做奇函数。

（2）如果对于函数定义域内的任意一个x，都有f(-x)=f(x)，那么函数f(x)就叫做偶函数。

（3）如果对于函数定义域内的任意一个x，f(-x)=-f(x)与f(-x)=f(x)同时成立，那么函数f(x)既是奇函数又是偶函数，称为既奇又偶函数。

第二章 函数§2.1 函数及其性质一、函数的基本性质：1. 函数图像的对称性（1） 奇函数与偶函数：奇函数图像关于坐标原点对称，对于任意x D ∈，都有()()f x f x -=-成立；偶函数的图像关于y 轴对称，对于任意x D ∈，都有()()f x f x -=成立。

（2） 原函数与其反函数：原函数与其反函数的图像关于直线y x =对称。

若某一函数与其反函数表示同一函数时，那么此函数的图像就关于直线y x =对称。

（3） 若函数满足()(2)f x f ax =-，则()f x 的图像就关于直线x a =对称；若函数满足()(2)f x f a x =--，则()f x 的图像就关于点(,0)a 对称。

（4） 互对称知识：函数()()y f x a y f a x =-=-与的图像关于直线x a =对称。

2．函数的单调性函数的单调性是针对其定义域的某个子区间而言的。

判断一个函数的单调性一般采用定义法、导数法或借助其他函数结合单调性的性质（如复合函数的单调性）特别提示：函数(0)ay x a x=+>的图像和单调区间。

3．函数的周期性对于函数()y f x =，若存在一个非零常数T ，使得当x 为定义域中的每一个值时，都有()()f x T f x +=成立，则称()y f x =是周期函数，T 称为该函数的一个周期。

若在所有的周期中存在一个最小的正数，就称其为最小正周期。

（1） 若T 是()y f x =的周期，那么()nT n Z ∈也是它的周期。

（2） 若()y f x =是周期为T 的函数，则()(0)y f ax b a =+≠是周期为Ta的周期函数。

（3） 若函数()y f x =的图像关于直线x a x b ==和对称，则()y f x =是周期为2()a b -的函数。

（4） 若函数()y f x =满足()()(0)f x a f x a +=-≠，则()y f x =是周期为2a 的函数。

(2) /(航+如型三角函数的奇偶性（i ） g （x ） = /沏（颜+如（x€ R）(x)为偶函数匕鼠U 力（而+ 出=j4sin （-<at + 炉）（x W 氏）0 sin 曲匚*0=。

（工 W R ）7Tcos 卯=。

=上7T+一1左 e Z ）由此得 2 ,同理，式夫4皿皈+双相的 为奇函数 =顺@=0/3=上网海2)（ii ）飙# =+劭SwR]妖N = .Aa 式题+钠为偶函数见双t")；就= 式以+如为奇函数7T=中=无产+ — (k e Z)3、周期性(1)基本公式(ii) 〃皈+⑺+氏型三角函数的周期竺y =+ G + 5 =加+中出 的周期为何；（一）三角函数的性质1、定义域与值域2、奇偶性(1)基本函数的奇偶性奇函数：y = sinx y= tanx ； 偶函数：y=cosx.(i )基本三角函数的周期的周期为；丁.y=sinx , y=cosx 的周期为 之并 ；y = tanx , y = cotx4-212yy=cotxy=tanx 3-32X 03 27 3,y=cosx-5-4 .7223 2322 5 2“如血的+朗+9=心服如+沟+用的周期为何.（2）认知⑴A =1/W +创型函数的周期y = |月劭（枷+或）| j = A 匚。

5（西+励|（ii ）若函数为,（收斗劭 型两位函数之和，则探求周期适于“最小公倍数法”. （iii ）探求其它“杂”三角函数的周期，基本策略是试验一一猜想一一证明.（3）特殊情形研究JT(i ) y = tanx — cotx 的最小正周期为27T（ii ） y=卜由H+|M 幻的最小正周期为，；7T（iii ） y = sin 4x + cos 4x 的最小正周期为，. _由此领悟“最小公倍数法”的适用类型，以防施错对象 .4、单调性（1）基本三角函数的单调区间（族）依从三角函数图象识证“三部曲”：①选周期：在原点附近选取那个包含全部锐角，单调区间完整，并且最好关于原点对称的 一个周期；②写特解：在所选周期内写出函数的增区问（或减区问）；③获通解：在②中所得特解区间两端加上有关函数的最小正周期的整数倍，即得这一函数 的增区间族（或减区间族）循着上述三部曲，便可得出课本中规范的三角函数的单调区间族 .揭示：上述“三部曲”也适合于寻求简单三角不等式的解集或探求三角函数的定义域（2） y=/（而+初 型三角函数的单调区问的周期为y = （助+切1_r= |达匚祖（姗+阖| 的周期为 7T(ii) > = 1/(耽+如+同3=0)的周期1y 二|金£血（为工卜8］妣+3）+甘¥ = |例如（而+5+上］ J = |总二加侬大+的+. 的周期为祠；,7T的周期为:. 均同它们不加绝对值时的周期相同，即对 数的周期不变.注意这一点与（i ）的区别.y=八加+◎+上的解析式施加绝对值后，该函此类三角函数单调区间的寻求“三部曲”为 ①换元、分解：令u =z 中,将所给函数分解为内、外两层：y = f (u) , u =®x+卯;②套用公式：根据对复合函数单调性的认知，确定出 f (u)的单调性，而后利用(1)中公 式写出关于u 的不等式；③还原、结论：将u =^+W 代入②中u 的不等式，解出x 的取值范围，并用集合或区间 形成结论.正弦、余弦、正切、余切函数的图象的性质:/y sinx y cosxy tanxy cotxy Asin x(A 、 >0)定义域 R R x | x R 且 x k 1 ,k Zx| x R 且x k ,k ZR值域 [1, 1][1, 1]R RA, A周期性 2 22奇偶性奇函数 偶函数奇函数 奇函数当 0,非奇非偶 当0,奇函数单调性[2 2k , —2k ] 2上为增函 数； [2 2k ,3——2k ] 2上为减函 数(k Z )[2k 1 , 2k ]上为增函 数[2k , 2k 1 ]上为减函数(k Z )一k ,一 k 2 2 上为增函数(k Z )k , k 1上为减函数(k Z )2k2(A),2k -2( A)上为增函数；2k 一------ 2— (A), 2k------ 2——(A)上为减函数(k Z )注意：①y sinx 与y sinx 的单调性正好相反；y cosx 与y cosx 的单调性也同样相反.一般 地，若y f(x)在［a,b ］上递增(减)，则y f (x)在［a,b ］上递减(增)y忖n x 与y cosx 的周期是.-(k Z),对称中心(k ,0); y cos( x )的对称轴方); y tan( x )的对称中心(工,0).,02③ y sin( x )或 y cos( x )0)的周期T 2y tan x 的周期为2 2 (T _ T 2，如图，翻折无效)④y sin( x )的对称轴方程是x k 程是x k (k Z ),对称中心(ky cos2x 原点对称 y cos( 2x) cos2x⑤ 当 tan tan 1, k ,(k Z) ; tan tan 1, k ,(k Z).⑥y cosx 与y s in x _ 2k是同一函数，而y ( x )是偶函数，则2 1 、，、y ( x ) sin( x k ) cos( x).2⑦函数y tanx 在R 上为增函数.(耳［只能在某个单调区间单调递增 .若在整个定义域,y tanx 为增函数，同样也是错误的］.⑧定义域关于原点对称是f (x)具有奇偶性的必要不充分条件.(奇偶性的两个条件：一是定义域 关于原点对称(奇偶都要)，二是满足奇偶性条件，偶函数：f( x) f(x),奇函数：f( x) f(x)) 奇偶性的单调性：奇同偶反.例如：y tanx 是奇函数，y tan(x 1)是非奇非偶.(定义域不 3 关于原点对称)奇函数特有性质：若0 x 的定义域，则f(x)一定有f(0) 0. (0 x 的定义域，则无此性质)⑨y sinx 不是周期函数；y sinx 为周期函数(T )； y cosx 是周期函数(如图)；y cosx 为周期函数(T )；y cos2x1的周期为(如图)，并非所有周期函数都有最小正周期,2y f (x) 5 f (x k),k R . ⑩ y a cos bsinVa 2 b 2sin( ) cos b 有 Va 2 b 2 y .、形如y Asin( x )的函数:11、几个物理量：A 一振幅；f 1—频率(周期的倒数)；x 一相包； 一初相；2、函数y Asin( x )表达式的确定：A 由最值确定； 由周期确定； 由图象上的特殊点确定，如 f(x) Asin( x )(A 0,0, | 3.函数 y Asin( x ) B (其中 A 0,0)最大值是A B,最小值是B A,周期是T —,最小正周期T 六频率是f「相位是x,初相是；其图象的对称轴是直线x k 7k Z),凡| "^0的图象如图所小，则f (x)(答：f(x)152sin(-2x -));y=| cos2x+1/2|图象是该图象与直线y B 的交点都是该图象的对称中心4、研究函数y Asin( x )性质的方法：类比于研究y sin x 的性质，只需将y Asin( x ) 中的x 看成y sinx 中的x,但在求y Asin( x )的单调区间时，要特别注意 A 和 的 符号，通过诱导公式先将 化正。

高中数学 14种函数图像和性质知识解析新人教A版必修1高中不得不掌握的函数图像与常用性质高中常用函数有14种，它们是:1.正比例函数；2.反比例函数；3.根式函数；4一次函数；5.二次函数；6双勾函数.；7..双抛函数；8.指数函数；9对数函数；10.三角函数；11分段函数.；12.绝对值函数；13.超越函数；14.抽象函数。

而函数的性质常见的有：1.定义域；2.值域；3.单调性；4.奇偶性；5.周期性；6.对称性；7.有界性；8.反函数；9.连续性.高中都是从函数解析式入手画出函数图像，再利用函数图像研究其性质，下面我们就函数的图像和性质做归纳总结。

1.正比例函数解析式图像定义域：值域：单调性：奇偶性：反函数：2.反比例函数解析式图像性质定义域：值域：单调性：奇偶性：反函数：对称性：定义域：值域：单调性：对称性：3根式函数解析式图像定义域：值域：单调性：奇偶性：反函数：4一次函数解析式图像定义域：值域：1 性质性质性质用心爱心专心单调性：反函数：5二次函数解析式图像定义域：值域：单调性：对称性：定义域：值域：单调性：对称性：6.双勾函数解析式图像定义域：值域：单调性：奇偶性：对称性：定义域：值域：单调性：奇偶性：对称性：7.双抛函数解析式图像定义域：值域：单调性：奇偶性：对称性：定义域：性质性质性质用心爱心专心值域：单调性：奇偶性：对称性：8.指数函数解析式图像定义域：值域：单调性：9.对数函数解析式图像定义域：值域：单调性：10.三角函数解析式图像单调性：周期性：奇偶性：有界性：对称性：定义域：值域：单调性：周期性：奇偶性：有界性：对称性：定义域：值域：单调性：周期性：奇偶性：有界性：对称性：定义域：值域：单调性：周期性：奇偶性：有界性：对称性：11.分段函数分段函数是在其定义域的不同子集上，分别用几个不同的式子来表示对应关系的函数，它是一类较特殊的函数。

其图像的画法是按定义域的划分分别作图。

1.4.2 正弦函数、余弦函数的性质第2课时 正、余弦函数的性质1．掌握y ＝sin x ，y ＝cos x 的性质：周期性、奇偶性，了解其图象的对称性． 2．掌握y ＝sin x ，y ＝cos x 的单调性，会结合它们的图象说出单调区间，并能根据单调性比较大小．3．掌握y ＝sin x ，y ＝cos x 的最大值、最小值，会求简单三角函数的值域或最值，并能指出取得最大(小)值时自变量x 的值的集合．1．正弦函数的图象与性质正弦函数的图象与性质如下表所示：____当x ＝____________时，y 取最大值1正弦曲线是中心对称图形，其所有的对称中心坐标为(k π，0)(k ∈Z )，即正弦曲线与x 轴的所有交点；正弦曲线也是轴对称图形，其所有的对称轴方程是x ＝k π＋π2(k ∈Z )，所有对称轴垂直于x 轴，且与正弦曲线交点的纵坐标是正弦函数的最大(小)值．【做一做1】 已知函数y ＝sin x ，x ∈R ，则下列说法不正确的是( ) A ．定义域是RB ．最大值与最小值的和等于0C ．在⎣⎢⎡⎦⎥⎤－π2，π2上是减函数 D ．最小正周期是2π2．余弦函数的图象与性质余弦函数的图象与性质如下表所示：__当x ＝________时，y 取最大值1余弦曲线是中心对称图形，其所有的对称中心坐标是⎝ ⎛⎭⎪⎫k π＋π2，0(k ∈Z )，即余弦曲线与x 轴的所有交点；余弦曲线也是轴对称图形，其所有的对称轴方程是x ＝k π(k ∈Z )，所有对称轴垂直于x 轴，且与余弦曲线交点的纵坐标是余弦函数的最大(小)值．【做一做2】 已知函数y ＝cos x ，x ∈R ，则下列说法错误的是( ) A ．值域为[－1,1]B ．是奇函数C ．在定义域上不是单调函数D ．在[0，π]上是减函数答案：1．R [－1,1] 2k π＋π2(k ∈Z ) 2k π－π2(k ∈Z ) 2π 奇 ⎣⎢⎡⎦⎥⎤2k π－π2，2k π＋π2⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋3π2【做一做1】 C2．R 2k π(k ∈Z ) 2k π＋π(k ∈Z ) 2π 偶 [(2k －1)π，2k π] [2k π，(2k ＋1)π]【做一做2】 B正、余弦函数的性质与图象的关系剖析：(1)定义域是R ，反映在图象上是所有垂直于x 轴的直线与图象有且只有一个交点．(2)正、余弦函数的单调性，反映在图象上是曲线的上升与下降的情况．(3)正、余弦函数的周期性，反映在图象上是曲线有规律地重复出现．相邻两对称中心的间隔是半个周期，相邻两对称轴的间隔也是半个周期，相邻的对称中心与对称轴的间隔是四分之一个周期．(4)正、余弦函数的奇偶性，反映在图象上是曲线关于原点或y 轴对称，即sin(－x )＝－sin x ，cos(－x )＝cos x .(5)正、余弦函数的最大值和最小值，反映在图象上，就是曲线的最高点和最低点．题型一 判断三角函数的奇偶性 【例1】 判断下列函数的奇偶性：(1)f (x )＝sin x cos x ；(2)f (x )＝1＋sin x －cos 2x1＋sin x.分析：先判断函数的定义域是否关于原点对称，再判断f (－x )与f (x )的关系，进而可确定函数的奇偶性．反思：1.判断函数奇偶性的依据是函数奇偶性的定义，定义域关于原点对称是函数有奇偶性的前提．另外还要注意诱导公式在判断f (x )与f (－x )之间关系时的应用．2．本例(2)中，易忽视f (x )的定义域，违背定义域优先的原则，而进行非等价变形，得f (x )＝sin x (1＋sin x )1＋sin x＝sin x ，从而导致结果错误．题型二 求三角函数的单调区间【例2】 求函数y ＝2sin ⎝⎛⎭⎪⎫3x ＋π4的单调递减区间． 反思：求函数y ＝A sin(ωx ＋φ)的单调区间时，利用整体思想，把ωx ＋φ看成一个整体，借助于正弦函数的单调区间来解决．题型三 求三角函数的值域(最值) 【例3】 求下列函数的值域： (1)y ＝3－2cos 2x ，x ∈R ；(2)y ＝cos 2x ＋2sin x －2，x ∈R .分析：(1)将2x 看成一个整体，利用余弦函数的值域求得；(2)把sin x 看成一个整体，利用换元法转化为求二次函数的值域．反思：求三角函数的值域的方法：①化为y ＝A sin(ωx ＋φ)＋b 或y ＝A cos(ωx ＋φ)＋b (A ＞0)，则其值域为[－A ＋b ，A ＋b ]．如本例(1)小题；②把sin x 或cos x 看成一个整体，利用换元法转化为求二次函数在闭区间上的值域，如本例(2)小题．题型四 比较三角函数值的大小 【例4】 比较下列各组数的大小： (1)sin 194°与cos 160°；(2)sin ⎝ ⎛⎭⎪⎫sin 3π8与sin ⎝⎛⎭⎪⎫cos 3π8.分析：(1)先将异名三角函数化为同名三角函数，并且利用诱导公式化到同一单调区间上．(2)先比较sin 3π8与cos 3π8的大小，然后利用正弦函数单调性求解．反思：比较三角函数值大小的步骤：①异名函数化为同名函数；②利用诱导公式把角化到同一单调区间上；③利用函数的单调性比较大小．题型五 易错辨析易错点 忽视x 的系数是－1【例5】 求y ＝sin ⎝ ⎛⎭⎪⎫π3－x 的单调递增区间．错解：令π3－x ＝t ，∵y ＝sin t 的递增区间为⎣⎢⎡⎦⎥⎤2k π－π2，2k π＋π2(k ∈Z )， ∴2k π－π2≤π3－x ≤2k π＋π2(k ∈Z )，解得－2k π－π6≤x ≤－2k π＋56π，即2k π－π6≤x ≤2k π＋5π6(k ∈Z )，即y ＝sin ⎝ ⎛⎭⎪⎫π3－x 的单调递增区间为⎣⎢⎡⎦⎥⎤2k π－π6，2k π＋5π6(k ∈Z )． 错因分析：在π3－x 中，x 的系数－1是负数，应整体代入正弦函数的单调递减区间，求原函数的单调递增区间．答案：【例1】 解：(1)定义域为R .f (－x )＝sin(－x )cos(－x )＝－sin x cos x ＝－f (x )，∴f (x )是奇函数．(2)要使函数有意义，自变量x 的取值应满足1＋sin x ≠0， ∴sin x ≠－1.∴x ≠2k π＋32π，k ∈Z .∴函数的定义域为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ∈R ，且x ≠2k π＋3π2，k ∈Z .f ⎝ ⎛⎭⎪⎫π2＝1＋sin π2－cos2π21＋sinπ2＝1，但f ⎝ ⎛⎭⎪⎫－π2无意义，∴函数f (x )既不是奇函数也不是偶函数． 【例2】 解：由于函数y ＝2sin x 的递减区间为⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋3π2(k ∈Z )． 令2k π＋π2≤3x ＋π4≤2k π＋3π2，得2k π3＋π12≤x ≤2k π3＋5π12(k ∈Z )． 故所求的单调递减区间为⎣⎢⎡⎦⎥⎤2k π3＋π12，2k π3＋5π12(k ∈Z )． 【例3】 解：(1)∵－1≤cos 2x ≤1，∴－2≤－2cos 2x ≤2. ∴1≤3－2cos 2x ≤5，即1≤y ≤5.∴函数y ＝3－2cos 2x ，x ∈R 的值域为[1,5]．(2)y ＝cos 2x ＋2sin x －2＝－sin 2x ＋2sin x －1＝－(sin x －1)2.∵－1≤sin x ≤1，∴函数y ＝cos 2x ＋2sin x －2，x ∈R 的值域为[－4,0]． 【例4】 解：(1)sin 194°＝sin(180°＋14°)＝－sin 14°， cos 160°＝cos(180°－20°)＝－cos 20°＝－sin 70°. ∵0°＜14°＜70°＜90°，∴sin 14°＜sin 70°， 从而－sin 14°＞－sin 70°，即sin 194°＞cos 160°. (2)∵cos 3π8＝sin π8，∴0＜cos 3π8＜sin 3π8＜1.而y ＝sin x 在(0,1)内递增，∴sin ⎝ ⎛⎭⎪⎫cos 3π8＜sin ⎝⎛⎭⎪⎫sin 3π8. 【例5】 正解：∵y ＝sin ⎝ ⎛⎭⎪⎫π3－x ＝－sin ⎝⎛⎭⎪⎫x －π3，∴要求原函数的单调递增区间，只需求y ＝sin ⎝⎛⎭⎪⎫x －π3的单调递减区间．令2k π＋π2≤x －π3≤2k π＋3π2(k ∈Z )，∴2k π＋5π6≤x ≤2k π＋116π(k ∈Z )．∴y ＝sin ⎝ ⎛⎭⎪⎫π3－x 的单调递增区间是 ⎣⎢⎡⎦⎥⎤2k π＋5π6，2k π＋116π(k ∈Z )．1．函数y ＝sin 2cos xx+是( )A ．奇函数B ．偶函数C ．既是奇函数又是偶函数D ．既不是奇函数也不是偶函数2．下列关系式中正确的是( ) A ．sin 11°＜cos 10°＜sin 168°B ．sin 168°＜sin 11°＜cos10°C ．sin 11°＜sin 168°＜cos 10°D ．sin 168°＜cos 10°＜sin11°3．函数y ＝sin 2x －cos x 的值域是__________． 4．函数y ＝3－2π32cos 33x ⎛⎫-+ ⎪⎝⎭的最大值为____________，此时自变量x 的取值集合是__________．5．求函数y ＝π2sin 4x ⎛⎫- ⎪⎝⎭的单调递增区间．答案：1．A 定义域为R ，f (－x )＝sin()2cos()x x -+-＝sin 2cos xx-+＝－f (x )，则f (x )是奇函数．2．C ∵sin 168°＝sin(180°－168°)＝sin 12°，cos 10°＝sin 80°， sin 11°＜sin 12°＜sin 80°， ∴sin 11°＜sin 168°＜cos 10°.3.51,4⎡⎤-⎢⎥⎣⎦设cos x ＝t ，－1≤t ≤1，则y ＝1－cos 2x －cos x ＝－t 2－t ＋1＝21524t ⎛⎫-++ ⎪⎝⎭. 由于－1≤t ≤1，则有－1≤y ≤54. 4．5 {x |x ＝3k π＋π，k ∈Z } 当2πcos 33x ⎛⎫+⎪⎝⎭＝－1时，y max ＝3－2×(－1)＝5.此时x 的取值集合为{x |x ＝3k π＋π，k ∈Z }． 5．解：y ＝π2sin 4x ⎛⎫- ⎪⎝⎭＝π2sin 4x ⎛⎫-- ⎪⎝⎭.令2k π＋π2≤x －π4≤2k π＋3π2 (k ∈Z )，得 2k π＋3π4≤x ≤2k π＋7π4(k ∈Z )．函数y ＝π2sin 4x ⎛⎫-⎪⎝⎭的递增区间为 3π7π2π,2π44k k ⎡⎤++⎢⎥⎣⎦(k ∈Z )．。