最新中考数学考前复习第22课时 矩形、菱形、正方形(5年真题)

矩形菱形正方形(39题)一、单选题1(2023·湖南·统考中考真题)如图，菱形ABCD中，连接AC，BD，若∠1=20°，则∠2的度数为()A.20°B.60°C.70°D.80°【答案】C【分析】根据菱形的性质可得BD⊥AC,AB∥CD，则∠1=∠ACD,∠ACD+∠2=90°，进而即可求解．【详解】解：∵四边形ABCD是菱形∴BD⊥AC,AB∥CD，∴∠1=∠ACD,∠ACD+∠2=90°，∵∠1=20°，∴∠2=90°-20°=70°,故选：C．【点睛】本题考查了菱形的性质，熟练掌握是菱形的性质解题的关键．2(2023·湖南常德·统考中考真题)如图1，在正方形ABCD中，对角线AC、BD相交于点O，E，F分别为AO，DO上的一点，且EF∥AD，连接AF,DE．若∠FAC=15°，则∠AED的度数为()A.80°B.90°C.105°D.115°【答案】C【分析】首先根据正方形的性质得到∠OAD=∠ODA=45°，AO=DO，然后结合EF∥AD得到OE= OF，然后证明出△AOF≌△DOE SAS，最后利用三角形内角和定理求解即可．【详解】∵四边形ABCD是正方形∴∠OAD=∠ODA=45°，AO=DO∵EF∥AD∴∠OEF=∠OAD=45°，∠OFE=∠ODA=45°∴∠OEF=∠OFE∴OE=OF又∵∠AOF=∠DOE=90°，AO=DO∴△AOF ≌△DOE SAS∴∠ODE =∠FAC =15°∴∠ADE =∠ODA -∠ODE =30°∴∠AED =180°-∠OAD -∠ADE =105°故选：C ．【点睛】此题考查了正方形的性质，全等三角形的性质和判定，等腰直角三角形三角形的性质等知识，解题的关键是熟练掌握以上知识点．3(2023·湖南常德·统考中考真题)下列命题正确的是()A.正方形的对角线相等且互相平分B.对角互补的四边形是平行四边形C.矩形的对角线互相垂直D.一组邻边相等的四边形是菱形【答案】A 【分析】根据正方形、平行四边形、矩形、菱形的各自性质和构成条件进行判断即可．【详解】A 、正方形的对角线相等且互相垂直平分，描述正确；B 、对角互补的四边形不一定是平行四边形，只是内接于圆，描述错误；C 、矩形的对角线不一定垂直，但相等，描述错误；D 、一组邻边相等的平行四边形才构成菱形，描述错误．故选：A ．【点睛】本题考查平行四边形、矩形、菱形、正方形的性质和判定，解题的关键是熟悉掌握各类特殊四边形的判定和性质．4(2023·浙江·统考中考真题)如图，在菱形ABCD 中，AB =1，∠DAB =60°，则AC 的长为()A.12B.1C.32D.3【答案】D 【分析】连接BD 与AC 交于O ．先证明△ABD 是等边三角形，由AC ⊥BD ，得到∠OAB =12∠BAD =30°，∠AOB =90°，即可得到OB =12AB =12，利用勾股定理求出AO 的长度，即可求得AC 的长度．【详解】解：连接BD 与AC 交于O ．∵四边形ABCD是菱形，∴AB∥CD，AB=AD，AC⊥BD，AO=OC=12AC，∵∠DAB=60°，且AB=AD，∴△ABD是等边三角形，∵AC⊥BD，∴∠OAB=12∠BAD=30°，∠AOB=90°，∴OB=12AB=12，∴AO=AB2-OB2=12-12 2=123，∴AC=2AO=3，故选：D．【点睛】此题主要考查了菱形的性质、勾股定理、等边三角形的判定和性质、30°角所对直角边等于斜边的一半，关键是熟练掌握菱形的性质．5(2023·上海·统考中考真题)在四边形ABCD中，AD∥BC,AB=CD．下列说法能使四边形ABCD 为矩形的是()A.AB∥CDB.AD=BCC.∠A=∠BD.∠A=∠D【答案】C【分析】结合平行四边形的判定和性质及矩形的判定逐一分析即可．【详解】A：∵AB∥CD，AD∥BC,AB=CD∴ABCD为平行四边形而非矩形故A不符合题意B：∵AD=BC，AD∥BC,AB=CD∴ABCD为平行四边形而非矩形故B不符合题意C：∵AD∥BC∴∠A+∠B=180°∵∠A=∠B∴∠A=∠B=90°∵AB=CD∴ABCD为矩形故C符合题意D：∵AD∥BC∴∠A+∠B=180°∵∠A=∠D∴∠D+∠B=180°∴ABCD不是平行四边形也不是矩形故D不符合题意故选：C．【点睛】本题主要考查平行线的性质，平行四边形的判定和性质及矩形的判定等知识，熟练掌握以上知识并灵活运用是解题的关键．6(2023·浙江宁波·统考中考真题)如图，以钝角三角形ABC 的最长边BC 为边向外作矩形BCDE ，连结AE ,AD ，设△AED ，△ABE ，△ACD 的面积分别为S ,S 1,S 2，若要求出S -S 1-S 2的值，只需知道()A.△ABE 的面积B.△ACD 的面积C.△ABC 的面积D.矩形BCDE 的面积【答案】C【分析】过点A 作FG ∥BC ，交EB 的延长线于点F ，DC 的延长线于点G ，易得：FG =BC ,AF ⊥BE ,AG⊥CD ，利用矩形的性质和三角形的面积公式，可得S 1+S 2=12S 矩形BCDE ，再根据S =S △ABC +S 矩形BCDE -S 1-S 2=S △ABC +12S 矩形BCDE ，得到S -S 1-S 2=S △ABC ，即可得出结论．【详解】解：过点A 作FG ∥BC ，交EB 的延长线于点F ，DC 的延长线于点G ，∵矩形BCDE ，∴BC ⊥BE ,BC ⊥CD ,BE =CD ，∴FG ⊥BE ,FG ⊥CD ，∴四边形BFGC 为矩形，∴FG =BC ,AF ⊥BE ,AG ⊥CD ，∴S 1=12BE ⋅AF ,S 2=12CD ⋅AG ，∴S 1+S 2=12BE AF +AG =12BE ⋅BC =12S 矩形BCDE ，又S =S △ABC +S 矩形BCDE -S 1-S 2=S △ABC +12S 矩形BCDE ，∴S -S 1-S 2=S △ABC +12S 矩形BCDE -12S 矩形BCDE =S △ABC ，∴只需要知道△ABC 的面积即可求出S -S 1-S 2的值；故选C ．【点睛】本题考查矩形的性质，求三角形的面积．解题的关键是得到S 1+S 2=12S 矩形BCDE 7(2023·湖南·统考中考真题)如图所示，在矩形ABCD 中，AB >AD ，AC 与BD 相交于点O ，下列说法正确的是()A.点O 为矩形ABCD 的对称中心B.点O 为线段AB 的对称中心C.直线BD 为矩形ABCD 的对称轴D.直线AC 为线段BD 的对称轴【答案】A【分析】由矩形ABCD是中心对称图形，对称中心是对角线的交点，线段AB的对称中心是线段AB的中点，矩形ABCD是轴对称图形，对称轴是过一组对边中点的直线，从而可得答案．【详解】解：矩形ABCD是中心对称图形，对称中心是对角线的交点，故A符合题意；线段AB的对称中心是线段AB的中点，故B不符合题意；矩形ABCD是轴对称图形，对称轴是过一组对边中点的直线，故C，D不符合题意；故选A【点睛】本题考查的是轴对称图形与中心对称图形的含义，矩形的性质，熟记矩形既是中心对称图形也是轴对称图形是解本题的关键．8(2023·四川宜宾·统考中考真题)如图，边长为6的正方形ABCD中，M为对角线BD上的一点，连接AM并延长交CD于点P．若PM=PC，则AM的长为()A.33-1B.333-2C.63-1D.633-2【答案】C【分析】先根据正方形的性质、三角形全等的判定证出△ADM≅△CDM，根据全等三角形的性质可得∠DAM=∠DCM，再根据等腰三角形的性质可得∠CMP=∠DCM，从而可得∠DAM=30°，然后利用勾股定理、含30度角的直角三角形的性质求解即可得．【详解】解：∵四边形ABCD是边长为6的正方形，∴AD=CD=6,∠ADC=90°,∠ADM=∠CDM=45°，在△ADM和△CDM中，DM=DM∠ADM=∠CDM=45°AD=CD，∴△ADM≅△CDM SAS，∴∠DAM=∠DCM，∵PM=PC，∴∠CMP=∠DCM，∴∠APD=∠CMP+∠DCM=2∠DCM=2∠DAM，又∵∠APD+∠DAM=180°-∠ADC=90°，∴∠DAM=30°，设PD=x，则AP=2PD=2x，PM=PC=CD-PD=6-x，∴AD=AP2-PD2=3x=6，解得x=23，∴PM=6-x=6-23，AP=2x=43，∴AM=AP-PM=43-6-23=63-1，故选：C．【点睛】本题考查了正方形的性质、勾股定理、含30度角的直角三角形的性质、等腰三角形的性质等知识点，熟练掌握正方形的性质是解题关键．9(2023·四川乐山·统考中考真题)如图，菱形ABCD 的对角线AC 与BD 相交于点O ，E 为边BC 的中点，连结OE ．若AC =6，BD =8，则OE =()A.2B.52C.3D.4【答案】B【分析】先由菱形的性质得AC ⊥BD ，OC =12AC =12×6=3，OB =12BD =12×8=4，再由勾股定理求出BC =5，然后由直角三角形斜边的中线等于斜边的一半求解．【详解】解：∵菱形ABCD ，∴AC ⊥BD ，OC =12AC =12×6=3，OB =12BD =128=4，∴由勾股定理，得BC =OB 2+OC 2=5，∵E 为边BC 的中点，∴OE =12BC =12×5=52故选：B ．【点睛】本考查菱形的性质，勾股定理，直角三角形的性质，熟练掌握菱形的性质，直角三角形的性质是解题的关键．10(2023·甘肃武威·统考中考真题)如图，将矩形ABCD 对折，使边AB 与DC ，BC 与AD 分别重合，展开后得到四边形EFGH ．若AB =2，BC =4，则四边形EFGH 的面积为()A.2B.4C.5D.6【答案】B【分析】由题意可得四边形EFGH 是菱形，FH =AB =2，GE =BC =4，由菱形的面积等于对角线乘积的一半即可得到答案．【详解】解：∵将矩形ABCD 对折，使边AB 与DC ，BC 与AD 分别重合，展开后得到四边形EFGH ，∴EF ⊥GH ，EF 与GH 互相平分，∴四边形EFGH 是菱形，∵FH =AB =2，GE =BC =4，∴菱形EFGH的面积为12FH⋅GE=12×2×4=4．故选：B【点睛】此题考查了矩形的折叠、菱形的判定和性质等知识，熟练掌握菱形的面积等于对角线乘积的一半是解题的关键．11(2023·浙江绍兴·统考中考真题)如图，在矩形ABCD中，O为对角线BD的中点，∠ABD=60°．动点E在线段OB上，动点F在线段OD上，点E,F同时从点O出发，分别向终点B,D运动，且始终保持OE =OF．点E关于AD,AB的对称点为E1,E2；点F关于BC,CD的对称点为F1,F2．在整个过程中，四边形E1E2F1F2形状的变化依次是()A.菱形→平行四边形→矩形→平行四边形→菱形B.菱形→正方形→平行四边形→菱形→平行四边形C.平行四边形→矩形→平行四边形→菱形→平行四边形D.平行四边形→菱形→正方形→平行四边形→菱形【答案】A【分析】根据题意，分别证明四边形E1E2F1F2是菱形，平行四边形，矩形，即可求解．【详解】∵四边形ABCD是矩形，∴AB∥CD，∠BAD=∠ABC=90°，∴∠BDC=∠ABD=60°，∠ADB=∠CBD=90°-60°=30°，∵OE=OF、OB=OD，∴DF=EB∵对称，∴DF=DF2，BF=BF1，BE=BE2,DE=DE1∴E1F2=E2F1∵对称，∴∠F2DC=∠CDF=60°，∠EDA=∠E1DA=30°∴∠E1DB=60°，同理∠F1BD=60°，∴DE1∥BF1∴E1F2∥E2F1∴四边形E1E2F1F2是平行四边形，如图所示，当E,F,O三点重合时，DO=BO，∴DE1=DF2=AE1=AE2即E1E2=E1F2∴四边形E1E2F1F2是菱形，如图所示，当E,F分别为OD,OB的中点时，设DB=4，则DF2=DF=1，DE1=DE=3，在Rt△ABD中，AB=2,AD=23，连接AE，AO，∵∠ABO=60°，BO=2=AB，∴△ABO是等边三角形，∵E为OB中点，∴AE⊥OB，BE=1，∴AE=22-12=3，根据对称性可得AE1=AE=3，∴AD2=12,DE21=9,AE21=3，∴AD2=AE21+DE21，∴△DE1A是直角三角形，且∠E1=90°，∴四边形E1E2F1F2是矩形，当F,E分别与D,B重合时，△BE1D,△BDF1都是等边三角形，则四边形E1E2F1F2是菱形∴在整个过程中，四边形E1E2F1F2形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形，故选：A．【点睛】本题考查了菱形的性质与判定，平行四边形的性质与判定，矩形的性质与判定，勾股定理与勾股定理的逆定理，轴对称的性质，含30度角的直角三角形的性质，熟练掌握以上知识是解题的关键．12(2023·重庆·统考中考真题)如图，在正方形ABCD中，O为对角线AC的中点，E为正方形内一点，连接BE，BE=BA，连接CE并延长，与∠ABE的平分线交于点F，连接OF，若AB=2，则OF的长度为()A.2B.3C.1D.2【答案】D【分析】连接AF ，根据正方形ABCD 得到AB =BC =BE ，∠ABC =90°，根据角平分线的性质和等腰三角形的性质，求得∠BFE =45°，再证明△ABF ≌△EBF ，求得∠AFC =90°，最后根据直角三角形斜边上的中点等于斜边的一半，即可求出OF 的长度．【详解】解：如图，连接AF ，∵四边形ABCD 是正方形，∴AB =BE =BC ，∠ABC =90°，AC =2AB =22，∴∠BEC =∠BCE ，∴∠EBC =180°-2∠BEC ，∴∠ABE =∠ABC -∠EBC =2∠BEC -90°，∵BF 平分∠ABE ，∴∠ABF =∠EBF =12∠ABE =∠BEC -45°，∴∠BFE =∠BEC -∠EBF =45°，在△BAF 与△BEF ,AB =EB∠ABF =∠EBF BF =BF，∴△BAF ≌△BEF SAS ，∴∠BFE =∠BFA =45°，∴∠AFC =∠BAF +∠BFE =90°，∵O 为对角线AC 的中点，∴OF =12AC =2，故选：D ．【点睛】本题考查了等腰三角形的判定和性质，三角形内角和定理，正方形的性质，直角三角形特征，作出正确的辅助线，求得∠BFE =45°是解题的关键．二、解答题13(2023·湖南怀化·统考中考真题)如图，矩形ABCD 中，过对角线BD 的中点O 作BD 的垂线EF ，分别交AD ，BC 于点E ，F ．(1)证明：△BOF ≌△DOE ；(2)连接BE 、DF ，证明：四边形EBFD 是菱形．【答案】(1)见解析；(2)见解析【分析】(1)根据矩形的性质得出AD ∥BC ，则∠1=∠2,∠3=∠4，根据O 是BD 的中点，可得BO =DO ，即可证明△BOF ≌△DOE AAS ；(2)根据△BOF ≌△DOE 可得ED =BF ，进而可得四边形EBFD 是平行四边形，根据对角线互相垂直的四边形是菱形，即可得证．【详解】(1)证明：如图所示，∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠1=∠2,∠3=∠4，∵O 是BD 的中点，∴BO =DO ，在△BOF 与△DOE 中∠1=∠2∠3=∠4BO =DO，∴△BOF ≌△DOE AAS ；(2)∵△BOF ≌△DOE∴ED =BF ，又∵ED ∥BF∴四边形EBFD 是平行四边形，∵EF ⊥BD∴四边形EBFD 是菱形．【点睛】本题考查了矩形的性质，全等三角形的性质与判定，菱形的判定，熟练掌握特殊四边形的性质与判定是解题的关键．14(2023·湖北随州·统考中考真题)如图，矩形ABCD 的对角线AC ，BD 相交于点O ，DE ∥AC ,CE ∥BD ．(1)求证：四边形OCED 是菱形；(2)若BC =3,DC =2，求四边形OCED 的面积．【答案】(1)见解析；(2)3【分析】(1)先根据矩形的性质求得OC =OD ，然后根据有一组邻边相等的平行四边形是菱形分析推理；(2)根据矩形的性质求得△OCD 的面积，然后结合菱形的性质求解．【详解】(1)解：∵ DE ∥AC ,CE ∥BD ，∴四边形OCED 是平行四边形，又∵矩形ABCD 中，OC =OD ，∴平行四边形OCED 是菱形；(2)解：矩形ABCD 的面积为BC ⋅DC =3×2=6，∴△OCD 的面积为14×6=32，∴菱形OCED 的面积为2×32=3．【点睛】本题考查矩形的性质、菱形的判定，属于中考基础题，掌握矩形的性质和菱形的判定方法，正确推理论证是解题关键．15(2023·湖南永州·统考中考真题)如图，已知四边形ABCD 是平行四边形，其对角线相交于点O ，OA =3,BD =8,AB =5．(1)△AOB 是直角三角形吗？请说明理由；(2)求证：四边形ABCD 是菱形．【答案】(1)△AOB 是直角三角形，理由见解析．(2)见解析【分析】(1)根据平行四边形对角线互相平分可得BO =12BD =4，再根据勾股定理的逆定理，即可得出结论；(2)根据对角线互相垂直的平行四边形是菱形，即可求证．【详解】(1)解：△AOB 是直角三角形，理由如下：∵四边形ABCD 是平行四边形，∴BO =12BD =4，∵OA 2+OB 2=32+42=52=AB 2，∴△AOB 是直角三角形．(2)证明：由(1)可得：△AOB 是直角三角形，∴∠AOB =90°，即AC ⊥BD ，∵四边形ABCD 是平行四边形，∴四边形ABCD 是菱形．【点睛】本题主要考查了平行四边形的性质，勾股定理的逆定理，菱形的判定，解题的关键是掌握平行四边形对角线互相平分，对角线互相垂直的平行四边形是菱形．16(2023·新疆·统考中考真题)如图，AD 和BC 相交于点O ，∠ABO =∠DCO =90°，OB =OC ．点E 、F 分别是AO 、DO的中点．(1)求证：OE =OF ；(2)当∠A =30°时，求证：四边形BECF 是矩形．【答案】(1)见解析；(2)见解析【分析】(1)直接证明△AOB ≌△DOC ASA ，得出OA =OD ，根据E 、F 分别是AO 、DO 的中点，即可得证；(2)证明四边形BECF 是平行四边形，进而根据∠A =30°，推导出△BOE 是等边三角形，进而可得BC =EF ，即可证明四边形BECF 是矩形．【详解】(1)证明：在△AOB 与△DOC 中，∠ABO =∠DCO =90°OB =OC∠AOB =∠DOC∴△AOB ≌△DOC ASA ，∴OA =OD ，又∵E 、F 分别是AO 、DO 的中点，∴OE =OF ；(2)∵OB =OC ，OF =OE ，∴四边形BECF 是平行四边形，BC =2OB ，EF =2OE ，∵E 为AO 的中点，∠ABO =90°，∴EB =EO =EA ，∵∠A =30°，∴∠BOE =60°，∴△BOE 是等边三角形，∴OB =OE ，∴BC =EF ，∴四边形BECF 是矩形．【点睛】本题考查了全等三角形的性质与判定，等边三角形的性质与判定，矩形判定，熟练掌握以上知识是解题的关键．17(2023·云南·统考中考真题)如图，平行四边形ABCD 中，AE 、CF 分别是∠BAD 、∠BCD 的平分线，且E 、F 分别在边BC 、AD 上，AE =AF ．(1)求证：四边形AECF 是菱形；(2)若∠ABC =60°，△ABE 的面积等于43，求平行线AB 与DC 间的距离．【答案】(1)证明见解析；(2)43【分析】(1)先证AD ∥BC ，再证AE ∥FC ，从而四边形AECF 是平行四边形，又AE =AF ，于是四边形AECF 是菱形；(2)连接AC ，先求得∠BAE =∠DAE =∠ABC =60°，再证AC ⊥AB ，∠ACB =90°-∠ABC =30°=∠EAC ，于是有33=AB AC，得AB =33AC ，再证AE =BE =CE ，从而根据面积公式即可求得AC =43．【详解】(1)证明：∵四边形ABCD 是平行四边形，∴AD ∥BC ，∠BAD =∠BCD ，∴∠BEA =∠DAE ，∵AE 、CF 分别是∠BAD 、∠BCD 的平分线，∴∠BAE =∠DAE =12∠BAD ，∠BCF =12∠BCD ，∴∠DAE =∠BCF =∠BEA ，∴AE ∥FC ，∴四边形AECF 是平行四边形，∵AE =AF ，∴四边形AECF 是菱形；(2)解：连接AC ，∵AD ∥BC ，∠ABC =60°，∴∠BAD =180°-∠ABC =120°，∴∠BAE =∠DAE =∠ABC =60°，∵四边形AECF 是菱形，∴∠EAC =12∠DAE =30°，∴∠BAC =∠BAE +∠EAC =90°，∴AC ⊥AB ，∠ACB =90°-∠ABC =30°=∠EAC ，∴AE =CE ，tan30°=tan ∠ACB =AB AC 即33=AB AC，∴AB =33AC ，∵∠BAE =∠ABC ，∴AE =BE =CE ，∵△ABE 的面积等于43，∴S △ABC =12AC ⋅AB =12AC ⋅33AC =36AC 2=83，∴平行线AB 与DC 间的距离AC =43．【点睛】本题考查了平行四边形的判定及性质，菱形的判定，角平分线的定义，等腰三角形的判定，三角函数的应用以及平行线间的距离，熟练掌握平行四边形的判定及性质，菱形的判定，角平分线的定义，等腰三角形的判定，三角函数的应用以及平行线间的距离等知识是解题的关键．18(2023·四川遂宁·统考中考真题)如图，四边形ABCD 中，AD ∥BC ，点O 为对角线BD 的中点，过点O 的直线l 分别与AD 、BC 所在的直线相交于点E 、F ．(点E 不与点D 重合)(1)求证：△DOE ≌△BOF ；(2)当直线l ⊥BD 时，连接BE 、DF ，试判断四边形EBFD 的形状，并说明理由．【答案】(1)见解析；(2)四边形EBFD 为菱形；理由见解析【分析】(1)根据AAS 证明△DOE ≌△BOF 即可；(2)连接EB 、FD ，根据△DOE ≌△BOF ，得出ED =BF ，根据ED ∥BF ，证明四边形EBFD 为平行四边形，根据EF ⊥BD ，证明四边形EBFD 为菱形即可．【详解】(1)证明：∵点O 为对角线BD 的中点，∴BO =DO ，∵AD ∥BC ，∴∠ODE =∠OBF ，∠OED =∠OFB ，在△DOE 和△BOF 中，∠ODE =∠OBF∠OED =∠OFB BO =DO，∴△DOE ≌△BOF AAS ；(2)解：四边形EBFD 为菱形，理由如下：连接EB 、FD ，如图所示：根据解析(1)可知，△DOE ≌△BOF ，∴ED =BF ，∵ED ∥BF ，∴四边形EBFD 为平行四边形，∵l ⊥BD ，即EF ⊥BD ，∴四边形EBFD 为菱形．【点睛】本题主要考查了三角形全等的判定和性质，菱形的判定，平行线的性质，解题的关键是熟练掌握三角形全等的判定方法和菱形的判定方法．19(2023·浙江嘉兴·统考中考真题)如图，在菱形ABCD 中，AE ⊥BC 于点E ，AF ⊥CD 于点F ，连接EF(1)求证：AE =AF ；(2)若∠B =60°，求∠AEF 的度数．【答案】(1)证明见解析；(2)60°【分析】(1)根据菱形的性质的三角形全等即可证明AE =AF ．(2)根据菱形的性质和已知条件可推出∠BAD 度数，再根据第一问的三角形全等和直角三角形的性质可求出∠BAE 和∠DAF 度数，从而求出∠EAF 度数，证明了等边三角形AEF ，即可求出∠AEF 的度数．【详解】(1)证明：∵菱形ABCD ，∴AB =AD ,∠B =∠D ，又∵AE ⊥BC ,AF ⊥CD ，∴∠AEB =∠AFD =90°．在△AEB 和△AFD 中，∠AEB =∠AFD∠B =∠D AB =AD，∴△ABE ≌△ADF (AAS )．∴AE =AF ．(2)解：∵菱形ABCD ，∴∠B +∠BAD =180°，∵∠B =60°，∴∠BAD =120°．又∵∠AEB =90°,∠B =60°，∴∠BAE =30°．由(1)知△ABE ≌△ADF ，∴∠BAE =∠DAF =30°．∴∠EAF =120°-30°-30°=60°．∵AE =AF ，∴△AEF 等边三角形．∴∠AEF =60°．【点睛】本题考查了三角形全等、菱形的性质、等边三角形的性质，解题的关键在于熟练掌握全等的方法和菱形的性质．20(2023·湖北鄂州·统考中考真题)如图，点E是矩形ABCD的边BC上的一点，且AE=AD．(1)尺规作图(请用2B铅笔)：作∠DAE的平分线AF，交BC的延长线于点F，连接DF．(保留作图痕迹，不写作法)；(2)试判断四边形AEFD的形状，并说明理由．【答案】(1)见解析；(2)四边形AEFD是菱形，理由见解析【分析】(1)根据题意结合尺规作角平分线的方法作图即可；(2)根据矩形的性质和平行线的性质得出∠DAF=∠AFE，结合角平分线的定义可得∠EFA=∠EAF，则AE=EF，然后根据平行四边形和菱形的判定定理得出结论．【详解】(1)解：如图所示：(2)四边形AEFD是菱形；理由：∵矩形ABCD中，AD∥BC，∴∠DAF=∠AFE，∵AF平分∠DAE，∴∠DAF=∠EAF，∴∠EFA=∠EAF，∴AE=EF，∵AE=AD，∴AD=EF，∵AD∥EF，∴四边形AEFD是平行四边形，又∵AE=AD，∴平行四边形AEFD是菱形．【点睛】本题主要考查了尺规作角平分线，矩形的性质，平行线的性质，等腰三角形的判定，平行四边形的判定以及菱形的判定等知识，熟练掌握相关判定定理和性质定理是解题的关键．21(2023·吉林长春·统考中考真题)将两个完全相同的含有30°角的直角三角板在同一平面内按如图所示位置摆放．点A，E，B，D依次在同一直线上，连结AF、CD．(1)求证：四边形AFDC是平行四边形；(2)己知BC=6cm，当四边形AFDC是菱形时．AD的长为cm．【答案】(1)见解析；(2)18【分析】(1)由题意可知△ACB≌△DFE易得AC=DF，∠CAB=∠FDE=30°即AC∥DF，依据一组对边平行且相等的四边形是平行四边形可证明；(2)如图，在Rt△ACB中，由30°角所对的直角边等于斜边的一半和直角三角形锐角互余易得AB=2BC= 12cm，∠ABC=60°；由菱形得对角线平分对角得∠CDA=∠FDA=30°，再由三角形外角和易证∠BCD=∠CDA即可得BC=BD=6cm，最后由AD=AB+BD求解即可．【详解】(1)证明：由题意可知△ACB≌△DFE，∴AC=DF，∠CAB=∠FDE=30°，∴AC∥DF，∴四边形AFDC地平行四边形；(2)如图，在Rt△ACB中，∠ACB=90°，∠CAB=30°，BC=6cm，∴AB=2BC=12cm，∠ABC=60°，四边形AFDC是菱形，∴AD平分∠CDF，∴∠CDA=∠FDA=30°，∵∠ABC=∠CDA+∠BCD，∴∠BCD=∠ABC-∠CDA=60°-30°=30°，∴∠BCD=∠CDA，∴BC=BD=6cm，∴AD=AB+BD=18cm，故答案为：18．【点睛】本题考查了全等三角形的性质，平行四边形的判定，菱形的性质，30°角所对的直角边等于斜边的一半和直角三角形锐角互余，三角形外角及等角对等边；解题的关键是熟练掌握相关知识综合求解．22(2023·湖南张家界·统考中考真题)如图，已知点A，D，C，B在同一条直线上，且AD=BC，AE= BF，CE=DF．(1)求证：AE∥BF；(2)若DF=FC时，求证：四边形DECF是菱形．【答案】(1)见解析；(2)见解析【分析】(1)根据题意得出AC=BD，再由全等三角形的判定和性质及平行线的判定证明即可；(2)方法一：利用全等三角形的判定和性质得出DE=CF，又EC=DF，再由菱形的判定证明即可；方法二：利用(1)中结论得出∠ECA=∠FDB，结合菱形的判定证明即可．【详解】(1)证明：∵AD=BC，∴AD+DC=BC+DC，即AC=BD在△AEC和△BFD中，AC=BDAE=BFCE=DF，∴△AEC≌△BFD SSS∴∠A=∠B，∴AE∥BF(2)方法一：在△ADE和△BCF中，AE=BF∠A=∠BAD=BC，∴△ADE≌△BCF SAS∴DE=CF，又EC=DF，∴四边形DECF是平行四边形∵DF=FC，∴▱DECF是菱形；方法二：∵△AEC≌△BFD，∴∠ECA=∠FDB∴EC∥DF，又EC=DF，∴四边形DECF是平行四边形∵DF=FC，∴▱DECF是菱形．【点睛】题目主要考查全等三角形的判定和性质，菱形的判定和性质，理解题意，熟练掌握运用这些知识点是解题关键．23(2023·湖南郴州·统考中考真题)如图，四边形ABCD是平行四边形．(1)尺规作图；作对角线AC的垂直平分线MN(保留作图痕迹)；(2)若直线MN分别交AD，BC于E，F两点，求证：四边形AFCE是菱形【答案】(1)见解析；(2)见解析【分析】(1)根据垂直平分线的作图方法进行作图即可；(2)设EF与AC交于点O，证明△AOE≌△COF ASA，得到OE=OF，得到四边形AFCE为平行四边形，根据EF⊥AC，即可得证．【详解】(1)解：如图所示，MN 即为所求；(2)∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠CAE =∠ACF ，如图：设EF 与AC 交于点O ，∵EF 是AC 的垂直平分线，∴AO =OC ，EF ⊥AC ，∵∠AOE =∠COF ，∴△AOE ≌△COF ASA ，∴OE =OF ，∴四边形AFCE 为平行四边形，∵EF ⊥AC ，∴四边形AFCE 为菱形．【点睛】本题考查基本作图-作垂线，平行四边形的判定和性质，全等三角形的判定和性质，菱形的判定．熟练掌握菱形的判定定理，是解题的关键．24(2023·湖北十堰·统考中考真题)如图，▱ABCD 的对角线AC ,BD 交于点O ，分别以点B ,C 为圆心，12AC ,12BD 长为半径画弧，两弧交于点P ，连接BP ,CP ．(1)试判断四边形BPCO的形状，并说明理由；(2)请说明当▱ABCD的对角线满足什么条件时，四边形BPCO是正方形？【答案】(1)平行四边形，见解析；(2)AC=BD且AC⊥BD【分析】(1)根据平行四边形的性质，得到BP=12AC=OC,CP=12BD=OB，根据两组对边分别相等的四边形是平行四边形判定即可．(2)根据对角线相等、平分且垂直的四边形是正方形判定即可．【详解】(1)四边形BPCO是平行四边形．理由如下：∵▱ABCD的对角线AC,BD交于点O，∴AO=OC,BO=OD，∵以点B,C为圆心，12AC,12BD长为半径画弧，两弧交于点P，∴BP=12AC=OC,CP=12BD=OB∴四边形BPCO是平行四边形．(2)∵对角线相等、平分且垂直的四边形是正方形，∴AC=BD且AC⊥BD时，四边形BPCO是正方形．【点睛】本题考查了平行四边形的判定和性质，正方形的判定和性质，熟练掌握判定和性质是解题的关键．25(2023·四川内江·统考中考真题)如图，在△ABC中，D是BC的中点，E是AD的中点，过点A作AF∥BC交CE的延长线于点F．(1)求证：AF=BD；(2)连接BF，若AB=AC，求证：四边形ADBF是矩形．【答案】(1)见解析；(2)见解析；【分析】(1)根据两直线平行，内错角相等求出∠AFE=∠DCE，然后利用“角角边”证明三角形全等，再由全等三角形的性质容易得出结论；(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形，再根据一个角是直角的平行四边形是矩形判定即可．【详解】(1)证明：∵AF∥BC，∴∠AFE=∠DCE，∵点E为AD的中点，∴AE=DE，在△AEF和△EDC中，∠AFE=∠DCE∠AEF=∠DECAE=DE，∴△EAF≌△EDC(AAS)；∴AF=CD，∵CD=BD，∴AF=BD；(2)证明：∵AF∥BD，AF=BD，∴四边形AFBD是平行四边形，∵AB=AC，BD=CD，∴∠ADB=90°，∴平行四边形AFBD是矩形．【点睛】本题考查了矩形的判定，全等三角形的判定与性质，平行四边形的判定，是基础题，明确有一个角是直角的平行四边形是矩形是解本题的关键．26(2023·湖南岳阳·统考中考真题)如图，点M在▱ABCD的边AD上，BM=CM，请从以下三个选项中①∠1=∠2；②AM=DM；③∠3=∠4，选择一个合适的选项作为已知条件，使▱ABCD为矩形．(1)你添加的条件是(填序号)；(2)添加条件后，请证明▱ABCD为矩形．【答案】(1)答案不唯一，①或②；(2)见解析【分析】(1)根据有一个角是直角的平行四边形是矩形进行选取；(2)通过证明△ABM≌△DCM可得∠A=∠D，然后结合平行线的性质求得∠A=90°，从而得出▱ABCD 为矩形．【详解】(1)解：①或②(2)添加条件①，▱ABCD为矩形，理由如下：在▱ABCD中AB=CD，AB∥CD，在△ABM和△DCM中AB=CD∠1=∠2 BM=CM ，∴△ABM≌△DCM ∴∠A=∠D，又∵AB∥CD，∴∠A+∠D=180°，∴∠A =∠D =90°，∴▱ABCD 为矩形；添加条件②，▱ABCD 为矩形，理由如下：在▱ABCD 中AB =CD ，AB ∥CD ，在△ABM 和△DCM 中AB =CDAM =DM BM =CM，∴△ABM ≌△DCM ∴∠A =∠D ，又∵AB ∥CD ，∴∠A +∠D =180°，∴∠A =∠D =90°，∴▱ABCD 为矩形【点睛】本题考查矩形的判定，全等三角形的判定和性质，掌握平行四边形的性质和矩形的判定方法(有一个角是直角的平行四边形是矩形)是解题关键．27(2023·四川乐山·统考中考真题)如图，在Rt △ABC 中，∠C =90°，点D 为AB 边上任意一点(不与点A 、B 重合)，过点D 作DE ∥BC ，DF ∥AC ，分别交AC 、BC 于点E 、F ，连接EF．(1)求证：四边形ECFD 是矩形；(2)若CF =2，CE =4，求点C 到EF 的距离．【答案】(1)见解析；(2)455【分析】(1)利用平行线的性质证明∠CED =∠CFD =90°，再利用四边形内角和为360°，证明∠EDF =90°，即可由矩形判定定理得出结论；(2)先由勾股定理求出EF =CF 2+CE 2=25，再根据三角形面积公式求解即可．【详解】(1)证明：∵DE ∥BC ，DF ∥AC ，∴四边形ECFD 为平行四边形，∵∠C =90°，∴四边形ECFD 是矩形．(2)解：∵∠C =90°，CF =2，CE =4，∴EF =CF 2+CE 2=25设点C 到EF 的距离为h ，∵S △CEF =12CE ⋅CF =12EF ⋅h ∴2×4=25h∴h=455答：点C到EF的距离为45 5．【点睛】本题考查矩形的判定，平行线的性质，勾股定理．熟练掌握矩形的判定定理和利用面积法求线段长是解题的关键．28(2023·浙江台州·统考中考真题)如图，四边形ABCD中，AD∥BC，∠A=∠C，BD为对角线．(1)证明：四边形ABCD是平行四边形．(2)已知AD>AB，请用无刻度的直尺和圆规作菱形BEDF，顶点E，F分别在边BC，AD上(保留作图痕迹，不要求写作法)．【答案】(1)见解析；(2)见解析【分析】(1)先证明∠ADB=∠CBD，再证明180°-∠ADB+∠A=180°-∠CBD+∠C，即∠ABD=∠CDB，从而可得结论；(2)作对角线BD的垂直平分线交AD于F，交BC于E，从而可得菱形BEDF．【详解】(1)证明：∵AD∥BC，∴∠ADB=∠CBD，∵∠A=∠C，∴180°-∠ADB+∠A=180°-∠CBD+∠C，即∠ABD=∠CDB．∴AB∥CD．∴四边形ABCD是平行四边形．(2)如图，四边形BEDF就是所求作的菱形．【点睛】本题考查的是平行四边形的判定与性质，作线段的垂直平分线，菱形的判定，熟练的利用菱形的判定进行作图是解本题的关键．三、填空题29(2023·黑龙江齐齐哈尔·统考中考真题)如图，在四边形ABCD中，AD=BC，AC⊥BD于点O．请添加一个条件：，使四边形ABCD成为菱形．【答案】AD∥BC(荅案不唯一)【分析】根据题意，先证明四边形ABCD是平行四边形，根据AC⊥BD，可得四边形ABCD成为菱形．【详解】解：添加条件AD∥BC∵AD=BC，AD∥BC∴四边形ABCD是平行四边形，∵AC⊥BD，∴四边形ABCD成为菱形．添加条件AB=CD∵AD=BC，AB=CD∴四边形ABCD是平行四边形，∵AC⊥BD，∴四边形ABCD成为菱形．添加条件OB=OD∵AC⊥BD，∴∠AOD=∠COB=90°∵AD=BC，OB=OD，∴Rt△AOD≌Rt△COB HL∴AD=BC，∴四边形ABCD是平行四边形，∵AC⊥BD，∴四边形ABCD成为菱形．添加条件∠ADB=∠CBD在△AOD与△COB中，∠ADB=∠CBD ∠AOD=∠COB AD=BC∴△AOD≌△COB∴AD=BC，∴四边形ABCD是平行四边形，∵AC⊥BD，∴四边形ABCD成为菱形．故答案为：AD∥BC(AB=CD或OB=OD或∠ADB=∠CBD等)．【点睛】本题考查了平行四边形的判定，菱形的判定，熟练掌握菱形的判定定理是解题的关键．30(2023·辽宁大连·统考中考真题)如图，在菱形ABCD中，AC、BD为菱形的对角线，∠DBC=60°, BD=10，点F为BC中点，则EF的长为．。

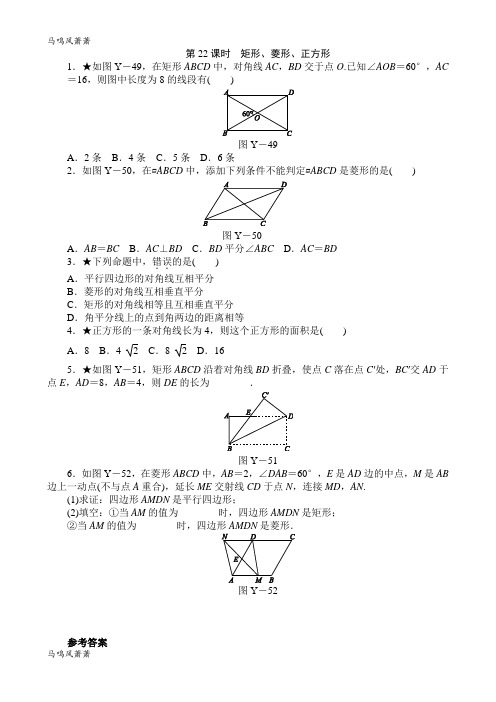
第22课时矩形、菱形、正方形1．★如图Y－49，在矩形ABCD中，对角线AC，BD交于点O.已知∠AOB＝60°，AC ＝16，则图中长度为8的线段有()图Y－49A．2条B．4条C．5条D．6条2．如图Y－50，在▱ABCD中，添加下列条件不能判定▱ABCD是菱形的是()图Y－50A．AB＝BC B．AC⊥BD C．BD平分∠ABC D．AC＝BD3．★下列命题中，错误．．的是()A．平行四边形的对角线互相平分B．菱形的对角线互相垂直平分C．矩形的对角线相等且互相垂直平分D．角平分线上的点到角两边的距离相等4．★正方形的一条对角线长为4，则这个正方形的面积是()A．8 B．4 2 C．8 2 D．165．★如图Y－51，矩形ABCD沿着对角线BD折叠，使点C落在点C′处，BC′交AD于点E，AD＝8，AB＝4，则DE的长为________．图Y－516．如图Y－52，在菱形ABCD中，AB＝2，∠DAB＝60°，E是AD边的中点，M是AB 边上一动点(不与点A重合)，延长ME交射线CD于点N，连接MD，AN.(1)求证：四边形AMDN是平行四边形；(2)填空：①当AM的值为________时，四边形AMDN是矩形；②当AM的值为________时，四边形AMDN是菱形．图Y－52参考答案1．D[解析] 因为矩形的对角线相等且互相平分，所以AO＝OC＝BO＝OD＝8.又因为∠AOB＝60°，所以△AOB是等边三角形，所以AB＝CD＝8，故有AO＝OC＝BO＝OD＝CD ＝AB＝8，故选D.此类问题容易出现的错误是不能判断出△AOB是等边三角形，造成解的遗漏．2．D[解析] 一组邻边相等的平行四边形是菱形，故A正确．对角线互相垂直的平行四边形是菱形，故B正确．对角线平分一组对角的平行四边形是菱形，故C正确．对角线相等的平行四边形是矩形，但不一定是菱形，故D错误．故选D.3．C[解析] 矩形的对角线互相平分且相等，不具备互相垂直的性质，C错误．故选C.4．A[解析] ∵正方形的一条对角线长为4，∴这个正方形的面积＝12×4×4＝8.故选A.此类问题容易出现忽视正方形是特殊的菱形而导致计算繁杂．5．5[解析] ∵∠CBD＝∠DBE，∠CBD＝∠ADB，∴∠DBE＝∠ADB，∴DE＝BE.设DE的长为x，则AE＝8－x.在Rt△ABE中，AB2＋AE2＝BE2，即42＋(8－x)2＝x2，解得x＝5.6．解：(1)证明：∵四边形ABCD为菱形，∴ND∥AM，∴∠NDE＝∠MAE，∠DNE＝∠AME.又∵E是AD边的中点，∴DE＝AE，∴△NDE≌△MAE，∴ND＝MA，∴四边形AMDN是平行四边形．(2)①1②2初中数学试卷鼎尚图文**整理制作。

2020年中考数学第一轮复习第二十二讲矩形菱形正方形【基础知识回顾】一、矩形：1、定义：有一个角是角的平行四边形叫做矩形2、矩形的性质：⑴矩形的四个角都⑵矩形的对角线3、矩形的判定：⑴用定义判定⑵有三个角是直角的是矩形⑶对角线相等的是矩形【注意：1、矩形是对称图形，对称中心是，矩形又是对称图形，对称轴有条2、矩形被它的对角线分成四个全等的三角形和两对全等的三角形3、矩形中常见题目是对角线相交成600或1200角时，利用直角三角形、等边三角形等图形的性质解决问题】二、菱形：1、定义：有一组邻边的平行四边形叫做菱形2、菱形的性质：⑴菱形的四条边都⑵菱形的对角线且每条对角线3、菱形的判定：⑴用定义判定⑵对角线互相垂直的是菱形⑶四条边都相等的是菱形【注意：1、菱形既是对称图形，也是对称图形，它有条对称轴，分别是2、菱形被对角线分成四个全等的三角形和两对全等的三角形3、菱形的面积可以用平行四边形面积公式计算，也可以用两对角线积的来计算4、菱形常见题目是内角为1200或600时，利用等边三角形或直角三角形的相关知识解决的题目】三、正方形：1、定义：有一组邻边相等的是正方形，或有一个角是直角的是正方形2、性质：⑴正方形四个角都都是角，⑵正方形四边条都⑶正方形两对角线、且每条对角线平分一组内角3、判定：⑴先证是矩形，再证 ⑵先证是菱形，再证【注意：1、菱形、正方形具有平行四边形的所有性质，正方形具有以上特殊四边形的所有性质。

这四者之间的关系可表示为：2、正方形也既是 对称图形，又是 对称图形，有 条对称轴3、几种特殊四边形的性质和判定都是从 、 、 三个方面来看 的，要注意它们的区别和联系】【中考真题考点例析】考点一：与四边形有关的折叠问题例1（2019潍坊）如图，在矩形ABCD 中，AD =2．将∠A 向内翻折，点A 落在BC 上，记为A ′，折痕为DE ．若将∠B 沿EA ′向内翻折，点B 恰好落在DE 上，记为B ′，则AB = ．对应练习1－1（泸州）如图，点E 是矩形ABCD 的边CD 上一点，把△ADE 沿AE 对折，点D 的对称点F 恰好落在BC 上，已知折痕AE=105cm ，且tan ∠EFC=34，那么该矩形的周长为（ ）A ．72cmB ．36cmC ．20cmD ．16cm对应练习1－2（湖州）如图，已知四边形ABCD 是矩形，把矩形沿直线AC 折叠，点B 落在点E 处，连接DE ．若DE ：AC=3：5，则AD AB的值为（ ） A ．12 B ．33 C ．23D ．22 考点二：和菱形有关的的问题例2(2019聊城中考)在如图菱形ABCD 中，点P 是BC 边上一点，连接AP ，点,E F 是AP 上的两点，连接DE ，BF ，使得AED ABC ∠=∠，ABF BPF ∠=∠．（1）求证：ABF DAE V V ≌；（2）求证：DE BF EF =＋．对应练习2－1（2019潍坊）如图1，菱形ABCD的顶点A，D在直线l上，∠BAD=60°，以点A为旋转中心将菱形ABCD顺时针旋转α（0°＜α＜30°），得到菱形AB′C′D′．B′C′交对角线AC于点M，C′D′交直线l于点N，连接MN．（1）当MN∥B′D′时，求α的大小．（2）如图2，对角线B′D′交AC于点H，交直线l与点G，延长C′B′交AB于点E，连接EH．当△HEB′的周长为2时，求菱形ABCD的周长．对应练习2－2（泉州）如图，菱形ABCD的周长为85，对角线AC和BD相交于点O，AC：BD=1：2，则AO：BO= ，菱形ABCD的面积S= ．考点三：和矩形有关的题目例3（2019年山东临沂）如图，在□ABCD中，M，N是BD上两点，BM＝DN，连接AM，MC，CN，NA，添加一个条件，使四边形AMCN是矩形，这个条件是（）A．OM＝12AC B．MB＝MO C．BD⊥AC D．∠AMB＝∠CND对应练习3－1（2019青岛中考）如图，在□ABCD 中，对角线AC 与BD 相交于点O ，点E ，F 分别为OB ，OD 中点，延长AE 至G ，使EG＝AE ，连接CG ．（1）求证：△ABE≌△CDF ；（2）当AB 与AC 满足什么数量关系时，四边形EGCF 是矩形？请说明理由.考点四：和正方形有关的试题例4（2019年菏泽）如图，E,F 是正方形ABCD 的对角线AC 上的两点，AC=8,AE=CF=2,则四边形BEDF 的周长是____.对应练习4－1（2019年枣庄）如图，点E 是正方形ABCD 的边DC 上一点，把ADE ∆绕点A 顺时针旋转90︒到ABF ∆的位置．若四边形AECF 的面积为20，DE=2，则AE 的长为（ ）A. 4B. 25C. 6D. 26对应练习4－2（2019年山东临沂）如图，在正方形ABCD 中，E 是DC 边上一点，（与D 、C 不重合），连接AE ，将△ADE 沿AE 所在的直线折叠得到△AFE ，延长EF 交BC 于点G ，连接AG ，作GH ⊥AG ，与AE 的延长线交于点H ，连接CH ．显然AE 是∠DAF 的平分线，EA 是∠DEF 的平分线．仔细观察，请逐一找出图中其他的角平分线（仅限于小于180°的角的平分线），并说明理由．考点五：矩形的动点问题例5（2019年泰安）如图，矩形ABCD 中，4AB =，2AD =，E 为AB 的中点，F 为EC 上一动点，P 为DF 中点，连接PB ，则PB 的最小值是（ ）A. 2B. 4C. 2D. 22 考点六：平行四边形、矩形、菱形及正方形综合题例6（2019年泰安）在平面直角坐标系中，直线:1l y x =+与y 轴交于点1A ，如图所示，A BG C M FH DE依次作正方形111OA B C ，正方形1222C A B C ，正方形2333C A B C ，正方形3444C A B C ，…，点1A ，2A ，3A ，4A ，…在直线l 上，点1C ，2C ，3C ，4C ,…⑴x 轴正半轴上，则前n 个正方形对角线的和是_____.对应练习6－1（2019年莱芜）如图在坐标系中放置一菱形OABC ，已知∠ABC=60°，OA=1．先将菱形OABC 沿x 轴的正方向无滑动翻转，每次翻转60°，连续翻转2019次，点B 的落点依次为B 1，B 2，B 3，…，则B 2019的坐标为 ．对应练习6－2（2019年山东滨州）如图，矩形ABCD 中，点E 在边CD 上，将△BCE 沿BE 折叠，点C 落在AD 边上的点F 处，过点F 作FG ∥CD 交BE 于点G ，连接CG ．（1）求证：四边形CEFG 是菱形；（2）若AB ＝6，AD ＝10，求四边形CEFG 的面积．第二十二讲 矩形 菱形 正方形 参考答案【中考真题考点例析】考点一：与四边形有关的折叠问题例1 答案：3 解：在矩形ABCD 中，∠ADC =∠C =∠B =90°，AB =DC ．由翻折可知，∠AED =∠A 'ED =∠A 'EB =60°，∴∠A 'DE =∠ADE =30°，∴∠A 'DC =30°=∠A 'DB '，又∠A 'B 'D =∠B =∠C ，DA '＝DA '，∴△DB 'A '≌△DCA '（AAS ），∴DC =DB '．在Rt △ADE 中，tan30°=AD AE，即33=2AE ，解得AE =332．∴DE =334．设AB =DC =DB '=x ，则B 'E =BE =x －332，即有x －332+x =334，解得x =3．对应练习1－1 答案：A对应练习1－2 答案：A解析：∵矩形沿直线AC 折叠，点B 落在点E 处，∴∠BAC=∠EAC ，AE=AB=CD ，∵矩形ABCD 的对边AB ∥CD ，∴∠DCA=∠BAC ，∴∠EAC=∠DCA ，设AE 与CD 相交于F ，则AF=CF ，∴AE -AF=CD -CF ，即DF=EF ，∴AF EFFC DF =，又∵∠AFC=∠EFD ，∴△ACF ∽△EDF ，∴53==AC DE FC DF，设DF=3x ，FC=5x ，则AF=5x ，在Rt △ADF 中，AD=2222(3x)-(5x)DF -AF ==4x ，又∵AB=CD=DF+FC=3x+5x=8x ，∴2184==x x AB AD．故选A ．考点二：和菱形有关的的问题例2 答案：证明：（1）∵四边形ABCD 为菱形，∴AB AD =，AD BC ∥，∴BPA DAE ∠=∠.在ABP ∆和DAE ∆中，又∵ABC AED ∠=∠，∴BAF ADE ∠=∠.∵ABF BPF ∠=∠且BPA DAE ∠=∠，∴ABF DAE ∠=∠，又∵AB DA =，∴()ABF DAE ASA ≅V V .（2）∵ABF DAE ≅V V ，∴AE BF =，DE AF =.∵AF AE EF BF EF =+=+， ∴DE BF EF =+.对应练习2－1 答案：解：（1）∵MN ∥B ′D ′，∴D C B C D N B M ''''=''．又∵C ′B ′=C ′D ′，∴MB ′=ND ′．在AB ′M 和△AD ′N 中，∴AB ′=AD ′，∠AB ′M =∠AD ′N ， B ′M =D ′N ，∴△AB ′M ≌△AD ′N ，∴∠B ′AM =∠D ′AN ．又∵∠D ′AN =α，∴∠B ′AM =α．∴∠B ′AM =∠BAB ′=21∠BAC =41∠BAD =15°．即α=15°．（2）在△AB ′E 和△AD ′G 中，∠AB ′E =∠AD ′G ，∠EAB ′=∠GAD ′，AB ′=AD ′，∴△AB ′E ≌△AD ′G ，∴EB ′=GD ′，AE =AG ．在△AHE 和△AHG 中，AE =AG ，∠EAH =∠GAH ，AH =AH ，∴△AHE ≌△AHG ，∴EH ＝GH ．∵△HEB ′的周长为2，∴EH +EB ′+HB ′=2，∴GH +GD ′+B ′H =2，∴B ′D ′=BD =2，∴菱形ABCD 的周长为8．对应练习2－2 答案：1：2，16解析：∵四边形ABCD 是菱形，∴AO=CO ，BO=DO ，∴AC=2AO ，BD=2BO ，∴AO ：BO=1：2；∵菱形ABCD 的周长为58，∴AB=52，∵AO ：BO=1：2，∴AO=2，BO=4，∴菱形ABCD 的面积S=248⨯＝16 故答案为：1：2，16．考点三：和矩形有关的题目例3 答案：A解：在□ABCD 中，OA ＝OC ，OB ＝OD ，又∵BM ＝DN ，∴OM ＝ON ，∴四边形AMCN 是平行四边形．当OM ＝12AC 时，则OA ＝OM ＝OC ，∴∠OAM ＝∠OMA ，∠OCM ＝∠OMC ，∴∠AMC ＝180°÷2＝90°，∴□AMCN 是矩形．对应练习3－1 答案：解：（1）证明：∵四边形ABCD 是平行四边形，∴AB=CD ，AB ∥CD ，OB=OD ，OA=OC ，∴∠ABE=∠CDF ，∵点E ，F 分别为OB ，OD 的中点，∴BE=12OB ，DF=12OD ， ∴BE=DF ，在△ABE 和△CDF 中，AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩()ABE CDF SAS ∴≅V V（2）当AC=2AB 时，四边形EGCF 是矩形；理由如下：∵AC=2OA ，AC=2AB ，∴AB=OA ，∵E 是OB 的中点，∴AG ⊥OB ，∴∠OEG=90°，同理：CF ⊥OD ，∴AG ∥CF ，∴EG∥CF，∵EG=AE，OA=OC，∴OE是△ACG的中位线，∴OE∥CG，∴EF∥CG，∴四边形EGCF是平行四边形，∵∠OEG=90°，∴四边形EGCF是矩形．考点四：和正方形有关的试题例4 答案：解：连接BD，如图所示：因此OD=OB=OC=OA=12AC=4，AE=CF=2,因此OE=OF=8222--=2.所以DF=DE=BE=BF=222425+=，所以四边形BEDF的周长是4×25=85.对应练习4－1 答案：D解：ADE∆Q绕点A顺时针旋转90︒到ABF∆的位置．∴四边形AECF的面积等于正方形ABCD的面积等于20，25AD DC∴==，2DE=Q，Rt ADE∴∆中，2226AE AD DE=+=故选：D．对应练习4－2 答案：解：AG是∠BAF的平分线，GA是∠BGF的平分线，GH是∠EGC的平分线，CH是∠DCM 的平分线．证明如下：∵四边形ABCD为正方形，∴∠D＝∠B＝90°，AB＝AD．∵△ADE沿AE翻折至△AFE，∴AD＝AF，∠D＝∠AFE＝90°，∴AB＝AF．又∵AG＝AG，∴Rt△ABG≌Rt△AFGAB GC NFHDEM（HL ）．∴∠BAG ＝∠FAG ，∠BGA ＝∠FGA ，即GA 是∠BGF 的平分线，GH 是∠EGC 的平分线．∵GH ⊥AG ，∴∠AGH ＝90°，∴∠AGE+∠HGE ＝90°，∠AGB+∠HGC ＝90°， 又⑴∠AGB ＝∠AGE ，∴∠HGE ＝∠HGC ， 即GH 是∠EGC 的平分线．如图，过点H 作HN ⊥BC 于点N ，则∠GNH ＝∠ABG ＝90°∵∠AGB+∠HGC ＝90°，∠AGB+∠BAG ＝90°，∴∠HGC ＝∠BAG ． ∵∠GAE ＝21∠BAD ＝45°，∠AGH ＝90°，∴∠AHG ＝45°，∴AG ＝GH ， ∴△ABG ≌△GNH （AAS ），∴BG ＝HN ， GN ＝AB ＝BC ， ∴BG ＝CN ，∴CN ＝HN ，∴∠HCN ＝45°，∴∠ECH ＝45°， 即CH 是∠DCM 的平分线． 考点五：矩形的动点问题 例5 答案：D解：根据题意要使PB 最小，就必须使得DF 最长，因此可得当C 点和F 点重合时，才能使PB 最小.Q 当C 和F 重合时，P 点是CD 的中点2CP ∴=BP ∴===故选D.考点六：平行四边形、矩形、菱形及正方形综合题例6答案：(21n-解：根据根据题意可得11OA =,212A C =,324A C =,L 112n n n A C --=所以可得正方形111OA B C正方形1222C A B C 的对角线为正方形2333C A B C 的对角线为正方形3444C A B C 的对角线为L正方形1n n n n C A B C -的对角线为2n -所以前n 个正方形对角线的和为12(1248+2n n --++=++++L L (21n-故答案为(21n-对应练习6－1 答案：（1342，0）解：连接AC，如图所示．∠四边形OABC是菱形，∠OA=AB=BC=OC．∠∠ABC=90°，∠∠ABC是等边三角形．∠AC=AB．∠AC=OA．∠OA=1，∠AC=1．画出第5次、第6次、第7次翻转后的图形，如图所示．由图可知：每翻转6次，图形向右平移4．∠2019=335×6+4，∠点B4向右平移1340（即335×4）到点B2019．∠B4的坐标为（2，0），∠B2019的坐标为（2+1340，0），∠B2019的坐标为（1342，0）．对应练习6－2 答案：解：（1）证明：由题意可得，△BCE≌△BFE，∴∠BEC＝∠BEF，FE＝CE，∵FG∥CE，∴∠FGE＝∠CEB，∴∠FGE＝∠FEG，∴FG＝FE，∴FG＝EC，∴四边形CEFG是平行四边形，又∵CE＝FE，∴四边形CEFG是菱形；（2）∵矩形ABCD中，AB＝6，AD＝10，BC＝BF，∴∠BAF＝90°，AD＝BC＝BF＝10，∴AF＝8，∴DF＝2，设EF＝x，则CE＝x，DE＝6﹣x，∵FDE＝90°，∴22+（6﹣x）2＝x2，解得，x＝，∴CE＝，∴四边形CEFG的面积是：CE•DF＝×2＝．【聚焦中考真题】一、选择题1．（威海）如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB 于点E，且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是（）A．BC=AC B．CF⊥BFC．BD=DF D．AC=BF2．（枣庄）如图，在边长为2的正方形ABCD中，M为边AD的中点，延长MD至点E，使ME=MC，以DE为边作正方形DEFG，点G在边CD上，则DG的长为（）A．3- 1 B．3 -5C．5+ 1 D．5- 13．（凉山州）如图，菱形ABCD中，∠B=60°，AB=4，则以AC为边长的正方形ACEF 的周长为（）A．14B．15C．16 D．174．（铜仁地区）下列命题中，真命题是（）A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形5．（宜宾）矩形具有而菱形不具有的性质是（）A．两组对边分别平行B．对角线相等C．对角线互相平分D．两组对角分别相等6．（随州）如图，在菱形ABCD中，∠BAD=120°．已知△ABC的周长是15，则菱形ABCD 的周长是（）A．25B．20C．15D．107．（重庆）如图，矩形纸片ABCD中，AB=6cm，BC=8cm，现将其沿AE对折，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CE的长为（）A．6cm B．4cm C．2cm D．1cm8．（南充）如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE=2，DE=6，∠EFB=60°，则矩形ABCD的面积是（）A．12B．24C．123D．1639．（巴中）如图，菱形ABCD的两条对角线相交于O，若AC=6，BD=4，则菱形ABCD 的周长是（）A．24B．16C．43D．2310.茂名）如图，矩形ABCD的两条对角线相交于点O，∠AOD=60°，AD=2，则AC的长是（）A．2B．4C．2 3D．4311．（成都）如图，将矩形ABCD沿对角线BD折叠，使点C和点C′重合，若AB=2，则C′D的长为（）A．1B．2C．3D．412．（包头）如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是（）A．S1＞S2B．S1=S2C．S1＜S2D．3S1=2S213．（扬州）如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于（）A．50°B．60°C．70°D．80°14．（绵阳）如图，四边形ABCD是菱形，对角线AC=8cm，BD=6cm，DH⊥AB于点H，且DH与AC交于G，则GH=（）A．2825cm B．2120cm C．2815cm D．2521cm15．（雅安）如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△CEF=2S△ABE．其中正确结论有（）个．A．2B．3C．4D．5二、填空题16．（临沂）如图，菱形ABCD中，AB=4，∠B=60°，AE⊥BC，AF⊥CD，垂足分别为E，F，连接EF，则△AEF的面积是．17．（烟台）如图，正方形ABCD的边长为4，点E在BC上，四边形EFGB也是正方形，以B为圆心，BA长为半径画⌒AC，连结AF，CF，则图中阴影部分面积为．18．（济南）如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：①CE=CF；②∠AEB=75°；③BE+DF=EF；④S正方形ABCD=2+3．其中正确的序号是（把你认为正确的都填上）．19．（宿迁）如图，一个平行四边形的活动框架，对角线是两根橡皮筋．若改变框架的形状，则∠α也随之变化，两条对角线长度也在发生改变．当∠α为------度时，两条对角线长度相等．20．（淮安）若菱形的两条对角线分别为2和3，则此菱形的面积是．21．（无锡）如图，菱形ABCD中，对角线AC交BD于O，AB=8，E是CD的中点，则OE的长等于．22．（黔西南州）如图所示，菱形ABCD的边长为4，且AE⊥BC于E，AF⊥CD于F，∠B=60°，则菱形的面积为．23．（攀枝花）如图，在菱形ABCD中，DE⊥AB于点E，cosA=35，BE=4，则tan∠DBE的值是．24．（南充）如图，正方形ABCD的边长为2，过点A作AE⊥AC，AE=1，连接BE，则tanE= ．25．（苏州）如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD内部．将AF延长交边BC于点G．若1CGGB k=，则ADAB=用含k的代数式表示）．26．（哈尔滨）如图，矩形ABCD的对角线AC，BD相交于点O，过点O作OE⊥AC交AB于E，若BC=4，△AOE的面积为5，则sin∠BOE的值为．27．（北京）如图，O是矩形ABCD的对角线AC的中点，M是AD的中点．若AB=5，AD=12，则四边形ABOM的周长为．28．（南京）如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称中心O处，折痕为EF，若菱形ABCD的边长为2cm，∠A=120°，则EF= cm．29．（舟山）如图，正方形ABCD的边长为3，点E，F分别在边AB、BC上，AE=BF=1，小球P从点E出发沿直线向点F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球P第一次碰到点E时，小球P所经过的路程为．30．（桂林）如图，已知线段AB=10，AC=BD=2，点P是CD上一动点，分别以AP、PB 为边向上、向下作正方形APEF和PHKB，设正方形对角线的交点分别为O1、O2，当点P 从点C运动到点D时，线段O1O2中点G的运动路径的长是．31．（荆州）如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，连结AD1、BC1．若∠ACB=30°，AB=1，CC1=x，△ACD与△A1C1D1重叠部分的面积为s，则下列结论：①△A1AD1≌△CC1B；②当x=1时，四边形ABC1D1是菱形；③当x=2时，△BDD1为等边三角形；④s=38（x-2）2（0＜x＜2）；其中正确的是（填序号）．三、解答题32．（2019潍坊）如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中AF交EC于点M．（1）求证：△AHF为等腰直角三角形．（2）若AB=3，EC=5，求EM的长．33.（2019年泰安）如图，四边形ABCD 是正方形，EFC ∆是等腰直角三角形，点E 在AB 上，且90CEF ∠=︒，FG AD ⊥，垂足为点G . （1）试判断AG 与FG 是否相等？并给出证明.（2）若点H 为CF 的中点，GH 与DH 垂直吗？若垂直，给出证明；若不存在，说明理由. 34.（2019年日照）如图，在矩形ABCD 中，对角线AC 的中点为O ，点G ，H 在对角线AC 上，AG ＝CH ，直线GH 绕点O 逆时针旋转α角，与边AB 、CD 分别相交于点E 、F （点E 不与点A 、B 重合）．（1）求证：四边形EHFG 是平行四边形；（2）若∠α＝90°，AB ＝9，AD ＝3，求AE 的长．35．（济宁）如图1，在正方形ABCD 中，E 、F 分别是边AD 、DC 上的点，且AF ⊥BE ． （1）求证：AF=BE ；（2）如图2，在正方形ABCD 中，M 、N 、P 、Q 分别是边AB 、BC 、CD 、DA 上的点，且MP ⊥NQ ．MP 与NQ 是否相等？并说明理由．36．（青岛）已知：如图，在矩形ABCD 中，M ，N 分别是边AD 、BC 的中点，E ，F 分别是线段BM ，CM 的中点．（1）求证：△ABM ≌△DCM ；（2）判断四边形MENF 是什么特殊四边形，并证明你的结论；（3）当AD ：AB= 时，四边形MENF 是正方形（只写结论，不需证明） 37. （淄博）矩形纸片ABCD 中，AB=5，AD=4．（1）如图1，四边形MNEF 是在矩形纸片ABCD 中裁剪出的一个正方形．你能否在该矩形中裁剪出一个面积最大的正方形，最大面积是多少？说明理由；（2）请用矩形纸片ABCD剪拼成一个面积最大的正方形．要求：在图2的矩形ABCD中画出裁剪线，并在网格中画出用裁剪出的纸片拼成的正方形示意图（使正方形的顶点都在网格的格点上）．38．（济南）（1）如图1，已知△ABC，以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连接BE，CD，请你完成图形，并证明：BE=CD；（尺规作图，不写做法，保留作图痕迹）；（2）如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE，CD，BE与CD有什么数量关系？简单说明理由；（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长．39.（资阳）在一个边长为a（单位：cm）的正方形ABCD中，点E、M分别是线段AC，CD上的动点，连结DE并延长交正方形的边于点F，过点M作MN⊥DF于H，交AD于N．（1）如图1，当点M与点C重合，求证：DF=MN；（2）如图2，假设点M从点C出发，以1cm/s的速度沿CD向点D运动，点E同时从点A出发，以2cm/s速度沿AC向点C运动，运动时间为t（t＞0）；①判断命题“当点F是边AB中点时，则点M是边CD的三等分点”的真假，并说明理由．②连结FM、FN，△MNF能否为等腰三角形？若能，请写出a，t之间的关系；若不能，请说明理由．40．（营口）如图1，△ABC为等腰直角三角形，∠ACB=90°，F是AC边上的一个动点（点F与A、C不重合），以CF为一边在等腰直角三角形外作正方形CDEF，连接BF、AD．（1）①猜想图1中线段BF、AD的数量关系及所在直线的位置关系，直接写出结论；②将图1中的正方形CDEF，绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2、图3的情形．图2中BF交AC于点H，交AD于点O，请你判断①中得到的结论是否仍然成立，并选取图2证明你的判断．（2）将原题中的等腰直角三角形ABC改为直角三角形ABC，∠ACB=90°，正方形CDEF改为矩形CDEF，如图4，且AC=4，BC=3，CD=43，CF=1，BF交AC于点H，交AD于点O，连接BD、AF，求BD2+AF2的值．CF的长．（1）求证：△BCP≌△DCP；（2）求证：∠DPE=∠ABC；（3）把正方形ABCD改为菱形，其它条件不变（如图②），若∠ABC=58°，则∠DPE= 度．43．（南通）如图，AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE．求证：四边形BCDE是矩形．44．（广州）如图，四边形ABCD是菱形，对角线AC与BD相交于O，AB=5，AO=4，求BD的长．45．（厦门）如图所示，在正方形ABCD中，点G是边BC上任意一点，DE⊥AG，垂足为E，延长DE交AB于点F．在线段AG上取点H，使得AG=DE+HG，连接BH．求证：∠ABH=∠CDE．46．（黔东南州）如图，在正方形ABCD中，点M是对角线BD上的一点，过点M作ME ∥CD交BC于点E，作MF∥BC交CD于点F．求证：AM=EF．47．（铁岭）如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．（1）求证：四边形AEBD是矩形；（2）当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．48．（南宁）如图，在菱形ABCD中，AC为对角线，点E、F分别是边BC、AD的中点．（1）求证：△ABE≌△CDF；（2）若∠B=60°，AB=4，求线段AE的长．49．（贵阳）已知：如图，在菱形ABCD中，F是BC上任意一点，连接AF交对角线BD 于点E，连接EC．（1）求证：AE=EC；（2）当∠ABC=60°，∠CEF=60°时，点F在线段BC上的什么位置？说明理由．50．（曲靖）如图，点E在正方形ABCD的边AB上，连接DE，过点C作CF⊥DE于F，过点A作AG∥CF交DE于点G．（1）求证：△DCF≌△ADG．（2）若点E是AB的中点，设∠DCF=α，求sinα的值．51．（绥化）已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边做正方形ADEF，连接CF（1）如图1，当点D在线段BC上时．求证CF+CD=BC；（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD 三条线段之间的关系；（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；①请直接写出CF，BC，CD三条线段之间的关系；②若正方形ADEF的边长为22，对角线AE，DF相交于点O，连接OC．求OC的长度．52．（盘锦）如图，正方形ABCD的边长是3，点P是直线BC上一点，连接PA，将线段PA绕点P逆时针旋转90°得到线段PE，在直线BA上取点F，使BF=BP，且点F与点E 在BC同侧，连接EF，CF．（1）如图 ，当点P在CB延长线上时，求证：四边形PCFE是平行四边形；（2）如图 ，当点P在线段BC上时，四边形PCFE是否还是平行四边形，说明理由；（3）在（2）的条件下，四边形PCFE的面积是否有最大值？若有，请求出面积的最大值及此时BP长；若没有，请说明理由．53.（2019年济南）如图，在矩形纸片ABCD中，将AB沿BM翻折，使点A落在BC上的点N处，BM为折痕，连接MN；再将CD沿CE翻折，使点D恰好落在MN上的点F处，CE为折AD=，痕，连接EF并延长交BM于点P，若8AB=，求线段PE的长．5第二十二讲矩形菱形正方形参考答案【聚焦中考真题】一、选择题1-5 DDCCB5-10 BCDCB11-15 BBBBC二、填空题16.答案：3解析：∵四边形ABCD是菱形，∴BC=CD，∠B=∠D=60°，∵AE⊥BC，AF⊥CD，∴AB•AE=AD•AF，∠BAE=∠DAF=30°，∴AE=AF，∵∠B=60°，∴∠BAD=120°，∴∠EAF=120°-30°-30°=60°，∴△AEF是等边三角形，∴AE=EF，∠AEF=60°，∵AB=4，∴AE=2，∴EF=AE=2，如图，过A作AM⊥EF，∴AM=AE•sin60°=3，23.答案：2解析：∵四边形ABCD是菱形，∴AD=AB。