计算理论答案

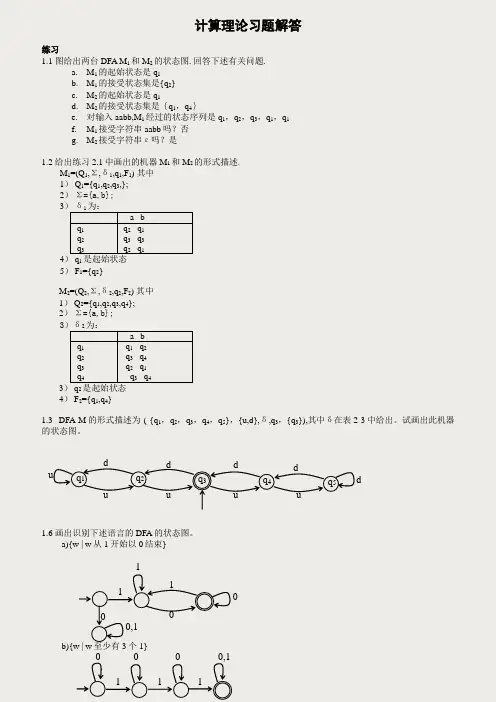
计算理论习题解答练习1.1 图给出两台DFA M 1和M 2的状态图. 回答下述有关问题.a. M 1的起始状态是q 1b. M 1的接受状态集是{q 2}c. M 2的起始状态是q 1d. M 2的接受状态集是｛q 1，q 4｝e. 对输入aabb,M 1经过的状态序列是q 1，q 2，q 3，q 1，q 1f. M 1接受字符串aabb 吗？否g. M 2接受字符串ε吗？是1.2 给出练习2.1中画出的机器M 1和M 2的形式描述.M 1=(Q 1,Σ,δ1,q 1,F 1) 其中 1） Q 1={q 1,q 2,q 3,}; 2） Σ={a,b}; 3） δ1为：a b q 1 q 2 q 3 q 2 q 1 q 3 q 3 q 2 q 1 4） q 1是起始状态 5） F 1={q 2}M 2=(Q 2,Σ,δ2,q 2,F 2) 其中 1） Q 2={q 1,q 2,q 3,q 4}; 2） Σ={a,b}; 3）δ2为：a b q 1 q 2 q 3 q 4 q 1 q 2 q 3 q 4 q 2 q 1 q 3 q 4 3） q 2是起始状态 4） F 2={q 1,q 4}1.3 DFA M 的形式描述为 ( {q 1，q 2，q 3，q 4，q 5}，{u,d},δ,q 3，{q 3}),其中δ在表2-3中给出。

试画出此机器的状态图。

1.6 画出识别下述语言的DFA 的状态图。

a){w | w 从1开始以0结束}b){w | w 至少有3个1}q 1 q 5 q 4 q 2 q 3 ud u u u u d d d d 00 1 11 0,1 0 0 1 0 0 1 10,1c) {w | w 含有子串0101}d) {w | w 的长度不小于3，且第三个符号为0}e) {w | w 从0开始且为奇长度，或从1开始且为偶长度}或f) {w | w 不含子串110}g) {w | w 的长度不超过5}h){w | w 是除11和111以外的任何字符}i){w | w 的奇位置均为1}j) {w | w 至少含有2个0，且至多含有1个1}k) {ε,0}l) {w | w 含有偶数个0，或恰好两个1}0,110 0 1 110 0,1 00,1 0,1 1 1 0,1 0 0,10,1 0,1 00,11 0,10 0,1 10,1 0111 00,1 0,1 0,1 0,1 0,10,10,11 1 1 0,1 0 0 00 0 10 0 1 11 1 1 0 0 0,1 0 0,1 0,11 1 00,1 0,1 1 01 1 0 0 0 0 0 0 1m) 空集 n) 除空串外的所有字符串1.7 给出识别下述语言的NFA ，且要求符合规定的状态数。

3.3 修改定理3.10以得到推论3.12的证明，即证明一个语言是可判定的当且仅当有非确定的TM判定它。

证明：若M是一个确定型判定器则，则M也是一个非确定型判定器。

现在设N是一个非确定的判定器，将构造一个与之等价的确定型判定器M。

模拟过程使用深度搜索。

设N的不确定性分支的最大个数为b。

M有三个带：一个输入带，一个工作带，一个地址带。

M按深度优先方式搜索N的不确定计算分支树。

M= “输入w，1)初始化，第一带上为w, 第二带为空，第三带为1;2)将第一带的内容复制到第二带上，3)按当前地址位数字选择N的一个不确定性分支，在第二带上模拟N运行一步；4)若当前地址位为i<b，且当前选择无效或按当前选择进入拒绝状态，则将当前地址位改为i+1, 转第2步；5)若当前地址位为i＝b，且当前选择无效或按当前选择进入拒绝状态，则将当前地址位改为空格, 左移并将当前地址位改为空格直到找到一个地址位其值<b，将当前地址位改为i+1, 转第2步；若到了地址带的最左端仍有当前地址位为b，则拒绝；6)若N进入接受状态，则接受；否则，右移一格，将空格上写入1，转第三步。

”由于N是非确定型判定器，所以对任意输入，由本题的提示M一定会停机。

3.4给出枚举器的形式定义。

解：枚举器E=(Q,∑,Γ,δ,q0,qaccept,qreject), 其中转移函数δ为：δ：Q×Γ→Q×Γ×{L,R}×∑*δ (q,a)=(r,b,s1,c)表示若E处于状态q,且在工作带上读到a，则状态转移为r，当前格改写为b并按s1作相应左或右移，打印带上写下字符串c，其中若c等于ε，则不打印。

另外E的起始格局只能是qv，这里v表示一个空格。

3.5检查图灵机的形式定义，回答下列问题并解释你的推测：a．图灵机能在它的带子上写下空白符吗b．带字母表Γ和输入字母表∑能相同吗？c．图灵机的读写头能在连续的两步中处于同一个位置吗？d．图灵机能只包含一个状态吗？解：a．能。

计算理论考研题目及答案### 计算理论考研题目及答案#### 题目一：确定性有限自动机（DFA）的定义和性质问题描述：给定一个确定性有限自动机（DFA）M，其状态集合为Q={q0, q1, q2}，字母表为Σ={a, b}，转换函数为δ，初始状态为q0，接受状态集合为F={q1, q2}。

请根据以下转换函数定义，判断字符串"aba"是否被M接受。

转换函数定义如下：- δ(q0, a) = q1- δ(q0, b) = q0- δ(q1, a) = q2- δ(q1, b) = q1- δ(q2, a) = q2- δ(q2, b) = q0答案：首先，根据转换函数，我们从初始状态q0开始，逐个读取字符串"aba"中的字符：1. 读取字符'a'，应用转换函数δ(q0, a)，状态变为q1。

2. 继续读取字符'b'，应用转换函数δ(q1, b)，状态变为q1。

3. 最后读取字符'a'，应用转换函数δ(q1, a)，状态变为q2。

由于状态q2是接受状态，因此字符串"aba"被DFA M接受。

#### 题目二：图灵机的停机问题问题描述：考虑一个图灵机T，其输入为一个二进制字符串。

请证明图灵机T是否能够解决以下问题：给定一个二进制字符串，判断该字符串是否能够被T在有限步内停机。

答案：这个问题是著名的停机问题，它是一个不可解问题。

根据图灵的停机问题的不可解性定理，不存在一个通用的算法来判断任意给定的图灵机和输入字符串是否停机。

因此，不能构造一个图灵机来判断所有图灵机的停机问题。

#### 题目三：P vs NP问题问题描述：简述P vs NP问题，并给出一个NP完全问题的例子。

答案：P vs NP问题是计算理论中的一个核心问题，它询问：所有那些可以快速验证解的问题（NP问题），是否也能快速找到解（即是否属于P类问题）。

什么是时间复杂度？请举例说 明。
时间复杂度是评价算法执行时 间快慢的一个指标，通常用大O 表示法来表示。例如，对于一 个简单的顺序查找算法，其时 间复杂度为O(n)，表示随着问 题规模n的增加，算法的执行时 间线性增长。
计算模型习题答案详解
习题1
解释图灵机的基本原理和工作过程。
答案
图灵机是一种理论上的计算模型，由一条无限长的纸带和一个读写头组成。读写头可以读取、写入和移动纸带上 的符号，根据当前状态和读取的符号来决定下一步的动作和状态转移。图灵机的工作过程可以模拟任何计算机程 序的执行过程。
RAM模型的扩展与优化
包括引入并行计算、分布式计算等概念，以 提高RAM模型的计算能力和效率。
其他计算模型
量子计算模型
利用量子力学原理进行计算的模型，具有在某些特定 问题上比传统计算机更高的计算效率。
生物计算模型
模拟生物体内信息处理过程的计算模型，如神经网络、 基因算法等。
光计算模型
利用光学原理进行计算的模型，具有高速并行处理和 低能耗等优点。
形式语言与自动机习题答案详解
习题1
解释什么是形式语言，并给出其定义和性质 。
答案
形式语言是பைடு நூலகம்于描述计算机程序的语法和语 义的一种数学工具。它由一组符号和一组规 则组成，可以表示各种不同类型的数据结构 和算法。形式语言具有确定性、封闭性和可 计算性等性质，这些性质使得我们可以对计
算机程序进行精确的描述和分析。
Python语言基础 掌握Python语言的基本语法、数 据类型、控制结构、函数等，以 及常用的Python库和框架。
其他编程语言 了解其他常见的编程语言，如C#、 JavaScript、Go等，以及它们的 特点和应用场景。

计算理论习题答案计算理论，也称为理论计算机科学，是研究算法和计算过程的数学理论基础的学科。

以下是一些计算理论习题的答案示例：1. 确定性图灵机（Deterministic Turing Machine, DTM）：- 习题：证明一个确定性图灵机可以模拟任何其他确定性图灵机。

- 答案：确定性图灵机可以读取输入，根据当前状态和读取到的符号，按照预定的转移规则移动磁带头并改变状态。

要模拟另一台确定性图灵机，只需要将被模拟机的状态转移表编码为模拟机的转移规则即可。

2. 非确定性图灵机（Nondeterministic Turing Machine, NTM）：- 习题：证明非确定性图灵机比确定性图灵机更强大。

- 答案：非确定性图灵机可以在多个可能的转移中选择，这使得它能够解决一些确定性图灵机无法解决的问题，例如哈密顿回路问题。

此外，任何确定性图灵机都可以被一个非确定性图灵机模拟，但反之则不成立。

3. 可计算性（Computability）：- 习题：证明某个特定的函数是可计算的。

- 答案：要证明一个函数是可计算的，需要展示一个算法或图灵机，它对于该函数的任何输入都能在有限步骤内给出输出。

例如，一个简单的加法函数f(x, y) = x + y是可计算的，因为它可以通过迭代或递归来实现。

4. 不可解问题（Undecidable Problems）：- 习题：解释停机问题（Halting Problem）为什么是不可解的。

- 答案：停机问题是不可解的，因为它涉及到预测一个图灵机是否会在有限步骤内停止。

如果存在一个算法能够解决停机问题，那么我们可以构造一个悖论，即一个图灵机可以模拟自身并决定自己是否会停止，这会导致自指的悖论。

5. 复杂性类（Complexity Classes）：- 习题：区分P类问题和NP类问题。

- 答案：P类问题是指可以在多项式时间内解决的问题，而NP类问题是指可以在多项式时间内验证一个解的问题。

计算机考博试题计算理论及答案计算理论字母表：⼀个有穷的符号集合。

字母表上的字符串是该字母表中的符号的有穷序列。

⼀个字符串的长度是它作为序列的长度。

连接反转Kleene星号L* ，连接L中0个或多个字符串得到的所有字符串的集合。

有穷⾃动机：描述能⼒和资源极其有限的计算机模型。

有穷⾃动机是⼀个5元组M=(K,∑,δ,s,F),其中1）K是⼀个有穷的集合，称为状态集2）∑是⼀个有穷的集合，称为字母表3）δ是从KX∑→K的函数，称为转移函数4）s∈K是初始状态5）F?K是接收状态集M接收的语⾔是M接收的所有字符串的集合，记作L(M).对于每⼀台⾮确定型有穷⾃动机，有⼀台等价的确定型有穷⾃动机有穷⾃动机接受的语⾔在并、连接、Kleene星号、补、交运算下是封闭的。

每⼀台⾮确定型有穷⾃动机都等价于某⼀台确定型有穷⾃动机。

⼀个语⾔是正则的当且仅当它被有穷⾃动机接受。

正则表达式：称R是⼀个正则表达式，如果R是1）a，这⾥a是字母表∑中的⼀个元素。

2）ε，只包含⼀个字符串空串的语⾔3），不包含任何字符串的语⾔4)(R1∪R2),这⾥R1和R2是正则表达式5）(R10R2),这⾥R1和R2是正则表达式6）(R1*),这⾥R1*是正则表达式⼀个语⾔是正则的当且仅当可以⽤正则表达式描述。

2000年4⽉1、根据图灵机理论,说明现代计算机系统的理论基础。

1936年，图灵向伦敦权威的数学杂志投了⼀篇论⽂，题为《论数字计算在决断难题中的应⽤》。

在这篇开创性的论⽂中，图灵给“可计算性”下了⼀个严格的数学定义，并提出著名的“图灵机”(Turing Machine)的设想。

“图灵机”不是⼀种具体的机器，⽽是⼀种思想模型，可制造⼀种⼗分简单但运算能⼒极强的计算机装置，⽤来计算所有能想像得到的可计算函数。

这个装置由下⾯⼏个部分组成：⼀个⽆限长的纸带，⼀个读写头。

（中间那个⼤盒⼦），内部状态（盒⼦上的⽅块，⽐如A,B,E,H），另外，还有⼀个程序对这个盒⼦进⾏控制。

计算理论习题答案CHAP2new2.2 a. 利用语言A={a m b n c n | m,n ≥0}和A={a n b n c m | m,n ≥0}以及例3.20，证明上下文无关语言在交的运算下不封闭。

b. 利用(a)和DeMorgan 律(定理1.10)，证明上下文无关语言在补运算下不封闭。

证明：a.先说明A,B 均为上下文无关文法，对A 构造CFG C 1S →aS|T|ε T →bTc|ε对B,构造CFG C 2S →Sc|R|ε R →aRb由此知 A,B 均为上下文无关语言。

但是由例3.20, A ∩B={a n b n c n |n ≥0}不是上下文无关语言，所以上下文无关语言在交的运算下不封闭。

b.用反证法。

假设CFL 在补运算下封闭，则对于(a)中上下文无关语言A,B ，A ,B 也为CFL ，且CFL 对并运算封闭，所以B A ⋃也为CFL ，进而知道BA ⋃为CFL ，由DeMorgan 定律B A ⋃＝A ∩B ，由此A ∩B 是CFL,这与(a)的结论矛盾，所以CFL 对补运算不封闭。

2.4和2.5 给出产生下述语言的上下文无关文法和PDA ，其中字母表∑={0,1}。

a. {w | w 至少含有3个1} S →A1A1A1A A →0A|1A|εε,1→1, 0, ε,1→ε,1→b. {w | w 以相同的符号开始和结束} S →0A0|1A1 A →0A|1A|εc. {w | w 的长度为奇数} S →0A|1A A →0B|1B|ε B →0A|1Ad. {w | w 的长度为奇数且正中间的符号为0} S →0S0|1S1|0S1|1S0|0e. {w | w 中1比0多} S →A1A1,ε→0,ε→0,ε→1,1→0,0→0,ε→1,ε→0,ε→0,ε→0,ε→0,0→ε,ε→ε,$→A →0A1|1A0|1A|AA|ε f. {w | w=w R } S →0S0|1S1|1|0 g. 空集 S →S2.6 给出产生下述语言的上下文无关文法：a ． 字母表{a,b}上a 的个数是b 的个数的两倍的所有字符串组成的集合。

46、我们若已接受最坏的，就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会，使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首，不会作诗也会吟。——孙洙 50、谁和我一样用功，谁就会和我一样成功。——莫扎特

计算理论课后习题答案
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ；权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊，可是金 子可以 拉着它 的鼻子 走。— —莎士 比

ELEMENTS OF COMPUTATION THEORY Chapter 3
Undergraduate Course College of Computer Science ZHEJIANG UNIVERSITY Fall-Winter, 2006
P 120-122 3.1.3 Construct CFGs that generate each of these languages. (c) {w ∈ {a, b}∗ : w = wR }.
(b) {a, b}∗ − {an bn : n ≥ 0} (c) {am bn cp dq : n = q, or m ≤ p or m + n = p + q } (d) {a, b}∗ − L where L is the language L = {babaabaaab . . . ban−1 ban b : n ≥ 1} Solution: (b) This language cab be expressed as {am bn | m = n} ∪ Σ∗ aΣ∗ bΣ∗ aΣ∗ ∪ Σ∗ bΣ∗ aΣ∗ bΣ∗ , all three of which are context free, so that their union is also context-free. (c) This language can be expressed as L1 ∪ L2 ∪ L3 , where L1 = {a∗ bn c∗ dn : n ≥ 0} L2 = {am b∗ cn d∗ : m ≤ n} L3 = {am bn cp dq : m + n = p + q } Each of these language can easily be recognized by a PDA created by modifying the one which accepts {an bn : n ≥ 0}. (d) The language is Σ∗ bbΣ∗ ∪ Σ∗ {ban bam : n + 1 = m}Σ∗ ∪ aΣ∗ ∪ Σ∗ a. Each of these languages is context-free, so is their union. 3.5.2 Use Theorem 3.5.2 and 3.5.3 to show that the following languages are not context-free. (c) {www : w ∈ {a, b}∗ }

第三章上下文没关语言略。

a. 利用语言 A={a m b n c n | m,n0} 和 A={a n b n c m | m,n0} 以及例，证明上下文没关语言在交的运算下不关闭。

b.利用 (a) 和 DeMorgan律( 定理，证明上下文没关语言在补运算下不关闭。

证明： a. 先说明 A,B 均为上下文没关文法，对 A 结构 CFG C1S aS|T|T bTc|对 B, 结构 CFG C2S Sc|R|R aRb由此知 A,B 均为上下文没关语言。

0} 不是上下文没关语言，所以上下文无可是由例 , A ∩B={a n b n c n|n 关语言在交的运算下不关闭。

b. 用反证法。

假定 CFL在补运算下关闭，则对于 (a) 中上下文没关语言A,B，A , B也为 CFL，且 CFL对并运算关闭，所以A B也为 CFL，从而知道 A B 为CFL，由DeMorgan定律 A B ＝A∩B，由此A∩B是CFL,这与 (a) 的结论矛盾，所以 CFL对补运算不关闭。

略。

和给出产生下述语言的上下文没关文法和PDA，其中字母表={0,1} 。

a.{w | w起码含有3个1}0,1,1S→A1A1A1A,1,1,1 A→0A|1A|b.{w | w以同样的符号开始和结束}S→0A0|1A10,1,A→0A|1A|0,00,01,11,1c. {w | w的长度为奇数}0,1,0,1,S →0A|1AA →0B|1B|B →0A|1Ad. {w | w 的长度为奇数且正中间的符号为 0}S →0S0|1S1|0S1|1S0|00, 0 0,0 1,1,0,$ 0,,$e. {w | w 中 1 比 0 多}1,00,1 0S →A1A0, ,11,1 ,$,1,$A →0A1|1A0|1A|AA|f. {w | w=w R }S →0S0|1S1|1|00, 0 0,0 1, 1 1,1 ,1, ,$$ 0,,g. 空集S →S给出产生下述语言的上下文没关文法：a ．字母表 {a,b} 上 a 的个数是b 的个数的两倍的全部字符串构成的会合。

Undergraduate Course ELEMENTS OF COMPUTATION THEORY College of Computer Science Chapter2ZHEJIANG UNIVERSITYFall-Winter,2006P602.1.1Let M be a deterministicfinite automaton.Under exactly what cir-cumstances is e∈L(M)?Prove your answer.Solution:e∈L(M)if and only if s∈F.Suppose e∈L(M).Then,by definition of L(M),(s,e) ∗M(q,e),where q∈F.Because it is not the case that(s,e) M(q,w)for any configuration(q,w)(w=e).(s,e) ∗M(q,e)must be in the reflexive transitive closure of M by virtue of reflexivity −that is,(s,e)=(q,e).Therefore,s=q and thus s∈F.Suppose s∈F.Because ∗M is reflexive,(s,e) ∗M(s,e).Because s∈F,we havee∈L(M)by definition of L(M).2.1.2Describe informally the languages accepted by the following DF A.Solution:(c)All strings with the same number of a s and b s and in which no prefix has more thantwo b s than a s,or a s than b s.(d)All strings with the same number of a s and b s and in which no prefix has more thanone more a than b,or vice-versa.2.1.3Construct DF A accepting each of the following languages.(c){w∈{a,b}∗:w has neither aa nor bb as a substring}.(e){w∈{a,b}∗:w has both ab and ba as a substring}.Solution:(c)M=(K,Σ,δ,sF),whereK={q0,q1,q2,q3},Σ={a,b},s=q0,F={q0,q1,q2}q aδ(q,a)q0a q1q0b q2q1a q3q1b q2q2a q1q2b q3q3a q3q3b q3(e)M=(K,Σ,δ,sF),whereK={q0,q1,q2,q3,q4,q5},Σ={a,b},s=q0,F={q5}q aδ(q,a)q0a q1q0b q2q1a q1q1b q3q2a q4q2b q2q3a q5q3b q3q4a q4q4b q5q5a q5q5b q5P742.2.2Which regular expression for the languages accepted by the NF A of Problem2.2.1.Solution:a)a∗b)a(ba∪baa)∗(b∪ba)2.2.6(a)Find a simple NF A accepting(ab∪aab∪aba)∗.(b)Convert the NF A of part(a)to a DF A by the method in section2.2.Solution:(a)M=(K,Σ,∆,sF),where K={q0,q1,q2,q3},Σ={a,b},s=q0,F={q0}(qσq i)(q0a q1)(q1a q2)(q1b q0)(q1b q3)(q2a q0)(q3b q0)(b)Determinizing the above machine results in the following DFA:K={{q0},{q1},{q3},{q0,q1},{q0,q2},{q1,q3},∅},Σ={a,b},s={q0},F={{q0},{q0,q1},{q0,q2}}{q}σ{δ(q,σ)}{q0}a{q1}{q0}b∅{q1}a{q3}{q1}b{q0,q2}{q0,q2}a{q0,q1}{q0,q2}b∅{q0,q1}a{q1,q3}{q0,q1}b{q0,q2}{q3}a∅{q3}b{q0}{q1,q3}a{q3}{q1,q3}b{q0,q2}∅a∅∅b∅2.2.10Describe exactly what happens when the construction of this sectionapplied to a F A that is already deterministic.Solution:Only |K |of the 2|K |states of the new automaton will be reachable.Each of these states will have {q }for some q ∈K .If we identify {q }with q ,we have a bijection between the states of the old automata and the reachable states of the new one.With respect to this bijection,δ,s ,and F will be identical between the old mach-ine and the new.Sinceis the same,there is a natural isomorphism between the old and the automaton formed from the new one by discarding unreachable states.P 83-842.3.4Using the construction in the proof of theorem 2.3.1,construct F A accepting these languages.(b )((a ∪b )∗(e ∪c )∗)∗.Solution:(b )Ommited.2.3.7Apply the construction in Example 2.3.2to obtain regular expressions responding to each of the F A above.Simplify the resulting regular expres-sions as much as you can.Solution:(a )a ∗b (ba ∗b ∪a )∗(b )((a ∪b )(a ∪b ))∗(c )(a ∪b )∗abaa (a ∪b )∗(d )(a ∪∅∗)(ba ∗a )∗b (b ∪a )∗P 902.4.5Using the pumping theorem and closure under intersection,show that the following are not regular.(a ){ww R :w ∈{a,b }∗}Solution:Assume L is regular,by the closure property under intersection so is L 1=L ∩a ∗bba ∗.Consider language L 1.Let k be the constant whose existence the pumping theorem guarantees.Choose string w =a k bba k ∈L 1.Clearly |w |≥k .So the pumping theorem must hold.Let w =xyz such that |xy |≤k and y =e ,then y =a i where i >0.But then xy n z =a k +(n −1)i bba k ,which is clearly asymmetric for any n =1.The theorem fails,and thus that L 1is not regular,therefore L is not regular.2.4.8Are the following statements true od false?Explain you answer in each case.(a )Every subset of a regular language is regular.(b )Every regular language has a regular proper subset.(c )If L is regular,then so is {xy |x ∈L and y ∈L }.(d ){w |w =w R }is regular.(e )If L is regular,then so is {w |w ∈L and w R ∈L }.(f )If C is any set of regular languages,then ∪C is a regular language.(g ){xyx R |x,y ∈Σ∗}is regular.Solution:(a )False.Every language,including those we know not to be regular,is a subset of theregular language∗.(b )False.The empty set,which is a regular language,has no proper subsets at all,so it certainly cannot have a proper subset which is also a regular.(c )True.{xy |x ∈L and y ∈L }=L ◦¯L.Since L is regular,so is its complement,and thus their concatenation is regular.(d )False.This can be shown by trying to pump the string a k ba k .y will have to consist only of a s and the resulting xy 2z will unbalanced.Note,however,that this language is regular over an alphabet of one symbol.(It is true when C is required to be finite).(e )True.This language is L ∩L R .If L is regular,then so is L R .Since both L and L R are regular,so is their intersection.Solution:(f)False.Any language can be written as the(possibly infinite)union of the singleton sets containing its individual elements.Since not every language is regular,this claim is false.(g)True.{xyx R|x,y∈Σ∗}=Σ∗.By letting x=e,y can vary over all the stringsofΣ∗.)。

8.1 证明对于任意函数f:N N，其中f(n)n，不论用单带TM模型还是用两带只读输入TM模型，所定义的空间复杂性类SPACE(f(n))总是相同的。

证明：为区别，记单带TM模型在f(n)空间内能判定的语言类为SPACE1(f(n)), 而记双带只读输入TM模型在f(n)空间内能判定的语言类为SPACE2(f(n))。

该题要证明的是SPACE1(f(n))＝SPACE2(f(n))。

首先SPACE1(f(n))SPACE2(f(n))。

这是因为设A SPACE1(f(n))，且设M设在f(n)空间内判定A的单带TM，如下构造双带TM只读输入TM N。

N=“对于输入串w：1)将w复制到工作带上。

2)在工作带上模拟M，直到停机。

3)若M接受，则接受；否则，拒绝。

”N在f(n)空间内运行，L(N)=L(M)=A，所以A SPACE2(f(n))。

首先SPACE2(f(n))SPACE1(f(n))。

设A SPACE2(f(n))，且N 为在f(n)空间内判定A的双带只读输入TM。

按照用单带TM模拟多带TM的常规方式构造M：M＝“对于输入串w：1)初始化工作带为＃w1’w2…w n#’.其中以’标记N的两个读写头。

2)模拟N运行直到停机。

每一步模拟，要两次扫描带子。

第一次扫描确定读写头下符号，第二次扫描根据N的转移函数完成改写和移动读写头的工作。

3)若N接受，则接受；否则，拒绝。

”L(M)=L(N)=A。

由于f(n)n，M的运行空间是f(n)+n+2＝O(f(n))。

8.3 考虑广义地理学游戏，其中起始节点就是又无源箭头指入的节点。

选手I有必胜策略吗？选手II呢？给出理由。

1 2 34 5 6I II I II I Winner2 3 6 I4 5 6 II由表上来看选手II有必胜策略I2II4(不能选3)I5II6(不能选2)I。

8.4 证明PSPACE在并、补和星号运算下封闭。

证明：(1) 并：对任意L1, L2PSPACE，设有n a空间图灵机M1和n b空间图灵机M2判定它们，且c=max{a,b}。

计算理论考试题库及答案一、选择题1. 计算理论中的“图灵机”是由谁提出的？A. 阿兰·图灵B. 约翰·冯·诺伊曼C. 克劳德·香农D. 艾伦·纽曼答案：A2. 下列哪项不是图灵机的基本组成部分？A. 带子B. 读写头C. 状态寄存器D. 随机数生成器答案：D3. 形式语言理论中的“递归可枚举”是指什么？A. 可以通过图灵机在有限步内确定一个字符串是否属于该语言B. 可以通过图灵机枚举出该语言的所有字符串C. 可以通过图灵机在有限步内生成该语言的所有字符串D. 可以通过图灵机在有限步内枚举出该语言的所有字符串答案：B4. 确定性图灵机与非确定性图灵机的区别在于：A. 确定性图灵机有确定的输入输出B. 非确定性图灵机在每一步有多个可能的转移C. 确定性图灵机没有状态寄存器D. 非确定性图灵机有多个读写头答案：B5. 形式语言理论中的“可判定性问题”是指：A. 该问题有一个确定的答案B. 该问题有一个算法可以解决C. 该问题可以通过图灵机在有限步内判断D. 该问题可以通过图灵机枚举出所有可能的解答案：C二、简答题1. 请简述图灵机的工作原理。

答：图灵机由一个无限长的带子、一个读写头、一组状态寄存器和一个转移函数组成。

带子上的每个单元格可以存储一个符号，读写头可以读取、写入或擦除带子上的符号，并在带子上左右移动。

状态寄存器记录当前的状态，转移函数根据当前的状态和带子上的符号来决定读写头的下一步操作和状态寄存器的下一个状态。

图灵机通过这样的方式模拟计算过程。

2. 什么是“图灵完备性”？答：图灵完备性是指一个系统能够模拟任何图灵机的计算过程，也就是说，如果一个问题可以用图灵机解决，那么这个问题也可以在这个系统中解决。

具有图灵完备性的系统能够执行任何可以形式化的算法。

3. 请解释“不可解问题”与“难解问题”的区别。

答：不可解问题是指不存在任何算法能够在有限步内解决的问题，即这些问题是图灵不可判定的。

q3
ε,$->ε
q4
0,ε->0
1,ε->ε
2,0->ε
ε,ε->$
ε,ε->ε
ε,ε->ε
ε,$->ε
q1
q2
q5
q6
q7
CFG G=(V, ∑,R,S)
V={A11,A12,A13,A14,…A88} ∑={0,1,2}
S=A18 R:
A18->A14A48 A14->0A231 A23->0A231|ε A48->A442|ε
3. 设集合T={0,1}，用T中元素构造序列，最多 可构造（ D ）条序列。 A、1 B、 2 C、3 D、无穷 4. DFA和NFA的区别在于（ A ）。 A、两者的转移函数的值域不同 B、NFA能够识别的语言DFA不一定能够识别 C、DFA能够识别的语言NFA不一定能够识别 D、NFA比DFA多拥有一个栈
假设A2是正则的，泵长度为p
令S=apbapbapb,S是A2成员，且S长度大于p，S 可以分成三部分S=xyz满足泵引理。根据条件 三y只包含a，xyyz不是A2成员，违反泵引理。 A2不是正则的
4.给出产生下述语言的上下文无关文法。 1）{w|w至少包含3个1}； S->A1A1A1A A->A0|A1|ε 2）{w|w以相同的符号开始和结束}； S->0A0|1A1|0|1 A->0A|1A|ε
3）{w|w的长度为奇数}; S->0A|1A A->0B|1B|ε B->0A|1A
5. 利用泵引理证明下述语言不是上下文无关 的。
1）{w#t|w,t{a,b}*,且w是t的子串}；
设该语言上下文无关，p为泵长度。取 S=0p1p#0p1p，由泵引理，S可以划分为uvxyz 五部分。因为S=uxz也在该语言中，所以vy不 包含#。vxy不落在#一边，否则两边长度不同。 则#∈x，则必存在不全为零的i,j使得vy=1i0j

一、证明：设M是一台识别语言B的DFA，交换M的接受状态与非接受状态得到一台新的DFA，则这台新DFA识别B的补集。

因而，正则语言类在补运算下封闭。

(8分)参考答案：设M’是一台将DFA M的接受态与非接受态交换后的DFA，接下来证明M识别B语言，则M’识别B的补集：假定M’识别x，则对于x 在M’上运行将结束于M’的一个接受态，因为M和M’交换了接受态与非接受态，因此对于x运行于M，将会结束于一个非接受态，所以x∈/B。

类似地，如果x不被M’接受，则它一定被M接受。

故M’恰好接受所有不被M接受的那些串，因此M’识别B的补集。

既然B是任意的正则语言，且我们已构造出一台自动机识别它的补集，它表明任何正则语言的补也是正则的。

因此，正则语言类在补运算下封闭。

二、令∑＝｛0，1，＋，＝｝和ADD＝｛x=y+z | x，y，z是二制整数，且x是y与z的和｝，证明ADD不是正则的。

(8分)参考答案：假定ADD是正则的。

让P作为泵引理中的泵长度，选择S的串形式为1P＝0P＋1P作为ADD的一个成员。

因为S有长度大于P，由泵引理保证它能分割成形如：S＝xyz的三部分，满足泵引理的条件。

泵引理的第三个条件有｜xy｜≤P，《它表明对于K≥1，y就是1K。

这是xy2z是串1P＋K＝OP＋1P，而它不是ADD的成员，由泵引理导出矛盾，因此ADD不是正则的。

三、请将下述CFG转换成等价的乔姆斯基范式文法。

(8分)A→BAB｜B｜εB→00｜ε参考答案：S0→AB｜CC｜BA｜BD｜BB｜εA→AB｜CC｜BA｜BD｜BBB→CCC→0D→AB四、请用泵引理证明语言A＝｛0n＃02n＃03n | n≥0 ｝不是上下文无关的。

(8分)参考答案：由泵引理，让P作为泵长度，s=0p＃02p＃03p ，接下来证明s=uvxyz不能进行泵抽取。

v和y都不能包含＃，否则，xv2wy2z将超过2个＃s ，因此，如果我们按＃’s将s分成三段如：0p，02p，03p，至少有一段不包含v或y。

计算理论习题解答练习1.1 图给出两台DFA M1和M2的状态图. 回答下述有关问题.a.M1的起始状态是q1b.M1的接受状态集是{q2}c.M2的起始状态是q1d.M2的接受状态集是｛q1，q4｝e.对输入aabb,M1经过的状态序列是q1，q2，q3，q1，q1f.M1接受字符串aabb吗？否g.M2接受字符串ε吗？是1.2 给出练习2.1中画出的机器M1和M2的形式描述.M1=(Q1,Σ,δ1,q1,F1) 其中1）Q1={q1,q2,q3,};2）Σ={a,b};3415）F1={q2}M2=(Q2,Σ,δ2,q2,F2) 其中1）Q2={q1,q2,q3,q4};2）Σ={a,b};33）q2是起始状态4）F2={q1,q4}1.3 DFA M的形式描述为( {q1，q2，q3，q4，q5}，{u,d},δ,q3，{q3}),其中δ在表2-3中给出。

试画出此机器的状态图。

1.6 画出识别下述语言的DFA 的状态图。

a){w | w 从1开始以0结束}b){w | w 至少有3个1}c) {w | w 含有子串0101}d) {w | w 的长度不小于3，且第三个符号为0}e) {w | w 从0开始且为奇长度，或从1开始且为偶长度}f) {w | w 不含子串110}g) {w | w 的长度不超过5}h){w | w 是除11和111以外的任何字符}i){w | w 的奇位置均为1}j) {w | w 至少含有2个0，且至多含有1个1}k) {ε,0}l) {w | w 含有偶数个0，或恰好两个1}m) 空集 n) 除空串外的所有字符串1.7 给出识别下述语言的NFA ，且要求符合规定的状态数。

0,11a. {w | w以00结束}，三个状态b. 语言｛w | w含有子串0101，即对某个x和y，w=x0101y｝，5个状态.c. 语言｛w | w含有偶数个0或恰好两个1｝，6个状态。

5.1 证明EQ CFG 是不可判定的。

解：只须证明ALL CFG ≤m EQ CFG 即可。

构造CFG G 1，使L(G 1)=∑*。

设计从ALL CFG 到EQ CFG 的归约函数如下：F=“对于输入＜G ＞，其中G 是CFG ： 1）输出＜G,G 1＞。

”若＜G ＞∈ALL CFG ，则<G,G 1>∈EQ CFG 。

若＜G ＞∉ALL CFG ，则<G, G 1>∉EQ CFG 。

F 将ALL CFG 归约到EQ CFG 即ALL CFG ≤m EQ CFG ∵ALL CFG 是不可判定的， ∴EQ CFG 是不可判定的。

5.2证明EQ CFG 是补图灵可识别的。

证明：注意到A CFG ={<G,w>|G 是能派生串w 的CFG}是可判定的。

构造如下TM ：F=“输入<G,H>，其中G,H 是CFG ， 1) 对于字符串S 1, S 2,⋯，重复如下步骤。

2) 检测S i 是否可以由G 和H 派生。

3)若G 和H 中有一个能派生w ，而另一个不能，则接受。

”F 识别EQ CFG 的补。

5.4 如果A ≤m B 且B 是正则语言，这是否蕴涵着A 也是正则语言？为什么？ 解：否。

例如：对非正则语言A={0n 1n |n ≥0}和正则语言B={0}，可以构造一个可计算函数f 使得：f(w)=⎩⎨⎧≠=nn n n 10w 1,10w 0, 于是w ∈A ⇔f(w)∈B,故A ≤m B 。

5.5 证明A TM 不可映射规约到E TM 。

证明：反证法假设A TM ≤m E TM ， 则有TM m TM E A ≤。

而A TM 的补不是图灵可识别的，从而可知E TM 的补也不是图灵可识别的。

下面构造一个识别E TM 的补的图灵机S ： S=“输入<M>，M 是TM,1) 对i=1,2,…重复下一步。

2) 对S 1,S 2,…,S i 模拟M 运行i 步，若有接受，则接受。