小学奥数横式数字谜

横式数字谜在一个数学式子(横式或竖式)中擦去部分数字，或用字母、文字来代替部分数字的不完整的算式或竖式，叫做数字谜题目。

解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。

例如，求算式324+□=528中□所代表的数。

根据“加数=和-另一个加数”知，□=582-324＝258。

又如，求右竖式中字母A，B所代表的数字。

显然个位数相减时必须借位，所以，由12-B＝5知，B＝12-5＝7；由A-1＝3知，A＝3＋1＝4。

解数字谜问题既能增强数字运用能力，又能加深对运算的理解，还是培养和提高分析问题能力的有效方法。

这一讲介绍简单的算式(横式)数字谜的解法。

解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。

由它们推演还可以得到以下运算规则：由(1)，得和-一个加数=另一个加数；其次，要熟悉数字运算和拆分。

例如，8可用加法拆分为8＝0＋8＝1＋7＝2＋6＝3＋5＝4＋4；24可用乘法拆分为24＝1×24=2×12＝3×8＝4×6(两个数之积)=1×2×12＝2×2×6=…(三个数之积)=1×2×2×6＝2×2×2×3=…(四个数之积)例1 下列算式中，□，○，△，☆，*各代表什么数？(1)□+5＝13-6； (2)28-○＝15＋7；(3)3×△=54； (4)☆÷3＝87；(5)56÷*＝7。

解：(1)由加法运算规则知，□=13-6-5＝2；(2)由减法运算规则知，○＝28-(15＋7)＝6；(3)由乘法运算规则知，△＝54÷3＝18；(4)由除法运算规则知，☆=87×3＝261；(5)由除法运算规则知，*＝56÷7＝8。

三年级奥数横式数字谜解这类问题时：第一步，要仔细审题；第二步，必须挑选突破口；第三步，实验求解。

灵活运用运算法则和整数的性质，仔细观察算式的特点，学会辨认出问题、分析问题。

研究和化解这类问题，有助于培育我们观测、分析、概括、推理小说等能力。

47；(4)36-150÷=96÷16。

练1代表什么数：(1)⨯9+6⨯=600÷2；(2)25⨯25-÷3=610。

基准2=6=，那么=。

例3在下列方框中填上适当的数，使等式成立：；(2)148÷=84。

练习3在下列方框中填上适当的数，使等式成立：(1)213÷=165；(2)÷9=305。

例4在下列等号左边的每两个数之间，添上加号或减号，也可以用括号，使算式成立。

12345=1练4在下面的式子里加之括号，并使等式设立。

(1)7⨯9+12÷3-2=23；(2)7⨯9+12÷3-2=75。

基准5迎上适度的加号或负号、乘号或除号，也可以用括号，并使下面的等式设立。

55555=10练5迎上适度的运算符号：加号或负号、乘号或除号，并使以下等式设立。

1234=1a+a+a+a则a+b=。

4、325⨯÷19=650=；2100÷(÷3)=70=。

5、把1～9分别插入下面九个圆圈中，并使等式设立。

===6=15应该是___________。

9、在等号左边适度的地方迎上括号，并使算式设立。

里，使等式成立，每个数字只能用一次。

10；(6)2⨯()=10。

11、把加号、减号、乘号、除号，分别填入下面等式中的圆圈内，使等式成立。

((9)=1212、把1，2，3，4，5，6使结果尽可能大，并求出结果。

×)=13、将1，2，3，4，5，6，7，8，9==14分别代表相同的三个数，并且1代表什么数：(1)⨯17+43=400；(2)(601+)⨯9=7209。

小学三年级奥数22横式数字谜本教程共30讲第22讲横式数字谜(二)第2讲我们初步介绍了简单的横式填数问题。

这一讲再继续介绍一些此类问题。

例1在下列各式的□里填上合适的数字：(1)237÷□□=□；(2)368÷□□=□□；(3)14×□□=3□8。

解：(1)将除法变为乘法，可以转化为“在237=□□×□中填入合适的数字”的问题。

因为 237＝237×1＝79×3，所以只有一种填法：(2)问题可以转化为“在368＝□□×□□中填入合适的数字”的问题。

因为368＝368×1＝184×2＝92×4＝46×8＝23×16，其中只有368＝23×16是两个两位数之积。

因而有如下两种填法：(3)由被乘数的个位数是4，积的个位数是8知，乘数的个位数只可能为2或7，再由被乘数的十位数是1，积的百位数是3知，乘数的十位数不能填大于3的数字。

所以乘数只可能是12，17，22，27，32或37。

经试算，符合题意的填法有两种：例2在下列各式的□里填上合适的数：(1)□÷32＝7……29；(2)480÷156＝□……12；(3)5367÷□＝83……55。

分析：根据有余数的除法(简称带余除法)知：被除数=不完全商×除数＋余数，被除数-余数=不完全商×除数。

上式说明，(被除数-余数)是不完全商或除数的倍数，并且有(被除数-余数)÷除数=不完全商，(被除数-余数)÷不完全商=除数。

由此分析，可以得到如下解法。

解：(1)由7×32＋29＝253，得到如下填法：(2)由(480-12)÷156＝3，得到如下填法：(3)由(5367-55)÷83＝64，得到如下填法：例3在下列各式的□里填入合适的数字，使等式成立：(1)□5□×23＝5□□2；(2)9□□4÷48=□0□。

三年级数学奥数讲座横式数字谜(一)三年级横式数字谜(一)在一个数学式子(横式或竖式)中擦去部分数字，或用字母、文字来代替部分数字的不完整的算式或竖式，叫做数字谜题目。

解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。

例如，求算式324+□=528中□所代表的数。

根据“加数=和-另一个加数”知，□=582-324＝258。

又如，求右竖式中字母A，B所代表的数字。

显然个位数相减时必须借位，所以，由12-B＝5知，B＝12-5＝7；由A-1＝3知，A＝3＋1＝4。

解数字谜问题既能增强数字运用能力，又能加深对运算的理解，还是培养和提高分析问题能力的有效方法。

这一讲介绍简单的算式(横式)数字谜的解法。

若再限制拆分成四个“不同的”数字的乘积，范围又缩小了。

按从小到大的次序排列只有下面一种：180＝2×3×5×6。

所以填的四个数字依次为2，3，5，6。

(3)首先，由□÷△=3知，□＞△，因此，在把48拆分为两数的乘积时，有48＝48×1＝24×2＝16×3＝12×4＝8×6，其中，只有48＝12×4中，12÷4=3，因此□=12，△=4。

这道题还可以这样解：由□÷△=3知，□=△×3。

把□×△=48中的□换成△×3，就有(△×3)×△＝48，于是得到△×△=48÷3＝16。

因为16＝4×4，所以△=4。

再把□=△×3中的△换成4，就有□=△×3=4×3=12。

这是一种“代换”的思想，它在今后的数学学习中应用十分广泛。

下面，我们再结合例题讲一类“填运算符号”问题。

例4 在等号左端的两个数中间添加上运算符号，使下列各式成立：(1)4 4 4 4＝24；(2)5 5 5 5 5=6。

名师堂学校讲义第十一讲年级：三姓名：0横式数字谜一、教学目标：1、弄清横式数字谜式题的特点和常用的解答方法。

2、能熟练地运用四则运算中各部份之间的关系。

3、能灵活快速的解答这类式题。

二、重点：理解和掌握用四则运算中各部份关系解答这类题三、关键：解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。

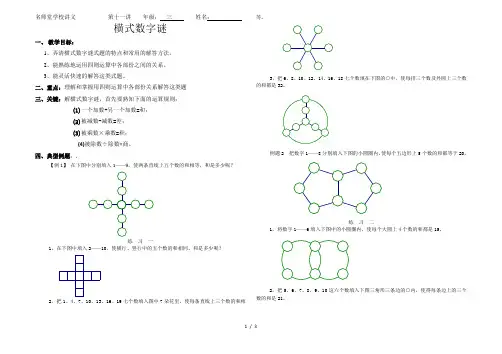
四、典型例题：.【例1】在下图中分别填入1——9，使两条直线上五个数的和相等，和是多少呢？练习一1，在下图中填入2——10，使横行、竖行中的五个数的和相同。

和是多少呢？2，把1、4、7、10、13、16、19七个数填入图中7朵花里，使每条直线上三个数的和相等。

3，把6、8、10、12、14、16、18七个数填在下图的○中，使每排三个数及外圆上三个数的和都是32。

例题2 把数字1——8分别填入下图的小圆圈内，使每个五边形上5个数的和都等于20。

练习二1，将数字1——6填入下图中的小圆圈内，使每个大圆上4个数的和都是15。

2，把5、6、7、8、9、10这六个数填入下图三角形三条边的○内，使得每条边上的三个数的和是21。

3，把1——8这八个数，分别填入下图的各个□内，使得每一横行、每一竖行的三个数的和是13。

例题3 在图中填入2——9，使每边3个数的和等于15。

练习三1，把1——8填入下图中，使每边3个数的和等于13。

2，将1——9这九个数填入下图中，使三角形每条边上四个数的和等于19，且有一个顶点的数字为1。

3，把1——10这十个数填入下图中，使每个正方形顶点圆圈内四个数之和都相等，而且最大。

这个和是多少？例题4 把1——8填入下图○内，使每边上三个数的和最大。

求最大的和是多少？练 习 四1，把3——10填入下图○中，使每边上三个数的和最大，求最大的和是多少？2，把1——8填入下图○中，使每边上三个数的和最小。

小学数学横式数字谜知识点归纳汇总在一个数学式子(横式或竖式)中擦去部分数字，或用字母、文字来代替部分数字的不完整的算式或竖式，叫做数字谜题目。

解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。

例如，求算式324+□=528中□所代表的数。

根据“加数=和-另一个加数”知，□=582-324＝258。

又如，求右竖式中字母A，B所代表的数字。

显然个位数相减时必须借位，所以，由12-B ＝5知，B＝12-5＝7；由A-1＝3知，A＝3＋1＝4。

解数字谜问题既能增强数字运用能力，又能加深对运算的理解，还是培养和提高分析问题能力的有效方法。

这一讲介绍简单的算式(横式)数字谜的解法。

解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。

由它们推演还可以得到以下运算规则：由(1)，得和-一个加数=另一个加数；其次，要熟悉数字运算和拆分。

例如，8可用加法拆分为8＝0＋8＝1＋7＝2＋6＝3＋5＝4＋4；24可用乘法拆分为24＝1×24=2×12＝3×8＝4×6(两个数之积)=1×2×12＝2×2×6=?(三个数之积)=1×2×2×6＝2×2×2×3=?(四个数之积)例1 下列算式中，□，○，△，☆，*各代表什么数？(1)□+5＝13-6； (2)28-○＝15＋7；(3)3×△=54；(4)☆÷3＝87；(5)56÷*＝7。

解：(1)由加法运算规则知，□=13-6-5＝2；(2)由减法运算规则知，○＝28-(15＋7)＝6；(3)由乘法运算规则知，△＝54÷3＝18；(4)由除法运算规则知，☆=87×3＝261；(5)由除法运算规则知，*＝56÷7＝8。

四年级奥数教程第3讲：横式数字谜例1：下列算式中， ○ □各代表什么数字？（1） ＋ ＋ =129解(1)△表示一个数,△+△+△=△×3,于是,△=129÷3=43;（2）8×□－51÷3=478×=47+17 口=64÷:8 =8（3）36－150÷ =96÷6 把150÷☆看成一个数,得到 150÷☆=36-6, 150÷☆=30,☆=150÷30, ☆=5例2：如果○＋□=6，□=○＋○，那么，□－○= 。

分析要求口-的值,必须求出□=?O=?将□=O+O 代入O+□=6中可求出出○的值,进而求出□的值. 也可以由条件口=O+O 分析得出□为偶数,这样6可以分解为2+4,从面求出O 、的值 解法一把□=+O 代入+=6中,得 +O+=6,即30=6,O=2, 这样□=4,口-O=4-2=2 解法二由□=O+O 知,口一定是个偶数,而O+=6,因此O 也 是偶数由6=2+4,得O=2,□=4,□-O=4-2=2. 说明此题含有两个未知数O 、口,要设法通过代入将其转化为只含有个未知数的式子,这样就可寻求突破随堂练习1：下列各式中，□代表什么数： （1）□×9＋6×□=600÷2 （2） 25×25－□÷3=610 (1)口×(9+6)=300,=300÷15, 口=20(2)625-□÷3=610, 口÷3=625-610, 口÷3=15=15×3 □=45.例3：将数字0、1、3、4、5、6填入下面的□内，使等式成立，每个空格只填入一个数字，并且所填数字不能重复。

□×□=□2=□□÷□分析上面等式中,因为积与商相等,所以被除数是较大的一个数,可以考虑6或7.先用7去试,只能7×1=7÷1,7与1不能重复用,排除7.再用6去 试,有三种情况(1)2×3=6÷1; (2)2×1=6÷3; (3)3×1=6:2 根据题意列式得到4+7-5=6; 4+5-7=2 说明(1)(2)符合题意,(3)不成立 解(1)2×3=6÷1=4+7-5; (2)2×1=6÷3=4+5-7例4：在下列等号左边的每两个数字之间，添上加号或减号，也可以用括号，使算式成立。