力的合成和分解实验完整版(20210105112653)

大学物理中的力的合成与分解实验力是物体之间相互作用的结果，它是物体产生加速度的原因。

在物理学中，力的合成与分解实验是一项基础性实验，它帮助我们理解和掌握力的概念及其运用。

本文将介绍大学物理中力的合成与分解实验的原理、实验步骤以及实验结果的分析。

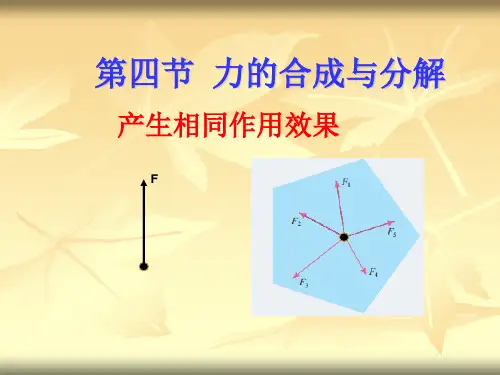
一、实验原理力的合成是指将两个力的作用效果合成为一个力的过程，力的合成可以用向量图形法和向量分析法进行计算。

向量图形法是通过将力的大小用力的箭头表示，箭头的方向表示力的方向，然后将两个力的箭头按顺序放在同一起点，以最后一个力的箭头为末端，连接起点与末端即可得到合力的箭头，合力的大小为各个力的箭头的矢量和。

向量分析法则是通过将力的大小与方向用坐标系表示，然后将各个力的坐标分量相加即可得到合力的坐标分量，进而求得合力的大小和方向。

力的分解是指将一个力按照特定方向分解成多个力的过程，力的分解可以将力分解为平行于某一方向的力和垂直于该方向的力。

分解一个力的关键是确定力的分解方向，常用的分解方向有水平方向与垂直方向。

分解一个力的水平分量和垂直分量时，可以使用几何分解法或三角函数法进行计算。

几何分解法是通过在力的作用线上选取适当的位置，作三条互相垂直的直线，将力的引起作用的点连接起来，并在各线上标出合适的长度，这些长度所决定的力互相垂直，并与原来的力的合成等效。

三角函数法则是运用正弦定理和余弦定理来计算力的分量，其中正弦函数用于计算垂直分力，余弦函数用于计算水平分力。

二、实验步骤1. 准备实验环境和实验装置。

2. 放置一个水平摩擦小的滑板，将两个力计放在滑板上，确保力计测量方向与滑板平行。

3. 保持一个力计固定不动，另一个力计按照一定的角度和大小施加力。

4. 测量两个力的大小和方向。

5. 重复实验多次，得到不同的数据。

6. 对实验数据进行处理和分析。

三、实验结果分析1. 合成力的实验结果分析：根据测得的两个力的大小和方向，利用向量图形法或向量分析法计算出合力的大小和方向，并与实验数据进行对比，分析误差的来源和大小。

力的合成和分解实验实验目的：验证互成角度的两个共点力合成的平行四边形定则..实验原理：一个力F的作用效果与两个共点力F1和F2的共点作用效果都是把橡皮筋拉伸到某点;所以F为F1和F2的合力..做出F的图示;再根据平行四边形定则做出F1和F2的合力Fˊ的图示;比较Fˊ和F是否大小相等;方向相同..实验仪器：方木板、橡皮筋、细绳套、工字钉..剪刀、弹簧测力计2只、铅笔、刻度尺、量角器、白纸、注意同一实验中的两只弹簧测力计的选取方法是：弹簧测力计应与板面平行..将两只弹簧测力计钩好后对拉;若两只弹簧测力计在拉的过程中读数相同;则可以;若不同;应更换弹簧测力计;直到相同为止；实验内容：(1)白纸用图钉固定在方木板上；橡皮筋一端用图钉固定在白纸上;另一端拴上两根细绳套..2用两只测力计沿不同方向拉细绳套;记下橡皮筋伸长到的位置O;在满足合力不超过弹簧测力计量程及橡皮筋形变不超过弹性限度的条件下;应使拉力尽量大一些;以减小误差..两只测力计的方向及读数F1、F2;做出两个力的图示;以两个力为临边做平行四边形;对角线即为理论上的合力Fˊ;量出它的大小..画力的图示时;应选定恰当的标度;尽量使图画得大一些;减少确定弹簧方向时的偶然误差;但也不要太大而画出纸外；要严格按力的图示要求和几何作图法作图.. (3)只用一只测力计钩住细绳套;将橡皮筋拉到O;记下测力计方向及读数F;做出它的图示..4在同一次实验中;橡皮筋拉长后的节点O位置一定要相同..(3)比较Fˊ与F的大小与方向..(4)改变两个力F1、F2的大小和夹角;重复实验两次..实验结论：在误差允许范围内;证明了平行四边形定则成立..注意事项：..231.我们这次做的实验是力的合成与分解..实验所需要的器材有：方木板、白纸、橡皮筋、细绳套2根、弹簧测力计2只、刻度尺、铅笔、工字钉若干个..2.接下来我们对弹簧测力计进行选取..将两只已调零的弹簧测力计钩好后对拉;若两只弹簧测力计在拉的过程中读数相同;则符合要求;若不同;则改换其他弹簧测力计;直到相同为止..3将橡皮筋的一端拴上两根细绳套..4做完上述准备工作后;便开始实验操作..我们将白纸用图钉固定在方木板上;将橡皮筋一端套在工字钉..4.用两只弹簧测力计沿不同方向拉细绳套;5.在满足合力不超过弹簧测力计量程及橡皮筋形变不超过弹性限度的条件下;应使拉力尽量大一些;以减小误差;并注意细绳与板面平行..6.记下橡皮筋拉长后的结点的位置O;并在两条细线距离结点较远处的位置进行标记;减小误差;7.以点O与两个标记点的连线来确定F1、F2的方向;并读出两个弹簧测力计的示数;作为F1、F2的大小..选定恰当的标度做出两个力的图示;可以尽量使图画得大一些;减少确定弹簧方向时的偶然误差;但也不要太大而画出纸外..然后以这两个力为邻边做平行四边形;对角线即为理论上的合力Fˊ;测量出它的大小..5.接下来用一只测力计钩住细绳套;将橡皮筋的结点拉到位置O;同样的;记下测力计方向及读数F;并做出它的图示..6.然后比较Fˊ与F的大小与方向..为了保证实验的准确性;我们通过改变F1、F2的大小和夹角;多次重复实验..7.最后可得出结论：在误差允许范围内;平行四边形定则成立..。

力的合成与分解的实验验证引言力是物体之间相互作用的结果，而力的合成与分解是力学中的基本概念。

力的合成指的是把多个力合并为一个力，而力的分解则是把一个力分解为多个力的过程。

在本文中，我们将通过实验来验证力的合成与分解原理。

实验目的本实验的目的是通过合成和分解力的实验，验证力的合成和分解原理。

实验材料1. 弹簧测力计2. 钢球3. 直尺实验步骤1. 准备工作：a. 将弹簧测力计固定在水平面上，并确保其刻度清晰可读。

b. 在弹簧测力计的下方放置一个平滑的水平台，以便测力计能够滑动自由。

2. 实验一：力的合成a. 将直尺放置在水平面上，并将其一端固定在横向位置。

b. 在直尺上标出两个固定点A和B，分别距离固定端10厘米和20厘米的位置。

c. 将钢球放置在A点的位置，并用弹簧测力计测量球对直尺的作用力F1。

d. 将钢球移动到B点的位置，并用弹簧测力计测量球对直尺的作用力F2。

e. 记录下F1和F2的数值。

3. 实验二：力的分解a. 将直尺仍然放置在水平面上，并将其一端固定在横向位置。

b. 在直尺上的固定点A处放置一个钢球，并用弹簧测力计测量球对直尺的作用力F1。

c. 将弹簧测力计移动到直尺的中间位置，然后从直尺的中间位置向B点方向用力拉动。

d. 在弹簧测力计达到平衡时，测量弹簧测力计显示的力F2。

e. 记录下F1和F2的数值。

实验结果实验一的结果显示，在A点和B点处施加的力分别为F1和F2。

实验结果表明，F1+F2的结果与通过实验一得到的合成力的结果大小相等。

实验二的结果显示，力F1被分解为F2和F3两个力。

实验结果表明，力F1的分解结果与通过实验二得到的分解力的结果大小相等。

结论通过以上实验，我们验证了力的合成与分解原理。

在实验一中，我们验证了合成力的大小与合并前的两个力的大小相等。

在实验二中，我们验证了分解力的大小与分解后的两个力的大小相等。

这些实验证明了力的合成与分解原理在物理学中的适用性，它们为我们理解和研究物体之间相互作用提供了基础。

物理实验探究力的合成与分解在物理学中，力是指物体之间相互作用的结果，进而导致物体产生加速度或变形。

力的合成与分解是物理学中的基本概念，通过实验探究，我们可以更深入地了解力的性质及其在现实世界中的应用。

本文将介绍一系列物理实验，旨在探究力的合成与分解原理及应用。

第一部分：力的合成实验一：平行力的合成在平行力的合成实验中，我们利用力的平行四边形法则来确定合力的大小和方向。

实验器材：1. 平滑水平桌面；2. 弹簧测力计；3. 平行力的拉力机构。

操作步骤：1. 将弹簧测力计固定在桌面上；2. 将两个平行力的拉力机构固定在弹簧测力计两侧；3. 调整拉力机构，使两个平行力的方向一致；4. 测量拉力机构施加的力，并记录结果；5. 切换拉力机构施加的力方向，再次测量并记录。

实验结果及结论：通过实验测量，我们可以得到平行力合成的结果。

根据力的平行四边形法则，我们可以确定合力的大小和方向。

实验结果表明，合力的大小与两个单力的大小之和相等，方向与两个单力的方向相同。

实验二：非平行力合成在非平行力的合成实验中，我们利用三角法则来确定合力的大小和方向。

实验器材：1. 平滑水平桌面；2. 弹簧测力计；3. 非平行力的拉力机构。

操作步骤：1. 将弹簧测力计固定在桌面上；2. 将非平行力的拉力机构固定在弹簧测力计两侧；3. 调整拉力机构，使两个非平行力的方向形成一个尖角；4. 测量拉力机构施加的力，并记录结果；5. 切换拉力机构施加的力方向，再次测量并记录。

通过实验测量，我们可以利用三角法则确定非平行力的合力大小和方向。

根据三角法则，我们可以将两个非平行单力作为两条边，以这两条边为邻边构造一个平行四边形，通过测量该平行四边形的对角线长度和方向，可以获得合力的大小和方向。

第二部分：力的分解实验三：力的平行分解在力的平行分解实验中，我们将一个力分解为两个平行力，以研究力的分解原理。

实验器材：1. 平滑水平桌面；2. 弹簧测力计；3. 力的平行分解装置。

物理教案：力的合成与分解实验力的合成与分解实验一、实验目的二、实验原理1. 合力的概念2. 力的合成3. 力的分解三、实验器材与药品四、实验步骤及操作要点1. 实验准备工作2. 实验步骤及操作指导五、实验数据记录与处理六、实验结果分析与讨论七、实验结论及思考题一、实验目的本次物理教案中，我们将学习有关力的合成与分解的知识。

通过合成和分解力的实际操作，加深对这些概念和原理的理解，提高运用力学知识解决问题的能力。

二、实验原理1. 合力的概念合力是指多个力共同对物体产生的一个结果，它可以改变物体受到的作用。

当多个力同时施加在一个物体上时，它们会产生一个等效于这些力之和的合力。

可以使用向量法或图示法来求解合力。

2. 力的合成如果两个或多个力以不同方向施加在一个物体上，并位于同一平面内，那么它们可以通过矢量相加得出一个等效于这些因素之和的合力。

合力的大小等于这些力的矢量的代数和，方向由这些矢量连线起点指向连线终点确定。

3. 力的分解当一个力施加在一个物体上时，它可以被分解为两个或多个部分，使得每个部分与原始力对物体产生相同效果。

这种将一个力拆解为多个部分的过程称为力的分解。

三、实验器材与药品1. 弹簧测压计2. 导轨3. 滑块4. 砝码组5. 字纸及夹子6. 记录表格四、实验步骤及操作要点1. 实验准备工作a) 将弹簧测压计固定在滑块上，并将其附加到导轨上。

b) 标出导轨上均匀间隔的位置，以便测量所需数据。

c) 安装好滑块，并保证其能够在导轨上自由运动。

2. 实验步骤及操作指导a) 将砝码组依次加在滑块上，并记录每增加一个砝码时弹簧测压计指示值。

b) 按计划调整滑块运动的角度，并记录对应的力合成值。

c) 重复上述步骤，在实验过程中要记录准确的数据。

五、实验数据记录与处理根据实验步骤操作并记录各个砝码对应的弹簧测压计指示值，以及在不同角度下得到的力合成值。

将这些数据整理成表格，并作适当的图像表示。

六、实验结果分析与讨论1. 分析数据a) 根据测量数据计算每个砝码对应的力大小。