重心法选址模型.doc

基于重心法的仓库选址方法分析摘要：在物流管理实践中，仓库选址是个很普遍的问题，如果盲目地进行仓储的选址与规划就会造成巨大的浪费。

而在解决这一问题的方法多样，有因素评分法、线性规划法和重心法。

其中，精确重心法是常用且有效的一种，通过控制总运输成本最低，从而在多个生产地和需求地区域内找到重心，设为仓库点。

但此方法并不适用于考虑实际地形、以及仓库建设成本的实际仓库选址问题，本文将对以上两种问题分析比较，并针对考虑建设成本的仓库选址问题进行实例分析。

一仓库选址问题概述在物流网络中，仓库连接着供应点和需求点，是两者之间的桥梁，在物流系统中起着重要作用。

选址在整个物流系统中占有重要的地位,是属于物流管理战略层的研究问题，仓储系统选址对企业商品流转速度和流通费用产生直接影响，并关于到企业对顾客的服务水平和服务质量。

如果不好好利用，反之盲目地进行仓储的选址与规划就会造成巨大的资源浪费，同时给企业经营带来很多不良后果。

二基于重心法原理的仓库选址问题1.重心法原理物流网络中仓库选址的实践中常用的方法是精确重心法（又称重心法）。

重心法是一种模拟方法，它将物流系统中的需求点和资源点看成是分布在某一平面范围内的物流系统，各点的需求量和资源量分别看成是物体的重量，物体系统的重心作为物流网点的最佳设置点，利用求物体系统重心的方法来确定物流网点的位置。

这种方法主要考虑的因素是现有设施之间的距离和要运输的货物量，将商品运输量作为影响商品运输费用的主要因素，仓库尽可能接近运量较大的网点，从而使较大的商品运量走相对较短的路程，就是求出本地区实际商品运输费用的重心所在的位置。

2.单个仓库选址理论模型重心法作为单一设施选址问题中最基本的方法之一，使用较为频繁，为了便于探讨问题,理想的重心法理论模型作出以下假设：只考虑现有设施之间的距离和要运输的货物量，1)模型常常假设需求量集中于某一点，各个需求点的位置和需求量已知而且不变，且运入和运出成本是相等的，不考虑在不满载的情况下增加的特殊运输费用；2)模型没有区分在不同地点建设仓库所需的资本成本,以及与在不同地点经营有关的其他成本的差别,而只是计算运输成本；3)模型中仓库与其他网络节点之间的路线通常是假定为直线，且运输费用只与配送中心和需求点的直线距离有关，不考虑城市交通状况；4)模型只考虑现有设施之间的距离和要运输的货物量，不考虑未来收入和成本及其他变化。

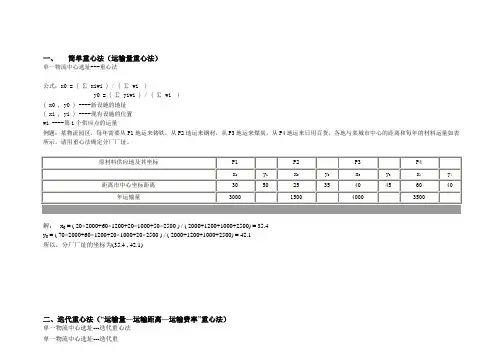
一、简单重心法（运输量重心法）单一物流中心选址---重心法公式：x0 = ( ∑ xiwi ) / ( ∑ wi )y0 = ( ∑ yiwi ) / ( ∑ wi )( x0 , y0 ) ----新设施的地址( xi , yi ) ----现有设施的位置wi ----第i个供应点的运量例题：某物流园区，每年需要从P1地运来铸铁，从P2地运来钢材，从P3地运来煤炭，从P4地运来日用百货，各地与某城市中心的距离和每年的材料运量如表所示。

请用重心法确定分厂厂址。

解：x0 = ( 20×2000+60×1200+20×1000+50×2500 ) / ( 2000+1200+1000+2500) = 35.4y0 = ( 70×2000+60×1200+20×1000+20×2500 ) / ( 2000+1200+1000+2500) = 42.1所以，分厂厂址的坐标为(35.4 , 42.1)二、迭代重心法（“运输量—运输距离—运输费率”重心法）单一物流中心选址---迭代重心法单一物流中心选址---迭代重公式：X = ( ∑Q i R i X i/D i) / ( ∑Q i R i/D i ) Y= ( ∑Q i R i Y i/D i) / ( ∑Q i R i/D i )D i= ( ( X i-X)2+(Y i-Y)2 )1/2F = ∑Q i R i D i(Xi , Yi)----现有目标的坐标位置Qi----运输量Ri----运输费率F----总运费(X , Y)----新仓库的位置坐标Di----现有目标到新仓库的距离解题方法：（1）令Di=1A、求出仓库的初始位置；B、将求出的仓库位置（X，Y）代入Di公式中，求出客户到仓库初始位置的距离；C、计算出仓库初始位置的总运费ΣQiRiDi；( 2 ) 迭代计算：A、将Di代入原公式，求出仓库的新位置坐标（X ，Y）；B、将求出的（X ，Y）代入Di公式中求出Di；C、计算出仓库新位置的总运费ΣiQiRiDi…不断迭代，直到求出的仓库位置和总运费越来越接近于不变，即为所得；注意：牵涉到运输费率要用重心法做；但如无费率，又要求用迭代重心法计算，则令费率为1。

配送中心选址的基本方法（一）单一配送中心的选址单一配送中心的选址方法有重心法、数值分析法等。

现以重心法为例进行计算说明。

1．重心法模型如图9-7所示，设有n 顾客，它们各自的坐标是()i i y x ,(i=1,2,3…,n)，配送中心的坐标是()00,y x ，有∑==nj jC H 1 （9-1）式中 H ---从配送中心到各顾客的总运输费用；jC -----从配送中心到各顾客的运输费用 而jC 又可以用下式来表示jj j j d w h C = （9-2）式中h: 表示从配送中心到顾客j 的运输费率 w : 表示从配送中心到零售店j 的发送量 jd ：从配送中心到顾客的运距。

jd 也可以写成如下形式()()[]212020j j j y y x x d -+-= （9-3）把（4-2）代入（4-1）中，得到jj nj j d w h H ∑==1（9-4）从式（9-3）和（9-4），可求出使H 为最小的0x 、y 。

解决这个问题的方法是运用下面的计算公式，令()0010=-=∂∂∑=j j j n j j d x x w h x H（9-5） ()0010=-=∂∂∑=j j j n j j d y y w h y H（9-6）从式（9-5）和式（9-6）中可分别求得最适合的*0x 和*0y ，即∑∑===dwh d x whx // （9-7）∑∑===dwh d y wh y 11*0// （9-8）因式（9-7）和式（9-8）右边还含有jd ，即还含有要求的未知数0x 、y ，而要从两式的右边完全消去0x 和y ，计算起来很复杂，故采用迭代法来进行计算。

2．迭代法的计算步骤（1）以所有顾客的重心坐标作为配送中心的初始地点（00x ，00y ）；（2）利用式（9-3）和（9-4），计算与（00x ，00y ）相应的总运费0H ；（3）把（00x ，00y ）分别代入式（9-3）、式（9-7）和式（9-8）中，计算配送中心的改善地点（10x ，10y ）；（4）利用式（9-3）和式（9-4），计算与（10x ，10y ）相应的总运费1H ；（5）把1H 和0H 进行比较，如果1H ＜0H ，则返回（3）的计算，再把（00x ，00y ）代入式（9-3）、式（9-7）和式（9-8）中，计算配送中心的再改善地点（20x ，20y ）。

运营管理设施选址的重心法1. 引言在现代企业运营中，选址策略扮演着至关重要的角色。

一个合理选择的设施选址，不仅可以提高运营效率，降低运营成本，还可以为企业带来更多的利润和竞争优势。

本文将介绍一种常用的选址方法——重心法，以帮助企业在选址时进行科学决策。

2. 重心法概述重心法，又称重力模型法或重心模型法，是一种通过计算和比较区域的贮运运距离，确定最佳设施选址的方法。

该方法基于货物运输成本最小化的原理，通过考虑各运输路径的距离和流量，找到最优的设施选址。

3. 重心法的步骤重心法的应用步骤可以分为以下几个步骤：3.1 数据收集收集相关数据是进行重心法选址的第一步。

数据收集包括但不限于以下内容：•地理数据：包括各个待选址点的经纬度、地形、交通、气候等信息；•运输数据：包括货物流量、运输成本、运输方式等信息。

3.2 距离计算根据收集到的地理数据，计算各个待选址点与潜在客户、供应商之间的距离。

常用的距离计算方法包括欧氏距离、曼哈顿距离等。

3.3 流量计算根据收集到的运输数据，计算各个待选址点与潜在客户、供应商之间的货物流量。

可以根据历史数据、市场需求等因素进行推算。

3.4 权重计算为了将距离和流量考虑在内，需要对其进行权重计算。

权重计算可以基于实际情况和经验进行决策，也可以使用数学模型进行计算。

3.5 重心计算根据计算出的距离和流量数据，使用重心模型计算出各个待选址点的重心。

重心可以用作选址的参考点，选择重心较优的位置作为设施选址。

3.6 选址决策最后，根据计算出的重心和其他相关因素，进行选址决策。

除了重心外，还需要考虑企业自身的战略目标、市场需求、竞争对手等因素。

4. 重心法的优势与局限性重心法作为一种常用的设施选址方法，具有以下优势：•相对简单：数据收集和计算过程相对简单，易于实施；•灵活性高：可以根据实际需求进行定制化的调整；•可解释性强：选址结果具有透明性，可以有效地向相关方进行解释。

然而，重心法也存在一些局限性：•假设前提：重心法假设距离和流量是选址的主要考虑因素，可能忽略其他重要因素；•数据依赖性：数据的准确性和完整性对选址结果有较大影响，如果数据不准确或缺失，选址结果可能不够准确。

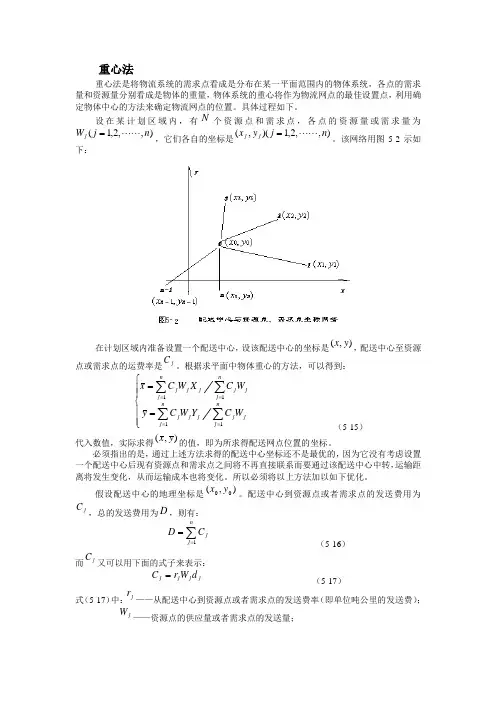
重心法重心法是将物流系统的需求点看成是分布在某一平面范围内的物体系统，各点的需求量和资源量分别看成是物体的重量，物体系统的重心将作为物流网点的最佳设置点，利用确定物体中心的方法来确定物流网点的位置。

具体过程如下。

设在某计划区域内，有N 个资源点和需求点，各点的资源量或需求量为),,2,1(n j W j =，它们各自的坐标是),,2,1)(,(n j y x j j =。

该网络用图5-2示如下：在计划区域内准备设置一个配送中心，设该配送中心的坐标是),(y x ，配送中心至资源点或需求点的运费率是jC 。

根据求平面中物体重心的方法，可以得到：⎪⎪⎩⎪⎪⎨⎧==∑∑∑∑====n j nj j j j j j n j nj j j j j j W C Y W C y W C X W C x 1111 （5-15）代入数值，实际求得),(y x 的值，即为所求得配送网点位置的坐标。

必须指出的是，通过上述方法求得的配送中心坐标还不是最优的，因为它没有考虑设置一个配送中心后现有资源点和需求点之间将不再直接联系而要通过该配送中心中转，运输距离将发生变化，从而运输成本也将变化。

所以必须将以上方法加以如下优化。

假设配送中心的地理坐标是),(00y x 。

配送中心到资源点或者需求点的发送费用为jC ，总的发送费用为D ，则有：∑==nj jC D 1（5-16）而jC 又可以用下面的式子来表示：jj j j d W r C = （5-17）式（5-17）中：j r——从配送中心到资源点或者需求点的发送费率（即单位吨公里的发送费）；jW ——资源点的供应量或者需求点的发送量；jd ——从配送中心到资源点或者需求点的直线距离。

其中，jd 也可以写成如下形式：][)(2)(2021j jj y yx x d --=- （5-18）把方程式（5-18）代入（5-17），得到：∑==nj jj j d W r D 1（5-19）从方程式（5-19）和方程式（5-16）可以求得使D 为最小的),(00y x 。