郑州2020届一测理科数学答案

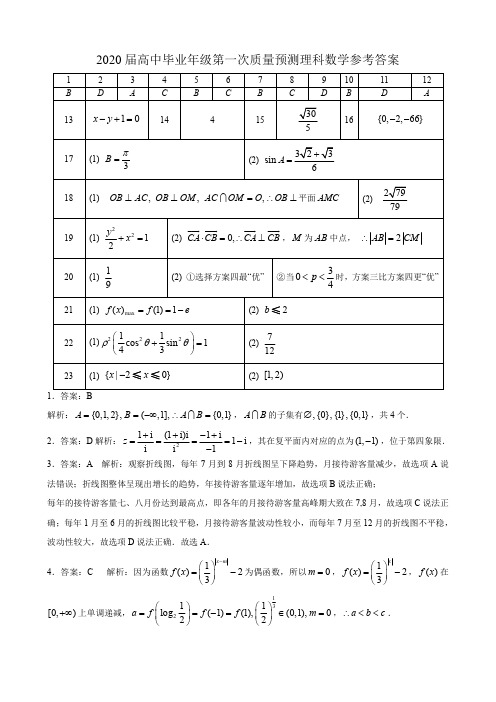
2020年高中毕业年级第一次质量预测数学（理科） 参考答案一、选择题1-12 BDACB CBCDB DA 二、填空题13. 14. 15. 16. 三、解答题17.解析：(I)∴即： ……3分∴ 因为所以……6分(II)若，由正弦定理，, ,由，故为锐角，……9分 ……12分 18. 解析：（I ）如图所示：连接，在中：.……2分在中：为的中点，则10;x y -+=4;;530{}.66,2,0--222(sin sin )()sin .R A B a c C -=-2222(sin sin )()sin 2,R R A B a c C R ⋅-=-⋅222.ac b ac +-=2221cos .22a cb B ac +-==0,B π<<3B π∠=12,8b c ==sin sin b cB C=sin 3C =b c >C ∠cos 3C =1sin sin()sin()32A B C C π=+=+=+=OM ABC ∆2,AB BC AC ===90,ABC BO ∠=︒=OB AC ⊥MAC ∆MA MC AC ===O ACCA，且……4分在中：根据勾股定理逆定理得到相交于，故平面………………….6分（Ⅱ）因为两两垂直，建立空间直角坐标系O−xyz如图所示．因为则……8分由所以，设平面的法向量为，则令……10分因为平面，所以为平面的法向量，所以与所成角的余弦为所以二面角的正弦值为.……12分19．（I）由题意知，.……1分又因为解得，……3分所以椭圆方程为. ……4分（Ⅱ）设过点直线为，设，OM AC⊥OM=MOB∆BO OM MB===222BO OM MB+=OB OM⊥,AC OM OOB⊥AMC,,OB OC OMMA MB MC AC====2AB BC==(0,A B C M23BN BC=u u u r u u u r33NMAN(,,)m x y z=u r(,(,,)0,3333(,,)0AN n x y z x yAM n x y z⎧⋅=⋅=+=⎪⎨⎪⋅=⋅=+=⎩u u u r ru u u u r ry=(1)m=--u rBO⊥AMC OB=uuu rAMC(1)m=--u rOB=uuu rcos,m OB<>==u r u u u u r2|sin,|79m OB<>===u r u u u u r1b=2ca=222a b c=+a=2212yx+=1(,0)3-13x ty=-()11,A x y()22,B x y由得，且. 则又因为，，，……10分 所以.因为线段的中点为，所以.……12分 20. 解析：(I)该混合样本达标的概率是，……2分 所以根据对立事件原理，不达标的概率为.……4分 (II)（i ）方案一：逐个检测，检测次数为4.方案二：由(1)知，每组两个样本检测时，若达标则检测次数为1，概率为；若不达标则检测次数为3，概率为.故方案二的检测次数记为ξ2，ξ2的可能取值为2,4,6. 其分布列如下，可求得方案二的期望为 221312x ty x y ⎧=-⎪⎪⎨⎪+=⎪⎩()2291812160t ty y +--=>0∆12212212,918616,918y y y t y t t ⎧+=⎪⎪+⋯⋯⎨⎪=-⎪+⎩分()111,CA x y =-u u u r ()221,CB x y =-u u u r()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y ⎛⎫⎛⎫⋅=--+=--+=+-++⎪⎪⎝⎭⎝⎭u u u r u u u r ()22216412161091839189t t t t t -=+-⋅+=++CA CB ⊥u u u ru u u rAB M ||2||AB CM =28()39=81199-=891926416119822()246818181819E ξ=⨯+⨯+⨯==方案四：混在一起检测，记检测次数为ξ4，ξ4可取1,5. 其分布列如下，可求得方案四的期望为. 比较可得，故选择方案四最“优”．……9分 (ii)方案三：设化验次数为，可取2,5.方案四：设化验次数为，可取；由题意得. 故当时，方案三比方案四更“优”．……12分 21解析：(I)，定义域，， 由，在增，在减，……4分 (II) 46417149()15818181E ξ=⨯+⨯=42()()4E E ξξ<<3η3η333()25(1)53E p p p η=+-=-4η4η1,54444()5(1)54E p p p η=+-=-34343()()53544E E p p p ηη<⇔-<-⇔<304p <<()ln xe f x x x x=--(0,)+∞221(1)(1)()()1x x e x x x e f x x x x ---'=--=1x e x x ≥+>()f x (0,1](1,)+∞max ()(1)1f x f e ==-1()()e 1xf x x bx x++-≥……6分令，令，在单调递增，，在存在零点，即……9分由于在单调递增，故即 在减，在增，所以.……12分22.解析：(I)将点代入曲线E 的方程，得解得，……2分所以曲线的普通方程为, 极坐标方程为.……5分(Ⅱ)不妨设点的极坐标分别为e e ln e 1x x xx x x bx x x⇔-+-++-≥ln e 10x x x x bx ⇔-++--≥e ln 1x x x xb x --+⇔≥min e ln 1(),x x x x b x --+⇔≥e ln 1()x x x x x x ϕ--+=2ln ()x x e xx xϕ+'=2()ln x h x x e x =+()h x (0,)+∞0,()x h x →→-∞(1)0h e =>()h x (0,1)0x 02000()ln 0xh x x e x =+=0001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=⇔=-=x y xe =(0,)+∞0001lnln ,x x x ==-001x e x =()x ϕ0(0,)x 0(,)x +∞000000min00e ln 111()2x x x x x x x x x ϕ--++-+===2b ≤3(1,)2P 1cos ,3,2a αα=⎧⎪⎨=⎪⎩24a =E 22143x y +=22211(cossin )143ρθθ+=,A B 1212()()00,2A B πρθρθρρ+>>，，，，，则即……8分,即……10分23. 解：(I)由，得，不等式两边同时平方，得，……3分 即，解得.所以不等式的解集为．……5分(Ⅱ)设g (x )＝|x －1|－|2x ＋1|，……8分因为，又恰好存在4个不同的整数n ，使得， 所以故的取值范围为. ……10分22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩2212111174312ρρ+=+=22117||||12OA OB +=()f x m ≥221)(21)x x ≥(－＋3(2)0x x +≤20x -≤≤()f x m ≥{|20}x x -≤≤()0()f n g n m ≥⇔≥-(2)(0)0g g -==(3)1,(4)2,(1) 3.g g g -=--=-=-()0f n ≥2 1.m -<-≤-m [1,2)12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩。

2020年高中毕业年级第一次质量预测数学（理科） 参考答案一、选择题1-12 BDACB CBCDB DA二、填空题13. 10;x y -+= 14.4; 15.;530 16.{}.66,2,0-- 三、解答题17.解析：(I)222(sinsin )()sin .R A B a c C -=- ∴2222(sinsin )()sin 2,R R A B a c C R ×-=-× 即：222.a c b ac +-= ……3分 ∴2221cos .22a cb B ac +-== 因为0,B p <<所以3B p Ð=……6分 (II)若12,8b c ==，由正弦定理，sin sin b c BC =, sin 3C =, 由b c >，故C Ð为锐角，cos 3C =……9分1sin sin()sin()323236A B C C p +=+=+=×+×=……12分 18. 解析：（I ）如图所示：连接OM ， 在ABC D中：2,AB BC AC ===，则90,ABC BO Ð=°AC .……2分 在MAC D 中：M A M C A C ===，O 为AC AC ^，且O M ……4分 在MOB D 中：BO OM MB ==222OM MB += 根据勾股定理逆定理得到OB OM ^ ,AC OM 相交于O ，故OB ^平面AMC ………………….6分（Ⅱ）因为,,OB OC OM 两两垂直，建立空间直角坐标系 − 如图所示． 因为M A M B M C AC ====,2AB BC ==则(0,A B C M ……8分 由23BN BC =uuu r uuu r所以，(,,0)33N 设平面MAN 的法向量为(,,)m x y z =u r ，则(,0)(,,)0,3333(,,)0AN n x y z x y AM n x y z ì×=×=+=ïíï×=×==îuuu r r uuuu r r令y =，得(1)m =--u r ……10分因为BO ^平面AMC，所以OB =uuu r为平面AMC 的法向量，所以(1)m =--u r与OB =uuu r所成角的余弦为cos ,m OB <u ruuuu r所以二面角的正弦值为2|sin ,|79m OB <=u ruuuu r .……12分 19．（I ）由题意知1b =，2c a =.……1分 又因为222a b c =+解得，a =……3分 所以椭圆方程为2212y x +=. ……4分 （Ⅱ） 设过点1(,0)3-直线为13x ty =-，设()11,A x y ，()22,B x y 由221312x ty x y ì=-ïïíï+=ïî得()2291812160t ty y +--=，且>0D . 则12212212,918616,918y y y t y t t ì+=ïï+¼¼íï=-ï+î分又因为()111,CA x y =-uuu r ，()221,CB x y =-uuu r ， ()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y æöæö×=--+=--+=+-++ç÷ç÷èøèøuuu r uuu r ()22216412161091839189t t t t t -=+-×+=++，……10分 所以C A C B ^uuu r uuu r .因为线段AB 的中点为M ，所以||2||AB CM =.……12分20. 解析：(I)该混合样本达标的概率是28(39=，……2分 所以根据对立事件原理，不达标的概率为81199-=.……4分 (II)（i ）方案一：逐个检测，检测次数为4. 方案二：由(1)知，每组两个样本检测时，若达标则检测次数为1，概率为89；若不达标则检测次数为3，概率为19.故方案二的检测次数记为ξ2，ξ2的可能取值为2,4,6.其分布列如下，可求得方案二的期望为26416119822()246818181819E x =´+´+´== 方案四：混在一起检测，记检测次数为ξ4，ξ4可取1,5. 其分布列如下，可求得方案四的期望为46417149()15818181E x =´+´=. 比较可得42()()4E E x x <<，故选择方案四最“优”．……9分 (ii)方案三：设化验次数为3h ，3h 可取2,5.3h2 5 p3p31p - 3333()25(1)53E p p p h =+-=-；方案四：设化验次数为4h ，4h 可取1,5 4h1 5 p4p 41p -4444()5(1)54E p p p h =+-=-；由题意得34343()()53544E E p p p h h <Û-<-Û<.故当304p <<时，方案三比方案四更“优”．……12分 21解析：(I)()ln x e f x x x x=--，定义域(0,)+¥， 221(1)(1)()()1x x e x x x e f x x x x---¢=--=， 由1x e x x ³+>，()f x 在(0,1]增，在(1,)+¥减，max ()(1)1f x f e ==-……4分 (II)1()()e 1x f x x bx x++-³ e e ln e 1x x x x x x bx x xÛ-+-++-³ ln e 10x x x x bx Û-++--³e ln 1x x x x b x --+Û³min e ln 1(,x x x x b x--+Û³……6分 令e ln 1()x x x x x x j --+=，2ln ()x x e x x xj +¢= 令2()ln x h x x e x =+，()h x 在(0,)+¥单调递增，0,()x h x ®®-¥，(1)0h e =>()h x 在(0,1)存在零点0x ，即02000()ln 0x h x x e x =+=0001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=Û=-=……9分 由于x y xe =在(0,)+¥单调递增，故0001ln ln ,x x x ==-即001x e x = ()x j 在0(0,)x 减，在0(,)x +¥增，000000min00e ln 111()2x x x x x x x x x j --++-+=== 所以2b £.……12分 22.解析：(I)将点3(1,)2P 代入曲线E 的方程，得1cos ,3,2a a a =ìïí=ïî解得24a =，……2分 所以曲线E 的普通方程为22143x y +=, 极坐标方程为22211(cos sin )143r q q +=.……5分 (Ⅱ)不妨设点,A B 的极坐标分别为1212()(00,2A B p r q r q r r +>>，，，，， 则22221122222211(cos sin )1,4311(cos (sin ()1,4232r q r q p p r q r q ì+=ïïíï+++=ïî 即22212222111cos sin ,43111sin cos ,43q q r q q r ì=+ïïíï=+ïî……8分 2212111174312r r +=+=,即22117||||12OA OB +=……10分 23. 解：(I)由()f x m ³，得，不等式两边同时平方，得221)(21)x x ³(－＋，……3分 即3(2)0x x +£，解得20x -££.所以不等式()f x m ³的解集为{|20}x x -££．……5分(Ⅱ)设g (x )＝|x －1|－|2x ＋1|， ……8分()0()f n g n m ³Û³-因为(2)(0)0g g -==，(3)1,(4)2,(1) 3.g g g -=--=-=- 又恰好存在4个不同的整数n ，使得()0f n ³， 所以2 1.m -<-£-故m 的取值范围为[1,2). ……10分 12,,21()3,1,22,1,x x g x x x x x ì+£-ïïï=--<£íï-->ïïî。

2020年高中毕业年级第一次质量预测数学（理科） 参考答案一、选择题1-12 BDACBCBCDB DA二、填空题13. 10;x y -+=14.4; 15.;53016.{}.66,2,0-- 三、解答题17.解析：(I)222(sinsin )()sin .R A B a c C -=- ∴2222(sinsin )()sin 2,R R A B a c C R ⋅-=-⋅ 即：222.a c b ac +-= ……3分∴2221cos .22a cb B ac +-== 因为0,B π<<所以3B π∠=……6分(II)若12,8b c ==，由正弦定理，sin sin b c B C=, sin C =, 由b c >，故C ∠为锐角，cos C =……9分 1sin sin()sin()32A B C C π=+=+=+=……12分 18. 解析：（I ）如图所示：连接OM ，在ABC ∆中：2,AB BC AC ===90,ABC BO ∠=︒=OB AC ⊥.……2分在MAC ∆中：MA MC AC ===O 为AC 的中点，则OM AC ⊥，且OM = ……4分在MOB ∆中：BO OM MB ===222BO OM MB += 根据勾股定理逆定理得到OB OM ⊥ ,AC OM 相交于O ，故OB ⊥平面AMC ………………….6分CA（Ⅱ）因为,,OB OC OM两两垂直，建立空间直角坐标系如图所示．因为MA MB MC AC====2AB BC==则(0,A B C M……8分由23BN BC=所以，33N设平面MAN的法向量为(,,)m x y z=，则2(,(,,)0,3333(,,)0AN n x y z x yAM n x y z⎧⋅=⋅=+=⎪⎨⎪⋅=⋅=+=⎩令y=(1)m=--……10分因为BO⊥平面AMC，所以(2,0,0)OB=为平面AMC的法向量，所以(1)m =--与(2,0,0)OB=所成角的余弦为cos,m OB<>==．所以二面角的正弦值为2|sin,|m OB<>===分19．（I）由题意知1b=，2ca=.……1分又因为222a b c=+解得，a=3分所以椭圆方程为2212yx+=. ……4分（Ⅱ）设过点1(,0)3-直线为13x ty=-，设()11,A x y，()22,B x y由221312x tyxy⎧=-⎪⎪⎨⎪+=⎪⎩得()2291812160t tyy+--=，且>0∆.则12212212,918616,918yy ytytt⎧+=⎪⎪+⋯⋯⎨⎪=-⎪+⎩分又因为()111,CA x y=-，()221,CB x y=-，()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y ⎛⎫⎛⎫⋅=--+=--+=+-++ ⎪⎪⎝⎭⎝⎭()22216412161091839189t t t t t -=+-⋅+=++，……10分 所以CA CB ⊥.因为线段AB 的中点为M ，所以||2||AB CM =.……12分20. 解析：(I)该混合样本达标的概率是28(39=，……2分 所以根据对立事件原理，不达标的概率为81199-=.……4分 (II)（i ）方案一：逐个检测，检测次数为4. 方案二：由(1)知，每组两个样本检测时，若达标则检测次数为1，概率为89；若不达标则检测次数为3，概率为19.故方案二的检测次数记为ξ2，ξ2的可能取值为2,4,6. 其分布列如下，可求得方案二的期望为26416119822()246818181819E ξ=⨯+⨯+⨯== 方案四：混在一起检测，记检测次数为ξ4，ξ4可取1,5.其分布列如下，可求得方案四的期望为46417149()15818181E ξ=⨯+⨯=. 比较可得42()()4E E ξξ<<，故选择方案四最“优”．……9分(ii)方案三：设化验次数为3η，3η可取2,5.333()25(1)53E p p p η=+-=-；方案四：设化验次数为4η，4η可取1,54444()5(1)54E p p p η=+-=-；由题意得34343()()53544E E p p p ηη<⇔-<-⇔<. 故当304p <<时，方案三比方案四更“优”．……12分 21解析：(I)()ln xe f x x x x=--，定义域(0,)+∞， 221(1)(1)()()1x x e x x x e f x x x x ---'=--=， 由1x e x x ≥+>，()f x 在(0,1]增，在(1,)+∞减，max ()(1)1f x f e ==-……4分 (II)1()()e 1x f x x bx x++-≥ e e ln e 1x x x x x x bx x x⇔-+-++-≥ ln e 10x x x x bx ⇔-++--≥e ln 1x x x x b x --+⇔≥min e ln 1(),x x x x b x--+⇔≥……6分 令e ln 1()x x x x x x ϕ--+=，2ln ()x x e x x xϕ+'= 令2()ln x h x x e x =+，()h x 在(0,)+∞单调递增，0,()x h x →→-∞，(1)0h e =>()h x 在(0,1)存在零点0x ，即02000()ln 0x h x x e x =+=0001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=⇔=-=……9分 由于x y xe =在(0,)+∞单调递增，故0001ln ln ,x x x ==-即001x e x =()x ϕ在0(0,)x 减，在0(,)x +∞增，000000min00e ln 111()2x x x x x x x x x ϕ--++-+=== 所以2b ≤.……12分 22.解析：(I)将点3(1,)2P 代入曲线E 的方程，得1cos ,3,2a αα=⎧⎪⎨=⎪⎩解得24a =，……2分 所以曲线E 的普通方程为22143x y +=, 极坐标方程为22211(cos sin )143ρθθ+=.……5分 (Ⅱ)不妨设点,A B 的极坐标分别为1212()()00,2A B πρθρθρρ+>>，，，，， 则22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩ 即22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩……8分2212111174312ρρ+=+=,即22117||||12OA OB +=……10分 23. 解：(I)由()f x m ≥，得，不等式两边同时平方，得221)(21)x x ≥(－＋，……3分 即3(2)0x x +≤，解得20x -≤≤.所以不等式()f x m ≥的解集为{|20}x x -≤≤．……5分(Ⅱ)设g (x )＝|x －1|－|2x ＋1|，……8分()0()f n g n m ≥⇔≥-因为(2)(0)0g g -==，(3)1,(4)2,(1) 3.g g g -=--=-=- 又恰好存在4个不同的整数n ，使得()0f n ≥， 所以2 1.m -<-≤-故m 的取值范围为[1,2). ……10分 12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩。

2020年郑州市高中毕业年级第一次质量预测数学（理科） 参考答案一、选择题1-12 BDACBCBCDB DA 二、填空题13. 10;x y -+=14.4; 15.;53016.{}.66,2,0-- 三、解答题17.解析：(I)222(sin sin )()sin .R A B a c C -=-∴2222(sin sin )()sin 2,R R A B a c C R ⋅-=-⋅即：222.ac b ac +-= ……3分∴2221cos .22a cb B ac +-== 因为0,B π<<所以3B π∠=……6分(II)若12,8b c ==，由正弦定理，sin sin b cB C=, sin C =,由b c >，故C ∠为锐角，cos C =……9分 1sin sin()sin()32A B C C π=+=+=+=……12分 18. 解析：（I ）如图所示：连接OM ， 在ABC ∆中：2,AB BC AC ===90,ABC BO ∠=︒=OB AC ⊥.……2分在MAC ∆中：MA MC AC ===O 为AC 的中点，则OM AC ⊥，且OM = ……4分在MOB ∆中：BO OM MB ===222BO OM MB +=根据勾股定理逆定理得到OB OM ⊥ ,AC OM 相交于O ， 故OB ⊥平面AMC ………………….6分CA（Ⅱ）因为,,OB OC OM两两垂直，建立空间直角坐标系如图所示．因为MA MB MC AC====2AB BC==则(0,A B C M……8分由23BN BC=所以，33N设平面MAN的法向量为(,,)m x y z=，则2(,(,,)0,3333(,,)0AN n x y z x yAM n x y z⎧⋅=⋅=+=⎪⎨⎪⋅=⋅=+=⎩令y=(1)m=--……10分因为BO⊥平面AMC，所以(2,0,0)OB=为平面AMC的法向量，所以(1)m =--与(2,0,0)OB=所成角的余弦为cos,m OB<>==．所以二面角的正弦值为2|sin,|m OB<>===分19．（I）由题意知1b=，2ca=.……1分又因为222a b c=+解得，a=3分所以椭圆方程为2212yx+=. ……4分（Ⅱ）设过点1(,0)3-直线为13x ty=-，设()11,A x y，()22,B x y由221312x tyxy⎧=-⎪⎪⎨⎪+=⎪⎩得()2291812160t tyy+--=，且>0∆.则12212212,918616,918yy ytytt⎧+=⎪⎪+⋯⋯⎨⎪=-⎪+⎩分又因为()111,CA x y=-，()221,CB x y=-，()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y ⎛⎫⎛⎫⋅=--+=--+=+-++⎪⎪⎝⎭⎝⎭()22216412161091839189t t t t t -=+-⋅+=++，……10分所以CA CB ⊥.因为线段AB 的中点为M ，所以||2||AB CM =.……12分20. 解析：(I)该混合样本达标的概率是28(39=，……2分 所以根据对立事件原理，不达标的概率为81199-=.……4分 (II)（i ）方案一：逐个检测，检测次数为4.方案二：由(1)知，每组两个样本检测时，若达标则检测次数为1，概率为89；若不达标则检测次数为3，概率为19.故方案二的检测次数记为ξ2，ξ2的可能取值为2,4,6. 其分布列如下，可求得方案二的期望为26416119822()246818181819E ξ=⨯+⨯+⨯== 方案四：混在一起检测，记检测次数为ξ4，ξ4可取1,5. 其分布列如下，可求得方案四的期望为46417149()15818181E ξ=⨯+⨯=. 比较可得42()()4E E ξξ<<，故选择方案四最“优”．……9分 (ii)方案三：设化验次数为3η，3η可取2,5.333()25(1)53E p p p η=+-=-；方案四：设化验次数为4η，4η可取1,54444()5(1)54E p p p η=+-=-；由题意得34343()()53544E E p p p ηη<⇔-<-⇔<. 故当304p <<时，方案三比方案四更“优”．……12分 21解析：(I)()ln xe f x x x x=--，定义域(0,)+∞，221(1)(1)()()1x x e x x x e f x x x x---'=--=， 由1x e x x ≥+>，()f x 在(0,1]增，在(1,)+∞减，max ()(1)1f x f e ==-……4分 (II)1()()e 1xf x x bx x++-≥ e e ln e 1x x xx x x bx x x⇔-+-++-≥ln e 10x x x x bx ⇔-++--≥e ln 1x x x xb x --+⇔≥min e ln 1(),x x x x b x --+⇔≥……6分令e ln 1()x x x x x x ϕ--+=，2ln ()x x e xx xϕ+'=令2()ln x h x x e x =+，()h x 在(0,)+∞单调递增，0,()x h x →→-∞，(1)0h e =>()h x 在(0,1)存在零点0x ，即02000()ln 0xh x x e x =+=001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=⇔=-=……9分由于x y xe =在(0,)+∞单调递增，故0001lnln ,x x x ==-即001x e x =()x ϕ在0(0,)x 减，在0(,)x +∞增，000000min00e ln 111()2x x x x x x x x x ϕ--++-+===所以2b ≤.……12分22.解析：(I)将点3(1,)2P 代入曲线E 的方程，得1cos ,3,2a αα=⎧⎪⎨=⎪⎩解得24a =，……2分所以曲线E 的普通方程为22143x y +=, 极坐标方程为22211(cossin )143ρθθ+=.……5分(Ⅱ)不妨设点,A B 的极坐标分别为1212()()00,2A B πρθρθρρ+>>，，，，，则22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩即22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩……8分 2212111174312ρρ+=+=,即22117||||12OA OB +=……10分 23. 解：(I)由()f x m ≥，得，不等式两边同时平方，得221)(21)x x ≥(－＋，……3分 即3(2)0x x +≤，解得20x -≤≤.所以不等式()f x m ≥的解集为{|20}x x -≤≤．……5分(Ⅱ)设g (x )＝|x －1|－|2x ＋1|，……8分()0()f n g n m ≥⇔≥-因为(2)(0)0g g -==，(3)1,(4)2,(1) 3.g g g -=--=-=-又恰好存在4个不同的整数n ，使得()0f n ≥， 所以2 1.m -<-≤-故m 的取值范围为[1,2). ……10分12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩。

2020年河南省郑州市中考数学一模试卷一、选择题（每小题3分，共30分，下列各小题均有四个答案，其中只有一个是正确的）1．（3分）﹣的相反数是（）A ．B ．﹣C ．D ．﹣2．（3分）华为Mate 30 5G 系列是近期相当火爆的5G 国产手机，它采用的麒麟990 5G 芯片在指甲盖大小的尺寸上集成了103亿个晶体管，将103亿用科学记数法表示为（）A ．1.03×109B ．10.3×109C ．1.03×1010D ．1.03×10113．（3分）下列运算正确的是（）A ．3x ﹣2x ＝xB ．3x+2x ＝5x 2C ．3x?2x ＝6xD ．3x ÷2x ＝4．（3分）如图是由5个完全相同的小正方体搭成的几何体，如果将小正方体A 放到小正方体B 的正上方，则它的（）A ．左视图会发生改变B ．俯视图会发生改变C ．主视图会发生改变D ．三种视图都会发生改变5．（3分）如图，平行四边形ABCD 中，AB ＝3，BC ＝5．以点C 为圆心，适当长为半径画弧，交BC 于点P ，交CD 于点Q ，再分别以点P ，Q 为圆心，大于PQ 的长为半径画弧，两弧相交于点N ，射线CN 交BA 的延长线于点E ，则AE 的长是（）A ．B ．C ．1D ．26．（3分）郑州市某中学获评“2019年河南省中小学书香校园”，学校在创建过程中购买了一批图书．已知购买科普类图书花费12000元，购买文学类图书花费10500元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普书的数量比购买文学书的数量少100本，求科普类图书平均每本的价格是多少元？若设科普类图书平均每本的价格是x元，则可列方程为（）A．﹣＝100B．﹣＝100C．﹣＝100D．﹣＝1007．（3分）2019年9月8日第十一届全国少数民族传统体育运动会在郑州奥体中心隆重开幕，某单位得到了两张开幕式的门票，为了弘扬劳动精神，决定从本单位的劳动模范小李、小张、小杨、小王四人中选取两人去参加开幕式，那么同时选中小李和小张的概率为（）A．B．C．D．8．（3分）已知有理数a≠1，我们把称为a的差倒数，如：2的差倒数是＝﹣1，﹣1的差倒数是＝，如果a1＝﹣2，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，…，依此类推，那么a2020的值是（）A．﹣2B．C．D．9．（3分）用三个不等式a＞b，ab＞0，＞中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题，组成真命题的个数为（）A．0B．1C．2D．310．（3分）使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m 3）与旋钮的旋转角度x（单位：度）（0°＜x≤90°）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用节能燃气灶烧开同一壶水的旋钮的旋转角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋转角度约为（）A．33°B．36°C．42°D．49°二、填空题（每小题3分，共15分）11．（3分）计算：（﹣1）0+（）﹣2＝．12．（3分）如图，五边形ABCDE是正五边形．若l1∥l2，则∠1﹣∠2＝°．13．（3分）如果一元二次方程9x 2﹣6x+m＝0有两个不相等的实数根，那么m的值可以为．（写出一个值即可）14．（3分）如图，四边形ABCD和四边形ACED都是平行四边形，点R为DE的中点，BR 分别交AC，CD于点P，Q．平行四边形ABCD的面积为6，则图中阴影部分的面积为．15．（3分）如图，在矩形ABMN中，AN＝1，点C是MN的中点，分别连接AC，BC，且BC＝2，点D为AC的中点，点E为边AB上一个动点，连接DE，点A关于直线DE的对称点为点F，分别连接DF，EF．当EF⊥AC时，AE的长为．三、解答题（共75分）16．（8分）已知分式1﹣÷（1+）．（1）请对分式进行化简；（2）如图，若m为正整数，则该分式的值对应的点落在数轴上的第段上．（填写序号即可）17．（9分）某年级共有150名女生，为了解该年级女生实心球成绩（单位：米）和一分钟仰卧起坐成绩（单位：个）的情况，从中随机抽取30名女生进行测试，获得了他们的相关成绩，并对数据进行整理、描述和分析．下面给出了部分信息．a．实心球成绩的频数分布如表所示：分组 6.2≤x＜6.6 6.6≤x＜7.07.0≤x＜7.47.4≤x＜7.87.8≤x＜8.28.2≤x＜8.6频数2m10621 b．实心球成绩在7.0≤x＜7.4这一组的是：7.0，7.0，7.0，7.1，7.1，7.1，7.2，7.2，7.3，7.3c．一分钟仰卧起坐成绩如图所示：根据以上信息，回答下列问题：（1）①表中m的值为；②一分钟仰卧起坐成绩的中位数为；（2）若实心球成绩达到7.2米及以上时，成绩记为优秀．①请估计全年级女生实心球成绩达到优秀的人数；②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如表所示：女生代A B C D E F G H码实心球8.17.77.57.57.37.27.0 6.5一分钟*4247*4752*49仰卧起坐其中有3名女生的一分钟仰卧起坐成绩未抄录完整，但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀，于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀，你同意体育委员的说法吗？并说明你的理由．18．（9分）在△ABC中，∠BAC＝90°，AD是BC边上的中线，点E为AD的中点，过点A作AF∥BC交BE的延长线于点F，连接CF．（1）求证：AD＝AF；（2）填空：①当∠ACB＝°时，四边形ADCF为正方形；②连接DF，当∠ACB＝°时，四边形ABDF为菱形．19．（9分）某校“趣味数学”社团开展了测量本校旗杆高度的实践活动．“综合与实践”小组制订了测量方案，并完成了实地测量．他们在该旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离．为了减小测量误差，该小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如表（不完整）课题测量旗杆的高度成员组长：xxx组员：xxx，xxx，xxx测量工具角度的仪器，皮尺等测量示意图说明：线段GH表示学校旗杆，测量角度的仪器的高度AC＝BD＝1.5m，测点A，B与H在同一条水平直线上，A，B之间的距离可以直接测得，且点G，H，A，B，C，D都在同一竖直平面内，点C，D，E在同一条直线上，点E在GH上．测量数据测量项目第一次第二次平均值∠GCE的度数26.4°26.6°26.5°∠GDE的度数32.7°33.3°33°A，B之间的距离 5.9m 6.1m ……任务一：两次测量A，B之间的距离的平均值＝m任务二：根据以上测量结果，请你帮助该“综合与实践”小组求出学校旗杆GH的高度．（参考数据：sin26.5°≈0.45，cos26.5°≈0.89，tan26.5°≈0.50，sin33°≈0.54，cos33°≈0.84，tan33°≈0.65）任务三：该“综合与实践”小组在制定方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳．你认为其原因可能是什么？（写出一条即可）20．（9分）如图，在平面直角坐标系中，已知点B（0，4），等边三角形OAB的顶点A在反比例函数y＝（x＞0）的图象上．（1）求反比例函数的表达式；（2）把△OAB沿y轴向上平移a个单位长度，对应得到△O'A'B'．当这个函数的图象经过△O'A'B'一边的中点时，求a的值．21．（10分）《郑州市城市生活垃圾分类管理办法》于2019年12月起施行．某社区要投放A，B两种垃圾桶，负责人小李调查发现：购买数量少于100个购买数量不少于100个购买数量种类A原价销售以原价的7.5折销售B原价销售以原价的8折销售若购买A种垃圾桶80个，B种垃圾桶120个，则共需付款6880元；若购买A种垃圾桶100个，B种垃圾桶100个，则共需付款6150元．（1）求A，B两种垃圾桶的单价各为多少元？（2）若需要购买A，B两种垃圾桶共200个，且B种垃圾桶不多于A种垃圾桶数量的，如何购买使花费最少，最少费用为多少元？请说明理由．22．（10分）（一）发现探究在△ABC中，AB＝AC，点P在平面内，连接AP并将线段AP绕点A顺时针方向旋转与∠BAC相等的角度，得到线段AQ，连接BQ．【发现】如图1，如果点P是BC边上任意一点，则线段BQ和线段PC的数量关系是；【探究】如图2，如果点P为平面内任意一点．前面发现的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．请仅以图2所示的位置关系加以证明（或说明）；（二）拓展应用【应用】如图3，在△DEF中，DE＝8，∠EDF＝60°，∠DEF＝75°，P是线段EF上的任意一点，连接DP，将线段DP绕点D顺时针方向旋转60°，得到线段DQ，连接EQ．请直接写出线段EQ长度的最小值．23．（11分）如图，在平面直角坐标系中，直线y＝﹣x+n与x轴，y轴分别交于点B，点C，抛物线y＝ax 2+bx+（a≠0）过B，C两点，且交x轴于另一点A（﹣2，0），连接AC．（1）求抛物线的表达式；（2）已知点P为第一象限内抛物线上一点，且点P的横坐标为m，请用含m的代数式表示点P到直线BC的距离；（3）抛物线上是否存在一点Q（点C除外），使以点Q，A，B为顶点的三角形与△ABC 相似？若存在，直接写出点Q的坐标；若不存在，请说明理由．2020年河南省郑州市中考数学一模试卷参考答案与试题解析一、选择题（每小题3分，共30分，下列各小题均有四个答案，其中只有一个是正确的）1．（3分）﹣的相反数是（）A ．B ．﹣C ．D ．﹣【解答】解：﹣的相反数是．故选：A ．2．（3分）华为Mate 30 5G 系列是近期相当火爆的5G 国产手机，它采用的麒麟990 5G 芯片在指甲盖大小的尺寸上集成了103亿个晶体管，将103亿用科学记数法表示为（）A ．1.03×109B ．10.3×109C ．1.03×1010D ．1.03×1011【解答】解：103亿＝103 0000 0000＝1.03×1010，故选：C ．3．（3分）下列运算正确的是（）A ．3x ﹣2x ＝xB ．3x+2x ＝5x 2C ．3x?2x ＝6xD ．3x ÷2x ＝【解答】解：A 、结果是x ，故本选项符合题意；B 、结果是5x ，故本选项不符合题意；C 、结果是6x 2，故本选项不符合题意；D 、结果是，故本选项不符合题意；故选：A ．4．（3分）如图是由5个完全相同的小正方体搭成的几何体，如果将小正方体A 放到小正方体B 的正上方，则它的（）A ．左视图会发生改变B ．俯视图会发生改变C ．主视图会发生改变D ．三种视图都会发生改变【解答】解：如果将小正方体A 放到小正方体B 的正上方，则它的主视图会发生改变，俯视图和左视图不变．故选：C．5．（3分）如图，平行四边形ABCD中，AB＝3，BC＝5．以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于PQ的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是（）A．B．C．1D．2【解答】解：∵由题意可知CE是∠BCD的平分线，∴∠BCE＝∠DCE．∵四边形ABCD是平行四边形，∴AB∥CD，∴∠DCE＝∠E，∴∠BCE＝∠AEC，∴BE＝BC＝5，∵AB＝3，∴AE＝BE﹣AB＝2，故选：D．6．（3分）郑州市某中学获评“2019年河南省中小学书香校园”，学校在创建过程中购买了一批图书．已知购买科普类图书花费12000元，购买文学类图书花费10500元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普书的数量比购买文学书的数量少100本，求科普类图书平均每本的价格是多少元？若设科普类图书平均每本的价格是x元，则可列方程为（）A．﹣＝100B．﹣＝100C．﹣＝100D．﹣＝100【解答】解：设科普类图书平均每本的价格是x元，则可列方程为：﹣＝100．故选：D．7．（3分）2019年9月8日第十一届全国少数民族传统体育运动会在郑州奥体中心隆重开幕，某单位得到了两张开幕式的门票，为了弘扬劳动精神，决定从本单位的劳动模范小李、小张、小杨、小王四人中选取两人去参加开幕式，那么同时选中小李和小张的概率为（）A．B．C．D．【解答】解：根据题意画图如下：共有12种等可能的结果数，其中同时选中小李和小张的有2种，则同时选中小李和小张的概率为＝；故选：D．8．（3分）已知有理数a≠1，我们把称为a的差倒数，如：2的差倒数是＝﹣1，﹣1的差倒数是＝，如果a1＝﹣2，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数，…，依此类推，那么a2020的值是（）A．﹣2B．C．D．【解答】解：∵a1＝﹣2，∴a2＝＝，a3＝＝，a4＝＝﹣2，……∴这个数列以﹣2，，依次循环，∵2020÷3＝673…1，∴a2020的值是﹣2．故选：A．9．（3分）用三个不等式a＞b，ab＞0，＞中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题，组成真命题的个数为（）A．0B．1C．2D．3【解答】解：①若a＞b，ab＞0，则＞；假命题：理由：∵a＞b，ab＞0，∴a＞b＞0，∴＜；②若ab＞0，＞，则a＞b，假命题；理由：∵ab＞0，∴a、b同号，∵＞，∴a＜b；③若a＞b，＞，则ab＞0，假命题；理由：∵a＞b，＞，∴a、b异号，∴ab＜0．∴组成真命题的个数为0个；故选：A．10．（3分）使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m 3）与旋钮的旋转角度x（单位：度）（0°＜x≤90°）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用节能燃气灶烧开同一壶水的旋钮的旋转角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋转角度约为（）A．33°B．36°C．42°D．49°【解答】解：由图象可知，物线开口向上，该函数的对称轴x ＞且x ＜54，∴36＜x ＜54，即对称轴位于直线x ＝36与直线x ＝54之间且靠近直线x ＝36，故选：C ．二、填空题（每小题3分，共15分）11．（3分）计算：（﹣1）0+（）﹣2＝5．【解答】解：原式＝1+4＝5．故答案为：5．12．（3分）如图，五边形ABCDE 是正五边形．若l 1∥l 2，则∠1﹣∠2＝72°．【解答】解：过B 点作BF ∥l 1，∵五边形ABCDE 是正五边形，∴∠ABC ＝108°，∵BF ∥l 1，l 1∥l 2，∴BF ∥l 2，∴∠3＝180°﹣∠1，∠4＝∠2，∴180°﹣∠1+∠2＝∠ABC ＝108°，∴∠1﹣∠2＝72°．故答案为：72．13．（3分）如果一元二次方程9x 2﹣6x+m ＝0有两个不相等的实数根，那么m 的值可以为．（写出一个值即可）【解答】解：根据题意得△＝（﹣6）2﹣4×9m ＞0，解得m＜1，所以m可取0．故答案为0．14．（3分）如图，四边形ABCD和四边形ACED都是平行四边形，点R为DE的中点，BR 分别交AC，CD于点P，Q．平行四边形ABCD的面积为6，则图中阴影部分的面积为．【解答】解：∵四边形ABCD和四边形ACED都是平行四边形，∴AD＝BC＝CE，AB∥CD，AC∥DE，∴平行四边形ACED的面积＝平行四边形ABCD的面积＝6，△BCP∽△BDE，△ABP∽△CQP∽△DQR，∴△ABC的面积＝△CDE的面积＝3，CP：ER＝BC：BE＝1：2，∵点R为DE的中点，∴CP：DR＝1：2，∴CP：AC＝CP：DE＝1：4，∵S△ABC＝3，∴S△ABP＝S△ABC＝，∵CP：AP＝1：3，∴S△PCQ＝S△ABP＝，∵CP：DR＝1：2，∴S△DQR＝4S△PCQ＝1，∴S阴影＝S△PCQ+S△DQR＝．故答案为：．15．（3分）如图，在矩形ABMN中，AN＝1，点C是MN的中点，分别连接AC，BC，且BC＝2，点D为AC的中点，点E为边AB上一个动点，连接DE，点A关于直线DE的对称点为点F，分别连接DF，EF．当EF⊥AC时，AE的长为或．【解答】解：∵四边形ABMN是矩形，∴AN＝BM＝1，∠M＝∠N＝90°，∵CM＝CN，∴△BMC≌△ANC（SAS），∴BC＝AC＝2，∴AC＝2AN，∴∠ACN＝30°，∵AB∥MN，∴∠CAB＝∠CBA＝30°，①如图1中，当DF⊥AB时，∠ADF＝60°，∵DA＝DF，∴△ADF是等边三角形，∴∠AFD＝60°，∵∠DFE＝∠DAE＝30°，∴EF平分∠AFD，∴EF⊥AD，此时AE＝．②如图2中，当△AEF是等边三角形时，EF⊥AC，此时EF＝．综上所述，满足条件的EF的值为或．三、解答题（共75分）16．（8分）已知分式1﹣÷（1+）．（1）请对分式进行化简；（2）如图，若m为正整数，则该分式的值对应的点落在数轴上的第①段上．（填写序号即可）【解答】解：（1）原式＝1﹣÷＝1﹣?＝1﹣＝＝；（2）∵原式＝1﹣，m为正整数且m＝1，∴该分式的值应落在数轴的①处，故答案为：①．17．（9分）某年级共有150名女生，为了解该年级女生实心球成绩（单位：米）和一分钟仰卧起坐成绩（单位：个）的情况，从中随机抽取30名女生进行测试，获得了他们的相关成绩，并对数据进行整理、描述和分析．下面给出了部分信息．a．实心球成绩的频数分布如表所示：分组 6.2≤x＜6.6 6.6≤x＜7.07.0≤x＜7.47.4≤x＜7.87.8≤x＜8.28.2≤x＜8.6频数2m10621 b．实心球成绩在7.0≤x＜7.4这一组的是：7.0，7.0，7.0，7.1，7.1，7.1，7.2，7.2，7.3，7.3c．一分钟仰卧起坐成绩如图所示：根据以上信息，回答下列问题：（1）①表中m的值为9；②一分钟仰卧起坐成绩的中位数为45；（2）若实心球成绩达到7.2米及以上时，成绩记为优秀．①请估计全年级女生实心球成绩达到优秀的人数；②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如表所示：女生代A B C D E F G H码实心球8.17.77.57.57.37.27.0 6.5一分钟*4247*4752*49仰卧起坐其中有3名女生的一分钟仰卧起坐成绩未抄录完整，但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀，于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀，你同意体育委员的说法吗？并说明你的理由．【解答】解：（1）①m＝30﹣2﹣10﹣6﹣2﹣1＝9，故答案为：9；②由条形统计图可得，一分钟仰卧起坐成绩的中位数为45，故答案为：45；（2）①∵实心球成绩在7.0≤x＜7.4这一组的是：7.0，7.0，7.0，7.1，7.1，7.1，7.2，7.2，7.3，7.3，∴实心球成绩在7.0≤x＜7.4这一组优秀的有4人，∴全年级女生实心球成绩达到优秀的人数是：150×＝65，答：全年级女生实心球成绩达到优秀的有65人；②同意，理由：如果女生E的仰卧起坐成绩未到达优秀，那么只有A、D、F有可能两项测试成绩都达到优秀，这与恰有4个人两项成绩都达到优秀，矛盾，因此，女生E的一分钟仰卧起坐成绩达到了优秀．18．（9分）在△ABC中，∠BAC＝90°，AD是BC边上的中线，点E为AD的中点，过点A作AF∥BC交BE的延长线于点F，连接CF．（1）求证：AD＝AF；（2）填空：①当∠ACB＝45°时，四边形ADCF为正方形；②连接DF，当∠ACB＝30°时，四边形ABDF为菱形．【解答】（1）证明：∵∠BAC＝90°，AD是BC边上的中线，∵AD＝CD＝BD，∵点E为AD的中点，∴AE＝DE，∵AF∥BC，∴∠AFE＝∠DBE，∵∠AF＝∠DEB，∴△AEF≌△DEB（AAS），∴AF＝BD，∴AD＝AF；（2）解：①当∠ACB＝45°时，四边形ADCF为正方形；∵AD＝AF，∴AF＝CD，∵AF∥CD，∴四边形ADCF是菱形，∴∠ACD＝∠ACF＝45°，∴∠DCF＝90°，∴四边形ADCF是正方形；②当∠ACB＝30°时，四边形ABDF为菱形；∵四边形ADCF是菱形，四边形ABDF是平行四边形，∴CD＝CF，∵∠ACB＝∠ACF＝30°，∴∠DCF＝60°，∴△DCF是等边三角形，∴DF＝CD，∴DF＝BD，∴四边形ABDF为菱形．故答案为：45，30．19．（9分）某校“趣味数学”社团开展了测量本校旗杆高度的实践活动．“综合与实践”小组制订了测量方案，并完成了实地测量．他们在该旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离．为了减小测量误差，该小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如表（不完整）课题测量旗杆的高度成员组长：xxx组员：xxx，xxx，xxx测量工具角度的仪器，皮尺等测量示意图说明：线段GH表示学校旗杆，测量角度的仪器的高度AC＝BD＝1.5m，测点A，B与H在同一条水平直线上，A，B之间的距离可以直接测得，且点G，H，A，B，C，D都在同一竖直平面内，点C，D，E在同一条直线上，点E在GH上．测量数据测量项目第一次第二次平均值∠GCE的度数26.4°26.6°26.5°∠GDE的度数32.7°33.3°33°A，B之间的距离 5.9m 6.1m ……任务一：两次测量A，B之间的距离的平均值＝6m任务二：根据以上测量结果，请你帮助该“综合与实践”小组求出学校旗杆GH的高度．（参考数据：sin26.5°≈0.45，cos26.5°≈0.89，tan26.5°≈0.50，sin33°≈0.54，cos33°≈0.84，tan33°≈0.65）任务三：该“综合与实践”小组在制定方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳．你认为其原因可能是什么？（写出一条即可）【解答】解：任务一：＝（5.9+6.1）＝6，故答案为：6；任务二：设EG＝xm，在Rt△DEG中，∠DEG＝90°，∠GDE＝33°，∵tan33°＝，∴DE＝，在Rt△CEG中，∠CEG＝90°，∠GCE＝25.7°，∵tan26.5°＝，CE＝，∵CD＝CE﹣DE，∴﹣＝6，∴x＝13，∴GH＝EG+EH＝13+1.5＝14.5，答：旗杆GH的高度为14.5米；任务三：没有太阳光，或旗杆底部不可能达到相等．20．（9分）如图，在平面直角坐标系中，已知点B（0，4），等边三角形OAB的顶点A在反比例函数y＝（x＞0）的图象上．（1）求反比例函数的表达式；（2）把△OAB沿y轴向上平移a个单位长度，对应得到△O'A'B'．当这个函数的图象经过△O'A'B'一边的中点时，求a的值．【解答】解：（1）∵点B（0，4），等边三角形OAB的顶点A在反比例函数y＝（x＞0）的图象上，∴点A的坐标为（2，2），∴2＝，得k＝4，即反比例函数的表达式是y＝；（2）当反比例函数y＝过边A′B′的中点时，∵边O′A′的中点是（，3+a），∴3+a＝，得a＝1；当反比例函数y＝过边O′A′的中点时，∵边A′B′的中点是（，1+a），∴1+a＝，得a＝3；由上可得，a的值是1或3．21．（10分）《郑州市城市生活垃圾分类管理办法》于2019年12月起施行．某社区要投放A，B两种垃圾桶，负责人小李调查发现：购买数量少于100个购买数量不少于100个购买数量种类A原价销售以原价的7.5折销售B原价销售以原价的8折销售若购买A种垃圾桶80个，B种垃圾桶120个，则共需付款6880元；若购买A种垃圾桶100个，B种垃圾桶100个，则共需付款6150元．（1）求A，B两种垃圾桶的单价各为多少元？（2）若需要购买A，B两种垃圾桶共200个，且B种垃圾桶不多于A种垃圾桶数量的，如何购买使花费最少，最少费用为多少元？请说明理由．【解答】解：（1）设A种垃圾桶的单价为x元，B种垃圾桶的单价为y元，根据题意得，解得，答：A种垃圾桶的单价为50元，B种垃圾桶的单价为30元；（2）设购买A种垃圾桶为a个，则购买B种垃圾桶为（200﹣a）个，根据题意得，解得a≥150；设购买A，B两种垃圾桶的总费用为W元，则W＝0.75×50a+30（200﹣a）＝7.5a+6000，∵k＝7.5＞0，∴W随x的增大而增大，∴当a＝150时，花费最少，最少费用为：7.5×150+6000＝7125（元）．答：购买A种垃圾桶150个，B种垃圾桶50个花费最少，最少费用为7125元．22．（10分）（一）发现探究在△ABC中，AB＝AC，点P在平面内，连接AP并将线段AP绕点A顺时针方向旋转与∠BAC相等的角度，得到线段AQ，连接BQ．【发现】如图1，如果点P是BC边上任意一点，则线段BQ和线段PC的数量关系是BQ ＝PC；【探究】如图2，如果点P为平面内任意一点．前面发现的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．请仅以图2所示的位置关系加以证明（或说明）；（二）拓展应用【应用】如图3，在△DEF中，DE＝8，∠EDF＝60°，∠DEF＝75°，P是线段EF上的任意一点，连接DP，将线段DP绕点D顺时针方向旋转60°，得到线段DQ，连接EQ．请直接写出线段EQ长度的最小值．【解答】解：【发现】由旋转知，AQ＝AP，∵∠P AQ＝∠BAC，∴∠P AQ﹣∠BAP＝∠BAC﹣∠BAP，∴∠BAQ＝∠CAP，∵AB＝AC，∴△BAQ≌△CAP（SAS），∴BQ＝CP，故答案为：BQ＝PC；【探究】结论：BQ＝PC仍然成立，理由：由旋转知，AQ＝AP，∵∠P AQ＝∠BAC，∴∠P AQ﹣∠BAP＝∠BAC﹣∠BAP，∴∠BAQ＝∠CAP，∵AB＝AC，∴△BAQ≌△CAP（SAS），∴BQ＝CP，【应用】如图3，在DF上取一点H，使DH＝DE＝8，连接PH，过点H作HM⊥EF于M，由旋转知，DQ＝DP，∠PDQ＝60°，∵∠EDF＝60°，∴∠PDQ＝∠EDF，∴∠EDQ＝∠HDP，∴△DEQ≌△DHP（SAS），∴EQ＝HP，要使EQ最小，则有HP最小，而点H是定点，点P是EF上的动点，∴当HM⊥EF（点P和点M重合）时，HP最小，即：点P与点M重合，EQ最小，最小值为HM，过点E作EG⊥DF于G，在Rt△DEG中，DE＝8，∠EDF＝60°，∴∠DEG＝30°，∴DG＝DE＝4，∴EG＝DG＝4，在Rt△EGF中，∠FEG＝∠DEF﹣∠DEG＝75°﹣30°＝45°，∴∠F＝90°﹣∠FEG＝45°＝∠FEG，FG＝EG＝4，∴DF＝DG+FG＝4+4，∴FH＝DF﹣DH＝4+4﹣8＝4﹣4，在Rt△HMF中，∠F＝45°，∴HM＝FH＝（4﹣4）＝2﹣2，即：EQ的最小值为2﹣2．23．（11分）如图，在平面直角坐标系中，直线y＝﹣x+n与x轴，y轴分别交于点B，点C，抛物线y＝ax 2+bx+（a≠0）过B，C两点，且交x轴于另一点A（﹣2，0），连接AC．（1）求抛物线的表达式；（2）已知点P为第一象限内抛物线上一点，且点P的横坐标为m，请用含m的代数式表示点P到直线BC的距离；（3）抛物线上是否存在一点Q（点C除外），使以点Q，A，B为顶点的三角形与△ABC 相似？若存在，直接写出点Q的坐标；若不存在，请说明理由．【解答】解：（1）点C（0，），则直线y＝﹣x+n＝﹣x+，则点B（3，0），则抛物线的表达式为：y＝a（x﹣3）（x+2）＝a（x2﹣x﹣6），故﹣6a＝，解得：a＝﹣，故抛物线的表达式为：y＝﹣x2+x+；（2）过点P作y轴的平行线交BC于点G，作PH⊥BC于点H，则∠HPG＝∠CBA＝α，tan∠CBA＝＝＝tanα，则cosα＝，设点P（m，﹣m2+m+），则点G（m，﹣m+），则PH＝PGcosα＝（﹣m2+m++m﹣）＝﹣m2+m；（3）①当点Q在x轴上方时，则点Q，A，B为顶点的三角形与△ABC全等，此时点Q与点C关于函数对称轴对称，则点Q（1，）；②当点Q在x轴下方时，（Ⅰ）当∠BAQ＝∠CAB时，△QAB∽△BAC，则＝，由勾股定理得：AC＝5，AQ＝＝＝10，过点Q作QH⊥x轴于点H，由△HAQ∽△OAC得：＝＝，∵OC＝，AQ＝10，∴QH＝6，则AH＝8，OH＝18﹣2＝6，∴Q（6，﹣6）；根据点的对称性，当点Q在第三象限时，符合条件的点Q（﹣5，﹣6）；故点Q的坐标为：（6，﹣6）或（﹣5，﹣6）；（Ⅱ）当∠BAQ＝∠CBA时，则直线AQ∥BC，直线BC表达式中的k为：﹣，则直线AQ的表达式为：y＝﹣x﹣2…②，联立①②并解得：x＝5或﹣2（舍去﹣2），故点Q（5，﹣），＝，而＝，故≠，即Q，A，B为顶点的三角形与△ABC不相似，故舍去，Q的对称点（﹣4，﹣）同样也舍去，即点Q的为：（﹣4，﹣）、（5，﹣）均不符合题意，都舍去；综上，点Q的坐标为：（1，）或（6，﹣6）或（﹣5，﹣6）．。