定积分的应用(体积、旋转体的侧面积)(精品课件).ppt
- 格式:ppt
- 大小:2.79 MB
- 文档页数:26








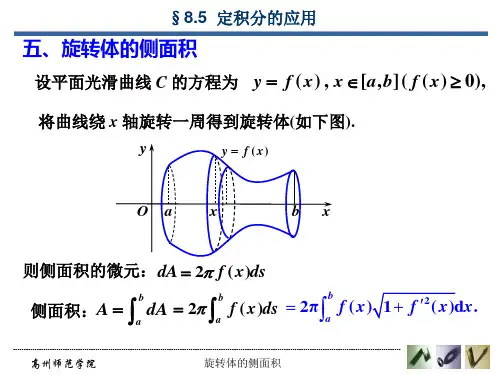

定积分在几何学上的应用之旋转体的侧面积x y o a b 旋转体的侧面积设平面光滑曲线求sy πS d 2=d 积分后得旋转体的侧面积x x f x f πS bad )(′+1)(2=2∫它绕x 轴旋转一周所得到的旋转曲面的侧面积.取侧面积元素:xyoa )(x f y bxxyo )(x f y ab xs y πS d 2=d 侧面积元素≠x y πd 2s d xd x y πd 2因为的线性主部.若光滑曲线由参数方程给出,则它绕x 轴旋转一周所得旋转体的不是薄片侧面积△S 的)(2t y πtt y t x d )(′+)(′22∫βαS =注意:侧面积为)(=t y y )(=t x x )≤≤(βt αxR y o例1.计算圆x 轴旋转一周所得的球台的侧面积S .解:对曲线弧应用公式得∫212=x xπS 22x R -2 1⎪⎭⎫ ⎝⎛+⋅22x R x --x d ∫21d 2=x xx R π)(2=12x x R π-当球台高h =2R 时, 得球的表面积公式24=RπS 1x 2x例 2. 求由星形线一周所得的旋转体的表面积S .解: 利用对称性∫222=ππS t a 3sin ()()22+t t a sin cos 32-t d ∫242d cos sin 12=πt t t a πsin 5112=52ta π2512=a πt t a cos sin 32绕x 轴旋转内容小结旋转体的侧面积=d2sS dyπ侧面积元素为(注意在不同坐标系下ds 的表达式)。