第三章3-3切割体的投影(截交线)
- 格式:ppt
- 大小:7.42 MB
- 文档页数:56




第3章立体的投影电子教案:3.1 基本立体的投影基本立体可分为平面立体和曲面立体。
表面均为平面的基本立体称为平面立体。
常见的有棱柱、棱锥,如图3-1所示。
表面由曲面和平面或完全由曲面组成的基本立体称为曲面立体。
最常见的曲面立体是回转体,包括圆柱、圆锥、球、圆环等,如图3-2所示。
将基本体放在三投影面体系中进行投射时,为了画图、读图的方便,通常将其“放平,摆正”。
放平——就是让基本体的底面处于平行面位置。
摆正——是在放平的基础上,让其余各面尽可能处于平行面或垂直面位置。
在以后画组合体视图或零件图时也要遵循这个原则。
图3-1 平面立体图3-2曲面立体3.1.1 平面立体的投影及其表面取点在投影图上表示平面立体就是把组成立体的平面和棱线表示出来,然后判别其可见性,把看得见的棱线投影画成实线,看不见的棱线投影画成虚线。
1.棱柱(1) 棱柱的投影常见的棱柱有正四棱柱和正六棱柱,图3-3(a)所示一正六棱柱,由六个相同的矩形棱面和上下底面(正六边形)所围成。
将其放平摆正后,上、下底面为水平面,其水平投影反映实形,另外两面投影积聚为直线。
正六棱柱的六个棱面中,前后两个面是正平面,正面投影反映实形;其余四个棱面均为铅垂面。
如图3-3(b)所示,作图过程如图3-4所示。
(a)(b)图3-3正六棱柱的投影及表面取点图3-4 正六棱柱的画图方法和步骤棱柱的投影特性是:在与棱线垂直的投影面上的投影为一多边形,它反映棱柱上、下底面的实形;另两个投影都是由粗实线或虚线组成的矩形线框,它反映棱面的实形或类似形。
(2) 在棱柱表面上取点在棱柱表面上取点,其原理和方法与在平面内取点相同。
该例中正六棱柱的各个表面都处于特殊位置,因此在其表面上取点均可利用平面投影积聚性的原理作图,并判别其可见性,如图3-3(b)所示。
2.棱锥(1) 投影分析和画法常见的棱锥有正三棱锥和正四棱锥,图3-5(a)所示为一正三棱锥,锥顶为S,其底面为等边△ABC,是水平面。

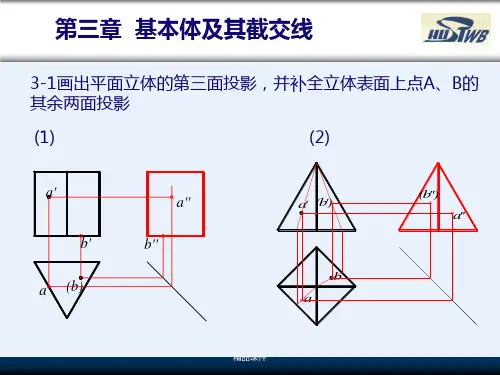



第三章基本立体的投影、截交线、相贯线§1立体的投影1.1平面立体的投影本节教学目标:掌握平面立体的投影特性和作图方法;掌握拉伸体的形成、投影及画法;熟悉平面立体表面中特殊位置的点、线的三面投影及画法。
重点:平面立体的投影特性及表面取点、取线的投影。
难点:平面立体表面中特殊位置处点、线的投影。
引入:通过对前面知识的学习已经知道,很多的机械零件都是由一些简单的基本形体组成,比如螺栓,我们可以将它分成正六棱柱、圆柱体和圆锥台三部分。
如果我们要绘制此螺栓的三视图,同学们都应该知道必须要绘制正六棱柱、圆柱体和圆锥台的三视图。
任何一个复杂的物体都可以看成由基本体组成,按组成基本体表面的性质进行分类,基本体可分为平面体和曲面体。
平面立体侧表面的交线称为棱线若平面立体所有棱线互相平行,称为棱柱。
若平面立体所有棱线交于一点,称为棱锥。
1.1.1棱柱的投影1. 以正六棱柱为例,分析平面立体的结构,(1)正六棱柱共有几个表面?有何关系?(2)正六棱柱共有几条侧棱?有何关系?提问:1)不同位置的投影有什么不同?2)应怎样放置最合理?提示:使尽可能多的表面和棱线处于特殊位置。
2.投影特性分析(1)投影分析:上、下两个底面——平行的两个侧面——其余的几个侧面(2)三面投影图分析(3)绘图步骤:1)建立投影面系;2)根据三等原则绘制三面投影;3)区分可见性。
3. 棱柱体的投影特性(重点:学生应掌握)(1)当棱柱的底面平行于某一投影面时,棱柱的投影在该面上为与底面相等的正多边形。
(2)另两面投影为几个相邻的矩形线框。
4. 棱柱表面取点、线重点:所取的点、线属于棱柱的哪个面上?进而再求三面投影。
***若点所在平面的投影可见,点的投影可见;若平面的投影积聚成直线,点的投影也可见。
例:例:已知四棱柱,试完成其V、H投影。
(图7-1)图7-1四棱柱的投影1.1.2棱锥的投影棱锥的投影是棱锥各顶点同面投影连线的集合。
1. 棱锥的定义2. 棱锥的形体分析(1)投影分析:下底面——顶点——其余的几个侧面(2)三面投影图分析(3)绘图步骤:1)建立投影面系;2)根据三等原则绘制三面投影;3)区分可见性。

§3-3 平面体的投影复杂物体都可以看成由若干基本体组合而成。
基本体有平面体和曲面体两类。
表面都是平面的立体称为平面体,如棱柱、棱锥;表面含有曲面的立体称为曲面体,常见的曲面体是回转体,如圆柱、圆锥、圆球等。
一、平面体的投影作图立体的投影图是立体各表面投影的总和。
平面体的表面都是平面,平面与平面的交线都是直线,因此画平面体投影图的实质就是画给定位置的若干平面和直线的投影。
运用前面所学的点、直线及平面投影特征,便可以完成平面体的投影作图。
1.棱柱的投影作图(以六棱柱为例)(1)首先将棱柱放置一个适当位置要尽可能多的让棱柱的主要表面和棱线与投影面平行或垂直,以方便画图和看图。
图3-43a 所示,六棱柱的顶、底面为水平面,前、后棱面为正平面,左、右两侧的棱面为铅锤面。
图3-43 正六棱柱的投影作图(2)具体画图1)画对称面的投影用细点画线画出立体对称面有积聚性的投影。
该六棱柱前后对称,对称面是正平面,用细点画线画出该平面有积聚性的投影(H面投影、W面投影);同理画出六棱柱左右对称面有积聚性的投影(V面投影、H面投影)。
2)画顶、底面的投影顶、底面是水平面,先画反映实形的H面投影(正六边形),再画有积聚性的V面投影和W面投影(图3-43b)3)画六个棱面的投影六个棱面的H面投影都积聚在正六边形的六条边上;前、后棱面V面投影相互重叠且反映实形,W面投影积聚为Z轴的平行线;左、右四棱面V面投影、W面投影都是缩小的类似形(矩形),并且投影发生重叠(图3-43c)。
4)检查加粗图线可见轮廓线的投影用粗实线绘制,不可见轮廓线的投影用细虚线绘制,对称面、轴线的投影用细点画线绘制(细点画线应超出图形2~5毫米),三种图线相互重叠时,优先表达前者(图3-43c)。
说明:画立体三面投影图的目的是用一组平面图形来表达物体的空间结构形状,将上述六棱柱放置在H面上或离H面一定距离,画出的三面投影图的图形是相同的,因此画立体三面投影时不必画出投影轴(图3-43d)。