北师大版数学七年级上册导学案：第三章《整式的加减》复习

整式及其加减班别： 姓名： 学号： 学习目标： 1、系统掌握相关知识内容； 2、掌握本章常见题型及其解题方法。

学习过程：一、复习1、字母可以表示任何数 （1）明明步行速度为3m/s ，那么他x 秒行走了 米；（2）温度由t ℃下降5℃后是 ℃；（3）今年李华m 岁，前年李华 岁，10年后李华 岁；（4）某商店上月收入为a 元，本月的收入比上月的2倍少500元，本月的收入是 元；（5）明明用t 秒走了100米，他的速度为 m/s 。

2、代数式的定义：用 把 连接而成的式子叫做代数式；单独一个 或一个 也是代数式。

（1）一个练习本x 元，一支铅笔y 元，买2个练习本和5支铅笔需要 元；（2）一个数x 的13与4的和用代数式表示是 （3）一个数a 的2倍与3的差用代数式表示是（4）代数式2()m n -表示（5）在21,,,13,4,4,2s a x y x pq t++=-<+中，有 个代数式；（6）若1,2x y ==-，则21xy y -+=3、整式的定义：单项式和多项式统称整式。

（1）单项式的定义：由 与 的乘积构成的代数式叫做单项式。

单独一个 或一个 也是单项式。

单项式中的 叫做这个单项式的系数；所有字母的 叫做单项式的次数。

（2）多项式的定义：几个单项式的 叫做多项式。

多项式中每个单项式叫做多项式的 ，次数 的项的次数叫做这个多项式的次数。

4、整式的加减（1）同类项的定义：所含 相同，并且相同字母的 也相同的项，叫做同类项。

合并同类项时，把同类项的 相加， 和 不变。

步骤：①先分类；②再合并。

（2）去括号法则： ①括号前是“＋”号，原括号里各项的符号都 ； ②括号前是“－”号，原括号里各项的符号都 。

（3）进行整式的加减运算时，如果遇到括号要先 ，再 。

二、例题与练习例1、填空（1）指出下列哪些是单项式？哪些是多项式？哪些是整式？2212,,,2,,3,,22x ya b r k k x y x x k +--+--++单项式{ }多项式{ }整式 { }（2）单项式232ab c -的系数是 ，次数是 ；（3）多项式32342x y xy xy -+-+有 项，次数是 。

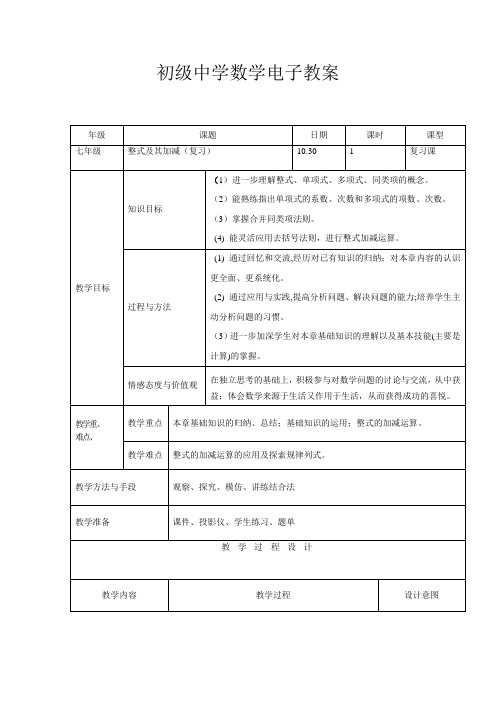
第三章整式及其加减1.理解并掌握单项式、多项式、整式等概念,弄清它们之间的区别与联系.2.理解同类项概念,掌握合并同类项的方法,掌握去括号时符号的变化规律,能正确地进行同类项的合并和去括号.在准确判断、正确合并同类项的基础上,进行整式的加减运算.3.理解整式中的字母表示数,整式的加减运算建立在数的运算的基础上;理解合并同类项、去括号的依据是分配律;理解数的运算律和运算律性质在整式的加减运算中仍然成立.4.建立数感、符号意识,初步形成运算能力,发展抽象思维.1.能分析实际问题中的数量关系,并列出整式表示.体会用字母表示数后,从算术到代数的进步.2.会求代数式的值,能解释值的实际意义,能根据代数式的值推断代数式反映的规律.渗透数学知识来源于生活,又要为生活而服务的辩证观点;经历由数的加减过渡到整式的加减的过程,培养学生由特殊到一般的思维;体会整式的加减实质上就是去括号,合并同类项,结果总是比原来简洁,体现了数学的简洁美.【重点】理解单项式、多项式的相关概念;熟练进行合并同类项和去括号的运算.【难点】准确地合并同类项,准确地处理去括号时的符号变化.专题一先化简再求值【专题分析】先把代数式化简,化简时,有括号的先去括号,再合并同类项,若有多重括号,可由里向外或由外向里逐层推进,尽可能减少去括号的次数和变号的项数.当x=1时,求x2 - x - (x2+x)的值.〔解析〕由外向内去括号,可减少变号的项数,再合并同类项,代入求值.解:原式=x2 - x+(x2+x)=x2 - x+x2+x=x2 - x.当x=1时,原式=×1 - ×1=1.[解题策略]先化简,再求值.【针对训练1】当x=1,y= - 1时,求xy - xy2 - {2xy+3xy2 - [xy2 - 4xy+(xy - 4xy2)]}的值.〔解析〕看清题,去多重括号时,可以由内向外逐层进行,也可以由外向内逐层进行,如果去括号法则掌握得较熟练,也可以内外同时去括号.解法1:(由内向外逐层去括号)原式=xy - xy2 - [2xy+3xy2 - (xy2 - 4xy+xy - 4xy2)]=xy - xy2 - [2xy+3xy2 - ( - 3xy2 - 3xy)]=xy - xy2 - (2xy+3xy2+3xy2+3xy)=xy - xy2 - (5xy+6xy2)=xy - xy2 - 5xy - 6xy2= - 4xy - 7xy2.当x=1,y= - 1时,原式= - 3.解法2:(由外向内去括号)原式=xy- xy2- 2xy- 3xy2+[xy2- 4xy+(xy- 4xy2)]= - xy- 4xy2+xy2- 4xy+(xy- 4xy2)= - 5xy- 3xy2+xy - 4xy2= - 4xy - 7xy2.当x=1,y= - 1时,原式= - 3.解法3:(内外同时去括号)原式=xy - xy2 - 2xy - 3xy2+(xy2 - 4xy+xy - 4xy2)= - xy - 4xy2+( - 3xy2 - 3xy)= - xy - 4xy2 - 3xy2 - 3xy= - 4xy - 7xy2.当x=1,y= - 1时,原式= - 3.[解题策略]化简时,去括号可由里到外,也可由外到里,还可以内外同时进行,然后再求值.专题二隐含条件求值法【专题分析】先通过隐含条件将字母的值求出,然后化简求值.若单项式x m+2y与单项式- 3x3y2n的和是一个单项式,求m+n的值.〔解析〕两个单项式能合并成一个单项式,说明这两个单项式是同类项.由同类项的定义可求得m和n的值,从而求出它们的和.解:由题意得m+2=3,2n=1,所以m=1,n=,所以m+n=.[解题策略]两个单项式能合并成一个单项式,隐含着这两个单项式为同类项的条件,同类项中相同字母的指数是相同的.【针对训练2】已知m,x,y满足:①(x - 5)2+|m|=0;②- 2ab y+1与4ab3是同类项.求代数式(2x2 - 3xy+6y2) - m(3x2 - xy+9y2)的值.〔解析〕因为(x - 5)2+|m|=0,所以(x - 5)2=0,|m|=0,又因为- 2ab y+1与4ab3是同类项,所以y+1=3.解:由题意可知(x - 5)2=0,|m|=0,所以x=5,m=0,又因为- 2ab y+1与4ab3是同类项,所以y+1=3,即y=2,将x=5,m=0,y=2代入代数式得(2x2 - 3xy+6y2) - m(3x2 - xy+9y2)=44.[解题策略]两个非负数的和为0时,每一个数都应为0,从而求出隐含条件中的x,m的值.专题三整体代入法及拆项构造法【专题分析】不求字母的值,将所求代数式变形成与已知条件有关的式子,如倍数关系、和差关系等.已知x2+xy=2,y2+xy=5,求x2+xy+y2的值.〔解析〕由x2+xy=2,y2+xy=5,我们很难求出x,y的值,所以把x2+xy,y2+xy分别看成一个整体,试着把x2+xy+y2变成与上面代数式有关的式子,即x2+xy+xy+y2=(x2+xy)+(xy+y2).解:x2+xy+y2=x2+xy+xy+y2=(x2+xy)+(xy+y2),当x2+xy=2,y2+xy=5时,原式=×2+×5=.[解题策略]变形时,xy拆成两项,从而构成与已知有关的式子,为整体代入提供了条件.【针对训练3】如果a2+ab=8,ab+b2=9,求a2 - b2的值.〔解析〕先将a2 - b2变形为a2+ab - ab - b2=(a2+ab) - (ab+b2),再进行计算.解:a2 - b2=a2+ab - ab - b2=(a2+ab) - (ab+b2)=8 - 9= - 1.[解题策略]为构造a2+ab与ab+b2的形式,在a2 - b2中间加上了ab,又减去ab,让所求的代数式中出现a2+ab与ab+b2的形式,再整体代入,从而计算出结果.专题四代数式的值为定值【专题分析】无论字母取何值,代数式的值不变,即代数式化简后,不含带有字母的项.若代数式(2x2+ax - y+b) - (2bx2 - 3x+5y - 1)的值与字母x的取值无关,求代数式3(a2 - ab - b2) - (4a2+ab+b2)的值.〔解析〕代数式(2x2+ax - y+b) - (2bx2 - 3x+5y - 1)的值与字母x的取值无关,说明合并同类项后不含带有x的项,也就是说凡是含有字母x的同类项合并后,系数为0.解:(2x2+ax - y+b) - (2bx2 - 3x+5y - 1)=2x2+ax - y+b - 2bx2+3x - 5y+1=(2 - 2b)x2+(a+3)x - 6y+b+1.由题意可知2 - 2b=0,a+3=0,所以b=1,a= - 3,所以3(a2 - ab - b2) - (4a2+ab+b2)=3a2 - 3ab - 3b2 - 4a2 - ab - b2= - a2 - 4b2 - 4ab= - 1.【针对训练4】有一道题目:当a=2,b= - 2时,求代数式3a3b3- a2b+b- 4a3b3- a2b- b2+a3b3+a2b- 2b2- 3的值.甲同学做题时把“a=2”错抄成“a= - 2”,乙同学没抄错题,且其他解题过程均正确,但他们做出的结果却一样.你说这是怎么回事呢?〔解析〕a的取值抄错了,还可以求出正确结果,说明这个代数式的值与字母a的取值无关.解:原式=3a3b3 - a2b+b - 4a3b3+a2b+b2+a3b3+a2b - 2b2 - 3= - b2+b - 3.此代数式经化简后不含字母a,即它的值与a的取值无关,所以甲同学把a的值抄错不会影响最后的结果.专题五探索图形拼接的规律【专题分析】近几年的中考中,涉及实际问题的考题比较多,而探索规律则是近年来中考命题的热点之一.一张正方形的桌子可坐4人,按照如图所示的方式将桌子拼在一起,回答下列问题.(1)两张桌子拼在一起可以坐几人?三张桌子拼在一起可以坐几人?n张桌子拼在一起可以坐几人?(2)一家酒楼有60张这样的正方形桌子,按如图所示的方式每4张拼成一张大桌子,则60张桌子可以拼成15张大桌子,共可坐多少人?(3)在(2)中若每4张桌子拼成一张大的正方形桌子,共可坐多少人?(4)对于这家酒楼,(2),(3)中哪种拼桌子的方式能使坐的人更多?〔解析〕根据图形的变化发现每加一张桌子,可以多坐2人,进而得到规律.解:(1)两张桌子拼在一起可以坐6人,三张桌子拼在一起可坐8人.每加一张桌子,可以多坐2人,则n张桌子拼在一起可以坐4+2(n - 1)=2n+2(人).(2)4张桌子拼在一起可以坐2×4+2=10(人),则60张桌子拼成15张大桌子后可以坐10×15=150(人).(3)易知每4张桌子拼成一张大的正方形桌子可以坐8人,则60张桌子总共可以坐8×15=120(人).(4)对于这家酒楼,(2)中拼桌子的方式能使坐的人更多.[解题策略]对实际问题要有数学建模思想,用适当的图形直观表达题意,为寻找规律带来方便.本题考查对于图形变化中的规律的总结能力,通过观察发现每加一张桌子,可以多坐2人.【针对训练5】小明用棋子摆成图形来研究数的规律,如图所示,图(1)中的棋子摆成三角形,其颗数3,6,9,12……称为三角形数;类似地,图(2)中4,8,12,16……称为正方形数.下列所给的四个数中既是三角形数又是正方形数的是()A.2010B.2012C.2014D.2016〔解析〕观察发现,三角形数都是3的倍数,正方形数都是4的倍数,所以既是三角形数又是正方形数的一定是12的倍数,然后对各选项进行计算判断即可.因为2010÷12=167……6,2012÷12=167……8,2014÷12=167……10,2016÷12=168,所以2016既是三角形数又是正方形数.故选D.。

北师大七年级上册第三章整式的加减导学案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN明德中学学生自主导学案 学习导学案 课 题 整式的加减（3）【学习目标】1．经历字母表示数量关系的过程，发展符号感。

2．会进行整式加减的运算，并能说明其中的算理，发展有条理的思考及语言表达能力。

【重点难点】教学重点：会进行整式加减的运算，并能说明其中的算理。

教学难点：正确地去括号、合并同类项及符号的正确处理。

【知识链接】 什么是合并同类项去括号是应该注意什么 【学法指导和使用说明】 利用自主课堂预习课本知识并完成导学案的第一部分，将预习中不能解决的问题标出来并记录下来。

【学习流程】 第一部分 一、课前练习1．填空：整式包括 和 。

2．单项式的系数是 、次数是 。

3．多项式3m 3− 2m −5+m 2是 次 项式，其中二次项系数是 ，一次项是 ，常数项是 。

4．下列各式，是同类项的一组是（ ）(A)22x 2y 与231yx (B) 2m 2n 与2mn 2 (C)ab 32与abc 5．去括号后合并同类项：(3a −b)+(5a+2b)−(7a+4b) =第二部分二、合作探究整式的加减 装订 线班 级： 组 别： 姓 名：学案编号： 编 写： 备课组长： 编写时间： 审 核：上课时间：1．如果用a 、b 分别表示一个两位数的十位数字和个位数字，那么这个两位数可以表示为 ，交换这个两位数的十位数字和个位数字后得到的两位数为____________，这两个两位数的和为_______________。

要点记录：2．如果用a 、b 、c 分别表示一个三位数的百位数字、十位数字和个位数字，那么这个三位数可以表示为 ，交换这个三位数的百位数字和个位数字后得到的三位数为_______；这两个三位数的差为________________。

●议一议：在上面的两个问题中，分别涉及到了整式的什么运算？说说你是如何运算的？▲归纳：一般地，几个整式相加减，如果有括号就然后再 。