奥数-初中数学竞赛辅导-多边形

【导语】奥林匹克数学竞赛或数学奥林匹克竞赛，简称奥数。

奥数对青少年的脑⼒锻炼有着⼀定的作⽤，可以通过奥数对思维和逻辑进⾏锻炼，对学⽣起到的并不仅仅是数学⽅⾯的作⽤，通常⽐普通数学要深奥⼀些。

下⾯是为⼤家带来的初⼀年级奥数知识点：多边形的内⾓和与外⾓和，欢迎⼤家阅读。

⼀、多边形的知识点1.n边形有n个顶点、n条边、n个内⾓.2.在多边形的知识中,难点是对⾓线.从⼀个顶点可以引(n-3)条对⾓线,则从n个顶点可引n(n-3)条.但是,从"这⼀点引向另⼀点"与"由另⼀点引向这⼀点"重复,所以,n边形共有n(n-3)/2条对⾓线.⼆、多边形的内⾓和定理多边形的内⾓和等于(n-2)·180°(n为多边形的边数).我们可以看到,内⾓和随着边数的变化⽽变化.边数每增加1,内⾓和就增加180°.试题分析：(1)①利⽤了四边形内⾓和为360°和直⾓三⾓形的性质求解;②根据三⾓形的外⾓等于与它不相邻的两个内⾓和求解;③根据①②可以直接写出结果;(2)根据(1)中所求得出各图形内⾓和的变化情况;(3)根据(1)中所求得出各图形内⾓和的变化情况.试题解析：(1)①∵四边形的内⾓和为360°，直⾓三⾓形中两个锐⾓和为90°∴∠1+∠2=360°-(∠A+∠B)=360°-90°=270°.∴∠1+∠2=270°.②∠1+∠2=180°+40°=220°，故答案是：220°;③∠1+∠2与∠A的关系是：∠1+∠2=180°+∠A;故答案为：∠1+∠2=∠A+180°;(2)如果剪去三⾓形的两个⾓，将它变成⼀个五边形时，剪去的两个⾓加上360°等于新⾓的和;剪去三⾓形的三个⾓，将它变成⼀个六边形时，剪去的三个⾓加上540°等于新⾓的和;(3)将四边形剪去⼀个⾓变成五边形，剪去的1个⾓加上180°等于新⾓的和;剪去两个⾓变成六边形，剪去的2个⾓加上360°等于新⾓的和;剪去三个⾓变成七边形，剪去的3个⾓加上540°等于新⾓的和与(2)中的相同.。

多边形在同一平面内，由一些线段首尾顺次相接组成的图形叫做多边形。

如果延长多边形的任一条边，整个多边形都在这条延长边的一侧，那么这样的多边形就叫做凸多边形。

下面所说的多边形均指凸多边形。

它的重要性质是：几边形的内角和是，由于这个结论与边数有关，所以这不是对多边形的最本质的刻划。

更加本质的是它的推论：任意多边形的外角和等于。

多边形中通过连结对角线中把多边形就分割为若干个三角形，这就把研究多边形的问题转化为研究三角形的问题，这是一种重要的研究思路，请读者在下面的解题过程中认真体会这种思路。

例1已知多边形的内角和是外角和的3倍，求这个多边形的边数。

思路设多边数的边数为n，然后通过已知条件列出n的方程，再求出n值。

解设这个多边形的边数为n，根据题意得解之得 n=8答：这个多边形的边数为8说明本题通过设边数为n，然后依题意列出n的方程，再求出n值。

这是运用方程的思想解几何题。

这种思想方法今后还会经常用到。

例2一个多边形的每个内角都等于，求这个多边形的边数。

思路1 利用多边形的内角和定理。

解法1 设这个多边形的边数为n，根据题意得解之得n=10思路2 利用多边形的外角和定理。

解法 2 因为这个多边形的每个内角都等于，所以每个外角都等于，而多边形的外角和是，所以这个多边形的边数是.说明当你们学习了解法1和解法2后，你们心里产生了怎样的想法呢？显然，解法1比较传统，解法2则标新立异，这就启发我们解题时选择恰当的出发点是多么重要。

例3一个多边形除了一个内角之外的所有内角和等于，求这个多边形的边数和这个内角的度数。

思路利用多边形的内角和定理。

解设这个多边形的边数为n，这个内角的度数为X，根据题意有.又解之得又由n是正整数得n=14说明在解题中要重视对题目隐含条件的发掘和利用。

如本题中的x取值范围是。

n是正整数等。

例4 求证：n边形的内角中，最多有3个锐角。

思路1 用反证法.证法1 假设n边形至少有4个锐角，取出4个锐角之后剩下的角记为，，，则有，得那么，，中至少有一个大于，而这与，，中的每一个都小于180矛盾。

2024年初二数学竞赛辅导计划样本为了提升学生在数学竞赛中的表现，增强其知识掌握的深度与广度，并且为优秀学生提供更加广阔的发展空间，以及展现其特殊才能，本学校决定举办七年级数学竞赛。

此项活动旨在培养数学领域的杰出人才，同时结合我校的具体情况，激发七年级学生对数学学习的热情，并营造积极的学习氛围，进一步奠定和提升我校起始年级数学教学的质量。

竞赛的参与对象为全体七年级学生，旨在培养以下能力：踏实认真的学习态度及吃苦耐劳的精神；勇于拼搏并具有竞争意识；思维敏捷以及快速解题的能力。

辅导工作将由初一年级的数学教师负责，利用每天下午第七节自习课的时间进行。

辅导地点定在七年级各班级教室。

辅导方式将结合集中辅导与个别辅导。

具体的辅导措施包括：1. 重视基础知识的训练，确保辅导内容与课本紧密结合，按照由浅入深、由易到难、由简到繁的顺序逐步深入，适时联系课本内容。

2. 在不脱离课本的基础上，适度扩展知识深度，教师需要基于课本内容进行延伸和拓宽，介绍新的知识。

3. 对竞赛题目进行精细讲解，激发学生的思维。

数学竞赛能够多方面培养学生的观察力、归纳能力和类比能力，为学生提供展示才华和发展智力的机会。

4. 授课时力求“一题多法”、“一法多题”、“一题多变”，以训练思维方法为主，突出数学模型的构建、基本解题思路及题目的重点和难点。

5. 设计专题训练，帮助学生掌握知识。

竞赛题目虽然难度大且具有创新性，但源于课本且高于课本，离不开基础知识和特有的思维规律。

因此，辅导中需要确定专题进行讲授和训练。

指导教师在设计专题时应注意题目的梯度和新鲜感，以真正达到培养能力的目的。

本通知由一三四团第一中学发布，具体日期请填写。

2024年初二数学竞赛辅导计划样本（二）针对初二数学辅导教学之浅见初二的学生往往面临学习上的分化和挑战，成绩相对落后的学生可能会对数学产生恐惧感，进而导致自信心的丧失，形成恶性循环。

要打破这一现状，除了改进教学方法之外，还需要深入探讨学习方法。

初中数学竞赛辅导资料为（46）完全平方数和完全平方式甲内容提要一定义1. 如果一个数恰好是某个有理数的平方，那么这个数叫做完全平方数.例如0，1，0.36，254，121都是完全平方数. 在整数集合里，完全平方数，都是整数的平方.2. 如果一个整式是另一个整式的平方，那么这个整式叫做完全平方式.如果没有特别说明，完全平方式是在实数范围内研究的.例如：在有理数范围 m 2, (a+b －2)2, 4x 2－12x+9, 144都是完全平方式.在实数范围 （a+3）2, x 2+22x+2, 3也都是完全平方式.二. 整数集合里，完全平方数的性质和判定1. 整数的平方的末位数字只能是0，1，4，5，6，9.所以凡是末位数字为2，3，7，8的整数必不是平方数.2. 若n 是完全平方数，且能被质数p 整除, 则它也能被p 2整除..若整数m 能被q 整除，但不能被q 2整除, 则m 不是完全平方数.例如：3402能被2整除，但不能被4整除，所以3402不是完全平方数.又如：444能被3整除，但不能被9整除，所以444不是完全平方数.三. 完全平方式的性质和判定在实数范围内如果 ax 2+bx+c (a ≠0)是完全平方式，则b 2－4ac=0且a>0；如果 b 2－4ac=0且a>0；则ax 2+bx+c (a ≠0)是完全平方式.在有理数范围内当b 2－4ac=0且a 是有理数的平方时，ax 2+bx+c 是完全平方式.四. 完全平方式和完全平方数的关系1. 完全平方式（ax+b ）2 中当a, b 都是有理数时, x 取任何有理数，其值都是完全平方数；当a, b 中有一个无理数时，则x 只有一些特殊值能使其值为完全平方数.2. 某些代数式虽不是完全平方式，但当字母取特殊值时，其值可能是完全平方数. 例如： n 2+9, 当n=4时，其值是完全平方数.所以，完全平方式和完全平方数，既有联系又有区别.五. 完全平方数与一元二次方程的有理数根的关系1. 在整系数方程ax 2+bx+c=0(a ≠0)中① 若b 2－4ac 是完全平方数，则方程有有理数根；② 若方程有有理数根，则b 2－4ac 是完全平方数.2. 在整系数方程x 2+px+q=0中① 若p 2－4q 是整数的平方，则方程有两个整数根；② 若方程有两个整数根，则p 2－4q 是整数的平方.乙例题例1. 求证：五个连续整数的平方和不是完全平方数.证明：设五个连续整数为m －2, m －1, m, m+1, m+2. 其平方和为S.那么S ＝（m －2）2＋（m －1）2＋m 2＋（m+1）2＋（m+2）2＝5（m 2+2）.∵m 2的个位数只能是0，1，4，5，6，9∴m 2+2的个位数只能是2，3，6，7，8，1∴m 2+2不能被5整除.而5（m 2+2）能被5整除，即S 能被5整除，但不能被25整除.∴五个连续整数的平方和不是完全平方数.例2 m 取什么实数时，（m －1）x 2+2mx+3m －2 是完全平方式？解：根据在实数范围内完全平方式的判定，得当且仅当⎩⎨⎧>-010m △＝时，（m －1）x 2+2mx+3m －2 是完全平方式 △=0，即（2m ）2－4(m －1)(3m －2)=0.解这个方程， 得 m 1=0.5, m 2=2.解不等式 m －1>0 ， 得m>1.即⎩⎨⎧>==125.0m m m 或 它们的公共解是 m=2.答：当m=2时，（m －1）x 2+2mx+3m －2 是完全平方式.例3. 已知： (x+a)(x+b)+(x+b)(x+c)+(x+c)(x+a)是完全平方式.求证： a=b=c.证明：把已知代数式整理成关于x 的二次三项式，得原式＝3x 2+2(a+b+c)x+ab+ac+bc∵它是完全平方式，∴△＝0.即 4(a+b+c)2－12(ab+ac+bc)=0.∴ 2a 2+2b 2+2c 2－2ab －2bc －2ca=0,(a －b)2+(b －c)2+(c －a)2=0.要使等式成立，必须且只需：⎪⎩⎪⎨⎧=-=-=-000a c c b b a解这个方程组，得a=b=c.例4. 已知方程x 2－5x+k=0有两个整数解，求k 的非负整数解.解：根据整系数简化的一元二次方程有两个整数根时，△是完全平方数.可设△= m 2 (m 为整数)，即（－5）2－4k=m 2 (m 为整数)，解得，k=4252m -. ∵ k 是非负整数，∴ ⎪⎩⎪⎨⎧-≥-的倍数是42502522m m 由25－m 2≥0， 得 5≤m ， 即－5≤m ≤5；由25－m 2是4的倍数，得 m=±1, ±3, ±5.以 m 的公共解±1, ±3, ±5，分别代入k=4252m -. 求得k= 6, 4, 0.答：当k=6, 4, 0时，方程x 2－5x+k=0有两个整数解例5. 求证：当k 为整数时，方程4x 2+8kx+(k 2+1)=0没有有理数根.证明： （用反证法）设方程有有理数根，那么△是整数的平方.∵△＝（8k ）2－16(k 2+1)＝16（3k 2－1）.设3k 2－1＝m 2 (m 是整数).由3k 2－m 2＝1，可知k 和m 是一奇一偶，下面按奇偶性讨论3k 2＝m 2＋1能否成立.当k 为偶数，m 为奇数时，左边k 2是4的倍数，3k 2也是4的倍数；右边m 2除以4余1，m 2＋1除以4余2.∴等式不能成立.； 当k 为奇数，m 为偶数时，左边k 2除以4余1，3k 2除以4余3右边m 2是4的倍数，m 2＋1除以4余1∴等式也不能成立.综上所述，不论k, m 取何整数，3k 2＝m 2＋1都不能成立.∴3k 2－1不是整数的平方， 16（3k 2－1）也不是整数的平方.∴当k 为整数时，方程4x 2+8kx+(k 2+1)=0没有有理数根丙练习461. 如果m 是整数，那么m 2+1的个位数只能是＿＿＿＿.2. 如果n 是奇数，那么n 2－1除以4余数是＿＿，n 2+2除以8余数是＿＿＿，3n 2除以4的余数是＿＿.3. 如果k 不是3的倍数，那么k 2－1 除以3余数是＿＿＿＿＿.4. 一个整数其中三个数字是1，其余的都是0，问这个数是平方数吗？为什么？5. 一串连续正整数的平方12，22，32，………，1234567892的和的个位数是＿＿.（1990年全国初中数学联赛题）6. m 取什么值时，代数式x 2－2m(x －4)－15是完全平方式？7. m 取什么正整数时，方程x 2－7x+m=0的两个根都是整数？8. a, b, c 满足什么条件时,代数式(c －b)x 2+2(b －a)x+a －b 是一个完全平方式？9. 判断下列计算的结果，是不是一个完全平方数：① 四个连续整数的积； ②两个奇数的平方和.10. 一个四位数加上38或减去138都是平方数，试求这个四位数.11. 已知四位数aabb 是平方数，试求a, b.12. 已知：n 是自然数且n>1. 求证：2n －1不是完全平方数.13. 已知：整系数的多项式4x 4+ax 3+13x 2+bx+1 是完全平方数，求整数a 和b 的值.14. 已知：a, b 是自然数且互质，试求方程x 2－abx+21(a+b)=0的自然数解. (1990年泉州市初二数学双基赛题)15.恰有35个连续自然数的算术平方根的整数部分相同，那么这个整数是( )(A) 17 (B) 18 (C) 35 (D) 36(1990年全国初中数学联赛题)。

多边形的面积奥数题《多边形的面积奥数题：一场奇妙的数学之旅》嘿，你知道吗？数学就像一个神秘的大宝藏，里面有好多好多有趣的东西呢。

多边形的面积奥数题呀，就像是这个宝藏里特别闪亮的宝石。

我记得有一次，老师在黑板上写了一道多边形面积的奥数题。

那道题就像一个小怪兽，看起来有点吓人。

题目是这样的：有一个不规则的六边形，给了我们几条边的长度，还有几个角的度数，让我们求这个六边形的面积。

我当时就想，哎呀，这可怎么算呀？这六边形歪歪扭扭的，又不是我们学过的那种规规矩矩的图形。

我同桌可积极了，他眼睛亮晶晶的，就像发现了新大陆一样。

他说：“咱们可以把这个六边形分成几个三角形呀。

”我一听，有点懵，就问他：“咋分呢？这又不是随随便便就能分的。

”他就拿起笔，在图形上比划着说：“你看，从这个顶点到那个顶点画一条线，这样就分成了一个三角形和一个五边形，然后再把五边形继续分。

”我看着他画的线，心里还是有点迷糊。

这时候，后面的学霸同学说话了：“你这样分太麻烦啦。

咱们可以找特殊的点，利用角和边的关系，用更巧妙的方法分。

”我赶紧转过头去，眼睛里充满了好奇，就像一只小馋猫看到了鱼一样，我说：“快说说，啥巧妙方法呀？”学霸同学笑了笑，然后在图形上又画了几条线，说：“我们可以把这个六边形补成一个大的长方形，然后用长方形的面积减去周围几个小三角形的面积，这样不就简单多了嘛。

”我和同桌都张大了嘴巴，就像看到了魔法一样。

这时候，我就想，哇，数学还能这么玩呢。

还有一道奥数题也特别有趣。

是一个四边形，只给了两条对角线的长度，还有它们相交的角度，让我们求四边形的面积。

我想了半天，感觉无从下手。

这时候，我们小组讨论起来了。

有个同学说：“这对角线就像交叉的树枝一样，是不是可以用它们做点文章呢？”另一个同学接着说：“我觉得可以把四边形分成四个三角形，然后用三角形面积公式试试。

”可是大家算了半天，发现还是很复杂。

这时候，老师走过来了，老师说：“同学们，你们有没有想过一种特殊的公式呀？对于这种只知道对角线和夹角求四边形面积的题，有个公式是面积等于对角线乘积的一半再乘以夹角的正弦值。

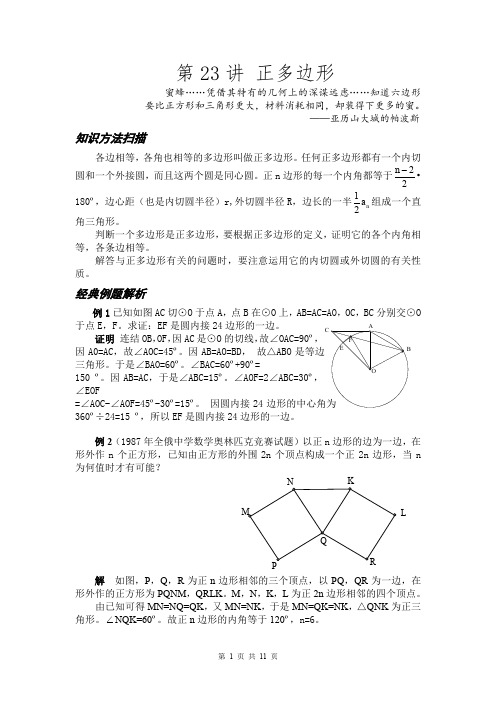
第23讲 正多边形蜜蜂……凭借其特有的几何上的深谋远虑……知道六边形要比正方形和三角形更大，材料消耗相同，却装得下更多的蜜。

——亚历山大城的帕波斯知识方法扫描各边相等，各角也相等的多边形叫做正多边形。

任何正多边形都有一个内切圆和一个外接圆，而且这两个圆是同心圆。

正n 边形的每一个内角都等于22n •180º，边心距（也是内切圆半径）r,外切圆半径R ，边长的一半12n a 组成一个直角三角形。

判断一个多边形是正多边形，要根据正多边形的定义，证明它的各个内角相等，各条边相等。

解答与正多边形有关的问题时，要注意运用它的内切圆或外切圆的有关性质。

经典例题解析例1已知如图AC 切⊙O 于点A ，点B 在⊙O 上，AB=AC=AO ，OC ，BC 分别交⊙O于点E ，F 。

求证：EF 是圆内接24边形的一边。

证明 连结OB ，OF ，因AC 是⊙O 的切线，故∠OAC=90º，因A0=AC ，故∠AOC=45º。

因AB=AO=BD ， 故△ABO 是等边三角形。

于是∠BAO=60º。

∠BAC=60º+90º=150 º。

因AB=AC ，于是∠ABC=15º。

∠AOF=2∠ABC=30º，∠EOF=∠AOC-∠AOF=45º-30º=15º。

因圆内接24360º÷24=15 º，所以EF 是圆内接24边形的一边。

例2（1987年全俄中学数学奥林匹克竞赛试题）以正n 边形的边为一边，在形外作n 个正方形，已知由正方形的外围2n 个顶点构成一个正2n 边形，当n 为何值时才有可能？L解 如图，P ，Q ，R 为正n 边形相邻的三个顶点，以PQ ，QR 为一边，在形外作的正方形为PQNM ，QRLK 。

M ，N ，K ，L 为正2n 边形相邻的四个顶点。

由已知可得MN=NQ=QK ，又MN=NK ，于是MN=QK=NK ，△QNK 为正三角形。

中考数学复习考点知识与题型专题讲解专题14 多边形【知识要点】多边形的相关知识：➢ 在平面中，由一些线段首尾顺次相接组成的图形叫做多边形，多边形中相邻两边组成的角叫做它的内角。

多边形的边与它邻边的延长线组成的角叫做外角。

➢ 连接多边形不相邻的两个顶点的线段叫做多边形的对角线。

➢ 一个n 边形从一个顶点出发的对角线的条数为（n －3）条，其所有的对角线条数为2)3( n n凸多边形 ：画出多边形的任何一条边所在的直线，如果多边形的其它边都在这条直线的同侧，那么这个多边形就是凸多边形。

正多边形 ：各角相等，各边相等的多边形叫做正多边形。

（两个条件缺一不可，除了三角形以外，因为若三角形的三内角相等，则必有三边相等，反过来也成立）⏹ 多边形的内角和➢ n 边形的内角和定理：n 边形的内角和为(n −2)∙180°➢ n 边形的外角和定理：多边形的外角和等于360°，与多边形的形状和边数无关。

【考查题型】考查题型一多边形截角后的边数问题【解题思路】多边形减去一个角的方法可能有三种：经过两个相邻点，则少了一条边；经过一个顶点和一边，边数不变；经过两条邻边，边数增加一条.典例1．（2018·云南昭通市模拟）把一个多边形纸片沿一条直线截下一个三角形后，变成一个18边形，则原多边形纸片的边数不可能是（）A．16B．17C．18D．19【答案】A【详解】一个n边形剪去一个角后，剩下的形状可能是n边形或（n+1）边形或（n-1）边形．故当剪去一个角后，剩下的部分是一个18边形，则这张纸片原来的形状可能是18边形或17边形或19边形，不可能是16边形.故选A.变式1-1．（2021·宁波市一模）把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是()A．六边形B．五边形C．四边形D．三角形【答案】A【解析】当剪去一个角后，剩下的部分是一个四边形，则这张纸片原来的形状可能是四边形或三角形或五边形，不可能是六边形.故选A.考查题型二计算多边形的周长【解题思路】考查多边形的周长，解题在于掌握计算公式典例2．（2021·隆化县模拟）下列图形中，周长不是32 m的图形是( )A．B．C．D．【答案】B【提示】根据所给图形，分别计算出它们的周长，然后判断各选项即可．【详解】A. L=(6+10)×2=32，其周长为32.B. 该平行四边形的一边长为10，另一边长大于6，故其周长大于32.C. L=(6+10)×2=32，其周长为32.D. L=(6+10)×2=32，其周长为32.采用排除法即可选出B故选B.变式2-1．（2017·海南中考模拟）如图，□ABCD纸片，∠A=120°，AB=4，BC=5，剪掉两个角后，得到六边形AEFCGH ,它的每个内角都是120°，且EF=1，HG=2，则这个六边形的周长为( )A．12B．15C．16D．18【答案】B【解析】如图，分别作直线AB、BC、HG的延长线和反向延长线使它们交于点B、Q、P.∵六边形ABCDEF的六个角都是120°，∴六边形ABCDEF的每一个外角的度数都是60°.∴△APH、△BEF、△DHG、△CQG都是等边三角形．∴EF=BE=BF=1，DG=HG=HD=2.∴FC=5-1=4，AH=5-2= 3，CG=CD-DG=4−2=2.∴六边形的周长为1+3+3+2+2+4=15.故选B.考查题型三计算网格中的多边形面积【解题思路】利用分割法即可解决问题典例3．（2021·辽宁葫芦岛市模拟）如图是边长为1的正方形网格，A、B、C、D均为格点，则四边形的面积为()A ．7B ．10C ．152D ．8 【答案】A 【提示】利用分割法即可解决问题.【详解】解：S 四边形ABCD ＝3×4﹣12×2×1×2﹣12×1×3×2＝12﹣5＝7，故选：A ． 变式3-1．（2021·山东烟台市模拟）如图，在边长为1的小正方形网格中，△ABC 的三个顶点均在格点上，若向正方形网格中投针，落在△ABC 内部的概率是()A ．12B ．14C ．38D ．516【答案】D【提示】用正方形的面积减去四个易求得三角形的面积，即可确定△ABC 面积，用△ABC 面积除以正方形的面积即可.【详解】解：正方形的面积＝4×4＝16，三角形ABC 的面积＝11116434221222-⨯⨯-⨯⨯-⨯⨯＝5， 所以落在△ABC 内部的概率是516， 故选D ．变式3-2．（2021·江西九年级零模）如图，在边长为1的小正方形网格中，小正方形的顶点叫格点，以格点为顶点的多边形叫格点多边形图中①，②，③，④四个格点多边形的面积分别记为1234,,,,S S S S 下列说法正确的是（）A ．12S SB ．23S S =C ．124S S S +=D ．134S S S +=【答案】B【提示】根据题意判断格点多边形的面积，依次将1234S S S S 、、、计算出来，再找到等量关系．【详解】观察图形可得12342.5,3,3,6,S S S S ====∴23234,6S S S S S =+==，故选：B ．考查题型四 计算多边形对角线条数【解题思路】熟记n 边形从一个顶点出发可引出（n-3）条对角线是解答此题的关键．典例4．（2017·山东济南市·中考真题）一个多边形的内角和比其外角和的2倍多180°，则该多边形的对角线的条数是（ ）A ．12B ．13C ．14D ．15【答案】C【解析】解：根据题意，得：（n ﹣2）•180=360°×2+180°，解得：n=7．则这个多边形的边数是7，七边形的对角线条数为7(73)2⨯-=14，故选C ． 变式4-1．（2018·山东济南市·中考模拟）若凸n 边形的每个外角都是36°，则从一个顶点出发引的对角线条数是（ ）A ．6B ．7C ．8D ．9【答案】B【解析】360°÷36°=10，10−3=7.故从一个顶点出发引的对角线条数是7.故选：B.变式4-2．（2021·莆田市二模）从n边形的一个顶点出发可以连接8条对角线，则n （）A．8B．9C．10D．11【答案】D【提示】根据n边形从一个顶点出发可引出（n-3）条对角线，可得n-3=8，求出n的值即可．【详解】解：由题意得：n-3=8，解得n=11，故选：D．变式4-3．（2021·湖南长沙市模拟）已知一个正n边形的每个内角为120°，则这个多边形的对角线有（）A．5条B．6条C．8条D．9条【答案】D【提示】多边形的每一个内角都等于120°，则每个外角是60°，而任何多边形的外角是360°，则求得多边形的边数；再根据多边形一个顶点出发的对角线＝n﹣3，即可求得对角线的条数．【详解】解：∵多边形的每一个内角都等于120°，∴每个外角是60度，则多边形的边数为360°÷60°＝6，则该多边形有6个顶点，则此多边形从一个顶点出发的对角线共有6﹣3＝3条．∴这个多边形的对角线有12（6×3）＝9条，故选：D．变式4-4．（2021·广东茂名市·中考模拟）若一个多边形从同一个顶点出发可以作5条对角线，则这个多边形的边数为（）A．6B．7C．8D．9【答案】C【提示】可根据n边形从一个顶点引出的对角线有n-3条，即可求解．【详解】解：设这个多边形的边数为n，则n-3=5，解得n=8，故这个多边形的边数为8，故选：C．变式4-5．（2021·河北模拟）过某个多边形的一个顶点的所有对角线，将这个多边形分成7个三角形，则这个多边形是（）A．六边形B．七边形C．八边形D．九边形【答案】D【提示】根据n边形从一个顶点出发可引出（n-3）条对角线，可组成n-2个三角形，依此可得n的值．【详解】解：设这个多边形是n边形，由题意得，n-2=7，解得：n=9，即这个多边形是九边形，故选:D．考查题型五多边形内角和问题【解题思路】考查多边形的内角和公式，解题关键是牢记多边形的内角和公式．典例5．（2018·山东济宁市·中考真题）如图，在五边形ABCDE中，∠A+∠B+∠E=300°，DP,CP分别平分∠EDC、∠BCD，则∠P的度数是( )A．60°B．65°C．55°D．50°【答案】A【解析】根据五边形的内角和等于540°，由∠A+∠B+∠E=300°，可求∠BCD+∠CDE的度数，再根据角平分线的定义可得∠PDC 与∠PCD 的角度和，进一步求得∠P 的度数．解：∵五边形的内角和等于540°，∠A+∠B+∠E=300°，∴∠BCD+∠CDE=540°﹣300°=240°，∵∠BCD 、∠CDE 的平分线在五边形内相交于点O ，∴∠PDC+∠PCD=（∠BCD+∠CDE ）=120°，∴∠P=180°﹣120°=60°．故选A ．变式5-1．（2021·甘肃庆阳市·中考真题）如图，足球图片正中的黑色正五边形的内角和是( )．A ．180°B ．360°C ．540°D ．720°【答案】C【提示】根据多边形内角和公式2180()n -⨯︒即可求出结果．【详解】解：黑色正五边形的内角和为：5218540(0)-⨯︒=︒，故选C ．变式5-2．（2021·湖南湘西土家族苗族自治州·中考真题）已知一个多边形的内角和是1080°，则这个多边形是（ ）A ．五边形B ．六边形C ．七边形D ．八边形【答案】D【提示】根据多边形的内角和=（n ﹣2）•180°，列方程可求解.【详解】设所求多边形边数为n ，∴（n ﹣2）•180°＝1080°，解得n ＝8.故选D.考查题型六正多边形内角和问题【解题思路】掌握并能运用多边形内角和公式是解题的关键典例6．（2021·湖南怀化市·中考真题）若一个多边形的内角和为1080°，则这个多边形的边数为（）A．6B．7C．8D．9【答案】C【提示】设这个多边形的边数为n，由n边形的内角和等于180°（n﹣2），即可得方程180（n﹣2）=1080，解此方程即可求得答案：n=8．故选C．变式6-1．（2021·湖北宜昌市·中考真题）游戏中有数学智慧，找起点游戏规定：从起点走五段相等直路之后回到起点，要求每走完一段直路后向右边偏行．成功的招数不止一招，可助我们成功的一招是（）．A．每走完一段直路后沿向右偏72°方向行走B．每段直路要短C．每走完一段直路后沿向右偏108°方向行走D．每段直路要长【答案】A【提示】根据题意可知封闭的图形是正五边形，求出正五边形内角的度数即可解决问题．【详解】根据题意可知，从起点走五段相等直路之后回到起点的封闭图形是正五边形，∵正五边形的每个内角的度数为：(52)1801085-⨯︒=︒∴它的邻补角的度数为：180°-108°=72°，因此，每走完一段直路后沿向右偏72°方向行走，故选：A．变式6-2．（2021·河北中考真题）正六边形的一个内角是正n边形一个外角的4倍，则n=_________．【答案】12【提示】先根据外角和定理求出正六边形的外角为60°，进而得到其内角为120°，再求出正n边形的外角为30°，再根据外角和定理即可求解．【详解】解：由多边形的外角和定理可知，正六边形的外角为：360°÷6=60°，故正六边形的内角为180°-60°=120°，又正六边形的一个内角是正n边形一个外角的4倍，∴正n边形的外角为30°，∴正n边形的边数为：360°÷30°=12．故答案为：12．∠变式6-3．（2021·福建中考真题）如图所示的六边形花环是用六个全等的直角三角形拼成的，则ABC 等于_______度．【答案】30【提示】先证出内部的图形是正六边形，求出内部小正六边形的内角，即可得到∠ACB的度数，根据直角三角形的两个锐角互余即可求解．【详解】解：由题意六边形花环是用六个全等的直角三角形拼成，可得BD=AC，BC=AF，∴CD=CF，同理可证小六边形其他的边也相等，即里面的小六边形也是正六边形，∴∠1=()1621801206-⨯︒=︒， ∴∠2=180°-120°=60°，∴∠ABC=30°，故答案为：30．考查题型七 截角后的内角和问题【解题思路】剪掉一个多边形的一个角，则所得新的多边形的角可能增加一个，也可能不变，也可能减少一个是解决本题的关键．典例7．（2021·五莲县一模）一个正方形被截掉一个角后，得到一个多边形，这个多边形的内角和是（ ）A ．360°B ．540°C ．180°或360°D ．540°或360°或180°【答案】D【提示】剪掉一个多边形的一个角，则所得新的多边形的角可能增加一个，也可能不变，也可能减少一个，根据多边形的内角和定理即可求解．【详解】n 边形的内角和是(n ﹣2)•180°，边数增加1，则新的多边形的内角和是(4+1﹣2)×180°＝540°，所得新的多边形的角不变，则新的多边形的内角和是(4﹣2)×180°＝360°，所得新的多边形的边数减少1，则新的多边形的内角和是(4﹣1﹣2)×180°＝180°，因而所成的新多边形的内角和是540°或360°或180°，故选D ．变式7-1．（2021·河北九年级其他模拟）一个多边形截去一个角后，形成另一个多边形的内角和为2520°，则原多边形的边数是（ ）A ．17B ．16C ．15D ．16或15或17【答案】D【详解】多边形的内角和可以表示成()2180n -⋅︒ (3n ≥且n 是整数)，一个多边形截去一个角后，多边形的边数可能增加了一条，也可能不变或减少了一条，根据()21802520,n -⋅︒=解得：n=16，则多边形的边数是15，16，17．故选D ．变式7-2．（2021·贵州铜仁市·九年级零模）一个多边形切去一个角后得到的另一个多边形的内角和为900︒，那么原多边形的边数为（）A ．6或7或8B ．6或7C ．7或8D ．7【答案】A【提示】首先求得内角和为900°的多边形的边数，即可确定原多边形的边数.【详解】解：设内角和为900°的多边形的边数是n ，则（n-2）•180°=900°，解得：n=7，如图，有如下几种切法，则原多边形的边数为6或7或8．故选：A ．考查题型八 正多边形的外角问题【解题思路】解决问题的关键是掌握多边形的外角和等于360度．典例8．（2021·江苏无锡市·中考真题）正十边形的每一个外角的度数为（）A．36︒B．30C．144︒D．150︒【答案】A【提示】利用多边形的外角性质计算即可求出值．【详解】解：360°÷10＝36°，故选：A．变式8-1．（2021·江苏扬州市·中考真题）如图，小明从点A出发沿直线前进10米到达点B，向左转45︒后又沿直线前进10米到达点C，再向左转45︒后沿直线前进10米到达点D……照这样走下去，小明第一次回到出发点A时所走的路程为（）A．100米B．80米C．60米D．40米【答案】B【提示】根据题意，小明走过的路程是正多边形，先用360°除以45°求出边数，然后再乘以10米即可．【详解】解：∵小明每次都是沿直线前进10米后再向左转45︒，∴他走过的图形是正多边形，边数n=360°÷45°=8，∴小明第一次回到出发点A时所走的路程=8×10=80米．故选：B．变式8-2．（2021·湖南娄底市·中考真题）正多边形的一个外角为60°，则这个多边形的边数为（）A．5B．6C．7D．8【答案】B【提示】根据正多边形的外角和以及一个外角的度数，求得边数．【详解】解：正多边形的一个外角等于60°，且外角和为360°，则这个正多边形的边数是：360°÷60°=6，故选：B．考查题型九多边形外角和的实际应用【解题思路】典例9．（2021·湖北黄冈市·中考真题）如果一个多边形的每一个外角都是36°，那么这个多边形的边数是（）A．7B．8C．9D．10【答案】D【提示】根据多边形的外角的性质，边数等于360°除以每一个外角的度数．【详解】∵一个多边形的每个外角都是36°，∴n=360°÷36°=10．故选D．变式9-1．（2021·山东德州市·中考真题）如图，小明从A点出发，沿直线前进8米后向左转45°，再沿直线前进8米，又向左转45°……照这样走下去，他第一次回到出发点A时，共走路程为（）A．80米B．96米C．64米D．48米【答案】C【提示】根据多边形的外角和即可求出答案．【详解】解：根据题意可知，他需要转360÷45=8次才会回到原点，所以一共走了8×8=64米．故选：C考查题型十多边形内角和与外角和的综合应用【解题思路】熟悉多边形的内角和公式：n边形的内角和是（n-2）×180°；多边形的外角和是360度．典例10．（2021·西藏中考真题）一个多边形的内角和是外角和的4倍，则这个多边形的边数是（）A．8B．9C．10D．11【答案】C【提示】利用多边形的内角和公式及外角和定理列方程即可解决问题．【详解】设这个多边形的边数是n，则有（n-2）×180°=360°×4，所有n=10．故选C．变式10-1．（2021·陆丰市模拟）一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（）A．108°B．90°C．72°D．60°【答案】C【提示】首先设此多边形为n边形，根据题意得：180（n-2）=540，即可求得n=5，再由多边形的外角和等于360°，即可求得答案．【详解】解：设此多边形为n边形，根据题意得：180（n-2）=540，解得：n=5，∴这个正多边形的每一个外角等于：3605=72°．故选C．变式10-2．（2021·中江县模拟）已知一个多边形的每一个外角都相等，一个内角与一个外角的度数之比是3：1，这个多边形的边数是()A．8B．9C．10D．12【答案】A【解析】试题提示：设这个多边形的外角为x°，则内角为3x°，根据多边形的相邻的内角与外角互补可的方程x+3x=180，解可得外角的度数，再用外角和除以外角度数即可得到边数．解：设这个多边形的外角为x°，则内角为3x°，由题意得：x+3x=180，解得x=45，这个多边形的边数：360°÷45°=8，故选A．变式10-3．（2021·西宁市模拟）一个多边形的内角和比它的外角和的2倍还大180°，这个多边形的边数是（）A．5B．6C．7D．8【答案】C【解析】解：设这个多边形的边数是n，根据题意得，（n-2）•180°=2×360°+180°， n=7．故选C．考查题型十一平面镶嵌【解题思路】几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．典例11.下列多边形中，不能够单独铺满地面的是（）A．正三角形B．正方形C．正五边形D．正六边形【答案】C【提示】由镶嵌的条件知，在一个顶点处各个内角和为360°．【详解】∵正三角形的内角=180°÷3=60°，360°÷60°=6，即6个正三角形可以铺满地面一个点，∴正三角形可以铺满地面；∵正方形的内角=360°÷4=90°，360°÷90°=4，即4个正方形可以铺满地面一个点，∴正方形可以铺满地面；∵正五边形的内角=180°－360°÷5=108°，360°÷108°≈3.3，∴正五边形不能铺满地面；∵正六边形的内角=180°－360°÷6=120°，360°÷120°=3，即3个正六边形可以铺满地面一个点，∴正六边形可以铺满地面．故选C．变式11-1小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板，他购买的瓷砖形状不可能．．．是（）A．正三角形B．正方形C．正五边形D．正六边形【答案】C【提示】平面图形镶嵌的条件：判断一种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角，若能构成360，则说明能够进行平面镶嵌；反之则不能.【详解】解：因为用一种正多边形镶嵌，只有正三角形，正四边形，正六边形三种正多边形能镶嵌成一个平面图案，所以小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板，他购买的瓷砖形状不可以是正五边形.故选：C变式11-2．能够铺满地面的正多边形组合是（）A．正六边形和正方形B．正五边形和正八边形C．正方形和正八边形D．正三角形和正十边形【答案】C【解析】A、正六边形的每个内角是120°，正方形的每个内角是90°，120m+90n=360°，显然n取任何正整数时，m不能得正整数，故不能铺满；B、正五边形每个内角是180°-360°÷5=108°，正八边形每个内角为135度，135m+108n=360°，显然n 取任何正整数时，m不能得正整数，故不能铺满；C、正方形的每个内角为90°，正八边形的每个内角为135°，两个正八边形和一个正方形刚好能铺满地面；D、正三角形每个内角为60度，正十边形每个内角为144度，60m+144n=360°，显然n取任何正整数时，m不能得正整数，故不能铺满．故选C．变式11-3下列边长相等的正多边形能完成镶嵌的是（）A．2个正八边形和1个正三角形B．3个正方形和2个正三角形C．1个正五边形和1个正十边形D．2个正六边形和2个正三角形【答案】D【提示】只需要明确几个几何图形在一点进行平铺就是几个图形与这一点相邻的所有内角之和等于360°即可。

专题14多边形的边与角阅读与思考主要是指多边形的边、内外角、对角线、凸多边形、凹多边形等基本概念和多边形内角和定理、外角和定理，其中多边形内、外角和定理是解有关多边形问题的基础．多边形的许多性质与问题往往可以利用三角形来说明、解决，将多边形问题转化为三角形问题是解多边形问.题的基本策略，转化的方法是连对角线或向外补形．多边形的内角和是随着多边形的边数变化而变化的，但外角和却总是不变的，所以，我们常以外角和的“不变”来制约内角和的“变”，把内角问题转化为外角问题来处理，这是解多边形相关问题的常用技巧．例题与求解【例1】两个凸多边形，它们的边长之和为12，对角线的条数之和为19，那么这两个多边形的边数分别是＿＿＿＿和＿＿＿＿．（“希望杯”邀请赛试题）解题思路：设两个凸多边形分别有m，n条边，分别引出(3)2m m-，(3)2n n-条对角线，由此得m，n方程组．【例2】凸边形有且只有3个钝角，那么n的最大值是（）A．5B．6C．7D．8解题思路：运用钝角、锐角概念，建立关于n的不等式，通过求解不等式逼近求解．【例3】凸n边形除去一个内角外，其余内角和为2570°，求n的值．（山东省竞赛试题）解题思路：利用n边形内角和公式，以及边数n为大于等于3的自然数这一要求，推出该角大小，进而求出n的值．【例4】如图，凸八边形ABCDEFGH的八个内角都相等，边AB，BC，CD，DE，EF，FG的长分为7，4，2，5，6，2，求该八边形的周长．（全国通讯赛试题）解题思路：该八边形每一内角均为135°，每一外角为45°，可将八边形问题转化为特殊三角形解决、特殊四边形加以解决．A BCD EFGH【例5】如图所示，小华从M点出发，沿直线前进10米后，向左转20°，再沿直线前进10米后，又向左转20°，…这样走下去，他第一次回到出发地M时，行走了多少米？解题思路：试着将图形画完，你也许就知道答案了．20︒20︒20︒M能力训练A级1．如图，凸四边形有＿＿＿个；∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＝＿＿＿．（重庆市竞赛试题）ABCD EF G第1题ABCD第2题2．如图，凸四边形ABCD的四边AB，BC，CD和DA的长分别为3，4，12和13，∠ABC＝90°，则四边形ABCD 的面积为＿＿＿．3．如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝＿＿＿．A BC DE F G 第3题AB CD247x第4题第7题4．如图，ABCD 是凸四边形，则x 的取值范围是＿＿＿．.5．一个凸多边形的每一内角都等于140°，那么，从这个多边形的一个顶点出发的对角线的条数是（）A ．9条B ．8条C ．7条D ．6条（“祖冲之杯”邀请赛试题）6．—个凸n 边形的内角和小于1999°，那么n 的最大值是（）（全国初中联赛试题）A ．11B ．12C ．13D ．147．如图，是一个正方形桌面，如果把桌面砍下一个角后，桌面还剩（）个角．A ．5个B ．5个或3个C ．5个或3个或4个D ．4个8．—个凸n 边形，除一个内角外，其余1n 个内角的和为2400°，则n 的值是（）A ．15B ．16C ．17D ．不能确定9．如图，在四边形ABCD 中，AB ＝AD ＝8，∠A ＝60°，∠D ＝150°，四边形周长为32，求BC 和DC 的长．ABCD10．—个凸n 边形的最小内角为95°，其他内角依次增加10°，求n 的值．（“希望杯”邀请赛试题）11．平面上有A，B，C，D四点，其中任何三点都不在一直线上，求证：在△ABC，△ABD，△ACD，△BDC中至少有—个三角形的内角不超过45°．（江苏省竞赛试题）12．我们常见到如图那样图案的地面，它们分别是全用正方形或全用正六边形形状的材料铺成的，这样形状的材料能铺成平整的、无空隙的地面．问：（1）像上面那样铺地面，能否全用正五边形的材料，为什么？（2）你能不能另外想出一个用一种多边形（不一定是正多边形）的材料铺地的方案？把你想到的方案画成草图．（3）请你再画出一个用两种不同的正多边形材料铺地的草图．（安徽省中考试题）B级1．一个正m边形恰好被正n边形围住（无重叠、无间隙，如图所示是m＝4，n＝8的情况），若m ＝10，则n＝＿＿＿＿．第1题AB CDEF第2题1A1B2A2B3B4B5B3A4A5A第3题2．如图，六边形ABCDEF中，∠A＝∠B＝∠C＝∠D＝∠E＝∠F，且AB＋BC＝11，FA CD＝3，则BC＋DE＝＿＿＿＿．（北京市竞赛试题）3．如图，延长凸五边形A 1A 2A 3A 4A 5的各边相交得到五个角：∠B 1，∠B 2，∠B 3，∠B 4，∠B 5，它们的和等于＿＿＿．若延长凸n 边形（n ≥5）的各边相交，则得到的n 个角的和等于＿＿＿＿．（第十二届“希望杯”邀请赛试题）4．如图，在四边形ABCD 中，AB＝4BC ＝1，CD ＝3，∠B ＝135°，∠C ＝90°，则∠D ＝（）A ．60°B ．67.5°C ．75°D ．不能确定（重庆市竞赛试题）ABCD第4题O ABCD第5题5．如图，已知O 是四边形ABCD 内一点，OA ＝OB ＝OC ，∠ABC ＝∠ADC ＝70°，则∠DAO ＋∠DCO 的大小是（）A ．70°B ．110°C ．140°D ．150°6．在一个多边形中，除了两个内角外，其余内角之和为2002°，则这个多边形的边数为（）A ．12B ．12或13C ．14D ．14或15（江苏省竞赛试题）7．一个凸十一边形由若干个边长为1的正方形或正三角形无重叠、无间隙地拼成，求此凸十一边形各个内角大小，并画出这样的凸十一边形的草图．（全国通讯赛试题）8．一块地能被n 块相同的正方形地砖所覆盖，如果使用较小的相同正方形地砖，那么需n ＋76块这样的地砖才能覆盖该块地，已知n 及地砖的边长都是整数，求n 的值．（上海市竞赛试题）9．设有一个边长为1的正三角形，记作A1如下左图，将A1的每条边三等分，在中间的线段上各向形外作正三角形，去掉中间的线段后得到的图形记作A2（如下中图）；将A2的每条边三等分，并重复上述过程，所得到的图形记作A3（如下右图）；再将A3的每条边三等分，并重复上述过程，所得到的图形记作A4，求A4的周长．A2A3A1（全国初中数学联赛试题）10．在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案．也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠（在几何里叫作平面镶嵌），这显然与正多边形的内角大小有关，当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角（360°）时，就拼成了一个平面图形．（1）请根据下列图形，填写表中空格：正多边形边数3456…n正多边形每个内角的度数60°90°（2）如果限于用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？（3）从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用这两种不同的正多边形镶嵌成的一个平面图形（草图）；并探索这两种正多边形共能镶嵌成几种不同的平面图形．说明你的理由．专题14多边形的边与角例157例2B例3n ＝17提示：设此角为x ，则（n －2）×180°＝x ＋2570°，得2570360180x n +︒+︒=︒，x ＝130°，此时n ＝17.例4双向延长AB ，CD ，EF ，GH 得四边形MNPQ ，如图，原八边形的内角都相等，其每一内角均为(82)1801358-⨯︒=︒，每一外角均为45°，因此MNPQ 为长方形，△BPC ，△DQE ，△FMG ，△ANH .＝x ，，由MQ ＝MF＋FE ＋EQ ＝NA ＋AB ＋BP 5226722y +=++，∴3y =-∵MN ＝QP ，∴x ＝3＋，∴周长＝7＋4＋2＋5＋6＋2＋3＋＋3＝32＋.例5将整个图形画完，就知道是一个边长为10米的正多边形，且每个外角的大小都是20°，由多边形的外角和等于360°知这是一个18边形，所以小华第一次回到M 点时走的总路程是180米.A 级1.7；540°2.363.540°4.1＜x ＜135.D6.C7.C8.A9.BC ＝10，DC ＝610.n ＝611.提示：分构成凸四边形和凹四边形两种情况讨论，并用反证法加以证明推出矛盾.12.(1)所用材料的形状不能是正五边形,因为,正五边形的每个内角都是108°,要铺成平整的,无空隙的地面,必须使若干个正五边形拼成一个周角，但找不到符合条件的以n ×108°=360°的n 值,故不能用形状是正五边形的材料铺地面.⑵⑶略.B 级1.5 2.143.180°;(n －4)180°4.B5.D 由OA=OB=OC 得∠BAO=∠ABO,∠BCO=∠OBC,所以∠DAO+∠DCO=360°－3×70°=150°6.D7.提示：因凸十一边形由正方形或正三角形拼成，故其内角的大小只能是60°,90°,120°,\150°四种可能,设这些角的个数分别为x ,y ,z ,w ,则116090120150(112)180x y z w x y z w +++=⎧⎨+++=-⨯⎩解得x =y =0,z =1,w =10.说明这个十一边形一个内角为120°,由两个正三角形的内角拼成，其余10个角均为150°,由一个正三角形内角与一个正方形内角拼成,图略.8.n =3249.649提示：从A 1开始,每进行一次操作,所得到的图形的周长是原来图形周长的43倍.10.(1)108°;120°;()02180n n-⨯(2)正三角形、正四边形(或正方形)正六边形.假定在接合处一共有k 块正边形地砖，由于正n 边形的所有内角都相等，则()002180360n k n-⨯= 即24222n k n n ==+--.因k 为整数，故n －2|4，n —2=1，2，4，得n=3,4或6，由此可见，只有三种正多边形的瓷砖，可以按要求铺地，即正三角形、正方形和正六边形.(3)如:正方形和正八边形，草图如下，设在一个顶点周围有m 个正方形的角，n 个正八边形的角，那么，m ，n 应是方程m ·90°+n ·135°=360°的整数解.即2m +3n =8的整数解.∵这个方程的整数解只有12m n =⎧⎨=⎩一组∴符合条件的图形只有一种.。

第20讲多边形内切圆【例题讲解】例题1、已知Rt △ABC ，AB ＝4，BC ＝3，求内切圆⊙O 的半径.方法一：利用切线长定理方法二：面积法如图，OD ＝OE ＝BE ＝BD ＝r ∵S △AOB ＋S △AOC ＋S △BOC ＝S △ABC∴AD ＝AF ＝4－r ，CE ＝CF ＝3－r ∴21⋅4⋅r ＋21⋅5⋅r ＋21⋅3⋅r ＝21⋅3⋅4∴4－r ＋3－r ＝5解得r ＝1解得r ＝1利用切线长定理，可推导出直角三角形内切圆半径r ＝2cb a -+（a 、b 为直角边，C 为斜边）利用面积法，可推导出直角三角形内切圆半径r ＝CS2（S 为面积，C 为周长）例题2、如图，△ABC 中，AB ＝AC ＝5，BC ＝6，点P 在边AB 上，以P 为圆心的⊙P 分别与边AC 、BC 相切于点E 、F ，则⊙P 的半径PE 的长为.答案：2411.例题3、如图，AB 为半圆O 的在直径，AD 、BC 分别切⊙O 于A 、B 两点，CD 切⊙0于点E ，连接OD 、OC ，下列结论：①∠DOC ＝90°，②AD ＋BC ＝CD ，③S △A 0D :S △BOC ＝AD 2：AO 2，④OD :OC ＝DE :EC ，⑤0D 2＝DE ·CD ，正确的有（）A .2个B .3个C .4个D .5个答案：D.例题4、如图，△ABC中，∠C＝90°，AC＝8cm，AB＝10cm，点P由点C出发以每秒2cm的速度沿线段CA向点A运动（不运动至A点），⊙0的圆心在BP上，且⊙0分别与AB、AC相切于点E、D，当点P运动2秒钟时，⊙O的半径是（）A.712cmB.512cmC.35cmD.2cm答案：A.【巩固练习】1、如图，在Rt△ABC中，BC＝8，AC＝6，以斜边AB上一点0为圆心作半圆，使它与BC、AC都相切，切点分别为D、E，则⊙O的半径为.2、如图，⊙O是Rt△ABC的内切圆，切点为D、F、E，若CE、BF的长是方程x2－13x＋30＝0的两个根，则△ABC的面积是.3、如图，⊙O是四边形ABCD的内切圆，E、F、G、H是切点，点P是优弧EFH上异于E、H的点，若∠A＝50°，则∠EPH＝.4、如图，在Rt△ABC中，∠B＝90°，以其三边为直径向三角形外作三个半圆，正方形EFGH的各边cm.分别与半圆相切且平行于AB或BC，如果正方形EFGH的面积是144cm2，则Rt△ABC的周长是E）上任一点P作⊙O的切线MN与AB，BC分别交于点M，N，若⊙O的半径为r，则Rt△MBN的5、如图，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切于点D、E，过劣弧DE（不包括端点D，周长为（用r表示）6、如图，以正方形ABCD的BC边为直径作半圆O，过点D作直线切半圆于点F，交AB边于点E，则三角形ADE和直角梯形EBCD的周长比为.3AE，7、如图，矩形ABCD中，AD＝4，O是BC边上的点，以OC为半径作⊙0交AB于点E，BE＝5把四边形AECD沿着CE所在的直线对折（线段AD对应AD），当⊙0与A’D’相切时，线段AB的长是.8、如图，在矩形ABCD 中，AB ＝8，AD ＝12，过点A ，D 两点的⊙0与BC 边相切于点E ，则⊙0的半径为.9、如图，一个半径为r 的⊙O 与矩形ABCD 的两边AB 、BC 都相切，BC ＝4.若将矩形的边AD 沿AE 对折后和⊙O 相切于点D ’，折痕AE 的长为5，则半径r 的值为.10、如图，圆O 与正方形ABCD 的两边AB 、AD 相切，且DE 与圆O 相切于E 点.若圆O 的半径为5，且AB ＝11，则DE 的长度为.11、如图，Rt △ABC 中，∠C ＝90°，AB ＝5，AC ＝3，点E 在中线AD 上，以E 为圆心的OE 分别与AB 、BC 相切，则OE 的半径为（）.A .78B .67C .56D .112、如图，正方形ABCD 的边长为4，点E 是AB 上的一点，将△BCE 沿CE 折叠至△FCE ，若CF ，CE 恰好与以正方形ABCD 的中心为圆心的⊙0相切，则折痕CE 的长为.13、如图，⊙0切△ABC 的三边于D 、E 、F ，那么三角形DEF 是（）A .锐角三角形B .直角三角形C .钝角三角形D .以上都有可能14、如图，在矩形ABCD 中，AB ＝4，AD ＝5，AD 、AB 、BC 分别与⊙0相切于E 、F 、G 三点，过点D 作⊙O 的切线交BC 于点M ，切点为N ，则DM 的长为.15、如图，OA 在x 轴上，OB 在y 轴上，OA ＝8，AB ＝10，点C 在边OA 上，AC ＝2，⊙P 的圆心P在线段BC 上，且⊙P 与边AB ，AO 都相切.若反比例函数y ＝k x（k ≠0）的图象经过圆心P ，则k ＝.16、如图，PA ，PB 切⊙0于A 、B 两点，CD 切⊙0于点E ，交PA ，PB 于C ，D .若⊙0的半径为r ，△PCD 的周长等于3r ，则tan ∠APB 的值是（）A .51312B .125C .3135D .213317、将正方形ABCD 绕点A 按逆时针方向旋转30°，得正方形AB 1C 1D 1，B 1C 1交CD 于点E ，AB＝3，则四边形AB 1ED 的内切圆半径为（）A .312+B .332-C .313+D .333-18、如图，AC 是矩形ABCD 的对角线，⊙0是△ABC 的内切圆，现将矩形ABCD 按如图所示的方式折叠，使点D 与点O 重合，折痕为FG ，点F ，G 分别在AD ，BC 上，连结OG ，DG ，若OG ⊥DG ，且⊙O 的半径长为1，则下列结论不成立的是（）A .BC －AB ＝2B .BC ＋AB 3＋4C .CD －DF 3－3D .CD ＋DF ＝419、（1）已知：如图①，△ABC的周长为1，面积为S，其内切圆圆心为0，半径为r，求证：r＝2s l（2）已知：如图②，△ABC中A、B、C三点的坐标分别为A（－3，0），B（2，0），C（0，4），若△ABC内心为D，求点D的坐标；（3）与三角形的一边和其他两边的延长线相切的圆，叫旁切圆，圆心叫旁心，请求出条件（2）中的△ABC位于第一象限的旁心的坐标。