实验四-离散时间系统的频域分析(附思考题程序)
- 格式:doc
- 大小:201.50 KB
- 文档页数:4

实验四离散信号的频域分析1. 计算序列的DTFT和DFT,观察栅栏效应设)()(4nRnx=,要求用MATLAB实现:(1)计算)(nx的傅里叶变换)(ωj eX,并绘出其幅度谱;(2)分别计算)(nx的4点DFT和8点DFT,绘出其幅度谱。
并说明它们和)(ωj eX的关系。
(提示:DFT变换可用MA TLAB提供的函数fft实现,也可以自己用C语言或matlab 编写)源程序:n1=4;n2=8;n=0:n1-1;k1=0:n1-1;k2=0:n2-1;w=2*pi*(0:2047)/2048;Xw=(1-exp(-j*4*w))./(1-exp(-j*w))xn=[(n>=0)&(n<4)];X1k=fft(xn,n1);X2k=fft(xn,n2);subplot(3,1,1)plot(w/pi,abs(Xw));title('x(n)的傅里叶变换的幅度谱')subplot(3,1,2)stem(k1,abs(X1k))title('4点的DFT[x(n)]=X1(k)的幅度谱')subplot(3,1,3)stem(k2,abs(X2k))title('8点的DFT[x(n)]=X1(k)的幅度谱')实验结果图:由实验结果图可知,X(k)是)(ωj e X 的等间隔采样,采样间隔是2π/N 。
2.计算序列的FFT ,观察频谱泄漏已知周期为16的信号)1612cos()1610cos()(n n n x ππ+=。
(1) 截取一个周期长度M=16点,计算其16点FFT 其频谱,并绘出其幅度谱;(2) 截取序列长度M=10点,计算其16点FFT 其频谱,绘出其幅度谱,并与(1)的结果进行比较,观察频谱泄漏现象,说明产生频谱泄漏的原因。
(1)源程序:T=16;fs=1/T;n=0:15;xn=cos(10*pi/16*n*T)+cos(12*pi/16*n*T);Xk=fft(xn,16)stem(n,abs(Xk))实验结果图:(2)源程序:T=16;fs=1/T;n=0:9;xn=cos(10*pi/16*n*T)+cos(12*pi/16*n*T); Xk1=fft(xn,16)stem(0:15,abs(Xk1))实验结果图:如图,可得出,当截取有限长信号时,频谱不再是单一的频谱,它的能量散布到整个频谱的各处。
实验四 离散信号的频域分析一、 实验目的1. 掌握序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换的Matlab 实现;2.学习用FFT 对连续信号和离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT 。
二、 实验原理及方法1. 离散非周期信号的谱分析 (1) 序列的傅里叶变换对于满足绝对可和的序列,即∞<∑∞∞-|)(|n x ,其傅里叶变换和反变换的定义为∑∞-∞=-=n nj j en x e X ωω)()( (4.1)ωπωππωd eeX n x nj j ⎰-=)(21)( (4.2)序列)(n x 是离散的,但)(ωj e X 是以π2为周期的ω的连续函数,为了能够在计算机上处理,需要对)(n x 进行截断,对频域进行离散化,近似处理后21()()kk n j j nn n X ex n eωω-==∑(4.3)其中2k k Mπω=,M 是对ω在一个周期内的采样,k 的取值由读者确定,若想观察一个周期内的频谱,0~1k M =-,若观察两个周期,0~21k M =-,以此类推。
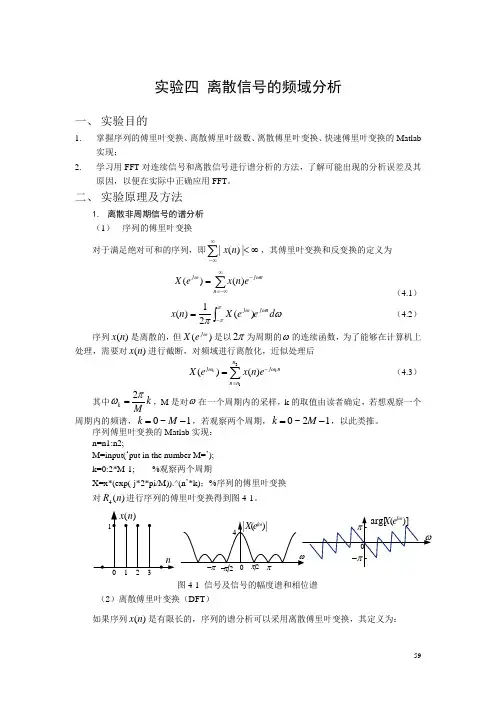
序列傅里叶变换的Matlab 实现: n=n1:n2;M=input(…put in the number M=‟); k=0:2*M-1; %观察两个周期X=x*(exp(-j*2*pi/M)).^(n ‟*k);%序列的傅里叶变换 对4()R n 进行序列的傅里叶变换得到图4-1。
图4-1 信号及信号的幅度谱和相位谱(2)离散傅里叶变换(DFT )如果序列)(n x 是有限长的,序列的谱分析可以采用离散傅里叶变换,其定义为:10,)()]([)(10-≤≤==∑-=N k W n x n x DFT k X N n knN(4.4)10,)(1)]([)(1-≤≤==∑-=-N n Wk X Nk X IDFT n x N k kn N(4.5)因为)(n x 与)(k X 都是离散的,所以可以利用计算机进行数值计算。

实验4 离散时间系统的频域分析一、实验目的(1)了解离散系统的零极点与系统因果性和稳定性的关系; (2)加深对离散系统的频率响应特性基本概念的理解; (3)熟悉MATLAB 中进行离散系统零极点分析的常用子函数; (4)掌握离散系统幅频响应和相频响应的求解方法。
二、知识点提示本章节的主要知识点是频率响应的概念、系统零极点对系统特性的影响;重点是频率响应的求解方法;难点是MATLAB 相关子函数的使用。
三、实验原理1.离散时间系统的零极点及零极点分布图设离散时间系统系统函数为NMzN a z a a z M b z b b z A z B z H ----++++++++==)1()2()1()1()2()1()()()(11 (4-1) MATLAB 提供了专门用于绘制离散时间系统零极点图的zplane 函数: ①zplane 函数 格式一:zplane(z, p)功能:绘制出列向量z 中的零点(以符号"○" 表示)和列向量p 中的极点(以符号"×"表示),同时画出参考单位圆,并在多阶零点和极点的右上角标出其阶数。
如果z 和p 为矩阵,则zplane 以不同的颜色分别绘出z 和p 各列中的零点和极点。
格式二:zplane(B, A)功能:绘制出系统函数H(z)的零极点图。
其中B 和A 为系统函数)(z H (4-1)式的分子和分母多项式系数向量。
zplane(B, A) 输入的是传递函数模型,函数首先调用root 函数以求出它们的零极点。
②roots 函数。
用于求多项式的根,调用格式:roots(C),其中C 为多项式的系数向量,降幂排列。
2.离散系统的频率特性MATLAB 提供了专门用于求离散系统频响特性的freqz 函数,调用格式如下: ①H = freqz(B,A,W)功能:计算由向量W (rad )指定的数字频率点上(通常指[0,π]范围的频率)离散系统)(z H 的频率响应)e (j ωH ,结果存于H 向量中。

南京邮电大学实验报告实验名称:离散时间信号与系统的时、频域表示离散傅立叶变换和z变换数字滤波器的频域分析和实现数字滤波器的设计课程名称数字信号处理A(双语) 班级学号B13011025姓名陈志豪开课时间2015/2016学年,第1学期实验名称:离散时间信号与系统的时、频域表示实验目的和任务:熟悉Matlab基本命令,理解和掌握离散时间信号与系统的时、频域表示及简单应用。
在Matlab环境中,按照要求产生序列,对序列进行基本运算;对简单离散时间系统进行仿真,计算线性时不变(LTI)系统的冲激响应和卷积输出;计算和观察序列的离散时间傅立叶变换(DTFT)幅度谱和相位谱。
实验内容:基本序列产生和运算:Q1.1~1.3,Q1.23,Q1.30~1.33离散时间系统仿真:Q2.1~2.3LTI系统:Q2.19,Q2.21,Q2.28DTFT:Q3.1,Q3.2,Q3.4实验过程与结果分析:Q1.1运行程序P1.1,以产生单位样本序列u[n]并显示它。
clf;n = -10:20;u = [zeros(1,10) 1 zeros(1,20)];stem(n,u);xlabel('Time index n');ylabel('Amplitude');title('Unit Sample Sequence');axis([-10 20 0 1.2]);Q1.2 命令clf,axis,title,xlabel和ylabel命令的作用是什么?答:clf命令的作用:清除图形窗口上的图形;axis命令的作用:设置坐标轴的范围和显示方式;title命令的作用:给当前图片命名;xlabel命令的作用:添加x坐标标注;ylabel c命令的作用:添加y坐标标注;Q1.3修改程序P1.1,以产生带有延时11个样本的延迟单位样本序列ud[n]。
运行修改的程序并显示产生的序列。
clf;n = -10:20;u = [zeros(1,21) 1 zeros(1,9)];stem(n,u);xlabel('Time index n');ylabel('Amplitude');title('Unit Sample Sequence');axis([-10 20 0 1.2]);Q1.23修改上述程序,以产生长度为50、频率为0.08、振幅为2.5、相移为90度的一个正弦序列并显示它。

离散时间系统频域分析离散时间系统的频域分析是研究离散时间信号在频域上的性质和行为的方法。
在离散时间系统频域分析中,使用离散时间傅里叶变换(Discrete Fourier Transform,DFT),来将离散时间信号从时域转换到频域。
通过分析信号在频域上的频谱分布和频谱特性,可以得到离散时间系统的频率响应和频域特性,对信号的频域分布和频率区间进行评估和分析。
离散时间傅里叶变换是时域信号分析的重要工具,它可以将离散时间信号从时域转换到频域。
离散时间傅里叶变换的定义可以表示为:X(k) = Σ[x(n) * exp(-j*2πkn/N)]其中,X(k)是离散时间信号在频域的频谱,x(n)是离散时间信号,N是信号的长度,k是频谱的索引。
离散时间傅里叶变换将时域信号分解成多个频率成分,通过频谱的幅度和相位信息,可以得到信号在频域上的分布情况。
通过离散时间傅里叶变换可以得到离散时间信号的频谱,进而分析信号在频域上的频率响应和频域特性。
频谱可以反映信号在不同频率上的能量分布情况,通过观察频谱的幅度和相位,可以得到信号的频率成分、频带宽度和频率特性等信息。
在离散时间系统频域分析中,常用的分析工具有频谱图、功率谱密度、频率响应等。
频谱图可以将信号的频谱以图形形式展示出来,通过观察频谱图的形状和分布,可以得到信号在频域上的特点。
功率谱密度是指信号在不同频率上的功率分布情况,可以评估信号在不同频率上的能量分布情况。
频率响应是指系统对不同频率信号的响应情况,可以评估系统对不同频率信号的滤波和增益特性。
离散时间系统频域分析的应用包括信号处理、通信系统、控制系统等领域。
在信号处理中,通过频域分析可以对信号进行滤波、去噪、频域变换等操作,提高信号的质量和分析能力。
在通信系统中,通过频域分析可以评估信号传输和接收的性能,并对系统进行优化和改进。
在控制系统中,通过频域分析可以评估系统的稳定性和控制特性,提高系统的响应速度和稳定性。

实验三 离散时间系统的时域分析1.实验目的(1)理解离散时间信号的系统及其特性。
(2)对简单的离散时间系统进行分析,研究其时域特性。
(3)利用MATLAB 对离散时间系统进行仿真,观察结果,理解其时域特性。
2.实验原理离散时间系统,主要是用于处理离散时间信号的系统,即是将输入信号映射成的输出的某种运算,系统的框图如图所示:][n x ][n y Discrete-timesystme(1)线性系统线性系统就是满足叠加原理的系统。
如果对于一个离散系统输入信号为12(),()x n x n 时,输出信号分别为12(),()y n y n ,即:1122()[()]()[()]y n T x n y n T x n ==。
而且当该系统的输入信号为12()()ax n bx n +时,其中a,b 为任意常数,输出为121212[()()][()][()]()()T ax n bx n aT x n bT x n ay n by n +=+=+,则该系统就是一个线性离散时间系统。
(2)时不变系统如果系统的响应与激励加于系统的时刻无关,则该系统是时不变系统。
对于一个离散时间系统,若输入()x n ,产生输出为()y n ,则输入为()x n k -,产生输出为()y n k -,即:若()[()]y n T x n =,则[()]()T x n k y n k -=-。
通常我们研究的是线性时不变离散系统。
3.实验内容及其步骤(1)复习离散时间系统的主要性质,掌握其原理和意义。
(2)一个简单的非线性离散时间系统的仿真 参考:% Generate a sinusoidal input signalclf; n = 0:200; x = cos(2*pi*0.05*n); % Compute the output signal x1 = [x 0 0]; % x1[n] = x[n+1] x2 = [0 x 0]; % x2[n] = x[n] x3 = [0 0 x];% x3[n] = x[n-1]y = x2.*x2-x1.*x3; y = y(2:202); % Plot the input and output signalssubplot(2,1,1) plot(n, x)xlabel('Time index n'); ylabel('Amplitude'); title('Input Signal')subplot(2,1,2) plot(n,y)xlabel('Time index n'); ylabel('Amplitude');title('Output signal');(3)线性与非线性系统的仿真参考:% Generate the input sequencesclf; n = 0:40; a = 2; b = -3;x1 = cos(2*pi*0.1*n); x2 = cos(2*pi*0.4*n);x = a*x1 + b*x2;num = [2.2403 2.4908 2.2403];den = [1 -0.4 0.75];ic = [0 0]; % Set zero initial conditionsy1 = filter(num,den,x1,ic); % Compute the output y1[n]y2 = filter(num,den,x2,ic); % Compute the output y2[n]y = filter(num,den,x,ic); % Compute the output y[n]yt = a*y1 + b*y2; d = y - yt; % Compute the difference output d[n] % Plot the outputs and the difference signalsubplot(3,1,1) stem(n,y); ylabel('Amplitude');title('Output Due to Weighted Input: a \cdot x_{1}[n] + b \cdot x_{2}[n]');subplot(3,1,2) stem(n,yt); ylabel('Amplitude');title('Weighted Output: a \cdot y_{1}[n] + b \cdot y_{2}[n]');subplot(3,1,3) stem(n,d); xlabel('Time index n'); ylabel('Amplitude');title('Difference Signal');(4)时不变与时变系统的仿真参考:% Generate the input sequencesclf; n = 0:40; D = 10; a = 3.0; b = -2;x = a*cos(2*pi*0.1*n) + b*cos(2*pi*0.4*n);xd = [zeros(1,D) x]; num = [2.2403 2.4908 2.2403]; den = [1 -0.4 0.75];ic = [0 0]; % Set initial conditions% Compute the output y[n]y = filter(num,den,x,ic);% Compute the output yd[n]yd = filter(num,den,xd,ic);% Compute the difference output d[n]d = y - yd(1+D:41+D);% Plot the outputssubplot(3,1,1) stem(n,y); ylabel('Amplitude'); title('Output y[n]'); grid;subplot(3,1,2) stem(n,yd(1:41)); ylabel('Amplitude');title(['Output due to Delayed Input x[n - ', num2str(D),']']); grid;subplot(3,1,3) stem(n,d); xlabel('Time index n'); ylabel('Amplitude');title('Difference Signal'); grid;4.实验用MATLAB函数介绍在实验过程中,MATLAB函数命令plot, figure, stem, subplot, axis, grid on, xlabel, ylabel, title, clc等在不同的情况下具体表述也有所不同,应该在实验中仔细体会其不同的含义。

实验二 离散时间系统的时域和频域分析1. 已知某系统的系统函数为21112.04.0121)(----++=zzz z H ,)()(n u n f =,要求:(1)从理论上求解系统的单位冲激响应和零状态响应,并根据求解结果用MA TLAB 绘制其时域波形;(2)试分别用MA TLAB 的impz()函数和filter()函数绘制系统的单位冲激响应和零状态响应。
理论分析: 6.075.12.075.2)6.0)(2.0(212.04.0121)(2211+--=+-+=-++=---z z z z z z z z zzz z H)()6.0(75.1)()2.0(75.2)(n u n u n h n n --=)(])6.0(6563.0)2.0(6875.03437.2[)(*)()(n u n h n f n y nn---==求解零状态响应:filter()函数y=filter(b,a,x) 由向量b 和a 组成的系统对输入x 进行滤波 求解单位序列响应:impz()函数h=impz(b,a,n)计算指定范围内(0: n-1)的单位序列响应的序列值 计算得:a=[1 0.4 -0.12]; b=[1 2 0]; 源程序:a=[1 0.4 -0.12]; b=[1 2 0]; n=0:1:10;subplot(2,2,1);h=2.75.*(0.2).^n-1.75.*(-0.6).^n; stem(n,h); xlabel('n'); ylabel('h(n)');subplot(2,2,2);y1=2.3437-(0.6875).*(0.2).^n-(0.6563).*(-0.6).^n; stem(n,y1); xlabel('n'); ylabel('y(n)'); subplot(2,2,3); impz(b,a,11); xlabel('n'); ylabel('h(n)'); subplot(2,2,4); x=ones(1,11); y2=filter(b,a,x);xlabel('n'); ylabel('y(n)'); 实验结果:510nh (n )510ny (n )510nh (n )Impulse Response510ny (n )2. 已知某系统的系统函数为5.0)(-=z z z H(1)绘制其零极点图(2)用freqz()函数绘出该系统的幅频特性曲线和相频特性曲线,并说明该系统的作用。

实验四离散信号与系统的离散频域分析(DFT)一、实验目的:1、掌握离散时间系统的DFT的MATLAB实现;2、熟悉DTFT和DFT之间的关系。
3、了解信号不同变形的DFT与原信号DFT之间的关系二、实验内容:自定义一个长为8点的信号,1、对信号分别做8点、16点、32点DFT,分别与DTFT合并作图并比较DFT与DTFT 之间的关系。
2、在信号后加零扩展至八点,每两个相邻样本之间插入一个零值,扩充为16点序列,作DFT,画出幅度谱和相位谱,并与原序列的DFT进行比较。
3、将信号以8为周期扩展,得到长为16的两个周期,作DFT,画出幅度谱和相位谱,并与原序列的DFT进行比较。
三、实验平台:MATLAB集成系统四、实验要求1、学习参考程序,理解程序内容,在重要程序段后作出文字说明;2、比较DFT和DTFT,以及扩充序列后与原信号的DFT的比较;3、对DFT的程序部分进行理解、分析。
参考程序:1.n=0:7;x=(0.9*exp(j*pi/3)).^n;x1=[x zeros(1,8)];x2=[x1 zeros(1,16)];N=8;WN=exp(-j*2*pi/N);nk=n'*n;WNnk=WN.^nk;Xk=x*WNnk;N1=16;n=0:15;WN=exp(-j*2*pi/N1);nk=n'*n;WNnk=WN.^nk;Xk1=x1*WNnk;N2=32;n=0:31;WN=exp(-j*2*pi/N2);nk=n'*n;WNnk=WN.^nk;Xk2=x2*WNnk;n=0:7;w=0:pi/100:2*pi;p=-100:100;X=x*(exp(-j*pi/100)).^(n'*p); magX=abs(X);angX=angle(X);magXk=abs(Xk);angXk=angle(Xk);magXk1=abs(Xk1);angXk1=angle(Xk1); magXk2=abs(Xk2);angXk2=angle(Xk2);subplot(4,2,1);plot(w/pi,magX);xlabel('w/pi');ylabel('幅度|X|');grid on; subplot(4,2,2);plot(w/pi,angX);xlabel('w/pi');ylabel('相位(rad/π)');subplot(4,2,3);stem(0:7,magXk);xlabel('k');ylabel('幅度|X(k)|');axis([0,8,0,6]); subplot(4,2,4);stem(0:7,angXk);xlabel('k');ylabel('相位(rad/π)');axis([0,8,-2,2]); subplot(4,2,5);stem(0:15,magXk1);xlabel('k');ylabel('幅度|X1(k)|');axis([0,16,0,6]); subplot(4,2,6);stem(0:15,angXk1);xlabel('k');ylabel('相位(rad/π)');axis([0,16,-2,2]); subplot(4,2,7);stem(0:31,magXk2);xlabel('k');ylabel('幅度|X2(k)|');axis([0,32,0,6]); subplot(4,2,8);stem(0:31,angXk2);xlabel('k');ylabel('相位(rad/π)');axis([0,32,-2,2]);0.51 1.520510w/pi幅度|X |0.51 1.52-202w/pi相位(r a d /π)02468k幅度|X (k )|2468k相位(r a d /π)051015k幅度|X 1(k )|51015k相位(r a d /π)102030k幅度|X 2(k )|102030k相位(r a d /π)2. n=0:7;x=(0.9*exp(j*pi/3)).^n;for i=1:8 %将原序列每两个相邻样本之间插入一个零值,扩展为长为16的序列 y1(2*i-1:2*i)=[x(i) 0]; endN=16;n=0:15;WN=exp(-j*2*pi/N);nk=n'*n; WNnk=WN.^nk; Yk1=y1*WNnk;magYk1=abs(Yk1);angYk1=angle(Yk1);y2=[x x]; %将信号以8为周期扩展,得到长为16的两个周期 N=16;n=0:15;WN=exp(-j*2*pi/N);nk=n'*n; WNnk=WN.^nk; Yk2=y2*WNnk;magYk2=abs(Yk2);angYk2=angle(Yk2); N=8;n=0:7;WN=exp(-j*2*pi/N);nk=n'*n; WNnk=WN.^nk; Xk=x*WNnk;magXk=abs(Xk);angXk=angle(Xk);subplot(3,2,1);stem(0:7,magXk);xlabel('k');ylabel('幅度|X(k)|'); subplot(3,2,2);stem(0:7,angXk);xlabel('k');ylabel('相位(rad/π)'); subplot(3,2,3);stem(0:15,magYk1);xlabel('k');ylabel('幅度|Y1(k)|'); subplot(3,2,4);stem(0:15,angYk1);xlabel('k');ylabel('相位(rad/π)'); subplot(3,2,5);stem(0:15,magYk2);xlabel('k');ylabel('幅度|Y2(k)|'); subplot(3,2,6);stem(0:15,angYk2);xlabel('k');ylabel('相位(rad/π)');02468k幅度|X (k )|02468k相位(r a d /π)51015k幅度|Y 1(k )|051015k相位(r a d /π)k幅度|Y 2(k )|51015k相位(r a d /π)。

实验四离散时间信号与系统分析实验四离散时间信号与系统分析一、实验目的1、理解离散信号及系统的时频域分析方法2、掌握Matlab进行信号的卷积、z变换及逆z变换的方法。
3、掌握Matlab进行离散系统时频域的分析方法二、实验时数:2学时三、实验相关知识(一)离散信号的卷积利用函数(,)可以计算离散信号的卷积和,c conv a b即c(n)=a(n)*b(n),向量c长度是a,b长度之和减1。
若a(n)对应的n的取值范围为:[n1, n2];b(n)对应的n的取值范围为:[n3, n4],则c(n)=a(n)*b(n)对应的n的取值范围为:[n1+n3, n2+n4]。
例4-1:已知两序列:x(k)={1,2,3,4,5;k=-1,0,1,2,3},y(k)={1,1,1;k=-1,0,1},计算x(k)*y(k),并画出卷积结果。
解:利用conv()函数进行离散信号的卷积,注意卷积信号的k 值范围k_x = -1:3;x=[1,2,3,4,5];k_y = -1:1;y=[1,1,1];z=conv(x,y);k_z= k_x(1)+k_y(1):k_x(end)+k_y(end); stem(k_z,z);(二)离散信号的逆z 变换离散序列的z 变换通常是z 的有理函数,可表示为有理分式的形式,因此可以现将X(z)展开成一些简单而常用的部分分式之和,然后分别求出各部分分式的逆变换,把各逆变换相加即可得到X(z)的逆变换x(n)。
设离散信号的z 变换式如下,120121212()()1()m m n n b b z b z b z num z X z a z a z a z den z ------++++==++++在Matlab 中进行部分分式展开的函数为residuez (),其调用形式如下:[r,p,k] = residuez(num,den)其中num=[b0, b1, …, bm]表示X(z)有理分式的分子多项式为12012m m b b z b z b z ---++++;den=[a0, a1, …, am]表示X(z)有理分式的分母多项式为12012m m b b z b z b z ---++++,注意分子分母多项式均为按z -1的降幂排列的多项式,缺项应补零。

实验四线性时不变离散时间系统的频域分析一、引言离散时间系统是指输入和输出都以离散的时间点进行采样的系统。
频域分析是通过将时域信号转换到频域来研究系统的特性和性能的一种方法。
实验四旨在通过频域分析方法研究线性时不变离散时间系统的特性。
二、理论分析线性时不变离散时间系统的输入输出关系可以表示为:y[n]=H(e^(jω))*x[n]其中,H(e^(jω))表示系统的频率响应,是输入和输出的傅里叶变换之比。
线性时不变离散时间系统的频率响应可以通过离散傅里叶变换(DFT)来求得。
DFT是时域序列经过离散采样后进行离散傅里叶变换得到频域表示的方法。
DFT的定义如下:X(k) = Σ[x(n)e^(-j2πkn/N)]其中,x(n)为时域序列,X(k)为频域序列,N为采样点数。
通过DFT可以将时域序列转换为频域序列,从而得到系统的频谱特性,包括幅度和相位。
三、实验步骤1.准备实验设备和软件:计算机、MATLAB软件。
2.设置实验输入信号:生成离散时间序列x[n]。
3.进行离散傅里叶变换:使用MATLAB软件进行离散傅里叶变换,得到频域序列X(k)。
4.计算幅度谱和相位谱:根据频域序列X(k)计算幅度谱和相位谱。
5.绘制频谱图:根据幅度谱和相位谱绘制频谱图。
6.分析系统特性:根据频谱图分析系统的频率响应特性。
四、实验注意事项1.在进行离散傅里叶变换时,注意采样点数N的选择,一般应满足N>2L,其中L为时域信号的长度。
2.在绘制频谱图时,注意选择适当的频率范围,以便观察频域特性。
五、实验结果分析实验通过离散傅里叶变换将时域信号转换为频域信号,得到了系统的频谱特性。
根据频谱图可以分析系统的频率响应,包括系统的幅度响应和相位响应。
六、实验总结通过实验四的实验,我们学习了线性时不变离散时间系统的频域分析方法。
通过离散傅里叶变换,我们可以将时域序列转换为频域序列,从而得到系统的频谱特性。
通过分析频谱图,我们可以了解系统的幅度响应和相位响应,进一步了解系统的特性和性能。

离散时间信号的频域分析实验报告实验名称:离散时间信号的频域分析⼀、实验⽬的1.对离散信号和系统在频域中进⾏分析,可以进⼀步研究它们的性质。
学会通过matlab,对离散时间序列的三种表⽰⽅法:离散时间傅⾥叶变换(DTFT)、离散傅⾥叶变换(DFT)和Z变换。
⼆、实验内容1、修改程序P3.1,计算如下有限长序列的离散时间傅⾥叶变换:g[n]=[1357911131517]并重做习题Q3.2。
讨论你的结果。
你能解释相位谱中的跳变吗?2、选取两个改变了长度的序列以及两个不同的时移值,重做习题Q3.73、编写⼀个MATLAB程序,⽤⼀个N点复数离散傅⾥叶变换计算两个长度为N的实数序列的N点离散傅⾥叶变换,并将结果同直接使⽤两个N点离散傅⾥叶变换得到的结果进⾏⽐较。
4、选取两个不同的时移量,重做习题Q3.335、选取两个不同长度的序列,重做习题Q.336、选取另外两组等长序列重做习题Q3.36三、主要算法与程序1、w=-4*pi:8*pi/511:4*pi;num=[1357911131517];den=[1];h=freqz(num,den,w);%Plot the DTFTsubplot(2,2,1)plot(w/pi,real(h));gridtitle('H(e^{j\omega})的实部')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,2)plot(w/pi,imag(h));gridtitle('H(e^{j\omega})的虚部')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,3)plot(w/pi,abs(h));gridtitle('|H(e^{j\omega})|幅度谱')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,4)plot(w/pi,angle(h));gridtitle('[H(e^{j\omega})]相位谱')xlabel('\omega/\pi');ylabel('以弧度为单位的相位');2、(1)序列为[9123456789],时移为30; %离散时间傅⽴叶变换的时移性质clf;w=-pi:2*pi/255:pi;wo=0.4*pi;D=30;num=[9123456789];h1=freqz(num,1,w);h2=freqz([zeros(1,D)num],1,w);subplot(2,2,1)plot(w/pi,abs(h1));gridtitle('原序列的幅度谱')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,2)plot(w/pi,abs(h2));gridtitle('时移D=30后序列的幅度谱')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,3)plot(w/pi,angle(h1));gridtitle('原序列的相位谱')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,4)plot(w/pi,angle(h2));gridtitle('时移D=30后序列的相位谱')xlabel('\omega/\pi');ylabel('振幅');(2)序列为[12345678910],时移为50;D=50;num=[12345678910];3、clf;g=[1124];h=[2321];x=g+i*h;N=length(x)-1;n=0:N;gk=fft(g);hk=fft(h);xk=fft(x);xk1=fft(conj(x));gk1=(xk+xk1)/2;hk1=(xk-xk1)/2i;subplot(4,2,1)stem(n,abs(gk));gridtitle('实部序列gk的离散傅⾥叶变换的幅度')xlabel('时间序号n');ylabel('振幅');subplot(4,2,2)stem(n,abs(hk));gridtitle('虚部序列gk的离散傅⾥叶变换的幅度')xlabel('时间序号n');ylabel('振幅');subplot(4,2,3)stem(n,abs(gk1));gridtitle('通过xk得到的gk1的离散傅⾥叶变换的幅度') xlabel('时间序号n');ylabel('振幅');subplot(4,2,4)stem(n,abs(hk1));gridtitle('通过xk得到的hk1的离散傅⾥叶变换的幅度') xlabel('时间序号n');ylabel('振幅');subplot(4,2,5)stem(n,angle(gk));gridtitle('实部序列gk的离散傅⾥叶变换的相位')xlabel('时间序号n');ylabel('以弧度为单位的相位'); subplot(4,2,6)stem(n,angle(hk));gridtitle('虚部序列hk的离散傅⾥叶变换的相位')xlabel('时间序号n');ylabel('以弧度为单位的相位'); subplot(4,2,7)stem(n,angle(gk1));gridtitle('通过xk得到的gk1的离散傅⾥叶变换的相位') xlabel('时间序号n');ylabel('以弧度为单位的相位'); subplot(4,2,8) stem(n,angle(hk1));gridtitle('通过xk得到的hk1的离散傅⾥叶变换的相位') xlabel('时间序号n');ylabel('以弧度为单位的相位');4、function y=circshift(x,M)if abs(M)>length(x)M=rem(M,length(x));endif M<0M=M+length(x);endy=[x(M+1:length(x))x(1:M)];%离散傅⾥叶变换的圆周时移性质,时移为10x=[0246810121416];N=length(x)-1;n=0:N;y=circshift(x,10);XF=fft(x);YF=fft(y);subplot(2,2,1);stem(n,abs(XF));gridtitle('原序列的离散傅⾥叶变换的幅度');xlabel('时间序号n');ylabel('振幅');subplot(2,2,2);stem(n,abs(YF));gridtitle('圆周移位10后的序列的离散傅⾥叶变换的幅度'); xlabel('时间序号n');ylabel('振幅'); subplot(2,2,3);stem(n,angle(XF));gridtitle('原序列的离散傅⾥叶变换的相位');xlabel('时间序号n');ylabel('相位');subplot(2,2,4);stem(n,angle(YF));gridtitle('圆周移位10后的序列的离散傅⾥叶变换的相位'); xlabel('时间序号n');ylabel('相位'); %离散傅⾥叶变换的圆周时移性质,时移为20y=circshift(x,20);5、序列为x=[0246810121416],时移为10;序列为x=[02468101214161820],时移为10;6、function y=circonv(x1,x2)L1=length(x1);L2=length(x2);if L1~=L2,error('长度不相等的序列'),endy=zeros(1,L1);x2tr=[x2(1)x2(L2:-1:2)];for k=1:L1sh=circshift(x2tr,1-k);h=x1.*sh;y(k)=sum(h);end%离散傅⾥叶变换的圆周卷积g1=[1234567];g2=[21-12-113];ycir=circonv(g1,g2);disp('圆周卷积的结果');disp(ycir)G1=fft(g1);G2=fft(g2);yc=real(ifft(G1.*G2));disp('离散傅⾥叶变换乘积的离散傅⾥叶逆变换的结果=');disp(yc)四、实验结果与分析图1图2.1图2.2图3图4.1图4.2图5.1序列长度9图5.2序列长度11Q6、圆周卷积的结果18183225393925离散傅⾥叶变换乘积的离散傅⾥叶逆变换的结果=18.000018.000032.000025.000039.000039.000025.0000、五、实验⼩结通过这次实验,我对离散信号和系统在频域中进⾏分析,进⼀步研究了它们的性质。
实验二 离散时间信号的频域分析一、实验目的信号的频域分析是信号处理中的一种有效的工具。
在离散信号的时域分析中,通常将信号表示成单位采样序列δ(n)的线性组合,而在频域中,将信号表示成复变量e -jwn 或e n N π2j -的线性组合。
通过这样的表示,可以将时域的离散序列映射到频域以便于进一步的处理。
本实验中,将学习利用MATLAB 计算离散时间信号的DTFT 和DFT ,并加深对其相互关系的理解。
二、实验原理(1) DTFT 和DFT 的定义及其相互关系。
序列x(n)的DTFT 定义:X(e -jw)=∑∞-∞=n n x )(e -jwn 它是关于自变量w 的复变函数,且是以2π为周期的连续函数。
X (e jw )可以表示为X(e jw )=X re (e jw )+jX im (e jw )其中,X re (e jw )和X im (e jw )分别是X(e jw )的实部和虚部;还可以表示为X(e jw )=|X(e jw)|e j θ(w)其中,|X(e jw)|和θ(w)=arg{X(e jw )}分别是X(e jw )的幅角函数和相位函数;它们都是w 的实函数,也是以2π为周期的函数。
序列X[n]的N 点DFT 定义: X[k]=X(k N2πj e)=∑-=-1Nπ2][N n kn jen X =∑-=1][N n kn N W n XX[k]是周期为N 的序列。
X(e jw )与X[k]的关系:X[k]是对X(e jw )在一个周期中的谱的等间隔N点采样,即:X[k]=X(e jw )|k Nπ2w =,而X(e jw )可以通过对X[k]内插获得,即X(e jw )=1)/2]-πk/N)][(N 2([1.)2Nπk 2sin()2πk2sin(][N 1---=∑--w j N k e wN wN k X三、实验内容(1)编程计算并画出下面DTFT 的实部,虚部,幅度和相位谱。
实验名称:离散时间信号的频域分析一、实验目的1.对离散信号和系统在频域中进行分析,可以进一步研究它们的性质。
学会通过matlab,对离散时间序列的三种表示方法:离散时间傅里叶变换(DTFT)、离散傅里叶变换(DFT)和Z变换。
二、实验内容1、修改程序P3.1,计算如下有限长序列的离散时间傅里叶变换:g[n]=[1357911131517]并重做习题Q3.2。
讨论你的结果。
你能解释相位谱中的跳变吗?2、选取两个改变了长度的序列以及两个不同的时移值,重做习题Q3.73、编写一个MATLAB程序,用一个N点复数离散傅里叶变换计算两个长度为N的实数序列的N点离散傅里叶变换,并将结果同直接使用两个N点离散傅里叶变换得到的结果进行比较。
4、选取两个不同的时移量,重做习题Q3.335、选取两个不同长度的序列,重做习题Q.336、选取另外两组等长序列重做习题Q3.36三、主要算法与程序1、w=-4*pi:8*pi/511:4*pi;num=[1357911131517];den=[1];h=freqz(num,den,w);%Plot the DTFTsubplot(2,2,1)plot(w/pi,real(h));gridtitle('H(e^{j\omega})的实部')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,2)plot(w/pi,imag(h));gridtitle('H(e^{j\omega})的虚部')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,3)plot(w/pi,abs(h));gridtitle('|H(e^{j\omega})|幅度谱')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,4)plot(w/pi,angle(h));gridtitle('[H(e^{j\omega})]相位谱')xlabel('\omega/\pi');ylabel('以弧度为单位的相位');2、(1)序列为[9123456789],时移为30; %离散时间傅立叶变换的时移性质clf;w=-pi:2*pi/255:pi;wo=0.4*pi;D=30;num=[9123456789];h1=freqz(num,1,w);h2=freqz([zeros(1,D)num],1,w);subplot(2,2,1)plot(w/pi,abs(h1));gridtitle('原序列的幅度谱')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,2)plot(w/pi,abs(h2));gridtitle('时移D=30后序列的幅度谱')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,3)plot(w/pi,angle(h1));gridtitle('原序列的相位谱')xlabel('\omega/\pi');ylabel('振幅');subplot(2,2,4)plot(w/pi,angle(h2));gridtitle('时移D=30后序列的相位谱')xlabel('\omega/\pi');ylabel('振幅');(2)序列为[12345678910],时移为50;D=50;num=[12345678910];3、clf;g=[1124];h=[2321];x=g+i*h;N=length(x)-1;n=0:N;gk=fft(g);hk=fft(h);xk=fft(x);xk1=fft(conj(x));gk1=(xk+xk1)/2;hk1=(xk-xk1)/2i;subplot(4,2,1)stem(n,abs(gk));gridtitle('实部序列gk的离散傅里叶变换的幅度')xlabel('时间序号n');ylabel('振幅');subplot(4,2,2)stem(n,abs(hk));gridtitle('虚部序列gk的离散傅里叶变换的幅度')xlabel('时间序号n');ylabel('振幅');subplot(4,2,3)stem(n,abs(gk1));gridtitle('通过xk得到的gk1的离散傅里叶变换的幅度') xlabel('时间序号n');ylabel('振幅');subplot(4,2,4)stem(n,abs(hk1));gridtitle('通过xk得到的hk1的离散傅里叶变换的幅度') xlabel('时间序号n');ylabel('振幅');subplot(4,2,5)stem(n,angle(gk));gridtitle('实部序列gk的离散傅里叶变换的相位')xlabel('时间序号n');ylabel('以弧度为单位的相位'); subplot(4,2,6)stem(n,angle(hk));gridtitle('虚部序列hk的离散傅里叶变换的相位')xlabel('时间序号n');ylabel('以弧度为单位的相位'); subplot(4,2,7)stem(n,angle(gk1));gridtitle('通过xk得到的gk1的离散傅里叶变换的相位') xlabel('时间序号n');ylabel('以弧度为单位的相位'); subplot(4,2,8)stem(n,angle(hk1));gridtitle('通过xk得到的hk1的离散傅里叶变换的相位') xlabel('时间序号n');ylabel('以弧度为单位的相位');4、function y=circshift(x,M)if abs(M)>length(x)M=rem(M,length(x));endif M<0M=M+length(x);endy=[x(M+1:length(x))x(1:M)];%离散傅里叶变换的圆周时移性质,时移为10x=[0246810121416];N=length(x)-1;n=0:N;y=circshift(x,10);XF=fft(x);YF=fft(y);subplot(2,2,1);stem(n,abs(XF));gridtitle('原序列的离散傅里叶变换的幅度');xlabel('时间序号n');ylabel('振幅');subplot(2,2,2);stem(n,abs(YF));gridtitle('圆周移位10后的序列的离散傅里叶变换的幅度'); xlabel('时间序号n');ylabel('振幅');subplot(2,2,3);stem(n,angle(XF));gridtitle('原序列的离散傅里叶变换的相位');xlabel('时间序号n');ylabel('相位');subplot(2,2,4);stem(n,angle(YF));gridtitle('圆周移位10后的序列的离散傅里叶变换的相位'); xlabel('时间序号n');ylabel('相位');%离散傅里叶变换的圆周时移性质,时移为20y=circshift(x,20);5、序列为x=[0246810121416],时移为10;序列为x=[02468101214161820],时移为10;6、function y=circonv(x1,x2)L1=length(x1);L2=length(x2);if L1~=L2,error('长度不相等的序列'),endy=zeros(1,L1);x2tr=[x2(1)x2(L2:-1:2)];for k=1:L1sh=circshift(x2tr,1-k);h=x1.*sh;y(k)=sum(h);end%离散傅里叶变换的圆周卷积g1=[1234567];g2=[21-12-113];ycir=circonv(g1,g2);disp('圆周卷积的结果');disp(ycir)G1=fft(g1);G2=fft(g2);yc=real(ifft(G1.*G2));disp('离散傅里叶变换乘积的离散傅里叶逆变换的结果=');disp(yc)四、实验结果与分析图1图2.1图2.2图3图4.1图4.2图5.1序列长度9图5.2序列长度11Q6、圆周卷积的结果18183225393925离散傅里叶变换乘积的离散傅里叶逆变换的结果=18.000018.000032.000025.000039.000039.000025.0000、五、实验小结通过这次实验,我对离散信号和系统在频域中进行分析,进一步研究了它们的性质。
实验3 离散时间系统的频域分析一、实验目的(1)了解DFS 、DFT 与DTFT 的联系;加深对FFT 基本理论的理解;掌握用MATLB 语言进行傅里叶变换时常用的子函数;(2)了解离散系统的零极点与系统因果性和稳定性的关系;加深对离散系统的频率响应特性基本概念的理解;熟悉MATLAB 中进行离散系统零极点分析的常用子函数;掌握离散系统幅频响应和相频响应的求解方法。
二、实验内容1. 已知离散时间系统函数为()432143213.07.05.11.112.01.03.01.02.0--------+-+-++++=zz z z z z z z z H 求该系统的零极点及零极点分布图,并判断系统的因果稳定性。
实验程序脚本文件:b=[0.2,0.1,0.3,0.1,0.2]; a=[1,-1.1,1.5,-0.7,0.3]; [z,p,k]=tf2zp(b,a); zplane(z,p)title('零极点分布图 ') 零极点图如下:因为系统函数的极点都在单位圆内部,所以该系统为因果稳定系统。
2. 已知离散时间系统的系统函数为()432143213.07.05.11.112.01.03.01.02.0--------+-+-++++=zz z z z z z z z H求该系统在π~0频率范围内的绝对幅频响应、相频响应。
实验程序脚本文件:b=[0.2 0.1 0.3 0.1 0.2]; a=[1 -1.1 1.5 -0.7 0.3]; [h,w]=freqz(b,a); subplot(2,1,1) plot(w,abs(h)); title('幅频响应'); subplot(2,1,2) plot(w,angle(h)) title('相频响应'); 运行以上程序可得:3. 已知()[]7,6,5,4,3,2,1,0=n x ,画出由离散时间傅里叶变换求得的幅度谱()()[]ωωj j e X e X a r g 和图形。
(1)复习傅里叶变换的定义及其性质,加深理解。
(2)熟悉离散时间傅里叶变换的概念及其性质。
参考一:计算离散时间傅里叶变换,并绘制图形。
已知有限长序列x(n)={1,2,3,4,5}。
n=-1:3;x=1:5;k=0:500;w=(pi/500)*k;X=x*(exp(-j*2*pi/500)).^(n'*k);magX=abs(X);angX=angle(X);realX=real(X);imagX=imag(X);subplot(2,2,1);plot(w/pi,magX);grid;xlabel('');ylabel('模值 ');title('模值部分');subplot(2,2,2);plot(w/pi,angX);grid;xlabel('pi为单位');ylabel('弧度');title('相角部分');subplot(2,2,3);plot(w/pi,realX);grid;xlabel('');ylabel('实部');title('实部部分');subplot(2,2,4);plot(w/pi,imagX);grid;xlabel('pi为单位');ylabel('虚部');title('虚部部分');参考二:计算离散时间傅里叶变换。
% Evaluation of the DTFT2()10.6iwiwiweH eeclf;% Compute the frequency samples of the DTFTw = -4*pi:8*pi/511:4*pi; num = [2 1];den = [1 -0.6];h = freqz(num, den, w); % Plot the DTFT subplot(2,1,1) ; plot(w/pi,real(h));grid title('Real part of H(e^{j\omega})')xlabel('\omega /\pi'); ylabel('Amplitude'); subplot(2,1,2) ; plot(w/pi,imag(h));grid title('Imaginary part of H(e^{j\omega})')xlabel('\omega /\pi'); ylabel('Amplitude'); pausesubplot(2,1,1) ; plot(w/pi,abs(h));gridtitle('Magnitude Spectrum |H(e^{j\omega})|')xlabel('\omega /\pi'); ylabel('Amplitude');subplot(2,1,2) ; plot(w/pi,angle(h));gridtitle('Phase Spectrum arg[H(e^{j\omega})]')xlabel('\omega /\pi'); ylabel('Phase in radians');(3)熟悉离散傅里叶变换的概念及其性质参考一:x(n)=sin(n*pi/8)+sin(n*pi/4)是一个N=16的序列,计算其傅里叶变换。
实验四 离散时间系统的频域分析1.实验目的(1)理解和加深傅里叶变换的概念及其性质。
(2)离散时间傅里叶变换(DTFT)的计算和基本性质。
(3)离散傅里叶变换(DFT)的计算和基本性质。
2.实验原理对离散时间信号进行频域分析,首先要对其进行傅里叶变换,通过得到的频谱函数进行分析。
离散时间傅里叶变换(DTFT ,Discrete-time Fourier Transform)是傅立叶变换的一种。
它将以离散时间nT (其中,T 为采样间隔)作为变量的函数(离散时间信号)f (nT )变换到连续的频域,即产生这个离散时间信号的连续频谱()iwF e ,其频谱是连续周期的。
设连续时间信号f (t )的采样信号为:()()()sp nf t t nT f nT ,并且其傅里叶变换为:()()(){}sp niwtf t f nT t nT dte 。
这就是采样序列f(nT)的DTFT::()()iwT inwTDTFT nF e f nT e,为了方便,通常将采样间隔T 归一化,则有:()()iw inwDTFT nF e f n e,该式即为信号f(n)的离散时间傅里叶变换。
其逆变换为:()1()2iw DTFT inw F e dw f n e 。
离散傅里叶变换(DFT ,Discrete-time Fourier Transform )是对离散周期信号的一种傅里叶变换,对于长度为有限长信号,则相当于对其周期延拓进行变换。
在频域上,DFT 的离散谱是对DTFT 连续谱的等间隔采样。
2112()()|()()DFT k DTFT k w NknT N N i iwTiwnTNn n F w F ef nT ef nT e长度为N 的有限长信号x(n),其N 点离散傅里叶变换为:10()[()]()kn N N n X k DFT x n x n W 。
X(k)的离散傅里叶逆变换为:101()[()]()kn N N k x n IDFT X k X k W N。
DTFT 是对任意序列的傅里叶分析,它的频谱是一个连续函数;而DFT 是把有限长序列作为周期序列的一个周期,对有限长序列的傅里叶分析,DFT 的特点是无论在时域还是频域都是有限长序列。
3.实验内容及其步骤(1)复习傅里叶变换的定义及其性质,加深理解。
(2)熟悉离散时间傅里叶变换的概念及其性质。
参考一:计算离散时间傅里叶变换,并绘制图形。
已知有限长序列x(n)={1,2,3,4,5}。
n=-1:3;x=1:5;k=0:500;w=(pi/500)*k;X=x*(exp(-j*2*pi/500)).^(n'*k); magX=abs(X);angX=angle(X);realX=real(X);imagX=imag(X); subplot(2,2,1);plot(w/pi,magX);grid;xlabel('');ylabel('模值 ');title('模值部分'); subplot(2,2,2);plot(w/pi,angX);grid;xlabel('pi 为单位');ylabel('弧度');title('相角部分'); subplot(2,2,3);plot(w/pi,realX);grid;xlabel('');ylabel('实部');title('实部部分'); subplot(2,2,4);plot(w/pi,imagX);grid;xlabel('pi 为单位');ylabel('虚部');title('虚部部分'); 参考二:计算离散时间傅里叶变换。
% Evaluation of the DTFT2()10.6iwiwiw e H eeclf;% Compute the frequency samples of the DTFTw = -4*pi:8*pi/511:4*pi; num = [2 1];den = [1 -0.6]; h = freqz(num, den, w); % Plot the DTFT subplot(2,1,1) plot(w/pi,real(h));grid title('Real part of H(e^{j\omega})')xlabel('\omega /\pi'); ylabel('Amplitude'); subplot(2,1,2) plot(w/pi,imag(h));grid title('Imaginary part of H(e^{j\omega})')xlabel('\omega /\pi'); ylabel('Amplitude'); pausesubplot(2,1,1) plot(w/pi,abs(h));grid title('Magnitude Spectrum |H(e^{j\omega})|')xlabel('\omega /\pi'); ylabel('Amplitude'); subplot(2,1,2) plot(w/pi,angle(h));grid title('Phase Spectrum arg[H(e^{j\omega})]')xlabel('\omega /\pi'); ylabel('Phase in radians'); (3)熟悉离散傅里叶变换的概念及其性质参考一:x(n)=sin(n*pi/8)+sin(n*pi/4)是一个N=16的序列,计算其傅里叶变换。
N=16;n=0:N-1;xn=sin(n*pi/8)+sin(n*pi/4);k=0:1:N-1;WN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^nk;Xk=xn*WNnk; subplot(2,1,1);stem(n,xn);subplot(2,1,2);stem(k,abs(Xk)); 参考二:计算x(n)=8*(0.4).^n,n 属于[0,20)的圆周移位2020()[(10)]()m n x n R n x 。
N=20;m=10;n=0:1:N-1;x=8*(0.4).^n;n1=mod((n+m),N);xm=x(n1+1);subplot(2,1,1);stem(n,x);title('original sequence');xlabel('n');ylabel('x(n)');subplot(2,1,2);stem(n,xm);title('circular shift equence');xlabel('n');ylabel('x((n+10))mod 20');4.实验用MATLAB函数介绍在实验过程中,MATLAB函数命令plot, figure, stem, subplot, axis, grid on, xlabel, ylabel, title, clc, mod, freqz等在不同的情况下具体表述也有所不同,应该在实验中仔细体会其不同的含义。
5.思考题(1)理解离散时间系统的频域分析,掌握和加深对傅立叶变换及其性质的理解。
(2)计算一个N=12的序列x(n)=cos(n*pi/6)的离散时间傅里叶变换。
>> N=12; n=0:N-1; k=0:1:N-1;>> x=cos(n*pi/6);>> X=x*(exp(-j*2*pi/N)).^(n'*k);>> subplot(2,1,1);stem(n,x);legend('x[n]');>> subplot(2,1,2);stem(n,abs(X));legend('X[k]');(3)求x1(n)=(0.8).^n,其中n属于[0,10]与x2(n)=(0.6).^n,并且n属于[0,18]的圆周卷积(N=20)。
先构造一个计算圆周卷积的函数进行计算。
function y=circonv(x1,x2,N)if length(x1)>Nerror('N should bigger than or equal to the length of x1!'); endif length(x2)>Nerror('N should bigger than or equal to the length of x2!'); endx1=[x1,zeros(1,N-length(x1))];x2=[x2,zeros(1,N-length(x2))];m=0:1:N-1;H=zeros(N,N);for n=1:1:NH(n,:)=cirshift(x2,n-1,N);endy=x1*H';function y=cirshift(x,m,N)if length(x)>Nerror('N should bigger than or equal to the length of x!'); endx=[x zeros(1,N-length(x))];n=0:1:N-1;n=mod(n-m,N);y=x(n+1);>> n1=0:10;x1=(0.8).^n1;>> n2=0:18;x2=(0.6).^n2;>> N=20;>> y=circonv(x1,x2,N);>> subplot(3,1,1);stem(n1,x1);legend('x1(n)');>> subplot(3,1,2);stem(n2,x2);legend('x2(n)');>> subplot(3,1,3);stem(0:N-1,y);legend('y(n)');6.实验报告要求(1)明确实验目的以及实验的原理。
(2)通过实验内容分析离散时间信号的性质。
(3)完成思考题的内容,对实验结果及其波形图进行分析对比,总结主要结论。