第3章效用函数
- 格式：ppt
- 大小：6.78 MB
- 文档页数：106
下载文档原格式
合集下载
经济学中效用函数的
矩估计法
定义
矩估计法是一种利用样本矩来估计总体参数的方法。它通过比较样本矩和总体矩的关系来估计总体参数。矩估计法的一个主要优点是它不需要知道数据的分布 假设，因此可以用于任何类型的数据。
优点
矩估计法的优点包括：简单易行、不需要知道数据的分布假设、可以用于任何类型的数据。此外，在某些情况下，矩估计法的解具有唯一性。
要点二
单调递减
如果对于所有的商品组合X和Y，只要X中的商品总价值 低于Y，那么消费者对于X的效用也低于Y。
03
效用函数的应用场景
消费者选择理论
01
描述消费者的偏好
效用函数能够量化描述消费者的 偏好，为研究消费者行为提供依 据。
02
消费者选择模型
基于效用函数构建消费者选择模 型，解释消费者如何在有限的资 源下做出最优的购买决策。
最大似然估计法
定义
优点
缺点
最大似然估计法是一种参数估计方法 ，它通过找到一组参数值，使得模型 预测的结果与实际观察到的数据之间 的似然性最大。换句话说，它试图找 到最有可能产生观察数据的参数值。
最大似然估计法是一种强大的参数估 计方法，因为它可以充分利用已知的 数据信息，并且对于大多数分布假设 ，其估计量是渐近正态的，这意味着 随着样本大小的增加，估计量的精度 也会提高。此外，最大似然估计法还 可以方便地处理缺失数据和异常值。
03
凸函数
一种常见的效用函数，其形式为U(x) = e^(ax)，其中a为常数。凸函数
的特点是随着商品数量的增加，效用值的增加速度逐渐加快。
02
效用函数的基本性质
偏好关系
完全偏好关系
如果消费者对于所有的商品组 合A和B，都更偏好A，那么我 们称A在偏好关系中完全优于B
效用论概述
四、无差异曲线的特殊形状 完全替代品：
MRS12 1
完全互补品：
水平部分： 垂直部分：
MRS12 0
MRS12
进口会增加消费者剩余增加：
第二节 无差异曲线
序数效用论者是用无差异曲线分析方法来 考察消费者行为的，并在此基础上推导出消 费者的需求曲线。
一、关于偏好的假定 第一个假定是偏好的完全性。
偏好的完全性指消费者总是可以比较和 排列所给出的不同商品组合。换言之，对 于任何两个商品组合A和B，消资者总是可 以作出，而且也仅仅只能作出以下三种判 断中的一种：对A的偏好大于对B的偏好； 对B的偏好大于对A的偏好；对A和B的偏好 相同（即A和B是无差异的）。
商品的需求价格是指消费者在一定时 期内对一定量的某种商品所愿意支付的 价格。
基数效用论者认为，商品的需求价格 取决于商品的边际效用。由于边际效用 递减规律的作用，随着消费者对某一种 商品消费量的连续增加，该商品的边际 效用是递减的，相应地，消费者为购买 这种商品所愿意支付的价格即需求价格 也是越来越低的。
P 1 X1 P 2 X 2 P n X n I ……限制条件
MU n MU1 MU 2 ……均衡条件 P P2 Pn 1
简化:
P 1 X1 P 2X2 I
MU1 MU 2 P P2 1
推理：
MU1 MU 2 若： P P2 1 说明一元钱购买商品1所得到的边际效用 小于购买商品2所得到的边际效用。这样， 理性的消费者就会调整这两种商品的购买数 量：减少对商品1的购买量，增加对商品2的 购买量。
3、消费者均衡 消费者均衡是指消费者把有限的货币收 入分配在各种商品的购买中，消费者实现 最大效用时既不想再增加、也不想再减少 任何商品购买数量的这么一种相对静止的 状态。
西方经济学第三章效用论
增加，其效用是不断递减的。每增加一元货币收入 给消费者带来的边际效用是越来越小的。
三章 效用论
10
钻石和木碗
有个穷人四处流浪，他只有一只旧木碗。 一天，穷人在渔船上帮工时遇到了特大风浪，被海水冲
到一个小岛上，岛上的酋长看见穷人头顶的木碗，感到 非常新奇，便用一大口袋珍珠宝石换走了木碗，派人把 穷人送回了家。 富翁听说木碗换回这么多宝贝，也想去碰碰运气。富翁 装了满满一船山珍海味和美酒，运到小岛。 酋长高兴地接受了富人送来的礼物，声称要送给他最珍 贵的东西。
均衡。 消费者的最优购买行为必须满足两个条件：一是
给消费者带来最大效用，二是购买的商品组合必 须在给定的预算线上。
三章 效用论
35
消费者均衡
X2
消费者收入既定，两种商
品价格既定，可以画出一
a
条预算线。
15
E点既在预算线上，又 在可能的最高的无差异曲
线上，是最优商品组合。 0
F
E
U3 b U1 U2
P1
P2
1
三章 效用论
13
Q
12 34 5 6 7 8
MU1 11 10 9 8 7 6 5 4 MU2 19 17 15 13 12 10 8 6
假设买4个商品1和4个商品2，MU1/P1<MU2/P2, 总效用为102，小于107，没有实现最大效用。
消费者必然增加商品2的购买，减少商品1的购买，使 总效用增加， 一直到MU1/P1=MU2/P2,。
x2 在维持效用水平 20 - A
不变的前提下，消 16 费者增加一单位某 种商品的消费时所 12 -
需要放弃的另一种 8 -
商品的消费数量， 4 -
B C D E
三章 效用论
10
钻石和木碗
有个穷人四处流浪，他只有一只旧木碗。 一天，穷人在渔船上帮工时遇到了特大风浪，被海水冲
到一个小岛上，岛上的酋长看见穷人头顶的木碗，感到 非常新奇，便用一大口袋珍珠宝石换走了木碗，派人把 穷人送回了家。 富翁听说木碗换回这么多宝贝，也想去碰碰运气。富翁 装了满满一船山珍海味和美酒，运到小岛。 酋长高兴地接受了富人送来的礼物，声称要送给他最珍 贵的东西。
均衡。 消费者的最优购买行为必须满足两个条件：一是
给消费者带来最大效用，二是购买的商品组合必 须在给定的预算线上。
三章 效用论
35
消费者均衡
X2
消费者收入既定，两种商
品价格既定，可以画出一
a
条预算线。
15
E点既在预算线上，又 在可能的最高的无差异曲
线上，是最优商品组合。 0
F
E
U3 b U1 U2
P1
P2
1
三章 效用论
13
Q
12 34 5 6 7 8
MU1 11 10 9 8 7 6 5 4 MU2 19 17 15 13 12 10 8 6
假设买4个商品1和4个商品2，MU1/P1<MU2/P2, 总效用为102，小于107，没有实现最大效用。
消费者必然增加商品2的购买，减少商品1的购买，使 总效用增加， 一直到MU1/P1=MU2/P2,。
x2 在维持效用水平 20 - A
不变的前提下，消 16 费者增加一单位某 种商品的消费时所 12 -
需要放弃的另一种 8 -
商品的消费数量， 4 -
B C D E
《效用函数》课件
在生产决策中，生产者需要考虑边际成本和边际 收益的关系，以实现利润最大化。在消费决策中 ，消费者需要考虑边际效用和边际成本的关系， 以实现效用最大化。
05
效用最大化问题
消费者剩余和生产者剩余
消费者剩余
消费者在购买某一商品时愿意支付的 最高价格与实际支付价格之间的差额 。消费者剩余反映了消费者对商品的 主观评价和实际支付之间的差异。
无差异曲线法
预算约束法
通过选择无差异曲线上的点来实现效用最 大化，无差异曲线上的点表示能给消费者 带来相同效用的不同商品组合。
在预算约束条件下，选择能够使总效用最 大的商品组合。
06
效用函数的发展趋势和未来展望
效用函数在经济学中的发展趋势
跨学科融合
随着经济学与其他学科的交叉研究， 效用函数的理论和应用将进一步融入 心理学、社会学和环境科学等领域， 以更全面地解释人类行为和经济现象 。
效用函数作为决策分析的重要工 具，为决策者提供了一套完整的 分析框架和方法。
04
效用函数的性质
边际替代效应
边际替代效应是指消费者在保持总效 用不变的情况下，通过改变消费组合 中不同商品的消费量，以获得最大效 用。
边际替代效应反映了消费者对于不同 商品之间的替代关系，是消费者行为 的一个重要特征。
对同一种商品的效用评价可能不同。
效用具有主观性和个体差异性，反映了消费者的个人偏好和价
03
值取向。
效用函数的定义
01
效用函数：表示消费者对不同消费组合的效用评价 的函数。
02
效用函数将商品的数量或消费组合映射到效用值上 ，反映了消费者的偏好和价值取向。
03
效用函数有多种形式，常见的有线性效用函数、二 次效用函数、对数效用函数等。
05
效用最大化问题
消费者剩余和生产者剩余
消费者剩余
消费者在购买某一商品时愿意支付的 最高价格与实际支付价格之间的差额 。消费者剩余反映了消费者对商品的 主观评价和实际支付之间的差异。
无差异曲线法
预算约束法
通过选择无差异曲线上的点来实现效用最 大化，无差异曲线上的点表示能给消费者 带来相同效用的不同商品组合。
在预算约束条件下，选择能够使总效用最 大的商品组合。
06
效用函数的发展趋势和未来展望
效用函数在经济学中的发展趋势
跨学科融合
随着经济学与其他学科的交叉研究， 效用函数的理论和应用将进一步融入 心理学、社会学和环境科学等领域， 以更全面地解释人类行为和经济现象 。
效用函数作为决策分析的重要工 具，为决策者提供了一套完整的 分析框架和方法。
04
效用函数的性质
边际替代效应
边际替代效应是指消费者在保持总效 用不变的情况下，通过改变消费组合 中不同商品的消费量，以获得最大效 用。
边际替代效应反映了消费者对于不同 商品之间的替代关系，是消费者行为 的一个重要特征。
对同一种商品的效用评价可能不同。
效用具有主观性和个体差异性，反映了消费者的个人偏好和价
03
值取向。
效用函数的定义
01
效用函数：表示消费者对不同消费组合的效用评价 的函数。
02
效用函数将商品的数量或消费组合映射到效用值上 ，反映了消费者的偏好和价值取向。
03
效用函数有多种形式，常见的有线性效用函数、二 次效用函数、对数效用函数等。
效用函数定义
3.Байду номын сангаас减的边际效用：效用函数对各个商品或服务的边际效用递减，即∂²U/∂Xi² <= 0。这意味着随着获得更多的一种商品或服务，个体对该商品或服务的额外满足感逐渐减少。
三、效用函数的应用
效用函数在经济学中有广泛的应用，特别是在消费者理论、福利经济学和行为经济学方面。
1.消费者理论：效用函数是描述消费者行为和偏好的重要工具。根据效用函数，经济学家可以分析个体如何根据自身的收入和价格来最大化效用。例如，当收入和价格发生变化时，效用函数可以帮助我们理解个体对商品或服务的消费决策如何做出调整。
二、效用函数的属性
1.非负性：效用函数输出值不能为负数，即U(X1, X2, ..., Xn) >= 0。这意味着个体对商品或服务的满足程度不能为负，越多的商品或服务应该获得越高的效用。
2.递增性：效用函数对各个商品或服务的边际效用应该是递增的。即∂U/∂Xi >= 0，表示当个体获得更多的一种商品或服务时，他的总效用应该增加。
四、效用函数的局限性
尽管效用函数在经济学中具有重要的应用，但它仍然存在一些局限性和争议。首先，效用函数的构建需要基于个体主观感受的假设，而个体的主观感受很难准确度量和比较。其次，效用函数的属性并不适用于所有情况，实际消费决策中，个体行为可能受到其他因素的影响，如心理因素、社会环境等。
综上所述，效用函数是经济学中一个重要的概念，用于量化个体对不同商品或服务的满足程度。它具有一些基本属性，并在消费者理论、福利经济学和行为经济学等领域有广泛应用。然而，我们也应该意识到效用函数的局限性，尤其是在对个体主观感受和非理性行为的解释方面。通过进一步研究和探索，可以不断完善和丰富效用函数理论，提高其在经济学中的适用性和准确性。
三、效用函数的应用
效用函数在经济学中有广泛的应用，特别是在消费者理论、福利经济学和行为经济学方面。
1.消费者理论：效用函数是描述消费者行为和偏好的重要工具。根据效用函数，经济学家可以分析个体如何根据自身的收入和价格来最大化效用。例如，当收入和价格发生变化时，效用函数可以帮助我们理解个体对商品或服务的消费决策如何做出调整。
二、效用函数的属性
1.非负性：效用函数输出值不能为负数，即U(X1, X2, ..., Xn) >= 0。这意味着个体对商品或服务的满足程度不能为负，越多的商品或服务应该获得越高的效用。
2.递增性：效用函数对各个商品或服务的边际效用应该是递增的。即∂U/∂Xi >= 0，表示当个体获得更多的一种商品或服务时，他的总效用应该增加。
四、效用函数的局限性
尽管效用函数在经济学中具有重要的应用，但它仍然存在一些局限性和争议。首先，效用函数的构建需要基于个体主观感受的假设，而个体的主观感受很难准确度量和比较。其次，效用函数的属性并不适用于所有情况，实际消费决策中，个体行为可能受到其他因素的影响，如心理因素、社会环境等。
综上所述，效用函数是经济学中一个重要的概念，用于量化个体对不同商品或服务的满足程度。它具有一些基本属性，并在消费者理论、福利经济学和行为经济学等领域有广泛应用。然而，我们也应该意识到效用函数的局限性，尤其是在对个体主观感受和非理性行为的解释方面。通过进一步研究和探索，可以不断完善和丰富效用函数理论，提高其在经济学中的适用性和准确性。
决策理论3_效用函数
决策理论3_效用函数决策理论是研究人类在面对不确定性和风险的情况下做出决策的理论。
效用函数是决策理论中的一个重要概念，用于衡量不同决策结果带来的效用或满足程度，从而指导人们做出最优决策。
效用函数的概念最早由经济学家边沁提出，他认为人们根据自身对事物的偏好程度，对不同结果赋予一定的效用值。
效用函数可以看作是将决策结果映射为实数的函数，而不同人对相同决策结果的效用值可能是不同的。
效用函数的具体形式和性质因人而异，常见的效用函数包括线性函数、指数函数、对数函数等。
线性函数在描述决策者对风险的态度时较为简单，即效用与结果成正比。
指数函数则可以很好地描述决策者对小概率事件的偏好，即决策者更容易选择高概率事件而放弃低概率事件。
对数函数则可以很好地描述决策者对较大收益的饱和效应，即对于相同数量级的收益，决策者的边际效用递减。
效用函数在决策分析中的应用非常广泛。
一方面，通过确定决策者的效用函数，可以将决策问题转化为一个最优化问题，通过求解最大效用值或最小效用值来确定最优决策。
例如，在投资决策中，决策者可以通过测量不同投资组合的效用值来选择最优的投资方案。
另一方面，效用函数也可以用来比较不同决策者之间的偏好，帮助决策者进行选择。
例如，在公共政策制定中，政府可以通过测量不同政策方案对公众的效用值来确定最优政策。
然而，在实际应用中，确定有效的效用函数并不容易。
一方面，人的偏好往往是主观和复杂的，难以用简单的函数来直接描述。
另一方面，效用函数的形式和参数可能随着决策情境和决策者的变化而变化，因此需要不断调整和修正。
为了解决这一问题，决策理论提出了一些方法，如实证研究、实验方法和专家调查等，以获得更准确和可靠的效用函数。
此外，效用函数还存在一些局限性和争议。
首先，效用函数假设人的决策行为完全理性，忽视了人们在面对复杂决策时可能存在的有限理性。
其次，效用函数所基于的价值观和陈述性规则可能因人而异，存在主观差异。
最后，效用函数往往难以考虑到所有的因素和权衡，可能导致决策结果与现实情况的偏离。
第3章关于效用函数
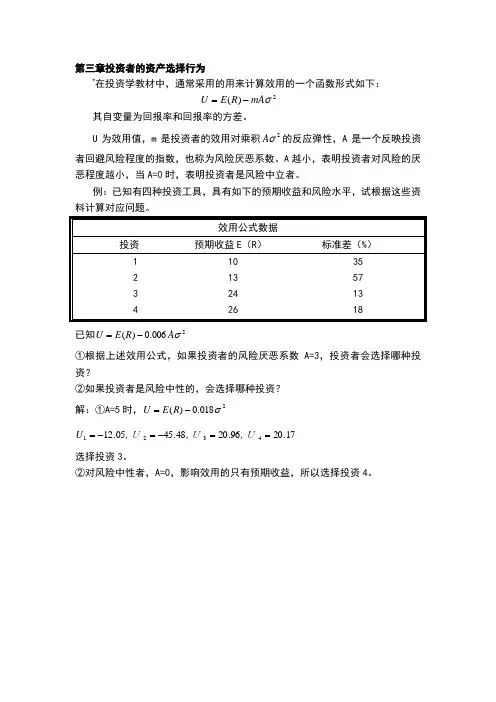
第三章投资者的资产选择行为
*在投资学教材中，通常采用的用来计算效用的一个函数形式如下：
其自变量为回报率和回报率的方差。
U 为效用值，m 是投资者的效用对乘积2σA 的反应弹性，A 是一个反映投资者回避风险程度的指数，也称为风险厌恶系数。
A 越小，表明投资者对风险的厌恶程度越小，当A=0时，表明投资者是风险中立者。
例：已知有四种投资工具，具有如下的预期收益和风险水平，试根据这些资料计算对应问题。
效用公式数据
投资 预期收益E （R ） 标准差（%）
1 10 35
2 1
3 57
3 2
4 13 4 26 18
已知2006.0)(σA R E U -=
①根据上述效用公式，如果投资者的风险厌恶系数A=3，投资者会选择哪种投资？
②如果投资者是风险中性的，会选择哪种投资？
解：①A=5时，2018.0)(σ-=R E U
17.2096.2048.4505.124321==-=-=，U ，U ，U U
选择投资3。
②对风险中性者，A=0，影响效用的只有预期收益，所以选择投资4。
2)(σmA R E U -=。
第三章 效用函数与风险厌恶
（5）局部非饱和性（local nonsatiation）
x C 和 〉0，总存在 y C, x y
使得 x y
在技术上，局部非饱和性和单调性保证了 无差异曲线具有一个负的斜率。
（6）凸性（convexity）
x, y, z C,ifx z, y z x (1) y z
严格凸性（strictly convexity）：
一、个体行为决策准则
（一）偏好关系
效用是一种纯主观的心理感受，因人因地因时 而异。
偏好是建立在消费者可以观察的选择行为之上 的。
偏好关系（preference relation)是指消费者 对不同商品或商品组合偏好的顺序。它可以用 一种两维（或二元）关系（binary relation） 表述出来。
u :C→R。
（三）消费者效用最大化问题
令 max u(.) 则最大化问题为：
s.tW
q (q1, , qm, , qM ) RM
max u(.) s.t.z C RM : qc W
上述约束式为瓦尔拉斯（walrasian budget set）预算集。
最优解：
u q 0
x, y, z C, ifx y, y z x z
（4）连续性（continunity）
对于任意的X、y，集合 x x y 和x x y是闭
集，则 x x y和 x x y是开集。
即如果x是一组至少与y一样好的消费束，而
且它趋近于另一消费束z，则z与y至少同样好。 这样就可以得到一条连续的无差异曲线。
ω1 ω2 ω3 ω4 ω5 xω 2 3 1 8 0
定义3.1 一个消费计划x(•)是对不同状态下消费品 的数量的描述。则
x : Z (Z R)
x C 和 〉0，总存在 y C, x y
使得 x y
在技术上，局部非饱和性和单调性保证了 无差异曲线具有一个负的斜率。
（6）凸性（convexity）
x, y, z C,ifx z, y z x (1) y z
严格凸性（strictly convexity）：
一、个体行为决策准则
（一）偏好关系
效用是一种纯主观的心理感受，因人因地因时 而异。
偏好是建立在消费者可以观察的选择行为之上 的。
偏好关系（preference relation)是指消费者 对不同商品或商品组合偏好的顺序。它可以用 一种两维（或二元）关系（binary relation） 表述出来。
u :C→R。
（三）消费者效用最大化问题
令 max u(.) 则最大化问题为：
s.tW
q (q1, , qm, , qM ) RM
max u(.) s.t.z C RM : qc W
上述约束式为瓦尔拉斯（walrasian budget set）预算集。
最优解：
u q 0
x, y, z C, ifx y, y z x z
（4）连续性（continunity）
对于任意的X、y，集合 x x y 和x x y是闭
集，则 x x y和 x x y是开集。
即如果x是一组至少与y一样好的消费束，而
且它趋近于另一消费束z，则z与y至少同样好。 这样就可以得到一条连续的无差异曲线。
ω1 ω2 ω3 ω4 ω5 xω 2 3 1 8 0
定义3.1 一个消费计划x(•)是对不同状态下消费品 的数量的描述。则
x : Z (Z R)
第3章效用函数
后来经济学家多数认为，消费理论可以基本上在 序数效用理论基础上展开。实际上，序数效用和 偏好映照是等同的概念。
•Chapter 1效用函数
基数效用和序数效用
序数效用(ordinal utility) 认为效用是心理现象，不可以度量，即不能用基数表 示，只能根据偏好的程度排列出顺序，即以序数第一 、第二、第三、…表示效用的高低。
•Chapter 1效用函数
消费者均衡的条件是使最后一单位货币购买各种商 品的边际效用都相等。钻石的边际效用高，所以价 格高昂，水的边际效用低，所以价格低廉，这样购 买水和钻石的每单位货币的边际效用相等。
或者说，人们愿意为边际效用高的钻石支付高价格 ，愿意为边际效用低的水支付低价格是理性行为。
效用最大化。 这被称作相等边际原则。
•Chapter 1效用函数
边际效用和边际替代率
边际效用均等法则 在既定的收入与商品价格下，消费者使得其花在所购买的每一种 商品上的最后一元钱所得到的边际效用相等。
• 数学证明
•Chapter 1效用函数
消费者行为的比较静态学
在经济学中将消费者选择的问题用一个 最优化模型来表示，即在预算约束下最
第3章效用函数
2020年6月6日星期六
本章概要
基数效用和序数效用 边际效用和边际替代率 预算约束下的效用最大化 凹效用函数和凸无差异曲线
•Chapter 1效用函数
效用与边际效用
效用Utility
人们在物品与劳务消费过程中（更一 般地在从事的行为中）所得到的欲望 的满足。
因人而异 因地而异 因时而异 不具伦理学意义：毒品 “多多益善”、 “过多则滥” 与“越多越糟”
•Chapter 1效用函数
•Chapter 1效用函数
•Chapter 1效用函数
基数效用和序数效用
序数效用(ordinal utility) 认为效用是心理现象，不可以度量，即不能用基数表 示，只能根据偏好的程度排列出顺序，即以序数第一 、第二、第三、…表示效用的高低。
•Chapter 1效用函数
消费者均衡的条件是使最后一单位货币购买各种商 品的边际效用都相等。钻石的边际效用高，所以价 格高昂，水的边际效用低，所以价格低廉，这样购 买水和钻石的每单位货币的边际效用相等。
或者说，人们愿意为边际效用高的钻石支付高价格 ，愿意为边际效用低的水支付低价格是理性行为。
效用最大化。 这被称作相等边际原则。
•Chapter 1效用函数
边际效用和边际替代率
边际效用均等法则 在既定的收入与商品价格下，消费者使得其花在所购买的每一种 商品上的最后一元钱所得到的边际效用相等。
• 数学证明
•Chapter 1效用函数
消费者行为的比较静态学
在经济学中将消费者选择的问题用一个 最优化模型来表示，即在预算约束下最
第3章效用函数
2020年6月6日星期六
本章概要
基数效用和序数效用 边际效用和边际替代率 预算约束下的效用最大化 凹效用函数和凸无差异曲线
•Chapter 1效用函数
效用与边际效用
效用Utility
人们在物品与劳务消费过程中（更一 般地在从事的行为中）所得到的欲望 的满足。
因人而异 因地而异 因时而异 不具伦理学意义：毒品 “多多益善”、 “过多则滥” 与“越多越糟”
•Chapter 1效用函数
•Chapter 1效用函数
效用函数ppt课件
14
理性行为公理：
公理1 连通性（或成对可比性）：如果P1, P2 ，则P1 或者P1 P2，或者P1 P2 。
P2，
公理2 传递性：如果P1, P2, P3，而且P1 P2，P2 P3，则必有
P1 P3 。
公理3 替代性：如果P1, P2 和Q，而且0<p<1，则
P1 P2 当且仅当 pP1 + (1-p)Q pP2 + (1-p)Q . 公理4 连续性（连续性或称偏好有界性）：
（1）概率的出现具有明显的客观性值，而且比较稳定； （2）决策不是解决一次性问题，而是解决多次重复的问题； （3）决策的结果不会对决策者带来严重的后果。 • 如果不符合这些情况，期望货币损益值准则就不适用，需要
采用其他标准。 • 用期望值作为决策准则的根本条件是，决策有不断反复的可
能。 4
所谓决策有不断重复的可能，包括下列三层涵义： 第一，决策本身即为重复性决策。 第二，重复的次数要比较多，尤其是当存在对于决策后果有重 大影响的小概率事件时，只有重复次数相当多时才能用期望值 来作为决策标准，因为只有这样其平均后果才接近于后果的期 望值。
Session 6 效用函数
1
Session Topic
• 期望货币损益值准则的局限 • 效用函数的定义和公理 • 效用函数的构成 • 风险和效用的关系 • 损失函数、风险函数和贝叶斯风险
2
期望货币损益值准则的局限
3
期望货币损益值准则的局限
• 以期望货币损益值为标准的决策方法一般只适用于下列几种 情况：
足。它是度量一定数量的金钱（或其它事务）在决策者心目中的
价值或者说决策者对待它们的态度的概念。或者说，效用是在有
风险的情况下，决策人对后果的爱好（称为偏好）的量化，可用
理性行为公理：
公理1 连通性（或成对可比性）：如果P1, P2 ，则P1 或者P1 P2，或者P1 P2 。
P2，
公理2 传递性：如果P1, P2, P3，而且P1 P2，P2 P3，则必有
P1 P3 。
公理3 替代性：如果P1, P2 和Q，而且0<p<1，则
P1 P2 当且仅当 pP1 + (1-p)Q pP2 + (1-p)Q . 公理4 连续性（连续性或称偏好有界性）：
（1）概率的出现具有明显的客观性值，而且比较稳定； （2）决策不是解决一次性问题，而是解决多次重复的问题； （3）决策的结果不会对决策者带来严重的后果。 • 如果不符合这些情况，期望货币损益值准则就不适用，需要
采用其他标准。 • 用期望值作为决策准则的根本条件是，决策有不断反复的可
能。 4
所谓决策有不断重复的可能，包括下列三层涵义： 第一，决策本身即为重复性决策。 第二，重复的次数要比较多，尤其是当存在对于决策后果有重 大影响的小概率事件时，只有重复次数相当多时才能用期望值 来作为决策标准，因为只有这样其平均后果才接近于后果的期 望值。
Session 6 效用函数
1
Session Topic
• 期望货币损益值准则的局限 • 效用函数的定义和公理 • 效用函数的构成 • 风险和效用的关系 • 损失函数、风险函数和贝叶斯风险
2
期望货币损益值准则的局限
3
期望货币损益值准则的局限
• 以期望货币损益值为标准的决策方法一般只适用于下列几种 情况：
足。它是度量一定数量的金钱（或其它事务）在决策者心目中的
价值或者说决策者对待它们的态度的概念。或者说，效用是在有
风险的情况下，决策人对后果的爱好（称为偏好）的量化，可用
第三章效用函数
在随机决策中，决策系统（Ω，A，F）中的 决策方案均是在状态空间背景中加以比较， 并按照某种规则，选出决策者最满意的行动 方案。
在本章中，我们用事态体表示在随机性状态 空间中的行动方案，方案的比较表示为事态 体的比较，并引入效用的概念，用以衡量事 态体（行动方案）的优劣。
§3.1 理性行为公理
3.1.1 事态体及其关系 1．事态体的概念 定义3.1
x 0.75
x 0.5
x 0.5
x 0
x* x0.5
x* x0
计算得：
x0.25
， x 2 0.75
2
2
效用曲线上新增两个点：
（ ε2, 0.25）,（2ε－ε2, 0.75）
u
1
0.75
0.5
0.25
0 ε2 ε 2ε－ε2 1
x
⑥ 若认为点数太少，效用曲线不够精确，可继续 按同样方法在新产生的区间内插入效用中点， 直到产生足够的点为止。
§3.2 效用函数的定义和构造
设有决策系统（Ω，A，F），在离散情况 下，结果值可以表示为决策矩阵：
o11 o12 ... o1n
O
(o ij
)
mn
o21
...
o22 ...
...
o2
n
... ...
om1
om 2
...
omn
§3.2 效用函数的定义和构造
矩阵O的第i行表示第i个可行方案的n个可能 结果值，即事态体
3.1.3 事态体的基本性质
性质3. 3 任一事态体无差异于一个简单事态体。
设有事态体T ＝（p1, o1；p2, o2 ；…；pn, on）则 必存在一个简单事态体
T’＝（p’, o*；1－p’, o0 ）～ T
在本章中，我们用事态体表示在随机性状态 空间中的行动方案，方案的比较表示为事态 体的比较，并引入效用的概念，用以衡量事 态体（行动方案）的优劣。
§3.1 理性行为公理
3.1.1 事态体及其关系 1．事态体的概念 定义3.1
x 0.75
x 0.5
x 0.5
x 0
x* x0.5
x* x0
计算得：
x0.25
， x 2 0.75
2
2
效用曲线上新增两个点：
（ ε2, 0.25）,（2ε－ε2, 0.75）
u
1
0.75
0.5
0.25
0 ε2 ε 2ε－ε2 1
x
⑥ 若认为点数太少，效用曲线不够精确，可继续 按同样方法在新产生的区间内插入效用中点， 直到产生足够的点为止。
§3.2 效用函数的定义和构造
设有决策系统（Ω，A，F），在离散情况 下，结果值可以表示为决策矩阵：
o11 o12 ... o1n
O
(o ij
)
mn
o21
...
o22 ...
...
o2
n
... ...
om1
om 2
...
omn
§3.2 效用函数的定义和构造
矩阵O的第i行表示第i个可行方案的n个可能 结果值，即事态体
3.1.3 事态体的基本性质
性质3. 3 任一事态体无差异于一个简单事态体。
设有事态体T ＝（p1, o1；p2, o2 ；…；pn, on）则 必存在一个简单事态体
T’＝（p’, o*；1－p’, o0 ）～ T
《效用函数》课件
效用最大化原则
1 什么是效用最大化
效用最大化是指消费者根据所拥有的收入和商品价格，选择能够带来最大满意度的消费 组合。
2 怎样实现效用最大化
我们将学习如何使用边际效用和预算约束条件来确定最优消费组合。
3 最优消费组合的条件
了解必要条件和充分条件，以便确定消费者达到效用最大化的最佳选择。
线性效用函数
定义
线性效用函数是一种简单直观的 效用函数形式，可以用一条直线 来表示。
线性效用函数的图像
通过图示，我们可以直观地理解 线性效用函数和消费者的选择行 为。
消费者选择和预算线
深入探究消费者如何在预算约束 下作出最优消费决策。
单位收益的效用函数
1
如何求出单位收益的效用函数
2
我们将学习如何通过计量经济数据和相
关工具来推导单位收益的效用函数。
3
什么是单位收益的效用函数
单位收益的效用函数是描述个体在某种 经济活动中所获得的满足感的函数。
解释单位收益的效用函数的实际 意义
深入探讨单位收益的效用函数在经济决 策和资源配置方面的重要性。
总结
效用函数的作用
效用函数帮助我们理解和量化 个体对商品或选择的偏好。
效用函数在经济学中 的应用
《效用函数》PPT课件
欢迎来到《效用函数》PPT课件！在本课程中，我们将深入探讨效用函数的定 义、性质、递减规律以及在经济学中的应用。让我们一起开始这个令人兴奋 且具有挑战性的学习之旅吧！
什么是效用函数？
定义
效用函数是描述个体或消费者对商品或选择的偏好程度的函数。
基本性质
效用函数是单调递增、连续且凸函数。
效用函数在消费理论、生产理 论和福利分析等方面具有广泛 的应用。
第3章---效用理论
第3章---效用理论1.效用U （ut ili ty ）消费者消费某种商品（或劳务）后的满足程度。
-----效用是一种主观评价。
2.基数效用理论：效用的大小可以用具体的数字进行度量的一种理论3.总效用TU （to tal ut ili ty ）：是指消费一定量的商品（或劳务）所得到的总满足程度。
例：假定，第一个包子的效用为5，第二个包子的效用为4，第三个包子的效用为3，第四个包子的效用为2，第五个包子的效用为1，第六个包子的效用为0，第七个包子的效用为-1，第八个包子的效用为-2. 那么：吃1个包子的总效用为5；吃2个包子的总效用为：5+4=9；吃3个包子的总效用为：5+4+3=12； 吃4个包子的总效用为：5+4+3+2=14； 吃5个包子的总效用为：5+4+3+2+1=15； 吃6个包子的总效用为：5+4+3+2+1+0=15； 吃7个包子的总效用为：5+4+3+2+1+0-1=14； 吃8个包子的总效用为：5+4+3+2+1+0-1-2=12；令：()Q f TU =，()51=f ，()92=f ，()123=f ...()128=f .4.总效用函数的特征：例：若某人的效用函数为Y X TU +=4，原来他消费9单位X ，8单位Y ，现在X 减少到4单位，问需要消费多少单位Y 才能与以前的满足相同？5.边际效用M U （ma rg ina l uti li ty ）：是指消费数量增加一个单位（或减少一个单位）时总效用的变动。
6.边际效用递减规律：在一定时间内消费者消费某种商品，随着对该商品消费数量的增加，消费者产生的满足程度的增量是递减的。
假定Q ∆保持不变，即每次增量相同，但TU ∆是递减的; 边际效用递减规律的数学语言：()Q f ''＜0或MU 是减函数。
7.货币的边际效用递减问题：货币的边际效用也是递减的，但是递减的速度很慢，一般忽略不计。
8.总效用与边际效用的关系：注意：本图不具有普遍性，边际效用曲线不一定是直线。
周惠中《微观经济学》(第3版)课后习题详解(效用函数)
第3章效用函数1．王五的效用函数如下：(),=。
王五原先消费9单位x和10单位y。
如U x y y果他所消费的x缩减为4单位，要给他多少单位y才能使他与原先一样满意？解：王五原先的效用为：()U==⨯+=9,1010231016当4x=，效用不变的前提下有：()u y y==，解得：4,16y=。
12所以要给他12单位y才能使他与原先一样满意。
2．“三只手”有两只左手，一只右手。
（1）画出“三只手”对左右手套的无差异曲线。
（2）我们称两只左手套、一只右手套为一“副”手套，并用拥有多少副手套来表示“三只手”的效用水平。
以()R L表示右（左）手套数，写出“三只手”的效用函数。
（3）如果2>，多一只左手套会增加多少效用？L R（4）如果2<，多一只左手套会增加多少效用？L R答：（1）“三只手”的左右手套为2:1的完全互补品，其无差异曲线如图3-1所示。
图3-1 无差异曲线（2）手套所带来的效用取决于左手套数目的半数取整与有手套数目的均值中的较小值，即()1,min ,2U L R R L ⎧⎫=⎨⎬⎩⎭；（3）如果2L R >，()1,min ,2U L R R L R ⎧⎫==⎨⎬⎩⎭，多一只左手套不会增加效用。
（4）若原先L 是奇数，初始效用为：()11,min ,22L U L R R L -⎧⎫==⎨⎬⎩⎭，增加一只左手套将增加一单位效用()()11,min ,22L L U L R R +⎧⎫+⎪⎪'==⎨⎬⎪⎪⎩⎭；若L 是偶数，初始效用()1,min ,22LU L R R L ⎧⎫==⎨⎬⎩⎭，增加一只左手套将不增加效用()1,min ,22L LU L R R +⎧⎫==⎨⎬⎩⎭。
3．还记得大大和小小吃冰棍的故事吗？（见第2章习题）（1）分别写出大大和小小对大、小冰棍的效用函数（以x 、y 分别表示大、小冰棍的数量）。
（2）试给出两个不同的大、小冰棍组合数，使得大大较喜欢其中一个组合，而小小则较喜欢另一个。
决策理论与方法第三章效用函数
决策理论与方法第三章：效用函数引言在决策理论与方法中，效用函数是一个重要的概念。
它是一种衡量个体对不同决策结果的偏好程度的数学函数。
效用函数的应用可以帮助人们在面临不同选择时做出最优的决策。
本文将介绍效用函数的定义、性质以及常见的应用方法。
定义效用函数是一种将不同决策结果与其对个体的满意程度相联系的函数。
它可以用来衡量个体对于不同选择的偏好程度。
一般来说，效用函数的取值范围是实数。
效用函数可以表示为U(x)，其中x是决策结果。
为了简化模型，我们常常假设效用函数是关于决策结果的单调递增函数。
这意味着，个体对于更好的决策结果拥有更高的满意度。
性质效用函数具有一些重要的性质，包括：•单调性：效用函数是一个单调递增函数，即对于任意的决策结果x和y，如果x>y，则U(x)>U(y)。
•凸性：效用函数是一个凸函数，即对于任意的决策结果x和y，以及0<α<1，有U(αx+(1-α)y)>αU(x)+(1-α)U(y)。
这意味着个体对于取得中间结果的满意度高于只取得x或y的满意度之和。
•边际效用递减性：边际效用指的是增加一个单位的某种决策结果对于个体总体满意度的变化。
效用函数具有边际效用递减性，即随着取得更多相同决策结果的数量增加，个体对于每个增加的单位的满意度递减。
常见的应用方法期望效用理论期望效用理论是一种将不确定性的决策问题转化为确定性的效用函数的方法。
它基于以下两个假设：个体具有一种对于结果的期望值，而且个体对于结果的满意程度是平凡的。
具体来说，期望效用理论将决策问题分为两个步骤：首先，通过量化不同结果的期望值，将不确定性问题转化为确定性问题；其次，通过效用函数对结果进行排名，选取满意度最高的决策。
风险偏好和风险厌恶在决策理论中，个体的风险偏好程度会直接影响其效用函数的形状。
风险偏好指的是个体对于不确定性决策结果的喜好程度。
具体来说，风险偏好可以分为风险厌恶、风险中性和风险喜好三种类型。
效用函数名词解释
效用函数名词解释一、什么是效用函数1.1 效用的概念效用在经济学中是一个基本的概念，它用于描述人们对不同选择的偏好程度。
效用是一个主观的概念，不同的人对同一种选择可能会赋予不同的效用。
1.2 效用函数的定义效用函数是用来表示人们对不同选择赋予的效用的函数。
它将不同的选择映射到一个数值上，数值越大则表示该选择对个体而言越有利。
效用函数是一种量化人们选择偏好的工具，通过它可以比较不同选择的效用大小。
二、效用函数的特点2.1 主观性效用函数的值是主观的，它取决于个体的偏好和价值观。
不同的人对同一种选择可能会有不同的效用函数。
2.2 正值性效用函数的值是正的，即效用函数的值不能为负。
这是因为效用是用来衡量个体对不同选择的好坏程度，若效用为负则表示该选择对个体来说是不利的。
2.3 边际效应递减性边际效应递减性是指随着某一选择数量的增加，对个体带来的额外效用逐渐减少。
例如，一个人一天喝一杯水可以获得一定的效用，但继续喝第二杯水时，获得的额外效用就会减少。
2.4 可比较性效用函数可以用来比较不同选择的效用大小。
通过效用函数，我们可以确定对个体来说哪种选择更优。
三、效用函数的形式3.1 效用函数的数学表达一般来说，效用函数可以用数学方程来表示。
常见的形式有线性效用函数、二次效用函数、指数效用函数等。
具体形式的选择取决于个体的偏好。
3.2 线性效用函数线性效用函数是一种简单的效用函数形式，它表示效用与选择数量成正比。
例如，一个人每天喝的咖啡数量和效用之间的关系可以用线性函数来描述。
3.3 二次效用函数二次效用函数是一种常用的效用函数形式，它表示效用与选择数量的平方成正比。
例如，一个人购买商品的数量和购买商品的效用之间的关系可以用二次函数来描述。
3.4 指数效用函数指数效用函数是一种常用的效用函数形式，它表示效用与选择数量的指数函数成正比。
例如，一个人对音乐会的参与人数和参与人数对自己的快乐感的影响可以用指数函数来描述。
第3章 效用函数
第3章 效用函数
3.1 引言 3.2 效用的定义和公理系统 3.3 效用函数的构造 3.4 风险与效用 3.5 货币的效用 3.6 阿莱斯悖论(Allais’s paradox)
3.1 引言
在定量评价可能的行动的各种后果时， 会遇到两个主要问题:
(1) 后果本身是用语言表述，可能没有任何 合适的直接测量标度。
（2）如他先有了10000元，要为100元钱去干这份让他讨厌的工作， 他就很可能不干了。
实际价值
0
100
钱 100000 100100
这个例子说明：即使是数值量表示的后果，它对决策人的实际价值仍有待确定。
3.1 引言
例3.2 决策人面临图3.1中决策树所示的选择：
①确定收入礼品1000元；
②参与一次抽奖：有50%的机会得0元，50%的机会得2500元。
⑴ 概率当量法
2．离散型后果的效用设定
后果为离散型随机变量时，后果集C 中元素为有限个，构造后果集上的 效用函数有两方面的内容: (1)确定各后果之间的优先序; (2)确定后果之间的优先程度。
离散型后果效用值的设定可以采用 概率当量法，简称NM法。
NM法步骤如下：
例3.6
例3.6 天气预报说球赛时可能有雨，一个足球爱好者要决定是否去球场看球。
圣彼得堡悖论的解释3：
(三)效用上限论
也有一种观点认为奖金的效用可能有一个上限，这样，期望效用 之和就有了一个极限值。Menger认为效用上限是惟一能消解该悖论 的方法。设效用值等于货币值，上限为100 单位，则游戏的期望效用 为7.56l25，如表3所示。
圣彼得堡悖论的解释4：
(四)结果有限论
(1) 严格序“ ” a b(或者记作aPb)的含义是“a优于b”( a
3.1 引言 3.2 效用的定义和公理系统 3.3 效用函数的构造 3.4 风险与效用 3.5 货币的效用 3.6 阿莱斯悖论(Allais’s paradox)
3.1 引言
在定量评价可能的行动的各种后果时， 会遇到两个主要问题:
(1) 后果本身是用语言表述，可能没有任何 合适的直接测量标度。
（2）如他先有了10000元，要为100元钱去干这份让他讨厌的工作， 他就很可能不干了。
实际价值
0
100
钱 100000 100100
这个例子说明：即使是数值量表示的后果，它对决策人的实际价值仍有待确定。
3.1 引言
例3.2 决策人面临图3.1中决策树所示的选择：
①确定收入礼品1000元；
②参与一次抽奖：有50%的机会得0元，50%的机会得2500元。
⑴ 概率当量法
2．离散型后果的效用设定
后果为离散型随机变量时，后果集C 中元素为有限个，构造后果集上的 效用函数有两方面的内容: (1)确定各后果之间的优先序; (2)确定后果之间的优先程度。
离散型后果效用值的设定可以采用 概率当量法，简称NM法。
NM法步骤如下：
例3.6
例3.6 天气预报说球赛时可能有雨，一个足球爱好者要决定是否去球场看球。
圣彼得堡悖论的解释3：
(三)效用上限论
也有一种观点认为奖金的效用可能有一个上限，这样，期望效用 之和就有了一个极限值。Menger认为效用上限是惟一能消解该悖论 的方法。设效用值等于货币值，上限为100 单位，则游戏的期望效用 为7.56l25，如表3所示。
圣彼得堡悖论的解释4：
(四)结果有限论
(1) 严格序“ ” a b(或者记作aPb)的含义是“a优于b”( a
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第3章效用函数
一、效用的基本概念与符号
•(3) 弱序“≥” • 记作aRb，含义是“a不劣于b”，亦即a 优于或者无差异于b。
第3章效用函数
一、效用的基本概念与符号
(4) 展望(prospect) 展望指决策的可能的前景，即各种后果及后果
出现的概率的组合，记作P= <p1,c1; p2,c2;…; pr,cr; >.
3.1 引言
•例3.1 考虑钱对同一个人的价值。假设一个学生手头紧张，正好有机会挣 100元钱，但是所要做的是他相当讨厌的工作。 • （1）如他经济情况差，他会认为100元钱的实际价值足够大，所要做 的工作即使是相当讨厌的，他仍会去干； • （2）如他先有了10000元，要为100元钱去干这份让他讨厌的工作， 他就很可能不干了。 •
➢有人选确定性的1000元的收入。抽 奖的期望值虽大，风险也大，实际价 值还不如保险的1000元。 ➢而有人认为礼品不如抽奖，因为 抽奖提供了获得2500元的机会。
这个例子说明：决策人的风险态度影 响其对后果的实际价值判断。
第3章效用函数
圣彼得堡悖论 (St. Petersburg Paradox/game)
•公理3.3表明两个有序的展望各有相同的比例
被相等的量
替代后，优先关系不变.
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
例3.3 横过马路问题:效用有界性证明
第3章效用函数
3.2.3 效用的公理化定义和效用的存在性
第3章效用函数
3.2.3 效用函数的存在性
(四)结果有限论
n Gustason认为，要避免矛盾，必须对期望值概念进 行限制，其一是限制其结果的数目；其二是把其结果 值的大小限制在一定的范围内。
n 这是典型的结果有限论，这一观点是从实际出发的。 因为实际上，游戏的投掷次数总是有限的数。
n 比如对游戏设定某一个投掷的上限数L，在投掷到这个 数的时候，如果仍然没有成功，也结束游戏，不管你 还能再投多少，就按照L付钱。因为你即便不设定L， 实际上也总有投到头的时候，人的寿命总是有限的， 任何原因都可以使得游戏中止。现在设定了上限，期 望值自然也就可以计算了。
嚼起来又酥又松，味道美极了！” n 兔子和猫争论不休、相持不下，跑去请猴子评理。 n 猴子听了，不由得大笑起来：“瞧你们这两个傻瓜蛋，连这点儿
常识都不懂！世界上最好吃的东西是什么？是桃子！桃子不但美 味可口，而且长得漂亮。我每天做梦都梦见吃桃子。” n 兔子和猫听了，全都直摇头。那么，世界上到底什么东西最好吃？
第3章效用函数
复合展望
第3章效用函数
一、效用的基本概念与符号
•(5) 抽奖与确定当量 • 由机会点和该机会点发出的n个机会枝的概率及相应 后果构成的图形称为抽奖（lottery），抽奖又称彩票。
•若C1 ~ (p, C2; (1-P),C3), 则称 确定性后果C1为抽奖(p, C2; (1-P),C3)的确定当量（certainty equivalent）。
第3章效用函数
2020/11/26
第3章效用函数
3.1 引言
n 在定量评价可能的行动的各种后果时， 会遇到两个主要问题:
✓ (1) 后果本身是用语言表述，可能没有任何 合适的直接测量标度。
✓ (2) 即使有一个明确的标度可以测量后果， 按这个标度测得的量也可能并不反映后果对 决策人的真正价值。
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
传递性推导:
• P1
•
P2
•αP1+(1-α)P1 αP2+(1-α)P2
•αP1+(1-α)P3 αP2+(1-α)P3
•(一)边际效用递减论
• Daniel Bernoulli在提出这个问题的时候就给出一种解决 办法。他认为游戏的期望值计算不应该是金钱，而应该是金钱的 期望效用，即利用众所周知的“期望效用递减律”，将金钱的效 用测度函数用货币值的对数来表示:效用=log(货币值)，如表 2 所示。所有结果的效用期望值之和将为一个有限值log(4)≈ 0.60206，如果这里的效用函数符合实际，则理性决策应以4元 为界。
此只要有可能，应该尽可能使用概率当量法。
第3章效用函数
⑴ 概率当量法
第3章效用函数
2．离散型后果的效用设定
n 后果为离散型随机变量时，后果集C 中元素为有限个，构造后果集上的 效用函数有两方面的内容: (1)确定各后果之间的优先序; (2)确定后果之间的优先程度。
第3章效用函数
圣彼得堡悖论的解释2：
(二)风险厌恶论
n 圣彼得堡悖论对于奖金额大小没有限制。 n 比如连续投掷40次才成功的话，奖金为1.1万亿元。但是这一奖
金出现的概率极小，1.1万亿次才可能出现一次。实际上，游戏 有一半的机会，其奖金为 2元，四分之三的机会得奖4元和2元。 奖金越少，机会越大，奖金越大，机会越小。 n Hacking（1980）所说：花25元的费用冒险参与游戏将是非常 愚蠢的，虽有得大奖的机会，但是风险太大。 n 因此，考虑采用风险厌恶因素的方法可以消解矛盾。Pual Weirich就提出在期望值计算中加人一种风险厌恶因子，并得出 了游戏费用的有限期望值，认为这种方法实际上解决了该悖论。
第3章效用函数
一、效用的基本概念与符号
•(1) 严格序“ ” • a b(或者记作aPb)的含义是“a优于b”( a is preferred to b )；也就是说，若非外界因素 的强迫，决策人只会选择a而不会选择b。
第3章效用函数
一、效用的基本概念与符号
• (2) 无差异“～” • a～b(或记作aIb)的含义是“a无差异于b” (a is indifference to b)；也就是说，决策人 对选择或同样满意。
第3章效用函数
第3章效用函数
第3章效用函数
3.2 效用的定义和公理系统
n 3.2.1 效用的定义 n 3.2.2 效用存在性公理 n 3.2.3 效用的公理化定义和效用的存在性 n 3.2.4 基数效用与序数效用
第3章效用函数
3.2.1 效用的定义
n 效用（utility）：消费者从消费商品中得 到的满足程度。
第3章效用函数
圣彼得堡悖论的解释3：
•(三)效用上限论
• 也有一种观点认为奖金的效用可能有一个上限，这样，期望效用 之和就有了一个极限值。Menger认为效用上限是惟一能消解该悖论 的方法。设效用值等于货币值，上限为100 单位，则游戏的期望效用 为7.56l25，如表3所示。
第3章效用函数
圣彼得堡悖论的解释4：
以上的故事说明效用完全是个人的心理感觉。 不同的偏好决定了对同一种商品效用大小的不同评价。
第3章效用函数
3.2.1 效用的定义
n 在决策理论中，后果对决策人的实际价值，即决策人对 后果的偏好次序是用效用(utility)来描述的。
n 效用就是偏好的量化，是数(实值函数)。
n 1738年，Daniel Bernoulli就指出：若一个人面临从给定 行动集(风险性展望集)中作选择的决策问题，如果他知 道与给定行动有关的将来的自然状态，且这些状态出现 的概率已知或可以估计，则他应选择对各种可能后果的 偏好的期望值最高的行动。
n 圣彼得堡悖论是数学家丹尼尔·伯努利（Daniel Bernoulli）的表 兄尼古拉·伯努利(Nicolaus Bernoulli)在1738提出的一个概率 期望值悖论，它来自于一种掷币游戏，即圣彼得堡游戏(表1)。
•问题：你愿意花100元来参加一次圣彼得堡游戏吗？
第3章效用函数
圣彼得堡悖论的解释1：
第3章效用函数
3.1 引言
n 由上面例子可知：在进行决策分析时，存在如何描述 或表达后果对决策人的实际价值，以便反映决策的人 心目中各种后果的偏好次序（preference order）的问 题。
n 偏好次序是决策人的个性与价值观的反映，它与决策 人所处的社会地位、经济地位、文化素养、心理和生 理（身体）状态有关。
1．估计效用函数值的方法
•⑴ 概率当量法
⑵ 确定当量法
•⑶ 增益当量法
⑷ 损失当量法
•
• 从纯理论角度看，这四种方法并没有实质性的区
别；但是实验结果表明，使用确定当量法时决策人对
最优后果（增益）的保守性和对损失的冒险性都比概
率当量法严重(Hershey，1982）；采用增益当量法
与损失当量法时产生的误差也比用概率当量法大，因
•实际价值
•0
00100
100000
这个例子说明：即使是数值量表示的后果，它对决策人的实际价值仍有待确定。
第3章效用函数
3.1 引言
例3.2 决策人面临图3.1中决策树所示的选择：
①确定收入礼品1000元；
②参与一次抽奖：有50%的机会得0元，50%的机会得2500元。
n 序数效用不反映偏好强度，(保序变换下唯一), 原序数列可变 换为16,9,4,1；或 8,6,4,2,或10,7,6,1等.
第3章效用函数
3.2.4 基数效用与序数效用
n 基数(cardinal number)效用：边际效用分析方法
n 总效用（TOTAL UTILITY，TU） ：消费者在一定时间内 从一定数量商品的消费中所得到的效用量的总和 ;
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
一、效用的基本概念与符号
•(3) 弱序“≥” • 记作aRb，含义是“a不劣于b”，亦即a 优于或者无差异于b。
第3章效用函数
一、效用的基本概念与符号
(4) 展望(prospect) 展望指决策的可能的前景，即各种后果及后果
出现的概率的组合，记作P= <p1,c1; p2,c2;…; pr,cr; >.
3.1 引言
•例3.1 考虑钱对同一个人的价值。假设一个学生手头紧张，正好有机会挣 100元钱，但是所要做的是他相当讨厌的工作。 • （1）如他经济情况差，他会认为100元钱的实际价值足够大，所要做 的工作即使是相当讨厌的，他仍会去干； • （2）如他先有了10000元，要为100元钱去干这份让他讨厌的工作， 他就很可能不干了。 •
➢有人选确定性的1000元的收入。抽 奖的期望值虽大，风险也大，实际价 值还不如保险的1000元。 ➢而有人认为礼品不如抽奖，因为 抽奖提供了获得2500元的机会。
这个例子说明：决策人的风险态度影 响其对后果的实际价值判断。
第3章效用函数
圣彼得堡悖论 (St. Petersburg Paradox/game)
•公理3.3表明两个有序的展望各有相同的比例
被相等的量
替代后，优先关系不变.
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
例3.3 横过马路问题:效用有界性证明
第3章效用函数
3.2.3 效用的公理化定义和效用的存在性
第3章效用函数
3.2.3 效用函数的存在性
(四)结果有限论
n Gustason认为，要避免矛盾，必须对期望值概念进 行限制，其一是限制其结果的数目；其二是把其结果 值的大小限制在一定的范围内。
n 这是典型的结果有限论，这一观点是从实际出发的。 因为实际上，游戏的投掷次数总是有限的数。
n 比如对游戏设定某一个投掷的上限数L，在投掷到这个 数的时候，如果仍然没有成功，也结束游戏，不管你 还能再投多少，就按照L付钱。因为你即便不设定L， 实际上也总有投到头的时候，人的寿命总是有限的， 任何原因都可以使得游戏中止。现在设定了上限，期 望值自然也就可以计算了。
嚼起来又酥又松，味道美极了！” n 兔子和猫争论不休、相持不下，跑去请猴子评理。 n 猴子听了，不由得大笑起来：“瞧你们这两个傻瓜蛋，连这点儿
常识都不懂！世界上最好吃的东西是什么？是桃子！桃子不但美 味可口，而且长得漂亮。我每天做梦都梦见吃桃子。” n 兔子和猫听了，全都直摇头。那么，世界上到底什么东西最好吃？
第3章效用函数
复合展望
第3章效用函数
一、效用的基本概念与符号
•(5) 抽奖与确定当量 • 由机会点和该机会点发出的n个机会枝的概率及相应 后果构成的图形称为抽奖（lottery），抽奖又称彩票。
•若C1 ~ (p, C2; (1-P),C3), 则称 确定性后果C1为抽奖(p, C2; (1-P),C3)的确定当量（certainty equivalent）。
第3章效用函数
2020/11/26
第3章效用函数
3.1 引言
n 在定量评价可能的行动的各种后果时， 会遇到两个主要问题:
✓ (1) 后果本身是用语言表述，可能没有任何 合适的直接测量标度。
✓ (2) 即使有一个明确的标度可以测量后果， 按这个标度测得的量也可能并不反映后果对 决策人的真正价值。
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
传递性推导:
• P1
•
P2
•αP1+(1-α)P1 αP2+(1-α)P2
•αP1+(1-α)P3 αP2+(1-α)P3
•(一)边际效用递减论
• Daniel Bernoulli在提出这个问题的时候就给出一种解决 办法。他认为游戏的期望值计算不应该是金钱，而应该是金钱的 期望效用，即利用众所周知的“期望效用递减律”，将金钱的效 用测度函数用货币值的对数来表示:效用=log(货币值)，如表 2 所示。所有结果的效用期望值之和将为一个有限值log(4)≈ 0.60206，如果这里的效用函数符合实际，则理性决策应以4元 为界。
此只要有可能，应该尽可能使用概率当量法。
第3章效用函数
⑴ 概率当量法
第3章效用函数
2．离散型后果的效用设定
n 后果为离散型随机变量时，后果集C 中元素为有限个，构造后果集上的 效用函数有两方面的内容: (1)确定各后果之间的优先序; (2)确定后果之间的优先程度。
第3章效用函数
圣彼得堡悖论的解释2：
(二)风险厌恶论
n 圣彼得堡悖论对于奖金额大小没有限制。 n 比如连续投掷40次才成功的话，奖金为1.1万亿元。但是这一奖
金出现的概率极小，1.1万亿次才可能出现一次。实际上，游戏 有一半的机会，其奖金为 2元，四分之三的机会得奖4元和2元。 奖金越少，机会越大，奖金越大，机会越小。 n Hacking（1980）所说：花25元的费用冒险参与游戏将是非常 愚蠢的，虽有得大奖的机会，但是风险太大。 n 因此，考虑采用风险厌恶因素的方法可以消解矛盾。Pual Weirich就提出在期望值计算中加人一种风险厌恶因子，并得出 了游戏费用的有限期望值，认为这种方法实际上解决了该悖论。
第3章效用函数
一、效用的基本概念与符号
•(1) 严格序“ ” • a b(或者记作aPb)的含义是“a优于b”( a is preferred to b )；也就是说，若非外界因素 的强迫，决策人只会选择a而不会选择b。
第3章效用函数
一、效用的基本概念与符号
• (2) 无差异“～” • a～b(或记作aIb)的含义是“a无差异于b” (a is indifference to b)；也就是说，决策人 对选择或同样满意。
第3章效用函数
第3章效用函数
第3章效用函数
3.2 效用的定义和公理系统
n 3.2.1 效用的定义 n 3.2.2 效用存在性公理 n 3.2.3 效用的公理化定义和效用的存在性 n 3.2.4 基数效用与序数效用
第3章效用函数
3.2.1 效用的定义
n 效用（utility）：消费者从消费商品中得 到的满足程度。
第3章效用函数
圣彼得堡悖论的解释3：
•(三)效用上限论
• 也有一种观点认为奖金的效用可能有一个上限，这样，期望效用 之和就有了一个极限值。Menger认为效用上限是惟一能消解该悖论 的方法。设效用值等于货币值，上限为100 单位，则游戏的期望效用 为7.56l25，如表3所示。
第3章效用函数
圣彼得堡悖论的解释4：
以上的故事说明效用完全是个人的心理感觉。 不同的偏好决定了对同一种商品效用大小的不同评价。
第3章效用函数
3.2.1 效用的定义
n 在决策理论中，后果对决策人的实际价值，即决策人对 后果的偏好次序是用效用(utility)来描述的。
n 效用就是偏好的量化，是数(实值函数)。
n 1738年，Daniel Bernoulli就指出：若一个人面临从给定 行动集(风险性展望集)中作选择的决策问题，如果他知 道与给定行动有关的将来的自然状态，且这些状态出现 的概率已知或可以估计，则他应选择对各种可能后果的 偏好的期望值最高的行动。
n 圣彼得堡悖论是数学家丹尼尔·伯努利（Daniel Bernoulli）的表 兄尼古拉·伯努利(Nicolaus Bernoulli)在1738提出的一个概率 期望值悖论，它来自于一种掷币游戏，即圣彼得堡游戏(表1)。
•问题：你愿意花100元来参加一次圣彼得堡游戏吗？
第3章效用函数
圣彼得堡悖论的解释1：
第3章效用函数
3.1 引言
n 由上面例子可知：在进行决策分析时，存在如何描述 或表达后果对决策人的实际价值，以便反映决策的人 心目中各种后果的偏好次序（preference order）的问 题。
n 偏好次序是决策人的个性与价值观的反映，它与决策 人所处的社会地位、经济地位、文化素养、心理和生 理（身体）状态有关。
1．估计效用函数值的方法
•⑴ 概率当量法
⑵ 确定当量法
•⑶ 增益当量法
⑷ 损失当量法
•
• 从纯理论角度看，这四种方法并没有实质性的区
别；但是实验结果表明，使用确定当量法时决策人对
最优后果（增益）的保守性和对损失的冒险性都比概
率当量法严重(Hershey，1982）；采用增益当量法
与损失当量法时产生的误差也比用概率当量法大，因
•实际价值
•0
00100
100000
这个例子说明：即使是数值量表示的后果，它对决策人的实际价值仍有待确定。
第3章效用函数
3.1 引言
例3.2 决策人面临图3.1中决策树所示的选择：
①确定收入礼品1000元；
②参与一次抽奖：有50%的机会得0元，50%的机会得2500元。
n 序数效用不反映偏好强度，(保序变换下唯一), 原序数列可变 换为16,9,4,1；或 8,6,4,2,或10,7,6,1等.
第3章效用函数
3.2.4 基数效用与序数效用
n 基数(cardinal number)效用：边际效用分析方法
n 总效用（TOTAL UTILITY，TU） ：消费者在一定时间内 从一定数量商品的消费中所得到的效用量的总和 ;
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数
第3章效用函数