第七章 随机解释变量问题资料
- 格式：ppt
- 大小：396.50 KB
- 文档页数：29
下载文档原格式
合集下载
计量经济学(第七章 随机解释变量问题)1
多元 线性 模型 的正 规方 程组 X2为 与μ相 关的 随机 变量
ˆ ˆ ˆ ˆ Yi ( 0 1 X 1i 2 X 2i k X ki ) E (i ) 0 ˆ ˆ ˆ ˆ Yi X 1i ( 0 1 X 1i 2 X 2i k X ki ) X 1i E (i X 1i ) 0 ˆ ˆ ˆ ˆ Yi X 2i ( 0 1 X 1i 2i X 2i k X ki ) X 2i E (i X 2i ) 0 Y X ( X X X ) X E ( X ) 0 ˆ ˆ ˆ ˆ 0 1 1i 2 2i k ki ki i ki i ki
• 但是在单方程计量经济学模型中，凡是外生变量都 被认为是确定性的。
• 于是随机解释变量问题主要表现于：用滞后被解释 变量作为模型的解释变量的情况。
• 例如：
(1) 耐用品存量调整模型 耐用品的存量Qt由前一个时期的存量Qt-1和当期 收入It共同决定：
Qt=0+1It+2Qt-1+t
t=1,T
拟合结果
80000 70000 60000 50000 40000 30000 20000 10000 0 1980 1985 1990 1995 2000 2005
JMXF JMXFOLS
JMXFIV JMXFGMM
四、解释变量的内生性检验
Hausman检验
Yi 0 1 X i 2 Z i1 i
(1) 随机解释变量与随机误差项独立 (Independence)
Cov( X 2, ) E( x2 ) E( x2 )E() 0
(2) 随机解释变量与随机误差项同期无关 (contemporaneously uncorrelated)，但异期相关。 Cov( X 2i, i ) E( x2i i ) 0
第七章 随机解释变量问题
= β 0 (1 − λ ) + β 1 (1 − λ )Yt + λC t −1 + µ t − λµ t −1
Ct-1是一随机解释变量，且与 (µt-λµt-1)高度相关 （Why?）。
三、随机解释变量的后果
计量经济学模型一旦出现随机解释变量，如果仍采用 OLS法估计模型参数，不同性质的随机解释变量会产生 不同的后果。 以下分三种情况讨论： 1、x是随机变量但与u互相独立，则OLSE仍然无偏。 2、x是随机变量，与u不独立但不相关，则OLSE在小样 本下有偏、大样本下具有一致性，即在大样本下OLSE 会逐渐逼近真值。 3、 x是随机变量，且与u相关，则OLSE在小样本下有偏、 大样本下也不具有一致性，即在OLS失效。
ˆ β1 =
∑x y ∑x
i 2 i
i
不具有一致性。 在大样本下也不成立，OLS估计量不具有一致性 不具有一致性
如果选择Z为X的工具变量 工具变量，那么在上述估计 工具变量 过程可改为:
∑z y
i
i
= β 1 ∑ z i xi + ∑ z i µ i
利用E(ziµi)=0，在大样本下可得到：
β1
~
四、解决随机解释变量的方法： 解决随机解释变量的方法： 工具变量法
模型中出现随机解释变量且与随机误差项相 关时，OLS估计量是有偏的。 如果随机解释变量与随机误差项不相关，则 可以通过增大样本容量的办法来得到一致的估计 量； 但如果相关，即使增大样本容量也无济于事。 这时，最常用的估计方法是工具变量法 工具变量法 （Instrument variables）。
二、实际经济问题中的随机解释变量问题 随机解释变量出现的原因： （1）在实际经济问题中，经济变量往往都无 法控制，所以其取值无法确定，必然表现出 随机性。 （2）滞后被解释变量作为解释变量时必然是 随机变量。
Ct-1是一随机解释变量，且与 (µt-λµt-1)高度相关 （Why?）。
三、随机解释变量的后果
计量经济学模型一旦出现随机解释变量，如果仍采用 OLS法估计模型参数，不同性质的随机解释变量会产生 不同的后果。 以下分三种情况讨论： 1、x是随机变量但与u互相独立，则OLSE仍然无偏。 2、x是随机变量，与u不独立但不相关，则OLSE在小样 本下有偏、大样本下具有一致性，即在大样本下OLSE 会逐渐逼近真值。 3、 x是随机变量，且与u相关，则OLSE在小样本下有偏、 大样本下也不具有一致性，即在OLS失效。
ˆ β1 =
∑x y ∑x
i 2 i
i
不具有一致性。 在大样本下也不成立，OLS估计量不具有一致性 不具有一致性
如果选择Z为X的工具变量 工具变量，那么在上述估计 工具变量 过程可改为:
∑z y
i
i
= β 1 ∑ z i xi + ∑ z i µ i
利用E(ziµi)=0，在大样本下可得到：
β1
~
四、解决随机解释变量的方法： 解决随机解释变量的方法： 工具变量法
模型中出现随机解释变量且与随机误差项相 关时，OLS估计量是有偏的。 如果随机解释变量与随机误差项不相关，则 可以通过增大样本容量的办法来得到一致的估计 量； 但如果相关，即使增大样本容量也无济于事。 这时，最常用的估计方法是工具变量法 工具变量法 （Instrument variables）。
二、实际经济问题中的随机解释变量问题 随机解释变量出现的原因： （1）在实际经济问题中，经济变量往往都无 法控制，所以其取值无法确定，必然表现出 随机性。 （2）滞后被解释变量作为解释变量时必然是 随机变量。
计量经济学随机解释变量问题
P134.第四章习 题 第 2 题： 一元线性回归模 型 Yi = β0 + β 1 X i + µi；已知 var ( µi ) = σ i2 ,
Yi β 0 X i µi 1 模型： + β1 + ，对其进行 以权 变换得 二元 模型： = σi σi σi σi σi OLS 估计，证明该模型随机 干扰项满足同方差，并 求此 估计， 干扰项满足同方差， 估计量。 模型中 的 β 1 估计量。
λC t -1 − λµt -1 − λβ0 = β1Yt -1
e
随机解释变量问题. 模型存在 随机解释变量问题
随机解释变量问题对模型参数估计的影响
1. 不相关时， 当随机解释变量 X 2 与随机干扰项 µt 不相关时， 估计仍然无偏。 模型的 OLS 估计仍然无偏。 2.当 cov ( X 2 , µ ) ≠ 0时 , 模型的 OLS 估计是一定是有偏的， 估计是一定是有偏的，
* * Yi* = β0 X 1 + β1 X 2 + µ* (为二元线性回归模型 ) i
(
ˆ Y − Yi*
* i
) = ∑(
2
ˆ * ˆ * Y − β0 X 1 − β 1 X 2
* i
)
2
∂ ∑ e i2 =0 ˆ * ˆ * * 2∑ Yi* − β0 X 1 − β1 X 2 X 1 = 0; ∂β0 ⇒ 2 ˆ * ˆ * * ∂ ∑ ei 2∑ Yi* − β0 X 1 − β1 X 2 X 2 = 0; =0 ∂β 1
S4.4随机解释变量问题 随机解释变量问题
当单方程计量经济学模型的解释变 量不是假设当中的确定性变量， 量不是假设当中的确定性变量，而是随 机变量，并且与随机误差项相关时， 机变量，并且与随机误差项相关时，这 种情形我们称之为随机解释变量问题 随机解释变量问题。 种情形我们称之为随机解释变量问题。
Yi β 0 X i µi 1 模型： + β1 + ，对其进行 以权 变换得 二元 模型： = σi σi σi σi σi OLS 估计，证明该模型随机 干扰项满足同方差，并 求此 估计， 干扰项满足同方差， 估计量。 模型中 的 β 1 估计量。
λC t -1 − λµt -1 − λβ0 = β1Yt -1
e
随机解释变量问题. 模型存在 随机解释变量问题
随机解释变量问题对模型参数估计的影响
1. 不相关时， 当随机解释变量 X 2 与随机干扰项 µt 不相关时， 估计仍然无偏。 模型的 OLS 估计仍然无偏。 2.当 cov ( X 2 , µ ) ≠ 0时 , 模型的 OLS 估计是一定是有偏的， 估计是一定是有偏的，
* * Yi* = β0 X 1 + β1 X 2 + µ* (为二元线性回归模型 ) i
(
ˆ Y − Yi*
* i
) = ∑(
2
ˆ * ˆ * Y − β0 X 1 − β 1 X 2
* i
)
2
∂ ∑ e i2 =0 ˆ * ˆ * * 2∑ Yi* − β0 X 1 − β1 X 2 X 1 = 0; ∂β0 ⇒ 2 ˆ * ˆ * * ∂ ∑ ei 2∑ Yi* − β0 X 1 − β1 X 2 X 2 = 0; =0 ∂β 1
S4.4随机解释变量问题 随机解释变量问题
当单方程计量经济学模型的解释变 量不是假设当中的确定性变量， 量不是假设当中的确定性变量，而是随 机变量，并且与随机误差项相关时， 机变量，并且与随机误差项相关时，这 种情形我们称之为随机解释变量问题 随机解释变量问题。 种情形我们称之为随机解释变量问题。
第7章随机解释变量
第7章 随机解释变量单方程线性计量经济学模型假定解释变量是确定性变量，并且与随机误差项不相关，违背这一基本假设的问题被称为随机解释变量问题。
本章介绍了随机解释变量问题的概念、产生的原因和后果、检验方法以及解决方法。
随机解释变量问题的概念对于计量经济模型n 21i i k i k i 22i 110 ，，，ββββ=+++++=u X X X Y i （7.1.1）其中一个基本假设是解释变量k 21,,X X X 是确定性变量，即解释变量与随机扰动项不相关。
但是在现实经济生活中，这个假定不一定成立，这一方面是因为用于建模的经济变量的观测值一般会存在观测误差，另一方面是经济变量之间联系的普遍性使得解释变量可能在一定程度上依赖于应变量，即解释变量X 影响应变量Y ，而应变量Y 也会反过来影响解释变量X 。
模型中如果存在一个或多个随机变量作为解释变量，就称为模型出现了随机解释变量问题。
其中k x 可能与随机误差项u 不相关，就是说，解释变量121,,-k x x x 都是外生的，但k x 有可能在方程(4.4.1)中是内生的，则称原模型存在随机解释变量问题。
内生性可能源自于省略误差、测量误差，联立性等①。
为讨论方便，我们假设中2X 为随机解释变量。
在模型（）中，根据解释变量2X 与随机误差项的关系，可以分为三种类型： 1)随机解释变量与随机干扰项独立)()(),(),(222===u E x E u x E u X Cov (7.1.2)2)随机解释变量与随机干扰项同期无关但异期相关n 21i 0),(),(i 2i 2 ，，，===u x E u X Cov i i (7.1.3)n 21i 0),(),(s -i 2s -i 2 ，，，=≠=u x E u X Cov i i (7.1.4)3)随机解释变量与随机干扰项同期相关n 21i 0),(),(i 2i 2 ，，，=≠=u x E u X Cov i i (7.1.5)实际经济问题中的随机解释变量在许多经济现象中，自变量的非随机性假定有时是不符合实际的。
第七章 随机变量及其分布(章末小结课件)高二数学(人教A版2019选择性必修第三册)
（1）如图1，进行一次高尔顿板试验，求小球掉入5号球槽的概率.
（2）小红和小明在研究了高尔顿板后，利用高尔顿板来到社团文化节上进行盈利性“抽奖”活动.小红使用图1所示的高尔顿板，付费6元可以玩一次游戏，小球掉入 号球槽得到的奖金为 元，其中 .小明改进了高尔顿板（如图2），首先将小木块减少成5层，然后使小球在下落的过程中与小木块碰撞时，有 的概率向左， 的概率向右滚下，最后掉入编号为1， ， ， 的球槽内，改进高尔顿板后只需付费4元就可以玩一次游戏，小球掉入 号球槽得到的奖金为 元，其中 .两位同学的高尔顿板游戏火爆进行，很多同学参加了游戏，你觉得小红和小明谁的盈利多？请说明理由.
方法总结 求离散型随机变量的均值、方差的步骤： 明确随机变量的取值，以及取每个值的试验结果； 求出随机变量取各个值的概率； 列出分布列； 用期望、方差公式求解； 标准差代入公式 求解.本题渗透了数据分析、数学运算的素养.
题型7 正态分布
例7 某物理量的测量结果服从正态分布 ，则下列结论中不正确的是( ).
方法总结 正态曲线的应用及求解策略：解答此类题目的关键在于将待求的问题向 ， ， 这三个区间进行转化，然后利用上述区间的概率求出相应的概率.解题过程渗透了直观想象、数学运算以及数据分析的素养.
高尔顿与高尔顿板
一、高尔顿简介
弗朗西斯·高尔顿（ ， —1911）是英国著名的统计学家、心理学家和遗传学家.他是达尔文的表弟，虽然不像达尔文那样声名显赫，但也不是无名之辈.并且，高尔顿幼年是神童，长大是才子，九十年的人生丰富多彩，是个名副其实的博学家.他涉猎范围广泛，研究水平颇深，纵观科学史，在同辈学者中能望其项背之人寥寥可数.他涉足的领域包括天文、地理、气象、机械、物理、统计、生物、遗传、医学、生理、心理等，还有与社会有关的人类学、民族学、教育学、宗教学，以及优生学、指纹学、照相术、登山术等等.
（2）小红和小明在研究了高尔顿板后，利用高尔顿板来到社团文化节上进行盈利性“抽奖”活动.小红使用图1所示的高尔顿板，付费6元可以玩一次游戏，小球掉入 号球槽得到的奖金为 元，其中 .小明改进了高尔顿板（如图2），首先将小木块减少成5层，然后使小球在下落的过程中与小木块碰撞时，有 的概率向左， 的概率向右滚下，最后掉入编号为1， ， ， 的球槽内，改进高尔顿板后只需付费4元就可以玩一次游戏，小球掉入 号球槽得到的奖金为 元，其中 .两位同学的高尔顿板游戏火爆进行，很多同学参加了游戏，你觉得小红和小明谁的盈利多？请说明理由.
方法总结 求离散型随机变量的均值、方差的步骤： 明确随机变量的取值，以及取每个值的试验结果； 求出随机变量取各个值的概率； 列出分布列； 用期望、方差公式求解； 标准差代入公式 求解.本题渗透了数据分析、数学运算的素养.
题型7 正态分布
例7 某物理量的测量结果服从正态分布 ，则下列结论中不正确的是( ).
方法总结 正态曲线的应用及求解策略：解答此类题目的关键在于将待求的问题向 ， ， 这三个区间进行转化，然后利用上述区间的概率求出相应的概率.解题过程渗透了直观想象、数学运算以及数据分析的素养.
高尔顿与高尔顿板
一、高尔顿简介
弗朗西斯·高尔顿（ ， —1911）是英国著名的统计学家、心理学家和遗传学家.他是达尔文的表弟，虽然不像达尔文那样声名显赫，但也不是无名之辈.并且，高尔顿幼年是神童，长大是才子，九十年的人生丰富多彩，是个名副其实的博学家.他涉猎范围广泛，研究水平颇深，纵观科学史，在同辈学者中能望其项背之人寥寥可数.他涉足的领域包括天文、地理、气象、机械、物理、统计、生物、遗传、医学、生理、心理等，还有与社会有关的人类学、民族学、教育学、宗教学，以及优生学、指纹学、照相术、登山术等等.
第七章 随机解释变量
第七章 随机解释变量一、填空题1.随机解释变量X 与随机误差项u 相关，可表示为__________。
2.工具变量法并没有改变原模型，只是在原模型的参数估计过程中用工具变量“替代” __________。
3.对于模型i ik i i i u X X X Y +++++=322110ββββ ，i=1,2,…,n ，若用工具变量Z 代替其中的随机解释变量2X ，则采用工具变量法所得新的正规方程组仅仅是将原正规方程组中的方程2221102)(i ik k i i i i X X b X b X b b Y X ++++=∑∑ 用方程______________代替，而其他方程则保持不变。
4.狭义工具变量法参数估计量的统计性质是小样本下__________，大样本下_________。
5.对于线性回归模型i ik i i i u X X X Y +++++=322110ββββ ，i=1,2,…,n ，其矩阵表示为u X Y +=β。
若用工具变量Z 代替其中的随机解释变量2X ，则采用工具变量法所得参数估计量的矩阵表示为__________，其中Z 被称为__________。
二、简答题1. 什么是工具变量？2. 选择作为工具变量的变量必须满足哪些条件？参考答案一、填空题1.Cov(X,u)≠0;2.解释变量；3. i ik k i i i i Z X b X b X b b Y Z )(22110++++=∑∑ ;4.有偏；无偏；5. Y Z X Z b ''=-1)(;工具变量二、简答题1. 答：在模型估计过程中被作为工具使用，以替代模型中与随机误差项相关的随机解释变量。
2. 答：（1）与所替代的随机解释变量高度相关；（2）与随机误差项不相关；（3）与模型中其他解释变量不相关，以避免出现多重共线性。
计量经济学随机解释变量的问题
合理预期的消费函数模型
合理预期理论认为消费是由对收入的预期所决定 的，或者说消费是有计划的，而这个计划是根据对 收入的预期制定的。于是有：
Ct 0 1Yt e t
C t 1 0 1Yt e 1 t 1
e Y 其中 t 表示 t 期收入预期值。
而预期收入与实际收入之间存在差距，表现为：
0 (1 ) 1 (1 )Yt Ct 1 t t 1
在该模型中，作为解释变量的Ct-1不仅是一个随 机解释变量，而且与模型的随机误差项(t-t-1)高 度相关（因为Ct-1与t-1高度相关）。属于上述第3种 情况。
二、随机解释变量的后果
三、工具变量法 Instrumental Variables Method
1、工具变量的选取
工具变量：在模型估计过程中被作为工具使用， 以替代模型中与随机误差项相关的随机解释变量。
选择为工具变量的变量必须满足以下条件： （1）与所替代的随机解释变量高度相关； （2）与随机误差项不相关； （3）与模型中其它解释变量不相关，以避免出 现多重共线性。
此时，我们即可认为， a,b1,b2,b3这些参 数的估计准确度基本不受影响。
• 如果将i换成时间t，则表示的是同一块土地 上每年的要素投入量，试想一下，前面的 “同期不相关”指的是什么意思？
• 2.如果随机解释变量与随机扰动项之间，随 着样本数量的增多，而渐渐地不相关，那 么估计出的参数满足一致性。 • 例如，国家统计局的数据统计一年比一年 精确，那么如果用年度数据进行模型估计， 就会出现渐近不相关的现象。
• （二）对显著性假设检验的影响
仪器 : T
i 0 2
SSTi (1 Ri2 )
第七章 虚拟变量和随机解释变量 (2)
第七章 虚拟变量和随机解释变量本章将讨论两种不同的模型：虚拟变量模型和随机解释变量模型，以及模型设定的其它问题。
第一节 虚拟变量模型在我们以前考虑的模型中，解释变量都是定量变量（如成本、价格、收入、产出等），但在经济研究中，因变量经常受到一些定性变量的影响（如性别、种族、季节、不同历史时期等），我们把这类定性变量称为虚拟变量。
习惯上用Ｄ表示虚拟变量，虚拟变量的取值通常为0和1。
0表示变量具备某种属性，1表示变量不具备某种属性。
一、包含一个虚拟变量的模型如果我们要研究的问题中解释变量只分为两类。
则需引入一个模拟变量。
例9.1建立模型研究中国妇女在工作中是否受到歧视。
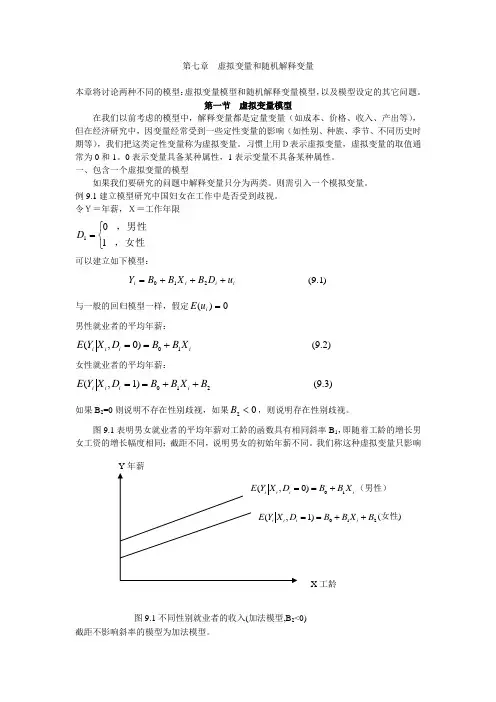
令Ｙ＝年薪，Ｘ＝工作年限⎩⎨⎧=，女性，男性101D 可以建立如下模型：i i i i u D B X B B Y +++=210 )1.9( 与一般的回归模型一样，假定0)(=i u E 男性就业者的平均年薪：i i i i X B B D X Y E 10)0,(+== )2.9(女性就业者的平均年薪：210)1,(B X B B D X Y E i i i i ++== )3.9(如果B 2=0则说明不存在性别歧视，如果02<B ，则说明存在性别歧视。
图9.1表明男女就业者的平均年薪对工龄的函数具有相同斜率B 1，即随着工龄的增长男女工资的增长幅度相同；截距不同，说明男女的初始年薪不同。
我们称这种虚拟变量只影响截距不影响斜率的模型为加法模型。
图9.1不同性别就业者的收入(加法模型,B 2<0)如果随着工龄增加，男性与女性的年薪差距也发生变化，则模型（9.1）就变为i i i i i u X D B X B B Y +++=210 )4.9(图9.2描绘了男性年薪增加较快的情况。
我们称虚拟变量只影响斜率而不影响截距的模型为乘法模型如（9.4）如果男性与女性的初始年薪和年薪增加速度都有差异，我们可以将加法模型和乘法模型结合起来，得到如下模型i i i i i i u D B X D B X B B Y ++++=3210 )5.9(模型（9.5）可以用来表示截距和斜率都发生变化的模型。
第七章 随机性解释变量与工具变量估计
第七章 随机性解释变量与工具变量估计Y X βε=+，古典假定中解释变量X 是非随机的。
如果存在一个或多个随机变量作为解释变量，则原模型出现随机性解释变量的问题。
产生随机性解释变量的情形： 1） 被解释变量的滞后项作为解释变量 1t t t t C Y C γαβε−=+++t2） 双向因果关系（联立方程） 12123t t t t t t Y X X Y Z ββμγγγ=++=+++ν，价格（）与需求（t Y t X ）互为因果，t Z 可以指收入。
解释变量的随机性在联立方程中不可避免。
3） 测量误差12Y X ββ=++ε，若解释变量X 存在测量误差：*X X ν=+，那么实际使用的解释变量是*X ，显然*X 随机。
一、随机性解释变量的导致的理论问题1ˆ(')'X X X ββε−=+， 1''ˆlim lim()lim()X X X p p p n nεββ−=+， 若X 非随机，有()ˆE ββ=，ˆlim p ββ=； 若X 随机，则?ˆ()E ββ=，?ˆlim p ββ= 注意：若(,)f X Y 是(,)X Y 的联合密度，是(,)h X Y (,)X Y 的函数，则：[(,)]{[(,)]}Y X E h X Y E E h X Y Y =若解释变量随机，则X 是随机矩阵（至少有一列是随机变量）。
设'lim()X Xp Q n=，有限，正定。
球形扰动即为：2(')n E X I εεσ=Case1： X 与ε独立（不相关）：(,)0i i Cov X ε=。
则有()E X ε0=，于是11ˆ()[(')'][(')'()]XE E X X X E X X X E X ββεβε−−=+=+=β最小二乘估计仍为无偏估计，其方差阵为：11112ˆˆˆ()[()()'][(')''(')] [(')'(')(')](')X Var E E X X X X X X E X X X E X X X X E X X βββββεεεεσ−−−−=−−===1−如果ε为条件正态分布，则 21ˆ(,('))N E X X ββσ−∼大样本性质：ˆlim p ββ=。
计量经济学随机解释变量问题
（4-16）
不相关，即
（4-17）
C o vZ ( i, 0 i)
3. 工具变量 Z 与模型中其他解释变量不相关，以避免出现多重共线性。
二、工具变量的应用（以一元回归模型为例说明）
记一元线性回归模型如下：
Y X i 0 1 i i
用普通最小二乘法估计模型(4-18)式 得正规方程组： 得正规方程组：
于是 （4-20）
于是
ˆ1
xy x
i 2 i
i
1
z y zx
i
i
（4-21）
i i
二、工具变量的应用（以多元线性回归模型为例说明）
其矩阵形式为
YX β
采用参数估计量得到的 正规方程组为
1 = ( Z X ) Z Y
采用工具变量法得到的 正规方程组为
Z Y= Z X
以一元线性回归模型为例进行说明。
图4-1
从图形 (图4-1)上看，如果随机解释变量与随机干扰项正相关，则在抽 取样本时，容易出现X值较小的点在总体回归线下方，而X值较大的点在总 体回归线上方的情况，因此，拟合的样本回归线则可能低估(underestimate) 了截距项，而高估(overestimate)斜率项。反之，如果随机解释变量与随机 干扰项负相关，则往往导致拟合的样本回归线高估截距项，而低估斜率项。
通常，对于没有选择另外的变量 作为工具变量的解释变量，可以认为 用自身作为工具变量。于是Z称为工 具变量矩阵。
（4-22）
Z
其中
1 Z1 X 21 X k1
1 Z2 X 22 X k2
1 Zn X 2n X kn
三、工具变量法估计量的性质
第七章 随机解释变量问题
【课外修炼】 阅读《计量经济学》（于俊年 编著） “十二五”普通高等教育本科国家级规划教材，高 等院校国际经贸专业规划教材，2014年9月（第三版）对 外经贸大学出版社出版。 一、作者简介 于俊年，对外经济贸易大学教授，研究领域包括计量经 济学、项目经济分析数量方法、投资项目可行性研究与项 目评估，出版并发表了多本著作和学术论文。 二、主要特点 全书分四篇共十七章。第一篇导论，第二篇系统地讲述 单方程回归模型的基本理论和方法，第三篇系统地讲述违 背经典回归假定的有关经济计量模型，第四篇讲述经济模 型构造理论与应用。由浅入深，循序渐进，
一方面由一些基本经济知识作一些判断，例如由于惯性的 存在，当期消费在一定程度上会受到前期的消费支出的影 响，但当期消费却不会对前期消费进行影响；另一方面豪 斯曼（Hauseman）检验从计量技术上给出了一种检验随 机解释变量是否具有内生性的有效方法。 豪斯曼检验的基本思想：已知某二元线性回归模型
Y X Z
任务7.1 随机解释变量问题概述 一、随机解释变量问题的概念 单方程线性计量经济学模型假设方程的解释变量为确定 性变量，同时解释变量还要与随机误差项不相关。如果违 背了这一基本假设，则我们将这样的问题称之为随机解释 变量问题（Stochastic explanatory variables problem） 对于模型 Yi 0 1 X1i 2 X 2i k X ki i 假定解释变量 X1, X2 ..., Xk 都是确定性变量， 即解释变量与随机扰动项不相关。但现实中，这个假设并 不一定成立，因为一方面模型中经济变量的观测值一般会 存在观测误差；
任务7.3 随机解释变量问题的修正 模型中出现随机解释变量与随机误差项相关时，普 通最小二乘法参数估计值是有偏的。如果随机解释变量 与随机误差项异期相关，则可以通过增大样本容量的办 法来得到一致的估计量；但如果是同期相关，即使增大 样本容量也无法起作用,这时通常使用工具变量法来进行 估计。
计量经济学—理论和应用4-4
（2）令MIN为该国的最低限度工资，它会与随
机干扰项相关吗？ （3）按照法律，各地区最低限度工资不得低于国 家最低工资，那么Gmin能成为Gmin1的工具 变量吗？ 2. 对模型 Yt 0 1 X1t 2 X 2t 3Yt1 t ,假设Yt-1与 t 相关。为了消除该相关性，采用工具变量法： ˆ 先求Yt关于X1t和X2t的回归，得到 Yt ，再做如 下回归
(xii)/n0
表明大样本下
ˆ 1
x y x
i 2 i
i
成立，即OLS估计量具有一致性。 然而，如果Xi与i相关，即使在大样本下，也 不存在 (xii)/n0 ，则
ˆ 1
x y x
i 2 i
i
在大样本下也不成立，OLS估计量不具有一致性。
工具变量法
如果选择Z为X的工具变量，那么在上述估计 过程可改为:
工具变量法是GMM的一个特例。
6、要找到与随机扰动项不相关而又与随机解释 变量相关的工具变量并不是一件很容易的事
可以用Xt-1作为原解释变量Xt的工具变量。
案例——中国居民人均消费函数
例4.4.1 在例2.5.1的中国居民人均消费函数的 估计中，采用OLS估计了下面的模型：
CONSP 0 1GDPP
Cov( X 2i, i ) E( x2i i ) 0
实际经济问题中的随机解释变量问题
在实际经济问题中，经济变量往往都具 有随机性。
但是在单方程计量经济学模型中，凡是外 生变量都被认为是确定性的。 于是随机解释变量问题主要表现于：用滞 后被解释变量作为模型的解释变量的情况。
实际经济问题中的随机解释变量问题
如果用GDPPt-1为工具变量，可得如下工具变 量法估计结果：
随机解释变量
随机解释变量带来什么后果取决于它与随 机误差项是否相关，以及什么程度的相关。
1. 随机解释变量与随机误差项不相关
这时采用OLS法估计模型参数，得到的参 数估计量仍然是无偏估计量。
2. 随机解释变量与随机误差项在小样本下相 关，在大样本下渐近无关
这时采用OLS法估计模型参数，得到的参 数估计量在小样本下是有偏的，在大样本下 具有渐进无偏性。
Yi X1i
YiZi
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X1i ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki Zi
M
Yi X ki
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X ki
• 求解这个方程组就可以得到原模型参数的工具 变量法估计量。
Yi X1i
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X1i
Yi X 2i
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X 2i
M
Yi X ki
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X ki
• 该方程组也可以看作是矩方法的结果。用每个 解释变量分别乘以模型的两边，并对所有样本点 求和：
E(X2) 0
（2）随机解释变量与随机误差项在小样本下相关， 在大样本下渐近无关。即
在小样本下 E( X 2 ) 0
在大样本下 Plim( X2ii n) 0
或
P lim( n
X 2ii n) 0 1
（3）随机解释变量与随机误差项在大样本下高 度相关。
Plim( X2ii n) 0
Yi 0 1X1i 2 X 2i L k X ki i
Yi X1i Yi X 2i
0 1X1i 2 X 2i L k X ki i X1i 0 1X1i 2 X 2i L k X ki i X 2i
1. 随机解释变量与随机误差项不相关
这时采用OLS法估计模型参数，得到的参 数估计量仍然是无偏估计量。
2. 随机解释变量与随机误差项在小样本下相 关，在大样本下渐近无关
这时采用OLS法估计模型参数，得到的参 数估计量在小样本下是有偏的，在大样本下 具有渐进无偏性。
Yi X1i
YiZi
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X1i ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki Zi
M
Yi X ki
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X ki
• 求解这个方程组就可以得到原模型参数的工具 变量法估计量。
Yi X1i
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X1i
Yi X 2i
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X 2i
M
Yi X ki
ˆ0 ˆ1X1i ˆ2 X 2i L ˆk X ki X ki
• 该方程组也可以看作是矩方法的结果。用每个 解释变量分别乘以模型的两边，并对所有样本点 求和：
E(X2) 0
（2）随机解释变量与随机误差项在小样本下相关， 在大样本下渐近无关。即
在小样本下 E( X 2 ) 0
在大样本下 Plim( X2ii n) 0
或
P lim( n
X 2ii n) 0 1
（3）随机解释变量与随机误差项在大样本下高 度相关。
Plim( X2ii n) 0
Yi 0 1X1i 2 X 2i L k X ki i
Yi X1i Yi X 2i
0 1X1i 2 X 2i L k X ki i X1i 0 1X1i 2 X 2i L k X ki i X 2i
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018/10/24 24
选择TSLS后打开下一个窗口
Hale Waihona Puke 2018/10/2425
模型设定
工具变量
估计方法
2018/10/24 26
工具变量法估计输出结果
2018/10/24
返回
27
六、运用工具变量法的实例
• • • • • 估计经济系统模型时常用TSLS估计 人民大学：《计量经济学教程》 第388页，美国季度宏观经济模型 资料：LX7\JKSH388Y.WF1 注意：有相应的SYSTEM模型文件
2018/10/24
22
4、工具变量法的局限
• 1 、 Z 难选，通常从前定变量（包括外生 变量）中选择或者用该变量的估计值作 为工具变量，例如X2^==>X2 • 2、Z不唯一 • 3、最小方差性不满足
返回
2018/10/24 23
五、EViews中实现工具变量法
• 工具变量法包含在TSLS中。设定模型后， 选择TSLS方法，打开一个要求给出工具 变量列表的对话框，填入适当的IV。 • Lx7\jksh388y.wf1 • cc=消费 • 采用TSLS估计 • 消费方程模型： cc c gnp cc(-1) • 工具变量：c gnp(-1) cc(-1)
6
2、运算法则 P lim ( X n Yn )＝P lim X n P lim Yn
n n n n n
P lim ( X n Yn )＝P lim X n P lim Yn
n n
P lim ( X n / Yn )＝P lim X n / P lim Yn
2018/10/24
X 随机，Cov(Xi, ui)0
1
教学内容
• • • • • • 一、随机解释变量问题 二、实际经济问题中的随机解释变量问题 三、随机解释变量问题的后果 四、工具变量法 五、工具变量法在EViews的实现 六、应用实例
2
2018/10/24
问题的提出：
在古典假定中要求解释 变量X是确定的变量， 并且与ui不相关，即： cov(xi , ui ) 0 但是从实际意义上看， 模型中的解释变量 与被模型省略的变量之 间完全可能相关。 于是， cov(xi , ui ) 0。因此，当上述古典假 定 不满足的时候，这时的 模型称为随机解释变 量模型。
2018/10/24
即Plim x2i ui n 0 1
返回
12
二、实际经济问题中的 随机解释变量问题
实际经济问题中，经济变量都具有随机性， 但是在模型中都将解释变量假定为外生的。 所谓随机解释变量问题主要表现在滞后被解 释变量做解释变量时。举例说明： （1）随机解释变量与随机误差项不相关 ——耐用品存量模型 （2）随机解释变量与随机误差项高度相关 ——合理预期的消费函数模型
2018/10/24 20
2、IV工具变量法
• IV法只是在估计过程中用IV替代了与随机误差项相关的变量， 并不是改变了原模型
• Y=XB+N • 采用工具变量Z=>正规方程： ZTXB^=Z`Y • B^=(ZTX)-1ZTY X2是随机解释变量
1 x11 Z z1 xk1 2018/10/24 1
n
ˆ (n) ) （ 且Var( 0 n ） ˆ ( n ) （一致无偏） 则有P lim
n
2018/10/24
10
一、随机解释变量问题
• 违反模型基本假定1——解释变量是确定性 变量的假定，某个或某些解释变量是随机 变量，称为随机解释变量问题。实际上是 指： X 随机，Cov(Xi, ui)0
2018/10/24
16
三、随机解释变量问题的后果
1、随机解释变量与随机误差项不相关 参数估计量仍然无偏估计量 2、随机解释变量与随机误差项在小样本下相关，在大样本下 渐进无关 参数估计量在小样本下是有偏的，在大样本下具有渐进无 偏性 3、随机解释变量与随机误差项高度相关 参数估计量在小样本下是有偏的，在大样本下不具有渐进 无偏性。而且； （1）随机误差项必然具有自相关 （2）DW检验失效，无论DW数值多大或多小均存在自相关
x z x
12 2
k2
1 x12 zn xkn
Z是X2的工具变量
其余解释变量用自身
作自己的工具变量 c是一个很好的IV
21
3、工具变量法估计量的特性
• （1）工具变量估计法得到的估计量是无偏 估计量 • （2）工具变量估计法得到的估计量是一致 估计量
2018/10/24 8
五、一致性 1、一致估计量 ˆ ( n ) , 则称 ˆ ( n )是的一致估计量。 若P lim
n
2、区别 ˆ (1) , ˆ ( 2) ,... ˆ ( n ) ,... ˆ (1) ) , E ( ˆ ( 2) ) ,... E ( ˆ ( n ) ) ,... 无偏性：E ( ˆ (1) ), E ( ˆ ( 2) ),... E ( ˆ ( n ) ),... （n ） 渐进无偏性：E ( 一致无偏性：
2018/10/24
5
三、概率极限 1、定义 设{ X n }为随机变量序列，若对任意给定的 0, 0 1存在N使得当n N时， P{| X n a | } 1 则称序列{ X n }依概率收敛于a, 记为 P lim X n a
n
2018/10/24
t 0 1 t 1 t 1 0 0 0 1 t t 1 0 t 1 t t 1 1 t t t 1 t 1 t 1 t t t t 1 t t 1 t 1 t 1
返回
2018/10/24
15
三、随机解释变量问题的后果
• • • • • • Y=XB+U B=(XTX)-1XTY B=(XTX)-1XTXB+U) B=（XTX）-1XTXB+(XTX)-1XTU E(B^)=B+(XTX)-1E(XTU) 因此估计量的优良性由E(XTU)确定
2 2
• 2、随机解释变量与随机误差项在小样本下相关，
E
x u 0
• 在大样本下渐进无关
P lim x2i ui n 0
即Plim x2i ui n 0 1
• 3、随机解释变量与随机误差项高度相关而且它们依概 率1都不存在不相关。
P lim x2i ui n 0
2018/10/24 17
大小样本特性
• 1、小样本特性： 样本容量有限时的统计特性 • 2、大样本特性： 小样本时不具备的统计性质，样本容量增大 时，随机量的统计特性 随机解释变量的特性问题，需要讨论概率极 限问题，请参阅其他读物（渐近无偏性， 一致性）
2018/10/24
返回
18
四、工具变量法
t
（ 1 λ ） I I λ I C （1 λ ） I λ I u （ 1 λ ） I λ C u u 合理预期消费函数 （ 1 λ ） （ 1 λ ） I λ C u λ u 属于第三类 （ 1 λ ） （ 1 λ ） I λ C v v u λ u v 与C 相关 C 与u 相关
2018/10/24 3
一些概念
一、大小样本特征 1、小样本特性：样本容量有限时的统计特性。
2、大样本特性：小样本时不具备的统计性质， 样本容量增大时，随机量的统计特性。
2018/10/24
4
二、序列 1、的估计量序列 — 随机序列 ˆ (n) } : ˆ (1) , ˆ ( 2) ,... ˆ ( n ) ,... { 2、期望序列 — 数值序列 ˆ ( n ) )} : E ( ˆ (1) ), E ( ˆ ( 2) ),... E ( ˆ ( n ) ),... {E ( 3、方差序列 — 数值序列 ˆ ( n ) )} : var( ˆ ( 2) )， ˆ ( 2) )， ˆ ( n ) )... {var( var( ... var(
2018/10/24
28
2018/10/24
返回 29
2018/10/24
ˆ (1)
,
ˆ ( 2)
,...
ˆ (n)
,... （n ）
9
p
3、一致性的性质 ˆ ( n ) ) ，则有P lim ˆ (n) （ 1 ）若E (
n
（无偏 一致无偏） ˆ ( n ) ) （渐进无偏） （2）若 lim E (
n n
注：假定上述极限存在且分母不为零。
2018/10/24
7
四、渐进性 1、渐进期望 ˆ (n) ) lim E (
n
2、渐进无偏 (n) ˆ E ( ) lim
n
3、渐进方差 1 (n) ˆ ˆ (n) E ( ˆ ( n ) )) 2 ] asyVar ( ) lim E[n( n n ＋
• • • • 1、工具变量 2、IV工具变量法 3、工具变量法估计量的特性 4、工具变量法的局限
2018/10/24
19
1、工具变量 Instrumental variables
• 功能：在OLS估计中被当成工具，用以替代与 随机误差项相关的随机解释变量。 • 工具变量满足的条件： • （1） Z与替代的随机解释变量Xj高度相关 • E(Xj,Z)0 • （2） Z与随机误差项uj无关 • E(uj,Z)=0 • （3） Z与模型中的其他解释变量Xi不相关 • E(Xi,Z)=0 i j
第七章 随机解释变量问题
回顾线性回归模型假设 • 假定1：在重复抽样中解释变量X是确定性变量——固定的（非随机， 而且解释变量之间不相关） • 假定2：随机误差项具有0均值。即， E(ui|Xi)=0 • 假定3：随机误差项具有同方差。即， Var(ui|Xi)=2 • 假定4：随机误差项在不同样本点之间是独立的。即， Cov(ui,uj)=0 • 假定5：随机误差项服从0均值、同方差的正态分布。即， ui ~ N(0,2) 假设6:解释变量之间不存在完全或近似的线性关系 违反模型基本假定1——解释变量是决定性变量的假定，称为随机解释变 量问题。
选择TSLS后打开下一个窗口
Hale Waihona Puke 2018/10/2425
模型设定
工具变量
估计方法
2018/10/24 26
工具变量法估计输出结果
2018/10/24
返回
27
六、运用工具变量法的实例
• • • • • 估计经济系统模型时常用TSLS估计 人民大学：《计量经济学教程》 第388页，美国季度宏观经济模型 资料：LX7\JKSH388Y.WF1 注意：有相应的SYSTEM模型文件
2018/10/24
22
4、工具变量法的局限
• 1 、 Z 难选，通常从前定变量（包括外生 变量）中选择或者用该变量的估计值作 为工具变量，例如X2^==>X2 • 2、Z不唯一 • 3、最小方差性不满足
返回
2018/10/24 23
五、EViews中实现工具变量法
• 工具变量法包含在TSLS中。设定模型后， 选择TSLS方法，打开一个要求给出工具 变量列表的对话框，填入适当的IV。 • Lx7\jksh388y.wf1 • cc=消费 • 采用TSLS估计 • 消费方程模型： cc c gnp cc(-1) • 工具变量：c gnp(-1) cc(-1)
6
2、运算法则 P lim ( X n Yn )＝P lim X n P lim Yn
n n n n n
P lim ( X n Yn )＝P lim X n P lim Yn
n n
P lim ( X n / Yn )＝P lim X n / P lim Yn
2018/10/24
X 随机，Cov(Xi, ui)0
1
教学内容
• • • • • • 一、随机解释变量问题 二、实际经济问题中的随机解释变量问题 三、随机解释变量问题的后果 四、工具变量法 五、工具变量法在EViews的实现 六、应用实例
2
2018/10/24
问题的提出：
在古典假定中要求解释 变量X是确定的变量， 并且与ui不相关，即： cov(xi , ui ) 0 但是从实际意义上看， 模型中的解释变量 与被模型省略的变量之 间完全可能相关。 于是， cov(xi , ui ) 0。因此，当上述古典假 定 不满足的时候，这时的 模型称为随机解释变 量模型。
2018/10/24
即Plim x2i ui n 0 1
返回
12
二、实际经济问题中的 随机解释变量问题
实际经济问题中，经济变量都具有随机性， 但是在模型中都将解释变量假定为外生的。 所谓随机解释变量问题主要表现在滞后被解 释变量做解释变量时。举例说明： （1）随机解释变量与随机误差项不相关 ——耐用品存量模型 （2）随机解释变量与随机误差项高度相关 ——合理预期的消费函数模型
2018/10/24 20
2、IV工具变量法
• IV法只是在估计过程中用IV替代了与随机误差项相关的变量， 并不是改变了原模型
• Y=XB+N • 采用工具变量Z=>正规方程： ZTXB^=Z`Y • B^=(ZTX)-1ZTY X2是随机解释变量
1 x11 Z z1 xk1 2018/10/24 1
n
ˆ (n) ) （ 且Var( 0 n ） ˆ ( n ) （一致无偏） 则有P lim
n
2018/10/24
10
一、随机解释变量问题
• 违反模型基本假定1——解释变量是确定性 变量的假定，某个或某些解释变量是随机 变量，称为随机解释变量问题。实际上是 指： X 随机，Cov(Xi, ui)0
2018/10/24
16
三、随机解释变量问题的后果
1、随机解释变量与随机误差项不相关 参数估计量仍然无偏估计量 2、随机解释变量与随机误差项在小样本下相关，在大样本下 渐进无关 参数估计量在小样本下是有偏的，在大样本下具有渐进无 偏性 3、随机解释变量与随机误差项高度相关 参数估计量在小样本下是有偏的，在大样本下不具有渐进 无偏性。而且； （1）随机误差项必然具有自相关 （2）DW检验失效，无论DW数值多大或多小均存在自相关
x z x
12 2
k2
1 x12 zn xkn
Z是X2的工具变量
其余解释变量用自身
作自己的工具变量 c是一个很好的IV
21
3、工具变量法估计量的特性
• （1）工具变量估计法得到的估计量是无偏 估计量 • （2）工具变量估计法得到的估计量是一致 估计量
2018/10/24 8
五、一致性 1、一致估计量 ˆ ( n ) , 则称 ˆ ( n )是的一致估计量。 若P lim
n
2、区别 ˆ (1) , ˆ ( 2) ,... ˆ ( n ) ,... ˆ (1) ) , E ( ˆ ( 2) ) ,... E ( ˆ ( n ) ) ,... 无偏性：E ( ˆ (1) ), E ( ˆ ( 2) ),... E ( ˆ ( n ) ),... （n ） 渐进无偏性：E ( 一致无偏性：
2018/10/24
5
三、概率极限 1、定义 设{ X n }为随机变量序列，若对任意给定的 0, 0 1存在N使得当n N时， P{| X n a | } 1 则称序列{ X n }依概率收敛于a, 记为 P lim X n a
n
2018/10/24
t 0 1 t 1 t 1 0 0 0 1 t t 1 0 t 1 t t 1 1 t t t 1 t 1 t 1 t t t t 1 t t 1 t 1 t 1
返回
2018/10/24
15
三、随机解释变量问题的后果
• • • • • • Y=XB+U B=(XTX)-1XTY B=(XTX)-1XTXB+U) B=（XTX）-1XTXB+(XTX)-1XTU E(B^)=B+(XTX)-1E(XTU) 因此估计量的优良性由E(XTU)确定
2 2
• 2、随机解释变量与随机误差项在小样本下相关，
E
x u 0
• 在大样本下渐进无关
P lim x2i ui n 0
即Plim x2i ui n 0 1
• 3、随机解释变量与随机误差项高度相关而且它们依概 率1都不存在不相关。
P lim x2i ui n 0
2018/10/24 17
大小样本特性
• 1、小样本特性： 样本容量有限时的统计特性 • 2、大样本特性： 小样本时不具备的统计性质，样本容量增大 时，随机量的统计特性 随机解释变量的特性问题，需要讨论概率极 限问题，请参阅其他读物（渐近无偏性， 一致性）
2018/10/24
返回
18
四、工具变量法
t
（ 1 λ ） I I λ I C （1 λ ） I λ I u （ 1 λ ） I λ C u u 合理预期消费函数 （ 1 λ ） （ 1 λ ） I λ C u λ u 属于第三类 （ 1 λ ） （ 1 λ ） I λ C v v u λ u v 与C 相关 C 与u 相关
2018/10/24 3
一些概念
一、大小样本特征 1、小样本特性：样本容量有限时的统计特性。
2、大样本特性：小样本时不具备的统计性质， 样本容量增大时，随机量的统计特性。
2018/10/24
4
二、序列 1、的估计量序列 — 随机序列 ˆ (n) } : ˆ (1) , ˆ ( 2) ,... ˆ ( n ) ,... { 2、期望序列 — 数值序列 ˆ ( n ) )} : E ( ˆ (1) ), E ( ˆ ( 2) ),... E ( ˆ ( n ) ),... {E ( 3、方差序列 — 数值序列 ˆ ( n ) )} : var( ˆ ( 2) )， ˆ ( 2) )， ˆ ( n ) )... {var( var( ... var(
2018/10/24
28
2018/10/24
返回 29
2018/10/24
ˆ (1)
,
ˆ ( 2)
,...
ˆ (n)
,... （n ）
9
p
3、一致性的性质 ˆ ( n ) ) ，则有P lim ˆ (n) （ 1 ）若E (
n
（无偏 一致无偏） ˆ ( n ) ) （渐进无偏） （2）若 lim E (
n n
注：假定上述极限存在且分母不为零。
2018/10/24
7
四、渐进性 1、渐进期望 ˆ (n) ) lim E (
n
2、渐进无偏 (n) ˆ E ( ) lim
n
3、渐进方差 1 (n) ˆ ˆ (n) E ( ˆ ( n ) )) 2 ] asyVar ( ) lim E[n( n n ＋
• • • • 1、工具变量 2、IV工具变量法 3、工具变量法估计量的特性 4、工具变量法的局限
2018/10/24
19
1、工具变量 Instrumental variables
• 功能：在OLS估计中被当成工具，用以替代与 随机误差项相关的随机解释变量。 • 工具变量满足的条件： • （1） Z与替代的随机解释变量Xj高度相关 • E(Xj,Z)0 • （2） Z与随机误差项uj无关 • E(uj,Z)=0 • （3） Z与模型中的其他解释变量Xi不相关 • E(Xi,Z)=0 i j
第七章 随机解释变量问题
回顾线性回归模型假设 • 假定1：在重复抽样中解释变量X是确定性变量——固定的（非随机， 而且解释变量之间不相关） • 假定2：随机误差项具有0均值。即， E(ui|Xi)=0 • 假定3：随机误差项具有同方差。即， Var(ui|Xi)=2 • 假定4：随机误差项在不同样本点之间是独立的。即， Cov(ui,uj)=0 • 假定5：随机误差项服从0均值、同方差的正态分布。即， ui ~ N(0,2) 假设6:解释变量之间不存在完全或近似的线性关系 违反模型基本假定1——解释变量是决定性变量的假定，称为随机解释变 量问题。