实验一 摩尔折射度的测定

一.实验的目的和意义1 .通过阿贝折射仪测水，糖水，玻璃的折射率，掌握阿贝折射仪的使用，同时了解掠入射法测定液体折射率，反射法和掠入法测固体折射率，即掌握使用阿贝折射仪测定物质折射率的方法，另外通过对葡萄糖溶液折射率的测定，确定其浓度。

2.通过自行搭建干涉装置，掌握分振幅法产生双光束以实现干涉的原理，观察非定域干涉条纹，掌握用干涉条纹计数法测量空气折射率的原理与方法。

3.通过研究对比空气和水在牛顿环里发生的干涉现象，更新了液体折射率的测试方法，使牛顿环的应用更加丰富，开拓了物理实验的新视野。

二.实验基础知识与实验原理1.阿贝折射仪是测物质折射率的专用仪器，他能快速而准确地测出透明液体，半透明液体或固体材料的折射率。

阿贝折射仪的光学系统由望远系统和读数系统组成，应用阿贝折射仪测量物质的折射率的方法是建立在全反射原理基础上的掠入射法，其中液体折射率由掠入射法测定而固体折射率由掠入法和反射法测定。

图 1 望远系统读数系统读书系统光路图图 2（阿贝折射仪）2.牛顿环测液体折射率,其中牛顿环是一种典型的等厚薄膜干涉现象，能充分显示光的波动性。

本文通过研究对比空气和水在牛顿环里发生的干涉现象，更新了液体折射率的测试方法，使牛顿环的应用更加丰富，开拓了物理实验的新视野。

图3（牛顿环）牛顿环是一种典型的等厚薄膜干涉现象，能充分显示光的波动性。

本文通过研究对比空气和水在牛顿环里发生的干涉现象，更新了液体折射率的测试方法，使牛顿环的应用更加丰富，开拓了物理实验的新视野。

设计原理当以波长为x 的钠黄光垂直照射到平凸透镜上时，由液体膜上，下表面反射光的光程差以及干涉相消。

即暗纹条件：)1......)(2,1,0(2/)12(2/2=+=+=n n ne λλδ 式中e 为某一暗纹中心，所在处的液体膜厚度，k 为干涉级次。

利用图中的几何关系，可得：R r e 2/2= (r 为条纹半径），代入（1）式，有图4......)2,1,0(2/)12(2//2=+=+=n n R nr λλδ （2）则暗纹半径......)2,1,0(/==n k nR r k λ （3）若取暗纹观察，则第m ，k 级对应的暗环半径的平方nmR r m /2λ= （4） knR r n /2λ= （5）两式相减得平凸透镜的曲率半径)/()(22n m n r r R n m --= （6）观察牛顿环时我们也将会发现牛顿环中心由于形变，灰尘，水等的影响，中心不是一点，而是一个不甚清晰的暗或亮的圆斑。

实验十四摩尔折光度的测定一、实验目的1.了解阿贝折光仪的结构和工作原理，正确掌握其使用方法。

2.测定某些化合物的折光率和密度，求算化合物、基团和原子。

二、实验原理摩尔折光度（R）是由于在光的照射下分子中电子云相对于分子骨架的相对运动的结果。

R可以作物为分子中电子极华率的量度。

R=(n2-1)M/(n2+2)ρN――折光度M――摩尔质量ρ――密度摩尔折光度有体积的因次，通常为cm3表示。

实验表明，摩尔折光度具有加和性。

三、仪器和药品阿贝折光仪；四氯化碳；乙醇；乙酸乙酯；乙酸甲酯；二氯乙烷。

四、实验步骤1.折光度的测定使用阿贝折光仪测定实验要求的几种物质的折光率。

2.用密度管法测定上述物质的密度。

阿贝折射仪的原理和操作方法阿贝折射仪是能测定透明、半透明液体或固体的折射率n D 和平均色散的n f -n c 仪器（其中以测透明液体为主），如仪器接上恒温器，则可测定温度为0~70℃内的折射率n D 。

折射率和平均色散是物质的重要光学常数之一，能借以了解物质的光学性能、 纯度、浓度及色散大小等。

（一）工作原理图5 图6 图7阿贝折射仪的基本原理即为折射定律：sin 1n α1=2n sin α2 1n 、2n 为交界面两侧的两种介质之折射率（图5）α1为入射角 ， α2为折射角若光线从光密介质进入光疏介质，入射角小于折射角，改变入射角可以使折射角达到900，此时的入射角称为临界角，本仪器测定折射率就是基于测定临界角的原理。

图6中当不同的角度光线射入AB 面时。

其折射角都大于i ，如果用一望远镜对射出光线观察，可以看到望远镜视场被分为明暗两部分，二者之间有明显的分界线。

见图7所示，明暗分界线为临界角的位置。

图7中ABCD 为一折射棱镜，其折射率n 2。

为AB 面上面是被测物体。

（透明固体或液体）其折射率为n 1，由折射定律得：sin 1n 90℃=2n sin α （1）2n sin β=sini （2）Ф=α+β则 α=Ф-β代入（1）式得1n =2n sin （Ф-β）=2n (sin Фcos β-cos Фsin β） (3)由（2）式得：222sin n β=sin 2i 22n (1-cos 2β) =sin 2i 22n -22n cos 2β=sin 2i cos β=22222/)sin (n i n -代入（3）式得：1n =sin Фi n 222sin --cos Фsini棱镜折射角Ф与折射率n 2均已知。

用小电容测量仪测偶极矩【实验目的】1. 掌握溶液法测定偶极矩的原理、方法和计算。

2. 熟悉小电容仪、折射仪的使用。

3. 用溶液法测定正丁醇的偶极矩，了解偶极矩与分子电性质的关系。

【实验原理】1.偶极矩与极化度分子呈电中性，但因空间构型的不同，正负电荷中心可能重合，也可能不重合，前者为非极性分子，后者称为极性分子，分子极性大小用偶极矩μ来度量，其定义为μ=gd(1)式中，g为正、负电荷中心所带的电荷量;d是正、负电荷中心间的距离。

偶极矩的SI单位是库米(C·m)。

而过去习惯使用的单位是德拜(D)，1D=×10-30C·m。

若将极性分子置于均匀的外电场中，分子将沿电场方向转动，同时还会发生电子云对分子骨架的相对移动和分子骨架的变形，称为极化。

极化的程度用摩尔极化度P来度量。

P是转向极化度(P转向)、电子极化度(P电子)和原子极化度(P原子)之和，P =P转向+ P电子+ P原子(2)其中，(3)式中，N A为阿佛加德罗(Avogadro)常数;K为玻耳兹曼(Boltzmann)常数;T为热力学温度。

由于P原子在P中所占的比例很小，所以在不很精确的测量中可以忽略P原子，(2)式可写成P = P转向 + P电子 (4)只要在低频电场(ν<1010s-1)或静电场中测得P;在ν≈1015s-1的高频电场(紫外可见光)中，由于极性分子的转向和分子骨架变形跟不上电场的变化，故P转向=0，P原子=0，所以测得的是P电子。

这样由(4)式可求得P转向，再由(3)式计算μ。

通过测定偶极矩，可以了解分子中电子云的分布和分子对称性，判断几何异构体和分子的立体结构。

2.溶液法测定偶极矩所谓溶液法就是将极性待测物溶于非极性溶剂中进行测定，然后外推到无限稀释。

因为在无限稀的溶液中，极性溶质分子所处的状态与它在气相时十分相近，此时分子的偶极矩可按下式计算:(5)式中，P∞2和R∞2分别表示无限稀时极性分子的摩尔极化度和摩尔折射度(习惯上用摩尔折射度表示折射法测定的P电子);T是热力学温度。

一、实验目的与实验仪器1.实验目的（1）学会使用读数显微镜测量固体和液体的折射率。

（2）学会使用全反射法测量液体的折射率。

（3）学会使用阿贝尔折射仪测量液体和固体的折射率。

2.实验仪器读数显微镜、待测折射率玻璃板、涂有红漆的玻璃片、小烧杯、底部涂有红漆标记的玻璃培养皿、全反射法测量液体折射率仪、钠光灯望远镜、阿贝尔折射仪、温度计、银粉、酒精、溴代萘。

二、实验原理1. 用读数显微镜测量液体和固体的折射率如图，透明介质中某物体S1发出的光经过空气和透明介质界面发生折射，在 S2位置成像。

当入射角i1和折射角i2很小时，有sin i 1 ≈ tan i 1 = PS 3S 3S 1sin i 2 ≈ tan i 2 =PS 3S 3S 2由折射定律知 n 1n 2=sini 2sini 1=S 3S 1S 3S 2将空气折射率 n 2=1 带入可得n 1 =S 3S 1S 3S 2式中S 3S 1为透明介质厚度，S 3S 2为物体成像距介质表面距离，即像的高度。

2.全反射法测液体折射率测量固体和液体折射率 实验报告在密封的两玻璃片中间的空气层放入一种液体中，当光通过后在各个面发生折射，由折射定律可以得出：n L sinα = n G sinβ = n A sini式中n L、n G、n A分别为液体、玻璃、空气的折射率。

当β足够大时，光线将在由玻璃射入空气时发生全反射，即i=90°，又由于n A=1。

只要测出正好达到全反射状态下的入射角即可计算出到液体的折射率，由折射定律：n L sinα = n G sinβ = 1即液体折射率n L =1 sinα上图便是用全反射法测量液体折射率的装置。

T 为望远镜；S为盛待测液体的容器；P 为中间有空气的玻璃系统，R为刻度盘。

调节仪器后，转动刻度盘，当望远镜视场中一半明亮一半昏暗时即达到全反射临界角。

3.阿贝折射仪测量固体和液体折射率 如图所示阿贝折射仪原理图，透明介质中光线以入射角α入射到直角玻璃棱镜ABC 的AB 面，进入棱镜中，再出射到空气中。

实验一 溶解热的测定一、目的1、了解电热补偿法测定热效应的基本原理及仪器使用。

2、测定硝酸钾在水中的积分溶解热，并用作图法求得其微分稀释热、积分稀释热和微分溶解热。

3、初步了解计算机采集处理实验数据、控制化学实验的方法和途径。

二、基本原理1、物质溶解于溶剂过程的热效应称为溶解热。

它有积分（或变浓）溶解热和微分（或定浓）溶解热两种。

前者是1 mol 溶质溶解在n 0 mol 溶剂中时所产生的热效应，以Q s 表示。

后者是1 mol 溶质溶解在无限量某一定浓度溶液中时所产生的热效应，即0,,s T p n Q n ∂⎛⎫⎪∂⎝⎭。

溶剂加到溶液中使之稀释时所产生的热效应称为稀释热。

它也有积分（或变浓）稀释热和微分（或定浓）稀释热两种。

前者是把原含1 mol 溶质和n 01 mol 溶剂的溶液稀释到含溶剂n 02 mol 时所产生的热效应，以Q d 表示，显然，Q d = Q s ，n02 – Q s ，n01。

后者是1 mol 溶剂加到无限量某一定浓度溶液中时所产生的热效应，即0,,s T p nQ n ⎛⎫∂⎪∂⎝⎭。

2、积分溶解热由实验直接测定，其它三种热效应则需通过作图来求：设纯溶剂、纯溶质的摩尔焓分别为H *m ，A 和H *m ，B ，一定浓度溶液中溶剂和溶质的偏摩尔焓分别为H m ，A 和H m ，B ，若由n A mol 溶剂和n B mol 溶质混合形成溶液，则混合前的总焓为 H = n A H *m ，A + n B H *m ，B 混合后的总焓为 H ΄ = n A H m ，A + n B H m ，B此混合（即溶解）过程的焓变为 ΔH = H ΄ – H = n A （H m ，A – H *m ，A ）+ n B （H m ，B – H *m ，B ） = n A ΔH m ，A + n B ΔH m ，B根据定义，ΔH m ，A 即为该浓度溶液的微分稀释热，ΔH m ，B 即为该浓度溶液的微分溶解热，积分溶解热则为： ,,0,,As m A m Bm AmBB Bn H Q H H n HHn n ∆==∆+∆=∆+∆ 故在Q s ~ n 0图上，某点切线的斜率即为该浓度溶液的微分稀释热，截距即为该浓度溶液的微分溶解热。

实验： 漫反射法测量玻璃折射率一．实验目的1.观察漫反射及全反射的实验现象。

2.用漫反射法测量玻璃折射率。

二．实验原理全反射：由折射定律可知，当光从光密介质进入光疏介质时（光密介质折射率2n 大于光疏介质折射率1n ），随着入射角的增加，折射角也会随之增加，当入射角增大到某角度时，折射角变成90度，继续增大入射角光线，光线将全部返回到光密介质中，折射光线消失，即光能量没有透射损失，这种现象称为全反射。

临界角：使折射角成90度的入射角称为临界角，由折射定律可知，临界角C θ满足 sin C θ=1n /2n 。

纸巾的作用是用来发散激光光束的。

本实验涉及三种不同折射率和两个全反射角。

空气折射率1n ≈1，待测玻璃折射率2n ，水的折射率3n ≈1.33。

三．实验主要步骤或操作要点 实验任务：1.在玻璃表面贴上蘸水的面巾纸，用激光笔照射纸巾产生光环，观察并记录其特征；将玻璃另一面浸入水中观察光环消失的现象。

2.用几何光学中的全反射原理分析解释光环产生和消失的物理机理，推导出玻璃折射率与暗环直径间的关系。

3.用直尺测量一块玻璃产生的暗环的直径，并测量玻璃的厚度，从而测得玻璃的折射率。

实验步骤：1. 用水蘸湿纸巾，将其贴到玻璃片上；2. 激光笔照射玻璃上的纸巾产生光环；3. 用直尺测量产生的暗环直径和玻璃厚度（在不同位置测5次以上）。

4.观测完光环后，将任意玻璃片的另一面浸入水中，观察光环消失的现象。

实验注意事项：1、禁用大功率激光。

2、不要让激光直射或者反射入眼睛，以免造成视力损伤。

3、玻璃或塑料片的边沿不要过于尖锐，以免划伤。

五．数据处理本实验默认玻璃（塑料）片下方是空气（1n ≈1）。

一般玻璃（塑料）的折射率2n 约为1.5，比空气和水的折射率都大，所以根据本实验的装置可知，只有在玻璃（塑料）片下表面会形成全反射条件，而玻璃（塑料）片上方覆盖的水膜厚度可以忽略不计，因此所观察到的暗环正是由于下表面的全反射产生的。

结构化学实验物质摩尔折射度的测定实验目的1. 掌握阿贝折射仪的使用方法。

2. 测定化合物的折射率和密度，求算化合物、基团和原子的摩尔折射度，判断各化合物的分子结构。

摩尔折射度摩尔折射度可以作为分子中电子极化的度量，用R 表示，其定义为：221R=2n M n ρ−×+n ：物质的折射率；M ：物质的摩尔质量g/mol ；ρ：物质的密度g/cm 3；R ：摩尔折射率cm 3/mol 实验原理实验原理摩尔折射度摩尔折射度具有加和性，等于分子中各原子的折射度以及形成化学键时折射度的增量之和。

利用这种加和性，就可以根据物质的化学式算出其各种同分异构体的摩尔折射度并于实验测量相比较，进而推断其化学键及分子结构。

仪器与试剂WAY型阿贝折光仪、比重瓶、滴管；纯水、四氯化碳、乙醇、乙酸甲酯、乙酸乙酯、二氯乙烷；实验步骤折射率的测定：使用阿贝折光仪测量每种液体的折射率。

密度的测定：用比重瓶测量上述每种液体的密度。

HO220H O 0=m m m m ρρ−×−m ：待测液体与比重瓶的总质量；m 0：比重瓶的质量；m H 20：水与比重瓶的总质量实验步骤数据记录及结果处理1. 列表记录实验数据。

2. 求算和液体的密度和合折射率并求出其摩尔折射度。

3.根据实验数据求出CH2，Cl，C，H等官能团的摩尔折射度。

思考题1.按实验书上表格6.1-1和6.1-2数据计算各化合物摩尔折射度的理论值，并与实验值相比较。

2. 试验中有哪些操作会引起测量结果的误差？结构化学实验结构化学实验。

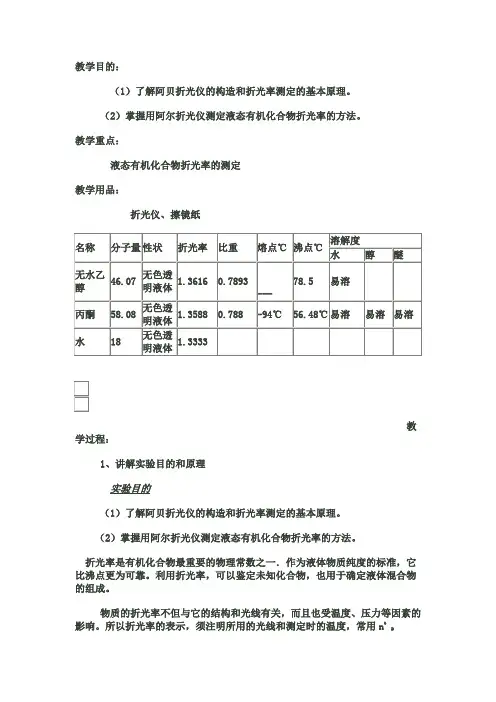
教学目的：（1）了解阿贝折光仪的构造和折光率测定的基本原理。

（2）掌握用阿尔折光仪测定液态有机化合物折光率的方法。

教学重点：液态有机化合物折光率的测定教学用品：折光仪、擦镜纸1、讲解实验目的和原理实验目的（1）了解阿贝折光仪的构造和折光率测定的基本原理。

（2）掌握用阿尔折光仪测定液态有机化合物折光率的方法。

折光率是有机化合物最重要的物理常数之一．作为液体物质纯度的标准，它比沸点更为可靠。

利用折光率，可以鉴定未知化合物，也用于确定液体混合物的组成。

物质的折光率不但与它的结构和光线有关，而且也受温度、压力等因素的影响。

所以折光率的表示，须注明所用的光线和测定时的温度，常用n tD基本原理一般地说，光在两个不同介质中的传播速度是不相同的，所以光线从一个介质进入另一个介质，当它的传播方向与两个介质的界面不垂直时，则在介面处的传播方向发生改变，这种现象称为光的折射现象。

光线在空气中的速度(v空)与它在液体中的速度（v液）之比定义为该液体的折光率（n）：n = v空／v液一个介质的折光率，就是光线从真空进入这个介质时的入射角的正弦与折射角的正弦之比，这种折光率称为该介质的绝对折光率。

通常是以空气为标准的。

折光率是物质的特性常数，固体、液体和气体都有折光率，尤其是液体，记载更为普遍。

不仅作为物质纯度的标志，也可用来鉴定未知物。

如分馏时，配合沸点，作为划分馏分的依据。

物质的折光率随入射光线波长不同而变，也随测定温度不同而变，通常温度升高1℃，液态化合物折光率降低3。

5～5。

5×10 ，所以，折光率（n）的表示需要注出所用光线波长和测定的温度。

2、介绍阿贝折光仪的构造：Abbe折光计的主要组成部分是两块直角棱镜，上面一块是光滑的，下面的表面是磨砂的，可以开启。

Abbe折光计的构造见附图1，左面有一个镜筒和刻度盘，上面刻有1。

3000～1。

7000的格子。

右面也有一个镜筒，是测量望远镜，用来观察折光情况的，筒内装消色散镜。

《实验：测定玻璃的折射率》讲义一、实验目的测定玻璃的折射率，加深对光的折射定律的理解。

二、实验原理当光线从空气斜射入玻璃时，入射角 i 和折射角 r 满足折射定律：n ＝ sin i ／ sin r ，其中 n 为玻璃的折射率。

通过测量入射角和折射角，就可以计算出玻璃的折射率。

三、实验器材玻璃砖、白纸、大头针、直尺、铅笔、量角器、平木板。

四、实验步骤1、把白纸平铺在平木板上，用铅笔在白纸上画出一条直线 aa'，作为界面。

2、把玻璃砖平放在白纸上，使玻璃砖的一个长边与直线 aa'对齐。

3、用大头针在玻璃砖的另一侧分别插上 P1、P2 两枚大头针，使P1、P2 的针尖大致在同一直线上。

4、眼睛在玻璃砖的另一侧观察，在白纸上分别插上 P3、P4 两枚大头针，使 P3 挡住 P1、P2 的像，P4 挡住 P3 和 P1、P2 的像。

5、移去玻璃砖和大头针，过 P1、P2 作直线 O1O2 交 aa'于 O 点，过 P3、P4 作直线 O3O4 交 aa'于 O'点，连接 OO'。

6、用量角器分别测量入射角 i 和折射角 r。

7、改变入射角，重复步骤 3 至 6，多测几组数据。

五、数据处理1、计算每次测量的折射率 n ＝ sin i ／ sin r 。

2、求折射率的平均值，得到玻璃的折射率。

六、注意事项1、玻璃砖要与纸面垂直。

2、插大头针时，要使大头针的针尖大致在同一直线上。

3、入射角不宜过大或过小，一般在 30°至 60°之间。

4、测量入射角和折射角时，要尽量准确。

七、误差分析1、测量误差：入射角和折射角的测量存在误差，可能导致折射率的计算不准确。

2、作图误差：在确定光线的光路时，作图不准确会引入误差。

3、仪器误差：量角器的精度有限，也会影响测量结果的准确性。

八、实验拓展1、思考如果玻璃砖的两个表面不平行，对实验结果会有什么影响？2、尝试用其他方法测定玻璃的折射率，比如利用全反射现象。

实验：测量玻璃的折射率[学习目标]1．能提出在“测量玻璃的折射率”实验中可能出现的问题。

2.能制订实验方案，能用相关器材收集数据。

3.能设计表格，分析数据，测得玻璃的折射率。

4.能撰写规范的实验报告，能有效陈述，能讨论交流实验过程中的问题。

5.注意提升实验设计能力，实验测量能力与误差分析能力。

一、实验目的掌握测量玻璃折射率的方法。

二、实验设计1．实验方案如图当光以一定的入射角透过一块两面平行的玻璃砖时，只要找出与入射光线AO 相对应的出射光线O′D，就能够画出光从空气射入玻璃后的折射光线OO′，于是就能测量入射角θ1、折射角θ2。

根据折射定律，就可以求出玻璃的折射率了。

2．实验原理用插针法确定光路，找出跟入射光线相对应的折射光线，用量角器测入射角θ1和折射角θ2，根据折射定律计算出玻璃的折射率n＝sin θ1sin θ2。

3．实验器材玻璃砖、白纸、木板、大头针四枚、图钉四枚、量角器、三角板(或直尺)、铅笔。

三、实验步骤1．如图所示，将白纸用图钉钉在平木板上。

2．在白纸上画出一条直线aa′作为界面(线)。

过aa′上的一点O画出界面的法线NN′，并画一条线段AO作为入射光线。

3．把长方形玻璃砖放在白纸上，使它的长边跟aa′对齐，画出玻璃砖的另一边bb′。

4．在直线AO上竖直插上两枚大头针P1、P2，透过玻璃砖观察大头针P1、P2的像，调整视线方向直到P2的像挡住P1的像。

再在观察者一侧竖直插上两枚大头针P3、P4，使P3挡住P1、P2的像，P4挡住P3及P1、P2的像，记下P3、P4的位置。

5．移去大头针和玻璃砖，过P3、P4所在处作直线O′B与bb′交于O′，直线O′B 就代表了沿AO方向入射的光线通过玻璃砖后的传播方向。

6．连接OO′，入射角θ1＝∠AON，折射角θ2＝∠O′ON′，用量角器量出入射角和折射角，从三角函数表中查出它们的正弦值，把这些数据记录在自己设计的表格中。

7．用上述方法求出入射角分别为30°、45°、60°时的折射角，查出它们的正弦值，填入表格中。

实验9. 偶极矩的测定一、实验目的：1. 测定氯仿在环己烷中的介电常数和偶极矩，了解偶极矩与分子电性质的关系。

2. 了解Clansius-Mosotti-Debye 方程的意义及公式的适用条件二、实验原理：1、偶极矩:分子结构可以近似地被石成是由电子。

和对于骨架（原子核及内层电子）所构成的。

由于分子空间构型的不同，其正、负电荷中心可能是重合的，也可能不重合，前者称为非极性分子，后者称为极性分子。

偶极矩”μ”是来度量分子极性的大小的概念，其定义是d q ⋅=μ式中 q 是正、负电荷中心所带的电荷量，d 为正、负电荷中心之间的距离，μ是一个向量，其方向规定从正到负。

因分子中原子间距离的数量级为1010-m ，电荷的数量级为2010-C ，所以偶极矩的数量级是3010-C·m 。

通过偶极矩的测定可以了解分子结构中有关电子云的分布和分子的对称性等情况，还可以用来判别几何异构体和分子的立体结构等。

克劳修斯、莫索蒂和德拜（Clausius －Mosotti －Debye ）从电磁理论得到了摩尔极化度P 与介电常数ε之间的关系式ρεεMP ⋅+-=21 式中，M 为被测物质的摩尔质量，ρ是该物质的密度，ε可以通过实验测定。

海德斯特兰（Hedestran ）首先利用稀溶液的近似公式()211x αεε+=溶()211x βρρ+=溶再根据溶液的加和性，推导出无限稀释时溶质摩尔极化度的公式()11211112112022123lim 2ρβεερεαεM M M P P P x -⋅+-+⋅+===→∞ 上述（5）、（6）、（7）式中，溶ε、溶ρ是溶液的介电常数和密度，2M 、2x 是溶质的摩尔质量和摩尔分数，1ε、1ρ和1M 分别是溶剂的介电常数、密度和摩尔质量，α、β在是分别与溶ε－2x 和溶ρ－2x 直线斜率有关的常数。

同时，可以推导得无限稀释时溶质的摩尔折射度的公式电子P ()122112111221212022621lim 2ργρβ++-⋅+-===→∞n M n M M n n R R x γ满足稀溶液近似公式：n aq =n 1(1+γx 2), 溶n 是溶液的折光率，n 1是溶剂的折光率，γ是与溶n －2x 直线斜率有关的常数。

测量玻璃折射率实验报告1.了解玻璃的光学性质并了解折射率的概念；2.学习使用正反射式法测量折射率。

实验原理：光线从一种介质进入另一种介质时，会因为介质密度不同而发生折射现象。

折射角和入射角之间的关系可以用折射定律表示：n1 sinθ1=n2 sinθ2其中，n1和n2分别表示入射介质和出射介质的折射率，θ1和θ2分别表示入射角和折射角。

在实验中，我们使用正反射式法测量玻璃的折射率。

如图所示，将光源L和观察屏S分别放置在玻璃板的两侧。

当光线从空气进入玻璃板时，发生折射现象。

当光线从玻璃板进入空气时，又发生折射现象。

此外，当光线从玻璃板表面反射时，仍然会有一部分光线透过玻璃板，发生了折射现象。

根据反射定律，入射角等于反射角，因此在上述实验中，入射角θ1等于反射角θ2。

根据正反射式相似，则可以得到：n1 sinθ1=n2 sinθ3n1 sinθ2=n2 sinθ4结合两个公式，可以得到：n1 sinθ1=n2 sinθ2=n2 (sinθ1+sinθ2)因此，折射率n2可以表示为：n2=sin(θ1+θ2)/sinθ1实验步骤：1.将光源和观察屏分别放置在玻璃板的两侧。

2.调节光源和观察屏的位置，使其与玻璃板成30度角。

3.调节光源的亮度和显微镜的放大倍数，使观察屏上出现最亮的环。

4.测量出环的直径d，并记录下实验数据。

5.将光源和观察屏的位置向玻璃板靠近，重复步骤2~4，测量出不同角度下的环直径。

6.根据实验数据计算出玻璃的折射率。

实验数据：入射角度θ1(°) 反射角度θ2(°) θ1+θ2(°) sinθ1 sin(θ1+θ2) sin(θ1+θ2)/sinθ1 折射率n230 30 60 0.5 0.866 1.732 1.73235 35 70 0.574 0.939 1.632 1.63240 40 80 0.642 1.114 1.733 1.73345 45 90 0.707 1.414 2 250 50 100 0.766 1.745 2.274 2.274实验结果：根据实验数据计算得到玻璃的折射率平均值为1.812。