1.静电场习题课
- 格式:ppt
- 大小:727.50 KB
- 文档页数:44





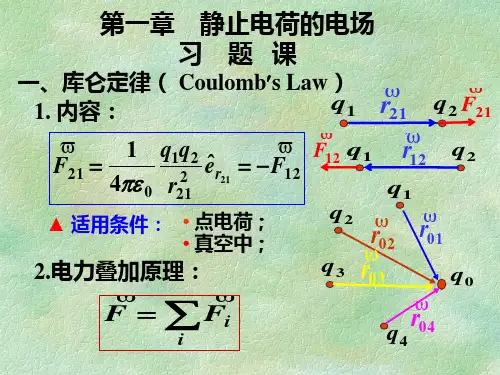
第1章 静电场的基本规律(习题课)一、 本章内容提要要求:理解和掌握各种物理量(概念)的定义和物理含义,掌握各种物理定理(律)的成立条件和运用方法。
1. 两种电荷、电荷守恒和电荷量子化2. 库仑定律 rr q q F ˆ412210⋅=πε 3. 电场强度 0q FE=4. 场强叠加原理 ∑=i E E5. 点电荷电场 r rqE ˆ4120⋅=πε 6. 电荷连续分布的带电体 三种电荷分布 ⎪⎩⎪⎨⎧===dl dq dS dq dVdq λσρ r r dq E d E 2041⋅==⎰⎰πε 计算电场分布的第一种方法(如何计算矢量积分?)7. 电场线及其性质发自正电荷(无穷远),终止于负电荷(无穷远),不在没有电荷处中断。
在静电场中,电场线不构成闭合曲线。
两条电场线不相交。
8. 高斯定理 电场的通量ε∑⎰⎰=⋅isqS d E(积分形式)ερ=⋅∇E (微分形式)电场的散度 E⋅∇=Ed i v , 有源场和无源场 高斯定理的意义——反映一般电场性质的规律。
哈密顿算符 z k y j x i ∂∂+∂∂+∂∂=∇ˆˆˆ,θϕθθϕ∂∂+∂∂⋅+∂∂=∇r e r e r er 1ˆsin 1ˆˆ计算电场分布的第二种方法(有条件的)9. 静电场的环路定理 电场的环量0l d =⋅⎰E L(积分形式)0=⨯∇E(微分形式)电场的旋度 E⨯∇=Er o t ,有旋场和无旋场 反映静电场性质的规律。
静电力是保守力,静电场是有势场。
10. 静电势能 l d 0⋅==-⎰QPPQ Q P E q A W W代表0q 与场源电荷之间的相互作用能 11. 电势差和电势l d 0⋅==-=-=⎰QPPQ QP Q P PQ E q A q W W U U Ul d ⋅=-=⎰o Po P p E U U U电势U 和静电势能W 参考零点的选择:(A )场源电荷分布于有限空间内,无穷远;(B )地面、金属外壳。


4.4解:如图所示建立坐标系,在半圆 环上取一小段圆弧,其长度为θRd则其带电量为θλ=Rd q d此段圆弧在环心O 点产生的电场强度为R4d R 4dq dE 020πεθλ=πε=由半圆环的对称性可知0点的场强E沿y 轴负向,所以有R4d sin sin dE dE 0y πεθθλ=θ=故环心处的电场强度大小R2R 4d sin dE E E 000y y πελ=πεθθλ===⎰⎰π所以 j R2E 0πελ-=4.5解:(1)两电荷同号时,在其连线外侧电场强度方向相同,内侧电场强度方向相反,故电场强度为零的点在两电荷连线内侧,设该点与q 1距离为r 1 ,(r 1>0),由场强叠加原理有0)(4421022101=--r d q rq πεπε 可得2111q q d q r +=(2)两电荷异号时,在其连线内侧电场强度方向相同,外侧电场强度方向相反。
故电场强度为零的点在两电荷连线外侧,又由于q 2>q 1 ,所以电场强度为零的点在q 1的外侧,设该点与q 1的距离为2r ,由场强叠加原理得0)r d (4q r 4q 22022201=+πε-πε可得 1212q q d q r -=4.7 解:建立如图所示的坐标系。
将带电 线分成两部分半圆环和两条半无 限长直线进行考虑。
设带电线线电荷密度为λ,分析半圆环部分:在半圆环上取一小段圆弧,其长度为dl ,则其带电量为 θλ=λ=d R dl dq 此段圆弧在环心0点产生的电场强度为: 20Rd R 41E d θλπε=电场分布关于x 轴对称:0=y E ,θθλπε=θ=sin R d R 41sin dE dE 20x所以R2d sin R 4sin R rd 41sin E E 000020πελ=θθπελ=θθλπε=θ=⎰⎰⎰ππ 方向沿x 轴正方向 分析两个半无限长直线:建立如图所示的坐标系,在带电直线上取电荷元dx dq λ=,它在O 点产生的电场强度大小为O ′)(4422020R x dxr dq dE +==πελπε 由带电线的对称性可知O 点的电场强度E沿x 轴负方向,所以有2/322022220)(4)(4cos R x xdxRx x R x dxdE dE x +=++==πελπελθ所以剩下部分在O 点产生的场强大小RR x xdxdE E E x x 002/32202)(4πελπελ=+===⎰⎰∞方向水平向左。


习题课(静电场中的导体和电介质)1、半径为R 1的导体球带正电Q 1其内外半径分别为R 2和R 3,球壳带正电Q 2(1)此带电系统的场强分布;(2)球的电势U 1和球壳的电势U 2; (3)球与球壳的电势差;(4)若用导线将球和球壳相连,U 1和U 2解:(1)电量均匀分布在球面上,即R 1球面电量为Q 1,R 2球面电量为-Q 1,R 3球面电量为Q 1+Q 2 ,利用均匀带电球面在空间任一点场强的结果和场强叠加原理,可求得场强分布为: r < R 1: E 1 = 0; R 1 < r <R 2 : E 2 = Q 1/4πε0r 2; R 2 < r < R 3 : E 3 = 0 r > R 3: E 4 = (Q 1+Q 2)/4πε0r 2(2) 30214243R Q Q dr E U Rπε+==⎰∞dr E dr E dr E U R R R R R ⎰⎰⎰∞++=332214321302121014)11(4R Q Q R R Q πεπε++-=(3) )11(421012112R R Q U U U -=-=πε (4) 3021214R Q Q U U πε+== 2、如图,在半径为a 的金属球外有一层外半径为b 的均匀电介质球壳,电介质的相对电容率为εr (1)介质层内外的场强大小;(2)介质层内外的电势; (3)金属球的电势;(4)电场的总能量; (5)解:(1)电量Q 均匀分布在半径为a r的球面为高斯面,利用高斯定理可求得场强分布 r < a : E 1 = 0; a < r < b : 2024rQ E r επε=; r > b : rQ E 034πε=(2) r > b : rQ dr E U r0334πε==⎰∞a < r <b : b Q b r Q dr E dr E U r bb r 003224)11(4πεεπε+-=+=⎰⎰∞r < a : b Q b a Q dr E dr E dr E U r bb a a r 0032114)11(4πεεπε+-=++=⎰⎰⎰∞(3)金属球的电势等于U 1(4)abb a a Q dV E dV E W r r b r baεπεεεεε022302208)(2121+-=+=⎰⎰∞ (5)ba a ab U Q C r r +-==εεπε014 3、在半径为R 的导体球壳薄壁附近与球心相距为d(d >R)的P 点处,放一点电荷q ,求:(1)球壳表面感应电荷在的球心O 处产生电势和场强; (2)空腔内任一点的电势和场强; (3)若将球壳接地,计算球壳表面感应电荷的总电量。