cplex教程六

IBMKnowledgeCenterCPLEX官方教程针对 C++ 用户的 Concert Technology 教程本教程向您说明如何结合使用 CPLEX 和 Concert Technology 来编写 C++ 应用程序。

在本教程中，您将学习：•Concert Technology C++ 应用程序中 CPLEX 的设计•CPLEX 对象对于 C++ 应用程序为必需。

•在 Concert Technology C++ 应用程序中编译 CPLEX•当您在 Concert Technology 中通过 C++ 库（如 CPLEX）编译C++ 应用程序时，需要告诉编译器要在何处查找CPLEX 和Concert include 文件（即头文件），并且还需要告诉链接器要在何处查找CPLEX 和Concert 库。

样本项目和 makefile 说明了如何为标准分发版中的示例执行这些关键步骤。

它们使用相对路径名来向编译器指示头文件的位置并向链接器指示库的位置。

•Concert Technology C++ 应用程序的剖析•Concert Technology 是 C++ 类库，因此 Concert Technology 应用程序由交互C++ 对象组成。

本主题对通常存在于完整Concert Technology CPLEX C++ 应用程序中的最重要类进行了简介。

•对使用 C++ 的小 LP 模型进行构建和求解•该样本对使用 C++ 的线性规划模型进行求解。

•编写和读取模型及文件•CPLEX 支持在 C++ 应用程序中从文件读取模型以及将模型编写到文件。

•选择优化器•根据问题类型选择 C++ 应用程序中的优化器。

•从文件读取问题：示例 ilolpex2.cpp•样本 ilolpex2.cpp 说明如何在 C++ 应用程序中从文件读取模型。

•修改和重新优化•CPLEX 提供了使用先前优化中的可用信息来修改模型并进行重新优化的方法。

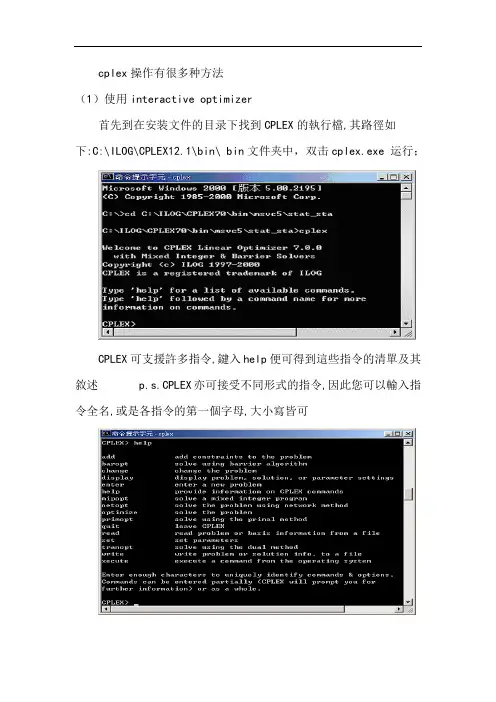
cplex操作有很多种方法（1）使用interactive optimizer首先到在安装文件的目录下找到CPLEX的執行檔,其路徑如下:C:\ILOG\CPLEX12.1\bin\ bin文件夹中，双击cplex.exe 运行；CPLEX可支援許多指令,鍵入help便可得到這些指令的清單及其敘述 p.s.CPLEX亦可接受不同形式的指令,因此您可以輸入指令全名,或是各指令的第一個字母,大小寫皆可當下達enter的指令後,Cplex會要求您給定新問題的名稱,接著問題必須如以下的順序來輸入(類似我們求解LP問題時所列的問題格式):objective function(目標函式)constraints(限制式)bounds(變數的個別範圍)輸入完整的問題後,記得在最後一行鍵入end,表示您已完成問題的輸入。

關於bounds: 若無特別規定個別變數的變動範圍,CPLEX 將會自動設定其default值return 的用法: 分隔過於冗長的限制式ex. time : -x1 + x2 + returnx3 <= 20 returnlabor : x1 – 3x2+x3 <=30 returnMatlab与cplex的混合编程1.安装matlab（cplex只支持>7.5版本的互联）和cplex12.12.点击matlab中file—setpath---添加安装盘中cplex安装文件下的matlab包，和example中的matlab示例。

3．在matlab的help中输入cplex，查找到cplex的教程，找到matlab和cplex互联教程，学习吧。

4．Matlab与cplex互联，默认的格式为min f*xst. Aineq*x <= bineqAeq*x = beqlb <= x <= ub编程时注意相互转换为标准格式。

5．。

CPLEX 12目录1. 简介 (3)2. 怎么用Cplex运行模型 (3)3. Cplex概览 (3)3.1线性规划 (3)3.2二次约束规划 (4)3.3混合整数规划 (4)3.4 可行松弛性 (5)3.5 解池：产生和保持多解 (5)4. GAMS选项 (9)5. Cplex选项总结 (10)5.1 预处理和一般选项 (10)5.2 单纯形法选项 (12)5.3 单纯形法的限制选项 (12)5.4 单纯形法的容限选项 (13)5.5 障碍特殊选项 (13)5.6 筛选特殊选项 (13)5.7 混合整数规划选项 (13)5.8 混合整数规划限制选项 (15)5.9 混合整数规划解池选项 (16)5.10 混合整数规划容许度选项 (16)5.11输出选项 (17)5.12 GAMS/Cplex选项文件 (17)6. 特殊备注 (18)6.1 物理内存限制 (18)6.2 使用特殊有序集 (18)6.3 使用半连续半整数变量 (19)6.4为求解MIP问题耗尽内存 (19)6.5 不能证明整数最优 (20)6.6 从混合整数规划的解开始 (20)6.7 使用可行松弛性 (21)7. GAMS/ CPLEX日志文件 (22)8. CPLEX选项的详细说明 (25)GAMS/Cplex是一种用于GAMS (The General Algebraic Modeling System，通用代数建模系统)的求解器，它使得用户可以把GAMS（通用代数建模系统的）的高级建模功能跟Cplex优化器的优势结合起来。

Cplex优化器是为能快速、最少用户干预地解决大型、复杂问题而设计的。

求解线性、二次约束和混合整数规划问题的Cplex算法现在已提供访问（针对恰当的许可证）。

尽管现存有多种求解工具，但是，GAMS/Cplex能自动地为特定问题计算最优值和设置大部分选项。

本文接下来总结了GAMS/Cplex的所有Cplex选项。

java如何调用cplexCplex是IBM公司的一个优化软件，可以用来求解线性规划(Linear Programming，LP)，二次规划(Quadratic Programming，QP)、混合整数规划(Mixed Integer Programming，MIP)问题。

下面就让店铺给大家说说java如何调用cplex吧。

java调用cplex的方法首先需要安装Cplex软件，我安装的版本是cplex_studio122.win-x86-32.exe下图安装后打开的Cplex自带的IDE，看上去跟Eclipse差不多。

在Cplex的安装目录下有许多值得我们学习的东西，还有一些examples，可供我们参考。

我是在Eclipse中使用Java调用Cplex，所以先把一些Cplex依赖加上。

运行依赖：cplex.jar(在..\cplex\lib目录下找到)和cplex122.dll(在..\cplex\bin目录下找到)。

将cplex.jar加到工程的Build Path中。

cplex122.dll可以设置到运行时的环境中(VM arguments)，或者添加到项目的Native library location。

接下来我们求解一个具体的线性规划问题。

例如，我们求解下面这样一个线性规划问题：Maximize x1 + 2x2 + 3x3subject to-x1 + x2 + x3 ≦20x1 - 3x2 + x3 ≦30with these bounds0 ≦x1 ≦400 ≦x2 ≦+∞0≦ x3≦ +∞先创建一个IloCplex对象，它是用来创建所有建模对象所需要的模型。

此时会抛出一个异常：IloException，需要try\catch。

代码如下：static public class Application {static public main(String[] args) {try {IloCplex cplex = new IloCplex();// create model and solve it} catch (IloException e) {System.err.println("Concert exception caught: " + e);}}}定义决策变量：double[] lb = {0.0, 0.0, 0.0};double[] ub = {40.0, Double.MAX_VALUE, Double.MAX_VALUE};IloNumVar[] x = cplex.numVarArray(3, lb, ub);定义目标函数：IloNumExpr expr = cplex.sum(x[0], cplex.prod(2.0, x[1]),cplex.prod(3.0, x[2]));cplex.addMaximize(expr);其中这个地方有许多写法，大家在使用的时候可以注意一下。

『实践』Yalmip+Ipopt+Cplex使⽤⼿册（⽂末附程序）Yalmip+Ipopt+Cplex使⽤⼿册(⽂末附程序)1.软件版本Cplex 12.6.2，Matlab R2014a， 3.12.9，2.Cplex添加⽅法破解版下载地址：其中community-edition可以免费试⽤，但最多只能计算1000个变量或1000个约束条件的优化问题。

点击安装，安装步骤默认操作即可。

点击Matlab中的，点击，找到路径并将其添加，最后点击即可。

然后在Matlab命令⾏窗⼝输⼊，出现帮助⽂档，代表添加成功。

3.Ipopt添加⽅法需要的组件：VC_redist.x64和ww_ifort_redist_intel64_2017.0.109.msi链接2：在打开的界⾯中选择图1-1即可。

图1Ipopt下载地址：（最新版本3.12.9）Ipopt下载链接：链接：https:///s/1tWBRJ7syW-WctcL1LkB06w 密码：1n3m （以前的版本3.12.6）下载下来后解压缩，打开⽂件，⽬录如下图1-2。

图2打开MATLAB，设置路径-》添加并包含⼦⽂件夹-》选择Ipopt路径-》保存。

见下图1-3。

图3右键运⾏图2中的opti_Install。

出现提⽰让你安装optiMEXFiles_mexw64_2_27，回车⼏下，弹出窗⼝，找到optiMEXFiles_mexw64_2_27（不需要⾃⼰⼿动解压）选中即可。

VC_redist.x64和ww_ifort_redist_intel64_2017.0.109.msi ，这两个组件⾃⼰⼿动安装，注意版本即可。

注意下图中框框中的组件我已经安装好了，如果没有安装，是会有提⽰的。

IPOPT 3.12.94.Yalmip添加⽅法下载地址：https://yalmip.github.io/（最新版本）下载链接：/s/1eRBhRlK 密码：dv4o（之前版本）将下载的⽂件解压，设置路径-》添加并包含⼦⽂件夹-》选择Yalmip路径-》保存。

cplex安装教程1. 首先，下载适用于您的操作系统的IBM ILOG CPLEX安装程序。

您可以从IBM官方网站或其它可信的软件下载网站获取该软件。

2. 执行安装程序并开始安装。

按照安装向导中的提示进行操作。

3. 在安装过程中，您可以选择安装C++和Java语言绑定，以便在这些语言中使用CPLEX。

根据您的需求选择适当的选项。

4. 在安装完成后，您需要设置环境变量，以便系统能够找到CPLEX的安装路径。

- 对于Windows用户，打开控制面板，并进入“系统和安全”->“系统”->“高级系统设置”。

在弹出的窗口中，选择“高级”选项卡，并点击“环境变量”按钮。

在系统变量中，找到“Path”变量，并将CPLEX的安装路径添加到变量值中。

- 对于Linux用户，在终端中使用文本编辑器打开~/.bashrc文件。

在文件末尾添加以下行，并保存文件。

```exportLD_LIBRARY_PATH=$LD_LIBRARY_PATH:/path/to/cplex/bin/x86-64_linux```5. 环境变量设置完成后，您可以打开终端或命令提示符并输入以下命令来验证CPLEX是否成功安装：```cplex```如果安装成功，您将看到CPLEX的命令行界面。

6. 安装完成后，您可以根据需要编写和运行CPLEX程序。

可以使用C++、Java或其它支持CPLEX的编程语言来编写程序。

- 对于C++，您需要包含适当的头文件并链接CPLEX库文件。

- 对于Java，您需要在您的项目中包含适当的JAR文件，并设置正确的类路径。

- 根据您选择的编程语言和开发环境，参考CPLEX的官方文档以获取更详细的安装和编程说明。

这样，您就可以完成CPLEX的安装并开始使用它来解决优化问题了。

注意，CPLEX是商业软件，您可能需要购买许可证才能使用全部功能。

python调用cplex算例如何使用Python调用Cplex算例介绍：在数学规划和操作研究中，IBM的CPLEX是一个广泛使用的解决方案。

它用于解决线性规划、整数规划、混合整数规划和二次规划等优化问题。

Python作为一种流行的编程语言，提供了丰富的库函数和工具，使得调用Cplex算例变得非常简单和灵活。

本文将一步一步地介绍如何使用Python调用Cplex算例，让您可以更好地利用这个强大的工具来解决实际问题。

步骤一：安装Cplex和Python首先，您需要安装Cplex软件包和Python。

可以从IBM官方网站上下载最新版本的Cplex，并按照安装指南进行安装。

然后，下载并安装Python，建议使用最新的Python 3.x版本。

步骤二：安装Cplex Python库在Cplex安装完成后，您需要安装Cplex Python库，这样Python才能够与Cplex进行通信。

打开终端或命令提示符，运行以下命令来安装Cplex Python库：pip install cplex步骤三：导入Cplex库打开Python开发环境（例如IDE或Jupyter Notebook），在代码的开头部分导入Cplex库：pythonimport cplex步骤四：创建Cplex问题使用Cplex库中的`Cplex`类来创建一个Cplex问题对象。

例如，下面的代码创建了一个空的Cplex问题：pythonproblem = cplex.Cplex()步骤五：添加变量和约束通过调用Cplex问题对象的方法，您可以添加变量和约束到问题中。

例如，下面的代码添加了一个变量和一个约束：pythonproblem.variables.add(names=['x'], lb=[0.0], ub=[1.0], types=['C']) problem.linear_constraints.add(lin_expr=[[[['x'], [1.0]]]], senses=['L'],rhs=[1.0])这个例子中，我们添加了一个名为`x`的连续变量，它的取值范围是从0到1。

【CPLEX教程02】配置Cplex的Java环境以及API说明因为⼩编⼀般⽤的C++和Java⽐较多，⽽且现在开发⼤型算法⽤这类⾯向对象的编程语⾔也⽅便得多。

基于上⾯的种种考虑，加上时间和精⼒有限，所以就暂时只做C++和Java的详细教程辣。

关于matlab和python的也许后续会补上的吧。

然后在开始之前，照例先把环境给配置好。

那么就先配置java的环境吧。

CPLEX系列教程可以关注我们的公众号哦！获取更多精彩消息！前⾯已经说了怎么下载和安装cplex了，如图：确保已经安装上这个版本，我们才能开始下⼀步的⼯作。

java⼩编⼀般⽤的ide是eclipse，就配置⼀下关于eclipse的。

其他的开发环境请⼤家⾃⾏设置哈。

新建⼀个⼯程，添加⼀个package，添加⼀个带main函数的类。

代码先别写。

在项⽬右键，选择build path -> Configure Build Path……找到Libraries->Add External JARs……，然后定位到\lib这个⽂件夹，把cplex.jar给添加进去。

到这⼀步还不⾏，还需要把CPLEX的动态运⾏库给添加进去，好让java程序运⾏的时候能够找到，具体做法是：在项⽬右键，选择build path -> Configure Build Path……，找到Libraries，点开JRE System Library，在Native library location那⾥点edit，把cplex下的\bin\x64_win64⽂件夹给添加进去，这⾥⾯有程序运⾏所需要动态库。

⼀个简单的线性规划问题：把下⾯代码复制进main函数⾥⾯：try {IloCplex cplex = new IloCplex(); // creat a modeldouble[] lb = {0.0, 0.0, 0.0};double[] ub = {40.0, Double.MAX_VALUE, Double.MAX_VALUE};IloNumVar[] x = cplex.numVarArray(3, lb, ub);double[] objvals = {1.0, 2.0, 3.0};cplex.addMaximize(cplex.scalProd(x, objvals));double[] coeff1 = {-1.0, 1.0, 1.0};double[] coeff2 = {1.0, -3.0, 1.0};cplex.addLe(cplex.scalProd(x, coeff1), 20.0);cplex.addLe(cplex.scalProd(x, coeff2), 30.0);if (cplex.solve()) {cplex.output().println("Solution status = " + cplex.getStatus());cplex.output().println("Solution value = " + cplex.getObjValue());double[] val = cplex.getValues(x);for (int j = 0; j < val.length; j++)cplex.output().println("x" + (j+1) + " = " + val[j]);}cplex.end();} catch (IloException e) {System.err.println("Concert exception caught: " + e);}点击运⾏，出现下⾯的结果就成功啦：最后，如果提⽰找不到build path ，share libraries什么的，请确保第⼆步配置正确！⾄此，我们已经能愉快使⽤cplex啦。

（个人总结的ILOG-CPLEX最简约的建模和使用方法，非常实用）数学规划模型可描述极为复杂的实际问题。

利用优化算法，应用程序能迅速找到这些问题模型的解决方案。

ILOG CPLEX 的速度非常快，可以解决现实世界中许多大规模的问题，并利用现在的应用系统快速提交可靠的解决方案。

这一特点可以从它在全球各地的使用情况和能在极端苛刻条件下应用的现状得到完全证明。

它能够处理有数百万个约束(constraint) 和变量，而且一直刷新数学规划的最高性能记录。

ILOG CPLEX接受的优化问题的一般形式：其中x中的决策变量可指定为连续类型（NumVarType.Float）或离散（整数）类型（NumVarType.Int）；下界lb最小至零（即决策变量非负），上届最大至C#可处理的最大值（System.Double.MaxValue）。

这里规定所有不等式约束的方向为“”。

调用CPLEX求解前需要给出：double[] c ——优化函数向量，数组长度为决策变量个数；这里要看看c能否为数组的数组，添加目标函数时能否按照数组的数组添加；double[][]var ——其行数为决策变量的组数，其列数应为决策变量的个数；double[][] A_le ——不等式约束矩阵，其列数应为决策变量的个数；double[] b_le ——不等式约束界，数组长度与A_le的行数保持一致；double[][] A_eq ——等式约束矩阵，其列数应为决策变量的个数；double[] b_eq ——等式约束界，数组长度与A_eq的行数保持一致；double[] lb ——决策变量的下界，数组长度与决策变量个数保持一致，若某个x[i]无下界则置为0；double[] ub ——决策变量的上界，数组长度与决策变量个数保持一致，若某个x[i]无上界则置为System.Double.MaxValue；double[] xt ——决策变量类型，数组长度与决策变量个数保持一致；xt[i] = NumVarType.Float 表示连续变量，xt[i] = NumVarType.Int表示整数变量；若混合整数规划问题退化为线性规划问题（即所有xt[i] = NumVarType.Int）则可省略xt；【注】为调用ILOG CPLEX，项目中需要添加引用——指定路径下的ILOG.CONCERT.DLL及ILOG.CPLEX.DLL，同时为调用求解器本身，需要加载CPLEX.DL L（可置于程序所在目录）；此外需要使用命名空间ILOG.CONCERT及ILOG.CPLEX。

CPLEX 12目录1. 简介 (3)2. 怎么用Cplex运行模型 (3)3. Cplex概览 (3)3.1线性规划 (3)3.2二次约束规划 (4)3.3混合整数规划 (4)3.4 可行松弛性 (5)3.5 解池：产生和保持多解 (5)4. GAMS选项 (9)5. Cplex选项总结 (10)5.1 预处理和一般选项 (10)5.2 单纯形法选项 (12)5.3 单纯形法的限制选项 (12)5.4 单纯形法的容限选项 (13)5.5 障碍特殊选项 (13)5.6 筛选特殊选项 (13)5.7 混合整数规划选项 (13)5.8 混合整数规划限制选项 (15)5.9 混合整数规划解池选项 (16)5.10 混合整数规划容许度选项 (16)5.11输出选项 (17)5.12 GAMS/Cplex选项文件 (17)6. 特殊备注 (18)6.1 物理内存限制 (18)6.2 使用特殊有序集 (18)6.3 使用半连续半整数变量 (19)6.4为求解MIP问题耗尽内存 (19)6.5 不能证明整数最优 (20)6.6 从混合整数规划的解开始 (20)6.7 使用可行松弛性 (21)7. GAMS/ CPLEX日志文件 (22)8. CPLEX选项的详细说明 (25)GAMS/Cplex是一种用于GAMS (The General Algebraic Modeling System，通用代数建模系统)的求解器，它使得用户可以把GAMS（通用代数建模系统的）的高级建模功能跟Cplex优化器的优势结合起来。

Cplex优化器是为能快速、最少用户干预地解决大型、复杂问题而设计的。

求解线性、二次约束和混合整数规划问题的Cplex算法现在已提供访问（针对恰当的许可证）。

尽管现存有多种求解工具，但是，GAMS/Cplex能自动地为特定问题计算最优值和设置大部分选项。

本文接下来总结了GAMS/Cplex的所有Cplex选项。

java cplex调用示例如何在Java中使用CPLEX进行求解使用IBM CPLEX是一种常见的求解线性规划和整数规划问题的方法。

CPLEX是一种高效的数学优化库，它提供了多种求解算法和优化策略。

在本文中，我将带你一步一步了解如何在Java中使用CPLEX进行求解，并提供一些示例代码。

1. 安装CPLEX库首先，你需要将CPLEX库安装到你的计算机上。

CPLEX可以从IBM官网上下载，并根据相应的操作系统进行安装。

安装完成后，你将获得一个包含CPLEX 库文件的文件夹。

2. 配置Java项目在Java项目中使用CPLEX之前，你需要配置相应的构建路径。

这可以通过在Eclipse或IntelliJ等集成开发环境中导入CPLEX库来完成。

你可以选择将CPLEX 库文件直接复制到项目的lib文件夹中，或者通过修改项目的构建路径来引用库文件。

完成后，你可以开始在Java代码中使用CPLEX库。

3. 导入CPLEX库在Java代码文件的顶部，你需要导入CPLEX库。

这可以通过使用Java的import 语句来完成。

例如，在使用CPLEX的线性规划功能之前，你需要导入IloCplex 类。

导入语句如下：javaimport ilog.concert.*;import ilog.cplex.*;4. 创建求解器在使用CPLEX进行求解之前，你需要创建一个求解器对象。

这个对象将提供CPLEX求解算法的接口，并负责加载问题和求解。

你可以使用IloCplex类来创建一个求解器对象。

示例代码如下：javaIloCplex cplex = new IloCplex();5. 定义决策变量在使用CPLEX求解问题之前，你需要定义问题的决策变量。

CPLEX使用IloNumVar类表示决策变量。

你需要指定决策变量的类型、上下界和名称。

示例代码如下：javaint numVars = 3;double[] lb = {0.0, 0.0, 0.0};double[] ub = {40.0, 3.0, Double.MAX_VALUE};IloNumVar[] x = cplex.numVarArray(numVars, lb, ub);在上面的示例中，我们定义了3个决策变量，它们的下界分别为0.0、0.0和0.0，上界分别为40.0、3.0和无穷大。

clpex,GLPK,lpsolve,yalmip简介与教程编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（clpex,GLPK,lpsolve,yalmip 简介与教程）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为clpex,GLPK,lpsolve,yalmip简介与教程的全部内容。

最近建立了一个网络流模型，是一个混合整数线性规划问题(模型中既有连续变量，又有整型变量).当要求解此模型的时候，发现matlab优化工具箱竟没有自带的可以求解这类问题的算法（只有bintprog求解器，但是只能求解不含连续变量的二值线性规划问题)。

于是在网上找了一些解决问题的途径，下面说说几种可能的解决方案. cplex 首先想到的是IBM公司大名鼎鼎的cplex。

cplex是IBM公司一款高性能的数学规划问题求解器，可以快速、稳定地求解线性规划、混合整数规划、二次规划等一系列规划问题。

CPLEX 的速度非常快,可以解决现实世界中许多大规模的问题,它能够处理有数百万个约束（constraint）和变量 (variable）的问题，而且一直刷新数学规划的最高性能记录。

他的标准版本是一个windows下的IDE应用软件，但是开发人员能通过组件库从其他程序语言调用 CPLEX 算法。

随标准版本一起发布的文件中包含一个名为matlab文件夹,将此文件夹添加到matlab的搜索路径下就可以在matlab下调用cplex高效地求解数学规划问题。

cplex IDE主界面（是不是很熟悉的界面？没错，cplex也是基于eclipse插件机制开发的。

）： bin目录下有matlab插件所必须的.mexw32文件和函数库API（。

如何在C#中引⼊CPLEX的dll（CPLEX系列-教程⼀）以前写在CSDN上的⽂章。

转到博客园之后，打算把这个教程移过来，顺便完善后⾯的教程。

主要是在+EF6⾥⾯使⽤cplex,完成⼀个最优⽣产计划的决策。

当时在查找如何在C#中引⽤cplex时，找到的⼤多是cplex在VS中的环境配置，⼤都还是以C++为例，⽽且觉得有些复杂。

所以想写⼀篇关于C#引⽤的教程。

关于下载我下载的版本是cplex studio12.8.0，可以去官⽹注册账号并下载试⽤版或者教育版。

其他下载途径⾃⾏百度。

安装下载之后，新建⼀个⽂件夹以备安装使⽤。

可以不⽤安装在C盘当中，安装后的⽂件夹如图所⽰：在这些⽂件夹当中，包含有C#、java、matlab、python等的教程（英⽂版），以及提供的样例。

以C#为例：教程位于~\cplex\dotnet.html当中。

样例在~\cplex\examples\x64_windows_vs2017\stat_mda当中。

双击打开其中的.sln⽂件，其中有很多C#的演⽰程序,可以⽤来学习。

.dll引⼊项⽬1. 打开VS2017，新建⼀个C#控制台应⽤程序，⽤来做配置效果的测试。

2. 点击“项⽬”-“添加引⽤”（或者直接在解决⽅案“引⽤”上，右键添加引⽤）3. 浏览⽂件夹，找到你的安装位置。

打开“~\cplex\bin\x64_win64”⽬录，选择其中的这两个添加⼊你的项⽬当中：4. 可以从样例代码中复制⼀个做测试，⽐如：using ILOG.Concert;using ILOG.CPLEX;public class Blend{internal static int _nbElements = 3;internal static int _nbRaw = 2;internal static int _nbScrap = 2;internal static int _nbIngot = 1;internal static double _alloy = 71.0;internal static double[] _cm = { 22.0, 10.0, 13.0 };internal static double[] _cr = { 6.0, 5.0 };internal static double[] _cs = { 7.0, 8.0 };internal static double[] _ci = { 9.0 };internal static double[] _p = { 0.05, 0.30, 0.60 };internal static double[] _P = { 0.10, 0.40, 0.80 };internal static double[][] _PRaw = {new double[] {0.20, 0.01},new double[] {0.05, 0.00},new double[] {0.05, 0.30}};internal static double[][] _PScrap = {new double[] {0.00, 0.01},new double[] {0.60, 0.00},new double[] {0.40, 0.70}};internal static double[][] _PIngot = {new double[] {0.10},new double[] {0.45},new double[] {0.45}};public static void Main(string[] args){try{Cplex cplex = new Cplex();INumVar[] m = cplex.NumVarArray(_nbElements, 0.0, System.Double.MaxValue); INumVar[] r = cplex.NumVarArray(_nbRaw, 0.0, System.Double.MaxValue);INumVar[] s = cplex.NumVarArray(_nbScrap, 0.0, System.Double.MaxValue);INumVar[] i = cplex.NumVarArray(_nbIngot, 0.0, System.Double.MaxValue);INumVar[] e = new INumVar[_nbElements];// Objective Function: Minimize Costcplex.AddMinimize(cplex.Sum(cplex.ScalProd(_cm, m),cplex.ScalProd(_cr, r),cplex.ScalProd(_cs, s),cplex.ScalProd(_ci, i)));// Min and max quantity of each element in alloyfor (int j = 0; j < _nbElements; j++){e[j] = cplex.NumVar(_p[j] * _alloy, _P[j] * _alloy);}// Constraint: produce requested quantity of alloycplex.AddEq(cplex.Sum(e), _alloy);// Constraints: Satisfy element quantity requirements for alloyfor (int j = 0; j < _nbElements; j++){cplex.AddEq(e[j],cplex.Sum(m[j],cplex.ScalProd(_PRaw[j], r),cplex.ScalProd(_PScrap[j], s),cplex.ScalProd(_PIngot[j], i)));}if (cplex.Solve()){if (cplex.GetStatus().Equals(Cplex.Status.Infeasible)){System.Console.WriteLine("No Solution");return;}double[] mVals = cplex.GetValues(m);double[] rVals = cplex.GetValues(r);double[] sVals = cplex.GetValues(s);double[] iVals = cplex.GetValues(i);double[] eVals = cplex.GetValues(e);// Print resultsSystem.Console.WriteLine("Solution status = " + cplex.GetStatus());System.Console.WriteLine("Cost:" + cplex.ObjValue);System.Console.WriteLine("Pure metal:");for (int j = 0; j < _nbElements; j++)System.Console.WriteLine("(" + j + ") " + mVals[j]);System.Console.WriteLine("Raw material:");for (int j = 0; j < _nbRaw; j++)System.Console.WriteLine("(" + j + ") " + rVals[j]);System.Console.WriteLine("Scrap:");for (int j = 0; j < _nbScrap; j++)System.Console.WriteLine("(" + j + ") " + sVals[j]);System.Console.WriteLine("Ingots : ");for (int j = 0; j < _nbIngot; j++)System.Console.WriteLine("(" + j + ") " + iVals[j]);System.Console.WriteLine("Elements:");for (int j = 0; j < _nbElements; j++)System.Console.WriteLine("(" + j + ") " + eVals[j]);}cplex.End();}catch (ILOG.Concert.Exception exc){System.Console.WriteLine("Concert exception '" + exc + "' caught");}System.Console.ReadKey();}}看了其他教程中，说要将解决⽅案启动配置为Release,但后⾯试了⼀下选为Debug也可以正常使⽤。

cplex语法CPLEX是一个用于求解复杂优化问题的软件工具。

它提供了一种高效的数学建模语言，可以描述和求解各种线性规划、整数规划、混合整数规划等数学模型。

本文将介绍CPLEX语法的一些基本知识和使用方法。

CPLEX语法主要由三个部分组成：参数设置、模型定义和求解过程。

首先，我们需要设置一些参数来指定求解器的行为。

例如，我们可以设置求解时间限制、容忍度等。

这些参数可以根据实际情况进行调整，以获得更好的求解效果。

接下来，我们需要定义数学模型。

在CPLEX中，可以使用变量、约束和目标函数来描述数学模型。

变量可以是连续型、整数型或二进制型，约束可以是等式或不等式，目标函数可以是最大化或最小化。

通过定义这些元素，我们可以构建一个数学模型，用于描述实际问题。

在模型定义完成后，我们可以使用CPLEX求解器来求解模型。

CPLEX 提供了多种求解算法，可以根据问题的性质选择合适的算法。

求解过程包括建立模型、设置参数、调用求解器进行求解和获取求解结果等步骤。

在求解过程中，CPLEX会尝试找到一个满足约束条件的最优解，或者证明问题无解。

除了基本的数学建模和求解功能，CPLEX还提供了一些高级功能，如约束编程、分布式求解和灵敏度分析等。

约束编程可以用于求解一些特殊类型的问题，如资源分配和调度问题。

分布式求解可以通过将求解任务分配给多台计算机来加速求解过程。

灵敏度分析可以用来评估模型对参数变化的敏感性，帮助我们理解问题的特性。

CPLEX语法具有良好的可读性和可扩展性。

它支持多种数学运算和逻辑运算，可以灵活地描述各种复杂问题。

此外，CPLEX还提供了丰富的文档和示例代码，帮助用户快速上手和解决实际问题。

CPLEX语法是一种强大的数学建模语言，可以帮助我们解决各种复杂优化问题。

通过合理地使用CPLEX语法，我们可以高效地建立数学模型，并利用CPLEX求解器来求解模型，从而得到最优解或近似最优解。

无论是在学术研究还是实际应用中，CPLEX都是一个非常有用的工具。