当前位置：文档之家 › 两个无约束优化的数值实验

两个无约束优化的数值实验

  • 格式：pdf
  • 大小：147.98 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

数学实验——无约束优化

数学实验——无约束优化

实验6无约束优化分1黄浩43实验目的1. 掌握用MATLAB优化工具箱的基本用法，对不同算法进行初步分析、比较2. 练习用无约束优化方法建立和求解实际问题模型（包括非线性最小二乘拟合）。

二、实验内容1. 《数学实验》第二版（问题2.1）问题叙述：取不同的初值计算非线性规划：尽可能求出所有局部极小点，进而找出全局极小点，并对不同算法（搜索方向、步长搜索、数值梯度与分析梯度等）的结果进行分析、比较。

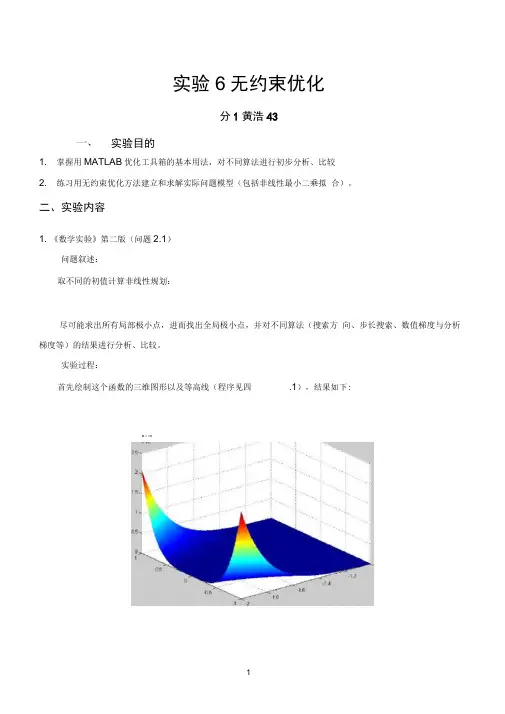
实验过程：首先绘制这个函数的三维图形以及等高线（程序见四.1），结果如下:s M tn0-”19 A8 A1G \ 5 -14 -13 \ 2 A1通过观察这两幅图，可以得到，x2确定时，x1越负，函数值越大，x1确定时，x2绝对值越大，函数值越大。

但对于x1正向偏离0的情况，并没有很好的反映，于是扩大绘图范围，做出下图（程序见四.2）：-1 -10由上面两幅图可见，方程像是一个四角被捏起的花布，而且z的最小值为0< 因此只要求解该方程的零点，即得到了方程的局部极小点，且若将原方程变形为:我们容易发现，该方程的零点为：x2=0或x1=0或x1=1或在求解零点之前，先针对一个零点，不妨用x1=1, x2=1，分析不同算法的优劣。

在matlab的无约束优化中，可以使用fminumc和fminsearch两种函数，搜索方向的算法有BFGS 公式、DFP公式和最速下降法三种（书中还提到的Gill-Murray 公式在matlab中已经不再使用），步长的一维搜索有混合二次三次多项式插值和三次多项式插值两种方法，另外，在求解函数梯度是也有数值方法和分析方法两种。

在对上述四类算法因素进行分析时，我们采用控制变量法，每次只保持一种或两种算法因素改变，分析它的精度及效率。

（一）分析fminumc与fminsearch两种方法的精度及效率选择初值为x1=0.8,x2=0.8，使用fminunc和fminsearch的默认算法及控制参数，输出结果如下（程序见四.3、四.4）：因为精确解为x1=1, z=0,我们便可以比较出不同算法的精度。

数学建模案例之多变量无约束最优化

数学建模案例之多变量无约束最优化

数学建模案例之多变量无约束最优化多变量无约束最优化问题是指在变量间没有限制条件的情况下，求解目标函数的最优值。

这类问题在数学建模中非常常见，实际应用非常广泛。

下面以一个实际案例说明多变量无约束最优化的建模过程。

假设地有几个旅游景点，现在需要制定一个旅游路线，使得游客的游玩时间最长，同时经济成本最低。

已知每个旅游景点之间的距离和游玩时间，以及游客每次游玩每公里所需的成本。

目标是找到一条旅游路线，使得游客在游览所有景点后，花费的经济成本最少。

首先，我们需要定义问题的数学模型。

假设有n个旅游景点，用x1, x2, ..., xn表示每个景点的游玩时间（单位：小时），用dij表示第i个景点和第j个景点之间的距离（单位：公里），用c表示游客游玩每公里所需的成本。

为了定义问题的数学模型，我们需要明确如下几个关键部分：1. 决策变量：定义一个n维向量X，其中每一个分量xi表示游客在第i个景点的游玩时间。

2. 目标函数：定义一个目标函数f(X)，表示游客花费的经济成本。

在本例中，目标函数可以定义为：f(X) = ∑dij * xi * c。

3.约束条件：由于是无约束最优化问题，这里没有额外的约束条件。

有了以上几个关键部分，我们可以将问题的数学模型表达为如下形式：最小化：f(X) = ∑dij * xi * c其中，i=1,2,...,n下一步是求解这个最优化问题。

可以使用各种数值优化算法，比如梯度下降法、牛顿法、遗传算法等。

具体的求解过程会涉及到算法的具体细节，这里不再详述。

最后，根据求解结果，我们可以得到游玩时间最长且经济成本最低的旅游路线。

这条路线就是我们需要制定的旅游路线。

总结起来，多变量无约束最优化问题在数学建模中的应用非常广泛。

通过定义合适的决策变量、目标函数和约束条件，可以将实际问题转化为数学模型，并通过数值优化算法求解这个模型，得到最优解。

在实际应用中，对于复杂的问题，可能需要结合多种算法和技巧来求解。

无约束常用优化方法

无约束常用优化方法

步长 ，作前进（或后退）试探．如试探成功（目
标函数值有所减小），则按步长序列
，加
大步长（注意每次加大步长都是由初始点算起），直
至试探失败（目标函数值比前一次的有所增加）时，
则取其前一次的步长作为沿这个坐标轴方向搜索的最
优步长，并计算出该方向上的终止点，而后以这个终
止点为始点再进行下一坐标轴方向的搜索，并重复上
处
显然 是二次函数，并且还是正定二次函数，所以 是凸函数且存在唯一全局极小点．为求此极小点，令
即可解得
即
（5.9）
对照基本迭代公式,易知，式（5.9）中的搜索方向
步长因子
方向
是直指点 处近似二次函数
的极小点的方向．此时称此方向为从点 出发的
Newton方向．从初始点开始，每一轮从当前迭代点出发，
沿Newton方向并取步长 的算法称为Newton法．
另外，共轭梯度法不要求精确的直线搜 索．但是，不精确的直线搜索可能导致迭代 出来的向量不再共轭，从而降低方法的效 能．克服的办法是，重设初始点，即把经过 n次迭代得到的Xn作为初始点重新迭代．
五、坐标轮换法
在坐标轮换法中，沿各个坐标轴方向进行一维搜索
时，常选用最优步长法或加速步长法．加速步长法从
初始点出发，沿搜索（坐标轴）方向先取一个较小的
三、共轭方向法
1、概念
通常，我们把从任意点
出发，依次沿某组共轭
方向进行一维搜索的求解最优化问题的方法，叫做共
轭方向法．
2、特点
• 一般地，在n维空间中可以找出n个互相共轭的方向，对于n元正 定二次函数，从任意初始点出发，顺次沿这n个共轭方向最多作n 次直线搜索就可以求得目标函数的极小点．这就是共轭方向法的 算法形成的基本思想．

实验10无约束优化

实验10无约束优化

实验10 无约束优化实验目的1． 1． 掌握用MA TLAB 优化工具箱的基本用法，对不同算法进行初步分析、比较。

2． 2． 练习用无约束优化方法建立和求解实际问题模型（包括非线性最小二乘拟合）。

实验内容第2题：取不同的初值计算下列非线性规划，尽可能求出所有局部极小点，进而找出全局极小点，并对不同算法（搜索方向、步长搜索、数值梯度与分析梯度等）的结果进行分析、比较。

（4）c a a c a a x x x x z T T 222111)()(1)()(1min +---+---=，2R ∈x 。

其中)73.0,7.0(),(21=c c ，T a )4,4(1=，Ta )8.3,5.2(2=。

★问题分析：首先用数学方法计算出真实值，),(21'=x x x ， 将T a )4,4(1=，T a )8.3,5.2(2=代入，化z 的表达式为：2222112221)8.3()5.2(1)4()4(1c x x c x x z +-+--+-+--=可见分母的值越小，z 越小。

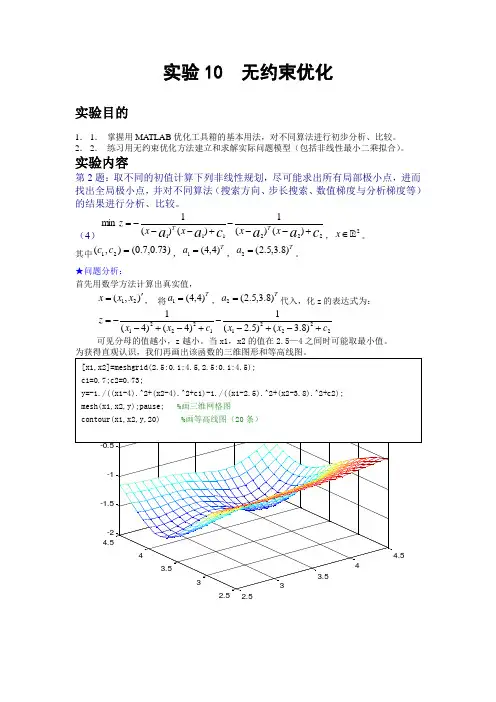
当x1，x2的值在2.5—4之间时可能取最小值。

2.53 3.54 4.52.533.544.5可以看出，z 存在两个最小值。

对z 求导：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+--++-+--+-+--++-+--=2122212212221221222112122211])8.3()5.2[()8.3(2])4()4[()4(2])8.3()5.2[()5.2(2])4()4[()4(2c x x x c x x x c x x x c x x x z ★ ★ Matlab 程序设计及结果： 下面用不同的算法进行计算：分别运行以上两程序，2222112221)8.3()5.2(1)4()4(1c x x c x x z +-+--+-+--=的求解无论用数值法还是分析法，无论用什么搜索方向，什么步长搜索都可以得到最优解和最优值。

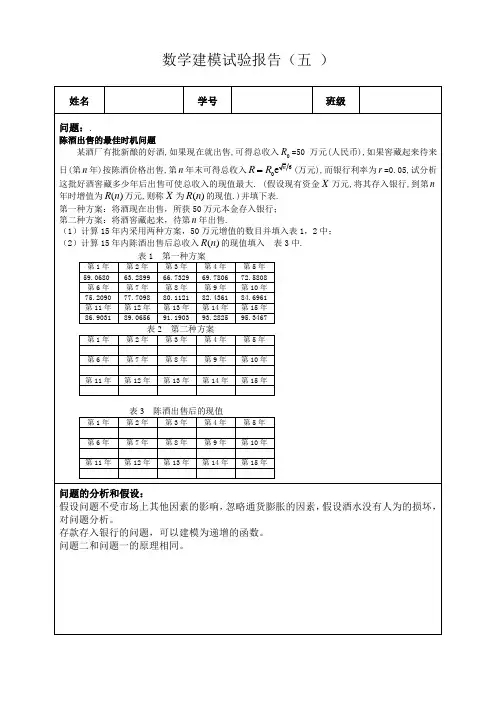
数学建模实验二 无约束优化

数学建模实验二 无约束优化

数学建模试验报告（五 ）姓名 学号 班级问题：.陈酒出售的最佳时机问题某酒厂有批新酿的好酒,如果现在就出售,可得总收入0R =50万元(人民币),如果窖藏起来待来日(第n 年)按陈酒价格出售,第n 年末可得总收入60en R R (万元),而银行利率为r =0.05,试分析这批好酒窖藏多少年后出售可使总收入的现值最大. (假设现有资金X 万元,将其存入银行,到第n 年时增值为()R n 万元,则称X 为()R n 的现值.)并填下表. 第一种方案：将酒现在出售，所获50万元本金存入银行； 第二种方案：将酒窖藏起来，待第n 年出售.（1）计算15年内采用两种方案，50万元增值的数目并填入表1，2中； （2）计算15年内陈酒出售后总收入()R n 的现值填入 表3中.表1 第一种方案第1年 第2年 第3年 第4年 第5年 59.0680 63.2899 66.7329 69.7806 72.5808 第6年 第7年 第8年 第9年 第10年 75.2090 77.7098 80.1121 82.4361 84.6961 第11年 第12年 第13年 第14年 第15年 86.9031 89.0656 91.1903 93.2825 95.3467 表2 第二种方案第1年 第2年第3年第4年第5年第6年第7年第8年第9年第10年第11年第12年第13年第14年第15年表3 陈酒出售后的现值第1年 第2年第3年第4年第5年第6年第7年第8年第9年第10年第11年第12年第13年第14年第15年问题的分析和假设：假设问题不受市场上其他因素的影响，忽略通货膨胀的因素，假设酒水没有人为的损坏， 对问题分析。

存款存入银行的问题，可以建模为递增的函数。

问题二和问题一的原理相同。

建模：第一种方案，过n年出售：设第n年的收益为bn，则根据题目，写出运算公式为：r=50bn=r*exp(sqrt(n)/6)第二种方案，立即出售，存款存入银行：可以设存入银行的年收入为r，初始值为r0=50（万元）则，第n年的时候r=r0*（1+0.05）^nr0=50求解的Matlab程序代码：第一种方案，过n年出售：在m文件种编辑：输入为，for n=1:15b(n)=50*exp(sqrt(n)/6);endbb =用来计算1-15年的收益。

实验7 无约束优化

实验7 无约束优化

在第一幅图中，最大的函数值的数量级已到 107，说明画图范围取得过大，函数值为 0 的,点在该图中均呈现一平面， 故需要缩小自变量的范围再绘图。 修改程序 guancha1.m 如下。
[x,y]=meshgrid(-0.1:0.01:1.1,-0.1:0.01:1.1);%选定x,y范围均为[-0.1,1.1] z=((x.*y).^2).*((1-x).^2).*((1-x-y.*((1-x).^5)).^2); mesh(x,y,z);%画三维图像 title('图2.1 三维图像'); pause contour(x,y,z,200) %画等高线 title('图2.2 等高线 ')
2.2 matlab 求解 2.2.1 输出三维图像和等高线，直观观察最优解所在位置 首先，先让 MATLAB 输出的三维图像，直观地观察最优解的大致范围。程序 guancha.m 如下。
[x,y]=meshgrid(-2:0.01:2,-2:0.01:2);%选定x,y范围均为[-2,2] z=((x.*y).^2).*((1-x).^2).*((1-x-y.*((1-x).^5)).^2); mesh(x,y,z);%画三维图像 title('图2.1 三维图像'); pause contour(x,y,z,30) %画等高线 title('图2.2 等高线 ')
3.42E-08 3.41E-08 2.21E-05 3.42E-08 3.41E-08 2.21E-05
2.42E-17 2.40E-17 1.00E-11 2.42E-17 2.40E-17 1.00E-11
18 18 99 18 18 99
2.比较分析梯度与数值梯度对结果的影响 首先计算 f(x)的梯度

求解非线性无约束优化问题的两种方法的分析

垫墼兰￡望叁兰堑圭兰垒篁塞１第一章预备知识§１．１共轭梯度方法§１．１．１引言共轭梯度法足最优化中最常用的方法之一。

它具有算法简便，存储需求小等优点，十分适合于大规模优化问题．在石油勘探，大气模拟，航天航空等领域出现的特大规模的优化问题是常常利用共轭梯度法求解。

在所有需要计算导数的优化方法中，最速下降是最简单的，但它速度太慢。

拟牛顿方法收敛速度很快，被广泛认为是非线性规划的最有效的方法。

但拟牛顿法需要存储矩阵以及通过求解线性方程组来计算搜索方向，这对于求解诸如上述问题等一些大规模问题几乎是不太可能办到的，共轭梯度法在算法的简便性，所需存储量等方面均与最速下降法差别不大，而收敛速度比最速下降法要快。

非线性共轭梯度法的收敛性分析的早期工作主要由Ｆｌｅｔｃｈｅｒ，Ｐｏｗｅｌｌ，Ｂｅａｌｅ等学者给出的，近年来，Ｎｏｃｅｄａｌ，Ｇｉｌｂｅｒｔ，Ｎａｚａｒｅｔｈ等学者在收敛性方面得到了不少的结果，使得共轭梯度法的研究由又热了起来．我国的学者也在共轭梯度法的理论研究中也取得了一定的成绩。

例如中科院应用数学所的韩继业，戴口等．§１．１．２共轭方向法共轭梯度法最本质的是共轭性质，共轭性是正交的一种推广。

定义１．１．２．１：设Ｗ∈咿×ｎ对称正定，ｄｌ，ｄ２，…，ｄ。

是咿中的一组非零向量，如果盯Ａｄｊ＝０，（ｉ≠Ｊ）．（１．１）则称ｄ１，ｄ２，…，ｄ。

是相互Ａ一共轭。

显然可见，如果ｄｌ，ｄ２，…，ｄ。

相互Ａ一共轭，则它们是线性无关的。

设Ｊ是单位阵则知，一共轭就是正交。

一般共轭方向法步骤如下：算法１．１．２．１：（一般共轭方向法）给出∞＋的初始点Ｘｌ，步ｌ：计算ｇｌ＝ｇ（Ｘ１）．步２：计算ｄｌ，使（ｆ｛’９ｌ＜０．步３：令女＝１．步４：计算口ｋ和Ｘｋ＋１，使得ｆ（ｘｋ－Ｆ‘１ｋｄｋ）。

Ｉ。

ｊ１１，‰十“呶），Ｘｋ＋１＝Ｘｋ＋ｖ。

ｋｄｋ．步５：计算以＋ｌ使得ｄ矗１Ｇｄｊ＝０，Ｊ＝１，２，…ｋ．步６：令ｋ：＝ｋ＋１，转步４．共轭方向法的一个基本性质是：只要执行精确线性搜索，就能得到二次终止性，这就足下面的共轭方向法基本定理。

实验7 无约束优化

数学实验作业（第八周）郭明钊 2012011880 化21一、原子位置问题1、 问题分析：题目中给出了各个原子之间的距离关系，所要求的就是每个原子在平面直角坐标系之中的具体位置。

则可以假设第i 个原子的坐标为(,)i i x y ，且假设第一个原子的位置为坐标原点，即(0,0)，则问题所求就转化为了使得2222[()()]i ji j ij ij x x y y d -+--∑达到最小值时的解。

这样问题就转化为了无约束优化：2222min [()()]i j i j ij ij x x y y d -+--∑，在这里，建立数组x ，其中有50个数，()i x i 为奇数为第i 个原子的横坐标，()i x i 为偶数为第i 个原子的纵坐标。

2、 使用matlab 中的lsqnonlin 函数实现：首先建立函数m 文件function y=distance(x,d)y(1)=(x(2*4-1))^2+(x(2*4))^2-d(1)^2;y(2)=(x(2*12-1))^2+(x(2*12))^2-d(2)^2;y(3)=(x(2*13-1))^2+(x(2*13))^2-d(3)^2;y(4)=(x(2*17-1))^2+(x(2*17))^2-d(4)^2;y(5)=(x(2*21-1))^2+(x(2*21))^2-d(5)^2;y(6)=(x(2*5-1)-x(2*2-1))^2+(x(2*5)-x(2*2))^2-d(6)^2;y(7)=(x(2*16-1)-x(2*2-1))^2+(x(2*16)-x(2*2))^2-d(7)^2;y(8)=(x(2*17-1)-x(2*2-1))^2+(x(2*17)-x(2*2))^2-d(8)^2;y(9)=(x(2*25-1)-x(2*2-1))^2+(x(2*25)-x(2*2))^2-d(9)^2;y(10)=(x(2*5-1)-x(2*3-1))^2+(x(2*5)-x(2*3))^2-d(10)^2;y(11)=(x(2*20-1)-x(2*3-1))^2+(x(2*20)-x(2*3))^2-d(11)^2;y(12)=(x(2*21-1)-x(2*3-1))^2+(x(2*21)-x(2*3))^2-d(12)^2;y(13)=(x(2*24-1)-x(2*3-1))^2+(x(2*24)-x(2*3))^2-d(13)^2;y(14)=(x(2*5-1)-x(2*4-1))^2+(x(2*5)-x(2*4))^2-d(14)^2;y(15)=(x(2*12-1)-x(2*4-1))^2+(x(2*12)-x(2*4))^2-d(15)^2;y(16)=(x(2*24-1)-x(2*4-1))^2+(x(2*24)-x(2*4))^2-d(16)^2;y(17)=(x(2*8-1)-x(2*6-1))^2+(x(2*8)-x(2*6))^2-d(17)^2;y(18)=(x(2*13-1)-x(2*6-1))^2+(x(2*13)-x(2*6))^2-d(18)^2;y(19)=(x(2*19-1)-x(2*6-1))^2+(x(2*19)-x(2*6))^2-d(19)^2;y(20)=(x(2*25-1)-x(2*6-1))^2+(x(2*25)-x(2*6))^2-d(20)^2;y(21)=(x(2*8-1)-x(2*7-1))^2+(x(2*8)-x(2*7))^2-d(21)^2;y(22)=(x(2*14-1)-x(2*7-1))^2+(x(2*14)-x(2*7))^2-d(22)^2;y(23)=(x(2*16-1)-x(2*7-1))^2+(x(2*16)-x(2*7))^2-d(23)^2;y(24)=(x(2*20-1)-x(2*7-1))^2+(x(2*20)-x(2*7))^2-d(24)^2;y(25)=(x(2*21-1)-x(2*7-1))^2+(x(2*21)-x(2*7))^2-d(25)^2;y(26)=(x(2*14-1)-x(2*8-1))^2+(x(2*14)-x(2*8))^2-d(26)^2;y(27)=(x(2*18-1)-x(2*8-1))^2+(x(2*18)-x(2*8))^2-d(27)^2;y(28)=(x(2*13-1)-x(2*9-1))^2+(x(2*13)-x(2*9))^2-d(28)^2;y(29)=(x(2*15-1)-x(2*9-1))^2+(x(2*15)-x(2*9))^2-d(29)^2;y(30)=(x(2*22-1)-x(2*9-1))^2+(x(2*22)-x(2*9))^2-d(30)^2;y(31)=(x(2*11-1)-x(2*10-1))^2+(x(2*11)-x(2*10))^2-d(31)^2;y(32)=(x(2*13-1)-x(2*10-1))^2+(x(2*13)-x(2*10))^2-d(32)^2;y(33)=(x(2*19-1)-x(2*10-1))^2+(x(2*19)-x(2*10))^2-d(33)^2;y(34)=(x(2*20-1)-x(2*10-1))^2+(x(2*20)-x(2*10))^2-d(34)^2;y(35)=(x(2*22-1)-x(2*10-1))^2+(x(2*22)-x(2*10))^2-d(35)^2;y(36)=(x(2*18-1)-x(2*11-1))^2+(x(2*18)-x(2*11))^2-d(36)^2;y(37)=(x(2*25-1)-x(2*11-1))^2+(x(2*25)-x(2*11))^2-d(37)^2;y(38)=(x(2*15-1)-x(2*12-1))^2+(x(2*15)-x(2*12))^2-d(38)^2;y(39)=(x(2*17-1)-x(2*12-1))^2+(x(2*17)-x(2*12))^2-d(39)^2;y(40)=(x(2*15-1)-x(2*13-1))^2+(x(2*15)-x(2*13))^2-d(40)^2;y(41)=(x(2*19-1)-x(2*13-1))^2+(x(2*19)-x(2*13))^2-d(41)^2;y(42)=(x(2*15-1)-x(2*14-1))^2+(x(2*15)-x(2*14))^2-d(42)^2;y(43)=(x(2*16-1)-x(2*14-1))^2+(x(2*16)-x(2*14))^2-d(43)^2;y(44)=(x(2*20-1)-x(2*16-1))^2+(x(2*20)-x(2*16))^2-d(44)^2;y(45)=(x(2*23-1)-x(2*16-1))^2+(x(2*23)-x(2*16))^2-d(45)^2;y(46)=(x(2*18-1)-x(2*17-1))^2+(x(2*18)-x(2*17))^2-d(46)^2;y(47)=(x(2*19-1)-x(2*17-1))^2+(x(2*19)-x(2*17))^2-d(47)^2;y(48)=(x(2*20-1)-x(2*19-1))^2+(x(2*20)-x(2*19))^2-d(48)^2;y(49)=(x(2*23-1)-x(2*19-1))^2+(x(2*23)-x(2*19))^2-d(49)^2;y(50)=(x(2*24-1)-x(2*19-1))^2+(x(2*24)-x(2*19))^2-d(50)^2;y(51)=(x(2*23-1)-x(2*21-1))^2+(x(2*23)-x(2*21))^2-d(51)^2;y(52)=(x(2*23-1)-x(2*22-1))^2+(x(2*23)-x(2*22))^2-d(52)^2;运行实现d=[0.9607 0.4399 0.8143 1.3765 1.2722 0.5294 0.6144 0.3766 0.6893 0.9488...0.8000 1.1090 1.1432 0.4758 1.3402 0.7006 0.4945 1.0559 0.6810 0.3587...0.3351 0.2878 1.3746 0.3870 0.7511 0.4439 0.8363 0.3208 0.1574 1.2736...0.5781 0.9254 0.6401 0.2467 0.4727 1.3840 0.4366 1.0307 1.3904 0.5725...0.7660 0.4394 1.0952 1.0422 1.8255 1.4325 1.0851 0.4995 1.2277 1.1271...0.7060 0.8052]';x0=[zeros(1,3),ones(1,47)]; %设初值[x,norms,res]=lsqnonlin(@distance,x0,[],[],[],d)a=reshape(x,2,25)'b=a(:,1)';c=a(:,2)';plot(b,c,'*') %在坐标系中显示出各个原子的位置3、结果如下：误差平方和：norms = 0.1625误差向量res =8.4224e-002 -5.6716e-002 5.4597e-0025.6860e-003 -1.1847e-001 5.8619e-0023.8879e-002 1.1819e-001 2.2805e-0023.8320e-002 -3.4772e-003 -3.9762e-0021.1452e-002 5.3897e-002 -4.3139e-0022.1071e-002 -4.4450e-002 9.6968e-003-5.6455e-002 4.0990e-002 2.7157e-0021.4843e-001 1.5864e-002 -3.7006e-003-1.3585e-001 2.6711e-002 -3.8390e-0039.0472e-003 2.9573e-002 -4.3175e-003-2.5224e-003 -4.7600e-004 1.2934e-002-2.4690e-002 7.6172e-003 2.5536e-003-5.2482e-003 7.3814e-002 -3.1225e-003-6.2153e-002 4.1666e-002 1.3685e-0016.4955e-002 2.3253e-003 -6.2132e-002-1.5985e-003 -5.7399e-002 -1.5199e-0021.3400e-002 -1.8521e-002 1.2003e-0013.1653e-003各个原子的坐标数值（第一列为横坐标，第二列为纵坐标）ans =0 00.2496 1.37301.6630 1.60100.7720 0.64120.7953 1.17011.2807 0.94921.4662 0.83651.2996 0.50230.3616 0.50871.1538 0.82271.1655 1.3985-0.3685 -0.03120.2287 0.81570.9857 0.85610.5856 0.44400.6025 1.9132-0.2599 1.35380.5372 0.16430.7983 1.36701.1261 1.01080.8162 0.91311.6189 0.70121.0248 0.15481.4666 0.46970.8870 1.0702 显示在坐标系中：当改变初值时x0=[zeros(1,2),ones(1,48)]; %设初值得norms =0.2298ans =0 00.7773 1.54251.2131 1.73990.8442 0.52390.6526 0.98631.4017 1.14390.7255 0.70991.0215 0.8220-0.0902 0.93201.2946 1.03960.7993 1.3167-0.4498 0.26080.4560 0.67820.6244 1.06130.1326 1.11251.2374 1.98050.5434 1.25021.2808 0.02161.3079 0.47031.0750 0.94510.2150 1.25031.0575 0.51940.1391 0.52860.3273 1.01521.0902 0.9464当换成其他初值时，答案也会明显不同。

Exp07_实验7_无约束优化

k T k k k k
k k T k k k k
T
(x ) f
k T
k
3.2 Broyden-Fletcher-Goldfarb-Shanno(BFGS)公式
G
k

f
k
(f
k T
k T
)
(f
) x
k T
k
k

G x (x ) G (x ) G x
k
k
k
k T k
k
k T
k
k
H
k
(1
(f ) H f (x ) f
x
k 1
x [ F ( x )]
k
k
1
F (x )
k
F ( x) f ( x)
3 拟Newton方法 目的 思路
x
k 1 k
不计算Hessian阵，克服病态、不正定、计 算复杂等缺陷，同时保持收敛较快的优点 回顾解方程组 F(x)=0的拟牛顿法
k 1
x [ F ( x )]
2 Newton方法 将f(xk+1)在xk点作泰勒展开至二阶项，用d替代dk
f (x
k 1
) f (x d ) f (x ) f
k k
T
( x )d
k
1 2
d f ( x )d
T 2 k
求d使f(xk+1)极小右端对d导数为0 f ( x k ) 2 f ( x k ) d 0 牛顿方程 牛顿方向 迭代格式
k 1
x
x d
k k
k
f (x
k 1
) f (x )
k

实验五：无约束优化

实验五：无约束优化班级 姓名 学号一、实验目的：学会用matlab 软件求解单变量和多变量无约束优化问题。

二、实验要求：1. 熟悉一维搜索的方法：进退法、黄金分割法、抛物线插值法、Armijo 准则；2. 熟悉求解多变量无约束问题的方法：变量轮换法、最速下降法、牛顿法、共轭梯度法；3. 会用matlab 软件求解无约束优化问题。

三、实验内容：1、试用matlab 优化工具箱中的fmincon 函数求解下列非线性规划问题：2221232212323123212223123m in ()8020..2023,,0f x x x x x x x x x x s t x x x x x x x =+++⎧-+≥⎪++≤⎪⎪--+=⎨⎪+=⎪⎪≥⎩(1)给出matlab 源代码； (2)求解结果粘贴.2、(精确一维搜索) 用0.618法求函数2()sin f x x x =-在[]0,1上的极小点，取自变量的允许误差为410δ-=，函数变量的允许误差为510ε-=。

3、(不精确一维搜索) Armijo 准则是许多非线性规划算法求步长时都必须执行的步骤。

Armijo 准则是指给定()0,1,(0,0.5),βσ∈∈令步长因子km k αβ=，其中km 是满足下列不等式的最小非负整数()()()mmTk k k k k f x d f x g d βσβ+≤+*这里k g 是函数()f x 在当前迭代点k x 处的梯度函数，k d 是当前迭代点k x 处的搜索方向. 可以证明()f x 若是连续可微的且满足0T k k g d <，则准则是有限终止的，即存在正数σ，使得对于充分大的正整数m ，()*成立.为了程序实现的方便，我们把Armijo 准则描述成下列详细的算法步骤： 算法1（Armijo 准则）步0：给定()0,1,(0,0.5),βσ∈∈令:0m =；步1：若不等式()()m m T k k k k k f x d f x g d βσβ+≤+成立， 置:,k m m = 1:km k k k x x d β+=+，停止.否则,转步2；步2：令:1m m =+，转步1.（1）试将上述的Armijo 准则编制成可重复利用的matlab 程序模块。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
89, 算法 4.3.1]代替 BFGS 中需要的 Wolfe 线搜索来确定步长. 请给出自 己算法中的参数设置. 4) 比较以上数值结果，完成以下表格： 表 1 求解问题(3)的各种方法的数值结果比较
初始点 方法 基本牛顿法 信赖域法 拟牛顿法 (0.8, 0.3) (1, 0.5)
⁄ ⁄ 0 , 0 , / 0 进行规范化，描述该反应的微分方程是： , 0 , 0 0,
0 , 这是一个线性常微分方程组问题，其解可以写成如下形式： exp , 1 1 exp exp , .
表 1 给出了对此系统测得的 10 组实验数据.
2. 无约束优化问题
问题描述如下 minimize with exp 0.8, 1 1 1 5, 26, 3 , 5.0893. , / 1 , 40, 1, 10 . 该问题的解
∗
∈
(3.a) (3.b) , (3.c) (3.d) (3.e)
其中 0.3, 0.6, 0.2 , 0.7395, 0.3144 ，最优值 ∗ 请回答以下问题： 1) 计算这个点处的梯度和 Hessian 阵，并说明其是否满足最优性条件. 2) 画出该问题在单位正方形内的等值线. 请问这个函数是凸函数吗？ (凸 函数的水平集是凸集，见[1]中 p .84, 引理 4.1.1). 画出这个函数 Hessian 阵的最小特征值的等值线. 请标出正负特征值区域. 这里为了观察牛顿法的性能， 给出了两个初始点， 一个是靠近解的(0.8, 0.3)， 一个是远离解的(1, 0.5). 针对这两个初始点，以梯度二范数小于1 10 为终止 条件，完成以下问题： 1) 给出基本牛顿法[[1],p.103]得到的迭代序列， 并画出迭代轨迹图. 描述所 得结果，并给出解释. 2) 给出信赖域型牛顿法[[1],p.137, 算法 6.1.1]得到的迭代序列， 并画出迭代 轨迹图. 描述所得结果，并给出解释. 这里的信赖域子问题(目标函数为 二次函数，约束为球约束)可以使用 Matlab 中的 fmincon.m 求解，也可 以使用 Steihaug 共轭梯度法求解[[1],p.148, 算法 6.3.2]. 请给出自己算法 中的参数设置. 3) 给出 BFGS 拟牛顿法[[1],p.119, 算法 5.3.1]得到的迭代序列， 并画出迭代 轨迹图. 描述所得结果， 并给出解释. 可以使用回溯 Armijo 线搜索[[1],p.
作为目标函数，这里的求和范围是规范化后的时间 处得到的浓度测量值
1
, , 和 ̂. 请完成以下问题： 1) 给出目标函数在区域 0,1.2 0,1 内的等值线 . 由图估计目标函数的 最小值和最小值点. 这个最小值点是动力学模型(1)关于实验数据在二范 数误差意义下的最佳拟合. 2) 分别以(0.5, 0.4)和(2, 2)为初始点，利用基本牛顿法[[1],p.103]求解参数估 计问题(2)，画出迭代点的轨迹； 3) 对初始点(2, 2)，利用带线搜索的牛顿法求解参数估计问题(2)，画出迭代 点的轨迹. 这里步长用回溯 Armijo 线搜索[[1],p. 89, 算法 4.3.1]确定. 请 说明线搜索中的参数设置，并统计每次迭代中为了确定步长而需要回溯 的次数. 4) 请描述 2)和 3)中出现的结果和现象，并进行分析，给出可能的解释.
0.0478 0.0915 0.1314 0.1679 0.2013 0.2318 0.2596 0.2851 0.3084 0.3296 ，将余量平方和 ̂
̂ 0.0382 0.0732 0.1051 0.1343 0.1610 0.1854 0.2077 0.2281 0.2467 0.2637 (2)
其中 表示迭代次数， 表示计算目标值的次数，
表示计算梯度的次数.
3. 小结
描述两到三个你遇到的问题及解决办法， 描述自己对无约束最优化算法的理 解. 其他任何你觉得有意义的内容.
参考文献
[1] 刘红英 , 夏勇 , 周水生 . 数学规划基础 [M]. 北京 : 北京航空航天大学出版 社,2012. [2] Lorenz T. Biegler, Nonlinear programming: concepts, algorithms, and applications to Chemical Processes [M]. Society for industrial and applied mathematics and the mathematical optimization society, Philadelphia, 2010.
两个无约束优化的数值实验
刘红英 本报告描述了两个无约束问题及其相关的若干数值实验。
1. 参数估计问题
考虑 A、 B、 C 在等温批式反应器(isothermal batch reactor) 遵循的一阶反应[[2], p.17, 例 2.1] ， 即 A → ，A→ 所发生的反应. 使用无量纲浓度 0 ，即用 A 的初始浓度 1, (1a) (1b) (1c)
3
表 1 一阶并行反应的浓度数据
time, 1 0.1 2 0.2 3 0.3 4 0.4 5 0.5 6 0.6 7 0.7 8 0.8 9 0.9 10 1.0 这里定义动力学参数作为变量 ∑
0.913 0.835 0.763 0.444 0.406 ,