2020选择填空专题答案.pdf

2020-2021年七年级英语上册选词填空选择题(难)（word）一、七年级英语上册选词填空专项目练习（含答案解析）1．用方框中所给单词或短语的适当形式补全对话。

B: Well, I travelled to Beijing and spent a happy holiday.A: Great! I look forward to going to Beijing. Tell me something interesting about it.B: OK. There are a lot of ________ and modern ________ in Beijing. I visited many ________ such as the Great Wall, the Palace Museum and the Summer Palace.A: I ________ about them. They are very famous. How long did you stay there?B: I spent a week staying there.A: Did you enjoy yourself?B: Yes, of course. I enjoyed not only its beautiful ________ scene, but also the delicious food.【答案】 traditional；buildings；places of interest；heard；natural【解析】【分析】本文是Andy去北京度假参观了几个景点的对话。

nature，自然，build，建筑，hear，听到，tradition，传统，place of interest，名胜（1）句意：北京有很多传统的和现代的建筑物。

根据 and modern 可知and前后一致，其前是形容词，根据提示词可知是traditional，形容词传统的，故填traditional。

2020年电力行业安全生产培训考试题库及答案（选择、填空、判断）一．选择1、《安规》中明确规定，单人值班不得单独从事（B）工作A、巡视B、修理C、检查2、高压设备上工作的安全措施分（B）类A、一B、三C、四3、10KV及以下电气设备不停电的安全距离是（B）米。

A、0.35B、0.7C、1.54、220KV电气设备不停电的安全距离是（C）米。

A、0.7B、2C、35、500KV电气设备不停电的安全距离是（C）米。

A、3B、4C、56、工作人员工作中正常活动范围与220KV带电设备的安全距离是（A）米。

A、3B、4C、57、工作人员工作中正常活动范围与500KV带电设备的安全距离是（C）米。

A、3B、4C、58、工作人员工作中正常活动范围与10KV及以下带电设备的安全距离是（A）米。

A、0.35B、0.7C、1.59、使用摇表测量高压设备绝缘，至少应由（B）人担任。

A、1B、2C、310、高压试验工作应（A）。

A、填写第一种工作票B、填写第二种工作票C、可以电话联系11、SF6设备工作区空气中SF6气体含量不得超过（B）ppm。

A、500B、1000C、150012、在运用中的高压设备上工作，分为（B）类：A、二B、三C、四13、设备运行后每（A）个月检查一次SF6气体含水量，直至稳定后，方可每年检测一次含水量。

A、三B、四C、五14、SF6设备运行稳定后方可（C）检查一次SF6气体含水量。

A、三个月B、半年C、一年15、工作人员进入SF6配电装置室，必须先通风（C）min，并用检漏仪测量SF6气体含量。

A、5B、10C、1516、短路变流器二次绕组，必须（A）A、使用短路片或使用短路线B、使用短路片搭接C、使用导线缠绕17、在电气设备上工作，应填用工作票或按命令执行，其方式有（A）种。

A、三B、四C、五18、带电作业和在带电设备外壳上的工作，应填用（B）。

A、电气第一种工作票B、电气第二种工作票C、热机工作票19、控制盘和低压配电盘、配电箱、电源干线上的工作，应填用（B）。

三下数学每日一练：选择合适的计量单位练习题及答案_2020年填空题版答案答案答案答案答案答案答案2020年三下数学：常见的量_选择合适的计量单位练习题~~第1题~~(2019镇江.三下期末) 在横线里填合适的单位．一个房间地面的面积是14________一头大象重5________一枚邮票的面积是6________一条铁路全长400________考点： 选择合适的计量单位;~~第2题~~(2019安溪.三下期末) 在横线上填上适当的单位。

黑板的长约4________ 一个足球场的面积约是7000________小明的身高是128________ 课桌桌面的面积约是35________考点： 选择合适的计量单位;~~第3题~~(2019龙岗.三下期末) 在横线上填上合适的单位。

一辆卡车能载重8________ 数学书封面的面积约为500________一张桌子高约70________ 一家超市的占地面积约1200________考点： 选择合适的计量单位;~~第4题~~(2019延安.三下期末) 在横线上填上合适的单位。

数学书封面的长大约是26________ 小学生每天睡觉9________学校操场的面积大约为900________ 一个绿皮西瓜重8.6________考点： 质量单位的选择;长度单位的选择;选择合适的计量单位;面积单位的选择;~~第5题~~(2019汉中.三下期末) 在横线上填上适当的单位名称。

一个鸡蛋约重50________ 我的一步长约30________数学书封面的面积约是5________ 一棵大树高约10________考点： 选择合适的计量单位;~~第6题~~(云南三下期末) 一间教室的面积大约是50________ 字典厚5________ 大树高16________考点： 厘米的认识与使用;选择合适的计量单位;平方厘米、平方分米、平方米的认识与使用;~~第7题~~(2016云南.三下期中) 云霄将军山海拔大约800________考点： 选择合适的计量单位;答案答案答案~~第8题~~(2019东海.三下期中) 填上合适的单位名称。

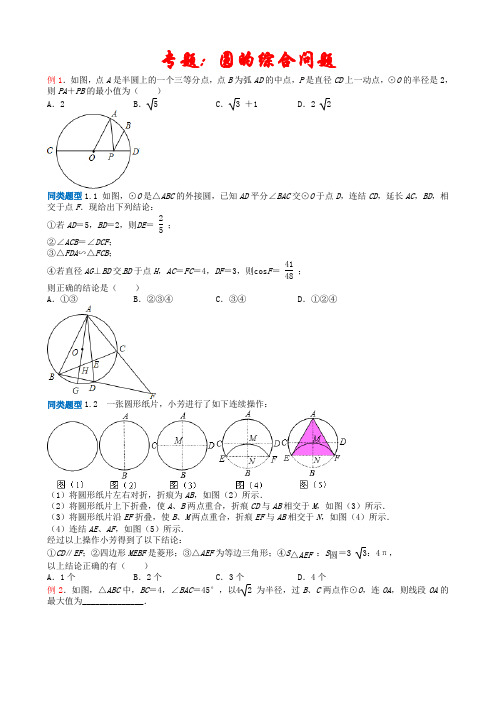
专题: 圆的综合问题例1．如图，点A是半圆上的一个三等分点，点B为弧AD的中点，P是直径CD上一动点，⊙O的半径是2，则PA＋PB的最小值为（）A．2 B． 5 C． 3 ＋1 D．2 2同类题型1.1 如图，⊙O是△ABC的外接圆，已知AD平分∠BAC交⊙O于点D，连结CD，延长AC，BD，相交于点F．现给出下列结论：①若AD＝5，BD＝2，则DE＝25；②∠ACB＝∠DCF；③△FDA∽△FCB；④若直径AG⊥BD交BD于点H，AC＝FC＝4，DF＝3，则cos F＝4148；则正确的结论是（）A．①③ B．②③④ C．③④ D．①②④同类题型1.2 一张圆形纸片，小芳进行了如下连续操作：（1）将圆形纸片左右对折，折痕为AB，如图（2）所示．（2）将圆形纸片上下折叠，使A、B两点重合，折痕CD与AB相交于M，如图（3）所示．（3）将圆形纸片沿EF折叠，使B、M两点重合，折痕EF与AB相交于N，如图（4）所示．（4）连结AE、AF，如图（5）所示．经过以上操作小芳得到了以下结论：①CD∥EF；②四边形MEBF是菱形；③△AEF为等边三角形；④S△AEF：S圆＝3 3：4π，以上结论正确的有（）A．1个 B．2个 C．3个 D．4个例2．如图，△ABC中，BC＝4，∠BAC＝45°，以4 2 为半径，过B、C两点作⊙O，连OA，则线段OA的最大值为______________．同类题型2.1 如图，已知⊙O的半径为1，锐角△ABC内接于⊙O，BD⊥AC于点D，OM⊥AB于点M，OM＝13，则sin∠CBD的值等于（）A．32B．13C．2 23D．12同类题型2.2 如图，直线l经过⊙O的圆心O，与⊙O交于A、B两点，点C在⊙O上，∠AOC＝30°，点P 是直线l上的一个动点（与圆心O不重合），直线CP与⊙O相交于点M，且MP＝OM，则满足条件的∠OCP 的大小为_______________．同类题型2.3 如图，△ABC中，∠BAC＝90°，AC＝12，AB＝10，D是AC上一个动点，以AD为直径的⊙O 交BD于E，则线段CE的最小值是（）A．5 B．6 C．7 D．8例3．如图，直线l1∥l2，⊙O与l1和l2分别相切于点A和点B．点M和点N分别是l1和l2上的动点，MN沿l1和l2平移．⊙O的半径为1，∠1＝60°．下列结论错误的是（）A．MN＝4 3 3B．若MN与⊙O相切，则AM＝ 3 C．若∠MON＝90°，则MN与⊙O相切 D．l1和l2的距离为2同类题型3.1 如图，已知A 、B 两点的坐标分别为（－2，0）、（0，1），⊙C 的圆心坐标为（0，－1），半径为1．若D 是⊙C 上的一个动点，射线AD 与y 轴交于点E ，则△ABE 面积的最大值是__________．同类题型 3.2 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l ：y ＝kx ＋4 3 与x 轴、y 轴分别交于A 、B ，∠OAB ＝30°，点P 在x 轴上，⊙P 与l 相切，当P 在线段OA 上运动时，使得⊙P 成为整圆的点P 个数是（ ）A ．6B ．8C ．10D ．12同类题型3.3 已知AC ⊥BC 于C ，BC ＝a ，CA ＝b ，AB ＝c ，下列图形中⊙O 与△ABC 的某两条边或三边所在的直线相切，则⊙O 的半径为ab a ＋b的是（ ） A ． B ． C ． D ．例4．如图，正方形ABCD 和正三角形AEF 都内接于⊙O ，EF 与BC ，CD 分别相交于点G ，H ，则EF GH的值为______________．同类题型4.1如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，以OB 为直径画圆M ，过D 作⊙M 的切线，切点为N ，分别交AC ，BC 于点E ，F ，已知AE ＝5，CE ＝3，则DF 的长是_______________．同类题型4.2 如图，已知△ABC 的外接圆⊙O 的半径为1，D 、E 分别是AB 、AC 上的点，BD ＝2AD ，EC ＝2AE ，则sin ∠BAC 的值等于线段（ ）A ．DE 的长B ．BC 的长 C ．23 DE 的长D ．32DE 的长例5．如图，AB 是⊙O 的直径，点C 是⊙O 上一点，AD 与过点C 的切线垂直，垂足为D ，直线DC 与AB 的延长线交于点P ，弦CE 平分∠ACB ，交AB 于点F ，连结BE ，BE ＝7 2 ．下列四个结论：①AC 平分∠DAB ；②PF 2 ＝PB ﹒PA ；③若BC ＝ 12 OP ，则阴影部分的面积为74π－ 494 3 ；④若PC ＝24，则tan ∠PCB ＝ 34．其中正确的是（ ）A ．①②B ．③④C ．①②④D ．①②③同类题型5.1 如图，在半径为2cm ，圆心角为90°的扇形OAB 中，分别以OA 、OB 为直径作半圆，则图中阴影部分的面积为_____________．同类题型5.2 某景区修建一栋复古建筑，其窗户设计如图所示．圆O 的圆心与矩形ABCD 对角线的交点重合，且圆与矩形上下两边相切（E 为上切点），与左右两边相交（F ，G 为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m ，根据设计要求，若∠EOF ＝45°，则此窗户的透光率（透光区域与矩形窗面的面积的比值）为_____________．同类题型5.3 如图，将半径为2，圆心角为120°的扇形OAB 绕点A 逆时针旋转60°，点O ，B 的对应点分别为O ′，B ′，连接BB ′，则图中阴影部分的面积是（ ）A ．2π3B ．2 3－ π3C ．2 3－ 2π3D ．4 3－ 2π3同类题型5.4 如图，已知矩形ABCD 中，AB ＝3，AD ＝2，分别以边AD ，BC 为直径在矩形ABCD 的内部作半圆O 1 和半圆O 2 ，一平行于AB 的直线EF 与这两个半圆分别交于点E 、点F ，且EF ＝2（EF 与AB 在圆心O 1和O 2 的同侧），则由⌒AE ，EF ，⌒FB ，AB 所围成图形（图中阴影部分）的面积等于_______．参考答案例1．如图，点A 是半圆上的一个三等分点，点B 为弧AD 的中点，P 是直径CD 上一动点，⊙O 的半径是2，则PA ＋PB 的最小值为（ ）A ．2B ． 5C ． 3 ＋1D ．2 2解：作A 关于MN 的对称点Q ，连接CQ ，BQ ，BQ 交CD 于P ，此时AP ＋PB ＝QP ＋PB ＝QB ，根据两点之间线段最短，PA ＋PB 的最小值为QB 的长度，连接OQ ，OB ，∵点A 是半圆上的一个三等分点，∴∠ACD ＝30°．∵B 弧AD 中点，∴∠BOD ＝∠ACD ＝30°，∴∠QOD ＝2∠QCD ＝2×30°＝60°，∴∠BOQ ＝30°＋60°＝90°．∵⊙O 的半径是2，∴OB ＝OQ ＝2，∴BQ ＝OB 2＋OQ 2＝2 2 ，即PA ＋PB 的最小值为22．选D ．同类题型1.1 如图，⊙O 是△ABC 的外接圆，已知AD 平分∠BAC 交⊙O 于点D ，连结CD ，延长AC ，BD ，相交于点F ．现给出下列结论：①若AD ＝5，BD ＝2，则DE ＝ 25； ②∠ACB ＝∠DCF ；③△FDA ∽△FCB ； ④若直径AG ⊥BD 交BD 于点H ，AC ＝FC ＝4，DF ＝3，则cos F ＝ 4148； 则正确的结论是（ ）A ．①③B ．②③④C ．③④D ．①②④解：①如图1，∵AD 平分∠BAC ，∴∠BAD ＝∠CAD ，∵∠CAD ＝∠CBD ，∴∠BAD ＝∠CBD ，∵∠BDE ＝∠BDE ，∴△BDE ∽△ADB ， ∴BD AD ＝DE BD， 由AD ＝5，BD ＝2，可求DE=45， ①不正确；②如图2，连接CD ，∠FCD ＋∠ACD ＝180°，∠ACD ＋∠ABD ＝180°，∴∠FCD ＝∠ABD ，若∠ACB ＝∠DCF ，因为∠ACB ＝∠ADB ，则有：∠ABD ＝∠ADB ，与已知不符，故②不正确；③如图3，∵∠F ＝∠F ，∠FAD ＝∠FBC ，∴△FDA ∽△FCB ；故③正确；④如图4，连接CD ，由②知：∠FCD ＝∠ABD ，又∵∠F ＝∠F ，∴△FCD ∽△FBA ， ∴FC FB ＝FD FA ， 由AC ＝FC ＝4，DF ＝3，可求：AF ＝8，FB ＝323， ∴BD ＝BF －DF ＝233， ∵直径AG ⊥BD ，∴DH ＝236， ∴FH ＝416， ∴cos F ＝FH AF ＝4148， 故④正确；故选：C ．同类题型1.2 一张圆形纸片，小芳进行了如下连续操作：（1）将圆形纸片左右对折，折痕为AB ，如图（2）所示．（2）将圆形纸片上下折叠，使A 、B 两点重合，折痕CD 与AB 相交于M ，如图（3）所示．（3）将圆形纸片沿EF 折叠，使B 、M 两点重合，折痕EF 与AB 相交于N ，如图（4）所示．（4）连结AE 、AF ，如图（5）所示．经过以上操作小芳得到了以下结论：①CD ∥EF ；②四边形MEBF 是菱形；③△AEF 为等边三角形；④S △AEF ：S 圆＝3 3：4π，以上结论正确的有（ ）A ．1个B ．2个C ．3个D ．4个解：∵纸片上下折叠A 、B 两点重合， ∴∠BMD ＝90°， ∵纸片沿EF 折叠，B 、M 两点重合，∴∠BNF ＝90°，∴∠BMD ＝∠BNF ＝90°，∴CD ∥EF ，故①正确；根据垂径定理，BM 垂直平分EF ，又∵纸片沿EF 折叠，B 、M 两点重合，∴BN ＝MN ，∴BM 、EF 互相垂直平分，∴四边形MEBF 是菱形，故②正确；如图，连接ME ，则ME ＝MB ＝2MN ，∴∠MEN ＝30°，∴∠EMN ＝90°－30°＝60°，又∵AM ＝ME （都是半径），∴∠AEM ＝∠EAM ， ∴∠AEM ＝12∠EMN ＝12×60°＝30°， ∴∠AEF ＝∠AEM ＋∠MEN ＝30°＋30°＝60°，同理可求∠AFE ＝60°，∴∠EAF ＝60°，∴△AEF 是等边三角形，故③正确；设圆的半径为r ，则MN ＝12 r ，EN ＝32r ， ∴EF ＝2EN ＝ 3 r ，AN ＝r ＋12r ＝32r ， ∴S △AEF ：S 圆＝（12×3r ×32r ）：πr 2＝3 3 ：4π，故④正确； 综上所述，结论正确的是①②③④共4个．选D ．同类题型1.3同类题型1.4例2．如图，△ABC 中，BC ＝4，∠BAC ＝45°，以4 2 为半径，过B 、C 两点作⊙O ，连OA ，则线段OA 的最大值为______________．解：作OF ⊥BC 于F ，则BF ＝CF ＝12 BC ＝2，如图，连结OB ，在Rt △OBF 中，OF ＝OB 2－BF 2＝(42)2－22＝27 ，∵∠BAC ＝45°，BC ＝4，∴点A 在BC 所对应的一段弧上一点，∴当点A 在BC 的垂直平分线上时OA 最大，此时AF ⊥BC ，AB ＝AC ，作BD ⊥AC 于D ，如图，设BD ＝x ，∵△ABD 为等腰直角三角形，∴AB ＝2BD ＝ 2 x ，∴AC ＝ 2 x ，在Rt △BDC 中，∵BC 2＝CD 2＋BD 2 ，∴42＝（2x －x ）2＋x 2 ，即x 2＝4（2＋ 2 ），∵12AF ﹒BC ＝12BD ﹒AC ， ∴AF ＝x ﹒2x4＝2 2 ＋2，∴AO ＝AF ＋OF ＝22＋2＋27 ，即线段OA 的最大值为22＋2＋27．同类题型2.1 如图，已知⊙O 的半径为1，锐角△ABC 内接于⊙O ，BD ⊥AC 于点D ，OM ⊥AB 于点M ，OM ＝ 13，则sin ∠CBD 的值等于（ ）A ．32B ．13C ．2 23D ．12解：连接AO ，∵OM ⊥AB 于点M ，AO ＝BO ，∴∠AOM ＝∠BOM ，∵∠AOB ＝2∠C∴∠MOB ＝∠C ，∵⊙O 的半径为1，锐角△ABC 内接于⊙O ，BD ⊥AC 于点D ，OM ＝13， ∴sin ∠CBD ＝sin∠OBM ＝MO OB ＝131＝13则sin ∠CBD 的值等于13． 选B ．同类题型2.2 如图，直线l 经过⊙O 的圆心O ，与⊙O 交于A 、B 两点，点C 在⊙O 上，∠AOC ＝30°，点P 是直线l 上的一个动点（与圆心O 不重合），直线CP 与⊙O 相交于点M ，且MP ＝OM ，则满足条件的∠OCP 的大小为_______________．解：①根据题意，画出图（1），在△QOC 中，OC ＝OM ，∴∠OMC ＝∠OCP ，在△OPM 中，MP ＝MO ，∴∠MOP ＝∠MPO ，又∵∠AOC ＝30°，∴∠MPO ＝∠OCP ＋∠AOC ＝∠OCP ＋30°，在△OPM 中，∠MOP ＋∠MPO ＋∠OMC ＝180°，即（∠OCP ＋30°）＋（∠OCP ＋30°）＋∠OCP ＝180°，整理得，3∠OCP ＝120°，∴∠OCP ＝40°．②当P 在线段OA 的延长线上（如图2）∵OC ＝OM ，∴∠OMP=（180°-∠MOC ）×12 ①， ∵OM ＝PM ，∴∠OPM=（180°-∠OMP ）×12②， 在△OMP 中，30°＋∠MOC ＋∠OMP ＋∠OPM ＝180°③，把①②代入③得∠MOC ＝20°，则∠OMP ＝80°∴∠OCP ＝100°；③当P 在线段OA 的反向延长线上（如图3），∵OC ＝OM ，∴∠OCP=∠OMC=（180°-∠COM ）×12①， ∵OM ＝PM ，∴∠P ＝（180°－∠OMP ）×12②， ∵∠AOC ＝30°，∴∠COM ＋∠POM ＝150°③，∵∠P ＝∠POM ，2∠P ＝∠OCP ＝∠OMC ④，①②③④联立得∠P ＝10°，∴∠OCP ＝180°－150°－10°＝20°．故答案为：40°、20°、100°．同类题型2.3 如图，△ABC 中，∠BAC ＝90°，AC ＝12，AB ＝10，D 是AC 上一个动点，以AD 为直径的⊙O 交BD 于E ，则线段CE 的最小值是（ ）A ．5B ．6C ．7D ．8解：如图，连接AE ，则∠AED ＝∠BEA ＝90°，∴点E 在以AB 为直径的⊙Q 上，∵AB ＝10，∴QA ＝QB ＝5，当点Q 、E 、C 三点共线时，QE ＋CE ＝CQ （最短），而QE 长度不变，故此时CE 最小，∵AC ＝12， ∴QC ＝AQ 2＋AC 2 ＝13，∴CE ＝QC －QE ＝13－5＝8，选D ．例3． 如图，直线l 1∥l 2 ，⊙O 与l 1 和l 2 分别相切于点A 和点B ．点M 和点N 分别是l 1 和l 2 上的动点，MN 沿l 1 和l 2 平移．⊙O 的半径为1，∠1＝60°．下列结论错误的是（ ）A ．MN ＝ 4 33B ．若MN 与⊙O 相切，则AM ＝ 3C ．若∠MON ＝90°，则MN 与⊙O 相切D ．l 1 和l 2 的距离为2解：A 、平移MN 使点B 与N 重合，∠1＝60°，AB ＝2，解直角三角形得MN ＝433 ，正确； B 、当MN 与圆相切时，M ，N 在AB 左侧以及M ，N 在A ，B 右侧时，AM ＝ 3 或33，错误； C 、若∠MON ＝90°，连接NO 并延长交MA 于点C ，则△AOC ≌△BON ，故CO ＝NO ，△MON ≌△MOC ，故MN 上的高为1，即O 到MN 的距离等于半径．正确；D 、l 1∥l 2 ，两平行线之间的距离为线段AB 的长，即直径AB ＝2，正确．选B ．同类题型3.1 如图，已知A 、B 两点的坐标分别为（－2，0）、（0，1），⊙C 的圆心坐标为（0，－1），半径为1．若D 是⊙C 上的一个动点，射线AD 与y 轴交于点E ，则△ABE 面积的最大值是__________．解：当射线AD 与⊙C 相切时，△ABE 面积的最大．连接AC ，∵∠AOC ＝∠ADC ＝90°，AC ＝AC ，OC ＝CD ，∴Rt △AOC ≌Rt △ADC （HL ），∴AD ＝AO ＝2，连接CD ，设EF ＝x ，∴DE 2 ＝EF ﹒OE ，∵CF ＝1， ∴DE ＝x (x ＋2) ，∵△CDE ∽△AOE ， ∴CD AO ＝CE AE， 即12＝x ＋12＋x (x ＋2) ， 解得x ＝23， S △ABE ＝BE ×AO 2＝2×(23＋1＋2)2＝113．同类题型 3.2 我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l ：y ＝kx ＋4 3 与x 轴、y 轴分别交于A 、B ，∠OAB ＝30°，点P 在x 轴上，⊙P 与l 相切，当P 在线段OA 上运动时，使得⊙P 成为整圆的点P 个数是（ ）A ．6B ．8C ．10D ．12解：∵直线l ：y ＝kx ＋4 3 与x 轴、y 轴分别交于A 、B ，∴B （0，4gh (3) ）， ∴OB ＝4 3 ，在RT △AOB 中，∠OAB ＝30°，∴OA ＝3OB ＝3×4 3 ＝12，∵⊙P 与l 相切，设切点为M ，连接PM ，则PM ⊥AB ，∴PM ＝12PA ， 设P （x ，0），∴PA ＝12－x ，∴⊙P 的半径PM ＝12PA ＝6－12x ， ∵x 为整数，PM 为整数，∴x 可以取0，2，4，6，8，10，6个数，∴使得⊙P 成为整圆的点P 个数是6．故选：A ．同类题型3.3 已知AC ⊥BC 于C ，BC ＝a ，CA ＝b ，AB ＝c ，下列图形中⊙O 与△ABC 的某两条边或三边所在的直线相切，则⊙O 的半径为ab a ＋b的是（ ） A ． B ． C ．D ．解：设⊙O 的半径为r ，A 、∵⊙O 是△ABC 内切圆，∴S △ABC ＝12（a ＋b ＋c ）﹒r ＝12 ab ， ∴r ＝ab a ＋b ＋c； B 、如图，连接OD ，则OD ＝OC ＝r ，OA ＝b －r ，∵AD 是⊙O 的切线，∴OD ⊥AB ，即∠AOD ＝∠C ＝90°，∴△ADO ∽△ACB ， ∴OA ：AB ＝OD ：BC ，即（b －r ）：c ＝r ：a ， 解得：r ＝ab a ＋c； C 、连接OE ，OD ，∵AC 与BC 是⊙O 的切线，∴OE ⊥BC ，OD ⊥AC ，∴∠OEB ＝∠ODC ＝∠C ＝90°，∴四边形ODCE 是矩形，∵OD ＝OE ，∴矩形ODCE 是正方形，∴EC ＝OD ＝r ，OE ∥AC ，∴OE ：AC ＝BE ：BC ，∴r ：b ＝（a －r ）：a ，∴r ＝ab a ＋b ； D 、解：设AC 、BA 、BC 与⊙O 的切点分别为D 、F 、E ；连接OD 、OE ；∵AC 、BE 是⊙O 的切线，∴∠ODC ＝∠OEC ＝∠DCE ＝90°；∴四边形ODCE 是矩形；∵OD ＝OE ，∴矩形ODCE 是正方形；即OE ＝OD ＝CD ＝r ，则AD ＝AF ＝b －r ；连接OB ，OF ， 由勾股定理得：BF 2＝OB 2－OF 2 ，BE 2＝OB 2－OE 2 ，∵OB ＝OB ，OF ＝OE ，∴BF ＝BE ，则BA ＋AF ＝BC ＋CE ，c ＋b －r ＝a ＋r ，即r ＝c ＋b －a 2． 故选C ．例4．如图，正方形ABCD 和正三角形AEF 都内接于⊙O ，EF 与BC ，CD 分别相交于点G ，H ，则EF GH的值为______________．解：如图，连接AC 、BD 、OF ，设⊙O 的半径是r ，则OF ＝r ，∵AO 是∠EAF 的平分线，∴∠OAF ＝60°÷2＝30°，∵OA ＝OF ，∴∠OFA ＝∠OAF ＝30°，∴∠COF ＝30°＋30°＝60°，∴FI=r ﹒sin60°=32r ，∴EF=32r ×2= 3 r ， ∵AO ＝2OI ，∴OI ＝12 r ，CI ＝r －12r ＝12r ， ∴GH BD ＝CI CO ＝12， ∴GH ＝12 BD ＝r ， ∴EF GH ＝3r r＝ 3 ．同类题型4.1如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，以OB 为直径画圆M ，过D 作⊙M 的切线，切点为N ，分别交AC ，BC 于点E ，F ，已知AE ＝5，CE ＝3，则DF 的长是_______________．解：延长EF ，过B 作直线平行AC 和EF 相交于P ，∵AE ＝5，EC ＝3，∴AO ＝CE ＋OE ，即有，OE ＝EN ＝1，又∵△DMN ∽△DEO ，且MN=13DM ， ∴DE ＝3OE ＝3，又∵OE ∥BP ，O 是DB 中点，所以E 也是中点，∴EP ＝DE ＝3，∴BP ＝2，又∵△EFC ∽△PFB ，相似比是3：2，∴EF=EP ×35＝1.8， 故可得DF ＝DE ＋EF ＝3＋1.8＝4.8．同类题型4.2 如图，已知△ABC 的外接圆⊙O 的半径为1，D 、E 分别是AB 、AC 上的点，BD ＝2AD ，EC ＝2AE ，则sin ∠BAC 的值等于线段（ ）A ．DE 的长B ．BC 的长 C ．23 DE 的长D ．32 DE 的长解：如图，作直径CF ，连接BF ，在Rt △CBF 中，sin ∠F ＝BC CF ＝BC 2 ； ∵BD ＝2AD ，EC ＝2AE ，∴AD ：AB ＝AE ：AC ＝1：3，又∵∠EAD ＝∠CAB ，∴△EAD ∽△CAB ，∴BC ＝3DE ，∴sin ∠A ＝sin ∠F ＝BC 2＝3DE 2＝32DE ． 选D ．例5．如图，AB 是⊙O 的直径，点C 是⊙O 上一点，AD 与过点C 的切线垂直，垂足为D ，直线DC 与AB 的延长线交于点P ，弦CE 平分∠ACB ，交AB 于点F ，连结BE ，BE ＝7 2 ．下列四个结论：①AC 平分∠DAB ；②PF 2 ＝PB ﹒PA ；③若BC ＝ 12 OP ，则阴影部分的面积为74π－ 494 3 ；④若PC ＝24，则tan ∠PCB ＝ 34．其中正确的是（ ）A ．①②B ．③④C ．①②④D ．①②③解：①连接O C ．∵OA ＝OC ，∴∠OAC ＝∠OC A ．∵PC 是⊙O 的切线，AD ⊥CD ，∴∠OCP ＝∠D ＝90°，∴OC ∥A D ．∴∠CAD ＝∠OCA ＝∠OA C ．即AC 平分∠DA B ．故正确；②∵AB 是直径，∴∠ACB ＝90°，∴∠PCB ＋∠ACD ＝90°，又∵∠CAD ＋∠ACD ＝90°，∴∠CAB ＝∠CAD ＝∠PC B ．又∵∠ACE ＝∠BCE ，∠PFC ＝∠CAB ＋∠ACE ，∠PCF ＝∠PCB ＋∠BCE ．∴∠PFC ＝∠PCF ．∴PC ＝PF ，∵∠P 是公共角，∴△PCB ∽△PAC ，∴PC ：PA ＝PB ：PC ，∴PC 2 ＝PB ﹒PA ，即PF 2 ＝PB ﹒PA ；故正确；③连接AE ．∵∠ACE ＝∠BCE ，∴⌒AE ＝⌒BE ，∴AE ＝BE ．又∵AB 是直径， ∴∠AEB ＝90°．∴AB=2BE=2×7 2 ＝14，∴OB ＝OC ＝7，∵PD 是切线，∴∠OCP ＝90°，∵BC ＝12OP ， ∴BC 是Rt △OCP 的中线， ∴BC ＝OB ＝OC ，即△OBC 是等边三角形，∴∠BOC ＝60°，∴S △BOC ＝4943 ，S _(扇形BOC )＝(60)/(360)×π×7^(2)＝(49)/(6)π， ∴阴影部分的面积为496π－4943 ；故错误；④∵△PCB ∽△PAC ， ∴PB PC ＝BC AC， ∴tan ∠PCB ＝tan ∠PAC ＝BC AC ＝PB PC ， 设PB ＝x ，则PA ＝x ＋14，∵PC 2 ＝PB ﹒PA ，∴242 ＝x （x ＋14），解得：x 1 ＝18，x 2 ＝－32，∴PB ＝18，∴tan ∠PCB ＝PB PC ＝1824＝34；故正确． 故选C ．同类题型5.1 如图，在半径为2cm ，圆心角为90°的扇形OAB 中，分别以OA 、OB 为直径作半圆，则图中阴影部分的面积为_____________．解：∵扇形OAB 的圆心角为90°，扇形半径为2，∴扇形面积为：90π×22360＝π（cm 2 ）， 半圆面积为：12×π×12＝π2（cm 2 ）， ∴S Q ＋S M ＝S M ＋S P ＝π2（cm 2 ）， ∴S Q ＝S P ，连接AB ，OD ，∵两半圆的直径相等，∴∠AOD ＝∠BOD ＝45°，∴S 绿色＝S △AOD ＝12×2×1＝1(cm 2)， ∴阴影部分Q 的面积为：S 扇形AOB －S 半圆－S 绿色＝π－π2－1＝π2－1(cm 2)．同类题型5.2 某景区修建一栋复古建筑，其窗户设计如图所示．圆O 的圆心与矩形ABCD 对角线的交点重合，且圆与矩形上下两边相切（E 为上切点），与左右两边相交（F ，G 为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m ，根据设计要求，若∠EOF ＝45°，则此窗户的透光率（透光区域与矩形窗面的面积的比值）为_____________．解：设⊙O 与矩形ABCD 的另一个交点为M ，连接OM 、OG ，则M 、O 、E 共线，由题意得：∠MOG ＝∠EOF ＝45°，∴∠FOG ＝90°，且OF ＝OG ＝1，∴S 透明区域＝180π×12360＋2×12×1×1＝π2＋1， 过O 作ON ⊥AD 于N ，∴ON ＝12FG ＝122 ， ∴AB ＝2ON ＝2×122＝ 2 ， ∴S 矩形＝2×2＝22，∴S 透光区域S 矩形＝π2＋122＝2(π＋2)8．同类题型5.3 如图，将半径为2，圆心角为120°的扇形OAB 绕点A 逆时针旋转60°，点O ，B 的对应点分别为O ′，B ′，连接BB ′，则图中阴影部分的面积是（ ）A ．2π3B ．2 3－ π3C ．2 3－ 2π3D ．4 3－ 2π3解：连接OO ′，BO ′，∵将半径为2，圆心角为120°的扇形OAB 绕点A 逆时针旋转60°，∴∠OAO ′＝60°，∴△OAO ′是等边三角形，∴∠AOO ′＝60°，∵∠AOB ＝120°，∴∠O ′OB ＝60°，∴△OO ′B 是等边三角形，∴∠AO ′B ＝120°，∵∠AO ′B ′＝120°，∴∠B ′O ′B ＝120°，∴∠O ′B ′B ＝∠O ′BB ′＝30°， ∴图中阴影部分的面积＝S △B ′O ′B －（S 扇形O ′OB －S △OO ′B ）＝12×1×23－（60﹒π×22360－12×2×3）＝23－2π3． 选C ．同类题型5.4 如图，已知矩形ABCD 中，AB ＝3，AD ＝2，分别以边AD ，BC 为直径在矩形ABCD 的内部作半圆O 1 和半圆O 2 ，一平行于AB 的直线EF 与这两个半圆分别交于点E 、点F ，且EF ＝2（EF 与AB 在圆心O 1和O 2 的同侧），则由⌒AE ，EF ，⌒FB ，AB 所围成图形（图中阴影部分）的面积等于_______．解：连接O 1O 2 ，O 1 E ，O 2 F ，则四边形O 1O 2 FE 是等腰梯形，过E 作EG ⊥O 1O 2 ，过FH ⊥O 1O 2 ，∴四边形EGHF 是矩形，∴GH ＝EF ＝2，∴O 1G ＝12， ∵O 1 E ＝1，∴GE ＝32， ∴O 1G O 1E ＝12； ∴∠O 1 EG ＝30°，∴∠AO 1 E ＝30°，同理∠BO 2 F ＝30°，∴阴影部分的面积＝S 矩形ABO 2O 1－2S 扇形AO 1E －S 梯形EFO 2O 1＝3－534－π6 ．。

武汉市2020-2021学年度第一学期期末考试八年级英语试卷题型汇编1 选择填空+六选五【东湖高新区2020-2021八年级上学期期末英语试卷】26. — Would you like to come to our class party, M Mary?— ________. I guess it will be fun.A. That's too badB. I'm afraid notC. SureD. My pleasure27. — Mike, can you make me a cup of tea?— ________. I'm coming.A. Good ideaB. No problemC. It sounds about rightD. It's OK28. — Do I have to add more honey, mom?— ________. Or it will be too sweet.A. no, that's itB. SureC. I guess soD. I hope so29. — Schools usually ________ New Year's parties on December 31st— You are right. We have a great time that day.A. organizeB. adviseC. inviteD. celebrate30. — Mary, do you know when your brother ________?— Oh, sorry, I have no idea. If he ________ I will tell you.A. comes; comesB. comes; will comeC. will come; comesD. will come; will come31. — The party is great success.— I think so. That's the result of good ________.1A. promisesB. pointsC. preparationsD. programs32. — What do you think of Mr. Zhang, Jack?— He is rea He always knows how we are feeling.A. carefulB. understandingC. seriousD. creative33. — How can I get into good college, Mom?— Mike ________ you work hard, you will never make it.A. unlessB. untilC. asD. before34. — What bad luck! My computer doesn’t work.— Don't be upset. Mike is ________. You can work on itA. emptyB. usefulC. availableD. new35. — I tried to ________ with him about our misunderstanding, but he wouldn't listen.— Don't waste your time. It's hard for him to change his mind.A. reasonB. fightC. solveD. agree36. — You don't look well. What's your trouble?— ________ at all. ________ is fine.A. Nothing; SomethingB. Anything; SomethingC. Anything; EverythingD. Nothing; Everything37— Linda, can you come to my birthday party this Saturday afternoon?— I'm sorry, ________ I can't. I have a dance classA. butB. andC. orD. then 38— Dinner is ready, Mike— Thanks, Carrie, but we ________ have some soup first.A. couldB. mightC. wouldD. will39. — Don't worry about the letter. I'm sure it'll ________.2— But it's important to me.A. turn upB. turn downC. turn onD. turn off40. — What are you doing, Mike?— Oh, I am calling to ask Mike ________A. when can he help meB. what is today’s homeworkC. if he will come to my partyD. how is he going to be a programmer五、词与短语选择填空(共5小题，每小题2分，满分10分)仔细阅读下面五个句子，然后用下面方框中所给的单词或短语填空，使每个句子在结构，句义和逻辑上正确。

专题 选择填空方法综述例1．如图1，E 为矩形ABCD 的边AD 上一点，点P 从点B 出发沿折线BE －ED －DC 运动到点C 停止，点Q 从点B 出发沿BC 运动到点C 停止，它们运动的速度都是1cm/s ．若点P 、点Q 同时开始运动，设运动时间为t （s ），△BPQ 的面积为y （cm 2），已知y 与t 之间的函数图象如图2所示．给出下列结论：①当0＜t ≤10时，△BPQ 是等腰三角形；②S △ABE ＝48cm 2；③当14＜t ＜22时，y ＝110－5t ；④在运动过程中，使得△ABP 是等腰三角形的P 点一共有3个；⑤△BPQ 与△ABE 相似时，t ＝14.5． 其中正确结论的序号是___________．同类题型1.1 如图，在四边形ABCD 中，DC ∥AB ，AD ＝5，CD ＝3，sin A ＝sin B ＝ 13，动点P 自A 点出发，沿着边AB 向点B 匀速运动，同时动点Q 自点A 出发，沿着边AD －DC －CB 匀速运动，速度均为每秒1个单位，当其中一个动点到达终点时，它们同时停止运动，设点P 运动t （秒）时，△APQ 的面积为s ，则s 关于t 的函数图象是（ ）A ．B ．C ．D ．同类题型1.2 如图1．在四边形ABCD 中，AB ∥CD ，AB ⊥BC ，动点P 从点B 出发，沿B →C →D →A 的方向运动，到达点A 停止，设点P 运动的路程为x ，△ABP 的面积为y ，如果y 与x 的函数图象如图2所示，那么AB 边的长度为____________．同类题型1.3 如图1，有一正方形广场ABCD ，图形中的线段均表示直行道路，⌒BD 表示一条以A 为圆心，以AB 为半径的圆弧形道路．如图2，在该广场的A 处有一路灯，O 是灯泡，夜晚小齐同学沿广场道路散步时，影子长度随行走路线的变化而变化，设他步行的路程为x （m ）时，相应影子的长度为y （m ），根据他步行的路线得到y 与x 之间关系的大致图象如图3，则他行走的路线是（ ）A．A→B→E→G B．A→E→D→C C．A→E→B→F D．A→B→D→C例2．如图，菱形ABCD的边长为6，∠ABC＝120°，M是BC边的一个三等分点，P是对角线AC上的动点，当PB＋PM的值最小时，PM的长是（）A．72B．2 73C．3 55D．264同类题型2.1 如图，已知菱形OABC的边OA在x轴上，点B的坐标为（8，4），点P是对角线OB上的一个动点，点D（0，2）在y轴上，当CP＋DP最短时，点P的坐标为____________．同类题型2.2 如图，在平面直角坐标系中，反比例函数y＝kx（x＞0）的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N两点．△OMN的面积为10．若动点P在x轴上，则PM＋PN的最小值是（）A．6 2 B．10 C．2 26 D．2 29同类题型2.3例3．如图，正方形ABCD中．点E，F分别在BC，CD上，△AEF是等边三角形．连接AC交EF于点G．过点G作GH⊥CE于点H，若S△EGH＝3，则S△ADF＝（）A．6 B．4 C．3 D．2同类题型3.1如图，在等腰Rt△ABC中，∠ABC＝90°，AB＝CB＝2，点D为AC的中点，点E，F分别是线段AB，CB上的动点，且∠EDF＝90°，若ED的长为m，则△BEF的周长是___________（用含m的代数式表示）．同类题型3.2 如图，在矩形ABCD中，AB＝2，AD＝2 2 ，点E是CD的中点，连接AE，将△ADE沿直线AE折叠，使点D落在点F处，则线段CF的长度是（）A．1 B．22C．23D．23同类题型3.3如图，在矩形ABCD中，BE⊥AC分别交AC、AD于点F、E，若AD＝1，AB＝CF，则AE＝__________．同类题型3.4 如图，正方形ABCD中，BC＝2，点M是边AB的中点，连接DM，DM与AC交于点P，点E在DC上，点F在DP上，且∠DFE＝45°．若PF＝56，则CE＝_________．例4．如图，正方形ABCD的边长为4，点E、F分别从点A、点D以相同速度同时出发，点E从点A向点D 运动，点F从点D向点C运动，点E运动到D点时，E、F停止运动．连接BE、AF相交于点G，连接CG．有下列结论：①AF⊥BE；②点G随着点E、F的运动而运动，且点G的运动路径的长度为π；③线段DG的最小值为2 5 －2；④当线段DG最小时，△BCG的面积S＝8＋855 ．其中正确的命题有____________．（填序号）同类题型4.1 如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为F，连结DF，下列四个结论：①△AEF∽△CAB；②tan∠CAD＝ 2 ；③DF＝DC；④CF＝2AF，正确的是（）A．①②③ B．②③④ C．①③④ D．①②④同类题型4.2 点E、F分别在平行四边形ABCD的边BC、AD上，BE＝DF，点P在边AB上，AP：PB＝1：n （n＞1），过点P且平行于AD的直线l将△ABE分成面积为S1、S2的两部分，将△CDF分成面积为S3、S4的两部分（如图），下列四个等式：①S1：S3＝1：n②S1：S4＝1：（2n＋1）③（S1＋S4）：（S2＋S3）＝1：n④（S3－S1）：（S2－S4）＝n：（n＋1）其中成立的有（）A．①②④ B．②③ C．②③④ D．③④同类题型4.3 如图，在矩形ABCD中，DE平分∠ADC交BC于点E，点F是CD边上一点（不与点D重合）．点P为DE上一动点，PE＜PD，将∠DPF绕点P逆时针旋转90°后，角的两边交射线DA于H，G两点，有下列结论：①DH＝DE；②DP＝DG；③DG＋DF＝ 2 DP；④DP﹒DE＝DH﹒DC，其中一定正确的是（）A．①② B．②③ C．①④ D．③④例5．如图，在平面直角坐标系中，经过点A的双曲线y＝kx（x＞0）同时经过点B，且点A在点B的左侧，点A的横坐标为 2 ，∠AOB＝∠OBA＝45°，则k的值为______________．同类题型5.1 如图，在平面直角坐标系xOy 中，已知直线y ＝kx （k ＞0）分别交反比例函数y ＝ 1x 和y ＝ 9x在第一象限的图象于点A ，B ，过点B 作 BD ⊥x 轴于点D ，交y ＝ 1x的图象于点C ，连结A C ．若△ABC 是等腰三角形，则k 的值是________．专题10 选择填空方法综述例1．如图1，E 为矩形ABCD 的边AD 上一点，点P 从点B 出发沿折线BE －ED －DC 运动到点C 停止，点Q 从点B 出发沿BC 运动到点C 停止，它们运动的速度都是1cm/s ．若点P 、点Q 同时开始运动，设运动时间为t （s ），△BPQ 的面积为y （cm 2），已知y 与t 之间的函数图象如图2所示．给出下列结论：①当0＜t ≤10时，△BPQ 是等腰三角形；②S △ABE ＝48cm 2；③当14＜t ＜22时，y ＝110－5t ；④在运动过程中，使得△ABP 是等腰三角形的P 点一共有3个；⑤△BPQ 与△ABE 相似时，t ＝14.5． 其中正确结论的序号是___________．解：由图象可以判定：BE ＝BC ＝10 cm ．DE ＝4 cm ，当点P 在ED 上运动时，S △BPQ ＝12BC ﹒AB ＝40cm 2，∴AB ＝8 cm ， ∴AE ＝6 cm ，∴当0＜t ≤10时，点P 在BE 上运动，BP ＝BQ ， ∴△BPQ 是等腰三角形， 故①正确；S △ABE ＝12AB ﹒AE ＝24 cm 2，故②错误；当14＜t ＜22时，点P 在CD 上运动，该段函数图象经过（14，40）和（22，0）两点，解析式为y ＝110－5t ，△ABP 为等腰三角形需要分类讨论：当AB ＝AP 时，ED 上存在一个符号题意的P 点，当BA ＝BO 时，BE 上存在一个符合同意的P 点，当PA ＝PB 时，点P 在AB 垂直平分线上，所以BE 和CD 上各存在一个符号题意的P 点，共有4个点满足题意， 故④错误；⑤△BPQ 与△ABE 相似时，只有；△BPQ ∽△BEA 这种情况，此时点Q 与点C 重合，即PC BC ＝AE AB ＝34，∴PC ＝7.5，即t ＝14.5． 故⑤正确．综上所述，正确的结论的序号是①③⑤．同类题型1.1 如图，在四边形ABCD 中，DC ∥AB ，AD ＝5，CD ＝3，sin A ＝sin B ＝ 13，动点P 自A 点出发，沿着边AB 向点B 匀速运动，同时动点Q 自点A 出发，沿着边AD －DC －CB 匀速运动，速度均为每秒1个单位，当其中一个动点到达终点时，它们同时停止运动，设点P 运动t （秒）时，△APQ 的面积为s ，则s 关于t 的函数图象是（ ）A ．B ．C ．D ．解：过点Q 做QM ⊥AB 于点M ．当点Q 在线段AD 上时，如图1所示，∵AP ＝AQ ＝t （0≤t ≤5），sin A ＝13，∴QM ＝13 t ，∴s ＝12AP ﹒QM ＝16t 2 ；当点Q 在线段CD 上时，如图2所示，∵AP ＝t （5≤t ≤8），QM ＝AD ﹒sin A ＝53，∴s ＝12AP ﹒QM ＝56t ；当点Q 在线段CB 上时，如图3所示，∵AP ＝t （8≤t ≤2023 ＋3（利用解直角三角形求出AB ＝2023 ＋3），BQ ＝5＋3＋5－t ＝13－t ，sin B ＝13，∴QM ＝13 （13－t ），∴s ＝12AP ﹒QM ＝－16（t 2－13t ），∴s ＝－16（t 2 －13t ）的对称轴为直线x ＝132．∵t ＜13， ∴s ＞0．综上观察函数图象可知B 选项中的图象符合题意． 选B ．同类题型1.2 如图1．在四边形ABCD 中，AB ∥CD ，AB ⊥BC ，动点P 从点B 出发，沿B →C →D →A 的方向运动，到达点A 停止，设点P 运动的路程为x ，△ABP 的面积为y ，如果y 与x 的函数图象如图2所示，那么AB 边的长度为____________．解：根据题意，当P 在BC 上时，三角形面积增大，结合图2可得，BC ＝4； 当P 在CD 上时，三角形面积不变，结合图2可得，CD ＝3； 当P 在DA 上时，三角形面积变小，结合图2可得，DA ＝5； 过D 作DE ⊥AB 于E ， ∵AB ∥CD ，AB ⊥BC ， ∴四边形DEBC 是矩形，∴EB ＝CD ＝3，DE ＝BC ＝4，AE ＝AD 2－DE 2＝52－42＝3， ∴AB ＝AE ＋EB ＝3＋3＝6．同类题型1.3 如图1，有一正方形广场ABCD ，图形中的线段均表示直行道路，⌒BD 表示一条以A 为圆心，以AB 为半径的圆弧形道路．如图2，在该广场的A 处有一路灯，O 是灯泡，夜晚小齐同学沿广场道路散步时，影子长度随行走路线的变化而变化，设他步行的路程为x （m ）时，相应影子的长度为y （m ），根据他步行的路线得到y 与x 之间关系的大致图象如图3，则他行走的路线是（ ）A ．A →B →E →G B ．A →E →D →C C ．A →E →B →FD ．A →B →D →C 解：根据图3可得，函数图象的中间一部分为水平方向的线段， 故影子的长度不变，即沿着弧形道路步行，因为函数图象中第一段和第三段图象对应的x 的范围相等，且均小于中间一段图象对应的x 的范围，又因为第一段和第三段图象都从左往右上升，所以第一段函数图象对应的路径为正方形的边AB 或AD ，第三段函数图象对应的路径为BC 或DC ， 故行走的路线是A →B →D →C （或A →D →B →C ）， 选D ．同类题型1.4例2．如图，菱形ABCD 的边长为6，∠ABC ＝120°，M 是BC 边的一个三等分点，P 是对角线AC 上的动点，当PB ＋PM 的值最小时，PM 的长是（ ）A ．72B ．2 73C ．3 55D ．264解：如图，连接DP ，BD ，作DH ⊥BC 于H ．∵四边形ABCD 是菱形，∴AC ⊥BD ，B 、D 关于AC 对称， ∴PB ＋PM ＝PD ＋PM ，∴当D 、P 、M 共线时，P ′B ＋P ′M ＝DM 的值最小，∵CM ＝13BC ＝2，∵∠ABC ＝120°，∴∠DBC ＝∠ABD ＝60°，∴△DBC 是等边三角形，∵BC ＝6， ∴CM ＝2，HM ＝1，DH ＝3 3 ，在Rt △DMH 中，DM ＝DH 2＋HM 2＝(33)2＋12＝27 ， ∵CM ∥AD ，∴P ′M DP ′＝CM AD ＝26＝13， ∴P ′M ＝14DM ＝72．选A ．同类题型2.1 如图，已知菱形OABC 的边OA 在x 轴上，点B 的坐标为（8，4），点P 是对角线OB 上的一个动点，点D （0，2）在y 轴上，当CP ＋DP 最短时，点P 的坐标为____________．解：如图连接AC ，AD ，分别交OB 于G 、P ，作BK ⊥OA 于K ．在Rt △OBK 中，OB ＝BK 2＋OK 2＝82＋42＝4 5 ， ∵四边形OABC 是菱形，∴AC ⊥OB ，GC ＝AG ，OG ＝BG ＝2 5 ，设OA ＝AB ＝x ，在Rt △ABK 中，∵AB 2＝AK 2＋BK 2，∴x 2＝（8－x ）2＋42 ， ∴x ＝5， ∴A （5，0），∵A 、C 关于直线OB 对称， ∴PC ＋PD ＝PA ＋PD ＝DA ， ∴此时PC ＋PD 最短，∵直线OB 解析式为y ＝12 x ，直线AD 解析式为y ＝－25x ＋2，由⎩⎨⎧y ＝12x y ＝－25x ＋2 解得⎩⎨⎧x ＝209y ＝109，∴点P 坐标（209 ，109）．同类题型2.2 如图，在平面直角坐标系中，反比例函数y ＝ kx（x ＞0）的图象与边长是6的正方形OABC 的两边AB ，BC 分别相交于M ，N 两点．△OMN 的面积为10．若动点P 在x 轴上，则PM ＋PN 的最小值是（ ） A ．6 2 B ．10 C ．2 26 D ．2 29解：∵正方形OABC 的边长是6，∴点M 的横坐标和点N 的纵坐标为6， ∴M （6，k 6 ），N （k6，6），∴BN ＝6－k 6 ，BM ＝6－k6， ∵△OMN 的面积为10，∴6×6－12×6×k 6－12×6×k 6－12×（6－k 6）2＝10，∴M （6，4），N （4，6），作M 关于x 轴的对称点M ′，连接NM ′交x 轴于P ，则NM ′的长＝PM ＋PN 的最小值，∵AM ＝AM ′＝4， ∴BM ′＝10，BN ＝2，∴NM ′＝BM ′2＋BN 2＝102＋22＝226 ， 选C ．同类题型2.3例3．如图，正方形ABCD 中．点E ，F 分别在BC ，CD 上，△AEF 是等边三角形．连接AC 交EF 于点G ．过点G 作GH ⊥CE 于点H ，若S △EGH ＝3，则S △ADF ＝（ ） A ．6 B ．4 C ．3 D ．2解：∵四边形ABCD 是正方形，∴AB ＝BC ＝CD ＝AD ，∠B ＝∠BCD ＝∠D ＝∠BAD ＝90°． ∵△AEF 等边三角形，∴AE ＝EF ＝AF ，∠EAF ＝60°． ∴∠BAE ＋∠DAF ＝30°． 在Rt △ABE 和Rt △ADF 中， ⎩⎨⎧AE ＝AF AB ＝AD， ∴Rt △ABE ≌Rt △ADF （HL ）， ∴BE ＝DF ， ∵BC ＝CD ，∴BC －BE ＝CD －DF ，即CE ＝CF ， ∴△CEF 是等腰直角三角形， ∵AE ＝AF ，∴AC 垂直平分EF ， ∴EG ＝GF ，∴GH ∥CF ，∴△EGH ∽△EFC ，∵S △EGH ＝3，∴S △EFC ＝12， ∴CF ＝2 6 ，EF ＝4 3 ，∴AF ＝4 3 ，设AD ＝x ，则DF ＝x －2 6 ，∵AF 2＝AD 2＋DF 2 ，∴（43）2＝x 2＋（x －26）2 ，∴x ＝6＋3 2 ，∴AD ＝6＋3 2 ，DF ＝32－ 6 ，∴S △ADF ＝12AD ﹒DF ＝6． 选A ．同类题型3.1如图，在等腰Rt △ABC 中，∠ABC ＝90°，AB ＝CB ＝2，点D 为AC 的中点，点E ，F 分别是线段AB ，CB 上的动点，且∠EDF ＝90°，若ED 的长为m ，则△BEF 的周长是___________（用含m 的代数式表示）．解：如图，连接BD ，在等腰Rt △ABC 中，点D 是AC 的中点，∴BD ⊥AC ， ∴BD ＝AD ＝CD ，∠DBC ＝∠A ＝45°，∠ADB ＝90°，∵∠EDF ＝90°，∴∠ADE ＝∠BDF ，在△ADE 和△BDF 中，⎩⎪⎨⎪⎧∠A ＝∠DBFAD ＝BD ∠ADE ＝∠BDF， ∴△ADE ≌△BDF （ASA ），∴AE ＝BF ，DE ＝DF ，在Rt △DEF 中，DF ＝DE ＝m ．∴EF ＝2DE ＝ 2 m ，∴△BEF 的周长为BE ＋BF ＋EF ＝BE ＋AE ＋EF ＝AB ＋EF ＝2＋ 2 m ．同类题型3.2 如图，在矩形ABCD 中，AB ＝2，AD ＝2 2 ，点E 是CD 的中点，连接AE ，将△ADE 沿直线AE 折叠，使点D 落在点F 处，则线段CF 的长度是（ ）A ．1B ．22C ．23D ．23解：过点E 作EM ⊥CF 于点M ，如图所示．在Rt △ADE 中，AD ＝2 2 ，DE ＝12AB ＝1， ∴AE ＝AD 2＋DE 2 ＝3．根据折叠的性质可知：ED ＝EF ，∠AED ＝∠AEF ．∵点E 是CD 的中点，∴CE ＝DE ＝FE ，∴∠FEM ＝∠CEM ，CM ＝FM ．∵∠DEA ＋∠AEF ＋∠FEM ＋∠MEC ＝180°，∴∠AEF ＋∠FEM ＝12×180°＝90°． 又∵∠EAF ＋∠AEF ＝90°，∴∠EAF ＝∠FEM ．∵∠AFE ＝∠EMF ＝90°，∴△AFE ∽△EMF ，∴MF FE ＝FE EA ，即MF 1＝13， ∴MF ＝13 ，CF ＝2MF ＝23． 选C ．同类题型3.3如图，在矩形ABCD 中，BE ⊥AC 分别交AC 、AD 于点F 、E ，若AD ＝1，AB ＝CF ，则AE ＝__________．解：∵四边形ABCD 是矩形，∴BC ＝AD ＝1，∠BAF ＝∠ABC ＝90°，∴∠ABE ＋∠CBF ＝90°，∵BE ⊥AC ，∴∠BFC ＝90°，∴∠BCF ＋∠CBF ＝90°，∴∠ABE ＝∠FCB ，在△ABE 和△FCB 中，⎩⎪⎨⎪⎧∠EAB ＝∠BFC ＝90°AB ＝CF ∠ABE ＝∠FCB， ∴△ABE ≌△FCB ，∴BF ＝AE ，BE ＝BC ＝1，∵BE ⊥AC ，∴∠BAF ＋∠ABF ＝90°，∵∠ABF ＋∠AEB ＝90°，∴∠BAF ＝∠AEB ，∵∠BAE ＝∠AFB ，∴△ABE ∽△FBA ， ∴AB BF ＝BE AB， ∴AB AE ＝1AB ， ∴AE ＝AB 2 ，在Rt △ABE 中，BE ＝1，根据勾股定理得，AB 2＋AE 2＝BE 2 ＝1，∴AE ＋AE 2 ＝1， ∵AE ＞0，∴AE ＝5－12．同类题型3.4 如图，正方形ABCD 中，BC ＝2，点M 是边AB 的中点，连接DM ，DM 与AC 交于点P ，点E 在DC 上，点F 在DP 上，且∠DFE ＝45°．若PF ＝ 56，则CE ＝_________．解：如图，连接EF ．∵四边形ABCD 是正方形，∴AB ＝BC ＝CD ＝DA ＝2，∠DAB ＝90°，∠DCP ＝45°，∴AM ＝BM ＝1，在Rt △ADM 中，DM ＝AD 2＋AM 2＝22＋12＝ 5 ，∵AM ∥CD ，∴AM DC ＝MP PD ＝12， ∴DP ＝253 ，∵PF ＝56， ∴DF ＝DP －PF ＝52， ∵∠EDF ＝∠PDC ，∠DFE ＝∠DCP ，∴△DEF ∽△DPC ， ∴DF DC ＝DE DP，∴522＝DE253，∴DE＝56，∴CE＝CD－DE＝2－56＝76．例4．如图，正方形ABCD的边长为4，点E、F分别从点A、点D以相同速度同时出发，点E从点A向点D 运动，点F从点D向点C运动，点E运动到D点时，E、F停止运动．连接BE、AF相交于点G，连接CG．有下列结论：①AF⊥BE；②点G随着点E、F的运动而运动，且点G的运动路径的长度为π；③线段DG的最小值为2 5 －2；④当线段DG最小时，△BCG的面积S＝8＋855 ．其中正确的命题有____________．（填序号）解：∵点E、F分别同时从A、D出发以相同的速度运动，∴AE＝DF，∵四边形ABCD是正方形，∴AB＝DA，∠BAE＝∠D＝90°，在△BAE和△ADF中，⎩⎪⎨⎪⎧AE＝DE∠BAE＝∠ADF＝90°AB＝AD，∴△BAE≌△ADF（SAS），∴∠ABE＝∠DAF，∵∠DAF＋∠BAG＝90°，∴∠ABE＋∠BAG＝90°，即∠AGB＝90°，∴AF⊥BE．故①正确；∵∠AGB＝90°，∴点G的运动路径是以AB为直径的圆所在的圆弧的一部分，由运动知，点E运动到点D时停止，同时点F运动到点C，∴点G的运动路径是以AB为直径的圆所在的圆弧所对的圆心角为90°，∴长度为90π×2180＝π，故命题②正确；如图，设AB的中点为点P，连接PD，∵点G是以点P为圆心AB为直径的圆弧上一点，∴当点G 在PD 上时，DG 有最小值，在Rt △ADP 中，AP ＝12 AB ＝2，AD ＝4，根据勾股定理得，PD ＝2 5 ， ∴DG 的最小值为2gh (5) －2，故③正确；过点G 作BC 的垂线与AD 相交于点M ，与BC 相交于N ，∴GM ∥PA ，∴△DMG ∽△DAP ，∴GM AP ＝DG DP， ∴GM ＝10－255， ∴△BCG 的高GN ＝4－GM ＝10＋255， ∴S △BCG ＝12×4×10＋255＝4＋455，故④错误， ∴正确的有①②③．同类题型4.1 如图，在矩形ABCD 中，E 是AD 边的中点，BE ⊥AC ，垂足为F ，连结DF ，下列四个结论：①△AEF ∽△CAB ；②tan ∠CAD ＝ 2 ；③DF ＝DC ；④CF ＝2AF ，正确的是（ ）A ．①②③B ．②③④C ．①③④D ．①②④解：如图，过D 作DM ∥BE 交AC 于N ，∵四边形ABCD 是矩形，∴AD ∥BC ，∠ABC ＝90°，AD ＝BC ，∵BE ⊥AC 于点F ，∴∠EAC ＝∠ACB ，∠ABC ＝∠AFE ＝90°，∴△AEF ∽△CAB ，故①正确；∵AD ∥BC ，∴△AEF ∽△CBF ，∴AE BC ＝AF CF， ∵AE ＝12AD ＝12BC ， ∴AF CF ＝12， ∴CF ＝2AF ，故④正确；∵DE ∥BM ，BE ∥DM ，∴四边形BMDE 是平行四边形，∴BM ＝DE ＝12BC ，∴BM ＝CM ，∴CN ＝NF ，∵BE ⊥AC 于点F ，DM ∥BE ，∴DN ⊥CF ，∴DM 垂直平分CF ，∴DF ＝DC ，故③正确；设AE ＝a ，AB ＝b ，则AD ＝2a ，由△BAE ∽△ADC ，有b a ＝2a b ，即b ＝ 2 a ， ∴tan ∠CAD ＝DC AD ＝b 2a ＝22．故②不正确； 正确的有①③④，选C ．同类题型4.2 点E 、F 分别在平行四边形ABCD 的边BC 、AD 上，BE ＝DF ，点P 在边AB 上，AP ：PB ＝1：n （n ＞1），过点P 且平行于AD 的直线l 将△ABE 分成面积为S 1 、S 2 的两部分，将△CDF 分成面积为S 3 、S 4 的两部分（如图），下列四个等式：①S 1 ：S 3 ＝1：n②S 1 ：S 4 ＝1：（2n ＋1）③（S 1＋S 4 ）：（S 2＋S 3 ）＝1：n④（S 3－S 1 ）：（S 2－S 4 ）＝n ：（n ＋1）其中成立的有（ ）A ．①②④B ．②③C ．②③④D ．③④解：由题意∵AP ：PB ＝1：n （n ＞1），AD ∥l ∥BC ，∴S 1S 1＋S 2＝（1n ＋1）2 ，S 3＝n 2S 1 ，S 3S 3＋S 4＝（n n ＋1）2 ， 整理得：S 2＝n （n ＋2）S 1 ，S 4＝（2n ＋1）S 1 ，∴S 1 ：S 4 ＝1：（2n ＋1），故①错误，②正确，∴（S 1＋S 4 ）：（S 2＋S 3）＝[S 1＋（2n ＋1）S 1]：[n （n ＋2）S 1＋n 2S 1]＝1：n ，故③正确，∴（S 3－S 1 ）：（S 2－S 4）＝[n 2S 1－S 1]：[n （n ＋2）S 1－（2n ＋1）S 1]＝1：1，故④错误，选B ．同类题型4.3 如图，在矩形ABCD 中，DE 平分∠ADC 交BC 于点E ，点F 是CD 边上一点（不与点D 重合）．点P 为DE 上一动点，PE ＜PD ，将∠DPF 绕点P 逆时针旋转90°后，角的两边交射线DA 于H ，G 两点，有下列结论：①DH ＝DE ；②DP ＝DG ；③DG ＋DF ＝ 2 DP ；④DP ﹒DE ＝DH ﹒DC ，其中一定正确的是（ ）A ．①②B ．②③C ．①④D ．③④解：∵∠GPF ＝∠HPD ＝90°，∠ADC ＝90°，∴∠GPH ＝∠FPD ，∵DE 平分∠ADC ，∴∠PDF ＝∠ADP ＝45°，∴△HPD 为等腰直角三角形，∴∠DHP ＝∠PDF ＝45°，在△HPG 和△DPF 中，∵⎩⎪⎨⎪⎧∠PHG ＝∠PDFPH ＝PD ∠GPH ＝∠FPD， ∴△HPG ≌△DPF （ASA ），∴PG ＝PF ；∵△HPD 为等腰直角三角形， ∴HD ＝ 2 DP ，HG ＝DF ，∴HD ＝HG ＋DG ＝DF ＋DG ，∴DG ＋DF ＝ 2 DP ；故③正确，∵DP ﹒DE ＝22 DH ﹒DE ，DC ＝22DE ， ∴DP ﹒DE ＝DH ﹒DC ，故④正确，由此即可判断选项D 正确，选D ．例5．如图，在平面直角坐标系中，经过点A 的双曲线y ＝ k x（x ＞0）同时经过点B ，且点A 在点B 的左侧，点A 的横坐标为 2 ，∠AOB ＝∠OBA ＝45°，则k 的值为______________．解：过A 作AM ⊥y 轴于M ，过B 作BD 选择x 轴于D ，直线BD 与AM 交于点N ，如图所示：则OD ＝MN ，DN ＝OM ，∠AMO ＝∠BNA ＝90°，∴∠AOM ＋∠OAM ＝90°，∵∠AOB ＝∠OBA ＝45°，∴OA ＝BA ，∠OAB ＝90°，∴∠OAM ＋∠BAN ＝90°，∴∠AOM ＝∠BAN ，在△AOM 和△BAN 中，⎩⎪⎨⎪⎧∠AOM ＝∠BAN∠AMO ＝∠BNA OA ＝BA， ∴△AOM ≌△BAN （AAS ），∴AM ＝BN ＝ 2 ，OM ＝AN ＝k 2 ， ∴OD ＝k 2＋ 2 ，BD ＝k 2－ 2 ， ∴B （k2＋ 2 ，k2－ 2 ），∴双曲线y ＝k x （x ＞0）同时经过点A 和B ，∴（k 2＋2）﹒（k 2－ 2 ）＝k ， 整理得：k 2 －2k －4＝0， 解得：k ＝1± 5 （负值舍去），∴k ＝1＋ 5 ．同类题型5.1 如图，在平面直角坐标系xOy 中，已知直线y ＝kx （k ＞0）分别交反比例函数y ＝ 1x 和y ＝ 9x在第一象限的图象于点A ，B ，过点B 作 BD ⊥x 轴于点D ，交y ＝ 1x的图象于点C ，连结A C ．若△ABC 是等腰三角形，则k 的值是________．解：∵点B 是y ＝kx 和y ＝9x 的交点，y ＝kx ＝9x， 解得：x ＝3k ，y ＝3k ，∴点B 坐标为（3k，3gh (k ) ）， 点A 是y ＝kx 和y ＝1x 的交点，y ＝kx ＝1x， 解得：x ＝1k ，y ＝k ，∴点A 坐标为（1k ，k ）， ∵BD ⊥x 轴，∴点C 横坐标为3k，纵坐标为13k ＝k 3 ， ∴点C 坐标为（3k ，k3 ），∴BA ≠AC ，若△ABC 是等腰三角形，①AB ＝BC ，则(3k －1k)2＋(3k －k )2＝3k －k 3 ， 解得：k ＝377； ②AC ＝BC ，则(3k －1k )2＋(k －k 3)2＝3k －k 3 ， 解得：k ＝155； 故k ＝377 或155．。

专题一 压轴选择填空题第4关 以圆或隐圆为背景的选择填空题【名师综述】直线与圆是高中数学的C 级知识点，是高中数学中数形结合思想的典型体现．近年来，高考对直线与圆的命题，既充分体现自身知识结构体系的命题形式多样化，又保持与函数或不等式或轨迹相结合的命题思路，呈现出“综合应用，融会贯通”的特色，充分彰显直线与圆的交汇价值．【典例解剖】类型一 以动点轨迹为圆考查直线与圆、圆与圆位置关系典例1．（2020上海控江中学高三月考）设三角形ABC 是位于平面直角坐标系xOy 的第一象限中的一个不等边三角形，该平面上的动点P 满足：222222||||||||||||PA PB PC OA OB OC ++=++，已知动点P 的轨迹是一个圆，则该圆的圆心位于三角形ABC 的（ ） A ．内心 B ．外心C ．重心D ．垂心【答案】C 【解析】【分析】可设(,)P x y ，()11,A x y ()22,B x y ，()33,C x y ，由222222||||||||||||PA PB PC OA OB OC ++=++列出关系式，由P 的轨迹为圆，求出圆心坐标即可【详解】设(,)P x y ，()11,A x y ()22,B x y ，()33,C x y ，由222222||||||||||||PA PB PC OA OB OC ++=++得：222222222222112233112233()()()()()()x x y y x x y y x x y y x y x y x y -+-+-+-+-+-=+++++ 展开整理，得22123123332()2()0x y x x x x y y y y +-++-++=．∴2222123123123123111[()][()][()()]339x x x x y y y y x x x y y y -+++-++=+++++． ∴圆的圆心坐标为1231(()3x x x ++，1231())3y y y ++，为三角形ABC 的重心，故选C ．【名师点睛】本题考查直线与圆的综合应用，圆的轨迹方程的求法，重心坐标公式的应用，计算量偏大，化简时需进行整体代换，简化运算难度，属于中档题． 【举一反三】（2020上海洋泾中学高三月考）已知定圆C ：()2245x y -+=，其圆心为()4,0C ，点A 为圆C 所在平面内一定点，点P 为圆C 上一个动点，若线段PA 的中垂线与直线PC 交于点Q ，则动点Q 的轨迹可能为______．（写出所有正确的序号）（1）椭圆；（2）双曲线；（3）抛物线；（4）圆；（5）直线；（6）一个点． 【答案】（1）（2）（4）（6） 【解析】（1）若点A 在圆C 外部，=QA QC PC AC ->Q 点的轨迹是以,A C 为焦点的双曲线；（2）若点A 在圆上，则C Q ，点重合，如图，点Q 点的轨迹为点C ；（3）若点A 在圆内部且不为圆心，则QA QC PC +==AC <Q 点的轨迹是以,A C 为焦点的椭圆；（4）若点A 在圆内部且为圆心，,A C 重合时，Q 为半径PA 的中点，所以点Q 是以C 为半径的圆．综上所述，Q 点的轨迹可能是（1）（2）（4）（6）四种情况 答案为：（1）（2）（4）（6）类型二 以圆中直角三角形建立函数关系式或方程或不等式典例2．（2020上海师大附中期中）已知点A ，B ，C 在圆221x y +=上运动，且AB ⊥BC ，若点P 的坐标为（2，0），则PA PB PC ++u u u r u u u r u u u r 的最大值为（ ）A ．6B ．7C ．8D ．9【答案】B 【解析】由题意，AC 为直径，所以24437PA PB PC PO PB PB ++=+≤+≤+=u u u r u u u r u u u r u u u r u u u r u u u r，当且仅当点B 为（-1，0）时，PA PB PC ++u u u r u u u r u u u r取得最大值7，故选B ．考点：直线与圆的位置关系、平面向量的运算性质 【名师点睛】与圆有关的最值问题是命题的热点内容，它着重考查数形结合与转化思想．由平面几何知识知，圆上的一点与圆外一定点距离最值在定点和圆心连线与圆的两个交点处取到．圆周角为直角的弦为圆的半径，平面向量加法几何意义这些小结论是转化问题的关键． 【举一反三】1．（2020上海七宝中学高三月考）已知a b v v 、是平面内两个互相垂直的单位向量，且此平面内另一向量c v 在满足()()340a c b c +-=v v v v，均能使c b k -≤v v 成立，则k 的最小值是_________．【答案】52【解析】【分析】根据题意，()()()1,0,0,1,,a b c x y v v v===，利用()()340a c b c +⋅-=r r r r ，求得,x y 的关系，利用圆的几何性质，再求出c b -vv 的最大值，从而求出k 的最小值．【详解】因为a b v v 、是平面内两个互相垂直的单位向量，所以可设 ()()()1,0,0,1,,a b c x y v v v ===， ()33,a c x y ∴+=+r r ，()4,4b c x y -=--r r，又()()340a c b c +⋅-=r r r r ，()()340x x y y ∴-++-=，即()22325224x y ⎛⎫++-= ⎪⎝⎭， 它表示的圆心在3,22M ⎛⎫- ⎪⎝⎭，半径为52的圆，c b -v v 表示圆上的点到(0,1)B 的距离，圆心M 到点(0,1)B 的距离为d =c b ∴-r r 的最大值为52=，要使c b k -≤r r 恒成立，52k ≥，即k 的最小值是52，故答案为52．【名师点睛】本题主要考查向量模的几何意义、轨迹方程的应用以及圆的几何意义，考查了转化思想的应用，属于难题．转化是数学解题的灵魂，合理的转化不仅仅使问题得到了解决，还可以使解决问题的难度大大降低，本题将不等式恒成立问题转化为圆上动点到定点距离的最值问题是解题的关键． 类型三 利用数形结合揭示与刻画直线与圆、圆与圆位置关系典例3．（2020上海青浦中学月考）在平面直角坐标系中，记d 为点()cos ,sin P θθ到直线20x my --=的距离，当θ、m 变化时，d 的最大值为（ ） A ．1 B ．2 C ．3 D ．4【答案】C 【解析】【分析】P 为单位圆上一点，而直线20x my --=过点()2,0A ，则根据几何意义得d 的最大值为1OA +． 【详解】22cos sin 1θθ+=∴Q ，P 为单位圆上一点，而直线20x my --=过点()2,0A ， 所以d 的最大值为1213OA +=+=，选C ． 【名师点睛】与圆有关的最值问题主要表现在求几何图形的长度、面积的最值，求点到直线的距离的最值，求相关参数的最值等方面．解决此类问题的主要思路是利用圆的几何性质将问题转化． 【举一反三】（2020上海徐汇区一模）若圆221:1C x y +=和圆222:680C x y x y k +---=没有公共点，则实数k 的取值范围是（ ） A ．(9,11)-B ．(25,9)--C ．(,9)(11,)-∞-+∞UD ．(25,9)(11,)--+∞U【答案】D【解析】化圆C 2：x 2+y 2﹣6x ﹣8y ﹣k ＝0为（x ﹣3）2+（y ﹣4）2＝25+k ，则k ＞﹣25，圆心坐标为（3，4）， 圆C 1：x 2+y 2＝1的圆心坐标为（0，0），半径为1．要使圆C 1：x 2+y 2＝1和圆C 2：x 2+y 2﹣6x ﹣8y ﹣k ＝0没有公共点，则|C 1C 2|1或|C 1C 2|1，即51或51，解得﹣25＜k ＜﹣9或k ＞11． ∴实数k 的取值范围是（﹣25，﹣9）∪（11，+∞），故选D ．【精选名校模拟】1．（2020上海七宝中学月考）已知实数x 、y 满足：22(2)1x y +-=，ω=的取值范围是（ ）A ．B ．[1,2]C ．(0,2]D ．2【答案】B 【解析】【分析】构造直线0x +=，过圆上一点P 作直线的垂线PM 2sin POM =∠，求出sin POM ∠的范围即可得出．【详解】设(,)P x y 为圆22(2)1x y +-=上的任意一点，则P 到直线0x +=的距离PM =P 到原点的距离OP =22sin PMPOM OP==∠． 设圆22(2)1x y +-=与直线y kx =1=，解得k =，POM ∴∠的最小值为30︒，最大值为90︒，1sin 12POM ∴∠剟，12sin 2POM ∴∠剟，故选B ．【名师点睛】本题主要考查直线与圆的位置关系，距离公式的应用，解题关键是数形结合思想的应用，能阅读出ω=2．（2020上海南模中学高三月考）设1x 、2x 是关于x 的方程220x mx m m ++-=的两个不相等的实数根，那么过两点211(,)A x x ，222(,)B x x 的直线与圆()2211x y -+=的位置关系是（ ）A ．相离．B ．相切．C ．相交．D ．随m 的变化而变化．【答案】D 【解析】22212121,ABx x k x x x x -==+∴-Q 直线AB 的方程为21121()()y x x x x x -=+-． 即1212()y x x x x x =+-，所以直线AB的方程为22,y mx m m d =-+-===因为2240,4()0,03m m m m ∆>∴-->∴<<， 所以221999225,(),(,),()()161616256t g t t t t g t g m =>∴=+∈+∞>=令，所以1615d =<=，所以直线AB 与圆可能相交，也可能相切，也可能相离． 3．（2020上海一模冲刺练）若对于任意角θ，都有cos (2)sin 1x y θθ+-=，则直线:cos (2)sin 1l x y θθ+-=围成的正多边形的最小面积是（ ）A．B ．4C．D ．不确定【答案】D 【解析】【分析】先根据点()02P ，到直线cos (2)sin 1x y θθ+-=的距离为1，确定直线为以()02，为圆心，1为半径的圆的切线，再取特殊直线运算否定ABC 即得选项． 【详解】由对于任意角θ，都有cos (2)sin 1x y θθ+-=，则点()02P ，到直线cos (2)sin 1x y θθ+-=1=，即此直线为以()02，为圆心，1为半径的圆的切线， 当三条切线如图所示时，则正三角形ABC 的面积11233S =⨯⨯=， 即存在直线:cos (2)sin 1l x y θθ+-=，即选项A ，B ，C 错误，故选D ．4．（2020上海交大附中月考）数学中有许多形状优美、寓意美好的曲线，曲线C ：221||x y x y +=+就是其中之一（如图）．给出下列三个结论：①曲线C 恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C ； ③曲线C 所围成的“心形”区域的面积小于3． 其中，所有正确结论的序号是 A ．① B ．②C ．①②D ．①②③【答案】C 【解析】【分析】将所给方程进行等价变形确定x 的范围可得整点坐标和个数，结合均值不等式可得曲线上的点到坐标原点距离的最值和范围，利用图形的对称性和整点的坐标可确定图形面积的范围．【详解】由221x y x y +=+得，221y x y x -=-，2222||3341,10,2443x x x y x ⎛⎫-=-- ⎪⎝⎭厔， 所以x 可为的整数有0，-1，1，从而曲线22:1C x y x y +=+恰好经过(0，1)，(0，-1)，(1，0)，(1，1)，(-1，0)，(-1，1)六个整点，结论①正确．由221x y x y +=+得，222212x y x y +++…，解得222x y +≤，所以曲线C 上任意一点到原点的距离都．结论②正确．如图所示，易知()()()()0,1,1,0,1,1,,0,1A B C D -， 四边形ABCD 的面积13111122ABCD S =⨯⨯+⨯=，很明显“心形”区域的面积大于2ABCD S ，即“心形”区域的面积大于3，说法③错误，故选C ．5．（2020上海浦东复旦附中高三月考）在平面直角坐标系中，A ，B 分别是 x 轴和 y 轴上的动点，若以 AB 为直径的圆 C 与直线 240x y +-= 相切，则圆 C 面积的最小值为___ ． 【答案】45π【解析】由题意，圆心C 到原点的距离与到直线的距离相等，所以面积最小时，圆心在原点到直线的垂线中点上，则d =r =，45S π=． 6．（2020上海二中高三期中考试）若定义域均为D 的三个函数f （x ），g （x ），h （x ）满足条件：对任意x ∈D ，点（x ，g （x ）与点（x ，h （x ）都关于点（x ，f （x ）对称，则称h （x ）是g （x ）关于f （x ）的“对称函数”．已知g （x ）f （x ）=2x+b ，h （x ）是g （x ）关于f （x ）的“对称函数”，且h （x ）≥g （x ）恒成立，则实数b 的取值范围是_____．【答案】)+∞ 【解析】【分析】根据对称函数的定义，结合h （x ）≥g （x ）恒成立，转化为点到直线的距离d≥1，利用点到直线的距离公式进行求解即可【详解】∵x ∈D ，点（x ，g （x ）） 与点（x ，h （x ））都关于点（x ，f （x ））对称，∴g （x ）+h （x ）=2f （x ）， ∵h （x ）≥g （x ）恒成立，∴2f （x ）=g （x ）+h （x ）≥g （x ）+g （x ）=2g （x ），即f （x ）≥g （x ）恒成立， 作出g （x ）和f （x ）的图象，则g （x ）在直线f （x ）的下方或重合， 则直线f （x ）的截距b ＞0，且原点到直线y=2x+b 的距离d≥1，1=≥⇒b ≤，即实数b 的取值范围是+∞），故答案为：)+∞．7．（2020上海育才中学高三月考）已知平面直角坐标系中两点12(,)A a a 、12(,)B b b ，O 为原点，有122112AOB S a b a b ∆=-．设11(,)M x y 、22(,)N x y 、33(,)P x y 是平面曲线2224x y x y +=-上任意三点，则12212332T x y x y x y x y =-+-的最大值为________【答案】20． 【解析】【分析】将圆的方程化为标准方程，得出圆心坐标和半径长，由题意得12212332T x y x y x y x y =-+-12212332222OMN OPN OMNP x y x y x y x y S S S ∆∆≤-+-=+=四边形，转化为圆内接四边形中正方形的面积最大，即可得出T 的最大值．【详解】将圆的方程化为标准方程得()()22125x y -++=，圆心坐标为()1,2-122123321221233222OMN OPN T x y x y x y x y x y x y x y x y S S ∆∆∴=-+-≤-+-=+2OMNP S =四边形，由于圆内接四边形中，正方形的面积最大，所以当四边形OMNP 为正方形时，T =所以2220T ≤⨯=，故答案为：20．8．（2020上海浦东新区高三期末）若函数2y ax a =+存在零点，则实数a 的取值范围是________．【答案】 【解析】【分析】将函数2y ax a =+()()2,()f x a x g x =+=像，观察图像得出实数a 的取值范围．【详解】设()()2,()f x a x g x =+=2y ax a =+存在零点等价于()()2,()f x a x g x =+=函数()()2f x a x =+的图像恒过点(2,0)-，当其和函数()g x =a ==，所以()()2,()f x a x g x =+=03a ≤≤，故答案为：．9．（2020永安三中高三期中考试）若曲线y =y x b =+始终有交点，则b 的取值范围是_______．【答案】[-【解析】由题设可知x b +=b x =有解，令借cos ,[0,]x θθπ=∈，则sin θ=，所以sin cos )4b πθθθ=-=-，由于0θπ≤≤，故3444πππθ-≤-≤，结合正弦函数的图像可知sin()124πθ-≤-≤，则)[4b πθ=-∈-，应填答案[-． 【名师点睛】解答本题的思路是依据题设条件将其转化为方程x b +=进而分离参数b x ，然后通过三角换元将其转化为求函数sin cos )4b πθθθ=-=-的值域问题，最后借助正弦函数的图像求出其值域使得问题获解．10．（2020上海四中高三期中考试）若点()1,1P 为圆2260x y x +-=的弦MN 的中点，则弦MN 所在直线方程为________． 【答案】210x y --=【解析】因为(1,1)P 为圆2260x y x +-=的弦MN 的中点，所以圆心坐标为()3,0，31201MN k -=-=-，MN 所在直线方程为()121y x -=-，化简为210x y --=，故答案为210x y --=． 11．（2020上海华师大二附中高三月考）设1234,,,a a a a R ∈，且14231a a a a -=，则代数式222212341324a a a a a a a a +++++的最小值为______．【解析】【分析】由222212341324a a a a a a a a +++++结构特征，构造向量12(,)OA a a a ==u u u r r ，34(,)OB b a a ==u u u r r，设,a b r r 的夹角为θ，14231,,a a a a a b -=r r 不共线，0θπ<<，222212341324a a a a a a a a +++++=22||||2||||a b a b a b a b ++⋅≥+⋅r r r r r r r r ，转化为求2||||a b a b +⋅r r r r的最小值，由14231a a a a -=，可得1||||,sin a b θ=r r cos sin a b θθ⋅=r r ，转化求2cos cos 2sin sin sin θθθθθ++=的最小值，即为(sin ,cos )M θθ与点(0,2)P -连线的斜率最小值，即可得结果．【详解】设12(,)OA a a a ==u u u r r ，34(,)OB b a a ==u u u r r，设,a b r r的夹角为θ，14231,,a a a a a b -=r r 不共线，0θπ<<，222212341324a a a a a a a a +++++=22||||2||||a b a b a b a b ++⋅≥+⋅r r r r r r r r，sin θ===1||||||||a b a b ==r r ， 1cos ||||,sin sin a b a b θθθ=⋅=r r r r ，2||||a b a b +⋅r r r r 2cos cos 2sin sin sin θθθθθ+=+= ① 设(sin ,cos )M θθ，（0θπ<<），(0,2)P -，①式表示点(0,2)P -与单位圆（y 轴右侧）的点M 连线斜率，当PM12．（2020上海建平中学高三期中）已知a v 、b v 、2c v是平面内三个单位向量，若a b ⊥v v ，则4232a c a b c +++-v v v v v的最小值是________【答案】【解析】【分析】设2(,)c e x y ==r r ，(1,0)a =r ，(0,1)b =r ，将问题转化为求|2||64|a e a b e +++-r r r r r的最小值，再证明|2||2|a e a e +=+r r r r ，从而将原问题转化为求|2||64|a e a b e +++-r r r r r的最小值． 【详解】令2c e =r r，设(1,0)a =r ，(0,1)b =r ，e r 对应的点C 在单位圆上，所以问题转化为求|2||64|a e a b e +++-r r r r r的最小值．因为2222(2)(2)330a e a e e a +-+=-=r r r r r r ，所以|2||2|a e a e +=+r r r r ，所以|64||2|a e a b e ++-=+r r r rr ，表示C 点到点(2,0)-和(6,4)的距离之和，过点(2,0)-和(6,4)的直线为220x y -+=，原点到直线220x y -+=1=<，所以与单位圆相交，所以|2||64|a e a b e +++-r r r r r的最小值为：点(2,0)-和(6,4)之间的距离，即13．（2020上海高三模拟考试）已知关于t 的一元二次方程2(2)2()0(,)t i t xy x y i x y R ++++-=∈，当方程有实数根时，则实数t 的取值范围________． 【答案】[4,0]- 【解析】【分析】根据方程有实数根，再结合复数相等，建立条件关系可得点的轨迹为以()1,1-为半径的圆，再结合直线t y x =-与圆的位置关系即可得解．【详解】因为关于t 的一元二次方程2(2)2()0(,)t i t xy x y i x y R ++++-=∈有实数根，得222()0t t xy t x y i +++++=，由复数相等的充要条件可得：2220t t xy t x y ⎧++=⎨+-=⎩，消t 得22(1)(1)2x y -++=，则所求点的轨迹为以()1,1-为半径的圆，直线t y x =-≤，解得40t -≤≤，故答案为[4,0]-．14．（2020上海南模中学高三期中）在平面直角坐标系中，记曲线C 为点(2cos 1,2sin 1)P θθ-+的轨迹，直线20x ty -+=与曲线C 交于A 、B 两点，则||AB 的最小值为________．【答案】【解析】 【分析】由2121x cos y sin θθ=-⎧⎨=+⎩消去θ得（x +1）2+（y ﹣1）2＝4，得曲线C 的轨迹是以C （﹣1，1）为圆心，2为半径的圆，再根据勾股定理以及圆的性质可得弦长的最小值． 【详解】 由2121x cos y sin θθ=-⎧⎨=+⎩消去θ得（x +1）2+（y ﹣1）2＝4，∴曲线C 的轨迹是以C （﹣1，1）为圆心，2为半径的圆， 又直线20x ty -+=恒过点D ()2,0-，且此点在圆内部 故当CD AB ⊥时|AB |最短，∴|AB |＝=故答案为：15．（2020上海青浦中学高三月考）已知AC 、BD 为圆()()22:1216O x y -+-=的两条相互垂直的弦，垂足为121,2M n n ⎛⎫+- ⎪⎝⎭则四边形ABCD 的面积n S 的极限值为___________．【答案】32 【解析】 【分析】由题意可得四边形ABCD 的面积n S 的表达式：2n AC BDS ⨯=，由于点121,2M nn ⎛⎫+- ⎪⎝⎭的极限位置是圆心，且此时四边形面积取到极限值，此时几何图形形状可求得面积的极限 【详解】由题可知，AC 、BD 为圆()()22:1216O x y -+-=的两条相互垂直的弦，垂足为121,2M n n ⎛⎫+- ⎪⎝⎭，由2n AC BDS ⨯=，由点121,2M nn ⎛⎫+- ⎪⎝⎭的极限位置是圆心()1,2，此时AC 、BD 都是直径，故n S 的极限值为22r ，4r =，n S 的极限值为32，圆内接四边形恰好为正方形 故答案为：32．16．（2020上海建平中学高三月考）在ABC ∆中，2BC =，45A ∠=︒，B Ð为锐角，点O 是ABC ∆外接圆的圆心，则OA BC ⋅u u u v u u u v的取值范围是______．【答案】(2,- 【解析】【分析】建立适当的直角坐标系，写出各点的坐标，进一步利用向量的数量积，将问题转化成求三角函数的值域问题，从而得到OA BC ⋅u u u r u u u r的取值范围．【详解】如图所示：||2BC =，90BOC ∠=°，45CAB ∠=︒，由于B Ð为锐角，则点A 只能在左半圆上，设AOB θ∠=，则)A θθ3()22ππθ<<，B ，C ，所以OA θ=u u u r )θ，(BC =u u u r ，2cos 2sin )4OA BC πθθθ⋅=-+=-u u u r u u u r ，因为322ππθ<<，所以5444πππθ<-<，则sin()124πθ-<-≤，所以2)4πθ-<-≤故答案为：(2,-．17．（2020上海松江区一模）若实数,0a b >，满足abc a b c =++，221a b +=，则实数c 的最小值为________【答案】- 【解析】【分析】先由题意，根据基本不等式，得到12≤ab ，得出112-≤-ab ，再由221a b +=，得到()212+-=a b ab ，根据abc a b c =++得()()()()22233+==+-+-+a b c a b a b a b ，令=+t a b ，根据题意得到(=+∈t a b ，由函数单调性，得到3=-y t t的最值，进而可求出结果． 【详解】因为,0a b >，221a b +=，所以2212a b ab +=≥，即12≤ab ，当且仅当a b =时，取等号；因此111122-≤-=-ab ， 又221a b +=，所以22212++=+a b ab ab ，即()212+-=a b ab ，由abc a b c =++得1+=-a b c ab ，所以()()()()22233+==+-+-+a b c a b a b a b ，令=+t a b，因为+===a b ，当且仅当a b =时取等号．所以(=+∈t a b ， 又易知函数3=-y tt在(t ∈上单调递增，因此32=-≤=-y tt，因此()()2233==≥=-+--+ca b ta b t即实数c的最小值为-，故答案为：-18．（2020江苏盐城中学月考）在平面直角坐标系xOy中，已知点()2,2A，E、F为圆()()22:114C x y-+-=上的两动点，且EF=，若圆C上存在点P，使得,0AE AF mCP m+=>u u u r u u u r u u u r，则m的取值范围为________．【答案】1⎤-⎦【解析】取EF中点为M，连接AM，则2+=u u u r u u u r u u u u rAE AF AM，又圆()()22:114C x y-+-=上存在点P，使得,0AE AF mCP m+=>u u u r u u u r u u u r，所以2=u u u u r u u u rAM mCP，因此22==u u u u r u u u rAM m CP m，即=u u u u rm AM；因为E、F为圆()()22:114C x y-+-=上的两动点，且EF=1==CM，设(,)M x y1=，即()()22111x y-+-=即为动点M的轨迹；所以AMu u u u r表示圆()()22111x y-+-=上的点与定点()2,2A之间的距离，因此11-≤≤+u u u urAC AM AC，11≤≤u uu u rAM11≤≤m，故答案为：1⎤⎦．。

2020-2021年七年级英语下册选词填空选择题练习（word）1一、七年级英语下册选词填空专项目练习（含答案解析）1．选择方框内的短语并用其适当的形式填空（2）The noise went on ________. I couldn't get any sleep.（3）It was a very strange feeling—l was afraid, but excited ________.（4）The little girl ________ the forest to visit her grandmother yesterday.（5）Tina came home late yesterday because she met an old friend ________ home and talked with him for a while.（6）Many builders are working on the ________ to build a house.（7）Jack ________ the door for several times, but nobody answered.（8）I didn't pass the exam again and my mother ________ it.【答案】（1）clean up（2）all night（3）at the same time（4）walked through（5）on her way（6）building site（7）knocked on（8）felt unhappy about【解析】【分析】building site建筑工地；all night整晚；at the same time与此同时；walk through步行穿过；feel unhappy about对......感觉不满意；knock on敲；on one's way在路上；clean up打扫干净（1）句意：在你出去之前你必须打扫干净你的房间，它是如此脏。

专题：四边形的综合问题例1．如图，△APB中，AB＝2 2 ，∠APB＝90°，在AB的同侧作正△ABD、正△APE和△BPC，则四边形PCDE面积的最大值是__________．同类题型1.1 如图，△APB中，AP＝4，BP＝3，在AB的同侧作正△ABD、正△APE和正△BPC，则四边形PCDE面积的最大值是___________．同类题型1.2 如图，在□ABCD中，分别以AB、AD为边向外作等边△ABE、△ADF，延长CB交AE于点G，点G在点A、E之间，连接CE、CF，EF，则以下四个结论一定正确的是（）①△CDF≌△EBC；②∠CDF＝∠EAF；③△ECF是等边三角形；④CG⊥AE．A．只有①② B．只有①②③ C．只有③④ D．①②③④同类题型1.3 如图，四边形ABCD是平行四边形，点E是边CD上的一点，且BC＝EC，CF⊥BE交AB于点F，P是EB延长线上一点，下列结论：①BE平分∠CBF；②CF平分∠DCB；③BC＝FB；④PF＝P C．其中正确的有______________．（填序号）同类题型1.4 如图，在□ABCD中，∠DAB的平分线交CD于点E，交BC的延长线于点G，∠ABC的平分线交CD于点F，交AD的延长线于点H，AG与BH交于点O，连接BE，下列结论错误的是（）A．BO＝OH B．DF＝CE C．DH＝CG D．AB＝AE例2．图甲是小明设计的带菱形图案的花边作品．该作品由形如图乙的矩形图案拼接而成（不重叠、无缝隙）．图乙中ABBC ＝67，EF＝4cm，上下两个阴影三角形的面积之和为54cm2，其内部菱形由两组距离相等的平行线交叉得到，则该菱形的周长为____________．同类题型2.1 如图，在菱形ABCD中，AB＝4cm，∠ADC＝120°，点E、F同时由A、C两点出发，分别沿AB、CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF 为等边三角形，则t的值为____________．同类题型2.2 如图，在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是____________．同类题型2.3 如图，在菱形ABCD中，边长为10，∠A＝60°．顺次连接菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连接四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连接四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…，则四边形A2017B2017C2017D2017的周长是______________．例3．如图，在矩形ABCD中，点E为AB的中点，EF⊥EC交AD于点F，连接CF（AD＞AE），下列结论：①∠AEF ＝∠BCE ；②S △CEF ＝S △EAF ＋S △CBE ；③AF ＋BC ＞CF ； ④若BC CD ＝ 32，则△CEF ≌△CDF ．其中正确的结论是____________．（填写所有正确结论的序号）同类题型3.1 如图，在矩形ABCD 中，AD ＝ 2 AB ，∠B AD 的平分线交BC 于点E ，DH ⊥AE 于点H ，连接BH 并延长交CD 于点F ，连接DE 交BF 于点O ，下列结论：①AED ＝∠CED ；②AB ＝HF ，③BH ＝HF ；④BC －CF ＝2HE ；⑤OE ＝OD ；其中正确结论的序号是____________．同类题型3.2 如图，在矩形ABCD 中，BC ＝ 2 AB ，∠ADC 的平分线交边BC 于点E ，AH ⊥DE 于点H ，连接CH 并延长交AB 边于点F ，连接AE 交CF 于点O ，给出下列命题：①AD ＝DE ②DH ＝2 2 EH ③△AEH ∽△CFB ④HO ＝12AE 其中正确命题的序号是________________（填上所有正确命题的序号）同类题型3.3 如图，在矩形ABCD 中，点E 是边BC 的中点，AE ⊥BD ，垂足为F ，则tan ∠BDE 的值是（ ）A ．24B ．14C ．13D ．23例4．已知：如图，在正方形ABCD 外取一点E ，连接AE ，BE ，DE ．过点A 作AE 的垂线AP 交DE 于点P ．若AE ＝AP ＝1，PB ＝ 6 ，下列结论：①△APD ≌△AEB ；②点B 到直线AE 的距离为 2 ；③EB ⊥ED ；④S △APD ＋S △APB ＝1＋ 6 ．⑤S 正方形ABCD ＝4＋ 6．其中正确结论的序号是___________________．同类题型4.1 如图，正方形ABCD 的边长为2，将长为2的线段QR 的两端放在正方形的相邻的两边上同时滑动．如果点Q 从点A 出发，沿图中所示方向按A →B →C →D →A 滑动到A 止，同时点R 从点B 出发，沿图中所示方向按B →C →D →A →B 滑动到B 止．点N 是正方形ABCD 内任一点，把N 点落在线段QR 的中点M 所经过的路线围成的图形内的概率记为P ，则P ＝（ ）A ．4－π4B ．π4C ．14D ．π－14同类题型4.2 如图，边长为2的正方形ABCD 中，AE 平分∠DAC ，AE 交CD 于点F ，CE ⊥AE ，垂足为点E ，EG ⊥CD ，垂足为点G ，点H 在边BC 上，BH ＝DF ，连接AH 、FH ，FH 与AC 交于点M ，以下结论：①FH ＝2BH ；②AC ⊥FH ；③S △ACF ＝1；④CE ＝ 12AF ；⑤EG 2 ＝FG ﹒DG ，其中正确结论的个数为（ ） A ．2 B ．3 C ．4 D ．5同类题型4.3 如图，边长为1的正方形ABCD 的对角线AC 、BD 相交于点O ．有直角∠MPN ，使直角顶点P 与点O 重合，直角边PM 、PN 分别与OA 、OB 重合，然后逆时针旋转∠MPN ，旋转角为θ（0°＜θ＜90°），PM 、PN 分别交AB 、BC 于E 、F 两点，连接EF 交OB 于点G ，则下列结论中正确的是 ______________．（1）EF ＝ 2 OE ；（2）S 四边形OEBF ：S 正方形ABCD ＝1：4；（3）BE ＋BF ＝ 2 OA ；（4）在旋转过程中，当△BEF 与△COF 的面积之和最大时，AE ＝ 34；（5）OG ﹒BD ＝AE 2＋CF 2 ．同类题型4.4 如图，四边形ABHK 是边长为6的正方形，点C 、D 在边AB 上，且AC ＝DB ＝1，点P 是线段CD 上的动点，分别以AP 、PB 为边在线段AB 的同侧作正方形AMNP 和正方形BRQP ，E 、F 分别为MN 、QR 的中点，连接EF ，设EF 的中点为G ，则当点P 从点C 运动到点D时，点G 移动的路径长为 _____________．参考答案例1．如图，△APB 中，AB ＝2 2 ，∠APB ＝90°，在AB 的同侧作正△ABD 、正△APE 和△BPC ，则四边形PCDE 面积的最大值是__________．解：如图，延长EP 交BC 于点F ，∵∠APB ＝90°，∠APE ＝∠BPC ＝60°，∴∠EPC ＝150°，∴∠CPF ＝180°－150°＝30°，∴PF 平分∠BPC ，又∵PB ＝PC ，∴PF ⊥BC ，设Rt △ABP 中，AP ＝a ，BP ＝b ，则CF ＝12CP ＝12b ，a 2＋b 2 ＝8， ∵△APE 和△ABD 都是等边三角形，∴AE ＝AP ，AD ＝AB ，∠EAP ＝∠DAB ＝60°，∴∠EAD ＝∠PAB ，∴△EAD ≌△PAB （SAS ），∴ED ＝PB ＝CP ，同理可得：△APB ≌△DCB （SAS ），∴EP ＝AP ＝CD ，∴四边形CDEP 是平行四边形，∴四边形CDEP 的面积＝EP ×CF ＝a ×12b ＝12ab ， 又∵（a －b ）2＝a 2－2ab ＋b 2 ≥0，∴2ab ≤a 2＋b 2 ＝8，∴12ab ≤2， 即四边形PCDE 面积的最大值为2．同类题型1.1 如图，△APB 中，AP ＝4，BP ＝3，在AB 的同侧作正△ABD 、正△APE 和正△BPC ，则四边形PCDE 面积的最大值是___________．解：∵△APE 和△ABD 是等边三角形，∴AE ＝AP ＝4，AB ＝AD ，∠EAP ＝∠DAB ＝60°，∴∠EAD ＝∠PAB ＝60°－∠DAP ，在△EAD 和△PAB 中⎩⎪⎨⎪⎧AE ＝AP∠EAD ＝∠PAB AD ＝AB∴△EAD ≌△PAB （SAS ），∴DE ＝BP ，同理△DBC ≌△ABP ，∴DC ＝AP ，∵△APE 和△BPC 是等边三角形，∴EP ＝AP ，BP ＝CP ，∴DE ＝CP ＝3，DC ＝PE ＝4，∴四边形PCDE 是平行四边形，当CP ⊥EP 时，四边形PCDE 的面积最大，最大面积是3×4＝12．同类题型1.2 如图，在□ABCD 中，分别以AB 、AD 为边向外作等边△ABE 、△ADF ，延长CB 交AE 于点G ，点G 在点A 、E 之间，连接CE 、CF ，EF ，则以下四个结论一定正确的是（ ）①△CDF ≌△EBC ；②∠CDF ＝∠EAF ；③△ECF 是等边三角形；④CG ⊥AE ．A ．只有①②B ．只有①②③C ．只有③④D ．①②③④解：∵△ABE 、△ADF 是等边三角形∴FD＝AD，BE＝AB∵AD＝BC，AB＝DC∴FD＝BC，BE＝DC∵∠B＝∠D，∠FDA＝∠ABE∴∠CDF＝∠EBC∴△CDF≌△EBC，故①正确；∵∠FAE＝∠FAD＋∠EAB＋∠BAD＝60°＋60°＋（180°－∠CDA）＝300°－∠CDA，∠FDC＝360°－∠FDA－∠ADC＝300°－∠CDA，∴∠CDF＝∠EAF，故②正确；同理可得：∠CBE＝∠EAF＝∠CDF，∵BC＝AD＝AF，BE＝AE，∴△EAF≌△EBC，∴∠AEF＝∠BEC，∵∠AEF＋∠FEB＝∠BEC＋∠FEB＝∠AEB＝60°，∴∠FEC＝60°，∵CF＝CE，∴△ECF是等边三角形，故③正确；在等边三角形ABE中，∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段∴如果CG⊥AE，则G是AE的中点，∠ABG＝30°，∠ABC＝150°，题目缺少这个条件，CG⊥AE不能求证，故④错误．选B．同类题型1.3 如图，四边形ABCD是平行四边形，点E是边CD上的一点，且BC＝EC，CF⊥BE交AB于点F，P是EB延长线上一点，下列结论：①BE平分∠CBF；②CF平分∠DCB；③BC＝FB；④PF＝P C．其中正确的有______________．（填序号）解：证明：∵BC＝EC，∴∠CEB＝∠CBE，∵四边形ABCD是平行四边形，∴DC∥AB，∴∠CEB＝∠EBF，∴∠CBE＝∠EBF，∴①BE平分∠CBF，正确；∵BC＝EC，CF⊥BE，∴∠ECF＝∠BCF，∴②CF平分∠DCB，正确；∵DC∥AB，∴∠DCF＝∠CFB，∵∠ECF＝∠BCF，∴∠CFB＝∠BCF，∴BF＝BC，∴③正确；∵FB＝BC，CF⊥BE，∴B点一定在FC的垂直平分线上，即PB垂直平分FC，∴PF＝PC，故④正确．答案为①②③④．同类题型1.4 如图，在□ABCD中，∠DAB的平分线交CD于点E，交BC的延长线于点G，∠ABC的平分线交CD于点F，交AD的延长线于点H，AG与BH交于点O，连接BE，下列结论错误的是（）A．BO＝OH B．DF＝CE C．DH＝CG D．AB＝AE解：∵四边形ABCD是平行四边形，∴AH∥BG，AD＝BC，∴∠H＝∠HBG，∵∠HBG＝∠HBA，∴∠H＝∠HBA，∴AH＝AB，同理可证BG＝AB，∴AH＝BG，∵AD＝BC，∴DH＝CG，故C正确，∵AH＝AB，∠OAH＝∠OAB，∴OH＝OB，故A正确，∵DF∥AB，∴∠DFH＝∠ABH，∵∠H＝∠ABH，∴∠H＝∠DFH，∴DF＝DH，同理可证EC＝CG，∵DH＝CG，∴DF＝CE，故B正确，无法证明AE ＝AB ，选D ．例2．图甲是小明设计的带菱形图案的花边作品．该作品由形如图乙的矩形图案拼接而成（不重叠、无缝隙）．图乙中ABBC ＝ 67，EF ＝4cm ，上下两个阴影三角形的面积之和为54cm 2 ，其内部菱形由两组距离相等的平行线交叉得到，则该菱形的周长为____________．解：如图乙，H 是CF 与DN 的交点，取CD 的中点G ，连接HG ，，设AB ＝6a cm ，则BC ＝7a cm ，中间菱形的对角线HI 的长度为x cm ，∵BC ＝7a cm ，MN ＝EF ＝4cm ，∴CN ＝7a ＋42， ∵GH ∥BC ， ∴GH CN ＝DG DC， ∴7a －x27a ＋42＝12， ∴x ＝3.5a －2…（1）； ∵上下两个阴影三角形的面积之和为54cm 2 ，∴6a ﹒（7a －x ）÷2＝54，∴a （7a －x ）＝18…（2）；由（1）（2），可得a ＝2，x ＝5，∴CD ＝6×2＝12（cm ），CN ＝7a ＋42＝7×2＋42＝9(cm) ， ∴DN ＝122＋92 ＝15（cm ）， 又∵DH ＝DG 2＋GH 2＝62＋(7×2－52)2 ＝7.5（cm ）， ∴HN ＝15－7.5＝7.5（cm ）， ∵AM ∥FC ，∴KN HK ＝MN CM ＝49－4＝45 ， ∴HK ＝54＋5×7.5＝256(cm) ， ∴该菱形的周长为：256×4＝503（cm ）．同类题型2.1 如图，在菱形ABCD 中，AB ＝4cm ，∠ADC ＝120°，点E 、F 同时由A 、C 两点出发，分别沿AB 、CB 方向向点B 匀速移动（到点B 为止），点E 的速度为1cm/s ，点F 的速度为2cm/s ，经过t 秒△DEF 为等边三角形，则t 的值为____________．解：延长AB 至M ，使BM ＝AE ，连接FM ，∵四边形ABCD 是菱形，∠ADC ＝120°∴AB ＝AD ，∠A ＝60°，∵BM ＝AE ，∴AD ＝ME ，∵△DEF 为等边三角形，∴∠DAE ＝∠DFE ＝60°，DE ＝EF ＝FD ，∴∠MEF ＋∠DEA ═120°，∠ADE ＋∠DEA ＝180°－∠A ＝120°，∴∠MEF ＝∠ADE ，∴在△DAE 和△EMF 中，⎩⎪⎨⎪⎧AD ＝ME∠MEF ＝∠ADE DE ＝EF∴△DAE ≌EMF （SAS ），∴AE ＝MF ，∠M ＝∠A ＝60°，又∵BM ＝AE ，∴△BMF 是等边三角形，∴BF ＝AE ，∵AE ＝t ，CF ＝2t ，∴BC ＝CF ＋BF ＝2t ＋t ＝3t ，∵BC ＝4，∴3t ＝4，∴t ＝43． 同类题型2.2 如图，在边长为2的菱形ABCD 中，∠A ＝60°，M 是AD 边的中点，N 是AB 边上的一动点，将△AMN 沿MN 所在直线翻折得到△A ′MN ，连接A ′C ，则A ′C 长度的最小值是____________．解：如图所示：∵MA ′是定值，A ′C 长度取最小值时，即A ′在MC 上时，过点M 作MF ⊥DC 于点F ，∵在边长为2的菱形ABCD 中，∠A ＝60°，M 为AD 中点，∴2MD ＝AD ＝CD ＝2，∠FDM ＝60°，∴∠FMD ＝30°，∴FD ＝12MD ＝12 ， ∴FM ＝DM ×cos30°＝32， ∴MC ＝FM 2＋CF 2＝7 ，∴A ′C ＝MC －MA ′＝7 －1．同类题型2.3 如图，在菱形ABCD 中，边长为10，∠A ＝60°．顺次连接菱形ABCD 各边中点，可得四边形A 1B 1C 1D 1 ；顺次连接四边形A 1B 1C 1D 1 各边中点，可得四边形A 2B 2C 2D 2 ；顺次连接四边形A 2B 2C 2D 2 各边中点，可得四边形A 3B 3C 3D 3 ；按此规律继续下去…，则四边形A 2017B 2017C 2017D 2017 的周长是______________．解：∵菱形ABCD 中，边长为10，∠A ＝60°，顺次连结菱形ABCD 各边中点，∴△AA 1D 1 是等边三角形，四边形A 2B 2C 2D 2 是菱形，∴A 1D 1 ＝5，C 1D 1＝12AC ＝5 3 ，A 2B 2＝C 2D 2＝C 2B 2＝A 2D 2 ＝5， 同理可得出：A 3D 3＝5×12 ，C 3D 3＝12C 1D 1＝12×5 3 ， A 5D 5＝5×（12）2 ，C 5D 5＝12C 3D 3＝（12）2×5 3 ， …∴四边形A 2015B 2015C 2015D 2015 的周长是：5＋5321007 ．例3． 如图，在矩形ABCD 中，点E 为AB 的中点，EF ⊥EC 交AD 于点F ，连接CF （AD ＞AE ），下列结论：①∠AEF ＝∠BCE ；②S △CEF ＝S △EAF ＋S △CBE ；③AF ＋BC ＞CF ； ④若BC CD ＝ 32，则△CEF ≌△CDF ．其中正确的结论是____________．（填写所有正确结论的序号）解：延长CB ，FE 交于点G ，∵∠AEF ＋∠BEC ＝90°，∠BEC ＋∠BCE ＝90°，∴∠AEF ＝∠BCE ，①正确；在△AEF 和△BEG 中，⎩⎪⎨⎪⎧∠FAE ＝∠GBE ＝90°AE ＝BE∠AEF ＝∠BEG， ∴△AEF ≌△BEG （ASA ），∴AF ＝BG ，EF ＝EG ，∵CE ⊥EG ，∴S △CEG ＝S △CEF ，CG ＝CF ，∴S △CEF ＝S △EAF ＋S △CBE ，②正确；∴AF ＋BC ＝BG ＋BC ＝CG ＝CF ，③错误；∵BC CD ＝32， ∴∠BCE ＝30°，∴∠FCE ＝∠FCD ＝30°，在△CEF 和△CDF 中，⎩⎪⎨⎪⎧∠D ＝∠FEC ＝90°∠DCF ＝∠ECFCF ＝CF， ∴△CEF ≌△CDF （AAS ），④正确．同类题型3.1 如图，在矩形ABCD 中，AD ＝ 2 AB ，∠BAD 的平分线交BC 于点E ，DH ⊥AE 于点H ，连接BH 并延长交CD 于点F ，连接DE 交BF 于点O ，下列结论：①AED ＝∠CED ；②AB ＝HF ，③BH ＝HF ；④BC －CF ＝2HE ；⑤OE ＝OD ；其中正确结论的序号是____________．解：∵在矩形ABCD 中，AE 平分∠BAD ，∴∠BAE ＝∠DAE ＝45°，∴△ABE 是等腰直角三角形，∴AE= 2 AB ，∵AD= 2 AB ，∴AE ＝AD ，在△ABE 和△AHD 中，⎩⎪⎨⎪⎧∠BAE ＝∠DAE∠ABE ＝∠AHD ＝90°AE ＝AD， ∴△ABE ≌△AHD （AAS ），∴BE ＝DH ，∴AB ＝BE ＝AH ＝HD ，∴∠ADE ＝∠AED ＝12（180°－45°）＝67.5°，∴∠CED ＝180°－45°－67.5°＝67.5°，∴∠AED ＝∠CED ，故①正确；∵∠AHB=12 （180°－45°）＝67.5°，∠OHE ＝∠AHB （对顶角相等）， ∴∠OHE ＝∠AED ，∴OE ＝OH ，∵∠DOH ＝90°－67.5°＝22.5°，∠ODH ＝67.5°－45°＝22.5°，∴∠DOH ＝∠ODH ，∴OH ＝OD ，∴OE ＝OD ＝OH ，故⑤正确；∵∠EBH ＝90°－67.5°＝22.5°，∴∠EBH ＝∠OHD ，又∵BE ＝DH ，∠AEB ＝∠HDF ＝45°在△BEH 和△HDF 中⎩⎪⎨⎪⎧∠EBH ＝∠OHDBE ＝DH ∠AEB ＝∠HDF∴△BEH ≌△HDF （ASA ），∴BH ＝HF ，HE ＝DF ，故③正确；由上述①、②、③可得CD ＝BE 、DF ＝EH ＝CE ，CF ＝CD －DF ，∴BC －CF ＝（CD ＋HE ）－（CD －HE ）＝2HE ，所以④正确；∵AB ＝AH ，∠BAE ＝45°，∴△ABH 不是等边三角形，∴AB ≠BH ，∴即AB ≠HF ，故②错误；综上所述，结论正确的是①③④⑤．同类题型3.2 如图，在矩形ABCD 中，BC ＝ 2 AB ，∠ADC 的平分线交边BC 于点E ，AH ⊥DE 于点H ，连接CH 并延长交AB 边于点F ，连接AE 交CF 于点O ，给出下列命题：①AD ＝DE ②DH ＝2 2 EH ③△AEH ∽△CFB ④HO ＝12AE 其中正确命题的序号是________________（填上所有正确命题的序号）解：在矩形ABCD 中，AD ＝BC ＝2AB ＝ 2 CD ，∵DE 平分∠ADC ，∴∠ADE ＝∠CDE ＝45°，∵AD ⊥DE ，∴△ADH 是等腰直角三角形，∴AD ＝ 2 AB ，∴AH ＝AB ＝CD ，∵△DEC 是等腰直角三角形，∴DE ＝ 2 CD ，∴AD ＝DE ，∴∠AED ＝67.5°，∴∠AEB ＝180°－45°－67.5°＝67.5°，∴∠AED ＝∠AEB ，∵AD ∥BC ，∴∠DAE ＝∠AEB ，∴∠DAE ＝∠AED ，∴AD ＝DE ，故①正确；设DH ＝1，则AH ＝DH ＝1，AD ＝DE ＝ 2 ，∴HE ＝ 2 ，∴22HE ＝22≠1，故②错误；∵∠AEH ＝67.5°，∴∠EAH ＝22.5°，∵DH ＝CD ，∠EDC ＝45°，∴∠DHC ＝67.5°，∴∠OHA ＝22.5°，∴∠OAH ＝∠OHA ，∴OA ＝OH ，∴∠AEH ＝∠OHE ＝67.5°，∴OH ＝OE ，∴OH ＝12 AE ，故④正确；∵AH ＝DH ，CD ＝CE ，在△AFH 与△CHE 中，⎩⎪⎨⎪⎧∠AHF ＝∠HCE ＝22.5°∠FAH ＝∠HEC ＝45°AH ＝CE， ∴△AFH ≌△CHE ，∴∠AHF ＝∠HCE ，∵AO ＝OH ，∴∠HAO ＝∠AHO ，∴∠HAO ＝∠BCF ，∵∠B ＝∠AH E ＝90°，∴△AEH ∽△CFB ，故③正确．答案为：①③④．同类题型3.3 如图，在矩形ABCD 中，点E 是边BC 的中点，AE ⊥BD ，垂足为F ，则tan ∠BDE 的值是（）A ．24 B ．14 C ．13 D ．23解：∵四边形ABCD 是矩形，∴AD ＝BC ，AD ∥BC ，∵点E 是边BC 的中点，∴BE ＝12BC ＝12 AD ，∴△BEF ∽△DAF ，∴EFAF ＝BEAD ＝12 ，∴EF ＝12 AF ，∴EF ＝13 AE ， ∵点E 是边BC 的中点，∴由矩形的对称性得：AE ＝DE ，∴EF ＝13DE ，设EF ＝x ，则DE ＝3x ， ∴DF ＝DE 2－EF 2＝2 2 x ，∴tan ∠BDE ＝EF DF ＝x 22x ＝24； 选A ．例4．已知：如图，在正方形ABCD 外取一点E ，连接AE ，BE ，DE ．过点A 作AE 的垂线AP 交DE 于点P ．若AE ＝AP ＝1，PB ＝ 6 ，下列结论：①△APD ≌△AEB ；②点B 到直线AE 的距离为 2 ；③EB ⊥ED ；④S △APD ＋S △APB ＝1＋ 6 ．⑤S 正方形ABCD ＝4＋ 6．其中正确结论的序号是___________________．解：①∵∠EAB ＋∠BAP ＝90°，∠PAD ＋∠BAP ＝90°，∴∠EAB ＝∠PAD ，又∵AE ＝AP ，AB ＝AD ，∵在△APD 和△AEB 中，⎩⎪⎨⎪⎧AE ＝AP∠EAB ＝∠PAD AB ＝AD， ∴△APD ≌△AEB （SAS ）；故此选项成立；③∵△APD ≌△AEB ，∴∠APD ＝∠AEB ，∵∠AEB ＝∠AEP ＋∠BEP ，∠APD ＝∠AEP ＋∠PAE ，∴∠BEP ＝∠PAE ＝90°，∴EB ⊥ED ；故此选项成立；②过B 作BF ⊥AE ，交AE 的延长线于F ，∵AE ＝AP ，∠EAP ＝90°，∴∠AEP ＝∠APE ＝45°，又∵③中EB ⊥ED ，BF ⊥AF ，∴∠FEB ＝∠FBE ＝45°，又∵BE ＝BP 2－PE 2 ＝2，∴BF ＝EF ＝ 2 ，故此选项正确；④如图，连接BD ，在Rt △AEP 中，∵AE ＝AP ＝1， ∴EP ＝ 2 ， 又∵PB ＝ 6 ，∴BE ＝2，∵△APD ≌△AEB ，∴PD ＝BE ＝2， ∴S △ABP ＋S △ADP ＝S △ABD －S △BDP ＝12 S 正方形ABCD －12×DP ×BE ＝12×（4＋6）－12×2×2＝62． 故此选项不正确．⑤∵EF ＝BF ＝ 2 ，AE ＝1，∴在Rt △ABF 中，AB 2＝（AE ＋EF ）2＋BF 2＝5＋2 2 ，∴S 正方形ABCD ＝AB 2＝5＋22，故此选项不正确．答案为：①②③．同类题型4.1 如图，正方形ABCD 的边长为2，将长为2的线段QR 的两端放在正方形的相邻的两边上同时滑动．如果点Q 从点A 出发，沿图中所示方向按A →B →C →D →A 滑动到A 止，同时点R 从点B 出发，沿图中所示方向按B →C →D →A →B 滑动到B 止．点N 是正方形ABCD 内任一点，把N 点落在线段QR 的中点M 所经过的路线围成的图形内的概率记为P ，则P ＝（ ）A ．4－π4B ．π4C ．14D ．π－14解：根据题意得点M 到正方形各顶点的距离都为1，点M 所走的运动轨迹为以正方形各顶点为圆心，以1为半径的四个扇形，∴点M 所经过的路线围成的图形的面积为正方形ABCD 的面积减去4个扇形的面积．而正方形ABCD 的面积为2×2＝4，4个扇形的面积为4×90π×12360＝π， ∴点M 所经过的路线围成的图形的面积为4－π，∴把N 点落在线段QR 的中点M 所经过的路线围成的图形内的概率记为P ，则P ＝4－π4． 选：A ．同类题型4.2 如图，边长为2的正方形ABCD 中，AE 平分∠DAC ，AE 交CD 于点F ，CE ⊥AE ，垂足为点E ，EG ⊥CD ，垂足为点G ，点H 在边BC 上，BH ＝DF ，连接AH 、FH ，FH 与AC 交于点M ，以下结论：①FH ＝2BH ；②AC ⊥FH ；③S △ACF ＝1；④CE ＝ 12AF ；⑤EG 2 ＝FG ﹒DG ，其中正确结论的个数为（ ） A ．2 B ．3 C ．4 D ．5解：①②如图1，∵四边形ABCD 是正方形，∴AB ＝AD ，∠B ＝∠D ＝90°，∠BAD ＝90°，∵AE 平分∠DAC ，∴∠FAD ＝∠CAF ＝22.5°，∵BH ＝DF ，∴△ABH ≌△ADF ，∴AH ＝AF ，∠BAH ＝∠FAD ＝22.5°，∴∠HAC ＝∠FAC ，∴HM ＝FM ，AC ⊥FH ，∵AE 平分∠DAC ，∴DF ＝FM ，∴FH ＝2DF ＝2BH ，故选项①②正确；③在Rt △FMC 中，∠FCM ＝45°，∴△FMC 是等腰直角三角形，∵正方形的边长为2，∴AC ＝2 2 ，MC ＝DF ＝2 2 －2，∴FC ＝2－DF ＝2－（22－2）＝4－2 2 ， S △AFC ＝12CF ﹒AD ≠1， 所以选项③不正确；④AF ＝AD 2＋DF 2＝22＋(22－2)2＝24－2 2 ，∵△ADF ∽△CEF ，∴AD CE ＝AF FC ， ∴2CE ＝24－224－22 ，∴CE ＝4－2 2 ，∴CE ＝12AF ， 故选项④正确；⑤延长CE 和AD 交于N ，如图2，∵AE⊥CE，AE平分∠CAD，∴CE＝EN，∵EG∥DN，∴CG＝DG，在Rt△FEC中，EG⊥FC，∴EG 2＝FG﹒CG，∴EG 2＝FG﹒DG，故选项⑤正确；本题正确的结论有4个，故选C．同类题型4.3 如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P 与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是 ______________．（1）EF＝ 2 OE；（2）S四边形OEBF：S正方形ABCD＝1：4；（3）BE＋BF＝ 2 OA；（4）在旋转过程中，当△BEF与△COF的面积之和最大时，AE＝34；（5）OG﹒BD＝AE2＋CF2．解：（1）∵四边形ABCD是正方形，∴OB＝OC，∠OBE＝∠OCF＝45°，∠BOC＝90°，∴∠BOF＋∠COF＝90°，∵∠EOF＝90°，∴∠BOF＋∠COE＝90°，∴∠BOE＝∠COF，在△BOE和△COF中，⎩⎪⎨⎪⎧∠BOE ＝∠COFOB ＝OC∠OBE ＝∠OCF， ∴△BOE ≌△COF （ASA ），∴OE ＝OF ，BE ＝CF ， ∴EF ＝ 2 OE ；故正确； （2）∵S 四边形OEBF ＝S △BOE ＋S △BOE ＝S △BOE ＋S △COF ＝S △BOC ＝14S 正方形ABCD ， ∴S 四边形OEBF ：S 正方形ABCD ＝1：4；故正确；（3）∴BE ＋BF ＝BF ＋CF ＝BC ＝ 2 OA ；故正确；（4）过点O 作OH ⊥BC ，∵BC ＝1，∴OH ＝12BC ＝12， 设AE ＝x ，则BE ＝CF ＝1－x ，BF ＝x ，∴S △BEF ＋S △COF ＝12BE ﹒BF ＋12CF ﹒OH ＝12x （1－x ）＋12（1－x ）×12＝－12（x －14）2＋932， ∵a ＝－12＜0， ∴当x ＝14时，S △BEF ＋S △COF 最大； 即在旋转过程中，当△BEF 与△COF 的面积之和最大时，AE ＝14；故错误；（5）∵∠EOG ＝∠BOE ，∠OEG ＝∠OBE ＝45°，∴△OEG ∽△OBE ，∴OE ：OB ＝OG ：OE ，∴OG ﹒OB ＝OE 2 ，∵OB ＝12 BD ，OE ＝22EF ， ∴OG ﹒BD ＝EF 2 ，∵在△BEF 中，EF 2＝BE 2＋BF 2 ，∴EF 2＝AE 2＋CF 2 ，∴OG ﹒BD ＝AE 2＋CF 2 ．故正确．故答案为：（1），（2），（3），（5）．同类题型4.4 如图，四边形ABHK 是边长为6的正方形，点C 、D 在边AB 上，且AC ＝DB ＝1，点P 是线段CD 上的动点，分别以AP 、PB 为边在线段AB 的同侧作正方形AMNP 和正方形BRQP ，E 、F 分别为MN 、QR 的中点，连接EF ，设EF 的中点为G ，则当点P 从点C 运动到点D时，点G 移动的路径长为 _____________．解：如图，设KH 的中点为S ，连接PE ，PF ，SE ，SF ，PS ， ∵E 为MN 的中点，S 为KH 的中点，∴A ，E ，S 共线，F 为QR 的中点，S 为KH 的中点，∴B 、F 、S 共线，由△AME ∽△PQF ，得∠SAP ＝∠FPB ，∴ES ∥PF ，△PNE ∽△BRF ，得∠EPA ＝∠FBP ，∴PE ∥FS ，则四边形PESF 为平行四边形，则G 为PS 的中点， ∴G 的轨迹为△CSD 的中位线，∵CD ＝AB －AC －BD ＝6－1－1＝4，∴点G 移动的路径长12 ×4＝2．。