课程名称(中文)调和分析

北京大学数学科学学院一、学院简介数学科学学院起源于1904年京师大学堂的算学门。

1912年5月1日京师大学堂改名为北京大学，理科中便含有数学门。

1913年秋北京大学数学门招收新生，标志着我国现代第一个大学数学系正式开始教学活动。

1919年秋，北大改“门”为“系”。

在确定各系的序列时，蔡元培校长指出：“大学宗旨，凡治哲学文学应用科学者，都要从纯粹科学入手；治纯粹科学者，都要从数学入手。

所以，各系秩序，列数学系为第一系”。

时至今日，数学科学学院在全校各院系中仍然位列第一。

1952年秋，为适应国家大规模经济建设的需要，全国高等学校进行了院系调整。

北京大学数学系与清华大学数学系、燕京大学数学系经调整后，组建了新的北京大学数学力学系。

1969年力学专业在陕西汉中北京大学分校成立了力学系。

1985年，概率统计专业独立成立了概率统计系。

随着事业的发展和形势的变化，在数学系与概率统计系的基础上，1995年成立了北京大学数学科学学院，是国内第一个数学科学学院。

九十年来，北京大学的数学学科经过几代人的艰苦创业、辛勤耕耘，面貌发生了巨大的变化，教学、科研和其他各项工作不断向前迈进：先后培养出了一大批优秀的数学家和计算机科学家，其中16位毕业生被选为中国科学院院士；数千名本科毕业生、六百余名硕士毕业生和百余名博士毕业生分布在国内外多种行业，很多人都是业务骨干，有的成为知名企业家，得到社会各界的高度评价。

数学科学学院现设五个系：数学系、概率统计系、科学与工程计算系、信息科学系、金融数学系。

数学学院现有教师93名，其中中国科学院院士6名，第三世界科学院院士3名，教授51名，副教授29名，博士生导师58名。

数学科学学院经国务院学位办公室批准具有按照一级学科（数学）授予博士学位的权力，不论在数学科学的哪个领域，只要研究生的学习成绩和论文达到了博士学位的要求，皆可授予博士学位。

数学科学学院的本科被教育部遴选为国家“理科基础科学研究和教学人才培养基地”。

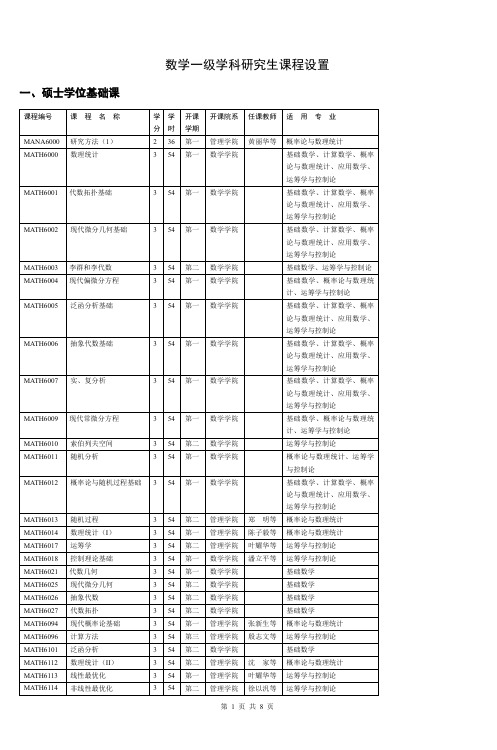
数学一级学科研究生课程设置一、硕士学位基础课课程编号课程名称学分学时开课学期开课院系任课教师适用专业MANA6000研究方法（1）236第一管理学院黄丽华等概率论与数理统计MATH6000数理统计354第一数学学院基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论MATH6001代数拓扑基础354第一数学学院基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论MATH6002现代微分几何基础354第一数学学院基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论MATH6003李群和李代数354第二数学学院基础数学、运筹学与控制论MATH6004现代偏微分方程354第一数学学院基础数学、概率论与数理统计、运筹学与控制论MATH6005泛函分析基础354第一数学学院基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论MATH6006抽象代数基础354第一数学学院基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论MATH6007实、复分析354第一数学学院基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论MATH6009现代常微分方程354第一数学学院基础数学、概率论与数理统计、运筹学与控制论MATH6010索伯列夫空间354第二数学学院运筹学与控制论MATH6011随机分析354第一数学学院概率论与数理统计、运筹学与控制论MATH6012概率论与随机过程基础354第一数学学院基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论MATH6013随机过程354第二管理学院郑明等概率论与数理统计MATH6014数理统计（I）354第一管理学院陈子毅等概率论与数理统计MATH6017运筹学354第二管理学院叶耀华等运筹学与控制论MATH6018控制理论基础354第一数学学院潘立平等运筹学与控制论MATH6021代数几何354第一数学学院基础数学MATH6025现代微分几何354第二数学学院基础数学MATH6026抽象代数354第二数学学院基础数学MATH6027代数拓扑354第二数学学院基础数学MATH6094现代概率论基础354第一管理学院张新生等概率论与数理统计MATH6096计算方法354第三管理学院殷志文等运筹学与控制论MATH6101泛函分析354第二数学学院基础数学MATH6112数理统计（II）354第二管理学院沈家等概率论与数理统计MATH6113线性最优化354第一管理学院叶耀华等运筹学与控制论MATH6114非线性最优化354第二管理学院徐以汎等运筹学与控制论MATH6117数值分析与科学计算354第一数学学院基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论MATH6118多元复分析基础354第一数学学院基础数学MATH6119数值代数及其应用354第一数学学院计算数学MATH6120应用分析中的科学计算354第三数学学院计算数学二、硕士学位专业课课程编号课程名称学分学时开课学期开课院系任课教师适用专业ECON6075高等计量金融学354第二管理学院胡瑾瑾等概率论与数理统计MATH6019变分迭代法354第二数学学院计算数学MATH6022完全交叉和孤立奇点354第三数学学院基础数学MATH6023代数曲面354第四数学学院基础数学MATH6029代数曲线354第三数学学院基础数学MATH6030极小子流形理论354第三数学学院基础数学MATH6031孤立子理论354第二数学学院基础数学MATH6032调和映照354第三数学学院基础数学MATH6033规范场354第三数学学院基础数学MATH6034黎曼曲面354第三数学学院基础数学MATH6035平面拟共形映射354第四数学学院基础数学MATH6036分形几何学354第四数学学院基础数学MATH6037非线性发展方程354第三数学学院基础数学、应用数学MATH6040偏微分方程函数论方法472第二数学学院基础数学MATH6041非线性泛函分析354第二数学学院基础数学MATH6042C*-代数（I）354第三数学学院基础数学MATH6043线性拓扑空间，Banach代数354第四数学学院基础数学MATH6044Banach空间概率论354第三数学学院基础数学MATH6045交换代数354第三数学学院基础数学MATH6046非交换代数354第三数学学院基础数学MATH6047拟线性双曲型方程组354第三数学学院基础数学、应用数学MATH6048拟微分算子354第三数学学院基础数学MATH6049二阶椭圆型方程354第三数学学院基础数学MATH6050动力系统354第二数学学院基础数学、运筹学与控制论MATH6052微分拓扑354第三数学学院基础数学MATH6061几何算法设计与分析354第二数学学院应用数学MATH6067神经网络354第二数学学院应用数学MATH6074精算数学354第二数学学院应用数学MATH6082工程中的数学问题与方法354第二数学学院应用数学MATH6083概率极限定理354第三管理学院张新生等概率论与数理统计MATH6084线性模型354第二管理学院朱仲义等概率论与数理统计MATH6087最优控制理论354第二数学学院运筹学与控制论MATH6088随机控制理论354第三数学学院运筹学与控制论MATH6092最优化理论专题236第一管理学院朱道立等运筹学与控制论MATH6093统计中的大样本理论354第三管理学院郑明等概率论与数理统计MATH6095概率极限理论与渐近统计354第二管理学院汪嘉冈等概率论与数理统计MATH6097凸分析354第三管理学院徐以汎等运筹学与控制论MATH6103散乱数据拟合354第二数学学院应用数学MATH6104算子理论和算子代数基础354第三数学学院基础数学MATH6105应用偏微分方程354第三数学学院应用数学MATH6106代数数论354第三数学学院基础数学MATH6107反散射理论354第三数学学院基础数学MATH6108现代科学中的分析与计算354第二数学学院应用数学MATH6109多元复分析选讲354第三数学学院基础数学MATH6110信贷风险定量分析及衍生产品354第四数学学院计算数学MATH6111模型式和自守形式的算术354第二数学学院基础数学MATH6115随机最优化354第三管理学院徐以汎等运筹学与控制论MATH6116向量最优化引论354第三管理学院黄学祥等运筹学与控制论MATH6121几何分析354第三数学学院基础数学MATH6122几何测度论354第三数学学院基础数学MATH6123分圆域354第三数学学院基础数学MATH6124复解析系统基础354第三数学学院基础数学MATH6125双有理几何354第三数学学院基础数学MATH6126混合型方程354第三数学学院基础数学MATH6127Hopf代数及其应用354第三数学学院基础数学MATH6128同调代数354第三数学学院基础数学MATH6129几何Hilbert模与Toeplitz分析354第三数学学院基础数学MATH6130数学物理反问题选讲354第二数学学院计算数学MATH6131数学物理反问题及不适定问题数值方法354第二数学学院计算数学MATH6132微分方程数值解基础354第二数学学院计算数学MATH6133广义逆的理论与计算354第二数学学院计算数学MATH6134矩阵计算及其应用354第二数学学院计算数学MATH6135规划与算法354第二数学学院计算数学MATH6136凸分析354第二数学学院计算数学MATH6137整数规划与动态规划354第二数学学院计算数学MATH6138大规模科学计算基础354第二数学学院计算数学MATH6139非光滑分析354第二数学学院计算数学MATH6140马尔可夫链的数值计算方法354第二数学学院计算数学MATH6141应用科学中的反问题354第二数学学院计算数学MATH6142大规模科学计算与平行算法354第二数学学院计算数学MATH6143图上随机游动354第二数学学院概率论与数理统计MATH6144随机图354第二数学学院概率论与数理统计MATH6145偏微分方程概论354第二数学学院应用数学MATH6146计算几何与计算机辅助设计354第二数学学院应用数学MATH6147动力系统及其应用354第二数学学院应用数学MATH6148数值微分方程354第二数学学院应用数学MATH6149保险精算原理与方法354第二数学学院应用数学MATH6150数学物理变分方法354第二数学学院应用数学MATH6151混沌动力学354第二数学学院应用数学MATH6152调和分析与小波分析354第二数学学院应用数学MATH6153精算模型与软件354第二数学学院应用数学MATH6154数学金融学354第二数学学院运筹学与控制论MATH6155调和分析354第一数学学院李洪全基础数学三、硕士专业选修课课程编号课程名称学分学时开课学期开课院系任课教师适用专业ECON7192金融统计354第三管理学院周健等概率论与数理统计ECON7244社会学中的高级统计方法354第二管理学院郑明等概率论与数理统计MATH6027代数拓扑354第二数学学院运筹学与控制论MATH6036分形几何学354第四数学学院应用数学MATH6130数学物理反问题选讲354第二数学学院应用数学MATH6151混沌动力学354第二数学学院基础数学MATH7000物理学与偏微分方程354第三数学学院基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论MATH7001孤立子理论（Ⅱ）354第四数学学院基础数学MATH7003Morse理论354第四数学学院基础数学MATH7004子流形理论354第四数学学院基础数学MATH7005李代数表示354第五数学学院基础数学MATH7009泛函微分方程354第四数学学院基础数学MATH7010分支理论354第四数学学院基础数学MATH7015全纯函数的积分表示354第四数学学院基础数学MATH7016非交换代数几何354第四数学学院基础数学MATH7017循环同调论354第四数学学院基础数学MATH7018分次代数354第四数学学院基础数学MATH7019多复变函数论354第四数学学院基础数学MATH7023现代偏微分方程选讲354第三数学学院基础数学MATH7041模式识别354第三数学学院应用数学MATH7047非寿险数学354第三数学学院应用数学MATH7053应用统计354第四管理学院郑方贤等概率论与数理统计MATH7054可靠性与生存分析354第四管理学院郑明等概率论与数理统计MATH7055统计计算354第四管理学院徐勤丰等概率论与数理统计MATH7056随机模拟与统计软件354第四管理学院张新生等概率论与数理统计MATH7057随机过程（续）354第四管理学院郑明等概率论与数理统计MATH7058序贯分析354第四管理学院郑祖康等概率论与数理统计MATH7059统计专题讨论（I）354第四管理学院沈家等概率论与数理统计MATH7060统计专题讨论（II）354第五管理学院沈家等概率论与数理统计MATH7061生存分析354第三管理学院郑明等概率论与数理统计MATH7063非线性控制系统354第三数学学院运筹学与控制论MATH7064分布参数系统理论354第三数学学院运筹学与控制论MATH7071最优化方法讨论班236第三管理学院徐以汎等运筹学与控制论MATH7073运筹学应用专题236第二管理学院叶耀华等运筹学与控制论MATH7074运筹学方法讨论班236第四管理学院殷志文等运筹学与控制论MATH7075流形上的拓扑354第四数学学院基础数学MATH7076复几何354第四数学学院基础数学MATH7077概形与层354第三数学学院基础数学MATH7080有限元与边界元354第三数学学院应用数学MATH7081数学物理与可积系统专题讨论354第三数学学院基础数学MATH7082数学物理专题讨论354第三数学学院基础数学MATH7083孤立子专题讨论354第三数学学院基础数学MATH7084微分几何专题讨论354第三数学学院基础数学MATH7085几何分析专题讨论354第三数学学院基础数学MATH7086偏微分方程专题讨论354第三数学学院基础数学MATH7087椭圆型方程专题讨论354第三数学学院基础数学MATH7088算子代数专题讨论354第三数学学院基础数学MATH7089代数几何专题讨论354第三数学学院基础数学MATH7090代数K-理论专题讨论354第三数学学院基础数学MATH7091同调代数专题讨论354第三数学学院基础数学MATH7093非交换代数专题讨论354第三数学学院基础数学354第三数学学院基础数学MATH7094极值拟共形映射与泰希缪空间专题讨论MATH7095极值拟共形映射专题讨论354第三数学学院基础数学MATH7096多复变专题讨论354第三数学学院基础数学MATH7097复动力系统和渐近分析专题讨354第三数学学院基础数学论MATH7098分形在金融中的应用专题讨论354第三数学学院基础数学MATH7099泛函分析专题讨论354第三数学学院基础数学MATH7120随机分析354第四管理学院张新生等概率论与数理统计MATH7121非参数统计354第四管理学院沈家等概率论与数理统计MATH7122生物统计354第四管理学院张新生等概率论与数理统计MATH7123时间序列分析354第三管理学院陈子毅等概率论与数理统计MATH7124专题讨论354第三数学学院基础数学MATH7128金融衍生产品的定价和计算354第四数学学院计算数学MATH7130多元统计分析354第三管理学院徐勤丰等概率论与数理统计MATH7131Bayes统计354第三管理学院徐勤丰等概率论与数理统计MATH7132组合最优化354第三管理学院殷志文等运筹学与控制论MATH7133决策分析354第三管理学院徐庆等运筹学与控制论354第二管理学院张新生等概率论与数理统计MATH7134Markov链蒙特卡洛模拟与统计计算MATH7135示性类理论354第三数学学院基础数学MATH7136非线性发展方程（续）354第四数学学院基础数学、应用数学MATH7137高维代数簇专题讨论354第三数学学院基础数学MATH7138拓扑学专题讨论354第三数学学院基础数学MATH7139半正定规划354第四数学学院计算数学MATH7140变分不等式与补问题354第四数学学院计算数学MATH7141非线性规划与算法354第四数学学院计算数学MATH7142内点算法354第四数学学院计算数学MATH7143正则化算法354第四数学学院计算数学MATH7144数值代数与应用续论354第五数学学院计算数学MATH7145计算机图形学354第三数学学院应用数学MATH7146应用几何354第三数学学院应用数学MATH7147数字信号处理354第三数学学院应用数学MATH7148应用非线性偏微分方程354第三数学学院应用数学MATH7149渐近分析方法354第三数学学院应用数学MATH7150计算机学习理论专题选讲354第三数学学院应用数学MATH7151数学物理方法专题选讲354第三数学学院应用数学MATH7152工业数学模型专题选讲354第三数学学院应用数学MATH7153应用概率统计专题选讲354第三数学学院应用数学MATH7154动力系统专题选讲354第三数学学院应用数学MATH7155利息理论354第三数学学院应用数学MATH7156风险理论354第三数学学院应用数学MATH7157二阶椭圆型方程（续）54第三数学学院应用数学MATH7158金融计算354第三数学学院运筹学与控制论MATH7159生物数学354第三数学学院运筹学与控制论MATH7160最优控制理论与应用专题讨论354第三数学学院运筹学与控制论MATH7161随机控制与金融数学专题讨论354第三数学学院运筹学与控制论MATH7162具延迟的动力系统354第三数学学院运筹学与控制论MATH7163辛几何引论354第三数学学院东瑜昕基础数学MATH8025脉冲动力系统354第一数学学院运筹学与控制论MATH8038神经网络动力系统354第一数学学院运筹学与控制论四、博士学位专业课课程编号课程名称学分学时开课学期开课院系任课教师适用专业ECON8121现代统计计算方法354第一管理学院张新生等概率论与数理统计MATH6021代数几何354第一数学学院基础数学MATH6048拟微分算子354第三数学学院基础数学MATH6050动力系统354第二数学学院基础数学MATH6108现代科学中的分析与计算354第二数学学院应用数学MATH6119数值代数及其应用354第一数学学院计算数学MATH6142大规模科学计算与平行算法354第二数学学院计算数学MATH6154数学金融学354第二数学学院运筹学与控制论MATH8000分形几何选讲354第一数学学院基础数学MATH8001极值拟共形映射理论354第一数学学院基础数学MATH8002泰希缪勒空间理论354第二数学学院基础数学MATH8003随机过程354第一数学学院基础数学MATH8004高等数理统计354第一数学学院基础数学、应用数学MATH8005偏微分方程354第二数学学院基础数学MATH8006非线性偏微分方程354第二数学学院基础数学MATH8007双曲型守恒律方程组354第一数学学院基础数学、应用数学MATH8009指标理论354第一数学学院基础数学MATH8010算子代数K-理论354第一数学学院基础数学MATH8011几何分析354第一数学学院基础数学MATH8012调和映照续论354第二数学学院基础数学MATH8013可积系统和孤立子354第一数学学院基础数学MATH8014复解析动力系统354第一数学学院基础数学MATH8015循环上同调354第二数学学院基础数学MATH8017微分算子代数354第二数学学院基础数学MATH8018非交换代数几何354第一数学学院基础数学MATH8025脉冲动力系统354第一数学学院基础数学、运筹学与控制论MATH8026非线性波动方程354第二数学学院基础数学、应用数学MATH8029高等数理统计354第一管理学院郑祖康等概率论与数理统计MATH8030随机过程极限定理354第一管理学院郑祖康等概率论与数理统计MATH8031过程统计354第一管理学院郑明等概率论与数理统计MATH8032分布参数系统最优控制理论354第一数学学院运筹学与控制论MATH8033最优化理论354第一管理学院朱道立等运筹学与控制论MATH8034微分对策理论354第一数学学院运筹学与控制论MATH8036变分分析354第二管理学院朱道立等运筹学与控制论MATH8038神经网络动力系统354第一数学学院运筹学与控制论MATH8066若干工程问题的并行算法354第一数学学院应用数学MATH8075数学金融学选讲354第一数学学院运筹学与控制论MATH8080数学物理基础472第二数学学院基础数学MATH8081可积系统和微分几何472第二数学学院基础数学MATH8082Hopf代数354第二数学学院基础数学MATH8083子流形续论354第一数学学院基础数学MATH8084几何中的偏微分方程354第二数学学院基础数学MATH8086数学物理反问题选讲354第一数学学院应用数学MATH8087算子理论和算子代数354第一数学学院基础数学MATH8088几何算子论354第二数学学院基础数学MATH8094微分分次同调代数354第一数学学院基础数学MATH8097鞅与随机微分方程354第一管理学院张新生等概率论与数理统计MATH8098Markov链蒙特卡洛随机模拟354第二管理学院张新生等概率论与数理统计MATH8099向量最优化理论354第二管理学院黄学祥等运筹学与控制论MATH8100随机最优化理论和模型354第一管理学院徐以汎等运筹学与控制论MATH8105代数几何选讲354第一数学学院基础数学MATH8106复代数几何354第一数学学院基础数学MATH8107Euler方程组与Navier-Stokes方程组354第三数学学院基础数学MATH8108变换群的一些基本理论354第一数学学院基础数学MATH8109规范场几何及其应用354第三数学学院基础数学MATH8110现代数学物理354第三数学学院基础数学MATH8111李群和李代数的表示354第三数学学院基础数学MATH8112黎曼几何续论354第三数学学院基础数学MATH8113数学物理反问题及其数值解法354第二数学学院计算数学MATH8114微分方程数值解及其应用354第二数学学院计算数学MATH8115优化理论及其应用354第一数学学院计算数学MATH8116概率中的计算问题354第二数学学院计算数学MATH8117鞅与随机积分354第一数学学院概率论与数理统计MATH8118大偏差理论354第一数学学院概率论与数理统计MATH8119物理学与偏微分方程选讲354第一数学学院应用数学MATH8120工业偏微分模型与方法354第一数学学院应用数学MATH8121KAM理论354第一数学学院应用数学MATH8122实体造型与虚拟现实354第一数学学院应用数学MATH8123统计学习理论354第一数学学院应用数学MATH8124多元逼近理论与方法354第一数学学院应用数学MATH8125无穷维动力系统354第一数学学院应用数学MATH8126随机系统的最优控制理论354第一数学学院运筹学与控制论五、博士专业选修课课程编号课程名称学分学时开课学期开课院系任课教师适用专业MATH6141应用科学中的反问题354第二数学学院计算数学MATH7000物理学与偏微分方程354第三数学学院基础数学MATH7154动力系统专题选讲354第三数学学院应用数学MATH7161随机控制与金融数学专题讨论354第三数学学院运筹学与控制论MATH8041KK-理论354第二数学学院基础数学MATH8042复结构的形变354第二数学学院基础数学MATH8045激波的数学理论354第二数学学院基础数学MATH8046偏微分方程的奇性分析354第二数学学院基础数学MATH8047现代微分算子理论354第三数学学院基础数学MATH8064神经网络专题讨论354第二数学学院应用数学MATH8065拟线性双曲型方程组与激波354第二数学学院应用数学MATH8067高等数理统计（续）354第二管理学院郑祖康等概率论与数理统计MATH8068随机过程极限定理（续）354第二管理学院郑祖康等概率论与数理统计MATH8069现代统计方法专题讨论（I）354第二管理学院郑祖康等概率论与数理统计MATH8070现代统计方法专题讨论（II）354第三管理学院郑祖康等概率论与数理统计MATH8076专题讨论354第三数学学院基础数学MATH8090决策理论与方法讨论班236第二管理学院朱道立等运筹学与控制论MATH8096Markov过程236第一管理学院张新生等概率论与数理统计MATH8101扩散过程236第二管理学院张新生等概率论与数理统计MATH8102贝叶斯统计分析354第二管理学院张新生等概率论与数理统计MATH8103现代分析理论与方法236第二管理学院徐以汎等运筹学与控制论MATH8104学术讨论班236第三管理学院朱道立等运筹学与控制论MATH8127非交换代数几何续论354第二数学学院基础数学MATH8128高维代数簇354第三数学学院基础数学MATH8129Torus作用及其在拓扑和组合354第二数学学院基础数学数学中的作用354第三数学学院基础数学MATH8130Moment映射、协边和哈密顿群作用354第三数学学院计算数学MATH8131数学物理反问题的直接数值方法MATH8132微分方程数值解法及其应用354第二数学学院计算数学MATH8133Markov过程引论354第二数学学院概率论与数理统计MATH8134Dirichlet型理论354第二数学学院概率论与数理统计MATH8135统计与精算专题选讲354第二数学学院应用数学MATH8136神经网络的模型与应用354第二数学学院应用数学MATH8137非线性发展方程选讲354第二数学学院应用数学MATH8138计算几何与多元逼近专题选讲354第二数学学院应用数学MATH8139计算几何与多元逼近专题讨论354第二数学学院应用数学MATH8140应用偏微分方程专题选讲354第二数学学院应用数学MATH8141应用偏微分方程专题讨论354第二数学学院应用数学MATH8142非线性抛物型和抛物双曲方程354第二数学学院应用数学MATH8143工业应用数学专题选讲354第二数学学院应用数学MATH8144工业应用数学专题讨论354第二数学学院应用数学MATH8145分布参数控制专题讨论354第二数学学院运筹学与控制论。

潮汐调和分析课程设计一、课程目标知识目标：1. 让学生掌握潮汐的基本概念，了解潮汐产生的原因及其变化规律。

2. 使学生掌握调和分析法的基本原理，并能运用该方法对潮汐数据进行处理和分析。

3. 让学生了解海洋潮汐对地理环境及人类活动的影响。

技能目标：1. 培养学生运用调和分析法处理潮汐数据的能力，提高数据分析与解决问题的技能。

2. 培养学生运用地理信息系统（GIS）软件进行潮汐数据可视化表达的能力。

情感态度价值观目标：1. 培养学生对海洋科学研究的兴趣，激发学生探索自然奥秘的热情。

2. 增强学生的环保意识，使其认识到海洋资源保护的重要性，培养学生的责任感。

本课程针对高中年级学生，结合地理学科特点，充分考虑学生的认知水平和兴趣，以实用性为导向，旨在提高学生对潮汐现象的理解和分析能力。

通过本课程的学习，学生将能够掌握潮汐相关知识，运用所学技能解决实际问题，并形成正确的情感态度价值观。

为实现课程目标，将目标分解为具体的学习成果，为后续教学设计和评估提供依据。

二、教学内容1. 潮汐基本概念：潮汐的定义、产生原因、主要类型（如：半日潮、全日潮）及其影响因素。

2. 潮汐变化规律：潮汐周期、潮高、潮时及潮流的变化规律，潮汐预测方法。

3. 调和分析法原理：介绍调和分析法的基本理论，包括傅里叶级数、调和常数及其计算方法。

4. 潮汐数据处理与分析：教授如何采集潮汐数据，运用调和分析法对数据进行处理，提取潮汐特征参数。

5. 潮汐数据可视化：运用GIS软件对潮汐数据进行可视化表达，分析潮汐空间分布特征。

6. 潮汐对地理环境及人类活动的影响：探讨潮汐现象在港口建设、海洋渔业、海洋旅游等方面的应用与影响。

教学内容依据课程目标，紧密结合教材相关章节，按照以下进度安排：1. 第一节课：潮汐基本概念及产生原因。

2. 第二节课：潮汐变化规律及预测方法。

3. 第三节课：调和分析法原理及计算方法。

4. 第四节课：潮汐数据处理与分析实践。

5. 第五节课：潮汐数据可视化及GIS应用。

数学专业学那些课程2楼：课程介绍：高等代数(I)3楼：课程介绍：整体微分几何4楼：课程介绍：微分几何5楼：课程介绍：偏微分方程选讲6楼：课程介绍：组合数学7楼：课程介绍：有限群8楼：课程介绍：微分流形9楼：课程介绍：微分动力系统10楼：课程介绍：调和分析选讲11楼：课程介绍：群表示论12楼：课程介绍：模形式13楼：课程介绍：密码学14楼：课程介绍：李群及其表示15楼：课程介绍：黎曼面16楼：课程介绍：黎曼几何17楼：课程介绍：代数拓扑学初步18楼：课程介绍：常微分方程选讲19楼：课程介绍：拓扑学20楼：课程介绍：实变函数21楼：课程介绍：数学物理方程22楼：课程介绍：解析几何23楼：课程介绍：复变函数24楼：课程介绍：泛函分析25楼：课程介绍：常微分方程26楼：课程介绍：初等数论27楼：课程介绍：抽象代数28楼：课程介绍：高等代数(II)29楼：课程介绍：数学分析课程编号：00132321课程名称：高等代数(I)课程类型：数学科学学院本科生必修课(主干基础课)学时学分：68+34学时，5学分先修要求：无基本目的：1．使学生掌握线性代数的初等部分：线性方程组与矩阵的基本理论，基本方法和基本技巧。

2．培养学生科学的思维方式，提高分析问题和解决问题的能力。

3．渗透现代数学研究结构的观点和分类的思想。

内容提要：1．线性方程组的解法：高斯消去法，线性方程组解的情况，数域。

2．行列式：n元排列，n级矩阵的行列式的定义，行列式的性质，行列式按一行(列)展开，Cramer 法则，Laplace定理。

3．线性方程组的理论：n维向量空间Kn及其线性子空间，线性相关性，基，维数，向量组的秩，矩阵的秩，线性方程组有解判别定理，齐次线性方程组的解空间，非齐次线性方程组的解的结构。

4．矩阵代数：映射，矩阵的运算，常用的特殊矩阵，矩阵乘积的秩，方阵的迹，矩阵的分块，分块矩阵的初等变换，矩阵乘积的行列式，可逆矩阵，求逆矩阵的方法，n 维欧几里得空间Rn，正交矩阵。

数学（0701）直博生培养方案一、培养目标本学科培养德、智、体全面发展，在基础数学、计算数学、概率论与数理统计、应用数学、运筹学与控制论等领域具有坚实的专业理论基础、独立从事科学研究能力或较强实际工作能力的高层次一流数学人才。

学位获得者有能力承担高等院校、科研机构的教学、科研工作，或企事业单位的研发和管理工作。

二、研究方向1、基础数学(1)代数(2)图论(3)拓扑学(4)常微分方程(5)偏微分方程(6)泛函分析(7)调和分析与逼近论(8)复分析(9)数理逻辑与数学基础(10)数论(11)微分几何学2、计算数学(1)线性与非线性规划(2)应用数值代数及并行计算(3)偏微分方程数值解法(4)应用软件(5)管理和决策的数值方法3、概率论与数理统计(1)估计与检验的方法与理论及随机规划(2)时间序列分析(3)排队论4、应用数学(1)反应及扩散系统的理论及数值方法(2)动力系统：微分动力系统、哈密顿动力系统(3)常微分方程(4)偏微分方程(5)流体力学中的数学理论5、运筹学与控制论(1)大系统优化问题的理论、方法和应用(2)人工神经网络在优化问题中的应用(3)多目标决策(4)模糊数学方法在决策分析中的应用(5)智能算法(6)最优化控制问题的数值方法三、招生对象应届本科毕业生、已获得推荐免试保研资格，并经复试合格者。

四、学习年限基本学制：五年五、课程设置1、除博士生政治课程、英语课程外，直博生需修满28学分硕士阶段课程。

2、公共基础课，包括：中国特色社会主义理论与实践研究（2学分，必修）；自然辩证法概论、马克思主义与社会科学方法论、马克思主义原著选读（以上三门任选一门，1学分）；中国马克思主义与当代、博士英语。

3、B类课程即公共学位课程8学分,包括：现代分析、基础代数。

4、C类课程即专业学位课程9-12学分；其中，基础数学、应用数学专业要在以下课程中选三门：代数拓扑、微分拓扑、流形与几何、偏微分方程、同调代数、紧黎曼曲面、动力系统、代数几何、代数数论、交换代数、数学的思想方法；计算数学、运筹与控制、概率论与数理统计专业要在以下课程中任选三门：概率论、多元迭代分析、数值代数、随机过程、偏微分方程、偏微分方程数值方法、数理统计基础、数学的思想方法。

数学专业硕士研究生培养方案（070100）一、培养目标为适应教育面向现代化、面向世界、面向未来的目标，培养社会主义建设事业需要的高层次专门人才，要求应用数学专业的硕士研究生：1.应具有较扎实的数学理论基础和基本数学素养；2.应系统地掌握本专业基本理论、基本研究方法和技巧；3.应具有较强的学术沟通能力和良好的团队协作精神；4.应具备创新意识和独立科研能力；5.应该熟练掌握一门外语，具有阅读外文资料和用外文写作论文的能力；6.应具有熟练地使用计算机进行科学计算以及借助互联网查阅专业资料的能力；7.身心健康，德才兼备。

二、培养方式与学习年限1．培养方式采用导师指导为主，导师与指导小组集体培养相结合的模式，通过课堂授课、专题讨论班、专家讲学、课题研究、参加学术报告（会议）等培养方式，使学生成为有学习积极性、主动性和创造性的高层次专门人才。

2．学习年限本专业的硕士研究生学制为三年，培养年限最长不超过五年。

三、研究方向基础数学，计算数学，概率论与数理统计，应用数学，运筹学与控制论。

四、课程设置五、学习要求与考核方式1.课程学习要求要求每位研究生至少修满35学分，其中学科基础课至少修满6学分，专业主干课至少修满6学分。

考核分为考试与考查。

必修课进行考试，选修课进行考试或考查。

考试成绩按百分制计分，考查成绩采用五级记分制。

2.实践环节要求实践内容包括教学实践（为本科生授课、辅导、批改作业、指导大学生毕业论文等）与科研实践（参与具体的科研项目、科研咨询、课题调研，参加学术报告或学术会议等）。

相关的要求见本培养方案有关条目。

3.科研成果数量要求本专业的硕士研究生在学习期间至少发表（含录用）1篇专业学术论文（除导师外，申请者须排名第一）。

特殊情况下，经导师同意并经学院学术委员会认定达到毕业水平者，可以不要求有学术论文在毕业前被发表或录用。

六、中期考核课程学习阶段完成后，学生最迟在入学后的第四学期末之前，参加学院组织的中期考核。

数学（0701）一级学科博士研究生培养方案一、培养目标培养掌握数学学科坚实宽广的基础理论和系统深入的专门知识、熟悉数学学科相关领域的前沿动态、具有独立从事数学及相关学科创新性研究及广阔国际视野的研究型人才；培养德智体全面发展适应国际化信息化时代要求的，能从事数学及相关学科领域的教学、科研工作的高素质、高层次的数学传播与研究人才。

具体要求如下：1. 具有较高的政治素质、良好的道德品质和团结协作精神，遵纪守法，学风严谨，热爱数学，有强烈的事业心和献身精神。

2. 掌握本专业坚实宽广的基础理论知识，能够独立地从事科学研究、教学工作或承担专门技术工作，而且具有主持科研、技术开发项目、探索和解决实际问题的能力。

3. 至少掌握一门外国语，并能运用该门外国语熟练地阅读本专业的外文资料，并具有一定的写作能力和国际学术交流能力。

第二外国语为选修，要求有阅读本专业外文资料的初步能力。

二、研究方向1．基础数学（1）代数学：本方向主要研究群、环、模、代数等运算系统的结构，以及它们的以线性形式、组合形式等形式出现的表示论性质；研究它们在数学各方向、在信息学、物理、化学等学科技术领域的代数形式和它们的应用。

（2）几何学：本方向主要研究黎曼流形的几何与分析，内容包括Kahler流形、Lie群与黎曼对称空间、Spin流形的曲率和拓扑性质、Laplace算子与Dirac算子的谱性质、调和映射与次椭圆调和映射的性质、Yang-Mills场理论、Seiberg-Witten 理论等。

（3）微分方程：本方向主要研究微分方程的基本理论及其应用。

主要侧重于研究非线性椭圆问题的多解及其性态、非线性抛物问题的解及其性态和有很强物理背景的Navier-Stokes 方程、Euler方程以及与化学反应和生物衍变有关的反应扩散方程的解的存在性及其性态等问题；同时，对常微分方程定性理论、分支理论以及动力系统也将进行探讨。

（4）函数论：本方向主要研究定义在各种域上取值为实值或复值的一般函数性质，以及各种函数类之间变换（算子）的性质，同时也研究这些内容和方法的抽象理论（如泛函分析理论等）；其研究结果和方法将应用于解决物理、工程等学科所提出的各种线性和非线性的解析问题。

微分方程2与调和分析课程学习建议微分方程2一、预备知识：不需要微分方程11、实分析：积分收敛定理、Holder/Young/Minkowski/Gronwall 不等式、卷积光滑化逼近、Lebesgue微分定理。

2、泛函分析：Riesz 表示定理（及其推论Lax-Milgram 定理）、紧算子的谱理论（Fredholm 二择一）、对称紧算子的谱、弱收敛的相关性质（见Evans 附录D）。

二、教材与参考书教材: Lawrence C. Evans: Partial Differential Equtaions (2nd edition).参考书：没有。

三、学习顺序：1、基本内容（普通班）第五章（Sobolev 空间）：5.1~5.7、5.8.1（Poincaré 不等式）、5.8.3（W1,∞=Lipschitz, 课本该定理证明出现大跳步，详见2017 年微分方程2 期中考试第三题）、5.9.1（H-1空间）；第六章（二阶线性椭圆方程）：6.1、6.2（存在性定理）、5.8.2（差商极限逼近导数）、6.3（正则性）、6.4（极大值原理）、6.5.1（对称椭圆算子的谱）；第七章（线性发展方程）：7.1（抛物方程弱解的Galerkin 方法）、波方程的存在性证明（见Luk Winghong (Jonathan)的波方程讲义第4节https:///~jluk/NWnotes.pdf）、7.2.4（双曲方程有限传播速度）。

（附）第5-7章用到泛函的地方：5.7 需要弱收敛和紧算子定义（附录D.4+D.5 的第一条定义）6.2.2 需要Lax-Milgram 定理(6.2.1 讲了, 需要Hilbert 空间的Riesz 表示定理结论)6.2.3 需要附录D.5（紧算子的谱Fredholm 二择一，真正用上的是726 页最下方那个Remark，类似线性方程组存在唯一解/齐次方程有非零解二择一）6.5.1 需要附录D.6（对称紧算子的谱，联想实对称方阵特征值的结论，一模一样）7.1 节需要自反空间的Banach-Alaoglu 定理（自反Banach 空间中，有界序列必有弱收敛子列）（附）第5-7章可以跳过的部分：5.3.3 整体光滑逼近的证明（知道思路即可，先有限覆盖边界，然后用个大球盖里面）；5.4节的延拓定理证明；5.5节的零迹定理的证明（但结论在第六章习题用到）；5.6.3（高阶Sobolev 不等式）的所有证明；6.3、7.1 节的所有高阶正则性证明（数学归纳法即可）和边界正则性证明（边界附近进行局部拉直，化成上半平面的情况）；6.4、7.1节的所有Harnack 不等式证明；7.2 节除了双曲方程的有限传播速度其它全部跳过。

目录高等数学<普通> (1)数学分析<数学系> (1)复变函数 (2)复变函数与积分变换 (2)实变函数论 (3)泛函分析 (3)高等数学续<数学系、计算机系> (3)高等数学<工科> (3)数学物理方程 (4)复分析 (4)数学史 (4)高等几何 (4)常微分方程I (5)常微分方程Ⅱ (5)大学文科数学 (5)运筹与优化 (6)概率论与数理统计<普通> (6)概率论 (6)解析几何 (6)离散数学（Ⅰ、Ⅱ） (7)数学模型 (7)计算方法<计算机> (7)高等代数 (8)几何学 (8)近世代数 (8)数学软件与数学实验 (8)计算方法<数学系> (9)数据分析 (9)信息与编码 (9)点集拓扑学 (10)组合数学 (10)数理经济学课程介绍 (10)应用随机过程 (11)金融数学引论 (11)保险与精算 (11)离散数学 (11)初等数论 (12)模糊数学 (12)微分几何 (12)高等代数选讲 (13)数学软件 (13)计量经济模型 (13)现代密码学 (14)信息工程概论 (14)概率论与数理统计<数学系> (14)▲ 课程名称：高等数学<普通>课程编码：110101(000102)学分：10 学时：160课程内容简介：一元函数微积分（一元函数的概念、极限、连续性、导数和微分、中值定理和导数的应用、不定积分、定积分和定积分的应用）；多元函数微积分（多元函数的概念、极限、连续性、偏导数和全微分及其应用、二重积分、三重积分）；微分方程初步（一阶微分方程和可降阶的二阶微分方程的解法、二阶常系数微分方程的解的结构和解法、差分方程的解法）；级数（级数的收敛、幂级数的求和、函数的幂级数展开及其应用）；向量代数与空间解析几何。

▲ 课程名称：数学分析 <数学系>课程编码：110104（110105、110106）学分：20 学时：320课程内容简介：一、分析基础：1、函数：掌握概念及表示方法，理解其单调性，有界性，奇偶性，周期性等基本性质；理解复合函数，反函数；基本初等函数，初等函数等概念。