2012年吉林省中考数学试题及答案

2012年吉林省中考数学试卷参考答案与试题解析一、选择题（每小题2分，共12分）1．（2012•吉林）在四个数0，﹣2，﹣1，2中，最小的数是（）A． 0 B ．﹣2 C．﹣1 D． 2考点：有理数大小比较。

分析：画出数轴，在数轴上标出各点，再根据数轴上右边的数总比左边的数大的特点进行解答．解答：解：如图所示：∵四个数中﹣2在最左边，∴﹣2最小．故选B．点评：本题考查的是有理数的大小比较，根据题意画出数轴．利用“数形结合”解答是解答此题的关键．2．（2012•吉林）如图，有5个完全相同的小正方体组合成一个立方体图形，它的俯视图是（）A．B．C．D．考点：简单组合体的三视图。

专题：常规题型。

分析：俯视图是从物体上面观看得到的图形，结合图形即可得出答案．解答：解：从上面看可得到一个有4个小正方形组成的大正方形．故选A．点评：本题考查了三视图的知识，俯视图是从物体的上面看得到的视图，属于基础题．A． 3a﹣a=2 B．a2+2a2=3a2C．a2•a3=a6D．（a+b）2=a2+b2考点：完全平方公式；合并同类项；同底数幂的乘法。

分析：利用合并同类项的法则、同底数幂的乘法的性质以及完全平方公式的知识求解，即可求得答案，注意排除法在解选择题中的应用．解答：解：A、3a﹣a=2a，故本选项错误；B、a2+2a2=3a2，故本选项正确；C、a2•a3=a5，故本选项错误；D、（a+b）2=a2+2ab+b2，故本选项错误．故选B．点评：此题考查了合并同类项、同底数幂的乘法以及完全平方公式的知识．此题比较简单，注意掌握指数的变化是解此题的关键．4．（2012•吉林）如图，在△ABC中，∠A=80°，∠B=40°．D、E分别是AB，AC上的点，且DE∥BC，则∠AED 的度数是（）A． 40°B． 60°C． 80°D． 120°考点：三角形内角和定理；平行线的性质。

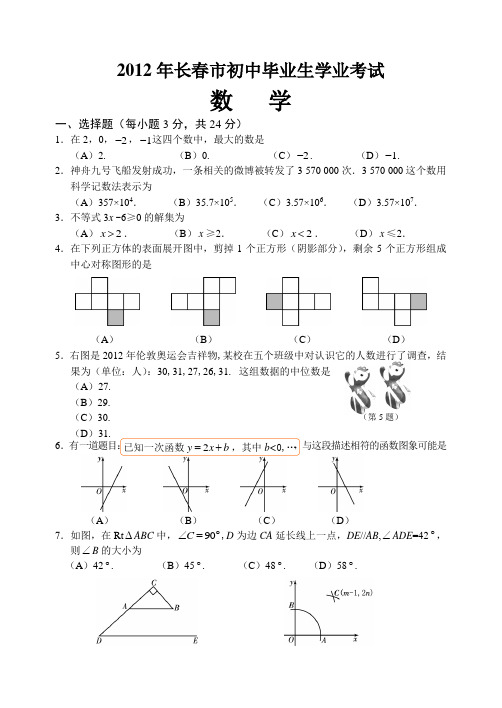
2012年长春市初中毕业生学业考试数 学一、选择题（每小题3分，共24分）1．在2，0，2-，1-这四个数中，最大的数是（A ）2. （B ）0. （C ）2-. （D ）1-.2．神舟九号飞船发射成功，一条相关的微博被转发了3 570 000次．3 570 000这个数用科学记数法表示为（A ）357×104． （B ）35.7×105． （C ）3.57×106． （D ）3.57×107．3．不等式3x -6≥0的解集为（A ）2x >． （B ）x ≥2． （C ）2x <． （D ）x ≤2．4．在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是（A ） （B ） （C ） （D ）5．右图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30,31,27,26,31. 这组数据的中位数是（A ）27.（B ）29.（C ）30. （D ）31.6．有一道题目： ，与这段描述相符的函数图象可能是（A ） （B ） （C ） （D ）7．如图，在Rt ∆ABC 中，90C ∠=︒,D 为边CA 延长线上一点，DE //AB ,∠ADE =42︒，则∠B 的大小为（A ）42︒. （B ）45︒. （C ）48︒. （D ）58︒.已知一次函数2y x b =+，其中b<0,… （第5题）2 （第7题） （第8题）8．如图，在平面直角坐标系中，在x 轴、y 轴的正半轴上，分别截取OA 、OB ，使OA =OB ；再分别以点A 、B 为圆心，以大于12AB 长为半径作弧，两弧交于点C .若点C 的坐标为（1m -，2n ），则m 与m 的关系为（A ）21m n += . （B ）21m n -=. （C ）21n m -=. （D ）21n m -=.二、填空题（每小题3分，共18分）9．计算：= .10．学校购买了一批图书，共a 箱，每箱有b 册.将这批图书的一半捐给社区，则捐给社区的图书有 册（用含a 、b 的代数式表示）.11．如图，⊙O 与正六边形OABCDE 的边OA 、OE 分别交于点F 、G ，则⌒FG 所对的圆周角∠FPG 的大小为 度.(第11题) (第12题)12．如图，在∆ABC 中，AB =5,AC =4,点D 在边AB 上，若ACD ∠=B ∠,则AD 的长为 .13．如图，□ABCD 的顶点B 在矩形AEFC 的边EF 上，点B 与点E 、F 不重合.若ACD∆的面积为3，则图中阴影部分两个三角形的面积和为 .(第13题) (第14题) 14．如图，在平面直角坐标系中，点A 是抛物线2(3)y a x k =-+与y 轴的交点，点B 是这条抛物线上另一点.且AB //x 轴，则以AB 为边的等边三角形ABC 的周长为 .三、解答题（每小题5分，共20分）15．先化简，再求值：2(2)(2)2(3)a a a +-++，其中13a =．16. 有甲、乙两个不透明的口袋，甲袋中有3个球，分别标有数字0,2,5；乙袋中有3个球，分别标有数字0,1,4 .这6个球除所标数字以外没有任何其他区别.从甲、乙两袋各随机摸出1个球，用画树状图（或列表）的方法，求摸出的两个球上数字之数学试题 第 页（共 6 页）3 和是6的概率.17. 某班有45名同学参加紧急疏散演练.对比发现：经专家指导后，平均每秒撤离的人数是指导前的3倍，这45名同学全部撤离的时间比指导前快30秒.求指导前平均每秒撤离的人数.18. 如图，在同一平面内，有一组平行线1l 、2l 、3l ，相邻两条平行线之间的距离均为4.点O 在直线1l 上，⊙O 与直线3l 的交点为A 、B ，AB =12，求⊙O 的半径.四、解答题（每小题6分，共12分）19．长春市某校准备组织七年级学生游园．供学生选择的游园地点有：东北虎园、净月潭、长影世纪城，每名学生只能选择其中一个地点．该校学生会从七年级学生中随机抽取了a 名学生，对他们选择各游园地点的情况进行了调查，并根据调查结果绘制成如下条形统计图．（1）求a 的值.（2）求这a 名学生选择去净月潭游园的学生人数的百分比.（3）按上述调查结果，估计该校七年级650名学生中选择去净月潭游园的人数.20．如图，有一个晾衣架放置在水平地面上.在其示意图中，支架OA 、OB 的长均为108cm ，支架OA 与水平晾衣杆OC 的夹角AOC 为59º，求支架两个着地点之间的距离AB ．（结果精确到0.1cm ）【参考数据：sin59º=0.86,cos59º=0.52,tan59º=1.66】4五、解答题（每小题6分，共12分）21. 图①、图②均为44⨯的正方形网格，线段AB 、BC 的端点均在格点上. 按要求在图①、图②中以AB 和BC 为边各画一个四边形ABCD .要求：四边形ABCD 的顶点D 在格点上，且有两个角相等（一组或两组角相等均可）；所画的两个四边形不全等.22. 如图，在平面直角坐标系中，□ABCO 的顶点A 、C 的坐标分别为A (2,0) 、C (1-,2),反比例函数(0)k y k x=≠的图象经过点B . （1）求k 的值.（2）将□ABCO 沿x 轴翻折，点C 落在点C ＇处.判断点C ’是否落在反比例函数(0)k y k x=≠的图象上，请通过计算说明理由.六、解答题（每小题7分，共14分）23．某加工厂为赶制一批零件，通过提高加工费标准的方式调动工人积极性.工人每天加工零件获得的加工费y （元）与加工个数x （个）之间的部分函数图象为折线OA -AB -BC ，如图所示.数学试题 第 页（共 6 页）5 （1）求工人一天加工零件不超过20个时每个零件的加工费.（2）求40≤x ≤60时y 与x 的函数关系式.（3）小王两天一共加工了60个零件，共得到加工费220元.在这两天中，小王第一天加工零件不足20个，求小王第一天加工的零件个数.24．感知：如图①，点E 在正方形ABCD 的BC 边上，BF ⊥AE 于点F ，DG ⊥AE 于点G .可知△ADG ≌△BAF .(不要求证明)拓展：如图②，点B 、C 在∠MAN 的边AM 、AN 上，点E 、F 在∠MAN 内部的射线AD 上, ∠1 、∠2分别是△ABE 、△CAF 的外角.已知AB =AC ，∠1 =∠2=∠BAC .求证：△ABE ≌△CAF .应用：如图③，在等腰三角形ABC 中， AB =AC ，AB >BC .点D 在边BC 上，CD =2BD ，点E 、F 在线段AD 上，∠1=∠2=∠BAC .若△ABC 的面积为9，则△ABE 与△CDF 的面积之和为 .七、解答题（每小题10分，共20分）25. 如图，在平面直角坐标系中，直线242y x =-+交x 轴于点A ，交直线y x =交于点B .抛物线22y ax x c =-+分别交线段AB 、OB 于点C 、D ，点C 和点D 的横坐标分别为16和4，点P 在这条抛物线上.6 (1)求点C 、D 的纵坐标.(2)求a 、c 的值.(3)若Q 为线段OB 上一点，且P 、Q 两点的纵坐标都为5，求线段PQ 的长.(4)若Q 为线段OB 或线段AB 上一点，PQ ⊥x 轴.设P 、Q 两点之间的距离为d （d >0），点Q 的横坐标为m ，直接写出d 随m 的增大而减小时m 的取值范围.【参考公式：二次函数2y ax bx c =++（a ≠0）图象的顶点坐标为24()24,b ac b a a--】26.如图，在Rt △ABC 中,∠ACB =90°，AC =8cm ,BC =4cm ,D 、E 分别为边AB 、BC 的中点，连结DE .点P 从点A 出发，沿折线AD -DE -EB 运动,到点B 停止．点P 在AD 上的速度运动，在折线DE -EB 上以1cm/s 的速度运动.当点P 与点A 不重合时，过点P 作PQ ⊥AC 于点Q ，以PQ 为边作正方形PQMN ，使点M 落在线段AC 上.设点P 的运动时间为t （s ）.（1）当点P 在线段DE 上运动时，线段DP 的长为 cm （用含t 的代数式表示）.（2）当点N 落在AB 边上时，求t 的值.（3）当正方形PQMN 与△ABC 重叠部分图形为五边形时，设五边形的面积为S (cm 2)，求S 与t 的函数关系式.（4）连结CD .当点N 与点D 重合时，有一点H 从点M 出发，在线段MN 上以2.5cm/s的速度沿M-N-M 连续做往返运动，直至点P 与点E 重合时，点H 停止往返运动；当点P 在线段EB 上运动时，点H 始终在线段MN 的中点处. 直接写出在点P 的整个运动过程中,点H 落在线段CD 上时t 的取值范围.。

历年吉林省中考数学试卷（持续更新中）2012年吉林省中考数学试卷（试卷答案及解析下期见）一、选择题（每小题2分，共12分）1．（2分）在四个数0，﹣2，﹣1，2中，最小的数是（）A．0 B．﹣2 C．﹣1 D．22．（2分）如图，有5个完全相同的小正方体组合成一个立方体图形，它的俯视图是（）3．（2分）下列计算正确的是（）A．3a﹣a=2 B．a2+2a2=3a2C．a2·a3=a6 D．（a+b）2=a2+b24．（2分）如图，在△ABC中，∠A=80°，∠B=40°．D、E分别是AB，AC上的点，且DE∥BC，则∠AED的度数是（）A．40° B．60° C．80° D．120°5．（2分）如图，菱形OABC的顶点B在y轴上，顶点C的坐标为（﹣3，2），若反比例函数y=（x＞0）的图象经过点A，则k的值为（）A．﹣6 B．﹣3 C．3 D．66．（2分）某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需的时间与原计划生产450台机器所需时间相同．设原计划每天生产x台机器，则可列方程为（）二、填空题（每小题3分，共24分）7．（3分）计算：﹣= ．8．（3分）不等式2x﹣1＞x的解集为．9．（3分）若方程x2﹣x=0的两根为x1，x2（x1＜x2），则x2﹣x1= ．10．（3分）若甲，乙两个芭蕾舞团参加演出的女演员人数相同，平均身高相同，身高的方差分别为=1.5，=2.5，则芭蕾舞团参加演出的女演员身高更整齐（填：“甲”或“乙”）．11．（3分）如图，A，B，C是⊙O上的三点，∠CAO=25°，∠BCO=35°，则∠AOB=度．12．（3分）如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点A为圆心，AC长为半径画弧，交AB于点D，则BD= ．13．（3分）如图，AB是⊙O的直径，BC为⊙O的切线，∠ACB=40°，点P在边BC上，则∠PAB的度数可能为（写出一个符合条件的度数即可）14．（3分）如图，在等边△ABC中，D是边AC上一点，连接BD．将△BCD绕点B逆时针旋转60°得到△BAE，连接ED．若BC=10，BD=9，则△AED的周长是．三、解答题（每小题5分，共20分）16．（5分）如图，在东北大秧歌的踩高跷表演中，已知演员身高是高跷长度的2倍，高跷与腿重合部分的长度为28cm，演员踩在高跷上时，头顶距离地面的高度为224cm．设演员的身高为xcm，高跷的长度为ycm，求x，y的值．17．（5分）如图，有一游戏棋盘和一个质地均匀的正四面体骰子（各面依次标有1，2，3，4四个数字）．游戏规则是游戏者每掷一次骰子，棋子按着地一面所示的数字前进相应的格数．例如：若棋子位于A处，游戏者所掷骰子着地一面所示数字为3，则棋子由A处前进3个方格到达B处．请用画树形图法（或列表法）求掷骰子两次后，棋子恰好由A处前进6个方格到达C处的概率．18．（5分）在如图所示的三个函数图象中，有两个函数图象能近似地刻画如下a，b两个情境：情境a：小芳离开家不久，发现把作业本忘在家里，于是返回了家里找到了作业本再去学校；情境b：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进．（1）情境a，b所对应的函数图象分别是、（填写序号）；（2）请你为剩下的函数图象写出一个适合的情境．四、解答题（每小题7分，共28分）19．（7分）在平面直角坐标系中，点A关于y轴的对称点为点B，点A关于原点O的对称点为点C．（1）若A点的坐标为（1，2），请你在给出的坐标系中画出△ABC．设AB与y轴的交点为D，则= ；（2）若点A的坐标为（a，b）（ab≠0），则△ABC的形状为．20．（7分）如图，沿AC方向开山修一条公路，为了加快施工速度，要在小山的另一边寻找点E同时施工．从AC上的一点B取∠ABD=127°，沿BD的方向前进，取∠BDE=37°，测得BD=520m，并且AC，BD和DE在同一平面内．（1）施工点E离D多远正好能使成A，C，E一条直线（结果保留整数）；（2）在（1）的条件下，若BC=80m，求公路段CE的长（结果保留整数）．（参考数据：sin37°=0.60，cos37°=0.80，tan37°=0.75）21．（7分）为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图．（1）小明一共调查了多少户家庭？（2）求所调查家庭5月份用水量的众数、平均数；（3）若该小区有400户居民，请你估计这个小区5月份的用水量．22．（7分）如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作▱ABDE，连接AD，EC．（1）求证：△ADC≌△ECD；（2）若BD=CD，求证：四边形ADCE是矩形．五、解答题（每小题8分，共16分）23．（8分）如图，在扇形OAB中，∠AOB=90°，半径OA=6．将扇形OAB沿过点B的直线折叠，点O恰好落在上点D处，折痕交OA于点C，求整个阴影部分的周长和面积．24．（8分）如图1，A，B，C为三个超市，在A通往C的道路（粗实线部分）上有一D点，D与B有道路（细实线部分）相通．A 与D，D与C，D与B之间的路程分别为25km，10km，5km．现计划在A通往C的道路上建一个配货中心H，每天有一辆货车只为这三个超市送货．该货车每天从H出发，单独为A送货1次，为B送货1次，为C送货2次．货车每次仅能给一家超市送货，每次送货后均返回配货中心H，设H到A的路程为xkm，这辆货车每天行驶的路程为ykm．（1）用含的代数式填空：当0≤x≤25时，货车从H到A往返1次的路程为2xkm，货车从H到B往返1次的路程为km，货车从H到C往返2次的路程为km，这辆货车每天行驶的路程y= ．当25＜x≤35时，这辆货车每天行驶的路程y= ；（2）请在图2中画出y与x（0≤x≤35）的函数图象；（3）配货中心H建在哪段，这辆货车每天行驶的路程最短？六、解答题（每小题10分，共20分）25．（10分）如图，在△ABC中，∠A=90°，AB=2cm，AC=4cm．动点P从点A出发，沿AB方向以1cm/s的速度向点B运动，动点Q从点B同时出发，沿BA方向以1cm/s的速度向点A运动．当点P到达点B时，P，Q两点同时停止运动，以AP为一边向上作正方形APDE，过点Q作QF∥BC，交AC于点F．设点P的运动时间为ts，正方形和梯形重合部分的面积为Scm2．（1）当t= s时，点P与点Q重合；（2）当t= s时，点D在QF上；（3）当点P在Q，B两点之间（不包括Q，B两点）时，求S与t之间的函数关系式．26．（10分）问题情境如图，在x轴上有两点A（m，0），B（n，0）（n＞m＞0）．分别过点A，点B作x轴的垂线，交抛物线y=x2于点C、点D．直线OC交直线BD于点E，直线OD交直线AC于点F，点E、点F的纵坐标分别记为yE，yF．特例探究填空：当m=1，n=2时，yE= ，yF= ；当m=3，n=5时，yE= ，yF= ．归纳证明对任意m，n（n＞m＞0），猜想yE与yF的大小关系，并证明你的猜想．拓展应用（1）若将“抛物线y=x2”改为“抛物线y=ax2（a＞0）”，其他条件不变，请直接写出yE与yF的大小关系；（2）连接EF，AE．当S四边形OFEB=3S△OFE时，直接写m与n的大小关系及四边形OFEA的形状．。

2012年长春市中考数学试卷一、填空题（共1小题；共5分）1. 计算：18−8= ______．二、解答题（共2小题；共26分）．2. 先化简，再求值：a+2a−2+2a2+3,其中a=133. 某班有45名同学参加紧急疏散演练．对比发现：经专家指导后，平均每秒撤离的人数是指导前的3倍，这45名同学全部撤离的时间比指导前快3秒．求指导前平均每秒撤离的人数．三、选择题（共3小题；共15分）4. 神舟九号飞船发射成功，一条相关的微博被转发了3570000次，3570000这个数用科学计数法表示为 A. 357×104 .B. 35.7×105C. 3.57×106D. 3.57×1075. 在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是______A. B.C. D.6. 有一道题目：已知一次函数y=2x+b，其中b<0，与这段描述相符的函数图像可能是______A. B.C. D.四、填空题（共1小题；共5分）7. 学校购买了一批图书，共a箱，每箱有b册，将这批图书的一半捐给社区，则捐给社区的图书为 ______册（用含a、b的代数式表示）．五、选择题（共2小题；共10分）8. 在2、0、−2、−1这四个数中，最大的数是______A. 2B. 0C. −2D. −19. 不等式3x−6≥0的解集为______A. x>2B. x≥2C. x<2D. x≤2六、填空题（共1小题；共5分）10. 如图，平行四边形ABCD的顶点B在矩形AEFC的边EF上，点B与点E，F不重合．若△ACD的面积为3，则图中的阴影部分两个三角形的面积和为 ______．答案第一部分1. 2第二部分2. 原式=a2−4+2a2+6=3a2+2.当a=13时，原式=3×132+2=213．3. 设指导前平均每秒撤离x人，根据题意，得：45 x −453x=3解得x=10．经检验：x=10是原分式方程的解，且符合题意．答：指导前平均每秒撤离10人．第三部分4. C5. D6. A第四部分7. 12ab第五部分8. A 9. B第六部分10. 3。

2012年长春市初中毕业生学业考试（数 学）参考答案本试卷包括七道大题，共26小题，共6页．全卷满分120分，考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回．卷和答题卡一并交回． 注意事项：1. 答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形区域内．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形区域内．2. 答题时，考试务必按照考试要求在答题卡上的指定区域作答，在草稿纸、试卷上答题无效．答题时，考试务必按照考试要求在答题卡上的指定区域作答，在草稿纸、试卷上答题无效． 一、选择题（每小题3分，共24分）[:]1. 在2、0、－2、－1这四个数中，最大的数是(A ) (A )2)2.. (B ) 0. (C ) －2. (D ) －1. 2. 神舟九号飞船发射成功，一条相关的微薄被转发了3570000次，3570000这个数用科学计数法表示为(C ) (A )435710´． (B ) 535.710´ (C ) 61057.3´ (D ) 73.5710´ 3.不等式3x －6³0的解集为(B ) (A ) x ＞2 (B ) x ≥2. (C )x ＜2 (D )x ≤2.4. 在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是(D ) 5.右图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，某校在五个班级中对认识它的人数进行了调查，结果为结果为（单位：人）：30，31，27，26，31.这组数据的中位数是(C ) (A ) 27 (B )29 (C ) 30 (D )31 6.有一道题目：已知一次函数y =2x +b ,其中b ＜0，…，与这段描述相符的函数图像可能是(A ) 7.如图，在Rt△ABC中，∠C=90°．D为边CA延长线上的一点，DE‖AB,∠ADE=42°，则∠B的大小为(C) (A) 42°(B) 45°(C) 48°(D)58°8. 如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A, B为1AB长为半径作弧，两弧交于点C．若点C的坐标为(m－1,2n),则m与n的关系为(B) 圆心，以大于2(A)m+2n=1 (B)m－2n=1 (C)2n－m=1 (D)n－2m=1 二、填空题（每小题3分，共18分）=39.计算：23-3___1 10.学校购买了一批图书，共a箱，每箱有b册，将这批图书的一半捐给社区，则捐给社区的图书为ab2的代数式表示）．册（用含a、b的代数式表示）．11.如图，⊙O 与正六边形OABCDE 的边OA 、OE 分别交于点F 、G ,则弧FG 所对的圆周角∠FPG 的大小为_60_度．度．12．如图，在△ABC 中，AB =5,AC =4,点D 在边AB 上，∠ACD =∠B ，则AD 的长为516.13.如图，ABCD 的顶点B 在矩形AEFC 的边EF 上，点B 与点E 、F 不重合．若△ACD 的面积为3，则图中的阴影部分两个三角形的面积和为图中的阴影部分两个三角形的面积和为 314.如图，在平面直角坐标系中，点A 是抛物线2(3)y a x k =-+与y 轴的交点，点B 是这条抛物线上的另一点，且AB ‖x 轴，则以AB 为边的等边三角形ABC 的周长为18. 三、解答题（每小题5分，共20分）15.先化简，再求值：21(2)(2)2(3),3a a a a +-++=其中312231331236242222=+÷øöçèæ´==+=++-=原式时当原式解，a a a a ： 16.有甲、乙两个不透明的口袋，甲袋中有3个球，分别标有数字0，2，5；乙袋中有3个球，分别标有数个球，分别标有数字0，1，4.这6个球除所标数字以外没有任何其他区别．从甲、乙两袋中各随机摸出1个球，用画树状个球，用画树状 图（或列表）的方法，求摸出的两个球上数字之是6的概率．的概率． 甲袋 乙袋和 0 1 4 2 3 6 5 6 9 所以()926=数学之和为P 17.某班有45名同学参加紧急疏散演练．对比发现：经专家指导后，平均每秒撤离的人数是指导前的3倍， 这45名同学全部撤离的时间比指导前快3秒．求指导前平均每秒撤离的人数．秒．求指导前平均每秒撤离的人数．0 2 5 0 1 4 0 1 4 0 1 4 。

2012年吉林省长春市中考数学试卷一、选择题（每小题3分，共24分）1．（3分）在2，0，﹣2，﹣1这四个数中，最大的数是（）A．2B．0C．﹣2D．﹣12．（3分）神舟九号飞船发射成功，一条相关的微博被转发了3570000次，3570000这个数用科学记数法表示为（）A．357×104B．35.7×105C．3.57×106D．3.57×107 3．（3分）不等式3x﹣6≥0的解集为（）A．x＞2B．x≥2C．x＜2D．x≤24．（3分）在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是（）A．B．C．D．5．（3分）如图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30，31，27，26，31．这组数据的中位数是（）A．27B．29C．30D．316．（3分）有一道题目：已知一次函数y=2x+b，其中b＜0，…，与这段描述相符的函数图象可能是（）A．B．C．D．7．（3分）如图，在Rt△ABC中，∠C=90°．D为边CA延长线上一点，DE∥AB，∠ADE=42°，则∠B的大小为（）A．42°B．45°C．48°D．58°8．（3分）如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、OB，使OA=OB；再分别以点A、B为圆心，以大于AB长为半径作弧，两弧交于点C．若点C的坐标为（m﹣1，2n），则m与n的关系为（）A．m+2n=1B．m﹣2n=1C．2n﹣m=1D．n﹣2m=1二、填空题（每小题3分，共18分）9．（3分）计算：=．10．（3分）学校购买了一批图书，共a箱，每箱有b册，将这批图书的一半捐给社区，则捐给社区的图书为册（用含a、b的代数式表示）．11．（3分）如图，⊙O与正六边形OABCDE的边OA、OE分别交于点F、G，则所对的圆周角∠FPG的大小为度．12．（3分）如图，在△ABC中，AB=5，AC=4，点D在边AB上，∠ACD=∠B，则AD的长为．13．（3分）如图，▱ABCD的顶点B在矩形AEFC的边EF上，点B与点E、F不重合，若△ACD的面积为3，则图中阴影部分两个三角形的面积和为．14．（3分）在平面直角坐标系中，点A是抛物线y=a（x﹣3）2+k与y轴的交点，点B是这条抛物线上的另一点，且AB∥x轴，则以AB为边的等边三角形ABC 的周长为．三、解答题（每小题5分，共20分）15．（5分）先化简，再求值：（a+2）（a﹣2）+2（a2+3），其中a=．16．（5分）有甲、乙两个不透明的口袋，甲袋中有3个球，分别标有数字0，2，5；乙袋中有3个球，分别标有数字0，1，4．这6个球除所标数字以外没有任何其它区别，从甲、乙两袋中各随机摸出1个球，用画树状图（或列表）的方法，求摸出的两个球上数字之和是6的概率．17．（5分）某班有45名同学参加紧急疏散演练，对比发现：经专家指导后，平均每秒撤离的人数是指导前的3倍，这45名同学全部撤离的时间比指导前快30秒．求指导前平均每秒撤离的人数．18．（5分）如图，在同一平面内，有一组平行线l1、l2、l3，相邻两条平行线之间的距离均为4，点O在直线l1上，⊙O与直线l3的交点为A、B，AB=12，求⊙O的半径．四、解答题（每小题6分，共12分）19．（6分）长春市某校准备组织七年级学生游园，供学生选择的游园地点有：东北虎园、净月潭、长影世纪城，每名学生只能选择其中一个地点．该校学生会从七年级学生中随机抽取了a名学生，对他们选择各游园地点的情况进行了调查，并根据调查结果绘制成如下条形统计图．（1）求a的值；（2）求这a名学生选择去净月潭游园的人数的百分比．（3）按上述调查结果，估计该校七年级650名学生中选择去净月潭游园的人数．20．（6分）如图，有一个晾衣架放置在水平地面上，在其示意图中，支架OA、OB的长均为108cm，支架OA与水平晾衣杆OC的夹角∠AOC为59°，求支架两个着地点之间的距离AB．（结果精确到0.1cm）[参考数据：sin59°=0.86，cos59°=0.52，tan59°=1.66]五、解答题（每小题6分，共12分）21．（6分）图①、图②均为4×4的正方形网络，线段AB、BC的端点均在格点上．按要求在图①、图②中以AB和BC为边各画一个四边形ABCD．要求：四边形ABCD的顶点D在格点上，且有两个角相等（一组或两组角相等均可）；所画的两个四边形不全等．22．（6分）如图，在平面直角坐标系中，▱OABC的顶点A、C的坐标分别为A（2，0）、C（﹣1，2），反比例函数y=（k≠0）的图象经过点B．（1）求k的值．（2）将▱OABC沿x轴翻折，点C落在点C′处，判断点C′是否在反比例函数y=（k ≠0）的图象上，请通过计算说明理由．六、解答题（每小题7分，共14分）23．（7分）某加工厂为赶制一批零件，通过提高加工费标准的方式调动工人积极性．工人每天加工零件获得的加工费y（元）与加工个数x（个）之间的函数图象为折线OA﹣AB﹣BC，如图所示．（1）求工人一天加工零件不超过20个时每个零件的加工费．（2）求40≤x≤60时y与x的函数关系式．（3）小王两天一共加工了60个零件，共得到加工费220元．在这两天中，小王第一天加工的零件不足20个，求小王第一天加工零件的个数．24．（7分）感知：如图①，点E在正方形ABCD的边BC上，BF⊥AE于点F，DG ⊥AE于点G，可知△ADG≌△BAF．（不要求证明）拓展：如图②，点B、C分别在∠MAN的边AM、AN上，点E、F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC，求证：△ABE≌△CAF．应用：如图③，在等腰三角形ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为9，则△ABE与△CDF的面积之和为．七、解答题（每小题10分，共20分）25．（10分）如图，在平面直角坐标系中，直线y=﹣2x+42交x轴于点A，交直线y=x于点B，抛物线y=ax2﹣2x+c分别交线段AB、OB于点C、D，点C和点D的横坐标分别为16和4，点P在这条抛物线上．（1）求点C、D的纵坐标．（2）求a、c的值．（3）若Q为线段OB上一点，P、Q两点的纵坐标都为5，求线段PQ的长．（4）若Q为线段OB或线段AB上一点，PQ⊥x轴，设P、Q两点间的距离为d （d＞0），点Q的横坐标为m，直接写出d随m的增大而减小时m的取值范围．[参考公式：二次函数y=ax2+bx+c（a≠0）图象的顶点坐标为（﹣，）]．26．（10分）如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=4cm．D、E分别为边AB、BC的中点，连接DE．点P从点A出发，沿折线AD﹣DE﹣EB运动，到点B停止．点P在线段AD上以cm/s的速度运动，在折线DE﹣EB上以1cm/s的速度运动．当点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M在线段AQ上．设点P的运动时间为t（s）．（1）当点P在线段DE上运动时，线段DP的长为cm（用含t的代数式表示）．（2）当点N落在AB边上时，求t的值．（3）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S （cm2），求S与t的函数关系式．（4）连接CD，当点N与点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s的速度沿M﹣N﹣M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中点处，直接写出在点P的整个运动过程中，点H落在线段CD上时t的取值范围．2012年吉林省长春市中考数学试卷参考答案与试题解析一、选择题（每小题3分，共24分）1．（3分）在2，0，﹣2，﹣1这四个数中，最大的数是（）A．2B．0C．﹣2D．﹣1【解答】解：这四个数在数轴上表示为：由数轴的特点可知，﹣2＜﹣1＜0＜2．故选：A．2．（3分）神舟九号飞船发射成功，一条相关的微博被转发了3570000次，3570000这个数用科学记数法表示为（）A．357×104B．35.7×105C．3.57×106D．3.57×107【解答】解：3 570 000=3.57×106．故选：C．3．（3分）不等式3x﹣6≥0的解集为（）A．x＞2B．x≥2C．x＜2D．x≤2【解答】解：移项得，3x≥6，系数化为1得，x≥2．故选：B．4．（3分）在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是（）A．B．C．D．【解答】解：A、不是中心对称图形，故本选项错误；B、不是中心对称图形，故本选项错误；C、不是中心对称图形，故本选项错误；D、是中心对称图形，故本选项正确．故选：D．5．（3分）如图是2012年伦敦奥运会吉祥物，某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30，31，27，26，31．这组数据的中位数是（）A．27B．29C．30D．31【解答】解：将这组数据从小到大排列为；26，27，30，31，31，所以这组数据的中位数是30，故选：C．6．（3分）有一道题目：已知一次函数y=2x+b，其中b＜0，…，与这段描述相符的函数图象可能是（）A．B．C．D．【解答】解：由一次函数y=2x+b中，k=2＞0，可知y随x的增大而增大，（故B、D错误）；又b＜0，因此当x=0时，y=b＜0，即函数图象与y轴的交点在y轴的负半轴，（故C错误，A正确）．故选：A．7．（3分）如图，在Rt△ABC中，∠C=90°．D为边CA延长线上一点，DE∥AB，∠ADE=42°，则∠B的大小为（）A．42°B．45°C．48°D．58°【解答】解：∵DE∥AB，∠ADE=42°，∴∠CAB=∠ADE=42°，∵在Rt△ABC中，∠C=90°，∴∠B=90°﹣∠CAB=90°﹣42°=48°．故选：C．8．（3分）如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA、OB，使OA=OB；再分别以点A、B为圆心，以大于AB长为半径作弧，两弧交于点C．若点C的坐标为（m﹣1，2n），则m与n的关系为（）A．m+2n=1B．m﹣2n=1C．2n﹣m=1D．n﹣2m=1【解答】解：∵OA=OB；分别以点A、B为圆心，以大于AB长为半径作弧，两弧交于点C，∴C点在∠BOA的角平分线上，∴C点到横纵坐标轴距离相等，进而得出，m﹣1=2n，即m﹣2n=1．故选：B．二、填空题（每小题3分，共18分）9．（3分）计算：=．【解答】解：原式=．故答案为：．10．（3分）学校购买了一批图书，共a箱，每箱有b册，将这批图书的一半捐给社区，则捐给社区的图书为册（用含a、b的代数式表示）．【解答】解：由题意得：这批图书共有ab册，则图书的一半是：册．故答案为：．11．（3分）如图，⊙O与正六边形OABCDE的边OA、OE分别交于点F、G，则所对的圆周角∠FPG的大小为60度．【解答】解：∵六边形OABCDE是正六边形，∴∠AOE==120°，即∠FOG=120°，∴∠FPG=∠FOG=60°．故答案为：60．12．（3分）如图，在△ABC中，AB=5，AC=4，点D在边AB上，∠ACD=∠B，则AD的长为．【解答】解：∵在△ABC与△ACD中，∠A=∠A，∠ACD=∠B，∴△ACD∽△ABC，∴=，∵AB=5，AC=4，∴=，解得AD=．故答案为：．13．（3分）如图，▱ABCD的顶点B在矩形AEFC的边EF上，点B与点E、F不重合，若△ACD的面积为3，则图中阴影部分两个三角形的面积和为3．【解答】解：∵四边形ABCD是平行四边形，∴AD=BC，DC=AB，∵在△ADC和△CBA中，∴△ADC≌△CBA，∵△ACD的面积为3，∴△ABC的面积是3，即AC×AE=3，AC×AE=6，∴阴影部分的面积是6﹣3=3，故答案为：3．14．（3分）在平面直角坐标系中，点A是抛物线y=a（x﹣3）2+k与y轴的交点，点B是这条抛物线上的另一点，且AB∥x轴，则以AB为边的等边三角形ABC 的周长为18．【解答】解：∵抛物线y=a（x﹣3）2+k的对称轴为x=3，且AB∥x轴，∴AB=2×3=6，∴等边△ABC的周长=3×6=18．故答案为：18．三、解答题（每小题5分，共20分）15．（5分）先化简，再求值：（a+2）（a﹣2）+2（a2+3），其中a=．【解答】解：（a+2）（a﹣2）+2（a2+3）=a2﹣4+2a2+6=3a2+2，当a=时，原式=3×+2=2．16．（5分）有甲、乙两个不透明的口袋，甲袋中有3个球，分别标有数字0，2，5；乙袋中有3个球，分别标有数字0，1，4．这6个球除所标数字以外没有任何其它区别，从甲、乙两袋中各随机摸出1个球，用画树状图（或列表）的方法，求摸出的两个球上数字之和是6的概率．【解答】解：画树状图得：∵共有9种等可能的结果，摸出的两个球上数字之和是6的有2种情况，∴摸出的两个球上数字之和是6的概率为：．17．（5分）某班有45名同学参加紧急疏散演练，对比发现：经专家指导后，平均每秒撤离的人数是指导前的3倍，这45名同学全部撤离的时间比指导前快30秒．求指导前平均每秒撤离的人数．【解答】解：设指导前平均每秒撤离的人数为x人，由题意得：﹣=30，解得：x=1，经检验：x=1是原分式方程的解，答：指导前平均每秒撤离的人数为1人．18．（5分）如图，在同一平面内，有一组平行线l1、l2、l3，相邻两条平行线之间的距离均为4，点O在直线l1上，⊙O与直线l3的交点为A、B，AB=12，求⊙O的半径．【解答】解：连接OA，过点O作OD⊥AB，∵AB=12，∴AD=AB=×12=6，∵相邻两条平行线之间的距离均为4，∴OD=8，在Rt△AOD中，∵AD=6，OD=8，∴OA===10．答：⊙O的半径为：10．四、解答题（每小题6分，共12分）19．（6分）长春市某校准备组织七年级学生游园，供学生选择的游园地点有：东北虎园、净月潭、长影世纪城，每名学生只能选择其中一个地点．该校学生会从七年级学生中随机抽取了a名学生，对他们选择各游园地点的情况进行了调查，并根据调查结果绘制成如下条形统计图．（1）求a的值；（2）求这a名学生选择去净月潭游园的人数的百分比．（3）按上述调查结果，估计该校七年级650名学生中选择去净月潭游园的人数．【解答】解：（1）a=12+18+20=50人；（2）选择去净月潭游园的人数的百分比为20÷50×100%=40%；（3）估计该校七年级650名学生中选择去净月潭游园的人数为650×40%=260人．20．（6分）如图，有一个晾衣架放置在水平地面上，在其示意图中，支架OA、OB的长均为108cm，支架OA与水平晾衣杆OC的夹角∠AOC为59°，求支架两个着地点之间的距离AB．（结果精确到0.1cm）[参考数据：sin59°=0.86，cos59°=0.52，tan59°=1.66]【解答】解：作OD⊥AB于点D，∵OA=OB∴AD=BD∵OC∥AB∴∠OAB=59°，在RtAOD中，AD=OA•cos59°，∴AB=2AD=2OA•cos59°=2×108×0.52≈112.3cm．答：支架两个着地点之间的距离AB约为112.3cm．五、解答题（每小题6分，共12分）21．（6分）图①、图②均为4×4的正方形网络，线段AB、BC的端点均在格点上．按要求在图①、图②中以AB和BC为边各画一个四边形ABCD．要求：四边形ABCD的顶点D在格点上，且有两个角相等（一组或两组角相等均可）；所画的两个四边形不全等．【解答】解：如图所示：．22．（6分）如图，在平面直角坐标系中，▱OABC的顶点A、C的坐标分别为A（2，0）、C（﹣1，2），反比例函数y=（k≠0）的图象经过点B．（1）求k的值．（2）将▱OABC沿x轴翻折，点C落在点C′处，判断点C′是否在反比例函数y=（k ≠0）的图象上，请通过计算说明理由．【解答】解：（1）∵四边形OABC是平行四边形，∴BC=AO，∵A（2，0），∴OA=2，∴BC=2，∵C（﹣1，2），∴CD=1，∴BD=BC﹣CD=2﹣1=1，∴B（1，2），∵反比例函数y=（k≠0）的图象经过点B，∴k=1×2=2；（2）∵▱OABC沿x轴翻折，点C落在点C′处，∴C′点坐标是（﹣1，﹣2），∵k=2，∴反比例函数解析式为y=，把C′点坐标（﹣1，﹣2）代入函数解析式能使解析式左右相等，故点C′在反比例函数y=的图象上．六、解答题（每小题7分，共14分）23．（7分）某加工厂为赶制一批零件，通过提高加工费标准的方式调动工人积极性．工人每天加工零件获得的加工费y（元）与加工个数x（个）之间的函数图象为折线OA﹣AB﹣BC，如图所示．（1）求工人一天加工零件不超过20个时每个零件的加工费．（2）求40≤x≤60时y与x的函数关系式．（3）小王两天一共加工了60个零件，共得到加工费220元．在这两天中，小王第一天加工的零件不足20个，求小王第一天加工零件的个数．【解答】解：（1）由图象可知，当0≤x≤20时，每个零件的加工费为60÷20=3元，即工人一天加工零件不超过20个时，每个零件的加工费为3元；（2）当40≤x≤60时，设y与x的函数关系式为y=kx+b，将B（40，140），C（60，240）代入，得，解得，所以，y与x的函数关系式为y=5x﹣60；（3）设小王第一天加工零件的个数为a，则第二天加工零件的个数为（60﹣a），依题意，得3（a+20）+4×20+（240﹣140）÷（60﹣40）×（60﹣20﹣20﹣a）=220，解得a=10，即：小王第一天加工零件的个数为10个．24．（7分）感知：如图①，点E在正方形ABCD的边BC上，BF⊥AE于点F，DG ⊥AE于点G，可知△ADG≌△BAF．（不要求证明）拓展：如图②，点B、C分别在∠MAN的边AM、AN上，点E、F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC，求证：△ABE≌△CAF．应用：如图③，在等腰三角形ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为9，则△ABE与△CDF的面积之和为6．【解答】拓展：证明：∵∠1=∠2，∴∠BEA=∠AFC，∵∠1=∠ABE+∠3，∠3+∠4=∠BAC，∠1=∠BAC，∴∠BAC=∠ABE+∠3，∴∠4=∠ABE，∴，∴△ABE≌△CAF（AAS）．应用：解：∵在等腰三角形ABC中，AB=AC，CD=2BD，∴△ABD与△ADC等高，底边比值为：1：2，∴△ABD与△ADC面积比为：1：2，∵△ABC的面积为9，∴△ABD与△ADC面积分别为：3，6；∵∠1=∠2，∴∠BEA=∠AFC，∵∠1=∠ABE+∠3，∠3+∠4=∠BAC，∠1=∠BAC，∴∠BAC=∠ABE+∠3，∴∠4=∠ABE，∴，∴△ABE≌△CAF（AAS），∴△ABE与△CAF面积相等，∴△ABE与△CDF的面积之和为△ADC的面积，∴△ABE与△CDF的面积之和为6，故答案为：6．七、解答题（每小题10分，共20分）25．（10分）如图，在平面直角坐标系中，直线y=﹣2x+42交x轴于点A，交直线y=x于点B，抛物线y=ax2﹣2x+c分别交线段AB、OB于点C、D，点C和点D的横坐标分别为16和4，点P在这条抛物线上．（1）求点C、D的纵坐标．（2）求a、c的值．（3）若Q为线段OB上一点，P、Q两点的纵坐标都为5，求线段PQ的长．（4）若Q为线段OB或线段AB上一点，PQ⊥x轴，设P、Q两点间的距离为d （d＞0），点Q的横坐标为m，直接写出d随m的增大而减小时m的取值范围．[参考公式：二次函数y=ax2+bx+c（a≠0）图象的顶点坐标为（﹣，）]．【解答】解：（1）∵点C在直线AB：y=﹣2x+42上，且C点的横坐标为16，∴y=﹣2×16+42=10，即点C的纵坐标为10；∵D点在直线OB：y=x上，且D点的横坐标为4，∴点D的纵坐标为4；（2）由（1）知点C的坐标为（16，10），点D的坐标为（4，4），∵抛物线y=ax2﹣2x+c经过C、D两点，∴，解得：a=，c=10，∴抛物线的解析式为y=x2﹣2x+10；（3）∵Q为线段OB上一点，纵坐标为5，∴Q点的横坐标也为5，∵点P在抛物线上，纵坐标为5，∴x2﹣2x+10=5，解得x1=8+2，x2=8﹣2，当点P的坐标为（8+2，5），点Q的坐标为（5，5），线段PQ的长为2+3，当点P的坐标为（8﹣2，5），点Q的坐标为（5，5），线段PQ的长为2﹣3．所以线段PQ的长为2+3或2﹣3．（4）根据题干条件：PQ⊥x轴，可知P、Q两点的横坐标相同，抛物线y=x2﹣2x+10=（x﹣8）2+2的顶点坐标为（8，2），联立，解得点B的坐标为（14，14），①当点Q为线段OB上时，如图所示，当0≤m＜4时，d随m的增大而减小，在BD段，d=x﹣（x2﹣2x+10），即d=﹣x2+3x﹣10，对称轴是x=12，当x≥12时，d随x的增大而减小．故当12≤m≤14时，d随m的增大而减小．则当0≤m＜4或12≤m≤14时，d随m的增大而减小；②当点Q为线段AB上时，如图所示，当14≤m＜16时，d随m的增大而减小，综上所述，当0≤m＜4或12≤m＜16时，d随m的增大而减小．26．（10分）如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=4cm．D、E分别为边AB、BC的中点，连接DE．点P从点A出发，沿折线AD﹣DE﹣EB运动，到点B停止．点P在线段AD上以cm/s的速度运动，在折线DE﹣EB上以1cm/s的速度运动．当点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M在线段AQ上．设点P的运动时间为t（s）．（1）当点P在线段DE上运动时，线段DP的长为（t﹣2）cm（用含t的代数式表示）．（2）当点N落在AB边上时，求t的值．（3）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S （cm2），求S与t的函数关系式．（4）连接CD，当点N与点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s的速度沿M﹣N﹣M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中点处，直接写出在点P的整个运动过程中，点H落在线段CD上时t的取值范围．【解答】解：（1）∵在Rt△ABC中，AC=8cm，BC=4cm，∴AB===D为AB中点，∴AD=，∴点P在AD段的运动时间为=2s．当点P在线段DE上运动时，DP段的运动时间为（t﹣2）s，∵DE段运动速度为1cm/s，∴DP=（t﹣2）cm．（2）当点N落在AB边上时，有两种情况，如下图所示：①如图（2）a，此时点D与点N重合，P位于线段DE上．由三角形中位线定理可知，DM=BC=2，∴DP=DM=2．由（1）知，DP=t﹣2，∴t﹣2=2，∴t=4；②如图（2）b，此时点P位于线段EB上．∵DE=AC=4，∴点P在DE段的运动时间为4s，∴PE=t﹣6，∴PB=BE﹣PE=8﹣t，PC=PE+CE=t﹣4．∵PN∥AC，∴PN：PB=AC：BC=2，∴PN=2PB=16﹣2t．由PN=PC，得16﹣2t=t﹣4，解得t=．所以，当点N落在AB边上时，t=4或t=．（3）当正方形PQMN与△ABC重叠部分图形为五边形时，有两种情况，如下图所示：①当2＜t＜4时，如图（3）a所示．DP=t﹣2，PQ=2，∴CQ=PE=DE﹣DP=4﹣（t﹣2）=6﹣t，AQ=AC﹣CQ=2+t，AM=AQ ﹣MQ=t．∵MN∥BC，∴FM：AM=BC：AC=1：2，∴FM=AM=t．S=S梯形AQPD﹣S△AMF=（DP+AQ）•PQ﹣AM•FM=[（t﹣2）+（2+t）]×2﹣t•t=﹣t2+2t；②当＜t＜8时，如图（3）b所示．PE=t﹣6，∴PC=CM=PE+CE=t﹣4，AM=AC﹣CM=12﹣t，PB=BE﹣PE=8﹣t，∴FM=AM=6﹣t，PG=2PB=16﹣2t，S=S梯形AQPG﹣S△AMF=（PG+AC）•PC﹣AM•FM=[（16﹣2t）+8]×（t﹣4）﹣（12﹣t）•（6﹣t）=t2+22t﹣84．＜＜综上所述，S与t的关系式为：S=＜＜（4）依题意，点H与点P的运动分为两个阶段，如下图所示：①当4＜t≤6时，此时点P在线段DE上运动，如图（4）a所示．此阶段点P运动时间为2s，因此点H运动距离为2.5×2=5cm，而MN=2，则此阶段中，点H将有3次机会落在线段CD上：第一次：此时点H由M→H运动时间为（t﹣4）s，运动距离MH=2.5（t﹣4）cm，∴NH=2﹣MH=12﹣2.5t；又DP=t﹣2，DN=DP﹣2=t﹣4，由DN=2NH得到：t﹣4=2（12﹣2.5t），解得t=；第二次：此时点H由N→H运动时间为t﹣4﹣=（t﹣4.8）s，运动距离NH=2.5（t﹣4.8）=2.5t﹣12；又DP=t﹣2，DN=DP﹣2=t﹣4，由DN=2NH得到：t﹣4=2（2.5t﹣12），解得t=5；②当6≤t≤8时，此时点P在线段EB上运动，如图（4）b所示．由图可知，在此阶段，始终有MH=MC，即MN与CD的交点始终为线段MN的中点，即点H．综上所述，在点P的整个运动过程中，点H落在线段CD上时t的取值范围是：t=或t=5或6≤t≤8．。

2012年长春市初中毕业生学业考试数 学本试卷包括七道大题，共26小题.共6页．全卷满分120分．考试时间为120分钟．考试结束后，将本试卷和答题卡一并交回． 注意事项：1．答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内．2．答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试题卷上答题无效．一、选择题（每小题3分，共24分） 1．在2，0，2-，1-这四个数中，最大的数是（A ）2. （B ）0. （C ）2-. （D ）1-.2．神舟九号飞船发射成功，一条相关的微博被转发了3 570 000次．3 570 000这个数用科学记数法表示为（A ）357×104． （B ）35.7×105． （C ）3.57×106． （D ）3.57×107． 3．不等式3x -6≥0的解集为（A ）2x >． （B ）x ≥2． （C ）2x <． （D ）x ≤2．4．在下列正方体的表面展开图中，剪掉1个正方形（阴影部分），剩余5个正方形组成中心对称图形的是（A ） （B ） （C ） （D ）5．右图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查，结果为（单位：人）：30,31,27,26,31. 这组数据的中位数是 （A ）27. （B ）29. （C ）30.（D ）31. 6．有一道题目： ，与这段描述相符的函数图象可能是（A ） （B ） （C ） （D ） 7．如图，在Rt ∆ABC 中，90C ∠=︒,D 为边CA 延长线上一点，DE //AB ,∠ADE =42︒，则∠B 的大小为（A ）42︒. （B ）45︒. （C ）48︒. （D ）58︒.已知一次函数2y x b =+，其中b<0,…（第5题）（第7题）（第8题）8．如图，在平面直角坐标系中，在x轴、y轴的正半轴上，分别截取OA、OB，使OA=OB；再分别以点A、B为圆心，以大于12AB长为半径作弧，两弧交于点C.若点C的坐标为（1m-，2n），则m与m的关系为（A）21m n+= .（B）21m n-=.（C）21n m-=.（D）21n m-=.二、填空题（每小题3分，共18分）9．计算：= .10．学校购买了一批图书，共a箱，每箱有b册.将这批图书的一半捐给社区，则捐给社区的图书有册（用含a、b的代数式表示）.11．如图，⊙O与正六边形OABCDE的边OA、OE分别交于点F、G，则⌒FG所对的圆周角∠FPG 的大小为度.(第11题) (第12题)12．如图，在∆ABC中，AB=5,AC=4,点D在边AB上，若ACD∠=B∠,则AD的长为.13．如图，□ABCD的顶点B在矩形AEFC的边EF上，点B与点E、F不重合.若ACD∆的面积为3，则图中阴影部分两个三角形的面积和为.(第13题) (第14题)14．如图，在平面直角坐标系中，点A是抛物线2(3)y a x k=-+与y轴的交点，点B是这条抛物线上另一点.且AB//x轴，则以AB为边的等边三角形ABC的周长为.三、解答题（每小题5分，共20分）15．先化简，再求值：2(2)(2)2(3)a a a+-++，其中13a=．16.有甲、乙两个不透明的口袋，甲袋中有3个球，分别标有数字0,2,5；乙袋中有3个球，分别标有数字0,1,4 .这6个球除所标数字以外没有任何其他区别.从甲、乙两袋各随机摸出1个球，用画树状图（或列表）的方法，求摸出的两个球上数字之和是6的概率.2数学试题 第 页（共 6 页）317. 某班有45名同学参加紧急疏散演练.对比发现：经专家指导后，平均每秒撤离的人数是指导前的3倍，这45名同学全部撤离的时间比指导前快30秒.求指导前平均每秒撤离的人数.18. 如图，在同一平面内，有一组平行线1l 、2l 、3l ，相邻两条平行线之间的距离均为4.点O 在直线1l 上，⊙O 与直线3l 的交点为A 、B ，AB =12，求⊙O 的半径.四、解答题（每小题6分，共12分）19．长春市某校准备组织七年级学生游园．供学生选择的游园地点有：东北虎园、净月潭、长影世纪城，每名学生只能选择其中一个地点．该校学生会从七年级学生中随机抽取了a 名学生，对他们选择各游园地点的情况进行了调查，并根据调查结果绘制成如下条形统计图．（1）求a 的值.（2）求这a 名学生选择去净月潭游园的学生人数的百分比.（3）按上述调查结果，估计该校七年级650名学生中选择去净月潭游园的人数.20．如图，有一个晾衣架放置在水平地面上.在其示意图中，支架OA 、OB 的长均为108cm ，支架OA 与水平晾衣杆OC 的夹角AOC 为59º，求支架两个着地点之间的距离AB ．（结果精确到0.1cm ）【参考数据：sin59º=0.86,cos59º=0.52,tan59º=1.66】4五、解答题（每小题6分，共12分）21. 图①、图②均为44⨯的正方形网格，线段AB 、BC 的端点均在格点上. 按要求在图①、图②中以AB 和BC 为边各画一个四边形ABCD .要求：四边形ABCD 的顶点D 在格点上，且有两个角相等（一组或两组角相等均可）；所画的两个四边形不全等.22. 如图，在平面直角坐标系中，□ABCO 的顶点A 、C 的坐标分别为A (2,0) 、C (1-,2),反比例函数(0)ky k x=≠的图象经过点B . （1）求k 的值.（2）将□ABCO 沿x 轴翻折，点C 落在点C ＇处.判断点C ’是否落在反比例函数(0)ky k x=≠的图象上，请通过计算说明理由.六、解答题（每小题7分，共14分）23．某加工厂为赶制一批零件，通过提高加工费标准的方式调动工人积极性.工人每天加工零件获得的加工费y （元）与加工个数x （个）之间的部分函数图象为折线OA -AB -BC ，如图所示.（1）求工人一天加工零件不超过20个时每个零件的加工费. （2）求40≤x ≤60时y 与x 的函数关系式.（3）小王两天一共加工了60个零件，共得到加工费220元.在这两天中，小王第一天加工零件不足20个，求小王第一天加工的零件个数.数学试题 第 页（共 6 页）5 24．感知：如图①，点E 在正方形ABCD 的BC 边上，BF ⊥AE 于点F ，DG ⊥AE 于点G .可知△ADG ≌△BAF .(不要求证明)拓展：如图②，点B 、C 在∠MAN 的边AM 、AN 上，点E 、F 在∠MAN 内部的射线AD上, ∠1 、∠2分别是△ABE 、△CAF 的外角.已知AB =AC ，∠1 =∠2= ∠BAC .求证：△ABE ≌△CAF .应用：如图③，在等腰三角形ABC 中， AB =AC ，AB >BC .点D 在边BC 上，CD =2BD ，点E 、F 在线段AD 上，∠1=∠2=∠BAC .若△ABC 的面积为9，则△ABE 与△CDF 的面积之和为 .七、解答题（每小题10分，共20分）25. 如图，在平面直角坐标系中，直线242y x =-+交x 轴于点A ，交直线y x =交于点B .抛物线22y ax x c =-+分别交线段AB 、OB 于点C 、D ，点C 和点D 的横坐标分别为16和4，点P 在这条抛物线上. (1)求点C 、D 的纵坐标. (2)求a 、c 的值.(3)若Q 为线段OB 上一点，且P 、Q 两点的纵坐标都为5，求线段PQ 的长.(4)若Q 为线段OB 或线段AB 上一点，PQ ⊥x 轴.设P 、Q 两点之间的距离为d （d >0），点Q 的横坐标为m ，直接写出d 随m 的增大而减小时m 的取值范围.【参考公式：二次函数2y ax bx c =++（a ≠0）图象的顶点坐标为24()24,b ac b a a --】26.如图，在Rt △ABC 中,∠ACB =90°，AC =8cm ,BC =4cm ,D 、E 分别为边AB 、BC 的中点，连结DE .点P 从点A 出发，沿折线AD -DE -EB 运动,到点B 停止．点P 在AD的速度运动，在折线DE -EB 上以1cm/s 的速度运动.当点P 与点A 不重合时，过点P 作PQ ⊥AC 于点Q ，以PQ 为边作正方形PQMN ，使点M 落在线段AC 上.设点P 的运动时间为t （s ）.（1）当点P 在线段DE 上运动时，线段DP 的长为 cm （用含t 的代数式表示）. （2）当点N 落在AB 边上时，求t 的值.（3）当正方形PQMN 与△ABC 重叠部分图形为五边形时，设五边形的面积为S (cm 2)，求S与t的函数关系式.（4）连结CD.当点N与点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s 的速度沿M-N-M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中点处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.6数学试题 第 页（共 6 页）7 2012年长春市初中毕业生学业考试数学参考答案及评分标准一、选择题（每小题3分，共24分）1．A 2．C 3．B 4．D 5．C 6．A 7．C 8．D 二、填空题（每小题3分，共18分） 910．2ab 11．60 12．16513．3 14．18 三、解答题（每小题5分，共20分）15．解：原式=22242632a a a -++=+． （3分）当13a =时，原式=2173()233⨯+=． （5分） 16．解：（3分）∴P （两个数字之和是6）=29． （5分） 17． 解：设指导前平均每秒撤离x 人． （1分）根据题意，得4545303x x-=． （3分） 解得1x =.经检验，1x =是原方程的解，且符合题意．答：指导前平均每秒撤离1人． （5分）18. 解：过点O 作OC ⊥AB 于C ，连结OA ． （1分）∴1112622AC AB ==⨯=． 在Rt △AOC 中，∠ACO =90°，OC =428⨯=， （3分） ∴10OA =．∴⊙O 的半径为10 ． （5分）或8四、解答题（每小题6分，共12分） 19．解：（1）18201250++=，所以a 值为50. （2分） （2）20100%40%50⨯=， 所以这50名学生选择去净月潭游园的人数的百分比为40%. （4分） （3）650×40％=260(人).所以该校七年级650名学生中会选择净月潭游园的人数约为260人.（6分）20．解：过点O 作OD ⊥AB 于D . （1分）∵OA =OB , ∴ AB=2 AD ． ∵CO ∥AB ,∴∠OAD =∠AOC =59º . （2分） 在Rt △ADO 中，∠ADO =90，cos ADOAD OA∠=， （4分） ∵OA =108，∴cos 108cos591080.5256.16AD OA OAD =⋅∠=⨯=⨯=. ∴AB =2×56.16=112.32≈112.3(cm).答：支架两个着地点之间的距离AB 约为112.3cm ． (6分)五、解答题（每小题6分，共12分） 21．解：以下答案供参考．画对一个得3分，共6分．(画出符合要求的凹四边形同样赋分)22．解：（1） ∵四边形OABC 是平行四边形，∴CB = OA , CB ∥OA . ∵A (2，0) ,C (1-，2),∴B （1，2）. （3分）数学试题 第 页（共 6 页）9 ∵反比例函数ky x=(k ≠0)的图象经过点B ， ∴21k=，2k =. （4分） （2） 点C ＇在反比例函数2y x=的图象上.理由：由翻折可知，点C ＇与点C 关于x 轴对称， ∵C (1-，2)， ∴C ＇（－1，－2）.由（1）知，反比例函数解析式为 2y x= . ∵当1x =-时，221y ==--， ∴点C ＇在反比例函数2y x=的图象上. (6分)六、解答题（每小题7分，共14分） 23．解：（1）∵60320=（元）， ∴工人一天加工零件不超过20个时每个零件的加工费为3元. （1分） （2）当40≤x ≤60 时，设y 与x 的函数关系式为y kx b =+.∵图象经过（40,140）、（60,240）,∴40140,60240.k b k b +=⎧⎨+=⎩解得5,60.k b =⎧⎨=-⎩∴当40≤x ≤60 时，y 与x 的函数关系式为560y x =- . （4分） （3）设小王第一天加工a 个零件,则第二天加工(60)a -个零件.∵小王第一天加工零件不足20个， ∴0≤a ＜20. ∴40＜60a -≤60. 根据题意，得()356060220a a +--= . 解得a =10.∴小王第一天加工10个零件. (7分)24.拓展: ∵1ABE BAE ∠=∠+∠， BAC CAF BAE ∠=∠+∠,又∵1BAC ∠=∠,∴ABE BAE CAF BAE ∠+∠=∠+∠.10∴ABE CAF ∠=∠. (2分) ∵∠1 =∠2, 1180AEB ∠+∠=︒，2180CFA ∠+∠=︒,∴AEB CFA ∠=∠. (4分) 又∵AB =AC ，∴△ABE ≌△CAF . (5分)应用: 6 (7分) 七、解答题（每小题10分，共20分）25．解：（1）在242y x =-+中，当x =16时，y =10.在y x =中，当x =4时y =4.∴点C 的纵坐标为10，点D 的纵坐标为4. （2分） （2）由（1）知，点C 的坐标为(16,10)，点D 的坐标为(4,4).∵抛物线图象经过点C 、D ，∴2563210,168 4.a c a c -+=⎧⎨-+=⎩解得1,810.a c ⎧=⎪⎨⎪=⎩ ∴a 的值为18， c 的值为10. （4分） （3） 在y x =中，当x =5时y =5.∴点Q 的横坐标为5.由（2）可知，抛物线的解析式为212108y x x =-+. 当y =5时，2121058x x -+=，解得8x =±∴点P的横坐标为8±①当点P 在点Q 左侧时，线段PQ的长为5(83--=. ②当点P 在点Q 右侧时，线段PQ的长为(853+-=+ ∴线段PQ的长为3或3+（8分） （4）当0≤m ＜4或12≤m ＜16时，d 随m 增大而减小. (10分)26．解：（1）（2t -） （不要求写t 的取值范围） （1分）（2）①当点P 在线段DE 上时，如图①.PD = PN =PQ =2.数学试题 第 页（共 6 页） 11 ∴22t -=.∴t =4.②当点P 在线段BE 上时，如图②.PN =2PB .∵PN =PC =(t －6)+2=t －4，BP=2-(t －6)=8－t ，∴42(8)t t -=-,解得 203t =. ∴当点N 落在AB 边上时，t 的值为4或203. （3分） （3）①当2＜t ＜4时，如图③，S =2212(4)4t --， 即2124S t t =-+. ②当203＜t ＜8时，如图④， S =()221(4)3204t t ---, 即2522844S t t =-+-. （7分） （4）143t =或5t =或6≤t ≤8. （10分） 提示：当点H 第一次落在线段CD 上时，12.5(4)(4)22t t -+-=，解得143t =. 当点H 第二次落在线段CD 上时，12.5(4)2(4)2t t --=-，解得5t =. 当点H 第三次落在线段CD 上时，16 2.5(4)(4)2t t --=-，解得6t =. 当6≤t ≤8时，点H 恒在线段CD 上.。

吉林省2012年初中毕业生学业考试数学试题数学试题共6页，包括六道大题，共26道小题．全卷满分120分．考试时间为120分钟．考试结束后，将本试题和答题卡一并交回．一．单项选择题（每小题2分，共12分）1.在四个数0，-2，-1，2中，最小的数是 （A ）0. （B ）-2. (C) -1 (D)2[答案]B 。

[考点]有理数大小的比较。

[解析] 根据正数大于负数，负数都小于0，两个负数之间，绝对值大的这个数反而小可得正确答案。

所以选B2. 如图，由5个完全相同的小正方形组合成一个立体图形，它的俯视图是[答案]A 。

[考点]三视图[解析]俯视图是在水平面上由上向下观察物理的图形，所以选A 。

3.下列计算正确的是(A)32a a -=； (B)22223a a a +=； (C)236a a a ⋅=； (D) 222()a b a b +=+．[答案] B .[考点] 整式的加减：合并同类项；整式的乘法：同底数幂的乘法；乘法公式：完全平方公式.[解析] 合并同类项：只把同类项的系数相加，所得的结果作为系数字母和字母的指数不变.所以22223a a a +=是正确的，故选B . 验证：32a a a -=；同底数的幂相乘，底数不变，指数相加，所以，23235a a a a +⋅==；完全平方公式：两数和的平方，等于它们的平方和加它们积的2倍，即：222()2a b a ab b +=++.所以，,,A C D 都是错的.4.如图，在ABC ∆中，80A ∠=︒，40B ∠=︒，D 、E 分别是AB 、AC 上的点，且DE BC ∥,则AED ∠的度数为(A)40° (B)60° (C) 80° (D)120°[答案] B .[考点] 平行线的性质；三角形的内角和.[解析] 由三角形的三个内角和为180︒，可得60C ∠=︒ ；又两直线平行，同位角相等，所以，由DE BC ∥，可得，AED C ∠=∠，所以60AED ∠=︒ 解：在ABC ∆中，180180804060C A B ∠=︒-∠-∠=︒-︒-︒=︒又DE BC ∥，AED C ∴∠=∠，所以60AED ∠=︒，故选B .5.如图，菱形OABC 的顶点B 在y 轴上，顶点C 的坐标为（-3，2）．若反比例函数ky x =（0x >）的图像经过点A ，则k 的值为(A) -6. (B) -3. (C) 3. (D) 6.[答案] D .[考点] 菱形的性质.直角坐标系内点的点与曲线方程的关系，求反比例函数中的待定系数.[解析] 如图，因为菱形OABC 的两条对角线互相垂直平分，又OB 在y 轴上，所以顶点C 、A 关于y 轴对称，已知C 的坐标为（-3，2），所以A 的坐标为（3，2）反比例函数k y x=（0x >）的图像经过点A ，则326k =⨯=，故选D . 6. 某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同．设原计划每天生产x 台机器，则可列方程为 50450600)(+=x x A . 50450600)(-=x x B . x x C 45050600)(=+. xx D 45050600)(=- [答案] C .[考点] 分式方程运用：列分式方程.[解析] 因为原计划每天生产x 台机器，现在平均每天比原计划多生产50台，所以，现在生产600台机器所需时间是60050x +天，原计划生产450台机器所需时间是450x天，故选C . 二．填空题（每小题3分，共24分）7.=_ ____.[答案.[考点] 二次根式：最简二次根式，根式的运算.[解析] 根式的运算顺序：先把各根式化为最简根式，然后合并同类根式.解：原式==8.不等式21x x ->的解集为__________.[答案] 1x >.[考点] 不等式：解一元一次不等式.[解析] 解一元一次不等式类似解一元一次方程，即把含未知数的项移到一边，数字项移到另一边，然后系数化1，但注意如果在不等式两边同时乘或除以一个负数，要把不等号改变方向.解：移项得：21x x ->合并得： 1x >所以原不等式的解集为1x >.9.若方程20x x -=，的两个根为1212,()x x x x <，则21x x -=______.[答案]1.[考点] 一元二次方程：解一元二次方程，一元二次方程的根与系数的关系（韦达定理）.[解析] 本题给出的一元二次方程较为简单，可直接求解，再求其差；也可利用根与系数的关系求出所需.常用的关系式有：12b x x a+=-，12c x x a ⋅=，学习中还可由求根公式总结出：2112)x x x x -=< 解：[方法一]2120(1)00,1x x x x x x -=⇒-=⇒==，21101x x -=-=.[方法二] 由根与系数的关系得：211x x -== 10. 若甲，乙两个芭蕾舞团参加演出的女演员人数相同，平均身高相同，身高的方差分别为2S 甲=1.5，2S 乙=2.5，则______芭蕾舞团参加演出的女演员身高更整齐（填“甲”或“乙”）． [答案] 甲.[考点] 数据的分析：数据的波动：方差.[解析] 方差越大，数据的波动性越大；方差越小，数据的波动性越小.两组平均数相同的数据，方差小的说明身高的整齐度高，所以甲芭蕾舞团参加演出的女演员身高更整齐.11.如图，,,A B C 是O 上的三点，25CAO ∠=︒．35BCO ∠=︒，则A O B ∠= 度．[答案] 120.[考点] 等腰三角形的性质；圆：圆内同弧所对的圆周角与圆心角的关系（圆周角定理）.[解析] 利用等腰三角形两底角相等，圆内同弧所对的圆周角都等于这条弧所对的圆心角的一半，即可求解.解：如图，在AOC ∆中，AO CO =，25CAO ACO ∴∠=∠=︒，25CAO ACO ∴∠=∠=︒.253560ACB ∴∠=︒+︒=︒又ACB ∠是AC 对的圆周角，AOB ∠是AC 对的圆心角2260120AOB ACB ∴∠=∠=⨯︒=︒12. 如图，在Rt ABC ∆中，90ACB ∠=︒，3AC =，4BC =,以点A 为圆心，AC 长为半径画弧，交AB 于点D ，则BD =______.[答案] 2.[考点] 圆：圆内半径外外相等；直角三角形：勾股定理.[解析] 如图，AC 、AD 为半径，3AC AD ∴==.再由勾股定理：勾三股四弦五得5AB =，532BD AB AD ∴=-=-=.13.如图，AB 是O 的直径，BC 是O 的切线，40ACB ∠=︒，点P 在边BC 上，则PAB ∠的度数可能为 （写出一个符合条件的度数即可）．[答案] 30︒.[考点] 圆：圆的切线的性质定理：圆的切线垂直于过切点半径（或直径），直角三角形：直角三角形的两个锐角互余 .[解析] 由圆的切线垂直于过切点半径（或直径），90ABC ∴∠=︒，再由直角三角形的两个锐角互余，40ACB ∠=︒，所以 50CAB ∠=︒，故只要写出在0︒到50︒间的一个角即可.14.如图，在等边ABC ∆中，D 是边AC 上的一点，连接BD ,将BCD ∆绕点B 逆时针旋转60︒，得到BAE ∆，连接ED ，若10BC =，9BD =，则AED ∆的周长是______.[答案] 19.[考点] 图形的旋转：旋转前、后的图形全等；正三角形，三角形周长.[解析] 由BCD BAE CD AE ∆≅∆⇒=.10AE AD AC BC ∴+===.又，9BD BE ==，60DBE ∠=︒，DBE ∴∆是正三角形9DE ⇒=.ADE ∴∆的周长：91019DE EA AD DE AD ++=+=+=三．解答题（每小题5分，共20分）15.先化简，再求值：2()()2a b a b a +-+，其中1a =,b =. [答案] 1.[考点] 化简求值. .[解析] 利用平方差公式，先作整式乘法运算，合并同类项，将原式化简，然后求值. 解：222222()()223a b a b a a b a a b +-+=-+=-，1a ∴=,b =时，原式22311=⨯-=.16.如图，在东北大秧歌的踩高跷表演中，已知演员身高是高跷长度的2倍，高跷与腿重合部分的长度是28cm ，演员踩在高跷上时，头顶距离地面的高度为224cm ．设演员的身高为xcm ，高跷的长度为ycm ，求x ,y 的值．[答案] x 的值为168，y 的值为84.[考点] 实际问题与二元一次方程组 .[解析] 找出能够表示应用题全部题意的两个相等关系，列出代数式，从而列出两个方程并组成方程组求解 .解：依题意得方程组：222428x y x y =⎧⎨+=+⎩，解得：16884x y =⎧⎨=⎩ 所以，x 的值为168，y 的值为84.17.如图，有一游戏棋盘和一个质地均匀的正四面体骰子（各面依次标有1,2,3,4，四个数字）．游戏规则是游戏者每投掷一次骰子，棋子按骰子着地一面所示的数字前进相应的格数．例如；若棋子位于A 处，游戏者所投掷骰子着地一面所示数字为3，则棋子由A 处前进3个方格到达B 处．请用画树形图法（或列表法）求投掷骰子两次后，棋子恰好由A 处前进6个方格到达C 处的概率．[答案] 316. [考点] 概率初步：随机事件与概率：用列举法（列表法或画树形图法）求概率.[解析] 为不重复不遗漏地列出所有可能的结果，通常采用列表法或用画树形图法求随机事件发生的概率.在一次试验n 次所有可能的结果中，事件A 件出现m 次的概率为()m P A n= [列表法] 在这次游戏中，投掷骰子两次，棋子恰好由A 处前进6个方格到达C 处，即，由表容易看出：投掷骰子两次，所有可能的结果有16种，而棋子恰好由A 处前进6个方格到达C 处的结果为3种，所以：P （棋子恰好由A 处前进6个方格到达C 处）316=. [画树形图法] 在这次游戏中，投掷骰子两次，棋子恰好由A 处前进6个方格到达C 处，即，两次投掷骰子着地一面所示数字和为6.而所有可能的结果画树图如下：由图容易看出：投掷骰子两次，所有可能的结果有16种，而棋子恰好由A 处前进6个方格到达C 处的结果为3种，所以：P （棋子恰好由A 处前进6个方格到达C 处）316=. 18.在如图所示的三个函数图像中，有两个函数图像能近似地刻画如下a 、b 两个情境：情境a ：小芳离开家不久，发现把作业本忘在家里，于是返回家里找到了作业本再去学校； 情境b ：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进．（1）情境a ，b 所对应的函数图像分别为 , .(填写序号)；（2）请你为剩下的函数图像写出一个适合的情境．[答案]（1）③,①；（2）小芳从家出发，到学校上学，放学回到了家.[考点] 函数的图象表示法.[解析] 从函数的图象能形象直观、清晰地呈现函数的一些性质.（1）情境a ：小芳离开家不久，发现把作业本忘在家里，于是返回家里找到了作业本再去学校，对应的函数图像为③；情境b ：小芳从家出发，走了一段路程后，为了赶时间，以更快的速度前进，对应的函数图像为①；（2）函数图像②能近似地刻画为：小芳从家出发，到学校上学，放学回到了家.此问答案不为一，只要注意到是从家里出发，出去后有停留，然后返回到家，满足了这三条就行。