中考数学复习微专题：对三角形内接矩形问题的探究

三角形内接矩形的关系式及其应用作者：沐文中来源：《中学数学杂志(初中版)》2013年第02期如果矩形有四个顶点都在三角形的边上，那么这个矩形称为此三角形的内接矩形.三角形及其内接矩形有一个应用广泛的关系式，现介绍如下：命题如图1，矩形EFGH的两个顶点E、H在BC上，另外两个顶点F、G分别在AB、AC上，若BC=a，BC边上的高AD=h，EF=Y，FG=x，则xa+yh=1.证明因为FG∥BC，所以△AFG∽△ABC，所以FGBC=AKAD，即xa=h-yh，所以xa+yh=1.这一关系或在课标入教版，北师大版，华师大版等教材中均有所介绍.下面就举例说明此关系式在中考中的应用.例1 （2012年山东日照）如图2，在Rt△ABC内有矩形PQMN，P、N分别在直角边AB、AC上，Q、M在斜边BC上，已知AB=3，AC=4，内接矩形PQMN的面积等于53，求BQ和MC的长.解因为AB=3，AC=4，所以BC=32+42=5.作AD⊥BC于D，则由AD·BC=AB·AC=2S△ABC得AD=3×45=125.设PQ=y，PN=x，则由关系式，得x5+y125=1. ①又xy=53（已知）②故解①、②得y=2或y=25.因为Rt△CMN∽Rt△CAB，所以CMMN=CAAB即CM=43y，所以CM=83或CM=815.同理可得BQ=34y，故BQ=32或BQ=310.点评本题借助三角形内接矩形的关系式和矩形面积公式列出二元一次方程组，简捷明快地先求得了PQ和PN的长度，然后再通过相似三角形求得BQ和MC的长度，使问题由繁变简，从而使复杂的问题简单化了.例2 （2012年辽宁大连）如图3，在Rt△ABC的斜边AB上任取一点P，过P点作AC、BC的平行线分别交BC、AC于N、M，则△APM和△PBN的面积之和不小于矩形MPNC的面积，试证明之.证明设AC=b，BC=a，PM=x，PN=y，S矩形MPNC=S1，S△APM+S△PBN=S由关系式点评本题应用上述关系式和面积公式，通过变形化简求得xa与yb的积与和，利用韦达定理的逆定理，构造出一元二次方程，再运用根的判别式得证.这种解题思路充分体现了构造法解题的科学性，符合新课程的理念要求，它能使抽象或隐含的条件清晰地显示出来，能把复杂的问题转化为简单的问题，因而解题时，就能化繁为简，变难为易.例3 （2012年云南大理）一张等腰三角形纸片，底边长15cm，底边上的高长225cm，现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条，如图4所示.已知剪得的纸条中有一张是正方形，则这张正方形纸条是第几张？所以这张正方形的纸条是第6张.点评本题是一道创新中考试题，通过六次运用本文的关系式，最后求得JK的长为3厘米，从而使实际问题得到了解决，如果不用三角形内接矩形的上述性质求解，将会使思路陷入困境.例4 （2012年山西大同）已知△ABC和内接矩形EFGH（如图5），问：在什么条件下，矩形EFGH的面积最大？解如图5，作AC边上的高BI，交EF于J，设BI=h，AC=b，则由题设条件，可设EH=x，所以由关系式得EFb+xh=1，故EF=bh（h-x），所以矩形EFGH的面积S=f（x）=EF·EH=bh（h-x）x=-bhx2+bx.因为-bh〈0，所以二次函数f（x）有最大值.故当x=--b2·bh=h2时，f（x）max=0-b24-bh=bh4=12S△ABC，这时，EF=bh（h-h2）=b2，所以，当内接矩形的长、宽分别等于三角形的底边和底边上的高的一半时，其面积最大.点评本题是运用本文的关系式和矩形面积公式先求得二次函数解析式，再运用二次函数求最大值的方法，求得矩形面积的最大值，方法新，过程简，易理解，要重视.综上述可知，应用本文关系式解中考问题，其关键在于要从问题的实际出发，根据题设去灵活应用.通过教学实践，笔者认为：注意对学生进行联系课本内容的专题讲座的训练，利于帮助学生理解课本内容提高学习数学的兴趣，利于拓宽学生的视野，提高解题水平，利于启迪学生思维，调动学习的积极性.因此在今后的教学过程中，注意对学生进行这类专题内容的探索与研究，是很有必要的.。

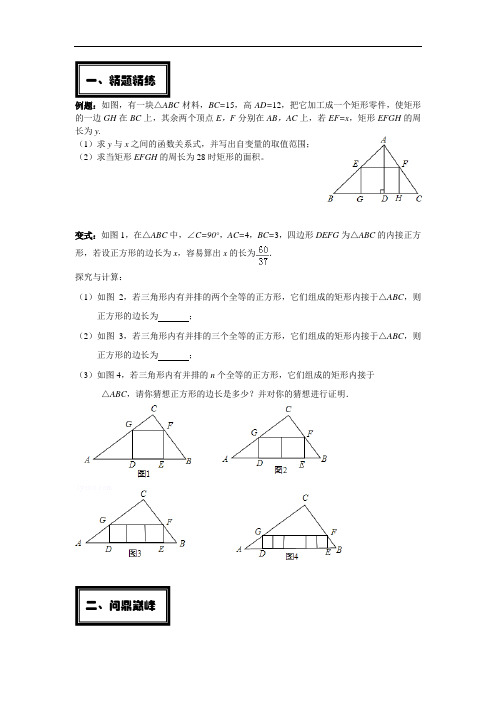
例题：如图，有一块△ABC 材料，BC=15，高AD=12，把它加工成一个矩形零件，使矩形的一边GH 在BC 上，其余两个顶点E ，F 分别在AB ，AC 上，若EF=x ，矩形EFGH 的周长为y .（1）求y 与x 之间的函数关系式，并写出自变量的取值范围；（2）求当矩形EFGH 的周长为28时矩形的面积。

变式：如图1，在△ABC 中，∠C=90°，AC=4，BC=3，四边形DEFG 为△ABC 的内接正方形，若设正方形的边长为x ，容易算出x 的长为．探究与计算：（1）如图2，若三角形内有并排的两个全等的正方形，它们组成的矩形内接于△ABC ，则正方形的边长为 ；（2）如图3，若三角形内有并排的三个全等的正方形，它们组成的矩形内接于△ABC ，则正方形的边长为 ；（3）如图4，若三角形内有并排的n 个全等的正方形，它们组成的矩形内接于△ABC ，请你猜想正方形的边长是多少？并对你的猜想进行证明．二、问鼎巅峰一、精题精练如图，（1）△ABC是斜边AB的长为3的等腰直角三角形，在△ABC内作第1个内接正方形A1B1D1E1（D1、E1在AB上，A1、B1分别在AC、BC上），再在△A1B1C内用同样的方法作第2个内接正方形A2B2D2E2，…如此下去，操作n次，则第一个内接正方形的边长是，第n个小正方形A n B n D n E n的边长是．（2）在△ABC中，BC=12，高AD=8，四边形PQMN为△ABC的内接矩形，（P在AB上，Q在AC上，M、N在BC上），①求当PQ为何值时，矩形PQMN面积最大．②若再在△APQ中作一个内接矩形P2Q2M2N2，如此下去，操作n次，求PnQn的长．（直接写出结果）（3）解完上述两题，根据其中一题你还能归纳出怎样的数学结论，请简单的写出一条．三、参考答案例题：∵四边形EFGH是矩形，∴EF∥BC，∴△AEF∽△ABC，∴=，即=，解得MD=12﹣x，∴y=2（EF+MD）=2（x+12﹣x）=24+x，∵矩形EFHG在△ABC内，∴0＜EF＜BC，即0＜x＜15，∴0＜x＜6，∴24＜24+x＜30，即24＜y＜30；（2）∵矩形EFGH的周长为28，∴24+x=28，解得x=10，∴MD=12﹣×10=4，∴S矩形EFGH=10×4=40．变式：（1）；（2）；（3）．证明，如图，过点C作CN⊥AB，垂足为N，交GF于点M，设小正方形的边长为x，∵四边形GDEF为矩形，∴GF∥AB，CM⊥GF，易算出CN=，∴，即，∴x=．即小正方形的边长是．问鼎巅峰：解：（1）1；．（2）①设PQ=x，矩形PQMN面积为y，AD交PQ于点E，∵PQ∥BC，∴△APQ∽△ABC，∴=，即=，∴PN=8﹣x．则y=PQ•PN=x•（8﹣x）=﹣（x﹣6）2+24．∵﹣＜0，∴该抛物线的开口方向向下，故当PQ=6时，矩形PQMN面积最大；②由①知，PQ=，同理：P1Q1=，P2Q2=，P n Q n=．（3）根据（1）的解题过程可以得到结论：第n个小正方形A n B n D n E n的面积是．根据（2）的解题过程可以得到：再在△APQ中作一个内接矩形P2Q2M2N2，如此下去，操作n 次，P n Q n 的长为．通过此小专题的学习，你对三角形内接矩形问题有较为深刻的理解了吗？此类问题主要考查了正方形，矩形的性质和相似三角形的性质．会利用三角形相似中的相似比来得到相关的线段之间的等量关系是解题的关键。

专题19三角形内接矩形相似模型【模型】如图，四边形DEFG 是△ABC 的内接矩形，EF 在BC 边上，D 、G 分别在AB 、AC 边上，则△ADG ∽△ABC ，△ADN ∽△ABM ，△AGN ∽△ACM .【例1】如图，在ABC 中，AD 是BC 边上的高，在ABC 的内部，作一个正方形PQRS ，若3BC =，2AD =，则正方形PQRS 的边长为（）A ．65B ．54C ．1D ．32【答案】A【分析】由四边形PQRS 是正方形，可得,SR BC ∥即可证得△ASR ∽△ABC ，设正方形PQRS 的边长为x ，然后由相似三角形对应高的比等于相似比，得方程：2,32x x -=解此方程即可求得答案．【解析】解：如图：记AD 与SR 的交点为E ，设正方形PQRS 的边长为x ，∵AD 是△ABC 的高，四边形PQRS 是正方形，∴SR BC ∥，AE 是△ASR 的高，则AE =AD -ED =2-x ，∴△ASR ∽△ABC ，,SR AE BC AD ∴=2,32x x -∴=解得：65x =，∴正方形PQRS 的边长为65．故选：A ．【例2】如图，已知三角形铁皮ABC 的边cm BC a =，BC 边上的高cm AM h =，要剪出一个正方形铁片DEFG ，使D 、E 在BC 上，G 、F 分别在AB 、AC 上，则正方形DEFG 的边长=________．【答案】aha h+【分析】设AM 交GF 于H 点，然后根据相似三角形的判定与性质求解即可．【解析】解：如图，设高AM 交GF 于H 点，∵四边形DEFG 为正方形，∴GF ∥DE ，即：GF ∥BC ，∴AH ⊥GF ，△AGF ∽△ABC ，∴GF AH BC AM=，设正方形的边长为x，∴x h xa h-=，解得：ahxa h =+，故答案为：ah a h+．【例3】如图，在△ABC中，∠C＝90°，AC＝BC，AB＝8．点P从点A出发，以每秒2个单位长度的速度沿边AB向点B运动．过点P作PD⊥AB交折线AC﹣CB于点D，以PD为边在PD右侧做正方形PDEF．设正方形PDEF与△ABC重叠部分图形的面积为S，点P的运动时间为t秒（0＜t＜4）．（1）当点D在边AC上时，正方形PDEF的边长为（用含t的代数式表示）．（2）当点E落在边BC上时，求t的值．（3）当点D在边AC上时，求S与t之间的函数关系式．（4）作射线PE交边BC于点G，连结DF．当DF＝4EG时，直接写出t的值．【答案】（1）2t；（2）43；（3）2244(0)34144832(2)3S t tS t t t⎧<≤⎪⎪⎨⎪+<≤⎪⎩＝＝﹣﹣；（4）t＝87或85【分析】（1）由等腰直角三角形的性质和正方形的性质可得：∠A＝∠ADP＝45°，即AP＝DP＝2t；（2）由等腰直角三角形的性质和正方形的性质可得：AB＝AP+PF+FB，即2t+2t+2t＝8，可求t的值；（3）分两种情况讨论，根据重叠部分的图形的形状，可求S与t之间的函数关系式；（4）分点E在△ABC内部和△ABC外部两种情况讨论，根据平行线分线段成比例，可求t的值．【解析】（1）∵∠C＝90°，AC＝BC，∴∠A＝45°＝∠B，且DP⊥AB，∴∠A＝∠ADP＝45°，∴AP＝DP＝2t，故答案为2t，（2）如图，∵四边形DEFP是正方形，∴DP＝DE＝EF＝PF，∠DPF＝∠EFP＝90°，∵∠A＝∠B＝45°，∴∠A＝∠ADP＝∠B＝∠BEF＝45°，∴AP＝DP＝2t＝EF＝FB＝PF，∵AB＝AP+PF+FB，∴2t+2t+2t＝8，∴t＝4 3；（3）当0＜t≤43时，正方形PDEF与△ABC重叠部分图形的面积为正方形PDEF的面积，即S＝DP2＝4t2，当43＜t≤2时，如图，正方形PDEF与△ABC重叠部分图形的面积为五边形PDGHF的面积，∵AP＝DP＝PF＝2t，∴BF＝8﹣AP﹣PF＝8﹣4t，∵BF＝HF＝8﹣4t，∴EH ＝EF ﹣HF ＝2t ﹣（8﹣4t ）＝6t ﹣8，∴S ＝S 正方形DPFE ﹣S △GHE ，∴S ＝4t 2﹣12×（6t ﹣8）2＝﹣14t 2+48t ﹣32，综上所述，S 与t 之间的函数关系式为2244(0)34144832(2)3S t t S t t t ⎧<≤⎪⎪⎨⎪+<≤⎪⎩＝＝﹣﹣.（4）如图，当点E 在△ABC 内部，设DF 与PE 交于点O，∵四边形PDEF 是正方形，∴DF ＝PE ＝2PO ＝2EO ，∠DFP ＝45°，∴∠DFP ＝∠ABC ＝45°，∴DF ∥BC ，∴PO PF PG PB=，∵DF ＝4EG ，∴设EG ＝a ，则DF ＝4a ＝PE ，PO ＝2a ＝EO ，∴PG ＝5a ，∴25PO PF a PG PB a ==，∴22825t t =-，∴t ＝87，如图，当点E 在△ABC 外部，设DF 与PE 交于点O，∵四边形PDEF 是正方形，∴DF ＝PE ＝2PO ＝2EO ，∠DFP ＝45°，∴∠DFP ＝∠ABC ＝45°，∴DF ∥BC ，∴PO PF PG PB=，∵DF ＝4EG ，∴设EG ＝a ，则DF ＝4a ＝PE ，PO ＝2a ＝EO ，∴PG ＝3a ，∵23PO PF a PG PB a ==，∴22823t t =-，∴t ＝85，综上所述：t ＝87或85.一、单选题1．如图，矩形EFGH 内接于ABC ，且边FG 落在BC 上，若2,3,2,3AD BC BC AD EF EH ⊥===，那么EH 的长为()A ．23B ．13C ．32D ．12【答案】C【分析】设EH =3x ，表示出EF ，由AD -EF 表示出三角形AEH 的边EH 上的高，根据三角形AEH 与三角形ABC 相似，利用相似三角形对应边上的高之比等于相似比求出x 的值，即为EH 的长．【解析】解：如图所示：∵四边形EFGH是矩形，∴EH∥BC，∴△AEH∽△ABC，∵AM⊥EH，AD⊥BC，∴AM EH AD BC=，设EH=3x，则有EF=2x，AM=AD-EF=2-2x，∴223 23x x -=，解得：12 x=，则32 EH=．故选：C．2．如图，在Rt△ABC中，∠C=90°，放置边长分别为3，4，x的三个正方形，则x的值为（）A．12B．7C．6D．5【答案】B【分析】根据已知条件可以推出△CEF∽△OME∽△PFN然后把它们的直角边用含x的表达式表示出来，利用对应边的比相等，即可推出x的值．【解析】解：∵在Rt△ABC中（∠C=90°），放置边长分别3，4，x的三个正方形，∴OM ∥AB ∥PN ∥EF ，EO ∥FP ，∠C =∠EOM =∠NPF =90°，∴△CEF ∽△OME ∽△PFN ，∴OE ：PN =OM ：PF ，∵EF =x ，MO =3，PN =4，∴OE =x -3，PF =x -4，∴（x -3）：4=3：（x -4），∴（x -3）（x -4）=12，即x 2-4x -3x +12=12，∴x =0（不符合题意，舍去）或x =7．故选：B ．3．如图，将一张面积为50的大三角形纸片沿着虚线剪成三张小三角形纸片与一张矩形纸片．根据图中标示的长度，则矩形纸片的面积为（）A ．12B ．18C ．24D ．30【答案】C 【分析】如图，由DE ∥BC ，可得△ADE ∽△ABC ，利用相似三角形的性质，可求得△ADE 的高，进而求得平行四边形的高，则问题可解．【解析】解：如图，设△ABC 的BC 边上的高为1h ，矩形DEFG 的FG 边上的高为2h ∵四边形DEFG 为矩形，∴DE ∥BC ，∴△ADE ∽△ABC ，DE =6，BC=10，∴12135h h DE h BC -==，∵S △ABC =50，∴15021010h ⨯==，∴2103105h -=，解得24h =，∴平行四边形纸片的面积为=26424DE h ⋅=⨯=．故选：C ．4．如图，在△ABC 中，AB 边上取一点P ，画正方形PQMN ，使Q ，M 在边BC 上，N 在边AC 上，连接BN ，在BN 上截取NE =NM ，连接EQ ，EM ，当3tan 4NBM ∠=时，则∠QEM 度数为（）A ．60°B ．70°C ．75°D ．90°【答案】D 【分析】证明BEQ BEM △∽△，可得BEQ BME ∠=∠，根据等腰三角形的性质可NEM NME ∠=∠，由90BME NME ∠+∠=︒，可得90BEQ NEM ∠+∠=︒，进而可得答案．【解析】PQMN 为正方形，QM NM ∴=，90BMN ∴∠=︒．3tan 4NBM ∠= ，∴在Rt △BMN 中，设3MN QM a ==，则4BM a =，∴BQ BM QM a =-=，5BN a ∴==．NE NM = ，NEM NME ∴∠=，3NE NM a ==，532BE BN NE a a a ∴=-=-=，∴122BQ a BE a ==，2142BE a BM a ==，BQ BE BE BM∴=．EBQ MBE∠=∠ ∴BEQ BEM △∽△，BEQ BME ∴∠=∠．90BME NME ∠+∠=︒ ，∴90BEQ NEM ∠+∠=︒，90QEM ∴∠=︒．故选D ．5．如图，在ABC 中，CH AB ⊥，CH h =，AB c =，若内接正方形DEFG 的边长是x ，则h 、c 、x 的数量关系为（）A ．222x h c +=B ．12x h c +=C ．2h xc =D ．111x h c=+【答案】D 【分析】先根据正方形的性质得到GF DE ∥，继而证明CGF CAB D D ，根据相似三角形的性质即可列出比例式，再通过证明四边形DHMG 是矩形表示出CM 的长度，即可求解．【解析】解：设CH 与GF 交于点M ，正方形DEFG ，GF DE ∴∥，90GDE DGF ∠=∠=︒，CGF CAB D D ∴ ，GF CM AB CH∴=， CH AB ⊥，90DHM ∴∠=︒，∴四边形DHMG 是矩形，DG MH ∴=，CH h =，AB c =，正方形DEFG 的边长是x ，MH x ∴=，CM CH MH h x ∴=-=-，x h x c h -∴=，整理得111x h c=+，故选：D ．6．我国古代数学著作《九章算法比类大全》有题如下：“方种芝麻斜种黍，勾股之田十亩无零数．九十股差方为界，勾差十步分明许．借问贤家如何取，多少黍田多少芝麻亩．算的二田无误处，智能才华算中举．”大意是：正方形田种芝麻，斜形（三角形）种黍，有一块直角三角形ABC 是10亩整．股差90AD =步，勾差10BF =步．请问黍田、芝麻各多少亩？（1亩240=平方步）答：（）A ．艺麻田3.75亩，黍田6.25亩B ．芝麻田3.25亩，黍田6.75亩C ．芝麻田3.70亩，黍田6.30亩D ．芝麻田3.30亩，黍田6.70亩【答案】A 【分析】首先判定AED EBF ∽，然后利用该相似三角形的对应边成比例和DE EF =求得30DE =；然后利用三角形和正方形的面积公式解答．【解析】解：根据题意知，AED EBF ∽，则AD EF DE FB=．又DE EF = ，30DE ∴==．所以，芝麻田的面积为：3030240 3.75S =⨯÷=芝麻（亩)．黍田的面积为：12402S AC CB S =⋅÷-黍芝麻()()12402AD DC CF FB S =++÷-芝麻1(9030)(3010)240 3.752=⨯++÷-6.25=（亩)．综上所述，芝麻田3.75亩，黍田6.25亩．故选：A ．二、填空题7．如图，在Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6．在其内并排放入（不重叠）n 个相同的小正方形纸片，使这些纸片的一边都在AB 上，首尾两个正方形各有一个顶点D ，E 分别在AC ，BC 上，则小正方形的边长为_____（用含n 的代数式表示）．【答案】1201225n +【分析】连接DE ，作CF ⊥AB 于点F ，根据勾股定理可得AB =10，再由22ABC AC BC AB CF S ⋅⋅== ，可得CF ＝245，然后根据△CDE ∽△CAB ，可得CG DE CF AB =，即可求解．【解析】解：连接DE ，作CF ⊥AB 于点F ，则DE AB ∥，∵∠C ＝90°，AC ＝8，BC ＝6．∴AB ＝10，∵22ABC AC BC AB CF S ⋅⋅== ，∴861022CF ⨯⋅=，解得∶CF ＝245，∵DE AB ∥，∴△CDE ∽△CAB ，CG DE ⊥，∴CG DE CF AB=，设小正方形的边长为x ，∴24524105x nx -=，解得x ＝1201225n +，故答案为：1201225n +．8．如图，在Rt △ABC 中，∠C =90°，AC =12，BC =5，在三角形内挖掉正方形CDEF ，则正方形CDEF 的边长为________．【答案】6017【分析】设EF ＝x ，则AF ＝12－x ，证明△AFE ∽△ACB ，可得EF AF BC AC =，由此构建方程即可解决问题．【解析】解：∵四边形CDEF 是正方形，∴EF ∥CD ，EF ＝FC ＝CD ＝DE ，设EF ＝x ，则AF ＝12－x ，∴△AFE ∽△ACB ，∴EF AF BC AC =，∴12512x x -=，解得x ＝6017，即正方形CDEF 的边长为6017，故答案为：6017．9．如图的△ABC 中有一正方形DEFG ，其中D 在AC 上，E 、F 在AB 上，直线AG 分别交DE 、BC 于M 、N 两点．若∠B ＝90°，AB ＝4，BC ＝3，EF ＝1，则BN 的长度为_____．【答案】127【分析】由∥DE BC 可得AE DE AB BC =，求出AE 的长，由GF BN ∥可得AE EF GF AB BN +=，将AE 的长代入可求得BN ．【解析】解：∵四边形DEFG 是正方形，∴,DE BC GF BN ∥∥，且DE =GF =EF =1，∴△ADE ∽△ACB ，△AGF ∽△ANB ，∴AE DE AB BC=①，AE EF GF AB BN +=②，由①可得，143AE =，解得：43AE =，将43AE =代入②，得：41134BN+=，解得：127BN =，故答案为：127．10．如图，矩形EFGH 内接于ABC ，且边FG 落在BC 上．若3BC =，2AD =，23EF EH =，AD BC ⊥，那么EH 的长为__．【答案】32【分析】根据矩形的性质得到EH BC ∥，得到AEH ABC ∽△△，根据相似三角形的性质得到比例式，列出方程，解方程即可．【解析】解：设AD 与EH 相交与点M ，四边形EFGH 是矩形，∴EH BC ∥，∴AEH ABC ∽△△，AM EH ⊥ ，AD BC ⊥，∴AM EH AD BC=，设3EH x =，则有2EF x =，22AM AD EF x =-=-，∴22323x x -=，解得：12x =，则32EH =．故答案为：32．11．如图，在ABC 中，点F 、G 在BC 上，点E 、H 分别在AB 、AC 上，四边形EFGH 是矩形，2,EH EF AD =是ABC 的高．8,6BC AD ==，那么EH 的长为____________．【答案】245【分析】通过四边形EFGH 为矩形推出EH BC ∥，因此△AEH 与△ABC 两个三角形相似，将AM 视为△AEH 的高，可得出AM EH AD BC=，再将数据代入即可得出答案．【解析】∵四边形EFGH 是矩形，∴EH BC ∥，∴AEF ABC ∽，∵AM 和AD 分别是△AEH 和△ABC 的高，∴,AM EH DM EF AD BC==，∴6AM AD DM AD EF EF =-=-=-，∵=2EH EF ，代入可得：6268EF EF -=，解得12=5EF ，∴1224=255EH ⨯=，故答案为：245．12．在Rt ABD △中，90ABD ∠=︒，点C 在线段AD 上，过点C 作CE AB ⊥于点E ，CF BD ⊥于点F ，使得四边形CEBF 为正方形，此时3cm AC =，4cm CD =，则阴影部分面积为_________2cm ．【答案】6【分析】由正方形的性质可得CE BD ∥，CE ＝CF ＝BF ＝BE ，得△AEC ∽△ABD ，设CE ＝CF ＝BF ＝BE ＝x ，利用相似三角形对应边成比例得到37AE x x AE x FD ==++，解得AE ＝34x ，FD ＝43x ，在Rt △AEC 中，由勾股定理得222AE CE AC +=，求得x 的值，进一步即可求得阴影部分的面积．【解析】解：∵四边形CEBF 为正方形，∴CE BD ∥，CE ＝CF ＝BF ＝BE ，∴△AEC ∽△ABD ，∴AE EC AC AB BD AD==，设CE ＝CF ＝BF ＝BE ＝x ，∴37AE x x AE x FD ==++，解得AE ＝34x ，FD ＝43x ，在Rt △AEC 中，由勾股定理得，222AE CE AC +=，即22334x x ⎛⎫+= ⎪⎝⎭，解得x ＝125，∴AE ＝34x ＝95（cm ），FD ＝43x ＝165（cm ），∴阴影部分面积为1912116126255255ACE CFD S S +=⨯⨯+⨯⨯= （2cm ）．故答案为：6三、解答题13．如图，己知直角三角形的铁片ABC 的两直角边BC 、AC 的长分别为3cm 和4cm ，分别采用（1）、（2）两种剪法，剪出一块正方形铁片，为使所得的正方形面积最大，问哪一种剪法好？为什么？【答案】（1）的情形下正方形的面积大，理由见解析【分析】求出两个正方形的边长，根据面积大的比较合理来选择．【解析】解：（1）设正方形边长为y cm ，则DE =CD =EF =CF =y cm ，∵DE ∥BC ，∴AD DE AC CB=，∴334y y -=，∴127y=；（2）5 AB=．作AB边上的高CH，交DE于点M．由1122ABCS AB CH AC BC=⋅=⋅△，得53422CH⨯=，解得12cm5CH=．∵DE∥AB，∴△CDE∽△CAB，∴CM DE CH AB=．设正方形DEFG的边长为cmx，则1251255x x-=，解得6037x=．∵6012 377<，∴（1）的情形下正方形的面积大．14．如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，∠DEB＝∠FCE，EF∥AB．(1)求证：△BDE∽△EFC；(2)设12AF FC =，△EFC 的面积是20，求△ABC 的面积．【答案】(1)见解析；(2)45【分析】（1）由平行线的性质得出DEB FCE ∠=∠，DBE FEC ∠=∠，即可得出结论；（2）先求出23FC AC =，易证EFC BAC ∆∆∽，由相似三角形的面积比等于相似比的平方即可得出结果．【解析】(1)解：证明：//EF AB ，DBE FEC ∴∠=∠，∵DEB FCE ∠∠＝，BDE EFC ∴∆∆∽；(2) 12AF FC =，∴23FC AC =，//EF AB ，EFC BAC ∴∆∆∽，∴222439EFC ABC S FC S AC ∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，99204544ABC EFC S S ∆∆∴==⨯=．15．如图，在ABC 中，点D 、E 、F 分别在AB 、BC 、AC 边上，DE AC ∥，EF AB ∥．(1)求证：BDE EFC △△∽．(2)若12BC =，12AF FC =，求线段BE 的长．【答案】(1)见解析；(2)4【分析】（1）由平行线的性质可得∠DEB ＝∠FCE ，∠DBE ＝∠FEC ，可得结论；（2）先证明四边形ADEF 是平行四边形，得到DE =AF ，推出12DE FC =，再由相似三角形的性质推出2EC BE =，由此求解即可．【解析】(1)解：∵DE ∥AC ，∴∠DEB ＝∠FCE ，∵EF ∥AB ，∴∠DBE ＝∠FEC ，∴△BDE ∽△EFC ；(2)解：∵DE ∥AC ，EF ∥AB ，∴四边形ADEF 是平行四边形，∴DE =AF ，∵12AF FC =，∴12DE FC =，∵△BDE ∽△EFC ，∴12BE DE EC FC ==，∴2EC BE =，∴312BE BC ==，∴4BE =．16．一块三角形的余料，底边BC 长1.8米，高AD ＝1米，如图．要利用它裁剪一个长宽比是3∶2的长方形，使长方形的长在BC 上，另两个顶点在AB 、AC 上，求长方形的长EH 和宽EF 的长．【答案】EH ＝911米，EF ＝611米【解析】根据比例设EH 、EF 分别为3k 、2k ，然后根据△AEH 和△ABC 相似，利用相似三角形对应高的比等于对应边的比列式比例式求出k 值，即可得解．【分析】解：∵长方形的长宽比是3∶2，∴设EH 、EF 分别为3k 、2k ，∴EH ∥BC ，∴△AEH ∽△ABC ，∴AM AD ＝EH BC ，即121k -＝31.8k ，解得k ＝311，∴EH ＝911米，EF ＝611米．17．我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用．例：已知x 可取任何实数，试求二次三项式261x x +-的最值．解：22226123331x x x x +-=+⨯⋅+--2(3)10x =+-∵无论x 取何实数，总有2(3)0x +≥．∴2(3)1010x +-≥-，即无论x 取何实数，261x x +-有最小值，是10-．(1)问题：已知247y x x =--+，试求y 的最值．(2)【知识迁移】在ABC 中，AD 是BC 边上的高，矩形PQMN 的顶点P 、N 分别在边AB AC 、上，顶点Q 、M 在边BC 上，探究一：12,6AD BC ==，求出矩形PQMN 的最大面积的值；（提示：由矩形PQMN 我们很容易证明APN ABC ∽△△，可以设PN x =，经过推导，用含有x 的代数式表示出该矩形的面积，从而求得答案．）(3)探究二：,AD h BC a ==，则矩形PQMN 面积S 的最大值___________．（用含a ，h 的代数式表示）【答案】(1)11；(2)18；(3)4ah【分析】（1）根据题意，使用配方法将二次三项式进行配方，再根据不等式的基本性质确定最值即可；（2）首先证明APN ABC ∽△△，根据相似三角形的性质，可以得到PN AE BC AD=，设PN x =，则162x AE =，得出2AE x =，从而得出122MN x =-，将矩形PQMN 面积S 用含x 的代数式表示，再进行配方，确定最值即可；（3）根据探究一，即可得出PN AE BC AD =，设PN x =，则x a h AE =，因此h AE x a =，从而得到h MN h x a=-，将矩形PQMN 面积S 用含x 的代数式表示，再进行配方，确定最值即可．【解析】（1）解：()()()22222247474227211y x x x x x x x =--+=-++=-++-+=-++∵无论x 取何实数，总有2(2)0x +≥，∴2(2)0x -+≤，∴2(2)1111x -++≤，即y 有最大值，是11；（2）探究一：∵四边形PQMN 是矩形，∴PN ∥BC ，∴∠APN ＝∠ABC ，∠ANP ＝∠ACB ，∴△APN ∽△ABC ，∴PNAEBC AD =，设PN ＝x ，∴162xAE=，∴2AE x =，由已知可得四边形EDMN 是矩形，∴122MN DE x ==-，∴()()()2222212221226332318S x x x x x x x =-=-+=--+-=--+，∵无论x 取何实数，总有2(3)0x -≥，∴22(3)0x --≤，∴22(3)1818x --+≤，∴矩形PQMN 的最大面积的值为18；（3）探究二：由探究一可知，△APN ∽△ABC ，∴PNAEBC AD =，设PN ＝x ，∴x a h AE=，∴h AE x a=，∴h MN h x a=-，∴()2222224424h h h h a a h a ah S x h x x hx x ax x ax x a a a a a ⎛⎫⎛⎫⎛⎫=-=-+=--=--+-=--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，∵无论x 取何实数，总有2()02a x -≥，∴2()02h a x a --≤，∴2(244h a ah ah x a --+≤，∴矩形PQMN 的最大面积的值为4ah ．18．如图，Rt ABC 为一块铁板余料，90B ∠=︒，6cm BC =，8cm AB =，要把它加工成正方形小铁板，有如图所示的两种加工方案，请你分别计算这两种加工方案的正方形的边长．【答案】方案①正方形边长247cm ，方案②正方形边长12037cm ．【分析】方案①：设正方形的边长为x cm,然后求出△AEF 和△ABC 相似，利用相似三角形对应边成比例列式计算即可得解．方案②：作BH ⊥AC 于H ，交DE 于K ，构造矩形DKHG 和相似三角形（△BDE ∽△BCA ），利用矩形的性质和等面积法求得线段BH 的长度，则BK ＝4.8−y ；然后由相似三角形的对应边成比例求得答案．【解析】解：设方案①正方形的边长为x cm ，90ABC ∠=︒ ，四边形BDFE 是正方形，EF BC ∴∥，AEF ABC ∴∆∆∽，∴EF AE BC AB=，即886x x -=，解得247x =，即加工成正方形的边长为247cm ．设方案②正方形的边长为y cm ，作BH AC ⊥于H ，交DE 于K ，∵四边形EDGF 是正方形，∴DE AC ∥，90EDG DGF ∠=∠=︒．∴BH DE ⊥于K ．∴90DKH ∠=︒．∴四边形DKHG 为矩形．设HK DG y ==．∵DE AC ∥．∴BDE BCA ∽．∴BK DE BH AC=．∵10AC ==．∴Δ11681022ABC S BH =⨯⨯=⨯⨯，∴ 4.8BH =，∴ 4.8BK y =-．∴4.84.810y y -=．解得12037y =．即方案②加工成正方形的边长为12037cm ．19．在△ABC 中，BC ＝2，BC 边上的高AD ＝1，P 是BC 上任一点，PE ∥AB 交AC 于E ，PF ∥AC 交AB 于F．(1)设BP ＝x ，将S △PEF 用x 表示；(2)当P 在BC 边上什么位置时，S 值最大．【答案】(1)S △PEF ＝﹣14x 2＋12x （0＜x ＜2）(2)当BP ＝1时，面积有最大值14【分析】（1）先求出△ABC 的面积，再用x 表示出PC ，然后再说明△CEP ∽△CAB 可得CEP CABS S ∆∆＝（22x -）2可得△CEP 的面积，同理可得S △BPF ＝24x ，然后结合图形根据平行四边形的对角线平分平行四边形解答即可；（2）先对（1）所得解析式配方，然后再根据二次函数的性质求最值即可．【解析】（1）解：（1）∵BC ＝2，BC 边上的高AD ＝1，∴S △ABC ＝12×2×1＝1，∵BP ＝x ，∴PC ＝2﹣x ，∵PE ∥AB ，∴△CEP ∽△CAB ，∴CEP CAB S S ∆∆＝（22x -）2，∴S △CEP ＝1﹣x ＋24x ，同理:S △BPF ＝24x ，∵四边形AEPF 为平行四边形，∴S △PEF ＝12S ▱AEPF ＝12（S △ABC ﹣S △CEP ﹣S △BPF ）＝﹣14x 2＋12x （0＜x ＜2）．∴S △PEF ＝﹣14x 2＋12x （0＜x ＜2）．（2）解：由（1）知S △PEF ＝﹣14x 2＋12x ＝﹣14（x ﹣1）2＋14，∵0＜x ＜2，∴当x ＝1时，面积有最大值14．20．课本中有一道作业题：有一块三角形余料ABC ，它的边BC ＝12m ，高线AD ＝8m ．要把它加工成正方形零件，使正方形的一边在BC 上，其余两个顶点分别在AB ，AC 上．问加工成的正方形零件的边长为多少米？小颖解得此题的答案为4.8m ．(1)你知道小颖是怎么做的吗？请你写出解答过程？(2)善于反思，她又提出了如下的问题，如果原题中所要加工的零件只是一个矩形，如图2，这样，此矩形零件的两条边长就不能确定，但这个矩形面积有最大值，求达到这个最大值时矩形零件的两条边长．(3)如图3，小颖想如果这块余料形状改为Rt △ABC 的斜板，已知∠A ＝90°，AB ＝8m ，AC ＝6m ，要把它加工成一个形状为平行四边形PQMN 的工件，使MQ 在BC 上，P 、N 两点分别在AB ，AC 上，且PN ＝8m ，则平行四边形PQMN 的面积为m 2．【答案】(1)见解析(2)达到这个最大值时矩形零件的两条边长4m =6mPQ PN =，(3)7.68【分析】（1）设正方形PQMN 的边长为x m ，则PN =PQ =ED =x m ，AE =AD -ED =（8-x ）m ，再证明△APN ∽△ABC ，得到AE PN AD BC =，即8812x x -=，由此求解即可；（2）设PN =x m ，矩形PQMN 的面积为2m S ，同理可证△APN ∽△ABC ，求出28m 3PQ x ⎛⎫=- ⎪⎝⎭，则()226243S PN PQ x =⋅=--+，由此利用二次函数的性质求解即可；（3）如图所示，过点A 作AD ⊥BC 于D ，交PN 于E ，同理可证△APN ∽△ABC ，AE ⊥PN ，得到AE PN AD BC=，利用勾股定理和面积法求出10m BC =， 4.8m AD =，从而求出0.96m DE =，则27.68m PQMN S PN DE =⋅=平行四边形．【解析】（1）解：由题意得四边形PQDE 是矩形，设正方形PQMN 的边长为x m ，则PN =PQ =ED =x m ，∴AE =AD -ED =（8-x ）m ，∵四边形PQMN 是正方形，∴PN QM ∥，∴△APN ∽△ABC ，∵AD ⊥BC ，∴AE ⊥PN ，∴AE PN AD BC =，即8812x x -=，解得 4.8x =，∴正方形PQMN 的边长为4.8m ；（2）解：设PN =x m ，矩形PQMN 的面积为2m S ，同理可证△APN ∽△ABC ，∴AE PN AD BC =，即8128x PQ -=，∴28m 3PQ x ⎛⎫=- ⎪⎝⎭，∴()2222288624333S PN PQ x x x x x ⎛⎫=⋅=-=-+=--+ ⎪⎝⎭，∵230a =-<，∴当6x =时，S 有最大值，最大值为224m ，∴4m PQ =，∴达到这个最大值时矩形零件的两条边长4m =6mPQ PN =，（3）解：如图所示，过点A 作AD ⊥BC 于D ，交PN 于E ，同理可证△APN ∽△ABC ，AE ⊥PN ，∴AE PN AD BC =，在Rt △ABC 中，∠A ＝90°，AB ＝8m ，AC ＝6m ，∴10m BC ==，∵1122ABC S AD BC AC AB =⋅=⋅△，∴ 4.8m AB AC AD BC⋅==，∴ 4.8AE AD DE DE =-=-，∴4.884.810DE -=，∴0.96m DE =，∴27.68m PQMN S PN DE =⋅=平行四边形，故答案为：7.68．。

相似三角形的应用——三角形的内接矩形问题一.复习提问：1．如图△ABC 中，DE ∥BC ，DE ＝2.5，BC ＝3.5，AF ⊥BC 于F ，交DE 于G ，AG ＝2。

求GF 的长。

二.例题讲解：已知在△ABC 中,BC=12,BC 边上的高AM=8,请回答下列问题: 1.如图⑴ ,四边形EFGH 为△ABC 的内接正方形,求正方形边长.2.如图⑵,三角形内有并排的两个全等的正方形,恰好组成了△ABC 的内接矩形EFGH,求每个小正方形边长.A BC D E GEM A C B E F G M A C B3.如图⑶, △ABC 内的内接矩形是由3个全等的正方形并排放置形成的，求小正方形边长。

4.如图⑷,三角形内并排的n 个全等的正方形组成的矩形内接于△ABC ，由以上结论猜测每个小正方形边长并验证。

三.变式训练 张师傅的困惑:如图,现有一木板余料,∠B=90°,BC=60cm,AB=80cm,我要把它加工成一个面积最大的正方形椅子面,下面有两位同学的加工方案,请同学们帮我选择哪位同学的加工方案好？小亮:如图,我充分利用直角三角形的直角,可使裁出的正方形面积最大,我的方案最好！小明:如图,我充分利用直角三角形中的最长边斜边,可使裁出的正方形面积最大,我的方案最好！FG E N FE N H M A C B M AC B B C A80c 60cABC 80c60c四．课堂检测：1、四边形DEFG 是△ABC 的内接矩形， AH ⊥BC 于H ，交DG 于M ，若BC=12cm ，AH=10cm ，DG=xcm ，DE=ycm（1）请用含x 的代数式表示y.（2）请用含x 的代数式表示矩形DEFG 的面积S.2. △ABC 是一张等腰直角三角形纸板，∠C=90度，AC=BC=2， (1)要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种 剪法(如图1)，比较甲、乙两种剪法，哪种剪法所得的正方形 面积大？请通过计算说明。