中考数学热点难题目几何三大变换

中考数学复习之几何三大变换学案知识梳理1. 平移、折叠、旋转统称为几何三大变换，它们都是全等变换，只改变图形的位置，不改变图形的大小和形状．2. 三大变换思考层次平移思考层次 （1）平移性质：①全等变换：对应线段①平行（或在一条直线上）且相等、对应角相等； ②对应点：②对应点所连线段平行（或在一条直线上）且相等． （2）组合搭配：平移会出现平行四边形． （3）应用：常应用在天桥问题、存在性问题等． 旋转思考层次 （1）旋转性质：①全等变换：对应线段相等、对应角相等；②对应点：对应点到旋转中心的距离相等；对应点与旋转中心的连线所成的角都等于旋转角；对应点所连线段的垂直平分线都经过旋转中心.（2）组合搭配：旋转会出现等腰三角形，特别地，旋转 60°会出现等边三角形，旋转90°会出现等腰直角三角形． （3）应用：当题目中出现等线段共端点时，会考虑构造旋转． （常见于图形中有正方形、等边三角形、等腰三角形等） 折叠（轴对称）思考层次 （1）轴对称性质：①全等变换：对应线段相等、对应角相等； ②对应点：对应点所连线段被对称轴垂直平分； 对称轴上的点到对应点的距离相等．（2）组合搭配：矩形背景下常出现等腰三角形；两次折叠常出现直角、60°角；折叠会出现圆弧等．（3）应用：常应用在最值问题等．例1：如图，四边形ABCD 是边长为9的正方形纸片，将该纸片折叠，使点B 落在CD 边上的点B′处，点A 的对应点为A′，折痕为MN ．若B′C=3，则AM 的长为__________．【思路分析】要求AM 的长，设AM=x ，则MD =9-x ．思路一：考虑利用折叠为全等变换转条件，得AM =A′M=x ， A′B′=AB=9．观察图形，∠A′=∠D =90°，∠MA′B′和∠MDB′都是直角三角形，MB′是其公共斜边，则MB′可分别在两个A'B'ADBCMN直角三角形中借助勾股定理表达，列方程．思路一 思路二思路二：MN 是对称轴，考虑利用对称轴上的点到对应点的距离相等转条件，得MB =MB′．观察图形，∠A =∠D =90°，MB ，MB′可分别放到Rt∠ABM 和Rt∠DB′M 中借助勾股定理表达，列方程．例2：如图，在四边形ABCD 中，∠BAD =∠BCD =90°，AB =AD ，若四边形ABCD 的面积为24，则AC 的长为____________．【思路分析】已知四边形ABCD 的面积，要求AC 的长，考虑借助AC 表达四边形ABCD 的面积．四边形ABCD 为不规则四边形，考虑割补法或转化法求面积．分析题目中条件AB =AD ，存在等线段共端点的结构，且隐含∠B +∠D =180°，故考虑通过构造旋转解决问题，可把∠ABC 绕点A 逆时针旋转90°．➢ 练习题1. 如图，将周长为8的△ABC 沿BC 方向平移1个单位得到△DEF ，则四边形ABFD的周长为（ ） A ．6 B ．8 C ．10 D ．122. 如图，在平面直角坐标系xOy 中，已知点A ，B 的坐标分别为(1，0)，(0，2)，将线段AB 平移至A 1B 1，若点A 1，B 1的坐标分别为(2，a )，(b ，3)，则a b +=___________．A'B'ADBCMN MC BDAB'A'D CBAF C E DB A 21ED CB A第2题图 第3题图3. 如图，AB =CD ，AB 与CD 相交于点O ，且∠AOC =60°，则AC +BD 与AB 的大小关系是（ ） A ．AC BD +>AB B ．AC +BD =AB C ．AC BD +≥AB D ．无法确定4. 如图，在44⨯的正方形网格中，△MNP 绕某点旋转一定的角度得到△M 1N 1P 1，则其旋转中心可能是（ ） A ．点AB ．点BC ．点CD ．点D第4题图 第5题图5. 如图，菱形OABC 的顶点O 在坐标原点，顶点A 在x 轴正半轴上，且∠B =120°，OA =2．将菱形OABC 绕原点O 顺时针旋转105°至菱形OA ′B ′C ′的位置，则点B ′的坐标为___________．6. 如图，两块完全相同的含30°角的直角三角板ABC 和A ′B ′C ′重合在一起，将三角板A ′B ′C ′绕其直角顶点C ′按逆时针方向旋转角α（090α<︒≤），则下列结论： ①当30α=︒时，A ′C 与AB 的交点恰好为AB 的中点； ②当60α=︒时，A ′B ′恰好经过点B ； ③在旋转过程中，始终存在AA ′⊥BB ′． 其中正确的是____________．（填写序号）第6题图 第7题图DOCBA11(C' ) CB'BA'AO'OCBAD EF CBA7. 如图，O 是等边三角形ABC 内一点，且OA =3，OB =4，OC =5．将线段OB 绕点B 逆时针旋转60°得到线段O′B ，则下列结论：①△AO′B 可以由△COB 绕点B 逆时针旋转60°得到； ②∠AOB =150°；③6AOBO'S =+四边形④6AOB AOC S S +=△△ 其中正确的是____________．（填写序号）8. 如图，将长为4cm ，宽为2cm 的矩形纸片ABCD 折叠，使点B 落在CD 边的中点E 处，压平后得到折痕MN ，则线段AM 的长为__________．9. 如图，在一张矩形纸片ABCD 中，AB =4，BC =8，点E ，F 分别在AD ，BC 边上，将纸片ABCD 沿直线EF 折叠，点C 落在AD 边上的一点H 处，点D 落在点G 处，则下列结论： ①四边形CFHE 是菱形； ②CE 平分∠DCH ；③当点H 与点A 重合时，EF= 其中正确的是____________．（填写序号）A ．B CD11.如图，在Rt △ABC 中，∠ACB =90°，∠B =30°，BC =3．D 是BC 边上一动点（不与点B ，C 重合），过点D 作DE ⊥BC ，交AB 于点E ，将∠B 沿直线DE 翻折，点B 落在射线BC 上的点F 处．当△AEF 为直角三角形时，BD 的长为________．B CFAEN MD GHFEDCBAE FD'A'CBDAABC12.13. 如图，在矩形ABCD 中，点E ，F 分别在BC ，CD 边上，将△ABE 沿AE 折叠，使点B 落在AC 上的点B′处，将△CEF 沿EF 折叠，使点C 落在EB ′与AD 的交点C ′处．若AB =1，则BC 的长为__________．14. 如图，将边长为2的等边三角形ABC 沿BC 方向平移1个单位得到△DEF ，则四边形ABFD的周长为_________．第1题图 第2题图15. 如图，已知△ABC 的面积为8，将△ABC 沿BC 方向平移到△A′B′C′的位置，使点B′和点C重合，连接AC ′，交A ′C 于点D ，则△CAC ′的面积为_________．16. 如图，在的方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（ ） A ．格点MB ．格点NC ．格点PD ．格点Q第3题图 第4题图17. 如图，已知OA ⊥OB ，等腰直角三角形CDE 的腰CD 在OB 上，∠ECD =45°，将△CDE 绕点CC'B'F ED CBAF E DC BA64⨯NMED C BOA D( B' )C'A'C B A逆时针旋转75°，点E 的对应点N 恰好落在OA 上，则的值为_________．18. 如图，E 是正方形ABCD 内一点，连接AE ，BE ，CE ，将△ABE 绕点B 顺时针旋转90°至△CBE′的位置．若AE =1，BE =2，CE =3，则∠BE′C =_________．19. 如图，在□ABCD 中，∠A =70°，将该平行四边形折叠，使点C ，D 分别落在点E ，F 处，折痕为MN ．若点E ，F 均在直线AB 上，则∠AMF =________．20. 如图，在正方形纸片ABCD 中，E ，F 分别是AD ，BC 的中点，沿过点B 的直线折叠，使点C落在EF 上，落点为N ，折痕交CD 边于点M ，BM 与EF 交于点P ，再展开．则下列结论：①CM =DM ；②∠ABN =30°；③；④△PMN 是等边三角形．其中正确的是____________．（填序号）第7题图 第8题图21. 已知一个矩形纸片OABC ，OA =6，点P 为AB 边上一点，AP =2，将△OAP 沿OP 折叠，点A落在点A′处，延长PA′交边OC 于点D ，经过点P 再次折叠纸片，点B 恰好落在点D 处，则AB 的长为____________．22. 如图，在矩形ABCD 中，AB =3，AD =9，将此长方形折叠，使点D 与点B 重合，点C 的对应点为点C′，折痕为EF ，则EF 的长为_________．OCCDFNM D CBA223AB CM NMPFE DCBAA'Q P DCOB AGC ′FE DC BA23. 如图，矩形纸片ABCD ，AB =5，BC =10，CD 上有一点E ，ED =2，AD 上有一点P ，PD =3，过P 作PF ⊥AD 交BC 于点F ，将纸片折叠，使点P 与点E 重合，折痕与PF 交于点Q ，与AD 交于点G ，则PQ 的长为_________．24. 如图，在四边形ABCD 中，已知△ABC 是等边三角形，∠ADC =30°，AD =3，BD =5，则CD 的长为________．参考答案1. C2. 23. C4. B5.，) 6.①②③ 7. ①②④ 8.9.①③ 10. A 11. 1或2 12. (-4，4) 13.14. 8 15. 8 16. B 17.18. 135° 19. 40° 20. ②③④QGF E PD CBA DCA13cm 8221. 12 22.23.24. 4134。

《中考压轴题》专题20：几何三大变换问题之轴对称（折叠）问题一、选择题1.将点P（﹣2，3）向右平移3个单位得到点P1，点P2与点P1关于原点对称，则P2的坐标是A．（﹣5，﹣3）B．（1，﹣3）C．（﹣1，﹣3）D．（5，﹣3）2.如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，点B为劣弧AN的中点．点P是直径MN上一动点，则PA+PB的最小值为A.2B.1C.2D.223.如图，在矩形ABCD中，AB=8，BC=16，将矩形ABCD沿EF折叠，使点C与点A重合，则折痕EF 的长为A．6B．12C．25D．454.如图，把矩形纸片ABCD沿对角线BD折叠，设重叠部分为△EBD，则下列说法错误的是A.AB=CDB.∠BAE=∠DCEC.EB=EDD.∠ABE一定等于30°5.如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，点B为劣弧AN的中点．点P是直径MN上一动点，则PA+PB的最小值为A.2B.1C.2D.226.如图，四边形ABCD是矩形，AB=6cm，BC=8cm，把矩形沿直线BD折叠，点C落在点E处，BE与AD相交于点F，连接AE，下列结论：①△FED是等腰三角形；②四边形ABDE是等腰梯形；③图中共有6对全等三角形；④四边形BCDF的周长为532cm；⑤AE的长为145cm．其中结论正确的个数为A.2个B.3个C.4个D.5个7.如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．则下列结论：①△ABG≌△AFG；②BG=CG；③AG∥CF；④S△EGC=S△AFE；⑤∠AGB+∠AED=145°．其中正确的个数是A．2B．3C．4D．58.如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE=13AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是A ．①②B ．②③C ．①③D ．①④9.如图，反比例函数k y x =（x ＜0）的图象经过点A （﹣1，1），过点A 作AB ⊥y 轴，垂足为B ，在y 轴的正半轴上取一点P （0，t ），过点P 作直线OA 的垂线l ，以直线l 为对称轴，点B 经轴对称变换得到的点B′在此反比例函数的图象上，则t 的值是A.152+ B.32 C.43 D.152-+10.如图，在正方形纸片ABCD 中，对角线AC 、BD 交于点O ，折叠正方形纸片ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合，展开后，折痕DE 分别交AB 、AC 于点E 、G ，连接GF.下列结论中错误的是A.∠AGE=67.5°B.四边形AEFG 是菱形C.B E=2OFD.DOG OGEF S :S 2:1∆=四边形11．如图，矩形ABCD 中，AB=3，BC=5，点P 是BC 边上的一个动点（点P 不与点B ，C 重合），现将△PCD 沿直线PD 折叠，使点C 落下点C 1处；作∠BPC 1的平分线交AB 于点E ．设BP=x ，BE=y ，那么y 关于x 的函数图象大致应为A. B. C. D.12.如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，有以下四个结论：①四边形CFHE是菱形；②EC平分∠DCH；③线段BF的取值范围为3≤BF≤4；④当点H与点A重合时，EF=25．以上结论中，你认为正确的有个．A.1B.2C.3D.413．如图，已知正方形ABCD，顶点A(1，3)、B(1,1)、C(3,1)．规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次变换．如此这样，连续经过2014次变换后，正方形ABCD的对角线交点M的坐标变为A．(—2012,2)B．（一2012，一2） C.(—2013,—2) D.(—2013,2)14.如图，矩形ABCD中，AD=5，AB=7.点E为DC上一个动点，把△ADE沿AE折叠，当点D的对应点D'落在∠ABC的角平分线上时，DE的长为.15．如图，四边形ABCD 中，AD ∥BC ，∠B=90°，E 为AB 上一点，分别以ED ，EC 为折痕将两个角（∠A ，∠B ）向内折起，点A ，B 恰好落在CD 边的点F 处．若AD=3，BC=5，则EF 的值是A ．15B ．215C ．17D ．21716．已知AD//BC ，AB ⊥AD ，点E 点F 分别在射线AD ，射线BC 上，若点E 与点B 关于AC 对称，点E 点F 关于BD 对称，AC 与BD 相交于点G ，则A.1tan ADB 2+∠=B.2BC 5CF=C.AEB 22DEF ∠+︒=∠ D.4cos AGB 6∠=17.如图，在Rt △ACB 中，∠ACB=90°，∠A=25°，D 是AB 上一点．将Rt △ABC 沿CD 折叠，使B 点落在AC 边上的B ′处，则∠ADB ′等于A ．25°B ．30°C ．35°D ．40°18.如图，已知直线a ∥b ，且a 与b 之间的距离为4，点A 到直线a 的距离为2，点B 到直线b 的距离为3，AB=230．试在直线a 上找一点M ，在直线b 上找一点N ，满足MN ⊥a 且AM+MN+NB 的长度和最短，则此时AM+NB=A ．6B ．8C ．10D ．1219.如图，正方形ABCD 中，AB=3，点E 在边CD 上，且CD=3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连接AG ，CF ．下列结论：①点G 是BC 中点；②FG=FC ；③F G C 9S 10∆=．其中正确的是A ．①②B ．①③C ．②③D ．①②③20如图，在平面直角坐标系中，Rt △OAB 的顶点A 在x 轴的正半轴上，顶点B 的坐标为（3，3），点C 的坐标为（12，0），点P 为斜边OB 上的一动点，则PA ＋PC 的最小值为【】A ．132B ．312C ．3192+D ．2721.如图①是3×3正方形方格，将其中两个方格涂黑，并且使得涂黑后的整个图案是轴对称图形，约定绕正方形ABCD 的中心旋转能重合的图案都视为同一种，例②中四幅图就视为同一种，则得到不同共有A ．4种B ．5种C ．6种D ．7种22.如图，在矩形ABCD 中，点E 是AD 的中点，∠EBC 的平分线交CD 于点F ，将△DEF 沿EF 折叠，点D 恰好落在BE 上M 点处，延长BC 、EF 交于点N ．有下列四个结论：①DF=CF ；②BF ⊥EN ；③△BEN 是等边三角形；④S △BEF =3S △DEF ．其中，将正确结论的序号全部选对的是A ．①②③B ．①②④C ．②③④D ．①②③④23.如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个直角三角形，展开后得到一个等腰三角形，则展开后的等腰三角形周长是A ．12B ．18C ．210+D ．2210+24.P 是∠AOB 内一点，分别作点P 关于直线OA 、OB 的对称点P 1、P 2，连接OP 1、OP 2，则下列结论正确的是A ．OP 1⊥OP 2B ．OP 1=OP 2C ．OP 1⊥OP 2且OP 1=OP 2D ．OP 1≠OP 225.如图，在Rt △ABC 中，∠C=90°，AC=3，BC=1，D 在AC 上，将△ADB 沿直线BD 翻折后，点A 落在点E 处，如果AD ⊥ED ，那么△ABE 的面积是A ．1B ．32C ．333+D ．1234+26.将一张宽为4cm 的长方形纸片（足够长）折叠成如图所示图形，重叠部分是一个三角形，则这个三角形面积的最小值是（）A ．338cm 2B ．8cm 2C ．3316cm 2D ．16cm 227.在平面直角坐标系中，若点P （m ，m ﹣n ）与点Q （﹣2，3）关于原点对称，则点M （m ，n ）在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限28.在如图所示的平面直角坐标系中，△OA 1B 1是边长为2的等边三角形，作△B 2A 2B 1与△OA 1B 1关于点B 1成中心对称，再作△B 2A 3B 3与△B 2A 2B 1关于点B 2成中心对称，如此作下去，则△B 2n A 2n +1B 2n +1（n 是正整数）的顶点A 2n +1的坐标是（）A ．（4n ﹣1，3）B ．（2n ﹣1，3）C ．（4n +1，3）D ．（2n +1，3）29.如图，在△ABC中，AB=10，AC=8，BC=12，AD⊥BC于D，点E、F分别在AB、AC边上，把△ABC沿EF 折叠，使点A与点D恰好重合，则△DEF的周长是（）A．14B．15C．16D．1730.如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，N是弧MB的中点，P是直径AB上的一动点．若MN=1，则△PMN周长的最小值为（）A．4B．5C．6D．731.如图，在矩形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E，则点D的坐标是（）A．（4，8）B．（5，8）C．（245，325）D．（225，365）32.如图，在边长为2的等边△ABC中，D为BC的中点，E是AC边上一点，则BE+DE的最小值为．二、填空题1.在Y ABCD 中，ABCD S 24=，AE 平分∠BAC ，交BC 于E.沿AE 将△ABE 折叠，点B 的对应点为F ，连结EF 并延长交AD 于G ，EG 将ABCD 分为面积相等的两部分.则ABE S ∆=.2.如图是长为40cm ，宽为16cm 的矩形纸片，M 点为一边上的中点，沿过M 的直线翻折．若中点M 所在边的一个顶点能．落在对边上，那么折痕．．长度为cm ．3.矩形纸片ABCD 中，已知AD=8，AB=6，E 是边BC 上的点，以AE 为折痕折叠纸片，使点B 落在点F 处，连接FC ，当△EFC 为直角三角形时，BE 的长为．4.如图，已知正方形ABCD 的边长为2，将正方形ABCD 沿直线EF 折叠，则图中折成的4个阴影三角形的周长之和为.5.如图1，正方形纸片ABCD 的边长为2，翻折∠B 、∠D ，使两个直角的顶点重合于对角线BD 上一点P 、EF 、GH 分别是折痕（如图2）．设AE=x （0＜x ＜2），给出下列判断：①当x=1时，点P 是正方形ABCD 的中心；②当x=12时，EF+GH ＞AC ；③当0＜x ＜2时，六边形AEFCHG 面积的最大值是114；④当0＜x ＜2时，六边形AEFCHG 周长的值不变．其中正确的是（写出所有正确判断的序号）．6.如图，在矩形ABCD中，AB=8，BC=10，E是AB上一点，将矩形ABCD沿CE折叠后，点B落在AD 边的F点上，则DF的长为．7.如图，AB、CD是⊙O两条弦，AB=8，CD=6，MN是直径，AB⊥MN于E,CD⊥MN于点F,P为EF上任意一点,，则PA+PC的最小值为．8.如图，将半径为3的圆形纸片，按下列顺序折叠．若»AB和»BC都经过圆心O，则阴影部分的面积是（结果保留π）9.如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF，如图2，展开再折叠一次，使点C 与点E重合，折痕为GH，点B的对应点为M，EM交AB于N，则tan∠ANE=.10.如图，折叠矩形纸片ABCD，使点B落在边AD上，折痕EF的两端分别在AB、BC上（含端点），且AB=6cm，BC=10cm．则折痕EF的最大值是cm．11.如图，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，如果AB：AD=2：3，那么tan∠EFC 值是.12．如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B处有乙滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁从外币A处到达内壁B处的最短距离为．13．将边长为1的正方形纸片按图1所示方法进行对折，记第1次对折后得到的图形面积为S1，第2次对折后得到的图形面积为S2，…，第n次对折后得到的图形面积为S n，请根据图2化简，S1+S2+S3+…+S2014=．14．如图，有一矩形纸片ABCD，AB=8，AD=17，将此矩形纸片折叠，使顶点A落在BC边的A′处，折痕所在直线同时经过边AB、AD（包括端点），设BA′=x，则x的取值范围是．15．如图，已知在矩形ABCD中，点E在边BC上，BE＝2CE，将矩形沿着过点E的直线翻折后，点C、D分别落在边BC下方的点C′、D′处，且点C′、D′、B在同一条直线上，折痕与边AD交于点F，D′F与BE 交于点G．设AB＝t，那么△EFG的周长为（用含t的代数式表示）．16．如图，将边长为6cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在Q 处，EQ与BC交于点G，则△EBG的周长是cm17．把标准纸一次又一次对开，可以得到均相似的“开纸”．现在我们在长为22、宽为1的矩形纸片中，画两个小矩形，使这两个小矩形的每条边都与原矩形纸的边平行，或小矩形的边在原矩形的边上，且每个小矩形均与原矩形纸相似，然后将它们剪下，则所剪得的两个小矩形纸片周长之和的最大值是．18.如图，在△ABC中，AB=AC，BC=8，3tanC2，如果将△ABC沿直线l翻折后，点B落在边AC的中点处，直线l与边BC交于点D，那么BD的长为．19.如图，菱形OABC的顶点O是坐标原点，顶点A在x的正半轴上，顶点B、C均在第一象限，OA=2，∠AOC=600，点D在边AB上，将四边形ODBC沿直线OD翻折，使点B和点C分别落在这个坐标平面的点B′和点C′处，且∠C′DB′=600。

《中考压轴题》专题22：几何三大变换问题之旋转（中心对称）问题一、选择题1.如图，已知△ABC 中，∠C=90°，AC=BC=，将△ABC 绕点A 顺时针方向旋转60°到△AB′C′的位置，连接C′B ，则C′B 的长为A ．22-B ．32C ．31-D ．12.如图，△AOB 为等腰三角形，顶点A 的坐标为（2，5），底边OB 在x 轴上．将△AOB 绕点B 按顺时针方向旋转一定角度后得△A'O'B ，点A 的对应点A'在x 轴上，则点O'的坐标为A ．（203，103）B ．（163，453）C ．（203，453）D ．（163，43）3.在平面直角坐标系中，函数y=x 2﹣2x （x≥0）的图象为C 1，C 1关于原点对称的图象为C 2，则直线y=a （a 为常数）与C 1、C 2的交点共有A.1个B.1个或2个C.个或2个或3个D.1个或2个或3个或4个4.如图，矩形ABCD 的长为6，宽为3，点O 1为矩形的中心，⊙O 2的半径为1，O 1O 2⊥AB 于点P ，O 1O 2=6．若⊙O 2绕点P 按顺时针方向旋转360°，在旋转过程中，⊙O 2与矩形的边只有一个公共点的情况一共出现A ．3次B ．4次C ．5次D ．6次5．如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使得点A′恰好落在AB上，则旋转角度为A．30°B．60°C．90°D．150°6.如图所示，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴围成的面积为A．122π+B．12π+C．1π+D．3-7.如图，直线y=2x与双曲线2yx=在第一象限的交点为A，过点A作AB⊥x轴于B，将△ABO绕点O旋转90°，得到△A′B′O，则点A′的坐标为A．（1.0）B．（1.0）或（﹣1.0）C．（2.0）或（0，﹣2）D．（﹣2.1）或（2，﹣1）8.如图，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF，连接CE、DF．将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置，则旋转角是A．45°B．60°C．90°D．120°9.如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（）A．△ABC绕点C顺时针旋转90°，再向下平移3B．△ABC绕点C顺时针旋转90°，再向下平移1 C．△ABC绕点C逆时针旋转90°，再向下平移1D．△ABC绕点C逆时针旋转90°，再向下平移3二、填空题1.如图，△ABC绕点A顺时针旋转45°得到△A'B'C'，若∠BAC=90°，AB=AC=2，则图中阴影部分的面积等于.2.如图，在在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB=90°，直角边AO在x轴上，且AO=1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O=2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O=2A1O…，依此规律，得到等腰直角三角形A2014OB2014，则点A2014的坐标为．3.如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1，此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=1+2；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=2+2；…，按此规律继续旋转，直至得到点P2014为止．则AP2014=．4.如图，在平面直角坐标系xOy中，已知点M0的坐标为（1，0），将线段OM0绕原点O逆时针方向旋转45°，再将其延长到M1，使得M1M0⊥OM0，得到线段OM1；又将线段OM1绕原点O逆时针方向旋转45°，再将其延长到M2，使得M2M1⊥OM1，得到线段OM2；如此下去，得到线段OM3，OM4，OM5，…根据以上规律，请直接写出OM2014的长度为．5.如图，将等边△ABC绕顶点A顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F，则∠EAF的度数是．6.如图，已知∠AOB=90°，点A绕点O顺时针旋转后的对应点A1落在射线OB上，点A绕点A1顺时针旋转后的对应点A2落在射线OB上，点A绕点A2顺时针旋转后的对应点A3落在射线OB上，…，连接AA1，AA2，AA3…，依次作法，则∠AA n A n+1等于度．（用含n的代数式表示，n为正整数）7.如图（1），有两个全等的正三角形ABC和ODE，点O、C分别为△ABC、△DEO的重心；固定点O，将△ODE顺时针旋转，使得OD经过点C，如图（2），则图（2）中四边形OGCF与△OCH面积的比为．8.如图在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1．先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2014次，点B的落点依次为B1，B2，B3，…，则B2014的坐标为．9.如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（53，0），B（0，4），则点B2014的横坐标为．10.通过对课本中《硬币滚动中的数学》的学习，我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程（如图①）．在图②中，有2014个半径为r的圆紧密排列成一条直线，半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位，则动圆C自身转动的周数为．11．如图，△COD是△AOB绕点O顺时针旋转40°后得到的图形，若点C恰好落在AB上，且∠AOD的度数为90°，则∠B的度数是．=上一点P（1，1），C为y轴上一点，连接PC，线段PC绕点12.如图，平面直角坐标系中，已知直线y xP顺时针旋转900至线段PD，过点D作直线AB⊥x轴。

专题21几何三大变换问题之平移问题轴对称、平移、旋转是平面几何的三大变换。

平移变换是指在同一平面内，将一个图形（含点、线、面）整体按照某个直线方向移动一定的距离，这样的图形变换叫做图形的平移变换，简称平移。

平移由两大要素构成：①平移的方向，②平移的距离。

平移有如下性质：1、经过平移，平移前后图形的形状、大小不变，只是位置发生改变，即平移前后的图形全等；2、平移前后图形的对应点所连的线段平行且相等；3、平移前后图形的对应线段平行且相等，对应角相等。

中考压轴题中平移问题，包括直线（线段）的平移问题；曲线的平移问题；三角形的平移问题；四边形的平移问题；其它曲面的平移问题。

一.直线（线段）的平移问题1.定义：P、Q分别是两条线段a和b上任意一点，线段PQ长度的最小值叫做线段与线段的距离.已知O(0，0)，A(4，0)，B(m，n)，C(m+4，n)是平面直角系中四点.（1）根据上述定义，当m=2，n=2时，如图1，线段BC与线段OA的距离是_____,当m=5，n=2时，如图2，线段BC与线段OA的距离(即线段AB的长)为______（2）如图3，若点B落在圆心为A，半径为2的圆上，线段BC与线段OA的距离记为d，求d关于m的函数解析式.（3）当m的值变化时，动线段BC与线段OA的距离始终为2，线段BC的中点为M.①求出点M随线段BC运动所围成的封闭图形的周长;②点D的坐标为(0，2)，m≥0，n≥0，作MH⊥x轴,垂足为H，是否存在m的值，使以A、M、H为顶点的三角形与△AOD相似，若存在，求出m的值；若不存在，请说明理由.【答案】（1）2；5（2）()()2m8m122m4d24m6<⎧-+-≤⎪=⎨≤≤⎪⎩（3）①16+4π②存在，m=1，m=3，m=143【解析】解：（1）2；5。

（2）∵点B落在圆心为A，半径为2的圆上，∴2≤m≤6。

当4≤m≤6时，根据定义， d=AB=2。

当2≤m＜4时，如图，过点B作BE⊥OA于点E，则根据定义，d=EB。

几何综合——三大变换【例1】已知△ABC ，AD ∥BE ，若∠CBE ＝4∠DAC ＝80°，求∠C 的度数。

CDEBA【例2】已知在梯形ABCD 中，AD ∥BC ，AB ＝DC ，且BD ＝BC ，AC ⊥BD 。

求证：AD ＋BC ＝2CM 。

MDCB A【例3】已知：如图，正方形ABCD 中，E 是AB 上一点，FG ⊥DE 于点H 。

⑴求证：FG ＝DE 。

⑵求证：FD EG 。

HGFEDC BA【例4】如图，△ABC 中，AB ＝AC ，D 、E 是AB 、AC 上的点且AD ＝CE 。

求证：2DE ≥BC 。

EDCB A【例5】(2007北京)如图，已知△ABC 。

⑴请你在BC 边上分别取两点D 、E (BC 的中点除外)，连结AD 、AE ，写出使此 图中只存在．．．两对．．面积相等的三角形的相应条件，并表示出面积相等的三角形；⑵请你根据使⑴成立的相应条件，证明AB ＋AC ＞AD ＋AE 。

板块二 轴对称变换【例6】把正方形沿着EF 折叠使点B 落在AD 上， B 'C '交CD 于点N ，已知正方形的边长为1，求△DB'N的周长。

NC'FEB'D C BA【例7】（2009山西太原）问题解决：如图1，将正方形纸片ABCD 折叠，使点B 落在CD 边上一点E （不与点C D 、重合），压平后得到折痕MN 。

当12CE CD 时，求AMBN的值。

图1N MF ED CBA【例8】⑴(2009浙江温州)如图，已知正方形纸片ABCD 的边长为8，⊙O 的半径为2，圆心在正方形的中心上，将纸片按图示方式折叠，使EA '恰好与⊙O 相切于点A '(△EF A '与⊙O 除切点外无重叠部分)，延长F A '交CD 边于点G ，则A 'G 的长是________。

G FC⑵将弧BC 沿弦BC 折叠交直径AB 于点D ，若AD ＝4，DB ＝5，则BC 的长是________。

中考几何变换专题复习（针对几何大题的讲解）几何图形问题的解决，主要借助于基本图形的性质（定义、定理等）和图形之间的关系(平行、全等、相似等）.基本图形的许多性质都源于这个图形本身的“变换特征”，最为重要和最为常用的图形关系“全等三角形”极多的情况也同样具有“变换”形式的联系.本来两个三角形全等是指它们的形状和大小都一样，和相互间的位置没有直接关系，但是，在同一个问题中涉及到的两个全等三角形，大多数都有一定的位置关系（或成轴对称关系，或成平移的关系，或成旋转的关系（包括中心对称）.这样，在解决具体的几何图形问题时，如果我们有意识地从图形的性质或关系中所显示或暗示的“变换特征”出发，来识别、构造基本图形或图形关系，那么将对问题的解决有着极为重要的启发和引导的作用.下面我们从变换视角以三角形的全等关系为主进行研究.解决图形问题的能力，核心要素是善于从综合与复杂的图形中识别和构造出基本图形及基本的图形关系，而“变换视角”正好能提高我们这种识别和构造的能力.1．已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）求证：EG=CG；（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．考点：旋转的性质；全等三角形的判定与性质；直角三角形斜边上的中线；正方形的性质。

专题：压轴题。

分析：（1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG=EG．（2）结论仍然成立，连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点；再证明△DAG≌△DCG，得出AG=CG；再证出△DMG≌△FNG，得到MG=NG；再证明△AMG≌△ENG，得出AG=EG；最后证出CG=EG．（3）结论依然成立．还知道EG⊥CG．解答：（1）证明：在Rt△FCD中，∵G为DF的中点，∴CG=FD，同理，在Rt△DEF中，EG=FD，∴CG=EG．（2）解：（1）中结论仍然成立，即EG=CG．证法一：连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点．在△DAG与△DCG中，∵AD=CD，∠ADG=∠CDG，DG=DG，∴△DAG≌△DCG，∴AG=CG；在△DMG与△FNG中，∵∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，∴△DMG≌△FNG，∴MG=NG；在矩形AENM中，AM=EN，在△AMG与△ENG中，∵AM=EN，∠AMG=∠ENG，MG=NG，∴△AMG≌△ENG，∴AG=EG，∴EG=CG．证法二：延长CG至M，使MG=CG，连接MF，ME，EC，在△DCG与△FMG中，∵FG=DG，∠MGF=∠CGD，MG=CG，∴△DCG≌△FMG．∴MF=CD，∠FMG=∠DCG，∴MF∥CD∥AB，∴EF⊥MF．在Rt△MFE与Rt△CBE中，∵MF=CB，EF=BE，∴△MFE≌△CBE∴∠MEF=∠CEB．∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°，∴△MEC为直角三角形．∵MG=CG，∴EG=MC，∴EG=CG．（3）解：（1）中的结论仍然成立．即EG=CG．其他的结论还有：EG⊥CG．点评：本题利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质．2．（1）如图1，已知矩形ABCD中，点E是BC上的一动点，过点E作EF⊥BD于点F，EG⊥AC于点G，CH⊥BD于点H，试证明CH=EF+EG；（2）若点E在BC的延长线上，如图2，过点E作EF⊥BD于点F，EG⊥AC的延长线于点G，CH⊥BD于点H，则EF、EG、CH三者之间具有怎样的数量关系，直接写出你的猜想；（3）如图3，BD是正方形ABCD的对角线，L在BD上，且BL=BC，连接CL，点E 是CL上任一点，EF⊥BD于点F，EG⊥BC于点G，猜想EF、EG、BD之间具有怎样的数量关系，直接写出你的猜想；（4）观察图1、图2、图3的特性，请你根据这一特性构造一个图形，使它仍然具有EF、EG、CH这样的线段，并满足（1）或（2）的结论，写出相关题设的条件和结论．考点：矩形的性质；全等三角形的判定与性质；等腰三角形的性质；正方形的性质。

【中考数学压轴题】十大类型之几何三大变换一、单选题(共1道，每道30分)1.如图，将矩形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕，AB=8，AD=4，则四边形ECGF的面积为（）A.6B.10C.12D.16答案：D解题思路：连接AC，交EF于点O，则AC被EF垂直且平分。

OC=OA，∵DC∥AB，∴∠OAE=∠OCF，∠CFO=∠OEA，∴△OFC的面积＝△OAE的面积。

所以所求四边形的面积等于△ACD的面积，为矩形面积一半，即16试题难度：三颗星知识点：翻折变换（折叠问题）二、解答题(共2道，每道35分)1.（2009湖南常德）如图1，若△ABC和△ADE为等边三角形，M，N分别是EB，CD的中点，易证：CD=BE，△AMN是等边三角形．（1）当把△ADE绕A点旋转到图2的位置时，CD=BE 是否仍然成立？若成立请证明，若不成立请说明理由；（2）当△ADE绕A点旋转到图3的位置时，△AMN是否还是等边三角形？若是，请给出证明，并求出当AB=2AD时，△ADE与△ABC及△AMN的面积之比；若不是，请说明理由．答案：答：（1）CD=BE．理由如下：∵△ABC和△ADE为等边三角形，∴AB=AC，AE=AD，∠BAC=∠EAD=60°，∵∠BAE=∠BAC-∠EAC=60°-∠EAC，∠DAC=∠DAE-∠EAC=60°-∠EAC，∴∠BAE=∠DAC，∴CD=BE．（2）△AMN是等边三角形．理由如下：∵△ABE≌△ACD，M、N分别是BE、CN的中点，∴AM=AN，NC=MB．∵AB=AC，∴△ABM≌△ACN，∴∠MAB=∠NAC，∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°，∴△AMN是等边三角形，设AD=a，则AD=AE=DE=a，AB=BC=AC=2a，易证BE⊥AC，∴，∴，∴，∵△ADE，△ABC，△AMN为等边三角形，∴．解题思路：（1）利用SAS判定△ABE≌△ACD，全等三角形的对应边相等，所以CD=BE．（2）证明△AMN是等边三角形，AD=a，则AB=2a，根据已知条件分别求得△AMN的边长，因为△ADE，△ABC，△AMN为等边三角形，所以面积比等于边长的平方的比．试题难度：三颗星知识点：中考压轴之实践操作、问题探究2.如图，抛物线y＝x 2－6x＋8与x 轴交于A、B两点（点A在点B的左侧），直线y＝x ＋2交y轴于点C，且过点D（8，m）．左右平移抛物线y＝x 2－6x＋8，记平移后点A的对应点为A′，点B的对应点为B′．（1）求线段AB、CD的长；（2）当抛物线向右平移到某个位置时，A′D＋B′D最小，试确定此时抛物线的表达式；（3）是否存在某个位置，使四边形A′B′DC的周长最小？若存在，求出此时抛物线的表达式和四边形A′B′DC的周长最小值；若不存在，请说明理由．答案：（1）（2）（3）存在，抛物线的表达式为，周长的最小值为解题思路：（1）令y＝x 2－6x＋8=0，解得x1=2，x2=4，由题意知A（2,0），B（4,0），则AB=2；将D（8，m）代入直线表达式y＝x＋2，可计算出D点坐标为（8,6）；C点坐标为（0,2），过D作DE⊥y轴于点E，则DE=8，CE=4，在Rt△CDE中，由勾股定理知（2）类似于“奶站模型”：我们可以认为A、B两定点为居民区，动点M在直线DE上运动为送奶站，要确定M点的位置，保证AM+BM最小；然后把A、B、M三点连同奶站模型和抛物线一起向右平移，当M点与D点重合时，M点向右平移几个单位，说明抛物线向右平移几个单位，此时A、B分别与A′、B′重合，能保证A′D＋B′D最小。

中考数学培优难题全优专题含答案解析 11：几何三大变换之旋转中考数学培优难题全优专题含答案解析11：几何三大变换之旋转高考数学综合素质训练专题一、中心对称和中心对称图形：题目：培养优秀问题的优秀题目【中考概论】题目11：几何的三种变换的旋转轴对称、平移和旋转是平面几何的三种变换。

旋转变换是指将图形（包括点、线和曲面）围绕固定点在同一平面上旋转固定角度。

这种图变换称为图旋转变换，简称旋转。

旋转由旋转中心、旋转方向和旋转角度决定。

旋转后，图形的形状和大小在旋转前后保持不变，但位置发生变化；旋转中心线与旋转中心线之间的距离相等，即旋转中心线与旋转中心线的相应平分点之间的距离；旋转前后图形的对应点与连接到旋转中心的线段之间的夹角等于旋转角度。

图形围绕某一点旋转360°/N（N是大于1的正整数）后，它与初始图形重合。

该图形称为旋转对称图形，该固定点称为旋转对称中心，旋转角度称为旋转角。

特别是，中心对称也是旋转对称的一种特殊形式。

将图形绕某一点旋转180°。

如果它能与另一个图形重合，则称这两个图形围绕这一点或中心对称。

这一点称为对称中心，两个图形的对应点称为围绕中心的对称点。

如果一个图形在围绕某一点旋转180度后可以与自身重合，则该图形是中心对称的。

在初中数学和日常生活中，有大量的旋转和变换知识，这是中学数学考试的必要内容。

结合全国各地的高考实例，从以下九个方面讨论了旋转变换：（1）中心对称图形和中心对称图形；（2）构造旋转图形；（3）相关点的旋转；（4）直线（线段）的旋转；（5）等腰（边）三角形的旋转；（6）直角三角形的旋转；（7）平行四边形、矩形和菱形的旋转；（8）关于正方形的旋转；（9）围绕其他形状旋转。

1例1（天津3点）在下列标志中，可以被视为中心对称图形的是【】（a）【答案】b。

（b）（c）（d）【考点】中心对称图形。

【分析】根据中心对称图形的概念：将图形围绕某一点旋转180°。

【中考数学热点难题】几何三大变换几何三大变
换
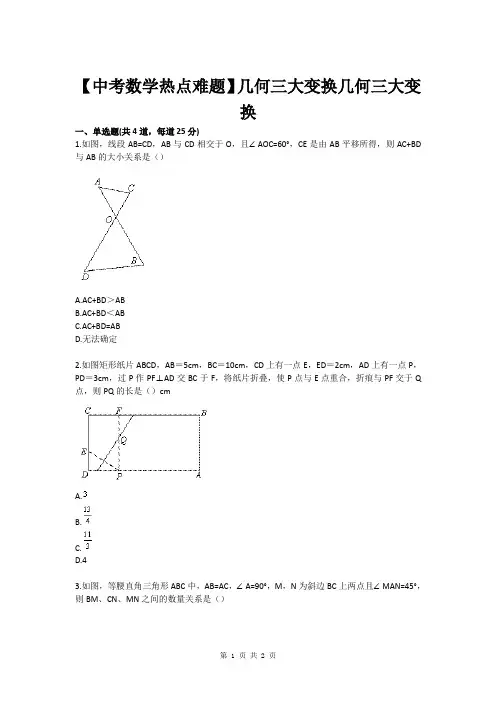
一、单选题(共4道，每道25分)
1.如图，线段AB=CD，AB与CD相交于O，且∠AOC=60°，CE是由AB平移所得，则AC+BD 与AB的大小关系是（）
A.AC+BD＞AB
B.AC+BD＜AB
C.AC+BD=AB
D.无法确定
2.如图矩形纸片ABCD，AB＝5cm，BC＝10cm，CD上有一点E，ED＝2cm，AD上有一点P，PD＝3cm，过P作PF⊥AD交BC于F，将纸片折叠，使P点与E点重合，折痕与PF交于Q 点，则PQ的长是（）cm
A.
B.
C.
D.4
3.如图，等腰直角三角形ABC中，AB=AC，∠A=90°，M，N为斜边BC上两点且∠MAN=45°，则BM、CN、MN之间的数量关系是（）
A.BM2+CN2=MN2
B.BM+CN=MN
C.2BM+CN=MN
D.无法确定
4.如图，在三角形纸片ABC中，∠ACB=90°，BC=3，AB=6．在AC上取一点E，以BE为折痕，使AB的一部分与BC重合，A与BC延长线上的点D重合，则CE的长度为（）
A.3
B.6
C.
D.。

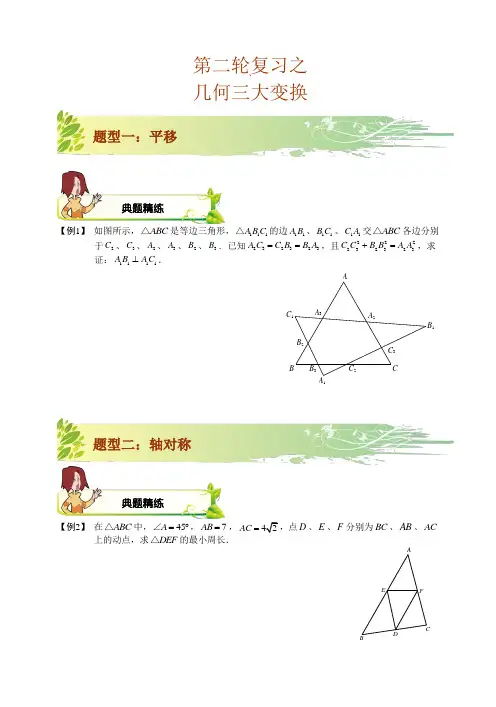
`【例1】 如图所示，ABC △是等边三角形，111A B C △的边11A B 、11B C 、11C A 交ABC △各边分别于2C 、3C 、2A 、3A 、2B 、3B ．已知232323A C C B B A ==，且222232323C C B B A A +=，求证：1111A B AC ⊥．C 3A 3B 3B 2A 2C 2C 1A 1B 1CBA【例2】 在ABC △中，45A =︒∠，7AB =，42AC =，点D 、E 、F 分别为BC 、AB 、AC 上的动点，求DEF △的最小周长．FEDCBA典题精练典题精练第二轮复习之几何三大变换题型二：轴对称题型一：平移【例3】 如图，已知60ABD ACD ∠=∠=︒，且1902ADB BDC ∠=︒-∠．求证：ABC △是等腰三角形．【例4】 在平面直角坐标系xOy 中，直线 6y x =+与x 轴交于点A ，与y 轴交于点B ．（1）求∠BAO 的度数；（2）如图1，P 为线段AB 上一点，在AP 上方以AP 为斜边作等腰直角三角形APD ．点 Q 在AD 上，连结PQ ，过作射线PF ⊥PQ 交x 轴于点F ，作PG ⊥x 轴于点G ． 求证：PF ＝PQ ；（3）如图2，E 为线段AB 上一点，在AE 上方以AE 为斜边作等腰直角三角形AED ．若P 为线段EB 的中点，连接PD 、PO ，猜想线段PD 、PO 有怎样的关系？并说明理由．图1 图2题型三：旋转B A【例5】 某学校活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程： ●操作发现：在等腰ABC △中，AB AC =，分别以AB 和AC 为斜边，向ABC △的外侧作等腰直角三角形，如图1所示，其中DF AB ⊥于点F ，EG AC ⊥于点G ，M 是BC 的中点，连接MD 和ME ，则下列结论正确的是（填序号即可）．①12AF AG AB ==；②MD ME =；③整个图形是轴对称图形；④DAB DM B ∠=∠． ●数学思考：在任意ABC △中，分别以AB 和AC 为斜边，向ABC △的外侧作等腰直角三角形，如图2所示，M 是BC 的中点，连接MD 和ME ，则MD 与ME 具有怎样的数量和位置关系？请给出证明过程； ●类比探究：在任意ABC △中，仍分别以AB 和AC 为斜边，向ABC △的内侧作等腰直角三角形，如图3所示，M 是BC 的中点，连接MD 和ME ，试判断MED △的形状． 答： ．图3EMC D BACM BEAD图2图1GF EM CBDA【例6】 在Rt △ABC 中，∠ACB =90°，∠A =30°，BD 是△ABC 的角平分线， DE ⊥AB 于点E ．（1）如图1，连接EC ，求证：△EBC 是等边三角形； （2）点M 是线段CD 上的一点（不与点C ，D 重合），以BM 为一边，在BM 的下方作∠BMG =60°，MG 交DE 延长线于点G ．请你在图2中画出完整图形，并直接写出MD ，DG 与AD 之间的数量关系；（3）如图3,点N 是线段AD 上的一点，以BN 为一边，在BN 的下方作∠BNG =60°，NG 交DE 延长线于点G ．试探究ND ，DG 与AD 数量之间的关系，并说明理由．图1 图2题型一 平移变换 巩固练习【练习1】 ⑴ 如图，三角形ABC 的底边BC 长3厘米，BC 边上的高是2厘米，将该三角形以每秒3厘米的速度沿高的方向向上平行移动2秒，这时， 该三角形扫过的面积（阴影部分）．⑵ 如图，线段AB 沿着四个方向①②③④都平移a 个单位长度，线 段AB 扫过的面积最大的是 ．（填序号） 题型二 轴对称变换 巩固练习【练习2】 如图所示，已知Rt ABC △中，90B ∠=︒，3AB =，4BC =，D ，E ，F 分别是三边AB ，BC ，CA 上的点，则DE EF FD ++的最小值为（ ）FEDCBAA ．125 B ．245C ．5D ．6题型三 旋转变换 巩固练习【练习3】 D 、E 是等腰Rt ABC △斜边BC 所在直线上的两点，满足135DAE ∠=︒；求证：222CD BE DE +=．EDCBA复习巩固②④①C'B'CB A。

中考热点难题目填空题目难题目技巧解析之探索规律几何三大变换专项备考练习
【中考热点难题】填空题难题技巧解析之探索规律、几何三大变换专项备考练习
一、填空题(共5道，每道20分)
1.（2011辽宁本溪）根据图中数字的规律，在最后一个空格中填上适当的数字.
2.(2011乌兰察布)将一些半径相同的小圆按如图所示的规律摆放，请仔细观察，第n个图形有个圆．（用含n的代数式表示）
3.（2011四川广安）如图所示，直线OP经过点P（4，），过x轴上的点1、3、5、7、9、11……分别作x轴的垂线，与直线OP相交得到一组梯形，其阴影部分梯形的面积从左至右依次记为S1、S2、…、Sn，则Sn关于n的函数关系式是．
4.（2011江苏淮安）如图，在Rt△ABC中，∠ABC=90°，∠ACB=30°，将
△ABC绕点A按逆时针方向旋转15°后得到△AB1C1，B1C1交AC于点D，如
果AD=，则△ABC的周长等于．
5.（2011江苏镇江）把棱长为4的正方体分割成29个棱长为整数的正方体（且没有剩余），其中棱长为1的正方体的个数为．。

C A B EF M N 图① CA BE M N 图②浅析天津中考几何压轴题从天津近五年中考之25题看天津中考几何压轴题之动向： 1、三大变换—平移、折叠、旋转（2008旋转与折叠，2009折叠，2010轴对称，2011旋转，2012折叠） 2、动点问题（常出现在最后一题或倒数第二题） 3、坐标系与几何图形的综合 （2009，2010,2011，2012） 4、几何图形与函数的综合 （2009，2011）5、全等三角形，相似三角形，勾股定理，平行四边形，特殊的平行四边形。

总之：综合性强，涉及知识点多。

25．（2009天津市10分）已知Rt △ABC 中，︒=∠90ACB ，CB CA =，有一个圆心角为︒45，半径的长等于CA 的扇形CEF 绕点C 旋转，且直线CE ，CF 分别与直线AB 交于点M ，N ． （Ⅰ）当扇形CEF 绕点C 在ACB ∠的内部旋转时，如图①，求证：222BN AM MN +=； 思路点拨：考虑222BN AM MN +=符合勾股定理的形式，需转化为在直角三角形中解决．可将△ACM 沿直线CE 对折，得△DCM ，连DN ，只需证BN DN =，︒=∠90MDN 就可以了．请你完成证明过程：（Ⅱ）当扇形CEF 绕点C 旋转至图②的位置时，关系式222BN AM MN +=是否仍然成立？若成立，请证明；若不成立，请说明理由．解题过程：（Ⅰ）证明 将△ACM 沿直线CE 对折，得△DCM ，连DN ， 则△DCM ≌△ACM ． ···················································································· 1分有CA CD =，AM DM =，ACM DCM ∠=∠，A CDM ∠=∠． 又由CB CA =，得 CB CD =． ···································· 2分 由DCM DCM ECF DCN ∠-︒=∠-∠=∠45，ACM ECF ACB BCN ∠-∠-∠=∠ ACM ACM ∠-︒=∠-︒-︒=454590，得BCN DCN ∠=∠． ································································································· 3分 又CN CN =，CA BEFDMN∴△CDN ≌△CBN ． ······················································································· 4分 有BN DN =，B CDN ∠=∠．∴︒=∠+∠=∠+∠=∠90B A CDN CDM MDN ． ·························································· 5分 ∴在Rt △MDN 中，由勾股定理，得222DN DM MN +=．即222BN AM MN +=． ···················································· 6分 （Ⅱ）关系式222BN AM MN +=仍然成立． ····················································· 7分 证明 将△ACM 沿直线CE 对折，得△GCM ，连GN ， 则△GCM ≌△ACM ． ················································ 8分 有CA CG =，AM GM =，ACM GCM ∠=∠，CAM CGM ∠=∠．又由CB CA =，得 CB CG =．由︒+∠=∠+∠=∠45GCM ECF GCM GCN ，ACM ACM ECF ACN ACB BCN ∠+︒=∠-∠-︒=∠-∠=∠45)(90．得BCN GCN ∠=∠． ····························································································· 9分 又CN CN =，∴△CGN ≌△CBN ．有BN GN =， 45=∠=∠B CGN ，︒=∠-︒=∠=∠135180CAB CAM CGM ， ∴ 9045135=-=∠-∠=∠CGN CGM MGN ． ∴在Rt △MGN 中，由勾股定理，得222GN GM MN +=．即222BN AM MN +=． ····················································· 10分25．（2009天津市10分）已知一个直角三角形纸片OAB ，其中9024AOB OA OB ∠===°，，．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB 交于点C ，与边AB 交于点D 。

初中数学几何三大变换（平移、旋转、轴对称）易错题汇总（含解析）典型易错题1（易错指数★★）下列图形中，对称轴的条数最少的图形是（）.【答案解析】A 、四条．B 、三条．C 、四条．D 、四条．故选：B ．典型易错题2（易错指数★★）下面几何图形中，一定是轴对称图形的有 .【答案解析】圆弧、角、等腰梯形都是轴对称图形.典型易错题3（易错指数★★★★）如图所示，在直角坐标系中放置一个边长为1的正方形，将正方形沿轴的正方向无滑动的在轴上滚动，当点离开原点后第一次落在轴上时，点运动的路径线与轴围成的面积为( ).【答案解析】典型易错题4（易错指数★★★★）【答案解析】先将 DABC 绕着 B?C 的中点旋转 180°，再将所得的三角形绕着 B?C? 的中点旋转180°，即可得到△ A?B?C?；先将 DABC 沿着 B?C 的垂直平分线翻折，再将所得的三角形沿着 B?C? 的垂直平分线翻折，即可得到△ A?B?C?；故选：D.典型易错题5（易错指数★★）答案解析】A ．等腰三角形底边上的高所在的直线是它的对称轴，正确；B ．线段和角都是轴对称图形，正确；C ．连接轴对称图形的对应点的线段必被对称轴垂直平分，正确；D ． DABC @ DDEF ，则 DABC 与 DDEF 不一定关于某条直线对称，错误；故选：D ．典型易错题6（易错指数★★★★）图中序号（1）（2）（3）（4）对应的四个三角形，都是这个图形进行了一次变换之后得到的，其中是通过轴对称得到的是A．（1） B．（2） C．（3） D．（4）【答案解析】Q轴对称是沿着某条直线翻转得到新图形， \通过轴对称得到的是（1）．故选：A典型易错题7（易错指数★★★★）【答案解析】典型易错题8（易错指数★★★★）【答案解析】。

中考数学压轴题分类解析汇编几何三大变换相关问题(含答案)汇总2022年全国数学中考真题,解析精辟专题7：几何三大变换相关问题.1. （2022年北京市7分）在△ABC中，BA=BC，BAC ，M是AC 的中点，P是线段BM上的动点，将线段PA绕点P顺时针旋转2 得到线段PQ。

（1）若且点P与点M重合（如图1），线段CQ的延长线交射线BM于点D，请补全图形，并写出∠CDB的度数；（2）在图2中，点P不与点B，M重合，线段CQ的延长线与射线BM交于点D，猜想∠CDB的大小（用含的代数式表示），并加以证明；（3）对于适当大小的，当点P在线段BM上运动到某一位置（不与点B，M重合）时，能使得线段CQ的延长线与射线BM交于点D，且PQ=QD，请直接写出的范围。

解：（1）补全图形如下：∠CDB=30°。

（2）作线段CQ的延长线交射线BM于点D，连接PC，AD，∵AB=BC，M是AC的中点，∴BM⊥AC。

∴AD=CD，AP=PC，PD=PD。

在△APD与△CPD中，∵AD=CD，PD=PD，PA=PC∴△APD≌△CPD（SSS）。

∴AP=PC，∠ADB=∠CDB，∠PAD=∠PCD。

又∵PQ=PA，∴PQ=PC，∠ADC=2∠CDB，∠PQC=∠PCD=∠PAD。

∴∠PAD+∠PQD=∠PQC+∠PQD=180°。

∴∠APQ+∠ADC=360°－（∠PAD+∠PQD）=180°。

∴∠ADC=180°－∠APQ=180°－2α，即2∠CDB=180°－2α。

汇总2022年全国数学中考真题,解析精辟∴∠CDB=90°－α。

（3）45°＜α＜60°。

旋转的性质，等边三角形的判定和性质，三角形内角和定理，全等三角形的判定和性质，等腰三角形的判定和性质，。

（1）利用图形旋转的性质以及等边三角形的判定得出△CMQ是等边三角形，即可得出答案：∵BA=BC，∠BAC=60°，M是AC的中点，∴BM⊥AC，AM=AC。

三大变换之--旋转作图（二）知识梳理1、中心对称:把一个图形绕着某个定点旋转180°，如果它能和另一个图形重合，那么这两个图形关于这个定点对称或中心对称。

这个定点叫做对称中心，两个图形中对应点叫做关于对称中心的对称点。

2、中心对称的性质：（1）对应点的连线都经过对称中心，并且被对称中心平分，即对称中心是两个对称点所连线段的中点。

（2）对应线段平行或共线。

教学重、难点作业完成情况典题探究1．如图，在直角坐标平面内，已知点A的坐标（﹣5，0），（1）图中B点的坐标是；（2）点B关于原点对称的点C的坐标是；点A关于y轴对称的点D的坐标是；（3）△ABC的面积是；（4）在直角坐标平面上找一点E，能满足S△ADE=S△ABC的点E有个；（5）在y轴上找一点F，使S△ADF=S△ABC，那么点F的所有可能位置是；（用坐标表示，并在图中画出）2．如图，在直角坐标系中，矩形纸片ABCD的点B坐标为（9，3），若把图形按要求折叠，使B、D两点重合，折痕为EF．（1）△DEF是否为等腰三角形？（不要说明理由）（2）图形中是否存在成中心对称的两个图形？如果存在请说明理由；如果不存在，也请说明理由．（图中实线、虚线一样看待）（3）求折痕EF的长及所在直线的解析式．3．我们知道，在平面内，如果一个图形绕着一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转的这个角称为这个图形的一个旋转角．例如，正方形绕着它的对角线的交点旋转90°后能与自身重合所以正方形是旋转对称图形，它有一个旋转角为90°．（1）判断下列说法是否正确（在相应横线里填上“对”或“错”）①正五边形是旋转对称图形，它有一个旋转角为144°．②长方形是旋转对称图形，它有一个旋转角为180°．（2）填空：下列图形中时旋转对称图形，且有一个旋转角为120°的是．（写出所有正确结论的序号）①正三角形②正方形③正六边形④正八边形（3）写出两个多边形，它们都是旋转对称图形，都有一个旋转角为72°，其中一个是轴对称图形，但不是中心对称图形；另一个既是轴对称图形，又是中心对称图形．4．某校园内有一人行道上镶嵌着如图①所示的水泥方砖，砖面上的小沟槽（如图②）EA、HD、GC、FB分别是方砖TPQR四边的中垂线，四边形HEFG是正方形，现请你根据上述信息解答下列问题．（1）方砖TPQR面上的图案_________A．是轴对称图形，但不是中心对称图形B．是中心对称图形，但不是轴对称图形C．是轴对称图形，又是中心对称图形D．既不是轴对称图形，也不是中心对称图形（2）若要使方砖TPQR的面积是正方形HEFG面积的9倍，求当方砖边长为24厘米时，小沟槽EA的长是多少．演练方阵A档（巩固专练）1．设点M（1，2）关于原点的对称点为M′，则M′的坐标为_________ ．2．在平面直角坐标系中，O是原点，A是x轴上的点，将射线OA绕点O旋转，使点A与双曲线y=上的点B重合，若点B的纵坐标是1，则点A的横坐标是_________ ．3．如图，将一朵小花放置在平面直角坐标系第一象限内，先将它向下平移4个单位后，再将它绕原点O 旋转180°，则小花顶点A的对应点A′的坐标为_________ ．4．在平面直角坐标系中，点P（5，﹣3）关于原点对称的点的坐标是_________ ．5．如图，在平面直角坐标系中，将△ABC绕点P旋转180°得到△DEF，则点P的坐标为_________ ．6．函数的图象如图所示，关于该函数，下列结论正确的是_________ （填序号）．①函数图象是轴对称图形；②函数图象是中心对称图形；③当x＞0时，函数有最小值；④点（1，4）在函数图象上；⑤当x＜1或x＞3时，y＞4．7．永州市新田县的龙家大院至今已有930多年历史，因该村拥有保存完好的“三堂九井二十四巷四十八栋”明清建筑，而申报为中国历史文化名村．如图是龙家大院的一个窗花图案，它具有很好的对称美，这个图案是由：①正六边形；②正三角形；③等腰梯形；④直角梯形等几何图形构成，在这四种几何图形中既是轴对称图形又是中心对称图形的是_________ （只填序号）．8．如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称或中心对称变换，若原来点A坐标是（a，b），则经过第2011次变换后所得的A点坐标是_________ ．9．在中国的园林建筑中，很多建筑图形具有对称性．如图是一个破损花窗的图形，请把它补画成中心对称图形．_________ ．10．在平面直角坐标系xOy中，已知A（﹣1，5），B（4，2），C（﹣1，0）三点．（1）点A关于原点O的对称点A′的坐标为_________ ，点B关于x轴的对称点B′的坐标为_________ ，点C关于y轴的对称点C的坐标为_________ ．（2）求（1）中的△A′B′C′的面积．B档（提升精练）11．如图，△ABO与△CDO关于O点中心对称，点E、F在线段AC上，且AF=CE．求证：FD=BE．12．如图，在平面直角坐标系中，O为坐标原点，每个小方格的边长为1个单位长度．正方形ABCD顶点都在格点上，其中，点A的坐标为（1，1）．（1）若将正方形ABCD绕点A顺时针方向旋转90°，点B到达点B1，点C到达点C1，点D到达点D1，求点B1、C1、D1的坐标．（2）若线段AC1的长度与点D1的横坐标的差恰好是一元二次方程x2+ax+1=0的一个根，求a的值．13．如图，在直角坐标系中，Rt△AOB的两条直角边OA，OB分别在x轴的负半轴，y轴的负半轴上，且OA=2，OB=1．将Rt△AOB绕点O按顺时针方向旋转90°，再把所得的像沿x轴正方向平移1个单位，得△CDO．（1）写出点A，C的坐标；（2）求点A和点C之间的距离．14．如图，图形中每一小格正方形的边长为1，已知△ABC．（1）AC的长等于_________ ；（2）先将△ABC向右平移2个单位得到△A′B′C′，则A点的对应点A′的坐标是_________ ；（3）再将△ABC绕点C按逆时针方向旋转90°后得到△A1B1C1，则A点对应点A1的坐标是_________ ．15．如图，平面直角坐标系中，△ABC为等边三角形，其中点A、B、C的坐标分别为（﹣3，﹣1）、（﹣3，﹣3）、（﹣3+，﹣2）．现以y轴为对称轴作△ABC的对称图形，得△A1B1C1，再以x轴为对称轴作△A1B1C1的对称图形，得△A2B2C2．（1）直接写出点C1、C2的坐标；（2）能否通过一次旋转将△ABC旋转到△A2B2C2的位置？你若认为能，请作出肯定的回答，并直接写出所旋转的度数；你若认为不能，请作出否定的回答（不必说明理由）；（3）设当△ABC的位置发生变化时，△A2B2C2、△A1B1C1与△ABC之间的对称关系始终保持不变．①当△ABC向上平移多少个单位时，△A1B1C1与△A2B2C2完全重合并直接写出此时点C的坐标；②将△ABC绕点A顺时针旋转α°（0≤α≤180），使△A1B1C1与△A2B2C2完全重合，此时α的值为多少点C 的坐标又是什么？16．如图①，在△AOB中，∠AOB=90°，OA=3，OB=4．将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转，分别得到图②、图③、…，则旋转得到的图⑩的直角顶点的坐标为_________ ．17．课外兴趣小组活动时，老师提出了如下问题：（1）如图1，在△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE=AD，再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE ＜8，则1＜AD＜4．[感悟]解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．（2）解决问题：受到（1）的启发，请你证明下列命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．求证：BE+CF＞EF，若∠A=90°，探索线段BE、CF、EF之间的等量关系，并加以证明．18．在平面直角坐标系中，O为坐标原点．（1）已知点A（3，1），连接OA，作如下探究：探究一：平移线段OA，使点O落在点B．设点A落在点C，若点B的坐标为（1，2），请在图1中作出BC，点C的坐标是_________ ；探究二：将线段OA绕点O逆时针旋转90度，设点A落在点D．则点D的坐标是_________ ；（2）已知四点O（0，0），A （a，b），C，B（c，d），顺次连接O，A，C，B．①若所得到的四边形为平行四边形，则点C的坐标是_________ ；②若所得到的四边形是正方形，请直接写出a，b，c，d应满足的关系式．19．如图，将边长为1的等边△OAP按图示方式，沿x轴正方向连续翻转2007次，点P依次落在点P1，P2，P3，P4，…，P2007的位置．试写出P1，P3，P100，P2007的坐标．20．如图，在平面直角坐标系xOy中，把矩形COAB绕点C顺时针旋转α度的角，得到矩形CFED，设FC与AB交于点H，且A（0，4）、C（8，0）．（1）当α=60°时，△CBD的形状是_________ ．（2）当AH=HC时，求直线FC的解析式．成长足迹课后检测三大变换之--旋转作图（二）参考答案典题探究例1解：（1）根据图示知，点B的坐标为（﹣3，4）；⊅（2）由（1）知，B（﹣3，4），∴点B关于原点对称的点C的坐标是（3，﹣4）；∵点A的坐标（﹣5，0），∴点A关于y轴对称的点D的坐标是（5，0）；（3）由勾股定理求得，AB=2，AC=4，BC=10，∴AB2+AC2=BC2，∴AB⊥AC，∴S△ABC=AB•AC=×2×4=20；（4）∵S△ADE=S△ABC，∴△ADE与△ABC的一条边的边长，和这条边上的高都相等，∵在该表格中，符合条件的点E由无数个；∴能满足S△ADE=S△ABC的点E有无数个；（5）∵AD=10，∴S△ADF=AD•OF=20，∴OF=4，∴点F的所有可能位置是（0，4）或（0，﹣4）；故答案是：（1）（﹣3，4）；（2）（3，﹣4）；（5，0）；（3）20；（4）无数．（每格1分）（5）（0，4）或（0，﹣4）．（2分）例2 解：（1）△DEF为等腰三角形．（2分）（2）连接BD交EF于M，∵B、D关于EF对称，∴BM=DM，EM⊥BD，易证EM=FM，∴E、F关于M成中心对称，B、D关于M成中心对称，又M为BD的中点，∴A、C关于M成中心对称，∴四边形AEFD与四边形CFEB关于M成中心对称．（6分）（3）设BE=OE=x，则AE=9﹣x，在直角三角形AED中，（9﹣x）2+32=x2，解得x=5，∴E（4，3），F（5，0），EF=，（9分）直线EF的解析式为y=﹣3x+15．（12分）例3解：（1）①=72°，∴正五边形是旋转对称图形，它有一个旋转角为144°，说法正确；②=90°，∴长方形是旋转对称图形，它有一个旋转角为180°，说法正确；（2）①正三角形的最小旋转角为=120°；②正方形的最小旋转角为=90°；③正六边形的最小旋转角为=60°；④正八边形的最小旋转角为=45°；则有一个旋转角为120°的是①③．（3）=72°，则正五边形是满足有一个旋转角为72°，是轴对称图形，但不是中心对称图形；正十边形有一个旋转角为72°，既是轴对称图形，又是中心对称图形．例4解：（1）通过图象观察和题意EA、HD、GC、FB分别是方砖TPQR四边的中垂线，且四边形HEFG是正方形就可以得出方砖TPQR面上的图案是轴对称图形，又是中心对称图形．（2）设小沟槽EA的长是xcm，则EG的长度为24﹣2x．∵四边形HEFG是正方形，∴HE=HG，∠GHE=90°，∴HE2+HG2=EG2．∴2HE2=（24﹣2x）2，∴HE2=2x2﹣48x+288．∵，∴，解得：x1=12+4（舍去），x2=12﹣4．∴EA=12﹣4．故答案为：C．演练方阵A档（巩固专练）1、解：点M（1，2）关于原点的对称点M′的坐标为（﹣1，﹣2），故答案为：（﹣1，﹣2）．2、解：如图所示：∵点A与双曲线y=上的点B重合，点B的纵坐标是1，∴点B的横坐标是，∴OB==2，∵A点可能在x轴的正半轴也可能在负半轴，∴A点坐标为：（2，0），（﹣2，0）．故答案为：2或﹣2．3、解：由平面直角坐标系可得A（3，1），向下平移4个单位后可得对应点的坐标为（3，﹣3），再将它绕原点O旋转180°可得对应点坐标为A′（﹣3，3），故答案为：（﹣3，3）．4、解：点P（5，﹣3）关于原点对称的点的坐标是（﹣5，3）．故答案为：（﹣5，3）．5、解：连接AD，∵将△ABC绕点P旋转180°得到△DEF，∴点A旋转后与点D重合，∵由题意可知A（0， 1），D（﹣2，﹣3）∴对应点到旋转中心的距离相等，∴线段AD的中点坐标即为点P的坐标，∴点P的坐标为（，），即P（﹣1，﹣1）．故答案为：（﹣1，﹣1）．6、解：①②当x变为﹣x时，y变为﹣y，可见，（x，y）对应点为（﹣x，﹣y），可见，函数图象是中心对称图形，不是轴对称图形，故②正确，①错误；③当x＞0时，函数图象有最低点，故函数有最小值，故本选项正确；④将点（1，4）代入解析式，等式成立，点（1，4）在函数图象上，故本选项正确：⑤当x=1和x=3时，y=4，可见，0＜x＜1或x＞3时，y＞4，故本选项错误；故答案为②③④．7、解：∵①此图形是中心对称图形，也是轴对称图形，故此选项正确；②此图形不是中心对称图形，但是轴对称图形，故此选项错误；③此图形不是中心对称图形，但是轴对称图形，故此选项错误；④此图形不是中心对称图形，也不是轴对称图形，故此选项错误．故答案为：①．8、解：∵2011÷3=670…1，第一次变换是各对应点关于x轴对称，点A坐标是（a，b），∴经过第2011次变换后所得的A点坐标是（a，﹣b）．故答案为（a，﹣b）．9、解：10、解：（1）∵A（﹣1，5），∴点A关于原点O的对称点A′的坐标为（1，﹣5）．∵B（4， 2），∴点B关于x轴的对称点B′的坐标为（4，﹣2）．∵C（﹣1，0），∴点C关于y轴的对称点C′的坐标为（1，0）．故答案分别是：（1，﹣5），（4，﹣2），（1，0）．（2）如图，∵A′（1，﹣5），B′（4，﹣2），C′（1，0）．∴A′C′=|﹣5﹣0|=5，B′D=|4﹣1|=3，∴S△A′B′C′=A′C′•B′D=×5×3=7.5，即（1）中的△A′B′C′的面积是7.5．11、证明：∵△ABO与△CDO关于O点中心对称，∴OB=OD，OA=OC，∵AF=CE，∴OF=OE，∵在△DOF和△BOE中∴△DOF≌△BOE（SAS），∴FD=BE．12、解：（1）如图，B1、C1、D1的坐标分别为：B1（2，﹣1），C1（4，0），D1（3，2）；（2）根据勾股定理，AC1==，∴线段AC1的长度与点D1的横坐标的差是﹣3，∴（﹣3）2+（﹣3）a+1=0，整理，10﹣6+9+（﹣3）a+1=0，∴（﹣3）a=﹣20+6，解得a=﹣2．故答案为：（1）B1（2，﹣1），C1（4，0），D1（3，2）；（2）a=﹣2．13、解：（1）点A的坐标是（﹣2，0），点C的坐标是（1，2）．（2）连接AC，在Rt△ACD中，AD=OA+OD=3，CD=2，∴AC2=CD2+AD2=22+32=13，∴AC=．14、解：（1）根据图形，可得出A的坐标为（﹣1，2），C的坐标为（0，﹣1），故AC的长等于=；（2）根据图形，可得出A的坐标为（﹣1，2），B的坐标为（3，1），C的坐标为（0，﹣1），将△ABC向右平移2个单位得到△A'B'C'，则A点的对应点A'的坐标是（1，2）；（3）根据旋转的规律，把△OAB的绕点O按逆时针方向旋转90°，就是把它上面的各个点按逆时针方向旋转90°，可得A1的坐标为（﹣3，﹣2）．15、解：（1）点C1、C2的坐标分别为（3﹣，﹣2）、（3﹣，2）．（2）能通过一次旋转将△ABC旋转到△A2B2C2的位置，所旋转的度数为180°；（3）①当△ABC向上平移2个单位时，△A1B1C1与△A2B2C2完全重合，此时点C的坐标为（﹣3+，0）（如图1）；②当α=180时，△A1B1C1与△A2B2C2完全重合，此时点C的坐标为（﹣3﹣，0）（如图2）．16、解：∵∠AOB=90°，OA=3，OB=4，∴AB===5，根据图形，每3个图形为一个循环组，3+5+4=12，所以，图⑨的直角顶点在x轴上，横坐标为12×3=36，所以，图⑨的顶点坐标为（36，0），又∵图⑩的直角顶点与图⑨的直角顶点重合，∴图⑩的直角顶点的坐标为（36，0）．故答案为：（36，0）．17、解：（1）延长FD到G，使得DG=DF，连接BG、EG．（或把△CFD绕点D逆时针旋转180°得到△BGD），∴CF=BG=DF=DG，∵DE⊥DF，∴EF=EG．在△BEG中，BE+BG＞EG，即BE+CF＞EF．（2）若∠A=90°，则∠EBC+∠FCB=90°，由（1）知∠FCD=∠DBG，EF=EG，∴∠EBC+∠DBG=90°，即∠EBG=90°，∴在Rt△EBG中，BE2+BG2=EG2，∴BE2+CF2=EF2．18、解：（1）探究一：∵点A（3，1），连接OA，平移线段OA，使点O落在点B．设点A落在点C，若点B的坐标为（1，2），则C的坐标为（4，3），如图1所示：探究二：∵将线段OA绕点O逆时针旋转90度，设点A落在点D．则点D的坐标是（﹣1，3），如图2所示；（2）∵四点O（0，0），A （a，b），C，B（c，d），顺次连接O，A，C，B．①若所得到的四边形为平行四边形，那么OA∥CB，∴OA平移到OB的位置，点C的坐标为（a+c，b+d）；②若所得到的四边形是正方形，那么根据正方形的性质可以得到a=d且b=﹣c或b=c且a=﹣d．19、解：P1（1，0）；∵等边△OAP的高为边长的倍，∴P3（，）；∵从P1开始，根据图形的旋转可得每三次翻转后和原来的状态一样，∴100=3×33+1，∴P100的纵坐标为0，横坐标为100，∴P100（100，0）；∵2007=3×669，∴P2007的纵坐标为，横坐标=2005+1.5=2006.5．∴P2007（2006.5，）．20、解：（1）∵矩形COAB绕点C顺时针旋转60度的角，得到矩形CFED，∴∠BCD=60°，CB=CD，∴△CBD为等边三角形；（2）∵A（0，4）、C（8，0），∴OA=BC=4，OC=AB=8，设AH=HC=x，则BH=8﹣x，CB=4，在Rt△CBH中，∵CH2=BH2+BC2，∴x2=（8﹣x）2+42，解得x=5，∴H点的坐标为（5，4），设直线FC的解析式为y=kx+b，把C（8，0）、H（5，4）代入得，解得，∴直线FC 的解析式为．21。

中考数学重难考点突破—几何变换题型分类解析考点1 轴对称与轴对称图形考点2 中心对称与中心对称图形► 类型之一 图形的折叠与轴对称 命题角度：图形的折叠与轴对称的关系．例2如图，在△ABC 中，∠C ＝90°，将△ABC 沿直线MN 翻折后，顶点C 恰好落在AB 边上的点D 处，已知MN ∥AB ，MC ＝6，NC ＝23，则四边形MABN 的面积是( C )A ．6 3B ．12 3C ．18 3D ．24 3[解析] 连接CD ，交MN 于E ，∵将△ABC 沿直线MN 翻折后，顶点C 恰好落在AB 边上的点D 处， ∴MN ⊥CD ，且CE ＝DE ，∴CD ＝2CE. ∵MN ∥AB ，∴△CMN ∽△CAB ， ∴S △CMN S △CAB ＝⎝ ⎛⎭⎪⎫CE CD 2＝14. ∵在△CMN 中，∠C ＝90°，MC ＝6，NC ＝23， ∴S △CMN ＝12CM·CN ＝12×6×23＝63， ∴S △CAB ＝4S △CMN ＝4×63＝24 3.∴S＝S△CAB－S△CMN＝243－63＝18 3.四边形MABN【方法技巧】图形折叠的本质是轴对称，折叠前后的两个部分全等．►类型之二轴对称图形与中心对称图形的概念命题角度：1. 轴对称的定义，轴对称图形的判断；2. 中心对称的定义，中心对称图形的判断．例1在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形，该小正方形的序号是(B)A．①B．②C．③D．④[解析] 如图，把标有序号②的白色小正方形涂黑，就可以使图中的黑色部分构成一个中心对称图形．【方法技巧】(1)把所要判断的图形沿一条直线折叠后，直线两旁的部分能够互相重合的图形是轴对称图形；(2)把所要判断的图形绕着某个点旋转180°后能与自身重合的图形是中心对称图形．►类型之三轴对称与中心对称有关的作图问题命题角度：1. 利用轴对称的性质作图；2. 利用中心对称的性质作图；3. 利用轴对称或中心对称的性质设计图案．例3 如图，⊙P的圆心P(－3，2)，半径为3，直线MN过点M(5，0)且平行于y轴，点N 在点M的上方．(1)在图中作出⊙P关于y轴对称的⊙P′，根据作图直接写出⊙P′与直线MN的位置关系；(2)若点N在(1)中的⊙P′上，求PN的长．[解析] (1)根据关于y轴对称的点的横坐标互为相反数，纵坐标相等找出点P′的位置，然后以3为半径画圆即可；再根据直线与圆的位置关系解答；(2)设直线PP′与MN相交于点Q，在Rt△QP′N中，利用勾股定理求出QN的长度，在Rt△QPN 中，利用勾股定理列式计算即可求出PN的长度．解：(1)作图如下．⊙P′与直线MN相交．(2)连接PP′并延长交MN于点Q，连接PN、P′N，由题意可知：在Rt△P′QN中，P′Q＝2，P′N＝3，由勾股定理可求出QN＝ 5.在Rt△PQN中，PQ＝3＋5＝8，QN＝5，由勾股定理可求出PN＝82＋（5）2＝69. 【方法技巧】此类作图问题的关键是根据轴对称与中心对称坐标特征求出对称点的坐标．【“输气管线路最短”问题的拓展创新】如图，要在燃气管道l上修建一个泵站，分别向A、B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？你可以在l上找几个点试一试，能发现什么规律？[解析]把管道l近似地看成一条直线，问题就是要在l上找一点C，使AC与CB的和最小．解：做A点关于直线l的对称点A'，连接A'B，与直线l的交点即是所求的的C点。