矩阵分解之Givens变换与Householder变换(PPT文档)

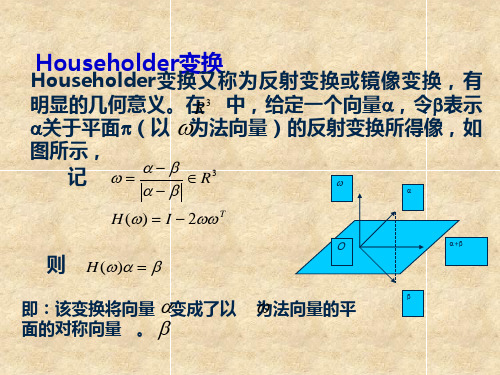
§2 Householder 变换镜像变换(Householder 变换)是把矩阵进行正交三角分解的有效方法。

一、Householder 变换及其性质考虑一向量x 分解为两个正交的分向量。

如下图所示，假定除了向量x 外还有另一已知向量v .现在,先将x 投影到v ,产生投影x P v .然后将x 投影到与v 垂直的超平面⊥v 上,产生另外一个投影x P v ⊥.投影x P v ⊥称为向量x 到向量v 的正交投影.于是,这两个投影就构成了以x 为对角线的矩形的两个边.根据向量加法规则, x 可以表示这两个投影的向量之和(合成向量),即x P x P x v v ⊥+= (1)向量x 的这一分解形式称为正交分解.在上述二维的例子中, ⊥v 是一直线,而x P v ⊥为一向量.在更高维的情况下,⊥v 变成一多维目标(超平面),而x P v ⊥仍然为包含在⊥v 内部的一向量.正交分解式(1)中的矩阵'),(1v v v v P v -= (2) '),(1v v v v I P I P v v -⊥-=-= (3)分别称为向量v 的投影矩阵和正交投影矩阵.如果我们不是像图3.1那样构造两个投影x P v 与x P v ⊥之和,而是构造二者之差,就会得到一个新向量x H v 如图3.2所示.图中,)1,2(),4,2(==v x ,因此)512,56(),58,516(-=--=-⊥x P x P v v ,于是, ).54,522(-=-=⊥x P x P x H v v v 矩阵v v I v v vv I v v v v I P P H v v v /,'2),/('2'),(21=-=-=-=-=-⊥ϖϖϖ (4)称为向量v 的Householder(变换)矩阵,而向量),(),(2),/('2)(v v x v vx v v x vv x x P x P x P P x H v v v v v -=-=-=-=⊥⊥ (5) 称为向量x 相对于向量⊥v 的Householder 镜像变换.这样设计的算法即节省了n n ⨯个存储单元,而且同样达到求解求逆的目的,这种改进的G-J 消去变换也称为紧凑或原地求逆变换.定义6.1 设0,)(≠=⨯ij m n ij a a A ,定义一个新的矩阵m n ij b ⨯=)(B ,其中j l i k a a a a b ij kj il kl kl ≠≠-=, ./ )1( i k a a b ij kj kj ≠-= ./ )2( j l a a b ij il il ≠= ./ )3(/1 )4(ij ij a b =按这个规则A 变成n ij ij ij I G A G A T -+=定义6.2 称)(A T ij 是对称矩阵A 施行以),(j i 为主元的消去变换，如果： ① 对A 作J G -消去变换，使其第j 列j a 变成i e ，即i j ij e a G =； ② 记i i ij g e G =，用i g 替代i ij A G 的第j 列i e . 由等价的定义，当A 为n 阶方阵时易得出n ij ij ij I G A G A T -+=消去变换ij T 的基本性质 性质1 反身性：A A T T ij ij =；设),(),()2()1()2()1()1(ij ij ij ij a A T A a A T A ≡=≡=，由（6.3）式可直接验证：m),1,2,j n;,1,2,(i )2( ===ij ij a a性质2 可交换性：当l j k i ≠≠,时，A T T A T T ij kl kl ij =； 由（6.3）式可直接验证两边元素对应相等.性质3 若)(为对称阵A A A ='，记)(αβb A T B kk ≡=，则⎪⎩⎪⎨⎧≠≠=≠-=k k b b kb b k k βαββααβββ,, , 对对称阵A 施行),(k k 消去变换后，得矩阵B .B 除第k 行k 列相差一个符号后，其余仍保持对称性，也称B 为绝对对称阵.性质4 行列置换与消去变换的次序变化关系：设A 为m n ⨯阵，ip P 为i 行和p 行交换的行置换阵，jq Q 为j 列和q 列交换的列置换阵，则①jq iq jq ij Q A T AQ T )()(=； ②)()(A T P A P T pj ip ip ij =； ③jq pq ip jq ip ij Q A T P AQ P T )()(=.证明 ①和②由（6.3）式及行列置换的定义可直接验证.下面利用①和②来证明③：jq pq ip jq pj ip jq ip ij jq ip ij Q A T P AQ T P AQ P T AQ P T )()]([)]([)(===性质5 设⎪⎪⎭⎫⎝⎛=22211211 A A A A A ，11A 为r 阶可逆矩阵，则⎪⎪⎭⎫ ⎝⎛--=------1211121122111211211111111 A A A A A A A A A A T T T r r . 证明 记),,2,1(,)1()()0(r k A G A A A k k k ===-，利用J G -消去变换的定义知：⎪⎪⎭⎫⎝⎛====--*22*12)0(121)1()( 0 A A I AG G G G AG Ar r r r r r . 记n r r r I G G G G J 121 -=.因k G 是由)1(-k A 的第k 列定义的J G -消去变换阵，即).,,,,,,(111n k k k k e e g e e G +-=对r k ,,2,1 =，k G 的第r 列以后各列均为单位向量，故有). (112111阶方阵为r J I J J J r n r ⎪⎪⎭⎫ ⎝⎛=- 由消去变换的定义 6.2，知消去变换等价于先做J G -变换然后进行替换.故有⎪⎪⎭⎫⎝⎛=-*2221*1211121 A J A J A T T T T r r . 利用0 0*22*12222112112111)0()(⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==-A A I A A A A I J J A J A r r n r r (6.4) 可得⎩⎨⎧=+=,0,2111211111A A J I A J r ,即⎪⎩⎪⎨⎧-==--.,111212111111A A J A J 把2111,J J 代入(6.4)式又得 ⎪⎩⎪⎨⎧-=+===--.,121112122221221*22121111211*12A A A A A A J A A A A J A 所以.A A A 121-1121221-112112-111-111121⎪⎪⎭⎫⎝⎛--=-A A A A A A A T T T T r r [证毕] 6.2 消去变换的应用(一)计算可逆矩阵的逆设A 为n 阶可逆矩阵.当A 为正定阵时,因A 的各阶主子式非零,故对A 依次施行消去变换时主元均不为零.于是有:A T T T T A n n 1211 --=,其中),,2,1(n k T k =是施行以),(k k 为主元的消去变换.对于一般可逆阵A ,有0≠A ,对A 依次以对角元为主元做消去变换时,当遇到某个0)1(=-k kka 时,一般先对矩阵作行列置换,使主元不为0,然后接着做消去变换,求出1-A .例6.2 求⎪⎪⎪⎭⎫⎝⎛=1 2 00 123 00A 的逆矩阵.解 因012≠=A ,A 为可逆矩阵.但011=a ,求1-A 时, 先进行行列置换后接着做消去变换,求出1-A .定理1（分块矩阵的正则逆） 设⎪⎭⎫⎝⎛=22211211A A A A A 可逆. 若011≠A , 则⎪⎪⎭⎫ ⎝⎛--+=⎪⎭⎫ ⎝⎛=-----------11.221112111.2211.22121111112111.22121111111222112111A A A A A A A A A A A A A A A A AA （1） 若022≠A , 则⎪⎪⎭⎫ ⎝⎛+--=----------1221212.112112212212.11211221221212.1112.111A A A A A A A A A A A A A A （2） 其中.,2112212112.111211121221.22A A A A A A A A A A ---=-= 证明 若011≠A , 则有(分块矩阵的初等变换)⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛---1.22111211122211211111210000A A I A A I A A A A I A A I （3） 此式证明了1.22A 的可逆性。

householder变换和奇异值分解标题：Householder变换与奇异值分解：线性代数中的两个重要概念引言：在线性代数中，Householder变换和奇异值分解是两个非常重要的概念。

它们在矩阵计算、数据处理以及信号处理等领域有着广泛的应用。

本文将以人类的视角，生动地介绍这两个概念，让读者感受到它们的实际应用和重要性。

1. Householder变换：矩阵的几何变换Householder变换是一种线性代数中常用的几何变换方法。

通过对矩阵进行反射操作，可以将向量投影到另一个向量上。

这个过程可以理解为在空间中对矩阵进行镜像，从而改变了矩阵的形状和性质。

例如，在计算机图形学中，我们可以利用Householder变换来实现图像的翻转、旋转和缩放等操作。

2. 奇异值分解：解析矩阵的秘密奇异值分解是一种将矩阵分解为三个矩阵乘积的方法。

这个过程可以将矩阵的结构和特征分解出来，从而更好地理解和处理矩阵的性质。

奇异值分解在数据处理、机器学习和信号处理等领域中非常常见。

例如，在数据降维中，我们可以利用奇异值分解将高维数据降低到低维空间，以减少计算量和提高算法效率。

3. Householder变换与奇异值分解的应用Householder变换和奇异值分解在实际应用中有着广泛的应用。

在图像处理中，我们可以利用Householder变换进行图像的翻转和旋转操作，从而实现图像的处理和增强。

而在数据处理和机器学习中，奇异值分解可以帮助我们降低数据维度，提取重要特征，并进行数据压缩和噪声去除等操作。

结论：Householder变换和奇异值分解作为线性代数中的两个重要概念，在实际应用中发挥着重要的作用。

它们不仅可以改变矩阵的形状和性质，还可以帮助我们更好地理解和处理数据。

通过深入学习和理解这两个概念，我们可以在各个领域中应用它们，从而提高问题的解决效率和准确性。

无论是在图像处理、数据处理还是机器学习中，Householder变换和奇异值分解都是不可或缺的工具，值得我们深入学习和探索。

§1-5 矩阵的QR 分解——一种正交变换思想：设[]nn RA ⨯∈[A]为一般非奇异方阵若[][][]R Q A =称为[A]的QR 分解其中:[Q]——正交矩阵，[R]——上三角阵[][][]I Q Q=T第5节矩阵的QR 分解法一G-S 正交化方法法二Householder 变换法三Givens 变换重点讲均可实现[A]=[Q][R]实现[A]的QR 分解的方法：重点要求掌握两种变换方法的思想：①Householder 变换②Givens 变换这是两种常用的正交相似变换！变换的目的使原矩阵简化，便于求特征解！第5节矩阵的QR 分解一、用Householder 变换实现QR 分解1、Householder 变换（简称H 变换）的定义和性质2、用H 变换将“给定向量”−→−H“指定方向”上去第5节矩阵的QR分解（进行一次最基本的H 变换）3、用H 变换将一般矩阵4、用H 正交相似变换，把一般矩阵[A]约化为上Hessenherg 阵[A]=[Q][R]下面介绍：（要通过n-1步最基本的H 变换才能实现）1、H 变换矩阵的定义和性质定义：设{}nRu ∈第5节矩阵的QR分解{}{}{}(){}{}{}{}222222,22u u u u u u u T====β[][]{}{}Tu u I P β-=称为Householder 变换矩阵！其中：（可推广到复空间）模的平方！若引入规范化向量（单位向量）：{}W {}{}{}2u u W ={}{}{}2u u W TT =第5节矩阵的QR 分解{}{}{}(){}{}()1,21212===W W W W W T{}{}1=W W T即则[][]{}{}TW W I P 2-=性质：（1）对称性：（2）正交性：[][]{}{}()[]P W W I P TTT=-=2[][][]I P P T=第5节矩阵的QR分解证：[][][]{}{}()[]{}{}()TT TW W I W W I P P 22--=[][]{}{}{}{}{}{}[]{}{}{}{}[]I W W W W I W W W W W W I I TTTTT=+-=+-=44422证毕。