正交数据处理例题(Excel)

格式：doc
大小：373.50 KB
文档页数：4

下载文档原格式

第4部分正交试验设计方案与数据处理

4.1 正交表及其用法
正交表记为 Ln（mk），m 是各因素的水平，k （列数）是因素的个数，n 是安排试验的次数（行数）。
L9（34）4因素3水平正交试验，共做9次试验，而全面试验要做 34=81 次，减少了72次。
L25（56） 6因素5水平正交试验，共做25次试验，而全面试验要做 56=15625 次，减少了15600次。
解这是4因素3水平的试验，可以选用正交表L9（34）安排出试验方案（这里有4个因素，正好将表排满），进行试验，将得出的结果列入表4-9中。
综合评分法是根据各个指标的重要性的不同，按照得出的试验结果综合分析，给每一个试验评出一个分数，作为这个试验的总指标。根据这个总指标作进一步的分析。
4.2.2 综合评分法（例4.3的解）
4.2.2 综合评分法（例4.3的解）
A1：时间，
25小时；
D1：加水量，
1：6；
B3：料中核酸含量，6.0；
C2：pH值，
6.0。
可以看出，这里分析出来的最好方案，在已经做过的9个试验中是没有的，可以按这个方案再试验一次，看能不能得出比第1号试验更好的结果，从而确定出真正最好的试验方案。
综合评分法是将多指标的问题，通过加权计算总分的方法化
4.2 多指标的分析方法
在例4.1中，试验指标只有一个，考察起来比较方便，但实际问题中，需要考察的指标往往不止一个，有时有两个、三个或更多。如何评价考察指标呢？两种方法。
4.2.1 综合平衡法通过具体的例子来加以说明。
例4.2 某陶瓷厂为了提高产品质量，要对生产的原料进行配方试验。要检验3项指标：抗压强度、落下强度和裂纹度，前两个指标越大越好，第3个指标越小越好。根据以往的经验，配方有3个重要因素：水分、粒度和碱度。它们各有3个水平，具体数据如表 4-6所示。试进行试验分析，找出最好的配方方案。

建立Excel宏快速处理正交试验设计数据

[作者简介]　陈翔(1972-),男,本科,主管技师,主要从事理化检验工作。

【实验室管理】建立Excel 宏快速处理正交试验设计数据陈翔1,梁卫玖2(11上海市徐汇区疾病预防控制中心,上海　200031;21上海市长宁区卫生检验所,上海　200051)[摘要]　目的:提高正交设计试验数据的处理速度。

方法:笔者以基于L 16(44)正交表的正交试验数据为例,利用Excel处理正交试验数据并建立了数据处理过程的宏。

结果:宏程序集合了极差分析、方差分析、趋势图绘制等正交试验数据处理的主要过程,具有快速和一次构建,反复使用的特点。

结论:针对不同的正交表可以建立不同的宏,使用这些宏能快速地处理基于相同正交表的试验数据。

[关键词]　Excel 宏;处理;正交试验设计[中图分类号]　R284 [文献标识码]　B [文章编号]　1004-8685(2009)11-2696-02 正交试验设计是理化检验工作中常用的研究和处理多因素多水平效应的科学实验方法,应用极为广泛,利用正交设计试验可以做到“多、快、好、省”,通过较少试验获得较优的试验条件组合,正交试验设计的数据处理过程较为繁琐,特别是方差分析涉及较多的计算和查表工作,利用Excel 建立宏能快速处理基于相同正交表的正交试验数据并对结果同时实现极差分析、方差分析和自动绘制因素水平趋势图,本文以基于L 16(44)正交表的石墨炉原子吸收法正交试验数据为例,介绍建立数据处理宏的过程。

1　材料与方法111　材料11111　石墨炉原子吸收测定化妆品中铬实验条件的正交试验设计数据[2]。

11112　M icr os oft OFF I CE 2003。

112　方法11211　打开宏的录制,开始宏的构建　新建一个Excel 工作簿,点击“工具”菜单中的“宏(M )”中的“录制新宏”,在出现的“录制新宏”对话框中键入宏的名称,同时可以设定宏的热键,按确定开始录制宏。

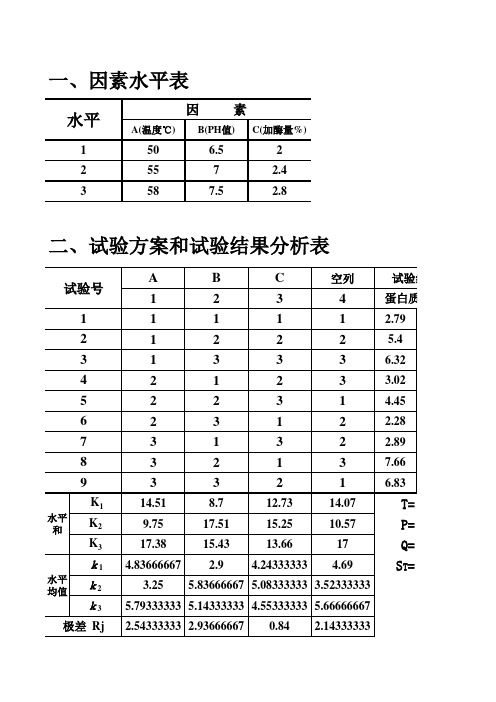
11212　建立正交试验数据处理表　在Sheet1“B1:E1”单元格中分别输入影响铬测定的实验条件因素名称,此处以A 、B 、C 、D 分别表示灰化温度、灰化时间、原子化温度、原子化时间,在单元格“A2:A17”中输入试验次数标签,在“B2:E17”中按L 16(44)正交表格式输入因素水平,在“F2:F17”中输入实验结果数据,此处为峰高值,在“A18:A21”中输入“K1～K4”,“A22:A25”中输入“K1’～K4’”,在“B18”中输入公式“S UM I F (B2:B17,1,F2:F17)”,以此类推直至在“E21”中输入“S UM I F (E2:E17,4,F2:F17)”,在“A22”中输入公式“A18/4”,拖动“A22”填充柄向下至“A25”,选中“A22:A25”,同样拖动填充柄至“E22:E25”区域,此时可得到如表1所示的正交试验数据处理表。

数据处理考试C8-6

规划求解所得的优方案为：pH值为3.5，反应时间2h，反应温度60℃；与6号实验一致，重复6、8号实验方案，确定其是否为优方案。
取决于反应pHx1(3.5~6.5)、反应时间x2(2~6h)、间的交互作用。试验指标Y为产量(g)，越低越好。水平试验。试验结果依次为1.71，1.56，1.79，
1.469 1.404 1.429
根据Significance F<0.01可知，建立的
F<0.01可知，建立的回归方程非常显著。
ificance F
Upper 95% 下限 95.0% 上限 95.0% 2.079569 0.689825 2.079569 0.121518 -0.14485 0.121518 0.072524 -0.07919 0.072524 0.013698 -0.01536 0.013698 0.005419 -0.00975 0.005419 0.002536 -0.00037 0.002536
x1 （反应温的交互作用）互作用）对
因素水平编码表：因素xj pH值x1/℃ 上水平（1） 6.5 下水平（-1） 3.5 零水平（0） 5 变化间距Δ j 1.5 选用正交表L8（27）：试验号 1 2 3 4 5 6 7 8 9 10 11反应时间x2/hFra bibliotek6 2 4 2
反应温度x3 100 60 80 20
z1 1 1 1 1 -1 -1 -1 -1 0 0 0
解的设置）
x1x2 39 39 13 13 21 21 7 7 20 20 20
x3 100 60 100 60 100 60 100 60 80 80 80
x1x3 650 390 650 390 350 210 350 210 400 400 400

K因素三水平正交试验处理Excel程序

7.99146667
4
1.99786667
F0.05( 2, 4)
总和
32.03
8
=6.94
方差分析的结果表明: 因素 A 对试验结果的影响高度显著,而因素 B 则达到了显著的水平.由于没有交互作用的影响,故因素 A 与 B 的好水平的搭配一定是最佳的.
因素的主次:
因素A(温度)为主要因素,并以水平A3(58℃)为最好;
B 则达到了显著的与 B 的好水平的搭
8℃)为最好; .5)为最好; 考虑后可任意取一 C1即可.
F0.1( 2, 4)
临界值
F0.01( 2, 2) =99.0
F0.05( 2, 2) =19.0
F0.10( 2, 2) =9.0
显著性
临界值显著性
F0.01( 2, 4) =18.0
F0.05( 2, 4) =6.94
FA
SA Se
2 79.57 , 4
FB
SB Se
2 11.37 . 4
方差来源平方和自由度均值
F值
临界值
因素A 9.90126667
2
4.95063333 2.47795982 F0.01( 2, 4)
因素B 14.1372667
2
7.06863333 3.53809063 =18.0
误差
因素B(PH值)为次要因素,并以水平B1(6.5)为最好;
因素C(加酶量:%)的作用太小,故在综合考虑后可任意取一个水平,比如,从用量最小的角度可以取水平C1即可.
最优方案:
A3 B1 C1
直观看的结果: A3 B1 C3
试验结果蛋白质: (%)
yi2

EXCEL和SPSS在回归分析、正交试验设计和判别分析中的应用

2) 将分组变量和自变量放入格子的列表里，如图所示，上面的是分组变量，选择”分类”，下面的是自变量，我们看到这里有个自变量: 舒张压和胆固醇。
3) 点击分组变量文本框，然后点击定义范围按钮，由于我们的数据是两分类的，分别为 1 和 2，设置如下图：
4) 点击统计量按钮，将 Box’s M 和 fisher 项打勾。如下图，点击继续回到判别分析主界面。点击确定，即可出现分析结果。
能力评分（1-100）；X2：病人年龄；X3：由诊断到进入研究时间（月）；X4：肿瘤类型（“0”表示鳞癌、 “1”表示小型细胞癌、 “2”表示腺癌、 “3”表示大型细胞癌）； X5：两种化疗方法（“1”表示常规、 “0”表示实验新法）； Y：病人的生存时间（“0”：表示生存时间短，即生存时间小于 200 天；“1”：表示生存时间长，即生存时间大于或等于 200 天。）根据上述分析流程对数据进行分析。
W1=8.294X1+8.055X2-72.740 W2=6.930X1+6.287X2-49.231 若有个样本的舒张压和胆固醇分别为：13.33(X1)和 5.96(X2)，带入上述两个判别式可知 W1=85.82682，W2=80.61642，W1>W2 属于分类 1。
习题：1991 年全国各省市区城镇平均消费情况如 data.xls 的 Sheet7 所示，是判别以下上海和西藏的归属类，数据见 sheet8。
系的。图 c 中的 Coefficients 为回归方程的系数，因此，回归结果为 y= — 285.0094+1.5598x1+03145x2，在使用面积不变的情况下，地产估价每增加 1 万元，房产销售的平均价格就会提高 1.5598 万元；在房地产估价不变的条件下，使用面积每增加 1 平方米，房产销售的平均价格就会提高 0.3145 元；图 a 中 Adjusted R Square 为调整复测定系数，本例中约为 0.71，它表示两个变量 x1,x2 对导致结果 y 的贡献，也就是说还有导致结果 y 的原因中有 29%是由除了 x1,x2 以外的因素造成的。习题：在黄芪提取工艺的研究中，选择了前煮时间、煎煮次数和加水量进行考察，实验数据见 data.xls 的 Sheet3，试对实验数据进行多元线性回归，对结果进行讨论。

excel正交试验设计模板 -回复

excel正交试验设计模板-回复标题：利用Excel进行正交试验设计的详细指南在科学研究、工程设计、产品质量优化等众多领域中，试验设计是一种非常重要的方法。

其中，正交试验设计因其效率高、效果好而被广泛应用。

本文将详细介绍如何使用Excel进行正交试验设计，以帮助读者更好地理解和应用这一工具。

一、理解正交试验设计正交试验设计是一种统计方法，主要用于研究多因素、多水平的试验问题。

其核心思想是通过选择最优的试验条件组合，用最少的试验次数获取最多的信息，从而达到优化试验过程、提高试验效率的目的。

二、准备试验因素和水平在进行正交试验设计之前，首先需要确定试验的因素和每个因素的水平。

例如，如果你正在研究影响产品产量的三个因素（温度、压力、原料质量），并且每个因素都有两个可选水平（高温/低温、高压/低压、优质原料/普通原料），那么你的试验因素就是温度、压力和原料质量，每个因素的水平数都是2。

三、选择正交表根据试验因素的数目和每个因素的水平数，选择合适的正交表。

正交表是一種特殊的设计表格，其行代表试验的运行次序，列代表试验的因素和水平。

在Excel中，我们可以使用“数据分析”工具中的“正交分析”功能来生成正交表。

四、填写正交表并进行试验在生成的正交表中，按照表中的顺序进行试验，并记录下每个试验的结果。

例如，在上述例子中，我们可能会在第一次试验中设定温度为高温、压力为高压、原料质量为优质，然后记录下产品的产量。

五、分析试验结果完成所有试验后，我们可以使用Excel的计算和图表功能来分析试验结果。

具体步骤如下：1. 计算每个因素在不同水平下的平均结果。

这可以通过使用Excel的“AVERAGEIF”函数实现。

2. 制作因素水平与结果的柱状图或线图，以便直观地看出各因素和水平对结果的影响。

3. 分析正交表的极差R和均方误差Sq，以确定各因素的重要性和最优水平。

一般来说，极差越大，说明该因素的影响越大；均方误差越小，说明该水平的效果越好。

常用正交表IQ

各种正交实验表说实在的，我对正交表也是一知半解，弄得不很清楚。

其数理统计原理更是摸不着火门。

好在本人收集了一系列的常用正交表，对付一般的正交试验应该没问题。

开始对正交表接触是在上《化工过程开发》那门课的时候，因为是考察科目，当时也没在意听。

现在觉得很后悔。

我搜集了很久，找了了这些常用的正交表，目的是想忠告那些与我一样上课没听的同学，好好把握来之不易上课时光。

现在大四了，成天在实验室做实验，写毕业论文，那还有闲心来看书。

我想以后工作了更是时间紧迫。

希望我搜集的这些常用正交表对你有所帮助。

至少给你一些启发。

废话不多说，转如正体。

由于博客系统自身的问题，上标和下标不能正常显示，采用字体颜色区分上标和下标。

红色为下标，蓝色为上标，请注意区分。

1、L4（23）序号 1 2 31 1 1 12 1 2 23 2 1 24 2 2 12、L8(27)序号 1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 1 1 2 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 17 2 2 1 1 2 2 18 2 2 1 2 1 1 23、L12(211)序号 1 2 3 4 5 6 7 8 9 10 111 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 23 1 1 2 2 2 1 1 1 2 2 24 1 2 1 2 2 1 2 2 1 1 25 1 2 2 1 2 2 1 2 1 2 16 1 2 2 2 1 2 2 1 2 1 17 2 1 2 2 1 1 2 2 1 2 18 2 1 2 1 2 2 2 1 1 1 29 2 1 1 2 2 2 1 2 2 1 110 2 2 2 1 1 1 1 2 2 1 211 2 2 1 2 1 2 1 1 1 2 212 2 2 1 1 2 1 2 1 2 2 14、L9（34）序号 1 2 3 41 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 15、L16（45）序号 1 2 3 4 51 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 310 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 26、L25（56）序号 1 2 3 4 5 61 1 1 1 1 1 12 1 2 2 2 2 23 1 3 3 3 3 34 1 4 4 4 4 45 1 5 5 5 5 56 2 1 2 3 4 57 2 2 3 4 5 18 2 3 4 5 1 29 2 4 5 1 2 310 2 5 1 2 3 411 3 1 3 5 2 412 3 2 4 1 3 513 3 3 5 2 4 114 3 4 1 3 5 215 3 5 2 4 1 316 4 1 4 2 5 317 4 2 5 3 1 418 4 3 1 4 2 519 4 4 2 5 3 120 4 5 3 1 4 221 5 1 5 4 3 222 5 2 1 5 4 323 5 3 2 1 5 424 5 4 3 2 1 525 5 5 4 3 2 1混合水平正交表7、L8（41×24）序号 1 2 3 4 51 1 1 1 1 12 1 2 2 2 23 2 1 1 2 24 2 2 2 1 15 3 1 2 1 26 3 2 1 2 17 4 1 2 2 18 4 2 1 1 28、L12（31×24）序号 1 2 3 4 51 1 1 1 1 12 1 1 1 2 23 1 2 2 1 24 1 2 2 2 15 2 1 2 1 16 2 1 2 2 27 2 2 1 2 28 2 2 1 2 29 3 1 2 1 29、L16（44×23）序号 1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 2附录1：常用正交表（1）L4（23）列号 1 2 3试验号1 1 1 12 1 2 23 2 1 24 2 2 1(2)L8(27)列号 1 2 3 4 5 6 7试验号1 1 1 1 1 1 1 12 1 1 1 2 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 17 2 2 1 1 2 2 18 2 2 1 2 1 1 2(3)L12(211)列号 1 2 3 4 5 6 7 8 9 10 11 试验号1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 23 1 1 2 2 2 1 1 1 2 2 24 1 2 1 2 2 1 2 2 1 1 25 1 2 2 1 2 2 1 2 1 2 16 1 2 2 2 1 2 2 1 2 1 17 2 1 2 2 1 1 2 2 1 2 18 2 1 2 1 2 2 2 1 1 1 29 2 1 1 2 2 2 1 2 2 1 110 2 2 2 1 1 1 1 2 2 1 211 2 2 1 2 1 2 1 1 1 2 212 2 2 1 1 2 1 2 1 2 2 1列号 1 2 3 4试验号1 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 1 （5）L16（45）列号 1 2 3 4 5试验号1 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 37 2 3 4 1 28 2 4 3 2 19 3 1 3 4 210 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 2 （6）L25（56）列号 1 2 3 4 5 6 试验号1 1 1 1 1 1 12 1 2 2 2 2 23 1 3 3 3 3 34 1 4 4 4 4 45 1 5 5 5 5 56 2 1 2 3 4 57 2 2 3 4 5 18 2 3 4 5 1 29 2 4 5 1 2 310 2 5 1 2 3 411 3 1 3 5 2 412 3 2 4 1 3 513 3 3 5 2 4 114 3 4 1 3 5 215 3 5 2 4 1 316 4 1 4 2 5 317 4 2 5 3 1 418 4 3 1 4 2 519 4 4 2 5 3 120 4 5 3 1 4 221 5 1 5 4 3 222 5 2 1 5 4 323 5 3 2 1 5 424 5 4 3 2 1 525 5 5 4 3 2 1 （7）L8（4×24）1 1 1 1 1 12 1 2 2 2 23 2 1 1 2 24 2 2 2 1 15 3 1 2 1 26 3 2 1 2 17 4 1 2 2 18 4 2 1 1 2 （8）L12（3×24）列号 1 2 3 4 5试验号1 1 1 1 1 12 1 1 1 2 23 1 2 2 1 24 1 2 2 2 15 2 1 2 1 16 2 1 2 2 27 2 2 1 2 28 2 2 1 2 29 3 1 2 1 210 3 1 1 2 111 3 2 1 1 212 3 2 2 2 1 （9）L16（44×23）列号 1 2 3 4 5 6 7 试验号1 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 2Excel表格在L9（34）正交试验数据处理中的应用L9（34）正交试验是医药工作中常用的实验方法之一。

EXCEL:用于多因素正交设计数据分析

EXCEL：用于多因素正交设计数据分析俞钟行【期刊名称】《中国质量》【年(卷),期】2011(000)006【摘要】摩托罗拉公司关于六西格玛管理的教材[1]第1章,就指出企业应用的质量管理方法像一个梯子:最底层是"救火",即处于无序状态;上一层是"产品检验",即质量是检验出来的;再上一层是"过程控制",即质量是制造出来的;最高层是"试验设计"(Design of Experiment,简称DOE),即质量是设计出来的.DOE可谓统计质量控制的最高境界.对试验所获数据的处理有各种方法."直接看":不作分析就可能获得理想的信息和成果."算一算":也就是极差分析,用一些比较简单的分析计算,可能获得比"直接看"更理想的信息和成果,但是否确实,需要经过验证.更为精密的方差分析、回归分析,既要有一定的统计学理论知识,又要进行比较繁复的计算,有时甚至非用软件不能解决实际问题.尽管Minitab、S-PLUS、JMP等统计软件应有尽有,但一则费用高,二则会用者少,常成为DOE推广应用的障碍.其实普及程度很高的EXCEL就有很强的统计功能,可在DOE数据分析中发挥强大威力.【总页数】3页(P91-93)【作者】俞钟行【作者单位】上海思科统计质量咨询服务有限公司【正文语种】中文【相关文献】1.基于多因素正交设计法采场结构参数数值模拟研究 [J], 陈辉;管伟明2.多因素正交设计建立切削力经验公式 [J], 秦乐3.Excel5.0的高级功能：数据分析,数据管理,宏,定制Excel [J], 袁洪;徐国平4.试验设计类型之可以考察部分交互作用的多因素设计:正交设计与均匀设计 [J], 张效嘉;胡良平5.Excel软件用于药学研究中的正交设计数据处理 [J], 朱海涛;邓雪华;陈吉炎;涂自良因版权原因，仅展示原文概要，查看原文内容请购买。

利用Excel进行正交设计及分析

Herald of M edicine Vol125 No13 M arch 2006
图 2 正交实验设计与结果示意图在单元格 A30输入“表 3 醇浸膏得率方差分析表 ”,合并 A30 ∶F30单元格 ;在 A31 ∶F31区域分别输入“误差来源 ”、 “SS”、“f”、“S”、“F”、“P”;在 A32 ∶A35 区域分别输入“A ”、 “B ”、“C”、“误差 ”; B32“ = 3 3 DEVSQ ( C21 ∶C23 ) ”, 拖动 B32复制柄至 B35,数据源分别改为“D21 ∶D23 ”、“E21 ∶ E23”、“F21 ∶F23 ”, C32 ∶C35 均为“2 ”, D32“ = B32 /C32 ”, 拖动 D32复制柄至 D35,在 E32 输入“ = D32 / ＄D ＄35 ”,拖动 E32复制柄至 E34,在 F32输入“ = IF ( E32 > = 99”,“ < 0. 01”, IF ( E32 > = 19,“ < 0. 05 ”,“ > 0. 05 ”) ) , 拖动 F32 复制柄至 F34。 (注意 : ＄和 ”是英文输入法状态下从键盘上输入的符号 , 不是插入的符号。) 在 A38 ∶F43区域输入“表 4 延胡索乙素含量方差分析表 ”,各单元格公式与表 3对应位置相同 (图 3) ,只是数据源发生改变。在 A46输入 "按指标 1较好的实验条件是 : ”, A47”= IF (C21 = MAX ( C21 ∶C23 ) ,“A1 ”, IF ( C22 = MAX ( C21 ∶ C23) ,“A2 ”,“A3 ”) ) ”, 拖动 A47 复制柄至 C47, 将“A1 ”、 “A2”、“A3”分别改为“B1 ”、“B2 ”、“B3 ”、“C1 ”、“C2 ”、“C3 ”。在 A48输入 "按指标 2较好的实验条件是 : ”, A49“ = IF ( C25 = MAX (C25 ∶C27) ,“A1”, IF (C26 =MAX ( C25 ∶C27) ,“A2”, “A3”) ) ”,拖动 D49复制柄至 F49,将“A1 ”、“A2 ”、“A3 ”分别改为“B1”、“B2”、“B3”、“C1”、“C2”、“C3”。保护工作表 [2 ] 。选定可更改数据的单元格区域 ,在菜单栏的“格式 ”中选择“单元格 ”项 ,打开其对话框 ,单击“保护 ”标签 ,取消“锁定 ”功能项的选择 ,再单击“工具 ”,单击下拉菜单 “保护 ”,单击“保护工作表 ”,这样 ,除了已取消锁定的单元格以外 ,其余单元格的公式、数据、格式等便不能被改动 ,防止错误操作将其破坏。将工作表以模板形式保存。

三因素三水平正交表例题

三因素三水平正交表例题例题1：某产品的质量受A、B、C三个因素影响，每个因素有三个水平。

A因素的三个水平为A1 = 10，A2 = 20，A3 = 30；B因素的三个水平为B1 = 5，B2 = 10，B3 = 15；C因素的三个水平为C1 = 2，C2 = 4，C3 = 6。

试用正交表安排试验，找出最佳的因素水平组合以提高产品质量（以产品质量指标越大越好）。

1. 选择正交表。

- 对于三因素三水平的试验，我们可以选用L9(3⁴)正交表。

2. 表头设计。

- 将A、B、C三个因素分别安排在正交表的三列上，例如A安排在第1列，B安排在第2列，C安排在第3列。

3. 确定试验方案。

- 根据正交表L9(3⁴)的安排进行试验。

例如，第1号试验的因素水平组合为A1、B1、C1；第2号试验为A1、B2、C2；第3号试验为A1、B3、C3；第4号试验为A2、B1、C2；第5号试验为A2、B2、C3；第6号试验为A2、B3、C1；第7号试验为A3、B1、C3；第8号试验为A3、B2、C1；第9号试验为A3、B3、C2。

4. 进行试验并记录结果。

- 假设经过试验得到9个试验结果分别为y1,y2,y3,y4,y5,y6,y7,y8,y9。

5. 分析试验结果。

- 计算各因素同一水平下试验结果的平均值。

- 对于A因素：- K1A=(y1 + y2+y3)/3，K2A=(y4 + y5 + y6)/3，K3A=(y7 + y8 + y9)/3。

- 计算极差RA = max(K1A,K2A,K3A)-min(K1A,K2A,K3A)。

- 对于B因素：- K1B=(y1 + y4 + y7)/3，K2B=(y2 + y5 + y8)/3，K3B=(y3 + y6 + y9)/3。

- 计算极差RB = max(K1B,K2B,K3B)-min(K1B,K2B,K3B)。

- 对于C因素：- K1C=(y1 + y6 + y8)/3，K2C=(y2 + y4 + y9)/3，K3C=(y3 + y5 + y7)/3。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

正交（全面）设计实验结果的直观分析：
1、看一看找条件。

指标最好的点对应的实验条件为最佳条件
根据正交（全面）设计数据可比的特点，表中指标最好的点为A3B3C2，
所对应的条件即为实验范围内的最佳工艺条件。

2、算一算极差确定主次因素。

极差大小顺序为因素主次顺序
K ij—第j个因素第i个水平的所有试验结果指标值的均值；
K11=（31+54+38）/3=41
K12=（31+53+57）/3=47
K23=（54+53+64）/3=57 MAX= MAX (K1j,，K2j，K3j)
MIN= MIN (K1j,，K2j，K3j)
极差R= MAX－MIN
表中计算结果显示极差的大小顺序为A>C>B，则实验范围内的主要影
响因素为A，其次为C，因素B影响最小。

Q j—均方和
Q j因素均方和，Q j=(K1j-K2j)2+(K1j-K3j)2+(K2j-K3j)2
Q1=（41-48）2+（41-61）2+（48-61）2=618
Q T总均方和，Q T=∑Q j，（如果不设计误差列，Q T=∑（y2）-（∑y）2/n）Q误差误差均方和，Q误差= Q T-∑Q j
f—自由度
f j：因素自由度，f j=因素j的水平数-1
f T：总自由度，f T=实验个数-1
f误差：误差自由度，f误差= f T-∑f j
MS—方差估计值
MS j因素方差值，MS j= Q j/ f j
MS误差误差方差值，MS误差= Q误差/ f误差
F值—统计检验量
F j因素检验量，F j= MS j/ MS误差
F0.1（f1，f2）标准检验量，根据检验水平和自由度查F表得到
（0.1为检验水平α，f1，f2分别为因素自由度和误差自由度，）显著性判断
F j > F0.01（f1，f2），高度显著因素
F j > F0.05（f1，f2），显著因素
F j > F0.1（f1，f2），较显著因素
用Excel进行直观分析简单、使用，要求同学们掌握。