指数函数的图像及性质的应用

指数函数的应用指数函数是高中数学中的重要内容之一，广泛应用于数学、物理、经济和工程等领域。

它具有独特的性质和广泛的应用场景，本文将介绍指数函数的概念、性质以及在不同领域的应用。

一、指数函数的概念和性质指数函数是以自然对数为底的幂函数，一般形式可以表示为f(x) = a^x，其中a为底数，x为指数。

指数函数的图像是曲线，通常具有以下性质：1. 当底数a大于1时，指数函数是递增函数；当底数a在0和1之间时，指数函数是递减函数。

2. 指数函数的定义域是实数集，值域是正实数集。

3. 指数函数在x轴上有一个特殊点，即f(0) = 1，该点被称为原点。

4. 指数函数在x轴的左侧逐渐趋近于0，但永远不会等于0；在x 轴的右侧逐渐趋近于正无穷大。

5. 指数函数的反函数是对数函数。

二、指数函数在数学中的应用指数函数在数学中具有广泛的应用，主要体现在以下几个方面：1. 指数函数在数列中的应用：指数函数可以用于描述数列的增长和衰减规律，比如等比数列中每一项与前一项的比值恒定，就可以表示为指数函数。

2. 指数函数在数学模型中的应用：指数函数可以用于建立各种数学模型，如人口增长模型、金融利息模型等，帮助我们理解和预测实际问题。

3. 指数函数在概率统计中的应用：指数函数在概率和统计中的分布函数中扮演着重要角色，如指数分布、正态分布的密度函数等。

三、指数函数在物理中的应用指数函数在物理学中也有重要的应用，尤其是描述自然界中各种现象的增长和衰减规律。

以下是一些常见的物理应用场景：1. 辐射衰减：核物质的衰变过程中，辐射的强度随着时间呈指数衰减，可以用指数函数来描述。

2. 指数增长和衰减：在电路中，电容器和电感器的电荷和电流的增长或衰减过程也可以用指数函数来表示。

3. 声音强度和光强度的衰减：声音和光的传播过程中，其强度随着距离增加呈指数衰减。

4. 热传导：热传导过程中，温度随着时间和空间的变化满足指数函数关系。

四、指数函数在经济和金融中的应用指数函数在经济学和金融学中也有广泛的应用，可以帮助分析和预测市场趋势和经济增长。

第2课时 指数函数的图像与性质的应用学习目标 1.进一步熟练掌握指数函数的图像、性质.2.能够利用指数函数的图像和性质比较大小、解不等式． 导语我们已经学习了指数函数的图像与性质，今天就探讨一下，利用这些知识去解决一些常见问题．一、指数函数图像的辨识例1 (1)已知函数f (x )＝ax ＋b 的图像如图所示，则函数g (x )＝a x ＋b 的图像可能是( )答案 B解析 由f (x )＝ax ＋b 的图像可得f (0)＝b <－1，f (1)＝a ＋b >0， 所以a >1，b <－1，故函数g (x )＝a x ＋b 为增函数，相对y ＝a x 向下平移大于1个单位，故B 符合．(2) (多选)已知实数a ，b 满足⎝⎛⎭⎫12a ＝⎝⎛⎭⎫13b ，给出下面几种关系，则其中可能成立的是( ) A ．0<a <b B ．0<b <a C ．a <b <0 D ．b ＝a答案 BCD解析 在同一坐标系中作出函数y ＝⎝⎛⎭⎫12x与函数y ＝⎝⎛⎭⎫13x 的图像，如图所示，若⎝⎛⎭⎫12a ＝⎝⎛⎭⎫13b>1，则a <b <0； 若⎝⎛⎭⎫12a ＝⎝⎛⎭⎫13b <1，则0<b <a ； 若⎝⎛⎭⎫12a ＝⎝⎛⎭⎫13b ＝1，则b ＝a ＝0.反思感悟 与指数函数相关的图像问题(1)熟记当底数a >1和0<a <1时，图像的大体形状． (2)注意图像平移问题：对于横坐标x 满足“左加右减”． (3)注意利用函数性质研究图像问题．跟踪训练1 (1)函数y ＝2x －1的图像一定不经过第________象限；若函数y ＝⎝⎛⎭⎫12x ＋b 的图像不经过第一象限，则实数b 的取值范围是________． 答案 二、四 (－∞，－1]解析 当x <0时，2x <1，y <0，在第三象限， 当x >0时，2x >1，y >0，在第一象限， 且当x ＝0时，y ＝0，故y ＝2x －1的图像一定不经过第二、四象限． 若函数y ＝⎝⎛⎭⎫12x ＋b 的图像不经过第一象限， 当x ∈[0，＋∞)时，y ＝⎝⎛⎭⎫12x ＋b ≤0， 又∵0<12<1，且x ∈[0，＋∞)，y ＝⎝⎛⎭⎫12x 是[0，＋∞)上的减函数， ∴0<⎝⎛⎭⎫12x ≤1，∴⎝⎛⎭⎫12x ＋b ≤1＋b ≤0， 解得b ≤－1.(2)已知直线y ＝2a 与函数y ＝|2x －2|的图像有两个公共点，求实数a 的取值范围．解 函数y ＝|2x －2|的图像如图中实线部分所示，要使直线y ＝2a 与该图像有两个公共点，则有0<2a <2，即0<a <1，故实数a 的取值范围为(0,1)．二、利用指数函数性质比较大小 例2 比较下列各组数的大小． (1)1.52.5与1.53.2； (2)56311⎛⎫⎪⎝⎭与56833⎛⎫⎪⎝⎭； (3)1.50.3与0.81.2.解 (1)∵函数y ＝1.5x 在R 上是增函数，2.5<3.2， ∴1.52.5<1.53.2.(2)指数函数y ＝⎝⎛⎭⎫311x 与y ＝⎝⎛⎭⎫833x 的图像(如图)，由图知56311⎛⎫⎪⎝⎭>56833⎛⎫ ⎪⎝⎭. (3)由指数函数的性质知1.50.3>1.50＝1， 而0.81.2<0.80＝1， ∴1.50.3>0.81.2.反思感悟 比较指数式大小的3种类型及处理方法跟踪训练2 比较下列各组数的大小： (1)0.8－0.1与1.250.2；(2)1.70.3与0.93.1；(3)a 0.5与a 0.6(a >0且a ≠1)． 解 (1)∵0<0.8<1， ∴y ＝0.8x 在R 上是减函数． ∵－0.2<－0.1，∴0.8－0.2>0.8－0.1， 而0.8－0.2＝⎝⎛⎭⎫45－0.2＝1.250.2， 即0.8－0.1<1.250.2.(2)∵1.70.3>1.70＝1,0.93.1<0.90＝1， ∴1.70.3>0.93.1.(3)a 0.5与a 0.6可看作指数函数y ＝a x 的两个函数值． 当0<a <1时，函数y ＝a x 在R 上是减函数． ∵0.5<0.6，∴a 0.5>a 0.6.当a >1时，函数y ＝a x 在R 上是增函数． ∵0.5<0.6，∴a 0.5<a 0.6.综上所述，当0<a <1时，a 0.5>a 0.6； 当a >1时，a 0.5<a 0.6.三、利用指数函数性质解不等式 例3 (1)不等式4x <42－3x的解集是________．答案 ⎝⎛⎭⎫－∞，12 解析 ∵4x <42－3x ，∴x <2－3x ，∴x <12.(2)解关于x 的不等式：a 2x ＋1≤a x －5(a >0且a ≠1)．解 ①当0<a <1时， ∵a 2x ＋1≤a x －5，∴2x ＋1≥x －5，解得x ≥－6. ②当a >1时，∵a 2x ＋1≤a x －5， ∴2x ＋1≤x －5，解得x ≤－6.综上所述，当0<a <1时，不等式的解集为{x |x ≥－6}； 当a >1时，不等式的解集为{x |x ≤－6}． 反思感悟 指数型不等式的解法(1)指数型不等式a f (x )>a g (x )(a >0且a ≠1)的解法： 当a >1时，f (x )>g (x )； 当0<a <1时，f (x )<g (x )．(2)如果不等式的形式不是同底指数式的形式，要首先进行变形将不等式两边的底数进行统一，此时常用到以下结论：1＝a 0(a >0且a ≠1)，a －x ＝⎝⎛⎭⎫1a x(a >0且a ≠1)等． 跟踪训练3 (1)已知不等式13≤3x <27，则x 的取值范围为( ) A ．－12≤x <3B.12≤x <3 C ．R D ．－12≤x <13答案 A解析 由题意可得123-≤3x <33，再根据函数y ＝3x 在R 上是增函数，可得－12≤x <3.(2)已知(a 2＋a ＋2)x >(a 2＋a ＋2)1－x ，则x 的取值范围是________． 答案 ⎝⎛⎭⎫12，＋∞ 解析 ∵a 2＋a ＋2＝⎝⎛⎭⎫a ＋122＋74>1， ∴(a 2＋a ＋2)x >(a 2＋a ＋2)1－x ⇔x >1－x ⇔x >12.∴x ∈⎝⎛⎭⎫12，＋∞.1．知识清单：(1)指数函数图像的应用． (2)利用指数函数性质比较大小． (3)利用指数函数性质解不等式．2．方法归纳：转化与化归、分类讨论、数形结合．3．常见误区：研究y ＝a f (x )型函数，易忽视讨论a >1还是0<a <1.1．(多选)下列判断正确的是( ) A ．2.52.5>2.53 B ．0.82<0.83 C ．π2>3πD ．0.90.3>0.90.5答案 CD解析 ∵y ＝πx 是增函数，且2>3， ∴π2>3π；∵y ＝0.9x 是减函数，且0.5>0.3， ∴0.90.3>0.90.5.故C ，D 正确．2．函数y ＝a x －1a(a >0且a ≠1)的图像可能是( )答案 D解析 当a >1时，y ＝a x －1a 为增函数，当x ＝0时，y ＝1－1a <1且y ＝1－1a >0，故A ，B 不符合．当0<a <1时，y ＝a x －1a 为减函数，当x ＝0时，y ＝1－1a <0，故C 不符合，D 符合．3．若a 3.1>a 3(a >0且a ≠1)，则实数a 的取值范围是________．答案 (1，＋∞)解析 因为3.1>3，且a 3.1>a 3， 所以函数y ＝a x 是增函数，所以a >1. 4．不等式225x >5x＋1的解集是________．答案 ⎝⎛⎭⎫－∞，－12∪(1，＋∞) 解析 由225x >5x ＋1得2x 2>x ＋1，解得x <－12或x >1.5．设0<a <1，则关于x 的不等式22232223x x x x a a >－＋＋－的解集为________．答案 (1，＋∞)解析 因为0<a <1，所以y ＝a x 在R 上是减函数， 又因为22232223x x x x aa>－＋＋－，所以2x 2－3x ＋2<2x 2＋2x －3，解得x >1.1．若2x ＋1<1，则x 的取值范围是( ) A ．(－1,1)B ．(－1，＋∞)C ．(0,1)∪(1，＋∞)D ．(－∞，－1)答案 D解析 ∵2x ＋1<1＝20，且y ＝2x 是增函数， ∴x ＋1<0，∴x <－1.2．已知函数f (x )＝(a 2－1)x ，若x >0时总有f (x )>1，则实数a 的取值范围是( ) A ．1<|a |<2 B ．|a |<2 C ．|a |>1D ．|a |> 2答案 D解析 由题意知a 2－1>1， 解得a 2>2， 即|a |> 2.3．函数①y ＝a x ；②y ＝b x ；③y ＝c x ；④y ＝d x 的图像如图所示，a ，b ，c ，d 分别是下列四个数：54，3，13，411中的一个，则a ，b ，c ，d 的值分别是( )A.54，3，13，411B.3，54，411，13C.411，13，3，54D.13，411，54， 3 答案 C解析 直线x ＝1与函数图像的交点的纵坐标从上到下依次为c ，d ，a ，b ，而3>54>411>13，所以a ，b ，c ，d 的值分别是411，13，3，54.4．函数y ＝a x (a >0且a ≠1)在[0,1]上的最大值与最小值的和为3，则函数y ＝2ax －1在[0,1]上的最大值是( ) A ．6 B ．1 C ．3 D.32答案 C解析 函数y ＝a x 在[0,1]上是单调的，最大值与最小值都在端点处取到，故有a 0＋a 1＝3，解得a ＝2，因此函数y ＝2ax －1＝4x －1在[0,1]上是增函数，当x ＝1时，y max ＝3. 5．在下列图像中，二次函数y ＝ax 2＋bx 及指数函数y ＝⎝⎛⎭⎫b a x的图像只可能是( )答案 A解析 根据指数函数的定义，可知a ，b 同号且不相等，∴－b2a <0，可排除B ，D ；由选项C中二次函数的图像，可知a －b >0，a <0，∴ba >1，∴指数函数y ＝⎝⎛⎭⎫b a x 单调递增，故C 不正确，排除C ，故选A.6．函数f (x )＝3x －3(1<x ≤5)的值域是________． 答案 ⎝⎛⎦⎤19，9 解析 因为1<x ≤5， 所以－2<x －3≤2.而函数y ＝3x 在(－2,2]上是增函数， 于是有19<f (x )≤32＝9，即所求函数的值域为⎝⎛⎦⎤19，9.7．已知a ＝0.80.7，b ＝0.80.9，c ＝1.20.8，则a ，b ，c 的大小关系是________．(用“>”连接) 答案 c >a >b解析 因为函数y ＝0.8x 是R 上的减函数， 所以a >b .又因为a ＝0.80.7<0.80＝1，c ＝1.20.8>1.20＝1， 所以c >a .故c >a >b .8．已知方程|2x －1|＝a 有两个不等实根，则实数a 的取值范围是________． 答案 (0,1)解析 函数y ＝|2x －1|＝⎩⎪⎨⎪⎧2x －1，x ≥0，－2x＋1，x <0，其图像如图所示．方程|2x －1|＝a 有两个不等实根等价于直线y ＝a 与y ＝|2x －1|的图像有两个交点，所以由图可知0<a <1.9．已知a－5x<a x －7(a >0且a ≠1)，求x 的取值范围．解 当a >1时，∵a －5x <a x －7，∴－5x <x －7， 解得x >76；当0<a <1时，∵a －5x <a x －7，∴－5x >x －7， 解得x <76.综上所述，当a >1时，x 的取值范围是⎝⎛⎭⎫76，＋∞； 当0<a <1时，x 的取值范围是⎝⎛⎭⎫－∞，76. 10．若函数f (x )＝(k ＋3)a x ＋3－b (a >0且a ≠1)是指数函数． (1)求k ，b 的值；(2)求解不等式f (2x －7)>f (4x －3)．解 (1)∵f (x )＝(k ＋3)a x ＋3－b (a >0且a ≠1)是指数函数， ∴k ＋3＝1且3－b ＝0，解得k ＝－2且b ＝3. (2)由(1)得f (x )＝a x (a >0且a ≠1)， 因为f (2x －7)>f (4x －3)，所以a 2x －7>a 4x －3.①当a >1时，f (x )＝a x 单调递增，则不等式等价于2x －7>4x －3，解得x <－2； ②当0<a <1时，f (x )＝a x 单调递减，则不等式等价于2x －7<4x －3，解得x >－2. 综上，当a >1时，原不等式的解集为{x |x <－2}； 当0<a <1时，原不等式的解集为{x |x >－2}．11．已知函数f (x )＝a －x (a >0且a ≠1)，且f (－2)>f (－3)，则a 的取值范围是( ) A ．a >0 B ．a >1 C ．a <1 D ．0<a <1答案 D解析 因为－2>－3，f (－2)>f (－3)，又f (x )＝a －x ＝⎝⎛⎭⎫1a x ，所以⎝⎛⎭⎫1a －2>⎝⎛⎭⎫1a －3，所以1a>1，所以0<a <1. 12．函数f (x )＝⎩⎪⎨⎪⎧ －x ＋3a ，x <0，a x ，x ≥0(a >0且a ≠1)是R 上的减函数，则a 的取值范围是( ) A ．(0,1) B.⎣⎡⎭⎫13，1C.⎝⎛⎦⎤0，13 D.⎝⎛⎦⎤0，23答案 B解析 由单调性定义，得f (x )为减函数应满足⎩⎪⎨⎪⎧ 0<a <1，3a ≥a 0，即13≤a <1.13．设y 1＝40.9，y 2＝80.48，y 3＝⎝⎛⎭⎫12－1.5，则( )A ．y 3>y 1>y 2B ．y 2>y 1>y 3C ．y 1>y 2>y 3D ．y 1>y 3>y 2答案 D解析 40.9＝21.8,80.48＝21.44，⎝⎛⎭⎫12－1.5＝21.5，由于y ＝2x 在R 上是增函数，所以21.8>21.5>21.44，即y 1>y 3>y 2.14．设函数f (x )＝⎩⎪⎨⎪⎧ 2－x ，x ≤0，1，x >0，则满足f (x ＋1)<f (2x )的x 的取值范围是() A ．(－∞，－1] B ．(0，＋∞)C ．(－1,0)D ．(－∞，0)答案 D解析 函数f (x )的图像如图所示，观察图像可知会有⎩⎪⎨⎪⎧2x <0，2x <x ＋1， 解得x <0，所以满足f (x ＋1)<f (2x )的x 的取值范围是(－∞，0)．15．设x <0，且1<b x <a x ，则( )A ．0<b <a <1B ．0<a <b <1C ．1<b <aD ．1<a <b答案 B解析 ∵1<b x <a x ，x <0，∴0<a <1,0<b <1.又当x ＝－1时，1b <1a， 即b >a ，∴0<a <b <1.16．已知函数f (x )＝b ·a x (其中a ，b 为常量，且a >0，a ≠1)的图像经过点A (1,6)，B (3,24)．(1)求f (x )；(2)若不等式⎝⎛⎭⎫1a x ＋⎝⎛⎭⎫1b x －m ≥0在x ∈(－∞，1]上恒成立，求实数m 的取值范围．解 (1)把A (1,6)，B (3,24)代入f (x )＝b ·a x ，得 ⎩⎪⎨⎪⎧ 6＝ab ，24＝b ·a 3，结合a >0且a ≠1， 解得⎩⎪⎨⎪⎧a ＝2，b ＝3.∴f (x )＝3·2x .(2)要使⎝⎛⎭⎫12x ＋⎝⎛⎭⎫13x ≥m 在(－∞，1]上恒成立，只需保证函数y ＝⎝⎛⎭⎫12x ＋⎝⎛⎭⎫13x 在(－∞，1]上的最小值不小于m 即可．∵函数y ＝⎝⎛⎭⎫12x ＋⎝⎛⎭⎫13x 在(－∞，1]上为减函数，∴当x ＝1时，y ＝⎝⎛⎭⎫12x ＋⎝⎛⎭⎫13x 有最小值56. ∴只需m ≤56即可． ∴m 的取值范围为⎝⎛⎦⎤－∞，56.。

指数函数对数函数与幂函数指数函数的性质与图像xx年xx月xx日CATALOGUE 目录•指数函数的定义与性质•对数函数的定义与性质•幂函数的定义与性质•指数函数、对数函数与幂函数的比较•指数函数、对数函数与幂函数的应用案例•总结与展望01指数函数的定义与性质指数函数的定义02指数函数：y=f(x)=a^x03a>0时，函数图像过一三象限；a<0时，函数图像过二四象限。

指数函数的性质函数图像恒过(0,1)点值域：R a>1时，函数为单调递增函数；0<a<1时，函数为单调递减函数奇偶性：当a>0时，为奇函数；当a=0时，既不是奇函数也不是偶函数；当a<0时，为偶函数指数函数的图像图像恒过(0,1)点当a>1时，函数的增长速度随着x的增大而逐渐加快；当0<a<1时，函数的增长速度随着x的增大而逐渐减慢。

a>1时，函数为单调递增函数，图像位于一三象限；0<a<1时，函数为单调递减函数，图像位于二四象限。

当a>1时，函数的最大值无限趋近于正无穷大；当0<a<1时，函数的最小值无限趋近于0。

02对数函数的定义与性质1 2 3自然对数：以数学常数e为底数的对数，记作ln(x)。

常用对数：以10为底数的对数，记作lg(x)。

底数为任意正数的对数，记作log(x)。

对数的运算性质log(a*b)=log(a)+log(b)；log(a/b)=log(a)-log(b)；log(a^n)=nlog(a)。

对数恒等式log(a/b)=log(a)-log(b)；log(a^n)=nlog(a)。

对数的运算律如果a>0且a不等于1，M>0，N>0，那么log(a)(MN)=log(a)M +log(a)N；log(a)(M/N)=log(a)M -log(a)N；log(a)M^n=nlog(a)M。

•对数函数的图像与性质：图像与x轴交点为1，当x>1时，函数值大于0；当0<x<1时，函数值小于0。

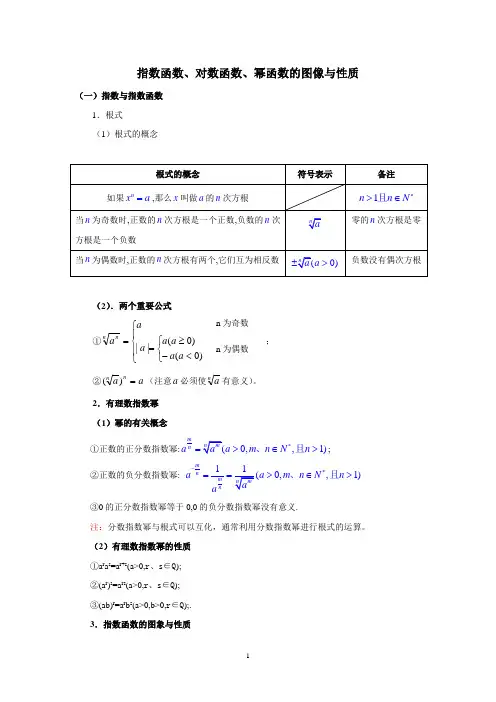
指数函数、对数函数、幂函数的图像与性质（一）指数与指数函数1．根式（1）根式的概念（2）．两个重要公式①⎪⎩⎪⎨⎧⎩⎨⎧<-≥==)0()0(||a a a a a aa nn ；②a a n n =)(（注意a 必须使n a 有意义）。

2．有理数指数幂 （1）幂的有关概念 ①正数的正分数指数幂:0,,1)m na a m n N n *=>∈>、且; ②正数的负分数指数幂: 10,,1)mnm naa m n N n a-*==>∈>、且③0的正分数指数幂等于0,0的负分数指数幂没有意义.注：分数指数幂与根式可以互化，通常利用分数指数幂进行根式的运算。

（2）有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q ); ②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r b s (a>0,b>0,r ∈Q );. 3．指数函数的图象与性质n 为奇数 n 为偶数注：如图所示，是指数函数（1）y=a x ,（2）y=b x,（3）,y=c x （4）,y=d x 的图象，如何确定底数a,b,c,d 与1之间的大小关系？提示：在图中作直线x=1，与它们图象交点的纵坐标即为它们各自底数的值，即c 1>d 1>1>a 1>b 1,∴c>d>1>a>b 。

即无论在轴的左侧还是右侧，底数按逆时针方向变大。

（二）对数与对数函数 1、对数的概念 （1）对数的定义如果(01)x a N a a =>≠且，那么数x 叫做以a 为底，N 的对数，记作log N a x =，其中a 叫做对数的底数，N 叫做真数。

（2）几种常见对数2、对数的性质与运算法则（1）对数的性质（0,1a a >≠且）：①1log 0a =，②lo g 1aa =，③lo g Na a N =，④lo g N a aN =。

指数函数与对数函数的图像与性质指数函数与对数函数是高中数学中常见的一类函数，它们在数学和科学领域中都有着广泛的应用。

本文将从图像和性质两个方面对指数函数与对数函数进行论述。

一、指数函数的图像与性质指数函数可以表示为f(x)=a^x(a>0, a≠1)的形式，其中a为底数，x 为指数。

指数函数的图像特点如下：1. a>1时，指数函数呈现上升趋势。

以y=2^x为例，当x增大时，2的x次方的结果也随之增大，因此函数图像呈现递增趋势。

2. 0<a<1时，指数函数呈现下降趋势。

以y=(1/2)^x为例，当x增大时，1/2的x次方的结果将逐渐变小，因此函数图像呈现递减趋势。

3. a<0时，指数函数的图像不能通过实数值来表示。

因为负数的幂是无法定义的。

除了这些基本性质外，指数函数还有以下几个重要特点：1. 零指数：任何数的零次幂都等于1，即a^0=1。

2. 幂运算法则：对于指数函数a^x和a^y，有a^x*a^y=a^(x+y)和(a^x)^y=a^(xy)。

这些法则可以简化指数函数的运算。

3. 指数函数的性质：指数函数存在且连续，且在定义域内单调递增或递减。

当指数函数的底数a>1时，函数在整个定义域上是严格递增的；当0<a<1时，函数在整个定义域上是严格递减的。

二、对数函数的图像与性质对数函数可以表示为f(x)=log_a(x)(a>0, a≠1)的形式，其中a为底数，x为实数。

对数函数的图像特点如下：1. a>1时，对数函数呈现上升趋势。

以y=log_2(x)为例，x增大时，log_2(x)的结果也随之增大，因此函数图像呈现递增趋势。

2. 0<a<1时，对数函数呈现下降趋势。

以y=log_(1/2)(x)为例，x增大时，log_(1/2)(x)的结果将逐渐减小，因此函数图像呈现递减趋势。

3. a<0时，对数函数的图像不能通过实数值来表示。

ʏ朱生亮指数函数是高中数学的重要内容,也是高考的考查重点,下面介绍指数函数的图像与性质在解题中的六种应用,供同学们学习与参考㊂一㊁根据函数判断图像例1 函数y =a x,y =x +a 在同一坐标系中的图像可能是( )㊂解:由题意知a >0且a ʂ1,则函数y =x +a 单调递增㊂当0<a <1时,y =a x单调递减,直线y =x +a 在y 轴上的截距大于0且小于1;当a >1时,y =a x单调递增,直线y =x +a 在y 轴上的截距大于1㊂应选D ㊂评注:函数图像的识别可以从以下几个方面入手:利用函数的定义域,判断图像的左右位置;利用函数的值域,判断图像的上下位置;利用函数的单调性,判断图像的变化趋势;利用函数的奇偶性,判断图像的对称性;利用函数的周期性,判断图像的循环往复;利用函数的特征点,排除不合要求的图像㊂二㊁已知函数图像判断新函数的图像 图1例2 已知函数f (x )=(x -a )(x -b )(其中a >b )的图像如图1所示,则函数g (x )=a x +b 的图像是( )㊂解:由已知函数f (x )=(x -a )(x -b )(其中a >b )的图像可知,0<a <1,b <-1,则g (x )是一个减函数,可排除C ,D ㊂根据g (0)=1+b <0,可排除B ㊂应选A ㊂评注:解答本题要仔细观察所给函数的图像,从图像中得出a ,b 的取值范围,再对照选项进行判断㊂三㊁求函数的图像恒过定点例3 函数f (x )=a x -2022+2022(a >0且a ʂ1)恒过的定点为㊂解:指数函数y =a x(a >0且a ʂ1)的图像恒过定点(0,1)㊂令x -2022=0,则x =2022,所以f (2022)=1+2022=2023,即函数f (x )=a x -2022+2022(a >0且a ʂ1)恒过的定点为(2022,2023)㊂评注:本题是利用特殊值法求解的,也可令a =2得到一个具体函数,再求此函数经过的定点㊂四㊁求方程解的个数例4 偶函数f (x )满足f (x -1)=f (x +1),且当x ɪ[0,1]时,f (x )=x ,则关于x 的方程f (x )=110x在x ɪ[0,4]上解的个数是㊂解:方程f (x )=110x在x ɪ[0,4]上解的个数就是函数y =f (x )与y =110x图像的交点个数㊂由f (x -1)=f (x +1),可知偶函数f (x )的周期T =2㊂当x ɪ[0,1]时,f (x )=x ㊂结合f (x )是偶函数,可画出y =f (x )与y =110x的图像,如图2所示㊂图2由图可知,方程f (x )=110x在x ɪ[0,4]上解的个数是4㊂评注:对于这类问题,直接解方程困难,可将求方程解的个数转化为两个函数图像的51知识结构与拓展高一数学 2022年11月Copyright ©博看网. All Rights Reserved.交点的个数㊂五㊁求函数的单调区间例5 函数f (x )=13-x 2+2x +1的单调减区间为㊂解:设u =-x 2+2x +1㊂因为y =13u在R 上为减函数,所以f (x )=13-x 2+2x +1的单调减区间为函数u =-x 2+2x +1的单调增区间㊂又u =-x 2+2x +1的单调增区间为(-ɕ,1],所以f (x )的减区间为(-ɕ,1]㊂评注:求解与指数函数有关的复合函数问题,要明确复合函数的构成,涉及单调区间㊁最值等问题时,要借助 同增异减 的法则进行判断㊂六㊁求参数的最值例6 已知函数f (x )=b a x(其中a ,b为常数,a >0且a ʂ1)的图像经过A (1,6),B (2,18)两点㊂若不等式2ax+1bx-m ȡ0在x ɪ(-ɕ,1]上恒成立,则实数m 的最大值为㊂解:由已知条件可得b a =6,b a 2=18,解得a =3,b =2,则原不等式为23 x+12 x-m ȡ0在x ɪ(-ɕ,1]上恒成立㊂设函数g (x )=23x+12x-m ㊂显然g (x )=23 x+12 x-m 在(-ɕ,1]上单调递减,所以g (x )ȡg (1)=23+12-m =76-m ,所以76-m ȡ0,所以m ɤ76㊂故实数m 的最大值为76㊂评注:分离参数求解恒成立问题,可将参数移到不等式的另一边,构造函数,将问题转化为函数的最值问题㊂本题的解题依据是:m ɤf (x )恒成立⇔m ɤf (x )m i n ,m ȡf (x )恒成立⇔m ȡf (x )m a x㊂1.定义一种运算:a ⊗b =a ,a ȡb ,b ,a <b ,已知函数f (x )=2x⊕(3-x ),那么函数y =f (x +1)的大致图像是( )㊂提示:由题意可得函数f (x )=2x⊕(3-x )=2x,x ȡ1,3-x ,x <1,所以y =f (x +1)=2x,x ȡ0,2-x ,x <0㊂应选B ㊂2.已知函数f (x )=|2x-1|,a <b <c且f (a )>f (c )>f (b ),则下列结论中一定成立的是( )㊂A .a <0,b <0,c <0B .a <0,b ȡ0,c >0C .2-a<2cD .2a+2c <2提示:作出函数f (x )=|2x-1|的图像,如图3所示㊂图3对于A ,由a <b <c ,可得a <b <c <0㊂函数f (x )=|2x-1|在(-ɕ,0)上单调递减,所以f (a )>f (b )>f (c ),与题设矛盾,A 不正确㊂对于B ,设a =-1,b =2,c =3,此时f (c )=|23-1|=7为最大值,与题设矛盾,B 不正确㊂对于C ,取a =0,c =3,可得2-a=1<2c=8成立,这时f (c )=7为最大值,与题设矛盾,C 不正确㊂对于D ,因为a <c ,且f (a )>f (c ),所以a <0<c ,所以f (a )=|2a -1|>f (c )=|2c -1|,即1-2a >2c -1,也即2a +2c<2,D 正确㊂应选D ㊂作者单位:湖北省巴东县第一高级中学(责任编辑 郭正华)61 知识结构与拓展 高一数学 2022年11月Copyright ©博看网. All Rights Reserved.。

指数函数一、根式与分数指数幂1. 根式定义根式：一般地，若x n=a（a为非负实数，n为正整数），则x叫做a的n次方根，记作或。

其中，n叫做根指数，a叫做被开方数。

2. 根式性质当n为奇数时，正数的n次方根为正数，负数的n次方根为负数。

当n为偶数时，正数的n次方根有两个，互为相反数；负数没有偶次方根。

0的任何次方根都是0。

3. 根式运算化简：通过因式分解、合并同类项等方法将复杂的根式化简为最简形式。

求值：将根号下的数按照因数分解的形式写出，然后求出完全平方数的平方根，最后相乘得到最终结果。

和（差）：将根式化为最简形式后，合并同类项。

积（商）：合并同类项，分解各个项，然后化简得到最终结果。

4. 分数指数幂定义分数指数幂：一个数的指数为分数，如（a>0，m,n∈N∗且n>1），其中a的次幂等于n次根号下a的m次方，即。

二、分数指数幂的运算性质1、同底数幂相乘：底数相同，指数相加2、同底数幂相除：底数相同，指数相减3、幂的乘方：指数相乘4、任何非零数的0次幂都等于15、负指数幂表示倒数三、实数指数幂的运算及其性质1、实数指数幂的基本概念实数指数幂指的是形如 a n 的数，其中 a 为实数（且 a≠0），n 为实数。

实数指数幂包括正整数指数幂、零指数幂、负整数指数幂、分数指数幂以及无理数指数幂。

2、运算性质同底数幂相乘：a m•a n=a m+n同底数幂相除：a m/a n=a m−n（a≠0）幂的乘方：(a m)n=a mn分数指数幂：（a>0，m,n 为正整数，n>1）负整数指数幂：（a≠0）零指数幂：a0=1（a≠0）四、无理数指数幂有理数指数幂逼近无理数指数幂的原理，基于数学中的极限思想和连续性概念。

由于无理数无法直接表示为两个整数的比，我们需要通过一系列越来越接近该无理数的有理数来逼近它，从而计算出对应的指数幂值。

这一过程体现了数学中的逼近和极限思想，是微积分等更高层次数学的基础。

指数函数的性质与应用指数函数作为数学中的一种重要函数，其性质与应用广泛存在于各个领域。

本文将探讨指数函数的基本性质，并通过具体的实际应用案例，展示其在数学、经济、物理等领域的实际应用。

1. 指数函数的定义与性质指数函数是以指数为自变量，底数为常数的函数。

一般表示为 f(x) = a^x，其中 a 为底数，x 为指数，a > 0，且a ≠ 1。

指数函数具有以下基本性质：（1）当指数 x 为整数时，指数函数表现为幂函数，即 f(x) = a^x。

（2）指数函数的定义域为全体实数。

（3）当底数 a > 1 时，函数呈增长趋势；当 0 < a < 1 时，函数呈衰减趋势。

（4）指数函数在 x 趋于无穷大时，取正无穷大或趋于零；在 x 趋于负无穷大时，取正数或趋于零。

（5）指数函数具有乘法性质，即 a^x * a^y = a^(x+y)。

2. 指数函数的应用2.1 数学领域在数学领域，指数函数广泛应用于研究数列、级数等。

例如在级数求和问题中，指数函数能够精确求解各项和的近似值，进而得到级数的性质和趋势。

此外，指数函数在微积分中也有广泛应用，特别是在研究变化速率和增长率等方面。

2.2 经济领域在经济领域，指数函数被广泛用于描述经济增长和消费模式。

例如在经济预测中，指数函数常被用来估计GDP、人口增长等指标。

同时，在复利计算中，指数函数的增长特性被应用于计算利息和投资回报率。

2.3 物理领域在物理领域，指数函数用于描述一些基本的自然现象。

例如在弹簧振动模型中，指数函数可以用来描述振幅的衰减；在放射性衰变中，指数函数可以用来描述放射性物质的衰减过程。

此外，指数函数还被应用于电路理论、流体力学等领域。

2.4 其他应用除了上述数学、经济、物理领域外，指数函数还在其他领域有着广泛的应用。

例如在计算机科学中，指数函数常用于算法的时间复杂度分析；在生态学中，指数函数用于描述生物种群的增长及其对环境的影响。