ug各种弹簧建模资料

弹簧的画法1、一般弹簧2、矩形弹簧、3、锥形螺旋弹簧（盘弹簧）4、纺锤形螺旋弹簧t=0xt=-sqrt(8)*(1-t)+sqr t(8)*tyt=2-0.25*xt^2zt=05、椭圆弹簧=1r1=2r2=1n=5a=0b=360s=(1-t)*a+t*bxt=r1*cos(n*s)yt=r2*sin(n*s)zt=t6、闭合端部的弹簧一个闭合端部的弹簧需要三条规律曲线：中间部分的一个简单螺旋线，在两端的可变螺距的螺旋线。

闭合端部必须相切到顶部z平面与主螺旋线，利用指数方程可以解决这个问题。

z值按照指数规律变化，指数等于主卷螺距除以闭合端的高度。

(1)建立单位为mm的新零件(2)输入公式Active_coils=11 //中间弹簧卷数Wire_dia=0.095 //弹簧线径Closed_height=Wire_dia+0.1 //考虑最后卷的间隙Dir=1 //改变螺旋旋转方向Free_length=7 //弹簧自由长度OD=2.19 //弹簧外直径Total_coils=13 //螺旋总卷数angle_offset=(Total_coils-trnc( Total_coils))*360 //0angle_offset_init=(Total_coils-Active_coils)/2*360 //360height=Free_length-Wire_dia-Closed_height*2 //中间螺旋高度pitch=height/Active_coils//中间螺旋螺距exp=(pitch/Closed_height*(To tal_coils-Active_coils)/2) //指数radius=(OD-Wire_dia/2) //螺旋线半径t=1 //规律参数xt=cos(Dir*360*Active_coils*t +angle_offset_init)*radius //中间螺旋x规律xt1=cos(Dir*360*(Total_coils-Active_coils)/2*t)*radius //上端部螺旋x规律xt2=cos(-Dir*360*(Total_coils -Active_coils)/2*t+angle_offse t)*radius //下端部螺旋x规律yt=sin(Dir*360*Active_coils*t +angle_offset_init)*radius //中间螺旋y规律yt1=sin(Dir*360*(Total_coils-Active_coils)/2*t)*radius //上端部螺旋y规律yt2=sin(-Dir*360*(Total_coils-Active_coils)/2*t+angle_offset )*radius //下端部螺旋y规律zt=t*height+Closed_height+Wire_dia/2 //中间螺旋z规律zt1=(t^(exp)*Closed_height)+ Wire_dia/2 //上端部螺旋z规律zt2=(-t^(exp)*Closed_height) +height+Closed_height*2+Wir e_dia/2 //下端部螺旋z规律---------------------------------------------------------------------------------------(3)利用law curve建立三条规律曲线(4)tube(Outerdiameter=Wire_dia,Inner Diameter-0)二.椭圆形弹簧公式：－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－n=10 //弹簧卷数pitch=5 //弹簧螺距startangle=0 //弹簧起始角endangle=360*n //弹簧终止角semimajor=30 //椭圆长半轴semiminor=20 //椭圆短半轴t=1s=(1-t)*startangle+endangle*txt=semimajor*cos(s)yt=semiminor*sin(s)zt=n*t*pitchwire_dia=3 //弹簧线径－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－本贴包三、圆形缠绕弹簧公式：－－－－－－－－－－－－－－－－－－－－－－－－－－－－R=120 //圆半径r=10 //螺旋半径angle=360n=40 //螺旋卷数t=1a=t*n*360b=t*angletempR=R+r*cos(a) //变化中的3D 圆半径xt=tempR*cos(b)yt=tempR*sin(b)zt=r*sin(a)wire_dia=5 //弹簧线径－－－－－－－－－－－－－－－－－－－－－－－－－－－－四、沿任意曲线缠绕弹簧（1）公式－－－－－－－－－－－－－－－－－－－－－－－r=10wire_dia=5n=25a=0b=n*360－－－－－－－－－－－－－－－－－－－－－(2)建立一条光顺样条(3)过样条端点正交样条建立基准面(4)过样条端点正交样条建立基准轴本贴包含图片附件:5)以基准平面为草图平面建立草图，在草图上画长度为r的直线，直线左端点在竖值的基准轴上。

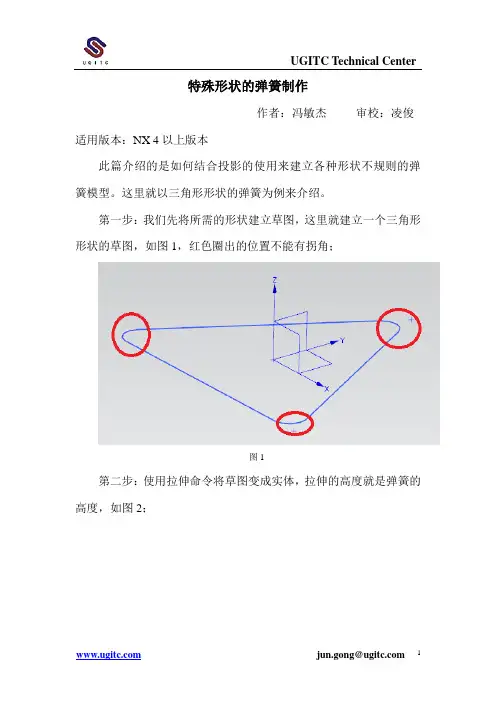
特殊形状的弹簧制作
作者：冯敏杰审校：凌俊适用版本：NX 4以上版本
此篇介绍的是如何结合投影的使用来建立各种形状不规则的弹簧模型。

这里就以三角形形状的弹簧为例来介绍。

第一步：我们先将所需的形状建立草图，这里就建立一个三角形形状的草图，如图1，红色圈出的位置不能有拐角；
图1
第二步：使用拉伸命令将草图变成实体，拉伸的高度就是弹簧的高度，如图2；
图2
第三步：制作螺旋线，其中需要注意的是螺旋线的直径需要大于拉伸出的实体，螺旋线的圈数和螺距便是最终弹簧的圈数和螺距，圈
数和螺距如图3所示，绘制完螺旋线后如图4；
图4
第四步：对螺旋线使用投影命令。

“要投影的曲线”选择螺旋线，要“投影的对象”选择实体的侧面，“投影方向”中选择“朝向直线”再选择Z轴（或实现在实体中心插入基准轴，然后选择基准轴）如图5，如图6三角形的螺旋线就绘制好了。

图6
第五步：选择三角形的螺旋线使用管道命令，如图7 输入半径，并且在“输出”选择“单段”，点击确定，并将弹簧以外的特征隐藏，三角形的弹簧就制作完成了，完成的效果如图8。

图7 图8。

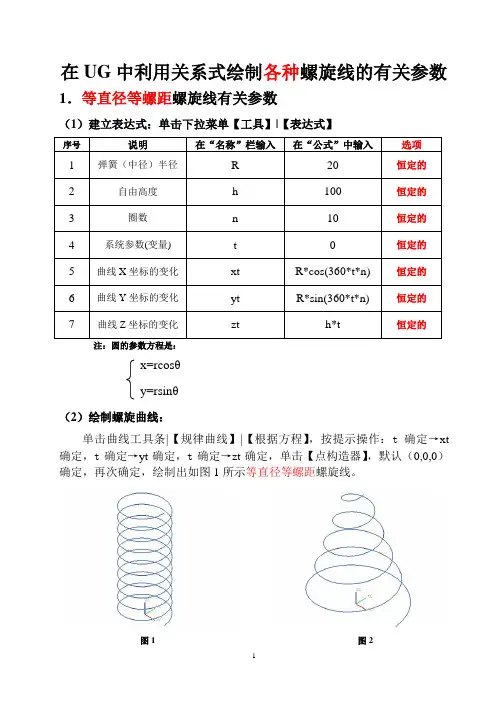
在UG中利用关系式绘制各种螺旋线的有关参数1．等直径等螺距螺旋线有关参数（1）建立表达式：单击下拉菜单【工具】|【表达式】注：圆的参数方程是：x=rcosθy=rsinθ（2）绘制螺旋曲线：单击曲线工具条|【规律曲线】|【根据方程】，按提示操作：t确定→xt 确定，t确定→yt确定，t确定→zt确定，单击【点构造器】，默认（0,0,0）确定，再次确定，绘制出如图1所示等直径等螺距螺旋线。

图1 图22．变直径等螺距螺旋线有关参数（1）建立表达式：单击下拉菜单【工具】|【表达式】（2）绘制螺旋曲线：单击曲线工具条|【规律曲线】|【根据方程】，按提示操作：t确定→xt 确定，t确定→yt确定，t确定→zt确定，单击【点构造器】，默认（0,0,0）确定，再次确定，绘制出如图2所示变直径等螺距螺旋线。

（3）创建基准平面：单击【基准平面】工具，创建水平基准平面XY平面，并向上偏置50(即h/2)，创建竖直基准平面XZ平面，偏置0。

（4）镜像螺旋线：在NX4版本中，单击【编辑】|【变换】|【用平面做镜像】|【复制】，选择图2螺旋线为镜像对象，选择水平面为镜像平面，得到图3所示螺旋线，再单击【编辑】|【变换】|【用平面做镜像】|【移动】，选择图3上半部螺旋线为镜像对象，选择竖直平面为镜像平面，得到图4螺旋线。

在NX6版本中，单击曲线工具条里的【镜像曲线】，选择图2螺旋线为镜像对象，选择水平面为镜像平面，【设置】选项输入曲线为“保持”得到图3所示螺旋线，再单击曲线工具条里的【镜像曲线】，选择图3上半部螺旋线为镜像对象，选择竖直平面为镜像平面，【设置】选项输入曲线为“隐藏”得到图4螺旋线。

3．等直径变螺距螺旋线有关参数（1）建立表达式：单击下拉菜单【工具】|【表达式】（2）绘制螺旋曲线：单击曲线工具条|【规律曲线】|【根据方程】，按提示操作：t 确定→xt 确定，t 确定→yt 确定，t 确定→zt 确定，单击【点构造器】，默认（0,0,0）确定，再次确定，绘制出如图5所示等直径变螺距螺旋线。

ug弹簧运动仿真技术介绍UG弹簧运动仿真技术介绍概要：UG软件是一款集成化的三维建模与仿真软件，拥有广泛的应用领域。

其中，UG弹簧运动仿真技术是UG软件中的一个重要功能，能够模拟和分析弹簧在运动过程中的力学行为，为设计师提供有力的辅助工具。

本文将深入探讨UG弹簧运动仿真技术的原理、应用场景和优点，并分享我在这方面的观点和理解。

第一部分：UG弹簧运动仿真技术的原理UG弹簧运动仿真技术基于弹簧的力学特性和UG软件的强大仿真计算能力，通过建立弹簧的几何模型和力学模型，模拟出弹簧在各种外部作用力下的运动行为。

其原理主要包括以下几个方面：1. 弹簧的刚度模型：在UG软件中，可以使用不同类型的刚度模型来描述弹簧的力学行为，常用的有线性刚度模型和非线性刚度模型。

线性刚度模型假设弹簧的应变与作用力成正比，而非线性刚度模型则考虑了弹簧的材料非线性特性，更加准确地描述了弹簧力学行为。

2. 外部作用力模型：UG软件可以根据实际需要，添加各种外部作用力，如重力、惯性力、弯曲力等，以模拟真实环境下弹簧的运动。

这些外部作用力可以通过UG软件的仿真计算功能进行定量分析，为设计师提供丰富的数据和结果。

3. 时间步长和计算方法：UG弹簧运动仿真技术中的时间步长和计算方法是保证仿真结果准确性的关键因素。

时间步长越小，仿真计算越精细，但同时计算量也更大。

UG软件提供了多种时间步长和计算方法的选择，以适应不同仿真场景和需求。

第二部分：UG弹簧运动仿真技术的应用场景UG弹簧运动仿真技术广泛应用于多个领域，以下列举几个典型的应用场景：1. 机械设计：在机械设计中，弹簧的运动行为往往是设计过程中的一个重要问题。

UG弹簧运动仿真技术能够模拟和分析弹簧在不同工况下的受力情况、受力分布以及变形情况，为设计师提供准确的数据，帮助他们进行设计评估和优化。

2. 汽车工程：汽车中使用大量的弹簧装置，如悬挂系统、减震器等。

UG弹簧运动仿真技术可以模拟和分析这些弹簧在不同路面条件下的运动行为，从而评估其性能和稳定性，并为优化设计提供指导。

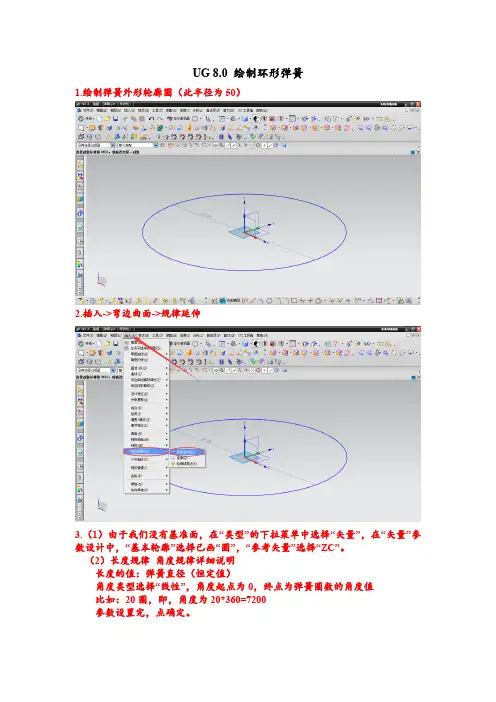
UG 8.0 绘制环形弹簧
1.绘制弹簧外形轮廓圆（此半径为50）
2.插入->弯边曲面->规律延伸
3.（1）由于我们没有基准面，在“类型”的下拉菜单中选择“矢量”，在“矢量”参数设计中，“基本轮廓”选择已画“圆”，“参考矢量”选择“ZC”。

（2）长度规律角度规律详细说明
长度的值：弹簧直径（恒定值）
角度类型选择“线性”，角度起点为0，终点为弹簧圈数的角度值
比如：20圈，即，角度为20*360=7200
参数设置完，点确定。

4.结果显示
5.提取边线，步骤：插入->来自体的曲线->抽取
抽取“边曲线”
抽取“边曲线”示意图
6.插入->扫掠->管道
管道设置参数：输出为“单段”
7.最终结果
Solidworks2013 绘制环形弹簧1.在“上视基准面”绘制R50的圆
2.建立与“前视基准面”相距半径长度的“基准面”
3在所建立的基准面上绘制弹簧丝的截面
4.插入->曲面->扫描曲面
曲面扫描：轮廓选弹簧丝截面，路径选弹簧基圆。

选项中：方向为“沿路径扭转”，定义方式为“旋转”，参数为圈数比如20圈，如下图。

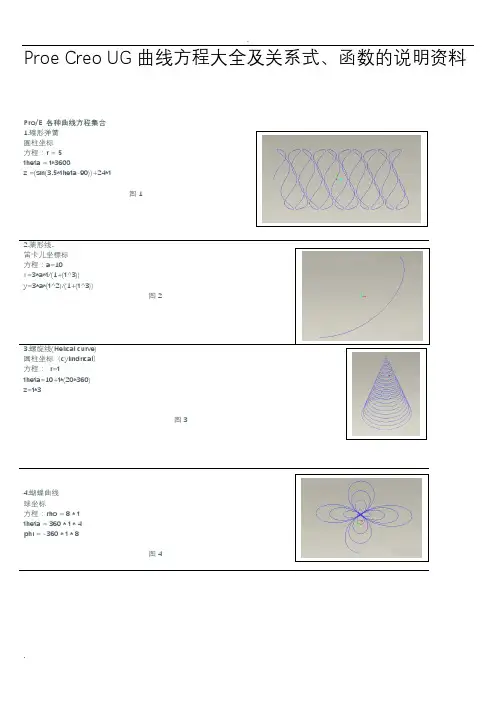
Proe Creo UG 曲线方程大全及关系式、函数的说明资料Pro/E 各种曲线方程集合 1.碟形弹簧 圓柱坐标 方程：r = 5 theta = t*3600z =(sin(3.5*theta-90))+24*t图1圆柱坐标（cylindrical ） 方程： r=ttheta=10+t*(20*360) z=t*3图34.蝴蝶曲线 球坐标方程：rho = 8 * t theta = 360 * t * 4 phi = -360 * t * 8图4图5笛卡儿坐标方程：x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t图611.心脏线圓柱坐标方程：a=10r=a*(1+cos(theta))theta=t*360Pro/E 各种曲线方程集合（二）Array22.外摆线迪卡尔坐标方程：theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta) Array图23 24.长短幅圆内旋轮线卡笛尔坐标方程：a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图2425.长短幅圆外旋轮线卡笛尔坐标方程：theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图2627.概率曲线！方程：笛卡儿坐标x = t*10-5y = exp(0-x^2)图2728.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图2829.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图2930.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图3031.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图3132.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图3233.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图3334.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图34 35.双曲正切y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图3536.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图3637.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图37r=t*(10*180)+1theta=10+t*(20*180)z=t图3839.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图39 40.封闭球形环绕曲线rho=2theta=360*tphi=t*360*10图4041.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0Pro/E 各种曲线方程集合（三）42.蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)图4243.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2图4344.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图4445.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2图4546.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图4647.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图4849.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16图4950 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程：a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图5152 簪形线球坐标方程：rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)图5354.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图5455. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)图5556.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图5657.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图5758.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图5859.环形二次曲线笛卡儿方程：x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图5960 蝶线球坐标：rho=4*sin(t*360)+6*cos(t*360^2)theta=t*360phi=log(1+t*360)*t*360图6061.正弦周弹簧笛卡尔：ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E 各种曲线方程集合（四）62.环形螺旋线x=（50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图6263.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图6364.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图6465.柱面正弦波线柱坐标：方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo （漩涡线）. 球坐标：rho=t*20^2theta=t*log(30)*60phi=t*7200图6667. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图6768.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图6869. 圆柱齿轮齿廓的渐开线方程：afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注：afa为压力角，取值范围是0到60，10为基圆半径。

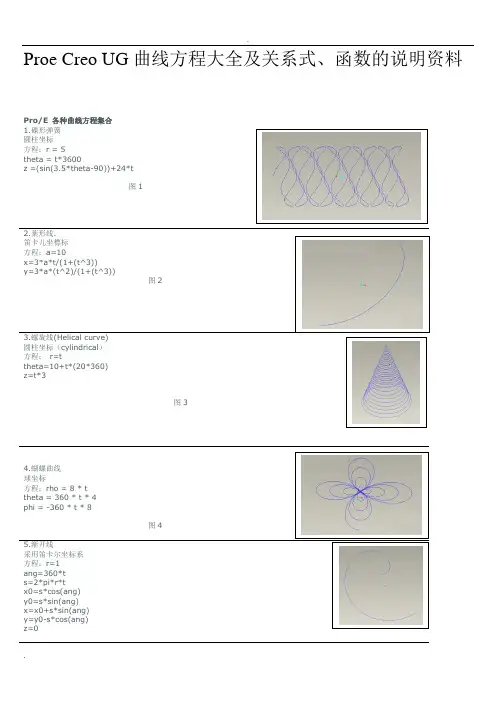
Proe Creo UG 曲线方程大全及关系式、函数的说明资料Pro/E 各种曲线方程集合 1.碟形弹簧 圓柱坐标 方程：r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t图12.葉形线.圆柱坐标（cylindrical ） 方程： r=ttheta=10+t*(20*360) z=t*3图3图5笛卡儿坐标方程：x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t图611.心脏线圓柱坐标方程：a=10r=a*(1+cos(theta))theta=t*360Pro/E 各种曲线方程集合（二）Array22.外摆线迪卡尔坐标方程：theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)图23 24.长短幅圆内旋轮线卡笛尔坐标b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图24 25.长短幅圆外旋轮线卡笛尔坐标方程：theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图2526. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图26 27.概率曲线！方程：笛卡儿坐标x = t*10-5y = exp(0-x^2)图27 28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图28 29.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图29 30.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图30 31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图31 32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图32 33.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图33 34.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图34 35.双曲正切y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图35 36.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图36 37.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图37r=t*(10*180)+1theta=10+t*(20*180)z=t图38 39.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图39 40.封闭球形环绕曲线rho=2phi=t*360*10图40 41.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0Pro/E 各种曲线方程集合（三）42.蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)图42 43.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2图43 44.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图44 45.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2图45 46.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图46 47.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图48 49.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16图49 50 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程：a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图51 52 簪形线球坐标方程：rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)图53 54.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图54 55. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)图55 56.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图5657.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图57 58.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图58 59.环形二次曲线笛卡儿方程：x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图59 60 蝶线球坐标：rho=4*sin(t*360)+6*cos(t*360^2)theta=t*360phi=log(1+t*360)*t*360图60 61.正弦周弹簧笛卡尔：ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E 各种曲线方程集合（四）62.环形螺旋线x=（50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图62 63.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图63 64.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图64 65.柱面正弦波线柱坐标：方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo （漩涡线）球坐标：rho=t*20^2theta=t*log(30)*60phi=t*7200图66 67. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图67 68.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图68 69. 圆柱齿轮齿廓的渐开线方程：afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注：afa为压力角，取值范围是0到60，10为基圆半径。

齿轮与弹簧出图
619 二、 将相关视图改为符合国标要求的简化画法
选择“菜单”/“GC 工具箱”/“齿轮”/“齿轮简化”命令，弹出“齿轮
简化”对话框。

从“类型”下拉列表框中选择“创建”选项。

“选择视图”按钮
处于被选中的状态，在图纸中选择全部3个视图作
为需要简化的视图。

在“齿轮简化”对话框的列表中选择“gear_1”锥齿轮作为要简化的
齿轮。

在“齿轮简化”对话框的“设置”选项组中确保选中“C ”复选框，设置
C 的值为3mm 。

在“齿轮简化”对话框中单击“确定”按钮，如图11-74所示。

图11-74 锥齿轮简化结果
11.4.2 弹簧出图
弹簧模型设计好之后，进入制图环境并创建所需图纸页后，使用“菜单”/“GC 工具箱”/“弹簧”级联菜单中的“弹簧简化画法”命令，可以根据弹簧三维模型的弹簧参数在图纸上自动生成采用简化画法的弹簧工程图，NX 会对简化后的视图进行部分关键尺寸的自动标注。

按照部件中的弹簧参数画出的弹簧简化视图示例如图11-75所示，该弹簧建模时采用的。

UGNX各种弹簧建模的参数资料UGNX是一款专业的计算机辅助设计（CAD）和计算机辅助制造（CAM）软件，广泛应用于各个工业领域。

在UGNX中，建模弹簧的方式有很多种，可以根据具体的需求选择不同的建模方法。

下面将介绍UGNX中几种常见的弹簧建模方法及其参数资料。

1.线弹簧建模：线弹簧是一种常见的弹簧结构，可以通过UGNX的“草图”模块进行建模。

线弹簧的主要参数包括弹簧的直径（D）、弹簧线经过的圈数（N）、弹簧的总长度（L）、弹簧的材料和弹性系数等。

2.螺旋弹簧建模：螺旋弹簧是一种具有螺旋线状结构的弹簧，也可以通过UGNX的“草图”模块进行建模。

螺旋弹簧的主要参数包括弹簧的直径（D）、螺旋线的半径（R）、螺旋线经过的圈数（N）、螺旋线的螺距（P）、弹簧的总长度（L）和弹簧的材料和弹性系数等。

3.液压弹簧建模：液压弹簧是一种基于液压原理工作的弹簧系统，可以通过UGNX的“组件建模”模块进行建模。

液压弹簧的主要参数包括弹簧的活塞直径（D）、活塞长度（L1）、活塞的活动范围（X1-X2）、油封的直径（D1/D2）、油封的材料和摩擦系数等。

4.薄壁波纹管弹簧建模：薄壁波纹管弹簧是一种由多个波纹组成的弹簧结构，可以通过UGNX的“板金”模块进行建模。

薄壁波纹管弹簧的主要参数包括波纹的高度（H）、波纹的角度（A）、波纹的数目（N）、波纹的材料和弹性系数等。

以上是UGNX中几种常见的弹簧建模方法及其参数资料，通过合理的选择方法和填写正确的参数，可以实现对各种弹簧的精准建模。

在实际应用中，还需要考虑到弹簧的工作环境和加载条件等因素，以保证设计的合理性和可靠性。

使用UGNX的强大建模功能，可以提高工作效率和准确性，为工程设计和制造提供有力的支持。

第4章常用通用件造型设计本章介绍常用通用件的三维实体设计，包括弹簧、螺栓、齿轮、凸轮和涡轮蜗杆等，通过这些常用件的练习，掌握三维造型的基本技巧。

4.1 弹簧设计本节通过3个实例讲解3种不同弹簧的三维建模方法。

例1设计圈数为10，螺距为30，半径为50，材料截面为圆形，直径为12，右旋弹簧。

（1）新建一个sping.prt文件，进入建模状态，单击【曲线】工具栏的按钮，图4-1所示【螺旋线】对话框，输入参数，单击按钮，结果如图4-2所示。

图4-1【螺旋线】对话框图4-2生成螺旋线（2）坐标系以X轴旋转90o，单击【实用工具】工具栏的按钮，弹出图4-3 所示对话框，选择和输入如图内容，单击按钮。

（3）绘制弹簧截面的圆。

单击【曲线】工具栏的按钮，弹出图4-4所示对话框，单击按钮，绘制螺旋线的端点为圆心，绘制半径为12的圆，结果如图4-5所示。

（4）沿导线扫掠。

单击【特征】工具栏的按钮，弹出图4-6所示【沿引导线扫掠】对话框，截面选择刚绘制的圆，引导线选择螺旋线，其他默认，单击按钮，结果如图4-6所示。

图4-3 【旋转WCS】对话框图4-4 【基本曲线】对话框图4-5 【沿引导线扫掠】对话框图4-6生成螺旋弹簧例2设计一圆锥螺旋弹簧，计圈数为7，螺距为30，半径由50线性变化到100，材料截面为10×16的矩形，右旋弹簧。

（1）新建一个screw_sping.prt的文件，进入建模状态，单击【曲线】工具栏的按钮，弹出图4-7 【螺旋线】对话框，输入圈数和螺距，单击单选一按钮，在弹出的对话框中单击按钮，输入如图4-8所示参数，生成如图4-9所示的结果。

（2）单击【特征】工具栏的按钮，在绘图区选择XOZ平面作为绘图平面，进入草图状态，绘制如图4-10所示的矩形截面，单击【草图生成器】工具栏上的按钮，回到建模状态。

图4-7 【螺旋线】对话框图4-8 半径的起始值图4-9 生成圆锥螺旋线图4-10 弹簧截面草图（3）单击【曲线】工具栏上的按钮，弹出图4-11【扫掠】对话框，单击截面的“选择曲线”，在绘图区选择刚绘制的矩形截面草图，单击引导线的“选择曲线”，选择螺旋线，单击定位方法的“指定矢量”按钮旁的下箭头，选择ZC，单击按钮，生成如图4-12所示的圆锥螺旋弹簧。