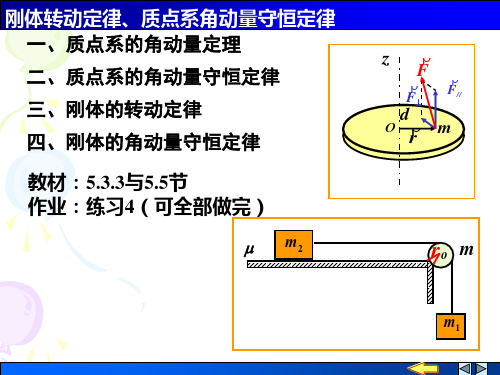
r r r L = r × mv = 恒矢量
r r r M = r ×F = 0
(1) F = 0 (2) F // r
(如有心力 如有心力) 如有心力
R O θ •A •B
如图所示,一半径为 例1.如图所示 一半径为 的光滑圆环置于 如图所示 一半径为R的光滑圆环置于 竖直平面内, 有一质量为m的小球穿在圆 竖直平面内 有一质量为 的小球穿在圆 环上, 并可在圆环上滑动. 环上 并可在圆环上滑动 小球开始静止 于圆环上的A点 该点通过环心 该点通过环心O的水平 于圆环上的 点(该点通过环心 的水平 面上), 然后从点A开始下滑 开始下滑.设小球与圆 面上 然后从点 开始下滑 设小球与圆 环间的摩擦略去不计.求小球滑到点 求小球滑到点B时 环间的摩擦略去不计 求小球滑到点 时 对环心O的角动量和角速度 的角动量和角速度. 对环心 的角动量和角速度
2 质点系对轴的角动量定理
质元 i 对 z 轴的角动量 Li =∆mi vi ri =∆mi ri2ω (方向沿 轴) 方向沿z轴 方向沿 所有质元对z轴的角动量为 所有质元对 轴的角动量为
上页
下页
返回
结束
z
O
ri • ∆ mi
L = ∑Li = ∑∆m r ω = Iω
2 i i
vi
其中
I = ∑∆mi ri2 称为转动惯量
L = Lxi + Ly j + Lz k
1、力矩 、 若外力F 作用在平面内某点P 若外力 作用在平面内某点
2.5.2 质点的角动量定理
O d
F 使物体产生转动,转点为 使物体产生转动 转点为O 转点为 OP = r , 力臂为 F对O点的 力臂为d. 对 点的 力矩为: 力矩为 M = Fd = Fr sinϕ 力矩的矢量表示: 力矩的矢量表示:



![[理学]第5章 刚体的定轴转动_OK](https://img.taocdn.com/s1/m/1edbe6d74b35eefdc8d333f9.png)