2017年浙江省高职考数学全真综合模拟试卷(十四)

2017年浙江省高职考数学全真综合模拟试卷（十八）一、选择题1. 已知集合{}是第四象限角x x M =，则下列结论正确的是 （ ) A 。

M ⊆︒30 B 。

{}M ∈︒-30 C.M ∈︒-30 D 。

{}︒<<︒=360270x x M2. 不等式262≤+-x 的解集用区间表示为 （ ） A 。

]4,2[- B 。

)4,2(- C. ]4,2[ D 。

]4,2(3. 已知命题2:=x p ，4:2=x q ，则下列结论正确的是 （ ）A 。

q p ⇒B 。

p q ⇒C 。

q p ⇒且p q ⇒D 。

以上均不对4. 已知函数⎩⎨⎧≥<=)0(10)0(10)(x x x x f ，则()[]=-7f f ( ） A.6 B.100 C 。

10- D 。

100-5. 如图，已知函数)(x f 的图像，则下列结论正确的是 （ ）A.函数)(x f 在区间]4,0[上单调递增B.函数最大值是4C 。

函数)(x f 在区间]2,1[上单调递减D 。

函数最小值是06. 已知二次函数122+-+=m x x y 与122-+=nx x y 的顶点相同，则n m +的值为（ ）A.10 B 。

8 C.7 D.97. 已知数列1,3，5，7，9，则其通项公式可记作 （ ） A 。

12-=n a n B.32-=n a n ()5,1∈nC 。

12-=n a n ]5,1[∈n D. 12-=n a n +∈N n 且]5,1[∈n8. 某小组有男生4名、女生3名，从中选3人参加学校组织的学习调研活动，要求至少1名女生参加,则有不同选派方法 （ ）A.35种B.18种C.30种D.31种9. 已知角α终边上一点)1,2(2---t ，则下列结论正确的是 ( ） A 。

0sin >α B.0cos >α C 。

0cos sin <αα D 。

0tan >α10. 化简)4sin()4cos(απαπ--+的结果是 （ ) A.αsin B 。

2017年浙江省高等职业技术教育招生考试模拟二数学试卷一、单项选择题(本大题共18小题，每小题2分，共36分)1、若集合{}22M x x =-≤<，{}0,1,2N =，则MN 等于（ ）A ．{}0B ．{}1C ．{}0,1,2D {}0,12、下列函数()f x 中，满足“对任意1x ，2x ∈（0，+∞），当1x <2x 时，都有1()f x >2()f x的是（ ） A ．()f x =1xB. ()f x =2(1)x - C .()f x =x sin D.()ln(1)f x x =+ 3、函数()=x f lg （x －2）x的定义域是（ ） A.[)3，＋∞ B.()3，＋∞ C.()2，＋∞ D.[)2，＋∞ 4、“m >n >0”是“方程mx 2＋ny 2＝1表示焦点在y 轴上的椭圆”的（ ） A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件5、已知α和β的终边关于x 轴对称，则下列各式中正确的是（ ） A.sinα=sinβ B. sin(α-π2) =sinβ C.cosα=cosβ D. cos(π2-α) =-cosβ6、已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a （ ）A ．1-B ．0C ．1D ．27、一个等差数列的前四项分别是x b x a ,,2,，则=ab（ ）A.21B.31C.1D.2 8、要从12人中选出5人去参加一项活动.A ，B ，C 三人至少一人入选有（ ）种不同选法A.666B.888C.444D.6689、已知点)6,(),4,3(a B A ，C 为AB 的中点，O 为原点，且25=OC ，则=a （ ） A ．7 B ．17 C ．7或17 D ．7或13-10、在ABC ∆中,若C B A 222sin sin sin <+,则ABC ∆的形状是（ ） A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定11、在平面直角坐标系xOy 中，四边形ABCD 的边AB ∥DC ，AD ∥BC ，已知点A (－2,0)，B (6,8)，C (8,6)，则D 点的坐标为（ ）A.(0，2)B.(0，－2)C.(2，－2)D.(2，2) 12、已知中心在原点的双曲线C 的右焦点为F （3，0），离心率等于32，则C 的方程是（ ）A ．22145x y -=B ．22145x y -=C ．22125x y -=D ．22125x y -=13、设l 是直线，a ，β是两个不同的平面（ ）A. 若l ∥a ，l ∥β，则a ∥βB. 若l ∥a ，l ⊥β，则a ⊥βC. 若a ⊥β，l ⊥a ，则l ⊥βD. 若a ⊥β, l ∥a ，则l ⊥β14、已知直线x =a （a >0）和圆（x －1）2+y 2=4相切，那么a 的值是（ ） A.5B.4C.3D.215、3sincos 23αα==若，则（ ） A ．23-B ．13-C ．13D ．2316、若使代数式的值在﹣1和2之间，x 可以取的整数有（ ） A.1个B.2个C ．3个D.4个17、若抛物线y 2=2px 的焦点坐标为（1,0）则准线方程为（ ） A.1=x B.1-=x C.2=x D ．2-=x18、在平面直角坐标系中，已知△AOB 三边所在直线的方程分别为x =0，y =0，2x +3y =30，则△AOB 内部和边上整点（即横、纵坐标均为整数的点）的总数是（ ） A.95 B.91 C.88 D.75二、填空题(本大题共8小题，每小题3分，共24分)19、已知t >0，则函数y ＝t 2－4t ＋1t的最小值为________．20、两袋分别装有写着0、1、2、3、4、5六个数字的6张卡片，从每袋中各任取一张卡片，所得两数之和等于7的概率为________．21、若cos(π4－θ)cos(π4＋θ)＝26，则cos2θ＝________．22、已知二次函数y =ax 2+bx +c 的顶点A （2，0），与y 轴的交点为B （0，－1），则其解析式为________．23、已知0,0ab bc <<，则直线ax by c +=通过第________象限.24、在等比数列{}n a （n ∈N*）中，若11a =，418a =，则该数列的前10项和为________．25、已知正方体1111ABCD A B C D -中，E 、F 分别为11BB CC 、的中点，那么异面直线AE与1D F 所成角的余弦值为____________.26、已知椭圆的中心在原点，且经过点()03，P ，b a 3=，则椭圆的标准方程为________．三、解答题(本大题共8小题，共60分)27、已知△ABC 是边长为2的正三角形，试用两种不同的方法在此三角形内分割出一个小三角形，分割出的小三角形的面积恰好是原来三角形面积的41，要求作出分割图形，并加以说明.28、在ABC ∆中,,,a b c 分别为内角,,A B C 所对的边，且满足sin 3cos 2A A +=.现给出三个条件：①2a =； ②45B =︒；③3c b =.试从中选出两个可以确定ABC ∆的条件，写出你的选择并以此为依据求ABC ∆的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分) .29、已知92⎪⎪⎭⎫ ⎝⎛x －x a 的展开式中，x 3的系数为49，求常数的a 值.30、已知函数⎩⎨⎧∈+-∈=]7,4(1)5(]4,1[log )(22x x x xx f ⑴ 在给定的直角坐标系内画出)(x f 的图象； ⑵ 写出)(x f 的单调递增区间（不需要证明）； ⑶ 写出)(x f 的最大值和最小值（不需要证明）．31、已知数集序列{1}, {3, 5}, {7, 9,11}, {13, 15, 17, 19},……,其中第n 个集合有n 个元素，每一个集合都由连续正奇数组成，并且每一个集合中的最大数与后一个集合最小数是连续奇数，(1) 求第n 个集合中最小数a n 的表达式； （2）求第n 个集合中各数之和S n 的表达式；32、已知函数2()sin sin cos 1f x x x x =++，(1)求函数()f x 的最小正周期;(2)求函数()f x 的单调递减区间.33、如图，在梯形ABCD中，AB∥CD，E，F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB=12，AD=5，BC=42，DE=4.现将△ADE，△CFB分别沿DE，CF折起，使A，B两点重合与点G，得到多面体CDEFG.（1）求证：平面DEG⊥平面CFG；（2）求多面体CDEFG的体积。

28 42017年浙江省高职考数学全真综合模拟试卷(十一)一、选择题1.已知I 为全集，集合M , N 是I 的子集，若M N = N ，则2.函数y 1 lg(x-1)的定义域是 x —23.函数y = 1( x = 0)的单调性为x4.直线3x - y-2 = 0的倾斜角为5•下列各式不能简化为 AD 的是A.是增函数B.是减函数C.在(0, •：：)上是减函数D.在(0,：：)上是增函数A. 30B.60C.120D.150A.&M -G NB. C | M 二 C | NC. M ND. M 二 NA.B. 'xxC. &x *1 且x 芒 0)D. fxx_1且 x = 2lA. (AB CD) BCB.OC CD - OAC. AD BC MB -MCD. MC DC - MA6•设a ，b 为实数，且a • b = 4， 则2a2b的最小值是A. 4B. 8 7.从不超过100的正数中每次任取一数, 3 11 A.B.-25100C.16 则该数能被11 C.-101D. 329整除的概率是1D.—108. “ a 二b ”是方程“ ax 2 by 2 =1 ”所表示的曲线为圆的A.必要非充分条件B.充分非必要条件9.下列条件能确定一个平面的是A. 3个点B. 一条直线和一个点c.充要条件 c.两条平行直线D.既非充分又非必要条件(D.空间的两条垂直直线10.已知数列 ①［前n 项和S n = n 2 • 2n 3，则 a 3 a 4 aC.27A. 1B .3811.已知sin 二tan J ::: 0 ,则二所在的象限为A.第一象限D. 49B.第二象限 12.下列抛物线中, 焦点到准线的距离为C.第三象限 1丄的是16D.第四象限A. y =8x 2B. y 二 4x2C.y 」x 21D. y x2 214•过圆（x-1） （y 2） =9的圆心且与直线A. 3x y -1 = 0B. 3x y 1 = 0C. x - 3y - 7 = 0D. x - 3y 7 = 015. A 、B 、C 、D 、E 五个人并排站成一排，如果 B 必须站在A 的右边（A 、B 可以不 相邻），不同的排法种数有 （）A. 24B. 60C. 90D.120二、填空题16. 函数f （x ）二- 5 -4x -x 2的定义域为 _____________ ，最小值为 _____________ ； 17.已知函数 fajr/x+Xx 〉0)，贝y f (2)= _____________ ，f(f(—2))=1 —x(x 兰0) 18.已知sin : =-，:•为第二象限角，贝U cos ：22 219.设双曲线亍-器1的左、右焦点分别为F 1、F 2，则左焦点已的坐标为一过已的直线与双曲线左支交于 A , B ，且AB =12，则卫ABF 2的周长为 _______________21.如图，将装在咼为 h 的圆柱形杯子中的饮料倒入杯口一样大，咼为-的圆锥形杯子中,2能倒 _________ 杯;三、解答题1,z7讥 兀22.计算 2— | + Ig1—3!+cos0 + tan —< 9丿 4223.已知方程x ■ ax （a 3^ 0有实数解，求a 的取值范围24. 已知 ABC 中，a ，b=8, c = 7, • C=60，求 ABC 的面积 S 「ABCQ25. 已知直线的斜率为 ，且直线被圆x -2x y 4^8所截得的弦长为 4，求此直4线的一般方程式26. 在等差数列 旨鳥中，已知a 3 =6 ,編=110 （1 ）求数列On f 的通项式13.设〉， （°，2）并且呎 4, tan ，则：一：一37JIA.—3 JIB.—4C. D.3x • y - 6 = 0平行的直线方程为_______ , tana =20. 1 3 5 ,2x -1) 2 4 6 2x 115 二的正整数解为116* 21題国（2 ）若从数列a ?依次按序取出a2, 34 , 38 ,…形成一个新的数列in /,求fbn?的第10项bio27•平面四边形ABCD 中，AB=BC=2，AD =CD =：訂5，. B=120，将ABC 沿四边形ABCD的对角线AC折起来，使DB的距离为,7，求:ABC所在平面与：ADC 所在平面所成二面角的平面角度数；第前厳田28•求（1 -3x）n展开式中的系数之和及第11项229. 已知函数f（x）=2s in x -si n（二2x），x R，求（1）函数f （x）的最小正周期（2）函数f （x）的值域2 230. 已知椭圆方程为-y 1，其右焦点为F4 3（1）求以F为焦点，以椭圆的中心点为顶点的抛物线方程（2）若直线y=2x+m被抛物线所截得的弦长AB =85，求m的值。

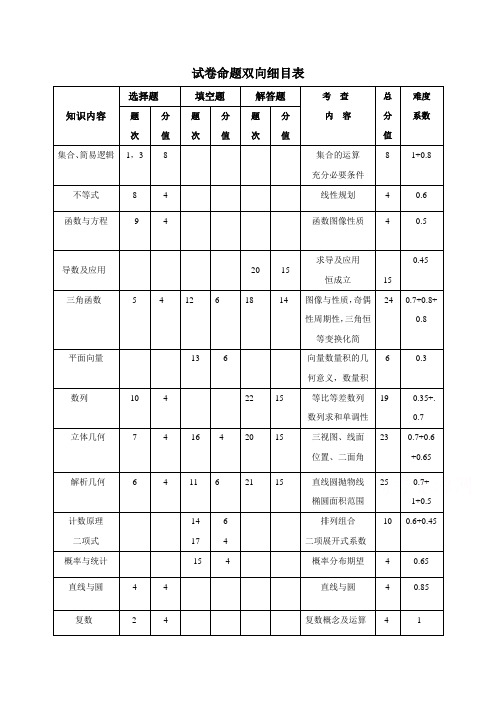
试卷命题双向细目表命题说明：1、试卷结构与2017年样卷保持基本一致⑴题型结构为， 10道选择、7道填空、5道解答的结构；⑵赋分设计为，选择每题4分、填空题前4题每题6分、每空3分，后3题每题4分，解答题共74分；⑶考查的内容，注重考查高中数学的主干知识：函数与导数，三角函数和解三角形，立体几何，解析几何，数列与不等式等。

2、立足基础，突出主干命题把重点放在高中数学课程中最基础、最核心的内容上，充分关注考生在学习数学和应用数学解决问题中必须掌握的核心观念、思想方法、基本概念和常用技能。

对基础知识的考查主要集中在小题上，具体知识点分布在集合、复数、向量、直线与圆、数列、函数图像、函数性质、线性规划、三视图、概率、三角函数、圆锥曲线性质、二项式等内容上，而且小题的考查直接了当，大部分是直接考查单一知识点，试卷对中学数学的核心内容和基本能力，特别是对高中数学的主干知识进行较为全面地考查。

注重了知识之间的内在联系，重点内容重点考，没有片面追求知识及基本思想、方法的覆盖面，反映了新课程的理念。

3、试题难度适中，层次分明试卷在三种题型中体现出明显的层次感，选择题、填空题、解答题，层层递进。

试卷的入口题和每种题型的入口题较好的把握了难度。

试卷对较难的解答题利用分步给分的设计方法，在化解难度的同时，又合理区分不同层次的考生。

试卷控制了较难题的比例，较难题基本集中在每种题型的最后一或两题，约占全卷的20%。

适合作为高考模拟试卷。

2017年高考模拟试卷 数学卷具体设计过程一、选择题：10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、（原题）已知R 为全集，B C A x x B x x A R 则},40|{},1|{<<=≤==（ ）A ．}4|{<x xB ．}10|{≤<x xC ．}0|{≤x xD ．}4|{≥x x（改编）定义集合A*B ＝｛x |x ∈A,且x ∉B ｝，若},40|{},1|{<<=≤=x x B x x A 则A*B=（ ）A ．}4|{<x xB ．}10|{≤<x xC ．}0|{≤x xD ．}4|{≥x x（命题意图：考查集合的含义及运算）2、（原题）在复平面内，复数zi i z +=+2对应的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限（改编）复数z 满足zi i z +=+2，则z 的虚部为 （ ）A ．i 23 B ．i 21C ．23D ．21（命题意图：考查复数加减乘除运算以及复数虚部的概念）3、（原题）已知p ：关于x 的不等式220x ax a +->的解集是R ，q :0a <,则p 是q 的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 （改编）已知p ：关于x 的不等式022≤-+a ax x 有解，q :1-<a ,则p 是q 的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 （命题意图：考查不等式知识及充要条件的判断）4．直线230x y --=与圆22:(2)(3)9C x y -++=交于,E F 两点，则ECF ∆的面积为 （ ▲ ）A ．23B ．52C ．553 D ． 43（命题意图：考查圆的几何问题）5、（原题）已知函数cosx -sinx cosx sinx ++=y ，关于下列说法正确的是 （ ）A.是奇函数，最小正周期为πB. 是偶函数，最小正周期为πC. 是奇函数，最小正周期为π2D. 是偶函数，最小正周期为π2(改编)已知函数)2sin(cos )cos(sin x x y +=，关于下列说法正确的是 （ ）A.是奇函数，最小正周期为πB. 是偶函数，最小正周期为πC. 是奇函数，最小正周期为π2D. 是偶函数，最小正周期为π2 （命题意图：考查三角函数图象与性质相关知识，理解奇偶性与周期性的定义）6、（原题）设点P 是双曲线22221(0,0)x y a b a b-=>>与圆2222x y a b +=+在第一象限的交点，其中12,F F分别是双曲线的左、右焦点，且12||2||PF PF =，则双曲线的离心率为_________________（改编）设双曲线C ：22221x y a b-=的左、右焦点分别为 F 1，F 2．若在双曲线的右支上存在一点P ，使得 |PF 1|＝3|PF 2|，则双曲线C 的离心率的取值范围为 ( )(A) (1,2](B)(C) (D)(1,2)（命题意图：考查双曲线定义和性质，利用性质求离心率）7、（原创）如图，正方体1111ABCD A B C D -的棱线长为1，线段11B D 上有两个动点E ，F ，且EF =，则下列结论中错误的是（ ） （A ）AC BE ⊥ （B ）//EF ABCD 平面（C ）三棱锥A BEF -的体积为定值 （D ）异面直线,AE BF 所成的角为定值 （命题意图：考查线面位置关系、线线角、三棱锥体积计算）8、（原题）实数y x ,满足⎪⎩⎪⎨⎧≤+≥+≥-.42,0,0y x y x y x λλ对任意的21>λ，该不等式组对应平面区域面积的最小值为( )（A ）4 （B ）518 （C ）516 （D ）3（改编）若不等式组13220x y x y λλ≤⎧⎪≤⎨⎪-+-≥⎩表示的平面区域经过四个象限，则实数λ的取值范围是（ ）A ．(,2)-∞B ．[1,1]-C ．[1,2)-D ．[1,)+∞ （命题意图：考查线性规划中的区域问题，同时考察数形结合的思想方法）9、（引用2016台州质检）已知函数(),()f x g x ''分别是二次函数()f x 和三次函数()g x 的导函数，它们在同一坐标系下的图象如图所示，设函数()()()h x f x g x =-，则（）A ．(1)(0)(1)h h h <<-B ．(1)(1)(0)h h h <-<C ．(0)(1)(1)h h h <-<D ．(0)(1)(1)h h h <<-（命题意图：考查导函数与原函数的关系及二次、三次函数的图象等知识）10、（引用2017温州一模）数列{}n a 的各项均为正数，n S 为其前n 项和，对于任意n N *∈，总有2,,n n na S a 成等差数列。

2017年浙江省高职考数学全真综合模拟试卷（十四）一、选择题设集合 , , 则 （ ）1. A.....B......C..... D.2. “1≤m ”是“方程022=+-m x x 有实根”的 （ ）3. A.充分非必要条...B.既非充分也非必要条..C.充要条..D.必要非充分条件设函数 在 上是增函数, 且 , 则 的取值范围是 （ ）4. A....... B...... C.......D.已知 , 则下式一定成立的是 （ ）5. A..... B......C........ D.6. 下列函数中1)0(=f 的是 （ ）A.⎩⎨⎧≤+->+=)0(2)0(1)(x x x x x f B.1)2()(2++=x x f C.1)(=x f D.12)(-=x x f 一工厂生产某种产品 件, 它们来自甲、乙、丙三条生产线。

已知从甲、乙、丙三条生产线上生产的个体数组成一个等差数列, 则乙生产线生产的产品件数为 （ ）A.8B.100C.60D.80在排列数的计算中, 根据 , 可知 的值等于 （ ）A.25B.24C.26D.23计算: （ ） A.23 B.21 C.21- D.23- 如果 是第三象限的角, 则 的值是 （ ）A.αsinB.αsin -C.αcosD.αcos -已知一个平面 与两条直线 , , 以下命题中正确的个数为 （ ）① , ② , ③ , ④A.1B.2C.3D.4当 , 时, 直线 通过 （ ）A.第一、二象限B.第二、三象限C.第三、四象限D.第一、四象限在 中, 为 中点, 若 , , 则 （ ）7. A...... B.......C...... D.设椭圆 的焦点为 , , 直线 过点 , 且与椭圆相交于 、 两点, 则 的周长为 （ ）A.6B.9C.12D.13若抛物线的顶点在原点, 对称轴为坐标轴, 且焦点到准线的距离为 , 则抛物线的方程是 （ ）A................B.8. C. 或.........D. 或9. 直线01234:=-+y x l 与两坐标轴围成的三角形的面积是 （ ）A.24B.12C.6D.18二、填空题10. 已知 , 则 的最小值是, 此时 ；11. 已知 （ ）满足 , 则 , ；12. 袋中装有 只乒乓球, 其中 只是白球, 只是黄球, 先后从袋中无放回的取出两球, 则取到 次白球 次黄球的概率是 ；13. 直线 与双曲线 仅有一个交点, 则 的值为 ；若直角三角形两直角边长分别为 和 , 则绕一条直角边旋转一周形成的几何体的最大侧面积为 , 最小侧面积为 ；函数 （ , ）的部分图像如图所示, 则该函数的最小正周期为 ；该函数的解析式为 ；三、解答题14. 若 , , 是一个集合中的三个元素, 实数 应满足什么条件15. 已知一次函数 满足 , 求 ；16. 已知 , 都是锐角, 且 , , 求 ；（1） 已知 的三个顶点 , , , 求：（2） 边AB 所在的直线方程17. 以 为原点, 且与 直线相切的圆的方程（1） 在等差数列 中, , , 求（2） 数列{}n a 的通项公式（3） 数列⎭⎬⎫⎩⎨⎧+11n n a a 的前n 项和如图所示, 在正三棱锥 中, 底边长等于 , 侧面与底面所成的二面角为 , 求:（1）正三棱锥ABC V -的体积；（2）侧棱VA 的长18. 如果 的二项展开式中的中间三项依次成等差数列, 求实数 的值19. 在 中, , , , 求 的周长（1） 已知中心在原点, 焦点在 轴上的双曲线的渐近线方程是 , 且过点 , 求（2） 双曲线方程（3） 双曲线被点)3,8(A 平分的弦PQ 所在的直线方程。

一、选择题1. 设{}1≤=x x P ，32=a ，则下列各式中正确的是 （ ） A.P a ⊆ B.P a ∉ C. {}P a ∈ D. {}P a ⊆2. 已知1>ab ，0<b ，则有 （ ） A.b a 1>B.b a 1<C.b a 1->D.ab 1> 3. 已知函数)(x f 在)5,2(-上是增函数，则下列各式正确的是 （ ） A. )3()2(f f <- B. )3()4(f f < C.)1()1(f f =- D.)1()0(->f f 4. 下列四个直线方程中有三个方程表示的是同一条直线，则表示不同直线的方程是 （ ） A.012=+-y x B.12+=x y C.112=+-yx D.)0(21-=-x y 5. 一次函数b kx y -=（0<k ，0>b ）的图象一定不经过的象限为 （ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限 6. 函数xx y -+=11的定义域是 （ ）A.[)()+∞,11,0YB. ()()+∞,11,0YC.),0(+∞D.[)1,1- 7. 若x 的不等式a x -≥-32的解集为R ，则实数a 的取值范围是 （ ） A.),3(+∞ B. ),3[+∞ C.)3,(-∞ D. ]3,(-∞ 8. 在数列{}n a 中，若95=a ，且1223+=++n n a a ，则=3a （ ） A.53 B.52 C.23 D.549. 若直线1l ：062=++y x 与2l ：013=-+ky x 互相不垂直，则k 的取值范围是 （ ）A.⎪⎭⎫ ⎝⎛+∞-⎪⎭⎫ ⎝⎛-∞-,2323,Y B. ⎪⎭⎫⎝⎛+∞⎪⎭⎫ ⎝⎛∞-,2323,YC. ⎪⎭⎫ ⎝⎛+∞-⎪⎭⎫ ⎝⎛-∞-,2323,I D. ⎪⎭⎫⎝⎛+∞⎪⎭⎫ ⎝⎛∞-,2323,I10. 已知平面//α平面β，且α⊂a ，β⊂b ，则直线a 与直线b （ ）A.平行B.相交C.异面D.没有公共点11. 抛掷两颗骰子，出现点数和为6的概率是 （ ） A.61 B.365C.121D.181 12. 已知)3,1(-=a ，若0a 是的单位向量，则下列各式正确的是 （ ）A.0a a >B.10=aC. ⎪⎪⎭⎫⎝⎛-=23,210a D. 02a a = 13. 若22sin -=α，α为第三象限角，则ααπcos )sin(--的值为 （ ） A.1- B.0 C.1 D.214. 抛物线22x y -=的焦点坐标是 （ ） A.⎪⎭⎫ ⎝⎛-0,21 B.)0,8(- C.⎪⎭⎫ ⎝⎛-81,0 D.)2,0(-15. 若方程1sin cos 22=-y x θθ表示焦点在y 轴上的双曲线，则θ是 （ ） A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角 二、填空题16. 已知0>x ，则xx 43--有最大值 ； 17. 直线l 过点)0,1(-且与直线01=-y 的夹角是︒60，则直线l 的一般式方程为 ；18. 若x ，y 是实数，则913113+-+-=x x y ，则=--32)(y x ；19. 将半径为4米的半圆围成圆锥的侧面，则圆锥的体积为 ； 20. 已知81cos sin -=θθ，⎪⎭⎫⎝⎛∈ππθ2,23，则=-θθcos sin ； 21. 若点),(y x M 满足0>xy ，0<+y x ，则以射线OM 为终边的对应角α为第 象限角； 三、解答题22. 求不等式02342>---x x x 的解集；23. 求以直线012=+-y x 与02=++y x 的交点为圆心，且与直线042=+-y x 相切的圆；24. 在ABC ∆中，已知︒=∠45B ，22=AC ，32=AB ，求C ∠；25. 求多项式5432)1()1()1()1()1(x x x x x -+-+-+-+-的展开式中含3x 的项；26. 已知双曲线C 与椭圆364922=+y x 有共同的焦点，且离心率为25，求： （1） 双曲线C 的标准方程； （2） 双曲线的渐近线方程；27. 已知正方形ABCD 的边长为1，分别取BC ，CD 的中点E ，F ，连结AE ，EF ，AF 以AE ，EF ，AF 为折痕折叠，使点B 、C 、D 重合于上点P ，求： （1） 二面角A EF P --的平面角的正弦值； （2） 三棱锥AEF P -的体积；28. 已知x x x x f cos sin 34sin 4)(2+=：求：（1） )(x f 的最小正周期； （2） )(x f 的最小值及相应x 的值；29. 已知数列{}n a 满足1a ，11-=-+n n a a ，数列{}n b 满足11a b =，241a a b b n n =+，求： （1） 数列{}n a 的通项公式； （2） 数列{}n b 的前10项和；30. 如图所示，在一张矩形纸的边上找一点E ，过E 点减去两个边长分别是AE 、DE 的正方形得到图形M （图中阴影部分）已知，，（1） 设x DE =，图形M 的面积为y ，写出y 与x 之间的函数关系式； （2） 当x 为何值时，图形M 的面积最大？ （3） 求出图形M 面积的最大值；。

2017年浙江省高职考数学全真综合模拟试卷（十五）一、选择题1. 设集合{}0>=x x A ，{}21≥-<=x x x B 或，则=B A （ ） A.{}2≥x x B. {}21≥-<x x x 或 C. {}01>-<x x x 或 D. {}0>x x2. “1>x ”是“312>+x ”的 （ ）A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件3. 如果31<<a ，24<<-b ，则b a +的取值范围是 （ ）A.)2,1(B.)5,1(-C.)5,3(-D.)3,1(4. 下列函数在区间),0(+∞上为增函数的是 （ ）A.13-=x yB.x x f 2log )(=C.x x g )21()(=D.x x h sin )(=5. 某物体一天当中的温度T （C ︒）是时间t （h ）的函数：603)(2+-=t t t T ，0=t 表示中午00:12，则下午00:16物体的温度是 （ ）A.C ︒60B.C ︒64C.C ︒68D.C ︒706. 对于向量下列等式一定成立的是 （ ）+=+ B. -=C. =λD. λ+=+7. 在等差数列{}n a 中，n a m =，m a n =，则=+n m a （ ）A.n m +B.n m -C.mnD.08. 从3名男生和5名女生中选出3人参加某个座谈会，若3人中必须有男有女，则不同的选法有 （ ）A.45种B.30种C.15种D.56种9. 下列方程表示椭圆的是 （ ） A. 1222=-y x B.122=+y x C. 12=x D. 1222=+y x 10. 在︒︒360~0范围内，与︒-880终边相同的角是 （ ）A.︒100B.︒120C.︒200D.︒22011. 抛物线24x y -=的准线方程是 （ ）A.1=xB.1-=xC.161-=yD. 161=y12. 若552cos =α，1010sin =β，且α与β均为锐角，则=+βα （ ） A.4π B.2π C.43π D.π 13. 下列命题中正确的个数有 （ ）①与同一个平面垂直的直线和平面（直线在该平面外）相互平行②与同一个平面垂直的两个平面相互垂直③与同一个平面垂直的两个平面相互平行④与同一个平面垂直的；两条直线垂直A.1个B.2个C.3个D.4个14. 已知0>m ，则mm 16+取得最小值的条件是当且仅当实数=m （ ） A.2 B.4 C.8 D.1615. 如图所示，防止的边长为1的正方形PABC 沿x 轴正方形 滚动，设顶点),(y x P 的轨迹方程是)(x f y =，设与其在x 轴两个相邻交点的图像与x 轴所围成区域面积为S ，则S 的值为 （ ） A.1+=πS B. 12+=πS C. 13+=πS D. π=S二、填空题16. 已知扇形的中心角为︒60，半径为10，那么扇形的弧长是 ，扇形的面积是 ；17. 已知{}n a 为等差数列，若π8951=++a a a ，则{}n a 前9项的和=n S ，)cos(73a a +的值为 ；18. 已知m =+ααcos sin ，则=α2sin ，=-ααcos sin ；19. 从6张不同的扑克牌中，每次任取一张，有放回地取两次，则两次取得同一张牌的概率是 ；20. 已知一个长方体共顶点的三条边长分别为1，2，3，则这个长方体的对角线长是 ；它的外接球的体积是 ；21. 若直线1-=kx y 与双曲线122=-x y 仅有一个交点，则k 的值为 ；三、解答题22. 当]2,1[-∈x 时，求函数3-=x a y （10<<a ）的取值范围23. 已知一个圆的圆心为)0,4(，并且此圆过原点（1） 求该圆的方程；（2） 求直线x y 3=被该圆截得的弦长24. 已知函数x x x x f cos sin 32cos 2)(2+-=（1） 将)(x f 化成B x A ++)sin(ϕω的形式；（2） 求)(x f 的最大值和最小正周期；25. 已知函数)34lg(2++=ax ax y 的定义域为R ，求实数a 的取值范围26. 已知8)(xa x -展开式中常数项为1120，求实数a 的值 27. 如图所示，已知AOB ∆是直角三角形，︒=∠90AOB ，︒=∠60OAB ，4=AB ，AOB ∆与AOC ∆全等，二面角B AO C --是直角二面角，点D 是AB 的中点，求直线AO 与CD 所成角的余弦值；28. 在ABC ∆中，3tan =B ，31cos =C ，63=AC ，求ABC ∆的面积 29. 某机床厂今年年初用98万元购进一台数控机床，并立即投入生产使用，计划第一年维修、保养费用12万元，从第二年开始，每年所需维修、保养费用比上一年增加4万元，该机床使用后，每年的总收入为50万元，设使用x 年后数控机床的盈利额为y 万元（1） 写出y 与x 之间的函数关系式（2） 从第几年开始，该机床开始盈利（盈利额为正值）？30. 已知抛物线的顶点在原点，焦点在圆03222=--+x y x 的圆心O 上，（1） 求抛物线的方程（2） 若过抛物线的焦点且倾斜角为︒45的直线与抛物线分别交于A 、B 两点，求AB ；。