【最新】武汉市硚口区八年级下册期中数学试卷(有答案)

2016-2017学年湖北省武汉市硚口区八年级（下）期中数学试卷一、选择題（共10小题，每小题3分，共30分下列各题均有四个备选选项，其中有且只有一个正确，请在答题卡上将正确答案的字母涂黑．1．若式子在实数范围内有意义，则a的取值范围是（）A．a＞3B．a≥3C．a＜3D．a≤32．若＝4﹣b，则b满足的条件是（）A．b＞4B．b＜4C．b≥4D．b≤43．以下列长度的线段为边，不能构成直角三角形的是（）A．2，3，4B．1，1，C．D．5，12，134．在平行四边形ABCD中，已知∠A＝60°，则∠D的度数是（）A．60°B．90°C．120°D．30°5．下列计算正确的是（）A．B．C．D．6．如图，一竖直的木杆在离地面4米处折断，木頂端落在地面离木杆底端3米处，木杆折断之前的高度为（）A．7米B．8米C．9米D．12米7．如图，▱ABCD的顶点坐标分别为A（1，4）、B（1，1）、C（5，2），则点D的坐标为（）A．（5，5）B．（5，6）C．（6，6）D．（5，4）8．如图，A（0，1），B（3，2），点P为x轴上任意一点，则PA+PB的最小值为（）A．3B．C．D．9．如图，在正方形网格中用没有刻度的直尺作一组对边长度为的平行四边形．在1×3的正方形网格中最多作2个，在1×4的正方形网格中最多作6个，在1×5的正方形网格中最多作12个，则在1×8的正方形网格中最多可以作（）A．28个B．42个C．21个D．56个10．如图，正方形ABCD中，点O为对角线的交点，直线EF过点O分别交AB、CD于E、F两点（BE＞EA），若过点O作直线与正方形的一组对边分別交于G、H两点，满足GH＝EF，则这样的直线GH（不同于直线EF）的条数共有（）A．1条B．2条C．3条D．无数条二、填空题（每小题3分，共18分11．16的平方根是．12．计算：÷＝．13．已知等边三角形的边长为6，则面积为．14．如图，菱形ABCD的周长为8，对角线BD＝2，则对角线AC为．15．如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点E的坐标．16．如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝5，DA＝5，则BD的长为．三、解答题（共8小題，共72分）17．（8分）计算：①；②．18．（8分）计算：①②19．（8分）一根直立于水中的芦节（BD）高出水面（AC）2米，一阵风吹来，芦苇的顶端D恰好到达水面的C处，且C到BD的距离AC＝6米，求水的深度（AB）为多少米？20．（8分）如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD．求证：四边形ABCD是菱形．21．（8分）如图，在4×4的正方形网格中，每个小正方形的边长都为1．（1）求△ABC的周长；（2）求证：∠ABC＝90°；（3）若点P为直线AC上任意一点，则线段BP的最小值为．22．（10分）如图1，点D、E、F、G分别为线段AB、OB、OC、AC的中点．（1）求证：四边形DEFG是平行四边形；（2）如图2，若点M为EF的中点，BE：CF：DG＝2：3：，求证：∠MOF＝∠EFO．23．（10分）已知点A为正方形BCDE内一动点，满足∠DAC＝135°，且b＝+5．（1）求a、b的值；（2）如图1，若线段AB＝b，AC＝a，求线段AD的长；（3）如图2，设线段AB＝m，AC＝n，AD＝h，请探究并直接写出三个量m2、n2、h2之间满足的数量关系．24．（12分）在正方形ABCD中，点E为边BC（不含B点）上的一动点，AE⊥EF，且AE＝EF，FG⊥BC的延长线于点G．（1）如图1，求证：BE＝FG；（2）如图2，连接BD，过点F作FH∥BC交BD于点H，连接HE，判断四边形EGFH的形状，并给出证明；（3）如图3，点P、Q为正方形ABCD内两点，AB＝BQ，且∠ABQ＝30°，BP平分∠QBC，BP ＝DP，若BC＝+1，求线段PQ的长．2016-2017学年湖北省武汉市硚口区八年级（下）期中数学试卷参考答案与试题解析一、选择題（共10小题，每小题3分，共30分下列各题均有四个备选选项，其中有且只有一个正确，请在答题卡上将正确答案的字母涂黑．1．若式子在实数范围内有意义，则a的取值范围是（）A．a＞3B．a≥3C．a＜3D．a≤3【分析】根据被开方数大于等于0列式计算即可得解．【解答】解：由题意得，a﹣3≥0，解得a≥3．故选：B．【点评】本题考查的知识点为：二次根式的被开方数是非负数．2．若＝4﹣b，则b满足的条件是（）A．b＞4B．b＜4C．b≥4D．b≤4【分析】根据二次根式的性质列出不等式，解不等式即可．【解答】解：∵＝4﹣b，∴4﹣b≥0，解得，b≤4，故选：D．【点评】本题考查的是二次根式的化简，掌握二次根式的性质：＝|a|是解题的关键．3．以下列长度的线段为边，不能构成直角三角形的是（）A．2，3，4B．1，1，C．D．5，12，13【分析】根据勾股定理的逆定理对四个选项进行逐一判断即可．【解答】解：A、∵22+32＝13≠42，∴不能构成直角三角形，故本选项符合要求；B、∵12+12＝（）2，∴能构成直角三角形，故本选项不符合要求；C、∵（）2+（）2＝（）2，∴能构成直角三角形，故本选项不符合要求；D、∵52+122＝132，∴能构成直角三角形，故本选项不符合要求．故选：A．【点评】本题考查的是勾股定理的逆定理，即如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形．4．在平行四边形ABCD中，已知∠A＝60°，则∠D的度数是（）A．60°B．90°C．120°D．30°【分析】根据平行四边形邻角互补的性质即可求解．【解答】解：∵在平行四边形ABCD中，∠A＝60°，∴∠D＝180°﹣60°＝120°．故选：C．【点评】此题主要考查了平行四边形的性质，关键是熟练掌握平行四边形邻角互补的知识点．5．下列计算正确的是（）A．B．C．D．【分析】根据二次根式的性质与同类二次根式的定义逐一计算可得．【解答】解：A、与不是同类二次根式，不能合并，此选项错误；B、4﹣3＝3，此选项错误；C、×＝，此选项正确；D、（3）2＝18，此选项错误；故选：C．【点评】本题主要考查二次根式的混合运算，解题的关键是熟练掌握二次根式的性质和二次根数混合运算顺序及其法则．6．如图，一竖直的木杆在离地面4米处折断，木頂端落在地面离木杆底端3米处，木杆折断之前的高度为（）A．7米B．8米C．9米D．12米【分析】由题意得，在直角三角形中，知道了两直角边，运用勾股定理即可求出斜边，从而得出这棵树折断之前的高度．【解答】解：∵一竖直的木杆在离地面4米处折断，頂端落在地面离木杆底端3米处，∴折断的部分长为＝5（米），∴折断前高度为5+4＝9（米）．故选：C．【点评】此题考查了勾股定理的应用，主要考查学生对勾股定理在实际生活中的运用能力．7．如图，▱ABCD的顶点坐标分别为A（1，4）、B（1，1）、C（5，2），则点D的坐标为（）A．（5，5）B．（5，6）C．（6，6）D．（5，4）【分析】由四边形ABCD是平行四边形，可得AB∥CD，AB＝CD，继而求得答案．【解答】解：∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∵A（1，4）、B（1，1）、C（5，2），∴AB＝3，∴点D的坐标为（5，5）．故选：A．【点评】此题考查了平行四边形的性质．注意平行四边形的对边平行且相等．8．如图，A（0，1），B（3，2），点P为x轴上任意一点，则PA+PB的最小值为（）A．3B．C．D．【分析】作点A关于x轴的对称点A′．连接BA′交x轴于点P，此时PA+PB的值最小．根据勾股定理求出BA′即可；【解答】解：作点A关于x轴的对称点A′．连接BA′交x轴于点P，此时PA+PB的值最小．PA+PB的最小值＝BA′＝＝3，故选：B．【点评】本题考查轴对称﹣最短问题，坐标用图形的性质等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型．9．如图，在正方形网格中用没有刻度的直尺作一组对边长度为的平行四边形．在1×3的正方形网格中最多作2个，在1×4的正方形网格中最多作6个，在1×5的正方形网格中最多作12个，则在1×8的正方形网格中最多可以作（）A．28个B．42个C．21个D．56个【分析】根据已知图形的出在1×n的正方形网格中最多作2×（1+2+3+…+n﹣2）个，据此可得．【解答】解：∵在1×3的正方形网格中最多作2＝2×1个，在1×4的正方形网格中最多作6＝2×（1+2）个，在1×5的正方形网格中最多作12＝2×（1+2+3）个，……∴在1×8的正方形网格中最多作2×（1+2+3+4+5+6）＝42个，故选：B．【点评】本题主要考查图形的变化规律，解题的关键是根据题意得出在1×n的正方形网格中最多作2×（1+2+3+…+n﹣2）个．10．如图，正方形ABCD中，点O为对角线的交点，直线EF过点O分别交AB、CD于E、F两点（BE＞EA），若过点O作直线与正方形的一组对边分別交于G、H两点，满足GH＝EF，则这样的直线GH（不同于直线EF）的条数共有（）A．1条B．2条C．3条D．无数条【分析】根据对称性以及旋转变换的性质，画出图形即可解决问题，如图所示；【解答】解：根据对称性以及旋转变换的性质可知满足条件的线段有3条，如图所示；故选：C．【点评】本题考查正方形的性质、旋转变换等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．二、填空题（每小题3分，共18分11．16的平方根是±4．【分析】根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2＝a，则x就是a的平方根，由此即可解决问题．【解答】解：∵（±4）2＝16，∴16的平方根是±4．故答案为：±4．【点评】本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．12．计算：÷＝3．【分析】根据二次根式是除法法则进行计算．【解答】解：原式＝＝＝＝3．故答案是：3．【点评】本题考查了二次根式的乘除法．二次根式的除法法则：÷＝（a≥0，b＞0）．13．已知等边三角形的边长为6，则面积为9．【分析】根据等边三角形三线合一的性质可得D为BC的中点，即BD＝CD，在直角三角形ABD 中，已知AB、BD，根据勾股定理即可求得AD的长，即可求三角形ABC的面积，即可解题．【解答】解：等边三角形高线即中线，故D为BC中点，∵AB＝6，∴BD＝3，∴AD＝＝3，∴等边△ABC的面积＝BC•AD＝×6×3＝9．故答案为：9．【点评】本题考查了勾股定理在直角三角形中的运用，等边三角形面积的计算，本题中根据勾股定理计算AD的值是解题的关键．14．如图，菱形ABCD的周长为8，对角线BD＝2，则对角线AC为2．【分析】设菱形的对角线相交于O，根据菱形性质得出AB＝BC＝CD＝AD，AC⊥BD，BO＝OD，AO＝OC，求出OB，根据勾股定理求出OA，即可求出AC．【解答】解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，AC⊥BD，BO＝OD，AO＝OC，∵菱形的周长是8，∴DC＝×8＝2，∵BD＝2，∴OD＝1，在Rt△DOC中，OC＝＝，∴AC＝2OC＝2，故答案为：2．【点评】本题考查了菱形的性质和勾股定理，注意：菱形的对角线互相垂直平分，菱形的四条边相等．15．如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点E的坐标（0，）．【分析】先证明EA＝EC（设为x）；根据勾股定理列出x2＝12+（3﹣x）2，求得x＝，即可解决问题．【解答】解：由题意知：∠BAC＝∠DAC，AB∥OC，∴∠ECA＝∠BAC，∴∠ECA＝∠DAC，∴EA＝EC（设为x）；由题意得：OA＝1，OC＝AB＝3；由勾股定理得：x2＝12+（3﹣x）2，解得：x＝，∴OE＝3﹣＝，∴E点的坐标为（0，）．故答案为：（0，）．【点评】该题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答；对综合的分析问题解决问题的能力提出了较高的要求．16．如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝5，DA＝5，则BD的长为．【分析】作DM⊥BC，交BC延长线于M，由勾股定理得出AC2＝AB2+BC2＝25，求出AC2+CD2＝AD2，由勾股定理的逆定理得出△ACD是直角三角形，∠ACD＝90°，证出∠ACB＝∠CDM，得出△ABC≌△CMD，由全等三角形的性质求出CM＝AB＝3，DM＝BC＝4，得出BM＝BC+CM ＝7，再由勾股定理求出BD即可．【解答】解：作DM⊥BC，交BC延长线于M，如图所示：则∠M＝90°，∴∠DCM+∠CDM＝90°，∵∠ABC＝90°，AB＝3，BC＝4，∴AC2＝AB2+BC2＝25，∴AC＝5，∵AD＝5，CD＝5，∴AC2+CD2＝AD2，∴△ACD是直角三角形，∠ACD＝90°，∴∠ACB+∠DCM＝90°，∴∠ACB＝∠CDM，∵∠ABC＝∠M＝90°，在△ABC和△CMD中∴△ABC≌△CMD，∴CM＝AB＝3，DM＝BC＝4，∴BM＝BC+CM＝7，∴BD＝＝＝，故答案为：．【点评】本题考查了全等三角形的判定与性质、勾股定理、勾股定理的逆定理；熟练掌握全等三角形的判定与性质，由勾股定理的逆定理证出△ACD是直角三角形是解决问题的关键．三、解答题（共8小題，共72分）17．（8分）计算：①；②．【分析】①先化简各二次根式，再合并同类二次根式即可得；②根据二次根式的乘法运算法则计算可得．【解答】解：①原式＝3﹣4+2＝；②原式＝＝＝3．【点评】本题主要考查二次根式的混合运算，解题的关键是熟练掌握二次根式的性质和二次根数混合运算顺序及其法则．18．（8分）计算：①②【分析】①先利用完全平方公式和平方差公式计算乘法和乘方，再合并同类二次根式即可得；②先化简各二次根式，再计算乘法，继而合并同类二次根式即可得．【解答】解：①原式＝2+6+4+3﹣6＝5+4；②原式＝6×﹣×6＝3﹣15＝﹣12．【点评】本题主要考查二次根式的混合运算，解题的关键是熟练掌握二次根式的性质及二次根式混合运算顺序和运算法则．19．（8分）一根直立于水中的芦节（BD）高出水面（AC）2米，一阵风吹来，芦苇的顶端D恰好到达水面的C处，且C到BD的距离AC＝6米，求水的深度（AB）为多少米？【分析】先设水深为x，则AB＝x，求出x的长，再由勾股定理即可得出结论．【解答】解：∵先设水深为x，则AB＝x，BC＝（x+2），∵AC＝6米，在△ABC中，AB2+AC2＝BC2，即62+x2＝（x+2）2，解得x＝8（米）．答：水深AB为8米．【点评】本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．20．（8分）如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD．求证：四边形ABCD是菱形．【分析】根据平行线的性质得出∠ADB＝∠DBC，∠DAC＝∠BCA，根据角平分线定义得出∠DAC ＝∠BAC，∠ABD＝∠DBC，求出∠BAC＝∠ACB，∠ABD＝∠ADB，根据等腰三角形的判定得出AB＝BC＝AD，根据平行四边形的判定得出四边形ABCD是平行四边形，即可得出答案．【解答】证明：∵AE∥BF，∴∠ADB＝∠DBC，∠DAC＝∠BCA，∵AC、BD分别是∠BAD、∠ABC的平分线，∴∠DAC＝∠BAC，∠ABD＝∠DBC，∴∠BAC＝∠ACB，∠ABD＝∠ADB，∴AB＝BC，AB＝AD∴AD＝BC，∵AD∥BC，∴四边形ABCD是平行四边形，∵AD＝AB，∴四边形ABCD是菱形．【点评】本题考查了等腰三角形的性质，平行四边形的判定，菱形的判定的应用，能得出四边形ABCD是平行四边形是解此题的关键．21．（8分）如图，在4×4的正方形网格中，每个小正方形的边长都为1．（1）求△ABC的周长；（2）求证：∠ABC＝90°；（3）若点P为直线AC上任意一点，则线段BP的最小值为2．【分析】（1）运用勾股定理求得AB，BC及AC的长，即可求出△ABC的周长．（2）运用勾股定理的逆定理求得AC2＝AB2+BC2，得出∠ABC＝90°．（3）过B作BP⊥AC，解答即可．【解答】解：（1）AB＝，BC＝，AC＝，△ABC的周长＝2++5＝3+5，（2）∵AC2＝25，AB2＝20，BC2＝5，∴AC2＝AB2+BC2，∴∠ABC＝90°．（3）过B作BP⊥AC，∵△ABC的面积＝，即，解得BP＝2，故答案为：2【点评】本题主要考查了勾股定理及勾股定理的逆定理，熟记勾股定理是解题的关键．22．（10分）如图1，点D、E、F、G分别为线段AB、OB、OC、AC的中点．（1）求证：四边形DEFG是平行四边形；（2）如图2，若点M为EF的中点，BE：CF：DG＝2：3：，求证：∠MOF＝∠EFO．【分析】（1）根据中位线定理得：DG∥BC，DG＝BC，EF∥BC，EF＝BC，则DG＝BC，DE ∥BC，根据一组对边平行且相等的四边形是平行四边形可得：四边形DEFG是平行四边形；（2）先根据已知的比的关系设未知数：设BE＝2x，CF＝3x，DG＝x，根据勾股定理的逆定理得：∠EOF＝90°，最后利用直角三角形斜边中线的性质可得OM＝FM，由等边对等角可得结论．【解答】证明：（1）∵D是AB的中点，G是AC的中点，∴DG是△ABC的中位线，∴DG∥BC，DG＝BC，同理得：EF是△OBC的中位线，∴EF∥BC，EF＝BC，∴DG＝EF，DG∥EF，∴四边形DEFG是平行四边形；（2）∵BE：CF：DG＝2：3：，∴设BE＝2x，CF＝3x，DG＝x，∴OE＝2x，OF＝3x，∵四边形DEFG是平行四边形，∴DG＝EF＝x，∴OE2+OF2＝EF2，∴∠EOF＝90°，∵点M为EF的中点，∴OM＝MF，∴∠MOF＝∠EFO．【点评】本题考查的是三角形中位线定理、平行四边形的判定、勾股定理的逆定理，掌握三角形中位线定理是解题的关键．23．（10分）已知点A为正方形BCDE内一动点，满足∠DAC＝135°，且b＝+5．（1）求a、b的值；（2）如图1，若线段AB＝b，AC＝a，求线段AD的长；（3）如图2，设线段AB＝m，AC＝n，AD＝h，请探究并直接写出三个量m2、n2、h2之间满足的数量关系．【分析】（1）根据二次根式有意义的条件列出不等式，解不等式得到答案；（2）把△CAD旋转90°得到△CA′B，根据勾股定理求出AA′，求出∠AA′B＝90°，根据勾股定理计算即可；（3）仿照（2）的计算方法解答．【解答】解：（1）由二次根式有意义的条件可知，a﹣3≥0，3﹣a≥0，∴a＝3，b＝5；（2）把△CAD旋转90°得到△CA′B，则AC＝A′C，∠A′CB＝∠ACD，AD＝A′B，∴∠ACA′＝90°，∴∠AA′C＝45°，AA′＝＝3，∴∠AA′B＝90°，∴A′B＝＝，∴AD＝A′B＝；（3）由（2）得，AA′＝＝n，∴m2﹣2n2＝h2．【点评】本题考查的是二次根式有意义的条件、旋转变换的性质、勾股定理的应用，掌握二次根式的被开方数是非负数、旋转变换的性质是解题的关键．24．（12分）在正方形ABCD中，点E为边BC（不含B点）上的一动点，AE⊥EF，且AE＝EF，FG⊥BC的延长线于点G．（1）如图1，求证：BE＝FG；（2）如图2，连接BD，过点F作FH∥BC交BD于点H，连接HE，判断四边形EGFH的形状，并给出证明；（3）如图3，点P、Q为正方形ABCD内两点，AB＝BQ，且∠ABQ＝30°，BP平分∠QBC，BP ＝DP，若BC＝+1，求线段PQ的长．【分析】（1）欲证明BE＝FG，只要证明△ABE≌△EGF，即可解决问题；（2）四边形EGFH是矩形．首先证明四边形ECMH是矩形，可得∠FHE＝∠HEG＝∠EGF＝90°，推出四边形EGFH是矩形；（3）如图3中，连接PC，作PE⊥BC于E，PF⊥BQ于F．∴由PCB≌△PCD，推出∠PCB＝∠PCD＝45°，可证PE＝EC，设PE＝EC＝a，在Rt△PEB中，由∠PBE＝30°，推出PB＝2PE，BE＝a，由BC＝+1，可得a+a＝+1，推出a＝1，再求出FQ、FP即可解决问题；【解答】解：（1）如图1中，∵FG⊥EG，AE⊥EF，四边形ABCD是正方形，∴∠B＝∠AEF＝∠G＝90°，∴∠BAE+∠AEB＝90°，∠AEB+∠FEG＝90°，∴∠BAE＝∠FEG，∵AE＝EF，∴△ABE≌△EGF，∴BE＝FG．（2）结论：四边形EGFH是矩形．理由：如图2中，设FH交CD于M．∵△ABE≌△EGF，∴AB＝EG＝BC，∴BE＝CG＝FG，∵FM∥CG，FG∥CM，∴四边形CMFG是平行四边形，∵GC＝FG，∠MCG＝90°，∴四边形CMFG是正方形，∴CM＝CG＝BE，∵BC＝CD，∴CE＝DM，∵FH∥BC，∴∠DMH＝∠DCB＝90°，∵∠MDH＝45°，∴∠MDH＝∠MHD＝45°，∴DM＝HM＝EC，∵HM∥EC，∴四边形CEHM是平行四边形，∵∠ECM＝90°，∴四边形ECMH是矩形，∴∠FHE＝∠HEG＝∠EGF＝90°，∴四边形EGFH是矩形．（3）如图3中，连接PC，作PE⊥BC于E，PF⊥BQ于F．∵PB＝PD，PC＝PC，BC＝CD，∴△PCB≌△PCD，∴∠PCB＝∠PCD＝45°，∵PE⊥EC，∴∠PCE＝∠EPC＝45°，∴PE＝EC，设PE＝EC＝a，在Rt△PEB中，∵∠PBE＝30°，∴PB＝2PE，BE＝a，∵BC＝+1，∴a+a＝+1，∴a＝1，∴PB＝2在Rt△PFB中，∵∠PBF＝30°，∴PF＝1，BF＝，∵BQ＝BQ＝BC＝+1，∴FQ＝1，∴PQ＝＝．【点评】本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、矩形的判定和性质、勾股定理、直角三角形30度角的性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．。

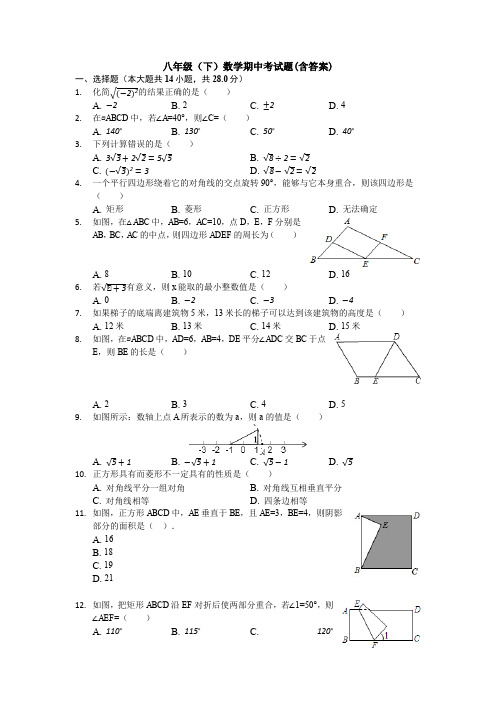
八年级（下）数学期中考试题(含答案)一、选择题（本大题共14小题，共28.0分）1.化简的结果正确的是（）A. B. 2 C. D. 42.在▱ABCD中，若∠A=40°，则∠C=（）A. B. C. D.3.下列计算错误的是（）A. B.C. D.4.一个平行四边形绕着它的对角线的交点旋转90°，能够与它本身重合，则该四边形是（）A. 矩形B. 菱形C. 正方形D. 无法确定5.如图，在△ABC中，AB=6，AC=10，点D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长为（）A. 8B. 10C. 12D. 166.若有意义，则x能取的最小整数值是（）A. 0B.C.D.7.如果梯子的底端离建筑物5米，13米长的梯子可以达到该建筑物的高度是（）A. 12米B. 13米C. 14米D. 15米8.如图，在▱ABCD中，AD=6，AB=4，DE平分∠ADC交BC于点E，则BE的长是（）A. 2B. 3C. 4D. 59.如图所示：数轴上点A所表示的数为a，则a的值是（）A. B. C. D.10.正方形具有而菱形不一定具有的性质是（）A. 对角线平分一组对角B. 对角线互相垂直平分C. 对角线相等D. 四条边相等11.如图，正方形ABCD中，AE垂直于BE，且AE=3，BE=4，则阴影部分的面积是（）．A. 16B. 18C. 19D. 2112.如图，把矩形ABCD沿EF对折后使两部分重合，若∠1=50°，则∠AEF=（）A. B. C.D.13.已知a+=，则a-的值为（）A. B. C. 2 D.14.如图，在Rt△ABC中，∠B=90°，AC=120cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B 匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒．过点D作DF⊥BC于点F，连接DE，EF．当四边形AEFD是菱形时，t的值为（）A. 20秒B. 18秒C. 12秒D. 6秒二、填空题（本大题共4小题，共12.0分）15.比较大小：______2．（填“＞”、“=”、“＜”）．16.如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1+∠2=______度．17.如图，在直角三角形ABC的三边上，向外做三个正方形，其中两个的面积为S3=110，S2=60，则另一个正方形的边长BC为______ ．18.若m分别表示3-的小数部分，则m2的值为______ ．（结果可以带根号）三、解答题（本大题共7小题，共60.0分）19.计算（1）-+．（2）（-）÷．20.当x=-时，求代数式x2-x+的值．21.如图，是由边长为1的小正方形组成的正方形网格，设顶点在这些小正方形顶点的三角形为格点三角形，图中已给出△ABC的一边AB的位置．（1）请在所给的网格中画出边长分别为2，2，4的一个格点△ABC；（2）根据所给数据说明△ABC是直角三角形．22.小敏的作法如下：23.如图所示，在一次夏令营活动中，小明从营地A点出发，沿北偏东60°方向走了5km到达B点，然后再沿北偏西30°方向走了5km到达目的地C点．（1）求A、C两点之间的距离；（2）确定目的地C在营地A的什么方向上．24.如图，在▱ABCD中，点E、F分别是BC，AD上的点，且BE=DF，对角线AC⊥AB．（1）求证：四边形AECF是平行四边形；（2）①当E为BC的中点时，求证：四边形AECF是菱形；②若AB=6，BC=10，当BE长为______ 时，四边形AECF是矩形．③四边形AECF有可能成为正方形吗？答：______ ．（填“有”或“没有”）25.如图，正方形ABCD的对角线AC，BD相交于点O，延长CB至点F，使CF=CA，连接AF，∠ACF的平分线分别交AF，AB，BD于点E，N，M，连接EO，已知BD=2．（1）求正方形ABCD的边长；（2）求OE的长；（3）①求证：CN=AF；②直接写出四边形AFBO的面积．答案和解析1.【答案】B【解析】解：原式=|-2|=2．故选：B．根据=|a|计算即可．本题考查了二次根式的性质与化简：=|a|．2.【答案】D【解析】解：∵在▱ABCD中∠A=40°，∴∠C=∠A=40°，．故选D．根据平行四边形的对角相等即可得出∠C的度数．本题考查平行四边形的性质，比较简单，解答本题的关键是掌握平行四边形的对角相等．3.【答案】A【解析】解：A、2与3不能合并，所以A选项的计算错误；B、原式=2÷2=，所以B选项的计算正确；C、原式=3，所以C选项的计算正确；D、原式=2-=，所以D选项的计算正确．故选A．根据二次根式的加减法对A、D进行判断；根据二次根式的除法法则对B进行判断；根据二次根式的性质对C进行判断．本题考查了二次根式的混合计算：先把二次根式化为最简二次根式，然后进行二次根式的运算，最后合并同类二次根式．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．4.【答案】C【解析】解：因为平行四边形对角线互相平分，绕着它的对角线的交点旋转90°，能够与它本身重合，说明对角线互相垂直平分且相等，所以该四边形是正方形．故选C．根据题意，该四边形的对角线互相垂直平分且相等．此题考查了平行四边形的性质及与特殊四边形的关系，属基础题．解题时要根据旋转的性质解答．5.【答案】D【解析】解：∵点D，E，F分别是AB，BC，AC的中点，∴DE∥AC，EF∥AB，DE=AC=5，EF=AB=3，∴四边形ADEF是平行四边形，∴AD=EF，DE=AF，∴四边形ADEF的周长为2（DE+EF）=16，故选：D．根据三角形的中位线定理，判断出四边形ADEF平行四边形，根据平行四边形的性质求出ADEF的周长即可．本题考查了三角形中位线定理，利用中位线定理判断出四边形ADEF为平行四边形是解题的关键．6.【答案】C【解析】解：∵有意义，∴x+3≥0，解得：x≥-3，∴x能取的最小整数值是：-3．故选：C．直接利用二次根式有意义的条件得出x的取值范围，进而得出答案．此题主要考查了二次根式有意义的条件，正确得出x的取值范围是解题关键．7.【答案】A【解析】解：如图所示，AB=13米，BC=5米，根据勾股定理AC===12米．故选：A．根据梯子、地面、墙正好构成直角三角形，再根据勾股定理解答即可．此题是勾股定理在实际生活中的运用，比较简单．8.【答案】A【解析】解：∵四边形ABCD是平行四边形，∴BC=AD=6，CD=AB=4，AD∥BC，∴∠ADE=∠DEC，∵DE平分∠ADC，∴∠ADE=∠CDE，∴∠CDE=∠DEC，∴EC=CD=4，∴BE=BC-EC=2．故选：A．由四边形ABCD是平行四边形，可得BC=AD=6，CD=AB=4，AD∥BC，得∠ADE=∠DEC，又由DE平分∠ADC，可得∠CDE=∠DEC，根据等角对等边，可得EC=CD=4，所以求得BE=BC-EC=2．此题考查了平行四边形的性质、角平分线的定义与等腰三角形的判定定理．注意当有平行线和角平分线出现时，会出现等腰三角形．9.【答案】C【解析】解：图中的直角三角形的两直角边为1和2，∴斜边长为：=，∴-1到A的距离是，那么点A所表示的数为：-1．故选：C．先根据勾股定理求出三角形的斜边长，再根据两点间的距离公式即可求出A点的坐标．本题考查的是勾股定理及两点间的距离公式，解答此题时要注意，确定点A的符号后，点A所表示的数是距离原点的距离．10.【答案】C【解析】解：正方形的性质：正方形的四条边相等，四个角都是直角，对角线互相垂直平分且相等，并且每一条对角线平分一组对角；菱形的性质：菱形的四条边相等，对角线互相垂直平分，并且每一条对角线平分一组对角；因此正方形具有而菱形不一定具有的性质是：对角线相等；故选：C．根据正方形和菱形的性质容易得出结论．本题考查了正方形和菱形的性质；熟练掌握正方形和菱形的性质是解题的关键；注意区别．11.【答案】C【解析】解：∵AE垂直于BE，且AE=3，BE=4，∴在Rt△ABE中，AB2=AE2+BE2=25，∴S阴影部分=S正方形ABCD-S△ABE=AB2-×AE×BE =25-×3×4=19．故选：C．由已知得△ABE为直角三角形，用勾股定理求正方形的边长AB，用S阴影部分=S正方形ABCD-S△ABE求面积．本题考查了勾股定理的运用，正方形的性质．关键是判断△ABE为直角三角形，运用勾股定理及面积公式求解．12.【答案】B【解析】解：根据题意得：∠2=∠3，∵∠1+∠2+∠3=180°，∴∠2=（180°-50°）÷2=65°，∵四边形ABCD是矩形，∴AD∥BC，∴∠AEF+∠2=180°，∴∠AEF=180°-65°=115°．故选B．根据折叠的性质，对折前后角相等．本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．13.【答案】B【解析】解：∵a+=，∴（a+）2=a2++2=6，∴a2+=4，∴a2+-2=2，∴a-=±．故选：B．首先求出（a+）2=a2++2=6，进而得出（a-）2=2，即可得出答案．此题主要考查了完全平方公式的应用，根据已知得出a2+的值是解题关键．14.【答案】A【解析】解：由题意CD=4t，AE=2t，∵DF⊥BC于F，∴∠DFC=90°在Rt△DFC中，∵∠C=30°，∴DF=CD=2t，∴DF=AE，∵∠CFD=∠B=90°，∴DF∥AE，∴四边形DFEA是平行四边形，∴当DF=AD时，四边形DFEA是菱形．∴120-4t=2t，∴t=20s，∴t=20s时，四边形DFEA是菱形．故选A．首先证明四边形DFEA是平行四边形，再根据AD=DF，列出方程求出t即可解决问题．本题考查菱形的性质、平行四边形的判定，一元一次方程等知识，解题的关键是灵活运用所学知识解决问题，学会构建方程解决问题，属于中考常考题型．15.【答案】＞【解析】解：∵2=，＞，∴＞2．故答案为：＞．本题需先把2进行整理，再与进行比较，即可得出结果．本题主要考查了实数大小关系，在解题时要化成同一形式是解题的关键．16.【答案】240【解析】解：∵四边形的内角和为（4-2）×180°=360°，∴∠B+∠C+∠D=360°-60°=300°，∵五边形的内角和为（5-2）×180°=540°，∴∠1+∠2=540°-300°=240°，故答案为：240．利用四边形的内角和得到∠B+∠C+∠D的度数，进而让五边形的内角和减去∠B+∠C+∠D的度数即为所求的度数．考查多边形的内角和知识；求得∠B+∠C+∠D的度数是解决本题的突破点．17.【答案】5【解析】解：∵∠ACB=90°，∴BC2+AC2=AB2，∵S1=BC2，S2=AC2，S3=AB2，∴S1+S2=S3，∴S1=100-60=50，∴BC=5．故答案为：5．根据正方形的面积公式，运用勾股定理可以证明S1+S2=S3，进而可得出结论．本题考查勾股定理，正方形面积公式，解题的关键是证明S1+S2=S3，记住这个结论在以后解题中会有帮助，属于基础题中考常考题型．18.【答案】6-4【解析】解：∵1＜＜，∴3-的小数部分是3--1=2-，∴m2的值为（2-）2=6-4．故答案为：6-4．根据1＜＜，可得m的值，根据代数式求值，可得答案．本题考查了估算无理数的大小，利用了算术平方根越大被开方数越大，代数式求值．19.【答案】解：（1）原式=4-3+，=+=；（2）原式=（4-3）÷，=÷=1．【解析】（1）首先化简二次根式，进而得出答案；（2）首先化简二次根式，进而利用二次根式除法运算法则求出答案．此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．20.【答案】解：当x=-时，原式=（-）2-（-）+=2-2+3-2++=3．【解析】将x的值代入代数式进行计算．本题考查二次根式运算，涉及公式的应用，代数式求值问题，属于基础问题．21.【答案】解：（1）如图，△ABC即为所求；（2）由图可知，AB=4，BC=2，AC=2，∵AB2+BC2=20，AC2=20，∴AB2+BC2=AC2，∴△ABC是直角三角形．【解析】（1）根据勾股定理找出C点，再顺次连接即可；（2）根据勾股定理的逆定理即可得出结论．本题考查的是作图-应用与设计作图，熟知勾股定理是解答此题的关键．22.【答案】解：小敏的作法正确．理由如下：∵线段AC的垂直平分线交AC于点O，∴AO=CO，∵BO=DO，∴四边形ABCD为平行四边形，∵∠ABC=90°，∴四边形ABCD为矩形．【解析】利用基本作图得到OA=OC，OB=OD，则利用平行四边形的判定方法可判断四边形ABCD为平行四边形，然后根据矩形的判定方法得到四边形ABCD为矩形．本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了矩形的判定．23.【答案】解：（1）过B点作直线EF∥AD，∴∠DAB=∠ABF=60°，∵∠EBC=30°，∴∠ABC=180°-∠ABF-∠EBC=180°-60°-30°=90°，∴△ABC为直角三角形，由已知可得：BC=5km，AB=5km，由勾股定理可得：AC2=BC2+AB2，所以AC==10（km），即：A、C两点之间的距离为10km；（2）在Rt△ABC中，∵BC=5km，AC=10km，∴∠CAB=30°，∵∠DAB=60°，∴∠DAC=30°，即点C在点A的北偏东30°的方向上．【解析】（1）根据平行线的性质，可得∠ABF，根据直角三角形的判定，可得∠ABC，根据勾股定理，可得答案；（2）根据直角三角形的性质，可得∠CAB，根据角的和差，可得答案．本题考查了勾股定理的应用，利用了方向角，平行线的性质，直角三角形的性质，勾股定理．24.【答案】（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∵BE=DF，∴AF=EC，∴四边形AECF人教版八年级（下）期中模拟数学试卷及答案一、选择题：共10小题，在每小题列出的四个选项中，选出符合题目要求的一项．1．（3分）下列各曲线中表示y是x的函数的是（）A．B．C．D．2．（3分）若点P（﹣1，3）在函数y＝kx的图象上，则k的值为（）A．﹣3B．3C．D．3．（3分）如图，一次函数y＝kx+b的图象经过点（﹣1，0）与（0，2），则关于x的不等式kx+b＞0的解集是（）A．x＞﹣1B．x＜﹣1C．x＞2D．x＜24．（3分）已知点（﹣3，y1），（2，y2）都在直线y＝2x+1上，则y1，y2的大小关系是（）A．y1＝y2B．y1＜y2C．y1＞y2D．不能确定5．（3分）已知2是关于x的方程3x2﹣2a＝0的一个解，则a的值是（）A．3B．4C．5D．66．（3分）如图，若DE是△ABC的中位线，△ABC的周长为1，则△ADE的周长为（）A．1B．2C．D．7．（3分）若m＜﹣1，则一次函数y＝（m+1）x+m﹣1的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限8．（3分）将矩形纸片ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE＝30°，BE ＝1，折叠后，点C落在AD边上的C1处，并且点B落在EC1边上的B1处．则EC的长为（）A．B．2C．3D．29．（3分）如图，平行四边形ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC＝60°，AB＝BC，连接OE．下列结论：①∠CAD＝30°；②S▱ABCD ＝AB•AC；③OB＝AB；④OE＝BC．其中成立的个数有（）A．1个B．2个C．3个D．4个10．（3分）如图1，在矩形MNPQ中，动点R从点N出发，沿着N→P→Q→M方向运动至点M处停止，设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则下列说法不正确的是（）A．当x＝2时，y＝5B．矩形MNPQ的面积是20C．当x＝6时，y＝10D．当y＝时，x＝10二、填空题：共8小题．11．（3分）函数中自变量x的取值范围是．12．（3分）若一元二次方程x2﹣2x﹣m＝0无实根，则m的取值范围是．13．（3分）将函数y＝2x+1的图象向上平移2个单位，所得的函数图象的解析式为．14．（3分）如图，等边三角形EBC在正方形ABCD内，连接DE，则∠ADE＝度．15．（3分）在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE＝3，若平行四边形ABCD的周长是16，则EC等于．16．（3分）根据如图所示的程序计算函数值，若输入x的值为，则输出的y值为．17．（3分）已知点A（2，﹣4），直线y＝﹣x﹣2与y轴交于点B，在x轴上存在一点P，使得P A+PB的值最小，则点P的坐标为．18．（3分）正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y＝kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则点B3的坐标是；点B2018的坐标是．三、解答题共8小题．解答应写出文字说明、演算步骤或证明过程．19．（20分）解一元二次方程：（1）（2x+1）2＝9；（2）x2+4x﹣2＝0；（3）x2﹣6x+12＝0；（4）3x（2x+1）＝4x+2．20．（6分）已知m是方程x2﹣x﹣3＝0的一个实数根，求代数式（m2﹣m）（m﹣+1）的值．21．（6分）已知直线l1的函数解析式为y＝x+1，且l1与x轴交于点A，直线l2经过点B，D，直线l1，l2交于点C．（1）求点A的坐标；（2）求直线l2的解析式；（3）求S△ABC的面积．22．（6分）如图，在△ABC中，AB＝AC，D是BC边的中点，点E，F分别在AD及其延长线上，且CE∥BF，连接BE，CF．（1）求证：四边形EBFC是菱形；（2）若BD＝4，BE＝5，求四边形EBFC的面积．23．（6分）已知：关于x的一元二次方程x2+（m+1）x+m＝0（1）求证：无论m为何值，方程总有两个实数根；（2）若x为方程的一个根，且满足0＜x＜3，求整数m的值．24．（7分）某游乐场普通门票价格40元/张，为了促销，新推出两种办卡方式：①白金卡售价200元/张，每次凭卡另收取20元；②钻石卡售价1000元/张，每次凭卡不再收费．促销期间普通门票正常出售，两种优惠卡不限次数，设去游乐场玩x次时，所需总费用为y元．（1）分别写出选择白金卡、普通门票消费时，y与x之间的函数关系式．（2）在同一坐标系中，若三种消费方式对应的函数图象如图所示，请求出点B，C的坐标．（3）请根据图象，直接写出选择哪种消费方式更合算．25．（7分）在平面直角坐标系xOy中，点P的坐标为（x1，y1），点Q的坐标为（x2，y2），且x1≠x2，y1≠y2．若P，Q为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”，下图①为点P，Q的“相关矩形”的示意图．已知点A的坐标为（1，0），（1）若点B的坐标为（3，1），求点A，B的“相关矩形”的面积；（2）点C在直线x＝3上，若点A，C的“相关矩形”为正方形，求直线AC的表达式；（3）若点D的坐标为（4，2），将直线y＝2x+b平移，当它与点A，D的“相关矩形”没有公共点时，求出b的取值范围．26．（8分）在矩形ABCD中，AB＝1，BC＝2，点P是边BC上一点（点P不与点B，点C 重合），点C关于直线AP的对称点为C'．（1）如果C'落在线段AB的延长线上．①在图①中补全图形；②求线段BP的长度；（2）如图②，设直线AP与CC'的交点为M，求证：BM⊥DM．2018-2019学年北京101中八年级（下）期中数学试卷参考答案与试题解析一、选择题：共10小题，在每小题列出的四个选项中，选出符合题目要求的一项．1．【解答】解：根据函数的意义可知：对于自变量x的任何值，y都有唯一的值与之相对应，故D正确．故选：D．2．【解答】解：∵点P（﹣1，3）在函数y＝kx的图象上，∴3＝﹣k，∴k＝﹣3，故选：A．3．【解答】解：由题意可得：一次函数y＝kx+b中，y＞0时，图象在x轴上方，x＞﹣1，则关于x的不等式kx+b＞0的解集是x＞﹣1，故选：A．4．【解答】解：∵点（﹣3，y1）和（2，y2）都在直线y＝2x+1上，∴y1＝2×（﹣3）+1＝﹣5，y2＝2×2+1＝5，∴y1＜y2．故选：B．5．【解答】解：把x＝2代入方程3x2﹣2a＝0得3×4﹣2a＝0，解得a＝6．故选：D．6．【解答】解：∵DE是△ABC的中位线，△ABC的周长为1，∴DE＝，AD＝，AE＝∴△ADE的周长为．故选：C．7．【解答】解：当m＜﹣1时，m+1＜0，m﹣1＜2，一次函数y＝（m+1）x+m﹣1的图象不经过第一象限，故选：A．8．【解答】解：∵矩形纸片ABCD，∠BAE＝30°，∴AE＝2BE＝2×1＝2，∠AEB＝90°﹣∠BAE＝90°﹣30°＝60°，∵AB沿AE翻折点B落在EC1边上的B1处，∴∠AEB1＝∠AEB＝60°，∵矩形对边AD∥BC，∴∠EAC1＝∠AEB1＝60°，∴△AEC1是等边三角形，∴BC1＝AE＝2，∵EC沿BF翻折点C落在AD边上的C1处，∴EC＝BC1＝2．故选：B．9．【解答】解：∵四边形ABCD是平行四边形，∴∠ABC＝∠ADC＝60°，∠BAD＝120°，∵AE平分∠BAD，∴∠BAE＝∠EAD＝60°∴△ABE是等边三角形，∴AE＝AB＝BE，∵AB＝BC，∴AE＝BC，∴∠BAC＝90°，∴∠CAD＝30°，故①正确；∵AC⊥AB，∴S▱ABCD＝AB•AC，故②正确，∵AB＝BC，OB＝BD，∵BD＞BC，∴AB≠OB，故③错误；∵∠CAD＝30°，∠AEB＝60°，AD∥BC，∴∠EAC＝∠ACE＝30°，∴AE＝CE，∴BE＝CE，∵OA＝OC，∴OE＝AB＝BC，故④正确．故选：C．10．【解答】解；由图2可知：PN＝4，PQ＝5．A、当x＝2时，y＝＝＝5，故A正确，与要求不符；B、矩形的面积＝MN•PN＝4×5＝20，故B正确，与要求不符；C、当x＝6时，点R在QP上，y＝＝10，故C正确，与要求不符；D、当y＝时，x＝3或x＝10，故错误，与要求相符．故选：D．二、填空题：共8小题．11．【解答】解：根据题意得：x+5≥0，解得x≥﹣5．12．【解答】解：∵关于x的一元二次方程x2﹣2x﹣m＝0无实根，∴△＝（﹣2）2﹣4×1×（﹣m）＜0，解得：m＜﹣1，故答案为：m＜﹣1．13．【解答】解：由“上加下减”的原则可知，将函数y＝2x+1的图象向上平移2个单位所得函数的解析式为y＝2x+3．故答案为：y＝2x+3．14．【解答】解：正方形ABCD中，BC＝CD，等边△BCE中，CE＝BC，∴CD＝CE，∵∠DCE＝90°﹣60°＝30°，∴∠CDE＝＝75°．∴∠ADE＝90°﹣75°＝15°．故答案为：15°．15．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，AB＝CD，AD＝BC，∴∠AEB＝∠DAE，∵平行四边形ABCD的周长是16，∴AB+BC＝8，∵AE是∠BAD的平分线，∴∠BAE＝∠DAE，∴∠BAE＝∠AEB，∴AB＝BE＝3，∴BC＝5，∴EC＝BC﹣BE＝5﹣3＝2；故答案为：2．16．【解答】解：x＝时，y＝﹣x+2＝﹣+2＝．故答案为：．17．【解答】解：作点B关于x轴的对称点B′，连接AB′，交x轴于P，连接PB，此时P A+PB的值最小．设直线AB′的解析式为y＝kx+b，把A（2，﹣4），B′（0，2）代入得到，解得，∴直线AB′的解析式为y＝﹣3x+2，令y＝0，得到x＝，∴P（，0），故答案为（，0）．18．【解答】解：∵B1的坐标为（1，1），点B2的坐标为（3，2），∴正方形A1B1C1O1边长为1，正方形A2B2C2C1边长为2，∴A1的坐标是（0，1），A2的坐标是：（1，2），代入y＝kx+b得，解得：．则直线的解析式是：y＝x+1．∵点B1的坐标为（1，1），点B2的坐标为（3，2），∴点B3的坐标为（7，4），…，∴Bn的横坐标是：2n﹣1，纵坐标是：2n﹣1．B n的坐标是（2n﹣1，2n﹣1）∴B2018的坐标是（22018﹣1，22017）．故答案为：（22018﹣1，22017）．三、解答题共8小题．解答应写出文字说明、演算步骤或证明过程．19．【解答】解：（1）2x+1＝±3，所以x1＝1，x2＝﹣2；（2）x2+4x＝2，x2+4x+4＝6，（x+2）2＝6，x+2＝±，所以x1＝﹣2+，x2＝﹣2﹣；（3）△＝（﹣6）2﹣4×1×12＜0，所以方程没有实数解；（4）3x（2x+1）﹣2（2x+1）＝0，（2x+1）（3x﹣2）＝0，2x+1＝0或3x﹣2＝0，所以x1＝﹣，x2＝．20．【解答】解：∵m是方程x2﹣x﹣3＝0的一个实数根，∴m2﹣m﹣3＝0，即m2＝m+3，∴（m2﹣m）（m﹣+1）＝（m+3﹣m）•＝3×＝3×2＝6．21．【解答】解：（1）在y＝x+1中，令y＝0，则x＝﹣1，∴A（﹣1，0）；（2）设直线l2的解析式为y＝kx+b，则，解得，∴y＝﹣2x+6；（3）解方程组，可得，∴C（，），∴S△ABC＝×（3+1）×＝．22．【解答】（1）证明：∵D是BC边的中点，∴BD＝CD，∵CE∥BF，∴∠DBF＝∠ECD，在△BDF和△CDE中，，∴△BDF≌△CDE（ASA），∴CE＝BF，又∵CE∥BF，∴四边形BFCE是平行四边形；∵AB＝AC，D是BC的中点，∴AD⊥BC，又∵四边形BFCE是平行四边形，∴四边形BFCE是菱形．（2）解：在Rt△BDE中，BE＝5，BD＝4，∴DE＝＝3，∵四边形BECF是菱形，∴EF＝2DE＝6，BC＝2BD＝8，∴菱形BECF的面积＝×6×8＝24．23．【解答】解：（1）∵△＝（m+1）2﹣4×1×m ＝m2+2m+1﹣4m＝m2﹣2m+1＝（m﹣1）2≥0，∴无论m为何值，方程总有两个实数根；（2）∵（x+1）（x+m）＝0，∴x+1＝0或x+m＝0，即x1＝﹣1、x2＝﹣m，∵0＜x＜3，∴0＜﹣m＜3，解得：﹣3＜m＜0，则整数m的值为﹣2、﹣1．24．【解答】解：（1）根据题意可得：白金卡：y＝20x+200．门票：y＝40x（2）将y＝40x代入y＝200+20x，得40x＝200+20x，解得x＝10，把x＝10代入y＝40x，得y＝400，所以B（10，400），把y＝1000代入y＝200+20x，得1000＝200+20x，解得x＝40，所以C（40，1000）；（3）当0＜x＜10时，选普通门票；当x＝10时，选普通门票和白金卡；当10＜x＜40时，选白金卡；当x＝40时，选白金卡和钻石卡；当x＞40时，选钻石卡25．【解答】解：（1）∵A（1，0），B（3，1）由定义可知：点A，B的“相关矩形”的底与高分别为2和1，∴点A，B的“相关矩形”的面积为2×1＝2；（2）由定义可知：AC是点A，C的“相关矩形”的对角线，又∵点A，C的“相关矩形”为正方形∴直线AC与x轴的夹角为45°，设直线AC的解析为：y＝x+m或y＝﹣x+n把（1，0）分别y＝x+m，∴m＝﹣1，∴直线AC的解析为：y＝x﹣1，把（1，0）代入y＝﹣x+n，∴n＝1，∴y＝﹣x+1，综上所述，若点A，C的“相关矩形”为正方形，直线AC的表达式为y＝x﹣1或y＝﹣x+1；（3）把A（1，0），D（4，2）分别代入y＝2x+b±2，得出b＝0，或b＝﹣8，∴b＞0或b＜﹣826．【解答】解：（1）①如图①所示：②连接AC，作PH⊥AC于H．则△APB≌△APH，∴AB＝AH＝1，PB＝PH，设PB＝PH＝x，∵AC＝＝，∴CH＝﹣1，在Rt△PCH中，x2+（﹣1）2＝（2﹣x）2，解得x＝，∴PB＝．（2）如图②中，连接AC、BD交于点O．连接OM．∵四边形ABCD是矩形，∴OA＝OB＝OC＝OD，∵∠AMC＝90°，∴OM＝OA＝OB＝OC＝OD，∴A、B、M、C、D五点共圆，∵BD是直径，∴∠BMD＝90°，∴BM⊥DM．最新人教版八年级数学下册期中考试试题(含答案)一、选择题（共10小题，每小题3分，满分30分）1、下列二次根式中，是最简二次根式的是（）A．2 B． C． D．2、在平行四边形、矩形、菱形、正方形中是轴对称图形的有（）A．4个 B．3 个 C．2个 D．1个3、如图，在▱ABCD中，对角线AC、BD相交于点O，AC=10，BD=6，AD=4，则▱ABCD的面积是（）A．12 B．12 C．24 D．304、下列各组数中，以a、b、c为边长的三角形不是直角三角形的是（）A．a=3，b=4，c=5 B．a=5，b=12，c=13C．a=1，b=3，c= D．a=，b=，c=5、下列计算正确的是（）A．4 B． C．2= D．3+的值为（）6、根式a a bA. 2B. 3C. 4D. 57、如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（）A．25海里 B．30海里 C．40海里 D．50海里8、如图，△ABC中，AB=AC，点D、E分别是边AB、AC的中点，点G、F在BC边上，四边形DEFG是正方形．若DE=2cm，则AC的长为（）A． cm B．4cm C． cm D． cm9、如图，平行四边形ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（）A．18 B．28 C．36 D．4610、如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB=65°，则∠AED′等于（）A．70° B．65° C．50° D．25°二、填空题（本题有6小题，每题3分，共18分）.11、如图，平行四边形ABCD中，对角线AC、BD相交于点O，AB=3，BC=5，则OA的取值范围为．12、一个直角三角形的两条直角边分别为6和8，那么这个直角三角形斜边上的高为。

2022-2023学年湖北省武汉市硚口区八年级（下）期中数学试卷1. 要使有意义，x 的取值范围是( )A. B. C. D.2. 下列各式计算正确的是( )A. B.C. D. 3. 在三边分别为下列长度的三角形中，不是直角三角形的是( )A. 3，4，5B. 1，2，C.，3D. 3，5，64. 在▱ABCD 中，若，则的大小是( )A.B.C.D.5. 如图，数轴上的点A 表示的数是，点B 表示的数是2，于点B ，且，以A 点为圆心，AC 为半径画弧交数轴于点D ，则点D 表示的数是( )A. B. C. D.6. 已知菱形ABCD 的对角线AC 、BD 长分别为8，6，则菱形的面积是( )A. 14B. 48C. 24D. 367. “方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心吉祥．如图，将边长为2cm 的正方形ABCD 沿对角线BD 方向平移1cm 得到正方形，形成一个“方胜”图案，则点D ，之间的距离为( )A. 1cmB. 2cmC. D.8. 如图，在矩形ABCD 中，E 是边AD 上一点，F ，G 分别是BE ，CE 的中点，连接AF ，DG ，FG ，若，，，则矩形ABCD 的面积是( )A. 44B. 46C. 48D. 509. 如图，已知点，，，，C为直线EF上一动点，则▱ACBD的对角线CD的最小值是( )A. B. 4 C. 5 D.10. 如图，点O是等边内一点，，，，则与的面积之和是( )A.B.C.D.11. 计算的结果是______.12. 计算的结果是______.13. 在中，，，则AB边的长是______ .14. “做数学”可以帮助我们积累数学活动经验．如图，已知三角形纸片ABC，第1次折叠使点B落在BC边上的点处，折痕AD交BC于点D；第2次折叠使点A落在点D处，折痕MN交于点若，则__________.15. 如图，在▱ABCD中，，，E，F是对角线上BD的动点，且，M，N分别是边AD，边BC上的动点.下列四个结论：①存在无数个平行四边形MENF；②存在无数个矩形MENF；③存在无数个菱形MENF；④存在两个正方形其中正确的结论是______ 填写序号16.如图，在中，，其中，设，，则BC的长是______ 用含m，n的式子表示17. 计算：；18. 先化简，再求值：，其中19. 如图，已知E，F分别是▱ABCD的边AB，CD上的两点，且求证：；求证：四边形DEBF是平行四边形.20. 如图，在四边形ABCD中，，，，求的度数．求四边形ABCD的面积．21. 如图，在正方形ABCD中，E是边BC上一点，于点F，交CD于点求证：；若E是BC的中点，连接BF，求证：22. 如图是由小正方形组成的网格，每个小正方形的顶点叫做格点．四边形ABCD 的四个顶点都是格点，仅用无刻度的直尺在给定网格中完成画图画图过程用虚线，画图结果用实线判断四边形ABCD的形状；在图1中，先在CD上画点E，使，再在AB上画点F，使；在图2中的CD上画点G，使23. 如图1，在菱形ABCD中，，点E，G分别在边AB，BC上，，，连接求证：是等边三角形；如图2，把沿BG翻折得到，连接FD，若，求FD的长；如图3，把绕点B顺时针旋转得到，连接DM，P是DM的中点，连接PC，PN，判断PC与PN的数量关系，并给出证明.24. 在平面直角坐标系中，四边形OABC为矩形，，，且，点E从B点出发沿BC运动，点F从B点出发沿BA运动，点G从O点出发沿OC运动.直接写出a，c的值；如图1，将沿OF折叠，点A恰好落在点E处，求E，F两点的坐标；如图2，若E，F两点以相同的速度同时出发运动，使，设点E的横坐标为m，求的值；如图3，已知点，若F，G两点以相同的速度同时出发运动，连接FG，作于H，直接写出DH的最大值.答案和解析1.【答案】A【解析】解：根据题意得：，解得故选：根据二次根式的意义，被开方数是非负数，可得，求解即可．本题主要考查了二次根式的意义和性质．概念：式子叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．2.【答案】C【解析】解：与不能合并，所以A选项不符合题意；B.，所以B选项不符合题意；C.，所以C选项不符合题意；D.，所以D选项不符合题意．故选：根据二次根式的加减法对A选项、B选项进行判断；根据二次根式的乘法法则对C选项进行判断；根据二次根式的性质对D选项进行判断．本题考查了二次根式的混合运算，熟练掌握二次根式的性质、二次根式的乘法和除法法则是解决问题的关键．3.【答案】D【解析】解：A、，，，长为3，4，5的三边能组成直角三角形，不符合题意；B、，，，长为1，2，的三边能组成直角三角形，不符合题意；C、，，，长为2，，3的三边能组成直角三角形，不符合题意；D、，，，，长为3，5，6的三边不能组成直角三角形，符合题意．故选：求出较小的两条边的平方和，将其与最大的边的平方比较，选其不等的选项即可得出结论．本题考查了勾股定理的逆定理，牢记“如果三角形的三边长a，b，c满足，那么这个三角形就是直角三角形”是解题的关键．4.【答案】B【解析】解：四边形ABCD是平行四边形，，又，，故选：由平行四边形的性质可得，结合，即可求的度数．本题考查了平行四边形的性质，掌握平行四边形的性质是本题的关键．5.【答案】C【解析】解：由图可得，，，，，，，，点D表示的数是，故选：根据图形和勾股定理可以得到AC的长，从而可以得到AD的长，然后再根据数轴，即可写出点D 表示的数．本题考查勾股定理、实数与数轴，解答本题的关键是明确题意，利用数形结合的思想解答．6.【答案】C【解析】解：四边形ABCD是菱形，，，，故选：根据菱形的面积等于对角线长乘积的一半即可解决问题．本题考查菱形的性质，解题的关键是记住菱形的面积等于对角线长乘积的一半，属于中考常考题型．7.【答案】D【解析】解：四边形ABCD为边长为2cm的正方形，，由平移的性质可知，，，故选：根据正方形的性质、勾股定理求出BD，根据平移的概念求出，计算即可．本题考查的是平移的性质、正方形的性质，根据平移的概念求出是解题的关键．8.【答案】C【解析】解：在矩形ABCD中，，，G分别是BE，CE的中点，，，FG是的中位线，，，，，，，，，，，是直角三角形，，，矩形ABCD的面积，故选：根据矩形的性质可得，根据F，G分别是BE，CE的中点，可得，，FG是的中位线，求出BE，CE和BC的长，进一步可知是直角三角形，，根据求出的面积，根据和矩形ABCD同底等高，可知矩形ABCD的面积，即可求出矩形ABCD的面积．本题考查了矩形的性质，三角形中位线定理，直角三边形斜边的中线的性质，勾股定理逆定理，熟练掌握这些性质是解题的关键．9.【答案】A【解析】解：设直线EF的解析式为，，，，解得，直线EF的解析式为，设，四边形ACBD是平行四边形，，，，，的最小值是8，的最小值是故选：利用待定系数法求出直线EF的解析式为，设，根据平行四边形的性质得，由勾股定理可得，根据非负数的性质可得的最小值是8，即可得CD的最小值．本题考查坐标与图形的性质，待定系数法，平行四边形的性质，勾股定理，非负数的性质，掌握待定系数法以及平行四边形的性质是解题的关键．10.【答案】A【解析】解：将绕点B顺时针旋转得，连接OD，，，，是等边三角形，，，，，，与的面积之和为，故选：将绕点B顺时针旋转得，连接OD，可得是等边三角形，再利用勾股定理的逆定理可得，从而解决问题．本题主要考查了等边三角形的判定与性质，勾股定理的逆定理，旋转的性质等知识，利用旋转将与的面积之和转化为，是解题的关键．11.【答案】2【解析】解：法一、；法二、故答案为：利用二次根式的性质计算即可．本题考查了二次根式的性质，掌握“”是解决本题的关键．12.【答案】【解析】解：原式故答案为利用完全平方公式计算．本题考查了二次根式的混合运算：在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．13.【答案】13或【解析】当AC、BC为直角边时，根据勾股定理得：，当BC为斜边，AC为直角边时，根据勾股定理得：，当答案为：13或从当此直角三角形的两直角边分别是5和12时，当此直角三角形的一个直角边为5，斜边为12时这两种情况分析，再利用勾股定理即可求出第三边．本题主要考查勾股定理的知识点，解答本题的关键是确定直角三角形的斜边，进行分类讨论，此题难度不大．14.【答案】6【解析】【分析】本题考查了三角形的中位线定理，折叠的性质，把图形补全证明GN是的中位线是解本题的关键．先把图补全，由折叠得：，，，证明GN是的中位线，得，可得答案．【解答】解：如图2，由折叠得：，，，，，是的中位线，，，故答案为：15.【答案】①②③【解析】解：连接AC，MN，且令AC，MN，BD相交于点O，四边形ABCD是平行四边形，，，，，只要，那么四边形MENF就是平行四边形，点E，F是BD上的动点，存在无数个平行四边形MENF，故①正确；只要，，则四边形MENF是矩形，点E，F是BD上的动点，存在无数个矩形MENF，故②正确；只要，，则四边形MENF是菱形，点E，F是BD上的动点，存在无数个菱形MENF，故③正确；只要，，，则四边形MENF是正方形，而符合要求的正方形只有一个，故④错误；故答案为：①②③．根据题意作出合适的辅助线，然后逐一分析即可．本题考查正方形的判定、菱形的判定、矩形的判定、平行四边形的判定，解答本题的关键是明确题意，作出合适的辅助线．16.【答案】【解析】解：作于D，作EF垂直平分AC，交AC于F，交BC于E，连接AE，则，，，，，又，，，，，，，，，，故答案为：作于D，作EF垂直平分AC，交AC于F，交BC于E，连接AE，由得，，得到，由勾股定理求出EF，由等积法求出AD，再由勾股定理求出DE，则本题考查了解直角三角形，有一定难度，合理添加辅助线，构造直角三角形是解题关键．17.【答案】解：原式；原式【解析】先把各二次根式化为最简二次根式，然后合并即可；根据二次根式的除法法则运算．本题考查了二次根式的混合运算，熟练掌握二次根式的性质、二次根式的除法法则是解决问题的关键．18.【答案】解：原式，当时，原式【解析】根据二次根式的加减混合运算进行化简，然后代入求值．本题考查了二次根式的化简求值：先根据二次根式的性质和已知条件把所求的式子进行化简，然后把满足条件的字母的值代入计算．19.【答案】证明：四边形ABCD为平行四边形，，，在与中，，≌，；四边形ABCD为平行四边形，，，，由得≌，，，即，四边形DEBF是平行四边形．【解析】由平行四边形的性质得，，再由ASA证明≌即可证得结论；由平行四边形的性质得，，则，再由全等三角形的性质得，得，即可得出结论．本题考查了平行四边形的判定与性质、全等三角形的判定与性质等知识；熟练掌握平行四边形的判定与性质，证明三角形全等是解题的关键．20.【答案】解：连结AC，，，，，，，，，，是直角三角形，，在中，，在中，【解析】由于，，利用勾股定理可求AC，并可求，而，，易得，可证是直角三角形，于是有，从而易求；连接AC，则可以计算的面积，根据AD，CD可以计算的面积，四边形ABCD的面积为和面积之和．本题考查了等腰三角形的性质、勾股定理、勾股定理的逆定理．解题的关键是连接AC，并证明是直角三角形．21.【答案】证明：四边形ABCD是正方形，，，又，，，≌，；如图所示，延长DE交AB的延长线于H，是BC的中点，，又，，≌，，即B是AH的中点，又，中，【解析】依据正方形的性质以及垂线的定义，即可得到，，，即可得出≌，由此可得结论；延长DE交AB的延长线于H，根据≌，即可得出B是AH的中点，进而得到本题主要考查了正方形的性质以及全等三角形的判定与性质，在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．22.【答案】解：，，四边形ABCD是平行四边形；如图1中，点E，点F即为所求；如图2中，点G即为所求．【解析】根据一组对边平行且相等的四边形是平行四边形即可；取格点T，连接AT，BT，BT交CD于点E，点E即为所求．连接AC，BD交于点O，连接EO，延长EO交AB于点F，点F即为所求；取格点R，连接AR，取AR的中点Q，连接BQ延长BQ交CD于点G，点G即为所求．本题考查作图-应用与设计作图，平行四边形的判定等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．23.【答案】证明：如图1，四边形ABCD是菱形，，，，，，是等边三角形；解：如图2，过点F作的延长线于点Q，过点G作的延长线于点H，四边形ABCD是菱形，，，，，，，由翻折可知是等边三角形，，，，，，，，，，，，，四边形GFQH是矩形，，，，；，理由如下：如图3，把绕点B顺时针旋转得到，延长CP交AB于点Q，连接CN、QN，是DM的中点，，四边形ABCD是菱形，，，，≌，，，，由旋转可知是等边三角形，，，，，≌，，，，，是等边三角形，，，，【解析】根据菱形的性质可得，，由，，可得，所以得到是等边三角形；过点F作交DC的延长线于点Q，过点G作的延长线于点H，由翻折可知是等边三角形，然后证明四边形GFQH是矩形，可得，，所以得，利用勾股定理即可解决问题；如图3，把绕点B顺时针旋转得到，P是DM的中点，延长CP交AB 于点Q，连接CN、QN，先证明≌，可得，，由旋转可知是等边三角形，再证明≌，可得，，得是等边三角形，再利用含30度角直角三角形即可解决问题．此题属于四边形综合题，考查菱形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理、解直角三角形等知识，解题的关键是正确地作出所需要的辅助线，此题难度较大，属于考试压轴题．24.【答案】解：又，，，；四边形OABC 为矩形，，，，，，由题意得：，在中，，，，，，即，设，则，在中，由勾股定理得，，解得：，，，；设直线EF 交y 轴于H 点，交x 轴于G 点；作，使，连接TH 、TE ；四边形OABC 为矩形，，，根据运动的特点可知：，，，，，，都为等腰直角三角形，，，，，，，，在和中，，≌，，，，，，，在和中，，≌，，，，，，即，，，，，；连接OB交GF于N点，取OA的中点M，取NA的中点L，连接MN、LH、LD，如图，根据运动的特点可知：，在矩形OABC中，，由勾股定理可得：，又：，≌，，即N为OB的中点，，的中点为M，，第21页，共21页，，，即点D 为M 的中点，又的中点为L ，，在中，，又，当且仅当L 、D 、H 三点共线时取等号，，即DH 的最大值为【解析】根据二次根式的非负性以及平方的非负性即可求解；即可得，，，由题意得：，在中，，，，即可得：，，即，设，则，利用勾股定理得，即可得，问题得解；设直线EF 交y 轴于H 点，交x 轴于G 点；作，使，连接TH 、TE ；根据运动的特点可知：，易证明，，，都为等腰直角三角形，，，，证明≌再证明≌，即有，则有²²，便可得，根据，则，，根据勾股定理可得，问题得解；连接OB 交GF 于N 点，，可证N 为OB 的中点，，取OA 的中点M ，则，取NA 的中点L ，点D 为MA 的中点，则，在中，，，即可解决问题．本题主要考查了矩形的性质，全等三角形的判定与性质，勾股定理，三角形的中位线的性质，直角三角形中斜边的中线等于斜边的一半，等腰三角形的判定与性质，构造合理的辅助线，掌握矩形的性质，是解答本题的关键．。

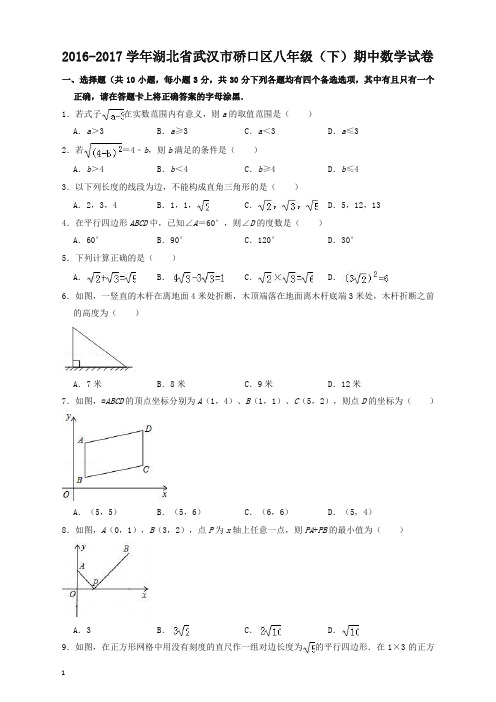
2016-2017学年湖北省武汉市硚口区八年级（下）期中数学试卷一、选择题（共10小题，每小题3分，共30分下列各题均有四个备选选项，其中有且只有一个正确，请在答题卡上将正确答案的字母涂黑．1．若式子在实数范围内有意义，则a的取值范围是（）A．a＞3 B．a≥3 C．a＜3 D．a≤32．若＝4﹣b，则b满足的条件是（）A．b＞4 B．b＜4 C．b≥4 D．b≤43．以下列长度的线段为边，不能构成直角三角形的是（）A．2，3，4 B．1，1，C．D．5，12，134．在平行四边形ABCD中，已知∠A＝60°，则∠D的度数是（）A．60°B．90°C．120°D．30°5．下列计算正确的是（）A．B．C．D．6．如图，一竖直的木杆在离地面4米处折断，木顶端落在地面离木杆底端3米处，木杆折断之前的高度为（）A．7米B．8米C．9米D．12米7．如图，▱ABCD的顶点坐标分别为A（1，4）、B（1，1）、C（5，2），则点D的坐标为（）A．（5，5）B．（5，6）C．（6，6）D．（5，4）8．如图，A（0，1），B（3，2），点P为x轴上任意一点，则PA+PB的最小值为（）A．3 B．C．D．9．如图，在正方形网格中用没有刻度的直尺作一组对边长度为的平行四边形．在1×3的正方形网格中最多作2个，在1×4的正方形网格中最多作6个，在1×5的正方形网格中最多作12个，则在1×8的正方形网格中最多可以作（）A．28个B．42个C．21个D．56个10．如图，正方形ABCD中，点O为对角线的交点，直线EF过点O分别交AB、CD于E、F两点（BE ＞EA），若过点O作直线与正方形的一组对边分别交于G、H两点，满足GH＝EF，则这样的直线GH（不同于直线EF）的条数共有（）A．1条B．2条C．3条D．无数条二、填空题（每小题3分，共18分11．16的平方根是．12．计算：÷＝．13．已知等边三角形的边长为6，则面积为．14．如图，菱形ABCD的周长为8，对角线BD＝2，则对角线AC为．15．如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点E的坐标．16．如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝5，DA＝5，则BD的长为．三、解答题（共8小题，共72分）17．（8分）计算：①；②．18．（8分）计算：①②19．（8分）一根直立于水中的芦节（BD）高出水面（AC）2米，一阵风吹来，芦苇的顶端D恰好到达水面的C处，且C到BD的距离AC＝6米，求水的深度（AB）为多少米？20．（8分）如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD．求证：四边形ABCD是菱形．21．（8分）如图，在4×4的正方形网格中，每个小正方形的边长都为1．（1）求△ABC的周长；（2）求证：∠ABC＝90°；（3）若点P为直线AC上任意一点，则线段BP的最小值为．22．（10分）如图1，点D、E、F、G分别为线段AB、OB、OC、AC的中点．（1）求证：四边形DEFG是平行四边形；（2）如图2，若点M为EF的中点，BE：CF：DG＝2：3：，求证：∠MOF＝∠EFO．23．（10分）已知点A为正方形BCDE内一动点，满足∠DAC＝135°，且b＝+5．（1）求a、b的值；（2）如图1，若线段AB＝b，AC＝a，求线段AD的长；（3）如图2，设线段AB＝m，AC＝n，AD＝h，请探究并直接写出三个量m2、n2、h2之间满足的数量关系．24．（12分）在正方形ABCD中，点E为边BC（不含B点）上的一动点，AE⊥EF，且AE＝EF，FG ⊥BC的延长线于点G．（1）如图1，求证：BE＝FG；（2）如图2，连接BD，过点F作FH∥BC交BD于点H，连接HE，判断四边形EGFH的形状，并给出证明；（3）如图3，点P、Q为正方形ABCD内两点，AB＝BQ，且∠ABQ＝30°，BP平分∠QBC，BP＝DP，若BC＝+1，求线段PQ的长．2016-2017学年湖北省武汉市硚口区八年级（下）期中数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，共30分下列各题均有四个备选选项，其中有且只有一个正确，请在答题卡上将正确答案的字母涂黑．1．若式子在实数范围内有意义，则a的取值范围是（）A．a＞3 B．a≥3 C．a＜3 D．a≤3【分析】根据被开方数大于等于0列式计算即可得解．【解答】解：由题意得，a﹣3≥0，解得a≥3．故选：B．【点评】本题考查的知识点为：二次根式的被开方数是非负数．2．若＝4﹣b，则b满足的条件是（）A．b＞4 B．b＜4 C．b≥4 D．b≤4【分析】根据二次根式的性质列出不等式，解不等式即可．【解答】解：∵＝4﹣b，∴4﹣b≥0，解得，b≤4，故选：D．【点评】本题考查的是二次根式的化简，掌握二次根式的性质：＝|a|是解题的关键．3．以下列长度的线段为边，不能构成直角三角形的是（）A．2，3，4 B．1，1，C．D．5，12，13【分析】根据勾股定理的逆定理对四个选项进行逐一判断即可．【解答】解：A、∵22+32＝13≠42，∴不能构成直角三角形，故本选项符合要求；B、∵12+12＝（）2，∴能构成直角三角形，故本选项不符合要求；C、∵（）2+（）2＝（）2，∴能构成直角三角形，故本选项不符合要求；D、∵52+122＝132，∴能构成直角三角形，故本选项不符合要求．故选：A．【点评】本题考查的是勾股定理的逆定理，即如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形．4．在平行四边形ABCD中，已知∠A＝60°，则∠D的度数是（）A．60°B．90°C．120°D．30°【分析】根据平行四边形邻角互补的性质即可求解．【解答】解：∵在平行四边形ABCD中，∠A＝60°，∴∠D＝180°﹣60°＝120°．故选：C．【点评】此题主要考查了平行四边形的性质，关键是熟练掌握平行四边形邻角互补的知识点．5．下列计算正确的是（）A．B．C．D．【分析】根据二次根式的性质与同类二次根式的定义逐一计算可得．【解答】解：A、与不是同类二次根式，不能合并，此选项错误；B、4﹣3＝3，此选项错误；C、×＝，此选项正确；D、（3）2＝18，此选项错误；故选：C．【点评】本题主要考查二次根式的混合运算，解题的关键是熟练掌握二次根式的性质和二次根数混合运算顺序及其法则．6．如图，一竖直的木杆在离地面4米处折断，木顶端落在地面离木杆底端3米处，木杆折断之前的高度为（）A．7米B．8米C．9米D．12米【分析】由题意得，在直角三角形中，知道了两直角边，运用勾股定理即可求出斜边，从而得出这棵树折断之前的高度．【解答】解：∵一竖直的木杆在离地面4米处折断，顶端落在地面离木杆底端3米处，∴折断的部分长为＝5（米），∴折断前高度为5+4＝9（米）．故选：C．【点评】此题考查了勾股定理的应用，主要考查学生对勾股定理在实际生活中的运用能力．7．如图，▱ABCD的顶点坐标分别为A（1，4）、B（1，1）、C（5，2），则点D的坐标为（）A．（5，5）B．（5，6）C．（6，6）D．（5，4）【分析】由四边形ABCD是平行四边形，可得AB∥CD，AB＝CD，继而求得答案．【解答】解：∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∵A（1，4）、B（1，1）、C（5，2），∴AB＝3，∴点D的坐标为（5，5）．故选：A．【点评】此题考查了平行四边形的性质．注意平行四边形的对边平行且相等．8．如图，A（0，1），B（3，2），点P为x轴上任意一点，则PA+PB的最小值为（）A．3 B．C．D．【分析】作点A关于x轴的对称点A′．连接BA′交x轴于点P，此时PA+PB的值最小．根据勾股定理求出BA′即可；【解答】解：作点A关于x轴的对称点A′．连接BA′交x轴于点P，此时PA+PB的值最小．PA+PB的最小值＝BA′＝＝3，故选：B．【点评】本题考查轴对称﹣最短问题，坐标用图形的性质等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型．9．如图，在正方形网格中用没有刻度的直尺作一组对边长度为的平行四边形．在1×3的正方形网格中最多作2个，在1×4的正方形网格中最多作6个，在1×5的正方形网格中最多作12个，则在1×8的正方形网格中最多可以作（）A．28个B．42个C．21个D．56个【分析】根据已知图形的出在1×n的正方形网格中最多作2×（1+2+3+…+n﹣2）个，据此可得．【解答】解：∵在1×3的正方形网格中最多作2＝2×1个，在1×4的正方形网格中最多作6＝2×（1+2）个，在1×5的正方形网格中最多作12＝2×（1+2+3）个，……∴在1×8的正方形网格中最多作2×（1+2+3+4+5+6）＝42个，故选：B．【点评】本题主要考查图形的变化规律，解题的关键是根据题意得出在1×n的正方形网格中最多作2×（1+2+3+…+n﹣2）个．10．如图，正方形ABCD中，点O为对角线的交点，直线EF过点O分别交AB、CD于E、F两点（BE ＞EA），若过点O作直线与正方形的一组对边分别交于G、H两点，满足GH＝EF，则这样的直线GH（不同于直线EF）的条数共有（）A．1条B．2条C．3条D．无数条【分析】根据对称性以及旋转变换的性质，画出图形即可解决问题，如图所示；【解答】解：根据对称性以及旋转变换的性质可知满足条件的线段有3条，如图所示；故选：C．【点评】本题考查正方形的性质、旋转变换等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．二、填空题（每小题3分，共18分11．16的平方根是±4 ．【分析】根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2＝a，则x就是a的平方根，由此即可解决问题．【解答】解：∵（±4）2＝16，∴16的平方根是±4．故答案为：±4．【点评】本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．12．计算：÷＝3．【分析】根据二次根式是除法法则进行计算．【解答】解：原式＝＝＝＝3．故答案是：3．【点评】本题考查了二次根式的乘除法．二次根式的除法法则：÷＝（a≥0，b＞0）．13．已知等边三角形的边长为6，则面积为9．【分析】根据等边三角形三线合一的性质可得D为BC的中点，即BD＝CD，在直角三角形ABD中，已知AB、BD，根据勾股定理即可求得AD的长，即可求三角形ABC的面积，即可解题．【解答】解：等边三角形高线即中线，故D为BC中点，∵AB＝6，∴BD＝3，∴AD＝＝3，∴等边△ABC的面积＝BC•AD＝×6×3＝9．故答案为：9．【点评】本题考查了勾股定理在直角三角形中的运用，等边三角形面积的计算，本题中根据勾股定理计算AD的值是解题的关键．14．如图，菱形ABCD的周长为8，对角线BD＝2，则对角线AC为2．【分析】设菱形的对角线相交于O，根据菱形性质得出AB＝BC＝CD＝AD，AC⊥BD，BO＝OD，AO＝OC，求出OB，根据勾股定理求出OA，即可求出AC．【解答】解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，AC⊥BD，BO＝OD，AO＝OC，∵菱形的周长是8，∴DC＝×8＝2，∵BD＝2，∴OD＝1，在Rt△DOC中，OC＝＝，∴AC＝2OC＝2，故答案为：2．【点评】本题考查了菱形的性质和勾股定理，注意：菱形的对角线互相垂直平分，菱形的四条边相等．15．如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点E的坐标（0，）．【分析】先证明EA＝EC（设为x）；根据勾股定理列出x2＝12+（3﹣x）2，求得x＝，即可解决问题．【解答】解：由题意知：∠BAC＝∠DAC，AB∥OC，∴∠ECA＝∠BAC，∴∠ECA＝∠DAC，∴EA＝EC（设为x）；由题意得：OA＝1，OC＝AB＝3；由勾股定理得：x2＝12+（3﹣x）2，解得：x＝，∴OE＝3﹣＝，∴E点的坐标为（0，）．故答案为：（0，）．【点评】该题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答；对综合的分析问题解决问题的能力提出了较高的要求．16．如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝5，DA＝5，则BD的长为．【分析】作DM⊥BC，交BC延长线于M，由勾股定理得出AC2＝AB2+BC2＝25，求出AC2+CD2＝AD2，由勾股定理的逆定理得出△ACD是直角三角形，∠ACD＝90°，证出∠ACB＝∠CDM，得出△ABC≌△CMD，由全等三角形的性质求出CM＝AB＝3，DM＝BC＝4，得出BM＝BC+CM＝7，再由勾股定理求出BD即可．【解答】解：作DM⊥BC，交BC延长线于M，如图所示：则∠M＝90°，∴∠DCM+∠CDM＝90°，∵∠ABC＝90°，AB＝3，BC＝4，∴AC2＝AB2+BC2＝25，∴AC＝5，∵AD＝5，CD＝5，∴AC2+CD2＝AD2，∴△ACD是直角三角形，∠ACD＝90°，∴∠ACB+∠DCM＝90°，∴∠ACB＝∠CDM，∵∠ABC＝∠M＝90°，在△ABC和△CMD中∴△ABC≌△CMD，∴CM＝AB＝3，DM＝BC＝4，∴BM＝BC+CM＝7，∴BD＝＝＝，故答案为：．【点评】本题考查了全等三角形的判定与性质、勾股定理、勾股定理的逆定理；熟练掌握全等三角形的判定与性质，由勾股定理的逆定理证出△ACD是直角三角形是解决问题的关键．三、解答题（共8小题，共72分）17．（8分）计算：①；②．【分析】①先化简各二次根式，再合并同类二次根式即可得；②根据二次根式的乘法运算法则计算可得．【解答】解：①原式＝3﹣4+2＝；②原式＝＝＝3．【点评】本题主要考查二次根式的混合运算，解题的关键是熟练掌握二次根式的性质和二次根数混合运算顺序及其法则．18．（8分）计算：①②【分析】①先利用完全平方公式和平方差公式计算乘法和乘方，再合并同类二次根式即可得；②先化简各二次根式，再计算乘法，继而合并同类二次根式即可得．【解答】解：①原式＝2+6+4+3﹣6＝5+4；②原式＝6×﹣×6＝3﹣15＝﹣12．【点评】本题主要考查二次根式的混合运算，解题的关键是熟练掌握二次根式的性质及二次根式混合运算顺序和运算法则．19．（8分）一根直立于水中的芦节（BD）高出水面（AC）2米，一阵风吹来，芦苇的顶端D恰好到达水面的C处，且C到BD的距离AC＝6米，求水的深度（AB）为多少米？【分析】先设水深为x，则AB＝x，求出x的长，再由勾股定理即可得出结论．【解答】解：∵先设水深为x，则AB＝x，BC＝（x+2），∵AC＝6米，在△ABC中，AB2+AC2＝BC2，即62+x2＝（x+2）2，解得x＝8（米）．答：水深AB为8米．【点评】本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．20．（8分）如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD．求证：四边形ABCD是菱形．【分析】根据平行线的性质得出∠ADB＝∠DBC，∠DAC＝∠BCA，根据角平分线定义得出∠DAC＝∠BAC，∠ABD＝∠DBC，求出∠BAC＝∠ACB，∠ABD＝∠ADB，根据等腰三角形的判定得出AB＝BC ＝AD，根据平行四边形的判定得出四边形ABCD是平行四边形，即可得出答案．【解答】证明：∵AE∥BF，∴∠ADB＝∠DBC，∠DAC＝∠BCA，∵AC、BD分别是∠BAD、∠ABC的平分线，∴∠DAC＝∠BAC，∠ABD＝∠DBC，∴∠BAC＝∠ACB，∠ABD＝∠ADB，∴AB＝BC，AB＝AD∴AD＝BC，∵AD∥BC，∴四边形ABCD是平行四边形，∵AD＝AB，∴四边形ABCD是菱形．【点评】本题考查了等腰三角形的性质，平行四边形的判定，菱形的判定的应用，能得出四边形ABCD是平行四边形是解此题的关键．21．（8分）如图，在4×4的正方形网格中，每个小正方形的边长都为1．（1）求△ABC的周长；（2）求证：∠ABC＝90°；（3）若点P为直线AC上任意一点，则线段BP的最小值为 2 ．【分析】（1）运用勾股定理求得AB，BC及AC的长，即可求出△ABC的周长．（2）运用勾股定理的逆定理求得AC2＝AB2+BC2，得出∠ABC＝90°．（3）过B作BP⊥AC，解答即可．【解答】解：（1）AB＝，BC＝，AC＝，△ABC的周长＝2++5＝3+5，（2）∵AC2＝25，AB2＝20，BC2＝5，∴AC2＝AB2+BC2，∴∠ABC＝90°．（3）过B作BP⊥AC，∵△ABC的面积＝，即，解得BP＝2，故答案为：2【点评】本题主要考查了勾股定理及勾股定理的逆定理，熟记勾股定理是解题的关键．22．（10分）如图1，点D、E、F、G分别为线段AB、OB、OC、AC的中点．（1）求证：四边形DEFG是平行四边形；（2）如图2，若点M为EF的中点，BE：CF：DG＝2：3：，求证：∠MOF＝∠EFO．【分析】（1）根据中位线定理得：DG∥BC，DG＝BC，EF∥BC，EF＝BC，则DG＝BC，DE∥BC，根据一组对边平行且相等的四边形是平行四边形可得：四边形DEFG是平行四边形；（2）先根据已知的比的关系设未知数：设BE＝2x，CF＝3x，DG＝x，根据勾股定理的逆定理得：∠EOF＝90°，最后利用直角三角形斜边中线的性质可得OM＝FM，由等边对等角可得结论．【解答】证明：（1）∵D是AB的中点，G是AC的中点，∴DG是△ABC的中位线，∴DG∥BC，DG＝BC，同理得：EF是△OBC的中位线，∴EF∥BC，EF＝BC，∴DG＝EF，DG∥EF，∴四边形DEFG是平行四边形；（2）∵BE：CF：DG＝2：3：，∴设BE＝2x，CF＝3x，DG＝x，∴OE＝2x，OF＝3x，∵四边形DEFG是平行四边形，∴DG＝EF＝x，∴OE2+OF2＝EF2，∴∠EOF＝90°，∵点M为EF的中点，∴OM＝MF，∴∠MOF＝∠EFO．【点评】本题考查的是三角形中位线定理、平行四边形的判定、勾股定理的逆定理，掌握三角形中位线定理是解题的关键．23．（10分）已知点A为正方形BCDE内一动点，满足∠DAC＝135°，且b＝+5．（1）求a、b的值；（2）如图1，若线段AB＝b，AC＝a，求线段AD的长；（3）如图2，设线段AB＝m，AC＝n，AD＝h，请探究并直接写出三个量m2、n2、h2之间满足的数量关系．【分析】（1）根据二次根式有意义的条件列出不等式，解不等式得到答案；（2）把△CAD旋转90°得到△CA′B，根据勾股定理求出AA′，求出∠AA′B＝90°，根据勾股定理计算即可；（3）仿照（2）的计算方法解答．【解答】解：（1）由二次根式有意义的条件可知，a﹣3≥0，3﹣a≥0，∴a＝3，b＝5；（2）把△CAD旋转90°得到△CA′B，则AC＝A′C，∠A′CB＝∠ACD，AD＝A′B，∴∠ACA′＝90°，∴∠AA′C＝45°，AA′＝＝3，∴∠AA′B＝90°，∴A′B＝＝，∴AD＝A′B＝；（3）由（2）得，AA′＝＝n，∴m2﹣2n2＝h2．【点评】本题考查的是二次根式有意义的条件、旋转变换的性质、勾股定理的应用，掌握二次根式的被开方数是非负数、旋转变换的性质是解题的关键．24．（12分）在正方形ABCD中，点E为边BC（不含B点）上的一动点，AE⊥EF，且AE＝EF，FG ⊥BC的延长线于点G．（1）如图1，求证：BE＝FG；（2）如图2，连接BD，过点F作FH∥BC交BD于点H，连接HE，判断四边形EGFH的形状，并给出证明；（3）如图3，点P、Q为正方形ABCD内两点，AB＝BQ，且∠ABQ＝30°，BP平分∠QBC，BP＝DP，若BC＝+1，求线段PQ的长．【分析】（1）欲证明BE＝FG，只要证明△ABE≌△EGF，即可解决问题；（2）四边形EGFH是矩形．首先证明四边形ECMH是矩形，可得∠FHE＝∠HEG＝∠EGF＝90°，推出四边形EGFH是矩形；（3）如图3中，连接PC，作PE⊥BC于E，PF⊥BQ于F．∴由PCB≌△PCD，推出∠PCB＝∠PCD＝45°，可证PE＝EC，设PE＝EC＝a，在Rt△PEB中，由∠PBE＝30°，推出PB＝2PE，BE＝a，由BC＝+1，可得a+a＝+1，推出a＝1，再求出FQ、FP即可解决问题；【解答】解：（1）如图1中，∵FG⊥EG，AE⊥EF，四边形ABCD是正方形，∴∠B＝∠AEF＝∠G＝90°，∴∠BAE+∠AEB＝90°，∠AEB+∠FEG＝90°，∴∠BAE＝∠FEG，∵AE＝EF，∴△ABE≌△EGF，∴BE＝FG．（2）结论：四边形EGFH是矩形．理由：如图2中，设FH交CD于M．∵△ABE≌△EGF，∴AB＝EG＝BC，∴BE＝CG＝FG，∵FM∥CG，FG∥CM，∴四边形CMFG是平行四边形，∵GC＝FG，∠MCG＝90°，∴四边形CMFG是正方形，∴CM＝CG＝BE，∵BC＝CD，∴CE＝DM，∵FH∥BC，∴∠DMH＝∠DCB＝90°，∵∠MDH＝45°，∴∠MDH＝∠MHD＝45°，∴DM＝HM＝EC，∵HM∥EC，∴四边形CEHM是平行四边形，∵∠ECM＝90°，∴四边形ECMH是矩形，∴∠FHE＝∠HEG＝∠EGF＝90°，∴四边形EGFH是矩形．（3）如图3中，连接PC，作PE⊥BC于E，PF⊥BQ于F．∵PB＝PD，PC＝PC，BC＝CD，∴△PCB≌△PCD，∴∠PCB＝∠PCD＝45°，∵PE⊥EC，∴∠PCE＝∠EPC＝45°，∴PE＝EC，设PE＝EC＝a，在Rt△PEB中，∵∠PBE＝30°，∴PB＝2PE，BE＝a，∵BC＝+1，∴a+a＝+1，∴a＝1，∴PB＝2在Rt△PFB中，∵∠PBF＝30°，∴PF＝1，BF＝，∵BQ＝BQ＝BC＝+1，∴FQ＝1，∴PQ＝＝．【点评】本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、矩形的判定和性质、勾股定理、直角三角形30度角的性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．。

2020-2021学年湖北省武汉市八年级（下）期中数学试卷一、选择题（本大题共10小题，共30.0分）1.下列实数中最小的是()A. 1B. −√17C. −4D. 02.下列式子中，属于最简二次根式的是()D. √5A. √9B. √20C. √133.下列运算正确的是()A. √(−3)2=−3B. (3√2)2=6C. √3+√2=√5D. √3×√5=√154.下列判断中正确的有()个(l)直角三角形的两边为3和4，则第三边长为5(2)有一个内角等于其它两个内角和的三角形是直角三角形(3)若三角形的三边满足b2=a2−c2，则△ABC是直角三角形(4)若△ABC中，∠A：∠B：∠C=8：15：17，则△ABC是直角三角形A. 1B. 2C. 3D. 45.下列说法中错误的是()A. 平行四边形的对边相等B. 正方形的对角线互相垂直平分且相等C. 菱形的对角线互相垂直平分D. 矩形的对角线互相垂直相等6.如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B，D恰好都落在点G处，已知BE=1，则EF的长为()A. 1.5B. 2.5C. 2.25D. 37.如图，在Rt△ABC中，∠ACB=90°，CD、CE分别是斜边上的高和中线，若AC=CE=6，则CD的长为()A. √3B. 3√3C. 6D. 6√38.如图，在一块平地上，停在一辆大客车前9m处有一棵大树．在一次强风中，这棵树从离地面6m处正对大客车方向折断倒下，若倒下部分的长是10m，则大树倒下时会碰到客车吗？()A. 不会B. 可能会C. 一定会D. 无法确定9.已知等腰三角形的两条中位线的长分别为3和5，则此等腰三角形的周长为()A. 22B. 26C. 22或26D. 1310.如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG，AC⏜，BC⏜的中点分别是M，N，P，Q.若MP+NQ= 14，AC+BC=20，则AB的长是()C. 13D. 16A. 9√2B. 907二、填空题（本大题共6小题，共18.0分）11.数轴上到−√2所表示的点的距离等于4的点所表示的数是______．12.若√a2=7，则实数a=______．13.在矩形ABCD中，AB=5，BC=12，点A在⊙B上，如果⊙D与⊙B相交，且点B在⊙D内，那么⊙D的半径长可以等于______.(只需写出一个符合要求的数)14.如图1，边长为a的正方形发生形变后成为边长为a的菱形，如果这个菱形的一组的值叫做这个菱形的“形变度”.例如，当形变后的对边之间的距离为h，我们把aℎ菱形是如图2形状(被对角线BD分成2个等边三角形)，则这个菱形的“形变度”为2：√3.如图3，正方形由16个边长为1的小正方形组成，形变后成为菱形，△AEF(A、E、F是格点)同时形变为△A′E′F′，若这个菱形的“形变度”k=16，则15 S△A′E′F′=______．15.已知直角三角形的两直角边分别为5㎝和12㎝.则它的斜边长为㎝.16.如图，AB为⊙O的弦，半径OC交AB于点D，AD=DB，OC=5，CD=2，则AB长为______．三、解答题（本大题共8小题，共72.0分）17.计算：(√3+√2)(√3−√2)−(1−√2)18.(1)(√13+√27)×√3；(2)√48÷√3−√12×√12+√24；(3)√24×√13−4×√18÷(1−√2)0．19.某地要开发一块三角形植物园，如图，测得AC=80cm，BC=60cm，AB=100cm．(1)若入口E在边AB上，且AB=2BE，求从入口E到出口C的最短路线的长；(2)若线段CD是一条水渠，且点D在边AB上，CD=CE，请直接写出DE的长度．20.如图，在⊙O上依次有A、B、C三点，BO的延长线交⊙O于E，AE⏜=CE⏜，过点C作CD//AB交BE的延长线于D，AD交⊙O于点F．(1)求证：四边形ABCD是菱形；(2)连接OA、OF，若∠AOF=3∠FOE且AF=3，求劣弧CF⏜的长．21.如图，在平面直角坐标系中，△ABC的顶点A(0,1)，B(3,2)，C(1,4)均在正方形网格的格点上．(1)画出△ABC关于x轴的对称图形△A1B1C1；(2)将△A1B1C1沿x轴方向向左平移4个单位得到△A2B2C2，画出△A2B2C2并写出顶点A2，B2，C2的坐标．22.阅读下列材料，解决问题：学习了勾股定理后我们知道：直角三角形两条直角边的平方和等于斜边的平方．根据勾股定理我们定义：如图①，点M、N是线段AB上两点，如果线段AM、MN、NB能构成直角三角形，则称点M、N是线段AB的勾股点解决问题(1)在图①中，如果AM=2，MN=3，则NB=______(2)如图②，已知点C是线段AB上一定点(AC<BC)，在线段AB上求作一点D，使得C、D是线段AB的勾股点．李玉同学是这样做的：过点C作直线GH⊥AB，在GH上截取CE=AC，连接BE，作BE的垂直平分线交AB于点D，则C、D是线段AB的勾股点你认为李玉同学的做法对吗？请说明理由(3)如图③，DE是△ABC的中位线，M、N是AB边的勾股点(AM<MN<NB)，连接CM、CN分别交DE于点G、H求证：G、H是线段DE的勾股点．23.如图，AC是正方形ABCD的对角线，AD=8，E是AC的中点．动点P从点A出发，沿AB方向以每秒1个单位的速度向终点B运动，同时动点Q从点B出发，以每秒2个单位的速度先沿BC方向运动到点C，再沿CD方向向终点D运动，以EP，EQ为邻边构造平行四边形PEQF，设点P运动的时间为t秒(0<t<8)．(1)当PE的长为5时，试求t的值．(2)当点F恰好落在线段AB上时，求BF的长．(3)在整个运动过程中，当平行四边形PEQF为菱形时，求t的值．(直接写出答案)24.在矩形ABCD中，AB=3，AD=4，动点Q从点A出发，以每秒1个单位的速度，沿AB向点B移动；同时点P从点B出发，仍以每秒1个单位的速度，沿BC向点C移动，连接QP，QD，PD.若两个点同时运动的时间为x秒(0<x≤3)，解答下列问题：(1)设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最大值？并求出最小值；(2)是否存在x的值，使得QP⊥DP？试说明理由．答案和解析1.【答案】B【解析】解：∵−√17<−4<0<1，∴实数中最小的是−√17．故选：B．根据实数大小比较的方法进行比较即可求解．考查了实数大小比较，任意两个实数都可以比较大小．正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小．2.【答案】D【解析】解：A、原式=3，故A不是最简二次根式，B、原式=2√5，故B不是最简二次根式，C、原式=√3，故C不是最简二次根式，3故选：D．根据最简二次根式的定义即可判断．本题考查最简二次根式，解题的关键是正确理解最简二次根式，本题属于基础题型．3.【答案】D【解析】解：A、原式=|−3|=3，所以A选项错误；B、原式=9×2=18，所以B选项错误；C、√2与√3不能合并，所以C选项错误；D、原式=√3×5=√15，所以D选项正确．故选：D．根据二次根式的性质对A、B进行判断；根据二次根式的加减法对C进行判断；根据二次根式的乘法法则对D进行判断．本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．4.【答案】B【解析】解：(l)直角三角形的两边为3和4，则第三边长为5或√7，原来的说法错误；(2)有一个内角等于其它两个内角和的三角形是直角三角形是正确的；(3)若三角形的三边满足b2=a2−c2，即b2+c2=a2，则△ABC是直角三角形是正确的；=76.5°，则△ABC不(4)若△ABC中，∠A：∠B：∠C=8：15：17，∠C=180°×178+15+17是直角三角形，原来的说法错误．故正确的有2个．故选：B．依据勾股定理的逆定理以及三角形内角和定理，即可得到三角形是否为直角三角形．本题主要考查了勾股定理的逆定理以及三角形内角和定理，如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．5.【答案】D【解析】解：矩形对角线一定相等，但不一定相互垂直，选D说法错误．其它三个选项说法均正确．故选：D．根据几种四边形的性质进行判断即可．本题主要考查了平行四边形以及三种特殊平行四边形的性质，熟悉这几种四边形的性质是解答关键．6.【答案】B【解析】解：∵正方形纸片ABCD的边长为3，∴∠C=90°，BC=CD=3，根据折叠的性质得：EG=BE=1，GF=DF，设DF=x，则EF=EG+GF=1+x，FC=DC−DF=3−x，EC=BC−BE=3−1=2，∵在Rt△EFC中，EF2=EC2+FC2，即(x+1)2=22+(3−x)2，解得：x=1.5，∴DF=1.5，EF=1+1.5=2.5．故选：B．由正方形纸片ABCD的边长为3，可得∠C=90°，BC=CD=3，由根据折叠的性质得：EG=BE=1，GF=DF，然后设DF=x，在Rt△EFC中，由勾股定理EF2=EC2+FC2，即可得方程，解方程即可求得答案．此题考查了正方形的性质、翻折变换以及勾股定理．此题难度适中，注意掌握数形结合思想与方程思想的应用．7.【答案】B【解析】解：∵∠ACB=90°，CE为斜边上的中线，∴AE=BE=CE=AC=6∴△ACE为等边三角形，∴∠AEC=60°，∴∠DCE=30°，∵CD⊥AE，AE=3，∴DE=12∴CD=√3DE=3√3，故选：B．AE，根据条件可求得AC=AE=CE=BE，可证得△ACE为等边三角形，可求得DE=12可求得DE，则可求得CD．本题主要考查直角三角形的性质及等边三角形的性质，根据直角三角形的性质求得BE、根据等边三角形的性质求得DE是解题的关键．8.【答案】A【解析】解：如图所示，AB=10米，AC=6米，在RtΔABC中，根据勾股定理得，BC=√AB2−AC2=√102−62=8<9．故选：A．由题意知树折断的两部分与地面形成一直角三角形，根据勾股定理求出BC的长即可解答．此题考查了勾股定理在生活中的应用．善于观察题目的信息是解题以及学好数学的关键．9.【答案】C【解析】解：等腰三角形的两条中位线长分别为3和5，根据三角形中位线定理可知，等腰三角形的两边长为6和10，当腰为10时，则三边长为10，10，6时，周长为26；当腰为6时，则三边长为6，6，10时，周长为22，故选：C．根据三角形中位线定理求出等腰三角形的两边长，分腰为10、腰为6两种情况，根据三角形的周长公式计算，得到答案．本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．10.【答案】D【解析】解：连接OP、OQ分别与AC、BC相交于点G、H，(AC+BC)=10，根据中点可得OG+OH=12MG+NH=AC+BC=20，∵MP+NQ=14，∴PG+QH=20−14=6，则OP+OQ=(OG+OH)+(PG+QH)=10+6=16，根据题意可得OP、OQ为圆的半径，AB为圆的直径，则AB=OP+OQ=16．故选：D．连接OP、OQ分别交AC、BC相交于点G、H，利用中位线定理求出OG+OH的长，根据AC+BC求出MG+NH的长，再由MP+NQ求出PG+QH的长，进而求出OP+OQ的长，即可确定出AB的长．此题考查了圆周角定理，垂径定理，以及正方形的性质，熟练掌握圆周角定理是解本题的关键．11.【答案】−√2−4或−√2+4【解析】解：根据题意得，当点在−√2的左边时，所表示的数为−√2−4，当点在−√2的右边时，所表示的数为−√2+4，故答案为：−√2−4或−√2+4．分两种情况：当这个点在−√2左边时，则比−√2小4；当这个点在−√2右边时，则比−√2大4.据此解答便可．本题主要考查了数轴上两点间的距离，关键是分情况讨论．12.【答案】±7【解析】解：由题意可知：|a|=7，∴a=±7，故答案为：±7根据二次根式的性质即可求出答案．本题考查二次根式，解题的关键是熟练运用二次根式的的性质，本题属于基础题型．13.【答案】14(答案不唯一)【解析】【分析】本题考查了圆与圆的位置关系、点与圆的位置关系，解题的关键是首先确定⊙B的半径，然后确定⊙D的半径的取值范围，难度不大．首先求得矩形的对角线的长，然后根据点A在⊙B上得到⊙B的半径为5，再根据⊙D与⊙B相交，得到⊙D的半径R满足8<R<18，再由点B在⊙D内，则13<R<18，在此范围内找到一个值即可．【解答】解：∵矩形ABCD中，AB=5，BC=12，∴根据勾股定理可得AC=BD=13，∵点A在⊙B上，∴⊙B的半径为5，∵如果⊙D与⊙B相交，∴⊙D的半径R满足8<R<18，∵点B在⊙D内，∴R>13，∴13<R<18，∴14符合要求，故答案为：14(答案不唯一)．14.【答案】154【解析】解：如图，在图2中，形变前正方形的面积为：a2，形变后的菱形的面积为：a⋅√32a=√32a2，∴菱形形变前的面积与形变后的面积之比：a2：√32a2=2：√3，∵这个菱形的“形变度”为2：√3．∴菱形形变前的面积与形变后的面积之比=这个菱形的“形变度”，S△AEF=12×2×2+12×2×2=4，∵若这个菱形的“形变度”k=1615，∴S△AEFS△A′E′F′=1615，即4S△A′E′F′=1615，∴S△A′E′F′=154．故答案为：154．求出形变前正方形的面积，形变后菱形的面积，两面积之比=菱形的“形变度”，求△AEF的面积，根据两面积之比=菱形的“形变度”，即可解答．本题考查了正方形的性质，菱形的性质以及四边形综合，根据题意得出菱形形变前的面积与形变后的面积之比是解题关键．15.【答案】13【解析】由勾股定理，得斜边=√52+122=13cm．16.【答案】8【解析】解：连接OB，如图所示：∵⊙O的半径为5，CD=2，∴OD=5−2=3．∵AD=DB，∴OC⊥AB，∴∠ODB=90°，∴BD=√OB2−OD2=√52−32=4，∴AB=2BD=8，故答案为：8．连接OB，根据⊙O的半径为5，CD=2得出OD的长，再由垂径定理的推论得出OC⊥AB，由勾股定理求出BD的长，进而可得出结论．本题考查的是垂径定理以及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．17.【答案】解：(√3+√2)(√3−√2)−(1−√2)=(√3)2−(√2)2−1+√2=(3−2)−1+√2=1−1+√2=√2．【解析】直接利用二次根式的性质结合平方差公式计算得出答案．此题主要考查了二次根式的混合运算，正确掌握相关运算法则是解题关键．18.【答案】解：(1)原式=√1×3+√27×33=1+9=10；(2)原式=√48÷3−√1×12+2√62=4−√6+2√6=4+√6；(3)原式=√24×1−√2÷13=2√2−√2=√2．【解析】(1)利用二次根式的乘法法则运算；(2)利用二次根式的乘除法则运算；(3)先利用零指数幂的意义计算，再利用二次根式的乘法法则运算，然后化简后合并即可．本题考查了二次根式的混合运算：先把各二次根式化简为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．19.【答案】解：(1)∵AC=80cm，BC=60cm，AB=100cm，∴AC2+BC2=AB2，∴△ABC为直角三角形，且∠ACB=90°，∵AB=2BE，∴E为AB的中点，即CE为AB边上的中线，∴CE=12AB=50cm；(2)作CF⊥AB，交AB于点F，∵CE=CD，∴EF=DF，∵S△ABC=12AC⋅BC=12AB⋅CF，∴CF=80×60100=48cm，在Rt△ACF中，根据勾股定理得：AF=√802−482=64cm，∴EF=AF−AE=64−50=14cm，则ED=2EF=28cm．【解析】(1)利用勾股定理的逆定理判断出三角形ABC为直角三角形，根据CE为斜边上的中线，利用直角三角形斜边上的中线等于斜边的一半求出即可；(2)作CF⊥AB，交AB于点F，由CE=CD，利用三线合一得到F为ED中点，利用面积法求出CF的长，再利用勾股定理求出AF的长，由AF−AE求出EF的长，即可确定出ED的长．此题考查了勾股定理的应用，熟练掌握勾股定理及逆定理是解本题的关键．20.【答案】(1)证明：∵AE⏜=CE⏜，∴∠CBD=∠ABD，∵CD//AB，∴∠ABD=∠CDB，∴∠CBD=∠CDB，∴CB=CD，∵BE是⊙O的直径，∴AB⏜=BC⏜，∴AB=BC=CD，∵CD//AB，∴四边形ABCD是菱形；(2)∵∠AOF=3∠FOE，设∠FOE=x，则∠AOF=3x，∠AOD=∠FOE+∠AOF=4x，∵OA=OF，∴∠OAF=∠OFA=12(180−3x)°，∵OA=OB，∴∠OAB=∠OBA=2x，∴∠ABC=4x，∵BC//AD，∴∠ABC+∠BAD=180°，∴4x+2x+12(180−3x)=180，x=20°，∴∠AOF=3x=60°，∠AOE=80°，∴∠COF=80°×2−60°=100°，∵OA=OF，∴△AOF是等边三角形，∴OF=AF=3，∴CF⏜的长=100π×3180=5π3．【解析】(1)先根据圆的性质得：∠CBD=∠ABD，由平行线的性质得：∠ABD=∠CDB，根据直径和等式的性质得：AB⏜=BC⏜，由一组对边平行且相等可得四边形ABCD是平行四边形，由AB=BC可得结论；(2)先设∠FOE=x，则∠AOF=3x，根据∠ABC+∠BAD=180°，列方程得：4x+2x+12(180−3x)=180，求出x的值，接着求CF⏜所对的圆心角和半径的长，根据弧长公式可得结论．本题考查平行四边形和菱形的判定和性质、等边三角形的判定和性质、弧长公式，平行线的性质等知识，解题的关键是学会设未知数，列方程求角的度数，证明三角形是等边三角形是解题的突破点，属于中考常考题型．21.【答案】解：(1)如图，△A1B1C1为所作；(2)如图，△A2B2C2为所作，点A2，B2，C2的坐标分别为(−4,−1)，(−1,−2)，(−3,−4)．【解析】(1)利用关于x轴对称的点的坐标特征写出A、B、C点的对应点A1、B1、C1的坐标，然后描点即可；(2)利用点平移的坐标特征写出点A2，B2，C2的坐标，然后描点即可．本题考查了作图−轴对称变换：几何图形都可看做是由点组成，我们在画一个图形的轴对称图形时，也是先从确定一些特殊的对称点开始的．也考查了平移变换．22.【答案】√13或√5【解析】解：(1)当BN是斜边时，BN=√22+32=√13．当MN是斜边时，BN=√32−22=√5，故答案为√13或√5．(2)如图②中，连接DE．∵点D在线段BE的垂直平分线上，∴DE=DB，∵GH⊥BC，∴∠ECD=90°，∴DE2=EC2+CD2，∵AC=CE，DE=DB，∴DB2=AC2+CD2，∴C、D是线段AB的勾股点．(3)如图3中，∵CD=DA，CE=EB，∴DE//AB，∴CG=GM，CH=HN，∴DG=12AM，GH=12MN，EH=12BN，∵BN2=MN2+AM2，∴14BN2=14MN2+14AM2，∴(12BN)2=(12MN)2+(12AM)2，∴EH2=GH2+DG2，∴G、H是线段DE的勾股点．(1)分两种情形分别求解即可解决问题．(2)想办法证明DB2=AC2+CD2即可．(3)利用三角形的中位线定理以及勾股定理证明EH2=GH2+DG2即可．本题考查作图−复杂作图，线段的垂直平分线的性质，勾股定理，三角形的中位线定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．23.【答案】解：(1)如图，取AB中点M，连接EM，∵四边形ABCD是正方形，∴AB=BC=CD=AD=8，∠ABC=90°，∵点M是AB中点，点E是AC中点，BC=4，EM//BC，∴AM=BM=4，EM=12∴∠AME=∠ABC=90°，当点P在点M上方时，∵PE=5，ME=4，∴PM=√PE2−EM2=√25−16=3，∴AP=AM−PM=1，=1(s)，∴t=11当点P在点M下方时，∵PE=5，ME=4，∴PM=√PE2−EM2=√25−16=3，∴AP=AM+PM=7，=7(s)，∴t=71综上所述：t的值为7或1；(2)如图2，∵四边形PEQF是平行四边形，∴PF=EQ，PF//EQ，当点F恰好落在线段AB上时，PF⊥BC，∴EQ⊥BC，又∵EM⊥AB，∠ABC=90°，∴四边形EMBQ是矩形，∴BQ=EM=4，EQ=BM=4，∴PF=4，∵动点Q从点B出发，以每秒2个单位的速度先沿BC方向运动到点C，∴t=4÷2=2，∴AP=2，∴BF=AB−AP=PF=2；(3)当▱PEQF为菱形时，PE=PQ，分四种情况：①当0<t≤2时，作EM⊥AB于M，EN⊥BC于N，如图3所示：∵PE2=PM2+EM2，EQ2=QN2+EN2，∴(4−t)2+42=(4−2t)2+42，(舍去)；解得：t=0(舍去)，或t=83②当2<t≤4时，同①得：(4−t)2+42=(2t−4)2+42，，解得：t=0(舍去)，或t=83∴t=8；3③当4<t≤6时，作EM⊥AB于M，EN⊥BC于N，如图4所示：∵PE 2=PM 2+EM 2，EQ 2=QN 2+EN 2，∴(t −4)2+42=(12−2t)2+42，解得：t =163，或t =8(舍去)， ∴t =163；④当6<t ≤8时，同③得：(t −4)2+42=(2t −12)2+42，解得：t =163(舍去)，或t =8(舍去)；综上所述：在整个运动过程中，当▱PEQF 为菱形时，t 的值为83或163．【解析】(1)取AB 中点M ，连接EM ，由三角形中位线定理可得AM =BM =4，EM =12BC =4，EM//BC ，∠AME =∠ABC =90°，由勾股定理可求PM 的长，分两种情况讨论可求AP 的长，即可求解；(2)由平行四边形的性质得出PF =EQ ，PF//EQ ，当点F 恰好落在线段AB 上时，得出EQ ⊥BC ，可证四边形EMBQ 是矩形，可得BQ =EM =4，EQ =BM =4，PF =4，可求AP =2，即可求出BF 的长；(3)由菱形的性质得出PE =PQ ，分四种情况：①当0<t ≤2时，作EM ⊥AB 于M ，EN ⊥BC 于N ；②当2<t ≤4时；③当4<t ≤6时，作EM ⊥AB 于M ，EN ⊥BC 于N ；④当6<t ≤8时；分别由勾股定理得出方程，解方程即可．本题是四边形综合题目，考查了正方形的性质，勾股定理，平行四边形的性质，三角形中位线定理，菱形的性质等知识；本题综合性强，有一定难度，特别是(3)中，需要通过作辅助线进行分类讨论，运用勾股定理得出方程才能得出结果．24.【答案】解：(1)∵四边形ABCD 为矩形，∴BC =AD =4，CD =AB =3，当运动x 秒时，则AQ =x ，BP =x ，∴BQ =AB −AQ =3−x ，CP =BC −BP =4−x ，∴S △ADQ =12AD ⋅AQ =12×4x =2x ，S △BPQ =12BQ ⋅BP =12(3−x)x =32x −12x 2，S △PCD =12PC ⋅CD =12⋅(4−x)⋅3=6−32x ，又S 矩形ABCD =AB ⋅BC =3×4=12，∴S=S矩形ABCD −S△ADQ−S△BPQ−S△PCD=12−2x−(32x−12x2)−(6−32x)=12x2−2x+6=12(x−2)2+4，即S=12(x−2)2+4，∴S为开口向上的二次函数，且对称轴为x=2，∴当0<x<2时，S随x的增大而减小，当2<x≤3时，S随x的增大而增大，又当x=0时，S=6，当S=3时，S=92，但x的范围内取不到x=0，∴S不存在最大值，当x=2时，S有最小值，最小值为4；(2)存在，理由如下：由(1)可知BQ=3−x，BP=x，CP=4−x，当QP⊥DP时，则∠BPQ+∠DPC=∠DPC+∠PDC，∴∠BPQ=∠PDC，且∠B=∠C，∴△BPQ∽△CDP，∴BQPC =BPCD，即3−x4−x=x3，解得x=7+√132(舍去)或x=7−√132，∴当x=7−√132时QP⊥DP．【解析】(1)可用x表示出AQ、BQ、BP、CP，从而可表示出S△ADQ、S△BPQ、S△PCD的面积，则可表示出S，再利用二次函数的增减性可求得是否有最大值，并能求得其最小值；(2)用x表示出BQ、BP、PC，当QP⊥DP时，可证明△BPQ∽△CDP，利用相似三角形的性质可得到关于x的方程，可求得x的值．本题为四边形的综合应用，涉及知识点有矩形的性质、二次函数的最值、相似三角形的判定和性质及方程思想等．在(1)中求得S关于x的关系式后，求S的最值时需要注意x 的范围，在(2)中证明三角形相似是解题的关键．本题考查知识点较多，综合性较强，难度适中．。

湖北省武汉市硚口区八年级（下）期中数学试卷一、选择題（共10小题，每小题3分，共30分下列各题均有四个备选选项，其中有且只有一个正确，请在答题卡上将正确答案的字母涂黑．1．若式子在实数范围内有意义，则a的取值范围是（）A．a＞3B．a≥3C．a＜3D．a≤32．若＝4﹣b，则b满足的条件是（）A．b＞4B．b＜4C．b≥4D．b≤43．以下列长度的线段为边，不能构成直角三角形的是（）A．2，3，4B．1，1，C．D．5，12，134．在平行四边形ABCD中，已知∠A＝60°，则∠D的度数是（）A．60°B．90°C．120°D．30°5．下列计算正确的是（）A．B．C．D．6．如图，一竖直的木杆在离地面4米处折断，木頂端落在地面离木杆底端3米处，木杆折断之前的高度为（）A．7米B．8米C．9米D．12米7．如图，▱ABCD的顶点坐标分别为A（1，4）、B（1，1）、C（5，2），则点D的坐标为（）A．（5，5）B．（5，6）C．（6，6）D．（5，4）8．如图，A（0，1），B（3，2），点P为x轴上任意一点，则PA+PB的最小值为（）A．3B．C．D．9．如图，在正方形网格中用没有刻度的直尺作一组对边长度为的平行四边形．在1×3的正方形网格中最多作2个，在1×4的正方形网格中最多作6个，在1×5的正方形网格中最多作12个，则在1×8的正方形网格中最多可以作（）A．28个B．42个C．21个D．56个10．如图，正方形ABCD中，点O为对角线的交点，直线EF过点O分别交AB、CD于E、F两点（BE＞EA），若过点O作直线与正方形的一组对边分別交于G、H两点，满足GH＝EF，则这样的直线GH（不同于直线EF）的条数共有（）A．1条B．2条C．3条D．无数条二、填空题（每小题3分，共18分11．16的平方根是．12．计算：÷＝．13．已知等边三角形的边长为6，则面积为．14．如图，菱形ABCD的周长为8，对角线BD＝2，则对角线AC为．15．如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点E的坐标．16．如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝5，DA＝5，则BD的长为．三、解答题（共8小題，共72分）17．（8分）计算：①；②．18．（8分）计算：①②19．（8分）一根直立于水中的芦节（BD）高出水面（AC）2米，一阵风吹来，芦苇的顶端D恰好到达水面的C处，且C到BD的距离AC＝6米，求水的深度（AB）为多少米？20．（8分）如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD．求证：四边形ABCD是菱形．21．（8分）如图，在4×4的正方形网格中，每个小正方形的边长都为1．（1）求△ABC的周长；（2）求证：∠ABC＝90°；（3）若点P为直线AC上任意一点，则线段BP的最小值为．22．（10分）如图1，点D、E、F、G分别为线段AB、OB、OC、AC的中点．（1）求证：四边形DEFG是平行四边形；（2）如图2，若点M为EF的中点，BE：CF：DG＝2：3：，求证：∠MOF＝∠EFO．23．（10分）已知点A为正方形BCDE内一动点，满足∠DAC＝135°，且b＝+5．（1）求a、b的值；（2）如图1，若线段AB＝b，AC＝a，求线段AD的长；（3）如图2，设线段AB＝m，AC＝n，AD＝h，请探究并直接写出三个量m2、n2、h2之间满足的数量关系．24．（12分）在正方形ABCD中，点E为边BC（不含B点）上的一动点，AE⊥EF，且AE＝EF，FG⊥BC的延长线于点G．（1）如图1，求证：BE＝FG；（2）如图2，连接BD，过点F作FH∥BC交BD于点H，连接HE，判断四边形EGFH的形状，并给出证明；（3）如图3，点P、Q为正方形ABCD内两点，AB＝BQ，且∠ABQ＝30°，BP平分∠QBC，BP ＝DP，若BC＝+1，求线段PQ的长．湖北省武汉市硚口区八年级（下）期中数学试卷参考答案与试题解析一、选择題（共10小题，每小题3分，共30分下列各题均有四个备选选项，其中有且只有一个正确，请在答题卡上将正确答案的字母涂黑．1．若式子在实数范围内有意义，则a的取值范围是（）A．a＞3B．a≥3C．a＜3D．a≤3【分析】根据被开方数大于等于0列式计算即可得解．【解答】解：由题意得，a﹣3≥0，解得a≥3．故选：B．【点评】本题考查的知识点为：二次根式的被开方数是非负数．2．若＝4﹣b，则b满足的条件是（）A．b＞4B．b＜4C．b≥4D．b≤4【分析】根据二次根式的性质列出不等式，解不等式即可．【解答】解：∵＝4﹣b，∴4﹣b≥0，解得，b≤4，故选：D．【点评】本题考查的是二次根式的化简，掌握二次根式的性质：＝|a|是解题的关键．3．以下列长度的线段为边，不能构成直角三角形的是（）A．2，3，4B．1，1，C．D．5，12，13【分析】根据勾股定理的逆定理对四个选项进行逐一判断即可．【解答】解：A、∵22+32＝13≠42，∴不能构成直角三角形，故本选项符合要求；B、∵12+12＝（）2，∴能构成直角三角形，故本选项不符合要求；C、∵（）2+（）2＝（）2，∴能构成直角三角形，故本选项不符合要求；D、∵52+122＝132，∴能构成直角三角形，故本选项不符合要求．故选：A．【点评】本题考查的是勾股定理的逆定理，即如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形．4．在平行四边形ABCD中，已知∠A＝60°，则∠D的度数是（）A．60°B．90°C．120°D．30°【分析】根据平行四边形邻角互补的性质即可求解．【解答】解：∵在平行四边形ABCD中，∠A＝60°，∴∠D＝180°﹣60°＝120°．故选：C．【点评】此题主要考查了平行四边形的性质，关键是熟练掌握平行四边形邻角互补的知识点．5．下列计算正确的是（）A．B．C．D．【分析】根据二次根式的性质与同类二次根式的定义逐一计算可得．【解答】解：A、与不是同类二次根式，不能合并，此选项错误；B、4﹣3＝3，此选项错误；C、×＝，此选项正确；D、（3）2＝18，此选项错误；故选：C．【点评】本题主要考查二次根式的混合运算，解题的关键是熟练掌握二次根式的性质和二次根数混合运算顺序及其法则．6．如图，一竖直的木杆在离地面4米处折断，木頂端落在地面离木杆底端3米处，木杆折断之前的高度为（）A．7米B．8米C．9米D．12米【分析】由题意得，在直角三角形中，知道了两直角边，运用勾股定理即可求出斜边，从而得出这棵树折断之前的高度．【解答】解：∵一竖直的木杆在离地面4米处折断，頂端落在地面离木杆底端3米处，∴折断的部分长为＝5（米），∴折断前高度为5+4＝9（米）．故选：C．【点评】此题考查了勾股定理的应用，主要考查学生对勾股定理在实际生活中的运用能力．7．如图，▱ABCD的顶点坐标分别为A（1，4）、B（1，1）、C（5，2），则点D的坐标为（）A．（5，5）B．（5，6）C．（6，6）D．（5，4）【分析】由四边形ABCD是平行四边形，可得AB∥CD，AB＝CD，继而求得答案．【解答】解：∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD，∵A（1，4）、B（1，1）、C（5，2），∴AB＝3，∴点D的坐标为（5，5）．故选：A．【点评】此题考查了平行四边形的性质．注意平行四边形的对边平行且相等．8．如图，A（0，1），B（3，2），点P为x轴上任意一点，则PA+PB的最小值为（）A．3B．C．D．【分析】作点A关于x轴的对称点A′．连接BA′交x轴于点P，此时PA+PB的值最小．根据勾股定理求出BA′即可；【解答】解：作点A关于x轴的对称点A′．连接BA′交x轴于点P，此时PA+PB的值最小．PA+PB的最小值＝BA′＝＝3，故选：B．【点评】本题考查轴对称﹣最短问题，坐标用图形的性质等知识，解题的关键是学会利用轴对称解决最短问题，属于中考常考题型．9．如图，在正方形网格中用没有刻度的直尺作一组对边长度为的平行四边形．在1×3的正方形网格中最多作2个，在1×4的正方形网格中最多作6个，在1×5的正方形网格中最多作12个，则在1×8的正方形网格中最多可以作（）A．28个B．42个C．21个D．56个【分析】根据已知图形的出在1×n的正方形网格中最多作2×（1+2+3+…+n﹣2）个，据此可得．【解答】解：∵在1×3的正方形网格中最多作2＝2×1个，在1×4的正方形网格中最多作6＝2×（1+2）个，在1×5的正方形网格中最多作12＝2×（1+2+3）个，……∴在1×8的正方形网格中最多作2×（1+2+3+4+5+6）＝42个，故选：B．【点评】本题主要考查图形的变化规律，解题的关键是根据题意得出在1×n的正方形网格中最多作2×（1+2+3+…+n﹣2）个．10．如图，正方形ABCD中，点O为对角线的交点，直线EF过点O分别交AB、CD于E、F两点（BE＞EA），若过点O作直线与正方形的一组对边分別交于G、H两点，满足GH＝EF，则这样的直线GH（不同于直线EF）的条数共有（）A．1条B．2条C．3条D．无数条【分析】根据对称性以及旋转变换的性质，画出图形即可解决问题，如图所示；【解答】解：根据对称性以及旋转变换的性质可知满足条件的线段有3条，如图所示；故选：C．【点评】本题考查正方形的性质、旋转变换等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．二、填空题（每小题3分，共18分11．16的平方根是±4．【分析】根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2＝a，则x就是a的平方根，由此即可解决问题．【解答】解：∵（±4）2＝16，∴16的平方根是±4．故答案为：±4．【点评】本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．12．计算：÷＝3．【分析】根据二次根式是除法法则进行计算．【解答】解：原式＝＝＝＝3．故答案是：3．【点评】本题考查了二次根式的乘除法．二次根式的除法法则：÷＝（a≥0，b＞0）．13．已知等边三角形的边长为6，则面积为9．【分析】根据等边三角形三线合一的性质可得D为BC的中点，即BD＝CD，在直角三角形ABD 中，已知AB、BD，根据勾股定理即可求得AD的长，即可求三角形ABC的面积，即可解题．【解答】解：等边三角形高线即中线，故D为BC中点，∵AB＝6，∴BD＝3，∴AD＝＝3，∴等边△ABC的面积＝BC•AD＝×6×3＝9．故答案为：9．【点评】本题考查了勾股定理在直角三角形中的运用，等边三角形面积的计算，本题中根据勾股定理计算AD的值是解题的关键．14．如图，菱形ABCD的周长为8，对角线BD＝2，则对角线AC为2．【分析】设菱形的对角线相交于O，根据菱形性质得出AB＝BC＝CD＝AD，AC⊥BD，BO＝OD，AO＝OC，求出OB，根据勾股定理求出OA，即可求出AC．【解答】解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，AC⊥BD，BO＝OD，AO＝OC，∵菱形的周长是8，∴DC＝×8＝2，∵BD＝2，∴OD＝1，在Rt△DOC中，OC＝＝，∴AC＝2OC＝2，故答案为：2．【点评】本题考查了菱形的性质和勾股定理，注意：菱形的对角线互相垂直平分，菱形的四条边相等．15．如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点E的坐标（0，）．【分析】先证明EA＝EC（设为x）；根据勾股定理列出x2＝12+（3﹣x）2，求得x＝，即可解决问题．【解答】解：由题意知：∠BAC＝∠DAC，AB∥OC，∴∠ECA＝∠BAC，∴∠ECA＝∠DAC，∴EA＝EC（设为x）；由题意得：OA＝1，OC＝AB＝3；由勾股定理得：x2＝12+（3﹣x）2，解得：x＝，∴OE＝3﹣＝，∴E点的坐标为（0，）．故答案为：（0，）．【点评】该题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答；对综合的分析问题解决问题的能力提出了较高的要求．16．如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝5，DA＝5，则BD的长为．【分析】作DM⊥BC，交BC延长线于M，由勾股定理得出AC2＝AB2+BC2＝25，求出AC2+CD2＝AD2，由勾股定理的逆定理得出△ACD是直角三角形，∠ACD＝90°，证出∠ACB＝∠CDM，得出△ABC≌△CMD，由全等三角形的性质求出CM＝AB＝3，DM＝BC＝4，得出BM＝BC+CM ＝7，再由勾股定理求出BD即可．【解答】解：作DM⊥BC，交BC延长线于M，如图所示：则∠M＝90°，∴∠DCM+∠CDM＝90°，∵∠ABC＝90°，AB＝3，BC＝4，∴AC2＝AB2+BC2＝25，∴AC＝5，∵AD＝5，CD＝5，∴AC2+CD2＝AD2，∴△ACD是直角三角形，∠ACD＝90°，∴∠ACB+∠DCM＝90°，∴∠ACB＝∠CDM，∵∠ABC＝∠M＝90°，在△ABC和△CMD中∴△ABC≌△CMD，∴CM＝AB＝3，DM＝BC＝4，∴BM＝BC+CM＝7，∴BD＝＝＝，故答案为：．【点评】本题考查了全等三角形的判定与性质、勾股定理、勾股定理的逆定理；熟练掌握全等三角形的判定与性质，由勾股定理的逆定理证出△ACD是直角三角形是解决问题的关键．三、解答题（共8小題，共72分）17．（8分）计算：①；②．【分析】①先化简各二次根式，再合并同类二次根式即可得；②根据二次根式的乘法运算法则计算可得．【解答】解：①原式＝3﹣4+2＝；②原式＝＝＝3．【点评】本题主要考查二次根式的混合运算，解题的关键是熟练掌握二次根式的性质和二次根数混合运算顺序及其法则．18．（8分）计算：①②【分析】①先利用完全平方公式和平方差公式计算乘法和乘方，再合并同类二次根式即可得；②先化简各二次根式，再计算乘法，继而合并同类二次根式即可得．【解答】解：①原式＝2+6+4+3﹣6＝5+4；②原式＝6×﹣×6＝3﹣15＝﹣12．【点评】本题主要考查二次根式的混合运算，解题的关键是熟练掌握二次根式的性质及二次根式混合运算顺序和运算法则．19．（8分）一根直立于水中的芦节（BD）高出水面（AC）2米，一阵风吹来，芦苇的顶端D恰好到达水面的C处，且C到BD的距离AC＝6米，求水的深度（AB）为多少米？【分析】先设水深为x，则AB＝x，求出x的长，再由勾股定理即可得出结论．【解答】解：∵先设水深为x，则AB＝x，BC＝（x+2），∵AC＝6米，在△ABC中，AB2+AC2＝BC2，即62+x2＝（x+2）2，解得x＝8（米）．答：水深AB为8米．【点评】本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．20．（8分）如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD．求证：四边形ABCD是菱形．【分析】根据平行线的性质得出∠ADB＝∠DBC，∠DAC＝∠BCA，根据角平分线定义得出∠DAC ＝∠BAC，∠ABD＝∠DBC，求出∠BAC＝∠ACB，∠ABD＝∠ADB，根据等腰三角形的判定得出AB＝BC＝AD，根据平行四边形的判定得出四边形ABCD是平行四边形，即可得出答案．【解答】证明：∵AE∥BF，∴∠ADB＝∠DBC，∠DAC＝∠BCA，∵AC、BD分别是∠BAD、∠ABC的平分线，∴∠DAC＝∠BAC，∠ABD＝∠DBC，∴∠BAC＝∠ACB，∠ABD＝∠ADB，∴AB＝BC，AB＝AD∴AD＝BC，∵AD∥BC，∴四边形ABCD是平行四边形，∵AD＝AB，∴四边形ABCD是菱形．【点评】本题考查了等腰三角形的性质，平行四边形的判定，菱形的判定的应用，能得出四边形ABCD是平行四边形是解此题的关键．21．（8分）如图，在4×4的正方形网格中，每个小正方形的边长都为1．（1）求△ABC的周长；（2）求证：∠ABC＝90°；（3）若点P为直线AC上任意一点，则线段BP的最小值为2．【分析】（1）运用勾股定理求得AB，BC及AC的长，即可求出△ABC的周长．（2）运用勾股定理的逆定理求得AC2＝AB2+BC2，得出∠ABC＝90°．（3）过B作BP⊥AC，解答即可．【解答】解：（1）AB＝，BC＝，AC＝，△ABC的周长＝2++5＝3+5，（2）∵AC2＝25，AB2＝20，BC2＝5，∴AC2＝AB2+BC2，∴∠ABC＝90°．（3）过B作BP⊥AC，∵△ABC的面积＝，即，解得BP＝2，故答案为：2【点评】本题主要考查了勾股定理及勾股定理的逆定理，熟记勾股定理是解题的关键．22．（10分）如图1，点D、E、F、G分别为线段AB、OB、OC、AC的中点．（1）求证：四边形DEFG是平行四边形；（2）如图2，若点M为EF的中点，BE：CF：DG＝2：3：，求证：∠MOF＝∠EFO．【分析】（1）根据中位线定理得：DG∥BC，DG＝BC，EF∥BC，EF＝BC，则DG＝BC，DE ∥BC，根据一组对边平行且相等的四边形是平行四边形可得：四边形DEFG是平行四边形；（2）先根据已知的比的关系设未知数：设BE＝2x，CF＝3x，DG＝x，根据勾股定理的逆定理得：∠EOF＝90°，最后利用直角三角形斜边中线的性质可得OM＝FM，由等边对等角可得结论．【解答】证明：（1）∵D是AB的中点，G是AC的中点，∴DG是△ABC的中位线，∴DG∥BC，DG＝BC，同理得：EF是△OBC的中位线，∴EF∥BC，EF＝BC，∴DG＝EF，DG∥EF，∴四边形DEFG是平行四边形；（2）∵BE：CF：DG＝2：3：，∴设BE＝2x，CF＝3x，DG＝x，∴OE＝2x，OF＝3x，∵四边形DEFG是平行四边形，∴DG＝EF＝x，∴OE2+OF2＝EF2，∴∠EOF＝90°，∵点M为EF的中点，∴OM＝MF，∴∠MOF＝∠EFO．【点评】本题考查的是三角形中位线定理、平行四边形的判定、勾股定理的逆定理，掌握三角形中位线定理是解题的关键．23．（10分）已知点A为正方形BCDE内一动点，满足∠DAC＝135°，且b＝+5．（1）求a、b的值；（2）如图1，若线段AB＝b，AC＝a，求线段AD的长；（3）如图2，设线段AB＝m，AC＝n，AD＝h，请探究并直接写出三个量m2、n2、h2之间满足的数量关系．【分析】（1）根据二次根式有意义的条件列出不等式，解不等式得到答案；（2）把△CAD旋转90°得到△CA′B，根据勾股定理求出AA′，求出∠AA′B＝90°，根据勾股定理计算即可；（3）仿照（2）的计算方法解答．【解答】解：（1）由二次根式有意义的条件可知，a﹣3≥0，3﹣a≥0，∴a＝3，b＝5；（2）把△CAD旋转90°得到△CA′B，则AC＝A′C，∠A′CB＝∠ACD，AD＝A′B，∴∠ACA′＝90°，∴∠AA′C＝45°，AA′＝＝3，∴∠AA′B＝90°，∴A′B＝＝，∴AD＝A′B＝；（3）由（2）得，AA′＝＝n，∴m2﹣2n2＝h2．【点评】本题考查的是二次根式有意义的条件、旋转变换的性质、勾股定理的应用，掌握二次根式的被开方数是非负数、旋转变换的性质是解题的关键．24．（12分）在正方形ABCD中，点E为边BC（不含B点）上的一动点，AE⊥EF，且AE＝EF，FG⊥BC的延长线于点G．（1）如图1，求证：BE＝FG；（2）如图2，连接BD，过点F作FH∥BC交BD于点H，连接HE，判断四边形EGFH的形状，并给出证明；（3）如图3，点P、Q为正方形ABCD内两点，AB＝BQ，且∠ABQ＝30°，BP平分∠QBC，BP ＝DP，若BC＝+1，求线段PQ的长．【分析】（1）欲证明BE＝FG，只要证明△ABE≌△EGF，即可解决问题；（2）四边形EGFH是矩形．首先证明四边形ECMH是矩形，可得∠FHE＝∠HEG＝∠EGF＝90°，推出四边形EGFH是矩形；（3）如图3中，连接PC，作PE⊥BC于E，PF⊥BQ于F．∴由PCB≌△PCD，推出∠PCB＝∠PCD＝45°，可证PE＝EC，设PE＝EC＝a，在Rt△PEB中，由∠PBE＝30°，推出PB＝2PE，BE＝a，由BC＝+1，可得a+a＝+1，推出a＝1，再求出FQ、FP即可解决问题；【解答】解：（1）如图1中，∵FG⊥EG，AE⊥EF，四边形ABCD是正方形，∴∠B＝∠AEF＝∠G＝90°，∴∠BAE+∠AEB＝90°，∠AEB+∠FEG＝90°，∴∠BAE＝∠FEG，∵AE＝EF，∴△ABE≌△EGF，∴BE＝FG．（2）结论：四边形EGFH是矩形．理由：如图2中，设FH交CD于M．∵△ABE≌△EGF，∴AB＝EG＝BC，∴BE＝CG＝FG，∵FM∥CG，FG∥CM，∴四边形CMFG是平行四边形，∵GC＝FG，∠MCG＝90°，∴四边形CMFG是正方形，∴CM＝CG＝BE，∵BC＝CD，∴CE＝DM，∵FH∥BC，∴∠DMH＝∠DCB＝90°，∵∠MDH＝45°，∴∠MDH＝∠MHD＝45°，∴DM＝HM＝EC，∵HM∥EC，∴四边形CEHM是平行四边形，∵∠ECM＝90°，∴四边形ECMH是矩形，∴∠FHE＝∠HEG＝∠EGF＝90°，∴四边形EGFH是矩形．（3）如图3中，连接PC，作PE⊥BC于E，PF⊥BQ于F．∵PB＝PD，PC＝PC，BC＝CD，∴△PCB≌△PCD，∴∠PCB＝∠PCD＝45°，∵PE⊥EC，∴∠PCE＝∠EPC＝45°，∴PE＝EC，设PE＝EC＝a，在Rt△PEB中，∵∠PBE＝30°，∴PB＝2PE，BE＝a，∵BC＝+1，∴a+a＝+1，∴a＝1，∴PB＝2在Rt△PFB中，∵∠PBF＝30°，∴PF＝1，BF＝，∵BQ＝BQ＝BC＝+1，∴FQ＝1，∴PQ＝＝．【点评】本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、矩形的判定和性质、勾股定理、直角三角形30度角的性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．21。

3 3 2 3 = = = = 8 2018~2019 学年度第二学期期中考试八年级数学答案一、选择题（共 10 小题，每小题 3 分，共 30 分）1.B2.B3.C4.C5.B6.B7.D8.A 9.C 10.D 二、填空题（共 6 小题，每小题 3 分，共 18 分）11. 12.5 13.96 14.﹣2 15. 2 16.40°16. 提示：延长 CM 到 E ，使 ME=MC ，连接 BE 、DE 、AE ，∵MA=MB，∴四边形 ACBE 为平行四边形，∴BE=AC，AE=BC ，∠AEB=∠ACB=100°，∵CA=MA，∴BE=MB， ∴可设∠BME=∠BEM=x，同理可设∠AED=∠ADE=y，∴∠DEM=180°﹣(x ＋y)= x ＋y ﹣100°，∴x＋y=140°，∴∠DEM=40°，∵N 为 CE 的中点，∴NM∥EE，∴∠NMC=∠DEM=40°． 三、解答题（共 8 小题，共 72 分）17.解: ⑴原式= 4 3 - 2 3 +12 ........................................ 3 分= (4 - 2 +12) 3 =14 …………………4 分 ．⑵原式= 5x + 5x - 2 5x .............................. 7 分=0 ........................... 8 分18.解：∵a =2＋ 3 ，b =2－ 3 ，∴a ＋b =4，ab =1，a ﹣b = 2 ， ................. 3 分（1）a ²＋b²=(a＋b)²﹣2ab =16﹣2=14； ......... 5 分（2） a - b a 2 - b 2 (a + b )(a - b ) 4⨯ ．......... 8 分 b a ab ab 1 (直接代值计算正确相应给分)19.证明：⑴∵DE∥AC，CE∥BD，∴四边形 OCED 是平行四边形， ........... 3 分∵四边形 ABCD 是矩形，∴OD= 1 BD ,2 1 = AC , 2 AC=BD ，......... 5 分 ∴OD=OC, ............................... 6 分∴四边形 OCED 为菱形． .................. 8 分20.解：连接 BD ，在 Rt △ABD 中，BD 2=AB 2＋AD 2=32＋42=52， .........................3 分在△CBD 中，CD 2=132，BC 2=122，而 122＋52=132，即 BC 2＋BD 2=CD 2， .................. 4 分∴∠DBC =90°， ............................................................ 5 分 ∴S 四边形 ABCD =S △BAD ＋S △DBC = 1 ·AD ·AB ＋ 1 DB ·BC = 1 ×4×3＋ 1 ×12×5=36， .........7 分 2 2 2 2 所以需费用 36×200=7200(元)答：要投入 7200 元 ........................................................ 8 分27 3 3 多等腰三角形角度转换变式，在MA 上取MF=MD ，连CF ， 效果相同.OC21. (1)证明：方法 1:延长 BA,CD 相交于点 O,∵AD∥BC，∴∠OAD=∠ABC , ∠ODA=∠DCB, ......... 1 分∵∠ABC=∠DCB, ∴∠OAD=∠ODA, ................. 2 分∴OA=OD,OB=OC, ................................ 3 分∴AB=DC ....................................... 4 分(方法 2:作 AM⊥BC 于 M, 作 DN⊥BC 于 N;方法 3：作 DH∥AB 交 BC 于 H)(2)画图略 ................................... 5 分由翻折题意可得：∠DCB=∠ECB, CD=CE .......... 6 分由（1）知：AB=DC ，∴AB=CE,又∠ABC=∠DCB，∴∠ABC=∠ECB∴AB∥CE ................................... 7 分∴四边形 ABEC 是平行四边形． .............. 8 分22.证明：（1）连接 EF,分别取 AP,BP 的中点 M,N,连接 NM,EM,FN, ......... 2 分可得：EF= 1 AB ，EF∥AB ； MN= 1AB ，MN∥AB;..................... 3 分2 2 ∴EF=MN，EF∥MN∴四边形 EFNM 是平行四边形, ................................. 5 分∴PF=PM,PE=PN∴AP=2PF. .................................................. 6 分（2） ∵AF⊥BE，AC=8,BC=6,∴PE 2+(2PF)2=AE 2,PF 2+(2PE)2=BF 2, .............. 7 分即∴PE 2+4PF 2=16 ,PF 2+4PE 2=9,∴5PE 2+5PF 2=25， ................................................ 8 分∴PE 2+PF 2=5 ， .................................................. 9 分∴EF= 5， AB=2EF= 2 5 ........................................................................................ 10 分23.解：⑴ a = -1，b=4，C(4,3)． ........... 4 分（1 分+1 分+2 分）⑵证明：连接 OM 交 DN 于E ，在 DN 上截取 DE=ON ，连接 ME ，1∵∠BOD=90°，M 为 BD 的中点，∴OM= 2 ∵CD⊥x 轴于 D ，C(4,3)，∴D(4,0)，∴OD=4=OB，∴OM⊥BD，∵ON⊥DN，∴∠OMD=∠OND=90°，∵∠DEM=∠OEN，∴∠MDF=∠MON，BD=MD ， .......... 5 分 ∴△MDF≌△MON(SAS)， ............................... 6 分∴MF=MN，∠DMF=∠OMN，∴∠MNF=∠OMD=90°，∴MN²＋MF²=NF²， ..................................... 7 分∴2MN²=MF²，∴MF= 2 MN ，∵DF＋NF=DN ，∴ 2 MN ＋ON=DN ． ........................ 8 分17 ⑶ 提示：取的 OB 中点 Q ，连接 PQ,CQ ，可得 PQ= 1OB = 2,2CQ = 7,∵ CP ≤ PQ + CQ ≤ 2 + 7,∴ 当点 P,Q,C 在同一直线上时，线段 CP 的最大值为2 + ． ............ 10 分（写值给 1 分，说明理由 1 分）24.⑴证明：∵四边形 ABCD 是正方形，∴AD=CD，∠ADB=∠CDB， ............ 1 分∵DM=DM，∴△ADM≌△CDM(SAS)， ...................... 2 分∴AM=CM． ............................................ 3 分⑵证明：连接 CM ，∵△ADM≌△CDM，∴∠DAM=∠DCM， AM=CM ，∵AM=MF，∴CM=MF，∴∠DCM=∠MFC， .......................... 4 分 ∵∠MFC＋∠MFD=180°，∴∠DAM＋∠MFD=180°，∴∠AMF＋∠ADC=180°， ∵∠ADC=90°，∴∠AMF=90°，∴∠MAF=∠MFA=45°， ........... 5 分 作 FG⊥AF 交 AE 的延长线于 G ，连接 HG 、AH 、BG ，∴∠AGF=45°=∠GAF，∴AF=GF， ............................. 6 分 ∵FH⊥CD，∴∠HFD=90°，∴∠AFD=∠GFH，∵∠BDC=45°，∴∠FHD=45°，∴FD=FH，∴△AFD≌△GFH(SAS)， ..................................... 7 分 ∴AD=GH，∠GHF=∠ADF=90°，∴∠GHF=∠HFD，∴HG∥CD，∵AB∥CD，∴AB∥GH，∵AD=AB，∴AB=GH，∴AB∥GH ，∴四边形 ABGH 是平行四边形， ................................ 8 分 ∴BM=HM，即 M 为 BH 的中点． ................................. 9 分⑶ 2 (写值给 1 分，说明简要理由给 2 分) ................................... 12 分。

最新人教版数学八年级下册期中考试试题及答案第Ⅱ卷（非选择题共84分）二、填空题（每小题3分，满分18分）13.比较大小：（填“＞、＜或＝”）14. 如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为 .15. 某地需要开辟一条隧道，隧道AB的长度无法直接测量。

如图所示，在地面上取一点C，使点C均可直接到达A，B两点，测量找到AC和BC的中点D，E，测得DE的长为1200m，则隧道AB的长度为__ _米。

三、解答题（满分66分）23.（14分）如图，在△ABC中，点O是AC边上一动点，过点O作BC的平行线交∠ACB的角平分线于点E，交∠ACB的外角平分线于点F(1)求证：EO=FO；(2)当点O运动到何处时，四边形CEAF是矩形?请证明你的结论。

(3)在第(2)问的结论下，若AE=3，EC=4，AB=12，BC=13，请求出凹四边形ABCE的面积.24.（14分）【问题情境】如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM.求证：AM=AD+MC.【探究展示】(2)若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，试判断AM=AD+MC是否成立?若成立，请给出证明，若不成立，请说明理由；【拓展延伸】(3)若(2)中矩形ABCD两边AB=6，BC=9，求AM的长。

参考答案一、BDCAA CABDC BC二、13. ＜14. 18米15. 2400米16. （5,4）17. 8=+18. (n最新人教版数学八年级下册期中考试试题及答案分△AFC的面积为 A. 6 B. 8 C. 10 D. 12第Ⅱ卷（非选择题共84分）二、填空题（每小题3分，满分18分）13.比较大小：（填“＞、＜或＝”）14. 如图,一棵大树在一次强台风中距地面5m处折断,倒下后树顶端着地点A距树底端B的距离为12m,这棵大树在折断前的高度为 .15. 某地需要开辟一条隧道，隧道AB的长度无法直接测量。

2022-2023学年湖北省武汉市硚口区八年级（下）期中数学试卷及参考答案一、选择题（共9小题，每小题3分，共30分）1．（3分）在二次根式√a+2中，a的取值范围是（）A．a＞﹣2B．a≥﹣2C．a≠﹣2D．a≤﹣22．（3分）下列计算错误的是（）A．3+2√2=5√2B．√8÷2=√2C．√2×√3=√6D．√8+√2=3√23．（3分）下列数组中，是勾股数的是（）A．6、8、10B．2、2、2C．1、1、√3D．1、2、34．（3分）若正方形的面积与长为6，宽为3的矩形面积相等，则该正方形的边长为（）A．3B．√3C．3√2D．√65．（3分）如图，在矩形ABCD纸片中，E为AD上一点，将△CDE沿CE翻折至△CFE．若点F恰好落在AB上，AF＝3，BC＝9，则AE＝（）A．9B．3√2C．2√3D．46．（3分）如图，两张等宽的矩形纸条交叉叠放在一起，重合部分构成的四边形一定是（）A．平行四边形B．矩形C．菱形D．正方形7．（3分）下列三个命题：①平行四边形的两组对边分别相等；②矩形的对角线相等；③直角三角形斜边上的中线等于斜边的一半，它们的逆命题是真命题的个数是（）A．0B．1C．2D．38．（3分）顺次连接菱形四边中点所得的四边形一定是（）A．平行四边形B．矩形C．菱形D．正方形9．（3分）如图，阴影部分表示以Rt△ABC的各边为直径的三个半圆所组成的两个新月形，面积分别记作S1和S2．若S1+S2＝7，AB＝6，则△ABC的周长是（）A ．12.5B ．13C ．14D ．15二、填空题（本大题共6个小题，每小题3分，共18分）10．（3分）计算：√9= ．11．（3分）边长为4cm 的等边三角形面积是 cm 2．12．（3分）如图，已知正方形ABCD 和等边△ABE ，连接EC ，则∠AEC ＝ °．13．（3分）在△ABC 中，AB ＝13，AC ＝20，BC 边上的高为12，则△ABC 的面积为 ．14．（3分）如图，在Rt △ABC 中，∠ACB ＝90°，D 、E 分别为AB 和AC 的中点，下列四个结论：①BC 2＝4DE 2；②BD 2﹣CE 2＝DE 2；③CD 2+BE 2＝7DE 2；④BE 2﹣CD 2＝3DE 2，其中正确的是 ．15．（3分）如图，在矩形ABCD 中，AB ＝6，AD ＝2，E 、F 分别是AB 和DC 上的两个动点，M 为BC 的中点，则DE +EF +FM 的最小值是 ；若∠EFD ＝45°，则DE +EF +FM 的最小值为 ．三、解答题（共8题，共72分）16．（8分）计算：（1）√12+√20+（√3−√5）；（2）23√9x +6√x 4． 17．（8分）已知：a ＝2+√3，b ＝2−√3．（1）直接写出：ab ＝ ，a +b ＝ ；（2）求1a +1b 的值． 18．（8分）我国古代数学著作《九章算术》中有这样一个问题：如图，有一个水池，其横截面是矩形，边长EF为10尺，在水池正中央有一根垂直于水面（BD）的芦苇（OA），它的顶端A高出水面1尺．如果把这根芦苇拉向水池一边，它的顶端A恰好到达池边的水面B处，求水池里水的深度（OC）是多少尺？19．（8分）如图，在正方形ABCD中，AB＝4，E是BC的中点，F是CD上一点，且DF＝3CF．（1）求证：AE⊥EF；（2）求四边形AEFD的面积．20．（8分）（1）如图1，E、F是▱ABCD对角线AC上的两点，且AE＝CF，连接BE、ED、DF、FB，求证：四边形BEDF是平行四边形．（2）如图2，在梯形ABCD中，AB∥CD，AD＝BC，求证：∠A＝∠B．21．（10分）无刻度直尺作图：（1）直接写出四边形ABCD的形状．（2）在图1中，先过E点画一条直线平分四边形ABCD的面积，再在AB上画点F，使得AF＝AE．（3）在图2中，先在AD上画一点G，使得∠DCG＝45°；连接AC，再在AC上画点H，使得GH＝GA．22．（10分）如图1，以▱ABCD的邻边AB和BC为边向外作正方形ABFE和正方形BCHG，连接BD、FG，线段BD和FG之间存在怎样的数量关系和位置关系？（1）先将问题特殊化，如图2，当∠ADC＝90°时，直接写出BD和FG之间的数量关系和位置关系．（2）再探究一般情况，当∠ADC≠90°时，证明（1）中的结论依然成立．（3）在（2）的条件下，连接EH，M为EH的中点，连接MF，试给出FM和BD的数量关系并证明．23．（12分）在菱形ABCD中，∠DCB＝120°，E为CD上一点．（1）如图1，若∠DAE＝30°，求证：BC＝2CE．（2）F为CB上一点，∠EAF＝30°．①如图2，连接EF，求证：EA平分∠DEF．②如图3，若BF＝2FC，求DECE的值．2021-2022学年湖北省武汉市硚口区八年级（下）期中数学试卷参考答案与试题解析一、选择题（共9小题，每小题3分，共30分）1．（3分）在二次根式√a+2中，a的取值范围是（）A．a＞﹣2B．a≥﹣2C．a≠﹣2D．a≤﹣2【解答】解：根据题意，得a+2≥0，解得a≥﹣2．故选：B．2．（3分）下列计算错误的是（）A．3+2√2=5√2B．√8÷2=√2C．√2×√3=√6D．√8+√2=3√2【解答】解：A、3与2√2不属于同类二次根式，不能运算，故A符合题意；B、√8÷2=√2，故B不符合题意；C、√2×√3=√6，故C不符合题意；D、√8+√2=3√2，故D不符合题意；故选：A．3．（3分）下列数组中，是勾股数的是（）A．6、8、10B．2、2、2C．1、1、√3D．1、2、3【解答】解：A、62+82＝102，三边是整数，同时能构成直角三角形，故符合题意．B、22+22≠22，不能构成直角三角形，故不符合题意；C、12+12≠（√3）2，不能构成直角三角形，故不符合题意；D、12+22≠32，不能构成直角三角形，故不符合题意；故选：A．4．（3分）若正方形的面积与长为6，宽为3的矩形面积相等，则该正方形的边长为（）A．3B．√3C．3√2D．√6【解答】解：设正方形的边长为x，由题意得：x2＝6×3，解得：x＝±3√2（负值不合题意舍去），即正方形的边长为3√2．故选：C．5．（3分）如图，在矩形ABCD纸片中，E为AD上一点，将△CDE沿CE翻折至△CFE．若点F恰好落在AB上，AF＝3，BC＝9，则AE＝（）A．9B．3√2C．2√3D．4【解答】解：设AE＝x，则DE＝AD﹣AE＝BC﹣AE＝9﹣x，∵△CDE沿CE翻折至△CFE，∴EF＝DE＝9﹣x，在Rt△AEF中，AF2+AE2＝EF2，∴32+x2＝（9﹣x）2，解得x＝4，∴AE＝4，故选：D．6．（3分）如图，两张等宽的矩形纸条交叉叠放在一起，重合部分构成的四边形一定是（）A．平行四边形B．矩形C．菱形D．正方形【解答】解：如图，∵AB∥CD，AD∥BC，∴四边形ABCD是平行四边形，作AE⊥BC于点E，AF⊥DC于点F，∵两张等宽的长方形纸条交叉叠放在一起，∴AE＝AF，∴S平行四边形ABCD＝BC•AE＝DC•AF，∴BC＝DC，∴▱ABCD是菱形．故选：C．7．（3分）下列三个命题：①平行四边形的两组对边分别相等；②矩形的对角线相等；③直角三角形斜边上的中线等于斜边的一半，它们的逆命题是真命题的个数是（）A．0B．1C．2D．3【解答】解：①平行四边形的两组对边分别相等的逆命题为两组对边分别相等的四边形是平行四边形，正确，是真命题，符合题意；②矩形的对角线相等的逆命题为对角线相等的四边形是矩形，错误，是假命题，不符合题意；③直角三角形斜边上的中线等于斜边的一半的逆命题为一条边上的中线等于这条边的一半的三角形是直角三角形，正确，是真命题，符合题意，逆命题为真命题的有2个，故选：C．8．（3分）顺次连接菱形四边中点所得的四边形一定是（）A．平行四边形B．矩形C．菱形D．正方形【解答】解：如图，四边形ABCD是菱形，且E、F、G、H分别是AB、BC、CD、AD的中点，则EH∥FG∥BD，EF＝FG=12BD；EF∥HG∥AC，EF＝HG=12AC，AC⊥BD．故四边形EFGH是平行四边形，又∵AC⊥BD，∴EH⊥EF，∠HEF＝90°∴边形EFGH是矩形．故选：B．9．（3分）如图，阴影部分表示以Rt△ABC的各边为直径的三个半圆所组成的两个新月形，面积分别记作S1和S2．若S1+S2＝7，AB＝6，则△ABC的周长是（）A．12.5B．13C．14D．15【解答】解：由勾股定理得，AC 2+BC 2＝AB 2，∵S 1+S 2＝7，∴12×π×（AC 2）2+12×π×（BC 2）2+12×AC ×BC −12×π×（AB 2）2＝7，∴AC ×BC ＝14，∴（AC +BC ）2＝AC 2+BC 2+2AC •BC ＝62+2×14＝64，∴AC +BC ＝8（负值舍去），∴△ABC 的周长＝AB +AC +BC ＝8+6＝14，故选：C ．二、填空题（本大题共6个小题，每小题3分，共18分）10．（3分）计算：√9= 3 ．【解答】解：∵32＝9，∴√9=3．故答案为：3．11．（3分）边长为4cm 的等边三角形面积是 4√3 cm 2．【解答】解：过点A 作AD ⊥BC 于点D ，如图所示：∵△ABC 是等边三角形，∴D 是BC 的中点，∵等边三角形边长为4cm ，∴AC ＝BC ＝4cm ，∴CD ＝2cm ，根据勾股定理，得AD =2√3cm ，∴△ABC 的面积为12×4×2√3=4√3（cm 2）， 故答案为：4√3．12．（3分）如图，已知正方形ABCD 和等边△ABE ，连接EC ，则∠AEC ＝ 45 °．【解答】解：在正方形ABCD 中，∠ABC ＝90°，AB ＝BC ．∵△ABE 是等边三角形，∴∠AEB ＝∠ABE ＝60°，AB ＝BE ，∴∠EBC ＝90°+60°＝150°，BE ＝BC ，∴∠BCE ＝∠BEC =12（180°﹣150°）＝15°，∴∠AEC ＝∠AEB +∠BEC ＝60°﹣15°＝45°．故答案为：45．13．（3分）在△ABC 中，AB ＝13，AC ＝20，BC 边上的高为12，则△ABC 的面积为 126或66 ．【解答】解：分两种情况：①当∠B 为锐角时，如图1所示，在Rt △ABD 中，BD =√AB 2−AD 2=√132−122=5，在Rt △ADC 中，CD =√AC 2−AD 2=√202−122=16，∴BC ＝BD +CD ＝21，∴△ABC 的面积为12×21×12＝126； ②当∠B 为钝角时，如图2所示，在Rt △ABD 中，BC ＝CD ﹣BD ＝16﹣5＝11，所以△ABC 的面积为12×11×12＝66； 故答案为：126或66．14．（3分）如图，在Rt△ABC中，∠ACB＝90°，D、E分别为AB和AC的中点，下列四个结论：①BC2＝4DE2；②BD2﹣CE2＝DE2；③CD2+BE2＝7DE2；④BE2﹣CD2＝3DE2，其中正确的是①②④．【解答】解：∵D，E分别是AB和AC的中点，∴DE是△ABC的中位线，∴BC＝2DE，CD＝AD＝BD=12AB，DE∥BC，∴BC2＝4DE2，故①正确；∵∠ACB＝90°，∴∠DEA＝∠DEC＝∠ACB＝90°，∴CD2﹣CE2＝DE2，∴BD2﹣CE2＝DE2，故②正确；∵BE2＝BC2+CE2，CE2＝CD2﹣DE2，∴BE2＝BC2+CD2﹣DE2，∵BC2＝4DE2，∴BE2﹣CD2＝4DE2﹣DE2＝3DE2，故④正确；∵BE2＝BC2+CE2，CD2＝CE2+DE2，∴CD2+BE2＝BC2+CE2+CE2+DE2＝5DE2+2CE2，∵CE≠DE，∴CD2+BE2≠7DE2，故③错误．故答案为：①②④．15．（3分）如图，在矩形ABCD中，AB＝6，AD＝2，E、F分别是AB和DC上的两个动点，M为BC的中点，则DE+EF+FM的最小值是√61；若∠EFD＝45°，则DE+EF+FM的最小值为5+2√2．【解答】解：作点D的对称点D'，作点M关于CD的对称点M'，连接D'M'，D'E，FM'，则DE+EF+FM＝D'E+EF+FM'，∴当D'，E，F，M'在同一条直线上时，所求的DE+EF+FM最小，最小值即为D'M'的长．过点M'作AD的垂线，交AD的延长线于点H，∴HM'＝AB＝6，∵M为BC的中点，AD＝BC＝2，∴MC＝CM'＝DH＝1，AD'＝AD＝2，∴HD'＝5，∴D'M'=√62+52=√61．故答案为：√61．（2）过点E作EP⊥CD于P，∵∠EFD＝45°，∴EP＝PF＝BC＝2，∴EF＝2√2，则DE+EF+FM＝DE+FM+2√2，∴求DE+FM+2√2的最小值即先求DE+FM的最小值．过点E作EM'＝FM，且EM'∥FM，∴DE+FM＝DE+EM'，∴当D ，E ，M '三点共线时，DE +EM '最小．此时DE ∥FM ，∴∠EDP ＝∠MFC ，∠EPD ＝∠MCF ，∴△DEP ∽△FMC ，∴EP MC =DP CF ，设CF ＝x ，则DP ＝DC ﹣PF ﹣CF ＝6﹣2﹣x ＝4﹣x ．∴21=4−x x， 解得x =43，∴CF =43，DP =83，DE =√DP 2+EP 2=103，FM ＝EM '=√CF 2+CM 2=53，∴DE +EM '＝5，∴DE +EF +FM 的最小值为5+2√2．故答案为：5+2√2．三、解答题（共8题，共72分）16．（8分）计算：（1）√12+√20+（√3−√5）；（2）23√9x +6√x 4． 【解答】解：（1）√12+√20+（√3−√5）=2√3+2√5+√3−√5＝3√3+√5；（2）23√9x +6√x 4 =23×3√x +6×√x 2＝2√x +3√x＝5√x ．17．（8分）已知：a ＝2+√3，b ＝2−√3．（1）直接写出：ab ＝ 1 ，a +b ＝ 4 ；（2）求1a +1b的值．【解答】解：（1）∵a＝2+√3，b＝2−√3，∴ab＝（2+√3）×（2−√3）＝1，a+b＝2+√3+2−√3=4，故答案为：1，4；（2）∵ab＝1，a+b＝4，∴1a +1b=a+bab=41=4，∴1a +1b的值为4．18．（8分）我国古代数学著作《九章算术》中有这样一个问题：如图，有一个水池，其横截面是矩形，边长EF为10尺，在水池正中央有一根垂直于水面（BD）的芦苇（OA），它的顶端A高出水面1尺．如果把这根芦苇拉向水池一边，它的顶端A恰好到达池边的水面B处，求水池里水的深度（OC）是多少尺？【解答】解：设水池里水的深度是x尺由题意得，x2+52＝（x+1）2，解得：x＝12，答：水池里水的深度（OC）是12尺．19．（8分）如图，在正方形ABCD中，AB＝4，E是BC的中点，F是CD上一点，且DF＝3CF．（1）求证：AE⊥EF；（2）求四边形AEFD的面积．【解答】（1）证明：∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD＝4，∵DF＝3CF，∴CF＝1，DF＝3，在Rt△ADF中，根据勾股定理可得：AF2＝AD2+DF2＝42+32＝25，∵E是BC的中点，∴BE＝EC=12BC＝2，∴AE2＝AB2+BE2＝42+22＝20，同理EF2＝EC2+CF2＝22+12＝5，∵EF2+AE2＝5+20＝25，AF2＝25，∴EF2+AE2＝AF2，∴△BEF是直角三角形，∴∠BEF＝90°．∴AE⊥EF；（2）解：S四边形AEFD＝S△AEF+S△ADF=12×AE•EF+12×AD•DF=12×2√5×√5+12×4×3＝5+6＝11．∴四边形AEFD的面积为11．20．（8分）（1）如图1，E、F是▱ABCD对角线AC上的两点，且AE＝CF，连接BE、ED、DF、FB，求证：四边形BEDF是平行四边形．（2）如图2，在梯形ABCD中，AB∥CD，AD＝BC，求证：∠A＝∠B．【解答】证明：（1）连接BD，交AC于点O，∵四边形ABCD是平行四边形，∴AO＝CO，BO＝DO，∵AE＝CF，∴AO﹣AE＝CO﹣CE，即EO＝FO，∴四边形BEDF为平行四边形（对角线互相平分的四边形是平行四边形）；（2）过C作CE∥AD，交AB于点E，∵AB∥DC，∴四边形ADCE是平行四边形，∴AD＝CE，∵AD＝BC，∴CE＝CB，∴∠B＝∠CEB，∵AD∥CE，∴∠A＝∠CEB，∴∠B＝∠A．21．（10分）无刻度直尺作图：（1）直接写出四边形ABCD的形状．（2）在图1中，先过E点画一条直线平分四边形ABCD的面积，再在AB上画点F，使得AF＝AE．（3）在图2中，先在AD上画一点G，使得∠DCG＝45°；连接AC，再在AC上画点H，使得GH＝GA．【解答】解：（1）四边形ABCD是菱形（理由是边长都是5）；（2）如图1中，直线OE，点F即为所求；（3）如图2中，点G，点H即为所求．22．（10分）如图1，以▱ABCD的邻边AB和BC为边向外作正方形ABFE和正方形BCHG，连接BD、FG ，线段BD 和FG 之间存在怎样的数量关系和位置关系？（1）先将问题特殊化，如图2，当∠ADC ＝90°时，直接写出BD 和FG 之间的数量关系和位置关系．（2）再探究一般情况，当∠ADC ≠90°时，证明（1）中的结论依然成立．（3）在（2）的条件下，连接EH ，M 为EH 的中点，连接MF ，试给出FM 和BD 的数量关系并证明．【解答】解：（1）如图，BD ＝FG ，BD ⊥FG ，理由如下：延长DB 交FG 于点Q ，∵四边形ABEF 和四边形BCHG 是正方形，∴∠DAB ＝∠EAB ＝∠ABF ＝∠BCD ＝∠BCH ＝90°，AB ＝BF ，BG ＝BC ，∵四边形ABCD 是平行四边形，∠ADC ＝90°，∴▱ABCD 是矩形，AB ＝CD ，∴∠ABC ＝90°，BF ＝CD ，∴∠FBG ＝90°，在△BCD 和△GBF 中，{CD =BF∠BCD =∠FBG BC =BG，∴△BCD ≌△GBF （SAS ），∴BD ＝FG ，∠CBD ＝∠BGF ，∵∠CBG ＝90°，∴∠CBD +∠GBM ＝90°，∴∠BGF +∠GBM ＝90°，∴∠GMB ＝90°，∴BD ⊥FG ；综上，BD ＝FG ，BD ⊥FG ；（2）如图1，（1）中的结论依然成立，理由如下：延长DB 交FG 于M ，∵四边形ABCD 是平行四边形，∴AB ∥CD ，AB ＝CD ，∴∠DCB ＝180°﹣∠ABC ，∵四边形ABFE 和四边形BCHG 是正方形，∴∠ABF ＝∠CBG ＝90°，BC ＝BG ，AB ＝BF ，∴∠FBG ＝360°﹣∠ABF ﹣∠CBG ﹣∠ABC ＝180°﹣∠ABC ，CD ＝BF ，∴∠BCD ＝∠FBG ，在△BCD 和△GBF 中，{CD =BF∠BCD =∠FBG BC =BG，∴△BCD ≌△GBF （SAS ），∴BD ＝FG ，∠CBD ＝∠BGF ，∵∠CBG ＝90°，∴∠CBD +∠GBM ＝90°，∴∠BGF +∠GBM ＝90°，∴∠GMB ＝90°，∴BD ⊥FG ；（3）解：如图2，连接MG ，延长FM 至Q ，使MQ ＝FM ，连接QH ，延长FB 交QH 于P ，在△EMF 和△HMQ 中，{EM =MH∠EMF =∠HMQ MF =QM，∴△EMF ≌△HMQ （SAS ），∴QH ＝EF ，∠EFM ＝∠FQH ，∴EF ∥QH ，∴∠BPH ＝∠EFB ＝90°，在四边形BPHG 中，∠PBG +∠PHG ＝360°﹣∠BGH ﹣∠BPH ＝360°﹣90°﹣90°＝180°，∵∠PBG +∠FBG ＝180°，∴∠FBG ＝∠PHG ，∵EF ＝BF ，∴BF ＝QH ，∴△FBG ≌△QHG （SAS ），∴FG ＝QG ，∠FGB ＝∠HGQ ，∴∠FGB +∠BGQ ＝∠HGQ +∠BGQ ＝∠BGH ＝90°，∴∠FGQ ＝90°，∴△FGQ 是等腰直角三角形，∴GM ＝FM ＝MQ =√22FG ，∵BD ＝FG ，∴FM=√22BD．23．（12分）在菱形ABCD中，∠DCB＝120°，E为CD上一点．（1）如图1，若∠DAE＝30°，求证：BC＝2CE．（2）F为CB上一点，∠EAF＝30°．①如图2，连接EF，求证：EA平分∠DEF．②如图3，若BF＝2FC，求DECE的值．【解答】（1）证明：如图1，∵四边形ABCD是菱形，∴AD＝CD＝BC，AD∥BC，∵∠DCB＝120°，∠DAE＝30°，∴∠D＝180°﹣∠DCB＝60°，∴∠AED＝90°，∴DE=12AD=12CD，∴CE＝CD﹣DE＝CD−12CD=12CD=12BC，∴BC＝2CE.（2）①证明：如图2，在DC上截取GD＝FC，连接AG、FG、AC，∵AD＝CD＝AB＝CB，∠B＝∠D＝60°，∴△ADC和△ABC都是等边三角形，∴AD＝AC，∠D＝∠ACF＝∠DAC＝60°，∴△ADG≌△ACF（SAS），∴AG＝AF，∠DAG＝∠CAF，∴∠F AG＝∠CAF+∠CAG＝∠BAG+∠CAG＝∠DAC＝60°，∵∠EAF＝30°，∴∠EAG＝∠EAF＝30°，∴AE垂直平分FG，∴EF＝EG，∴∠AEG＝∠AEF，EA 平分∠DEF ．②解：如图3，在DC 上截取GD ＝FC ，连接EF 、AG 、FG 、AC ，由①得AG ＝AF ，EF ＝EG ，∠F AG ＝60°，∴△AFG 是等边三角形，∵CD ﹣GD ＝CB ﹣FC ，∴BF ＝CG ，∵BF ＝2FC ，∴CG ＝2GD ，作GP ⊥AD 于点P ，FQ ⊥DC 交DC 的延长线于点Q ，则∠APG ＝∠GQF ＝90°，设PD ＝m ， ∵∠DPG ＝90°，∠D ＝60°，∴∠DGP ＝30°，∴GD ＝2PD ＝2m ，CG ＝2GD ＝4m ，∴AD ＝CD ＝2m +4m ＝6m ，∴P A ＝6m ﹣m ＝5m ，∵∠D ＝∠AGF ＝60°，AG ＝GF ，∴∠P AG ＝180°﹣∠D ﹣∠AGD ＝120°﹣∠AGD ，∠QGF ＝180°﹣∠AGF ﹣∠AGD ＝120°﹣∠AGD ， ∴∠P AG ＝∠QGF ，∴△P AG ≌△QGF （AAS ），∴PG ＝QF ，P A ＝QG ＝5m ，∴QF 2＝PG 2＝（2m ）2﹣m 2＝3m 2，∵QF 2+EQ 2＝EF 2，EF ＝EG ，EQ ＝5m ﹣EG ，∴3m 2+（5m ﹣EG ）2＝EG 2，解得EG =145m ， ∴DE ＝2m +145m =245m ，CE ＝6m ﹣2m −145m =65m ， ∴DE CE=245m 65m =4， ∴DE CE 的值是4．第21页（共21页）。

2023~2024学年度第二学期期中质量检测八年级数学试卷一、选择题（共10 小题，每小题3分，共30分）下列各题均有四个备选答案，其中有且只有一个是正确的，请在答题卡上将正确答案的代号涂黑．1.有意义，则x 的取值范围是（ ）A.x ＞3B. x ≠3 C. x ≥3 D. x ≤3【答案】C【解析】【分析】根据二次根式有意义的条件列出不等式，解不等式即可．【详解】解：由题意得，x-3≥0，解得，x ≥3．故选C ．【点睛】本题考查二次根式有意义的条件，掌握二次根式中的被开方数必须是非负数是解题关键．2. 下列各式计算正确的是（ ）A. B. C. D. 【答案】B 【解析】【分析】本题考查了二次根式的性质化简，二次根式的混合运算，掌握二次根式的混合运算法则是解题的关键．根据二次根式的混合运算法则逐一判定即可求解．【详解】解：A，原选项计算错误，不符合题意；B，原选项计算正确，符合题意；C不是同类二次根式，不能进行加减，原选项计算错误，不符合题意；D 、，原选项计算错误，不符合题意；故选： B ．3. 在中，，则的大小是（ ）A. B. C. D. 【答案】A 6=2÷==1-==2====ABCD Y 40A ∠=︒C ∠40︒140︒50︒70︒【解析】【分析】本题考查了平行四边的性质，掌握平行四边形的性质是解题的关键．根据平行四边形对角相等即可求解．【详解】解：∵四边形是平行四边形，∴，故选：A ．4. 在中，，， 的对边分别是，下列条件不能判断是直角三角形的是（ ）A. B. C. D. 【答案】B【解析】【分析】本题考查了勾股定理的逆定理，直角三角形的性质及判定方法，理解并掌握直角三角形的判定方法是解题的关键．根据直角三角形中，最大角的度数为可以判断A 、B 选项，运用勾股定理逆定理可判定C 、D 选项，由此即可求解．【详解】解：A 、∵，∴，则，能判定直角三角形，A 选项不符合题意；B 、，∴，即中最大角的度数为，∴不能判定是直角三角形，B 选项符合题意；C 、，设，∴，∴，即，能判定是直角三角形，C 选项不符合题意；D 、，能判定是直角三角形，不符合题意；故选：B ．5. 《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺，问折高者几何?意思是：一ABCD 40A C ∠=∠=︒ABC A ∠B ∠C ∠a b c ，，ABC A B ∠∠=︒+90::3:4:5A B C ∠∠∠=::3:4:5a b c =222a b c =+90︒90A B ∠+∠=︒180A B C ∠+∠+∠=︒90180C ︒+∠=︒90C ∠=︒::3:4:5A B C ∠∠∠=518075345C ∠=︒⨯=︒++ABC 75︒::3:4:5a b c =345a x b x c x ===，，()()()22222222239416525a x x b x x c x x ======，，22291625x x x +=222a b c +=222a c b =+根竹子，原高一丈（一丈尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部尺远，问折断处离地面的高度是多少?设折断处离地面的高度为 尺，则下列方程正确的是（ ）A. B. C. D. 【答案】A【解析】【分析】本题考查了勾股定理的运用，理解题意，掌握勾股定理的计算是解题的关键．根据题意，如图所示，【详解】解：根据题意作图如下，尺，尺，设，则，∴在直角中，，∴，故选：A ．6. 如图，在 中，下列结论中错误的是（ ）A. 当时，它是菱形B. 当平分 时，它是菱形C. 当时，它是矩形D. 当时，它是正方形【答案】D【解析】10=3x ()222310x x +=-()22310x x -=-()22310x x +=-()222310x x -=-10AB =3BC =BD x =10CD AB BD x =-=-BCD 222BC BD CD +=()222310x x +=-ABCD Y AB BC =AC BAD ∠OA OB =AC BD =【分析】本题考查了平行四边形的性质，菱形、矩形、正方形的判定和性质的综合，掌握平行四边形，特殊四边形的判定和性质是解题的关键．根据平行四边形的性质，菱形、矩形、正方形的判定逐一求解．【详解】解：∵四边形是平行四边形，∴当时，根据一组邻边相等的平行四边形是菱形，则A 选项正确，不符合题意；当平分时，，∴，∴平行四边形是菱形，B 选项正确，不符合题意；当时，，即，根据对角线相等的平行四边形是矩形，∴平行四边形是矩形，C 选项正确，不符合题意；当时，平行四边形是矩形，不是正方形，D 选项错误，符合题意；故选：D ．7. 如图，是菱形 的对角线的交点，是边中点，若，，则长是（ ）A. B. 3 C. D. 5【答案】A【解析】【分析】本题考查了菱形的性质，勾股定理，直角三角形斜边中线等于斜边的一半，掌握菱形的性质是解题的关键．根据菱形的性质可得直角，根据勾股定理求出的值，结合直角三角形斜边中线等于斜边的一半，根据点是的中点可得，由此即可求解．【详解】解：已知四边形是菱形，，∴，，∴是直角三角形，∴，∵点是的中点，ABCD AB BC =AC BAD ∠BAC CAD BCA ∠=∠=∠AB BC =ABCD OA OB =OA OC OB OD ===AC BD =ABCD AC BD =ABCD O ABCD E AD 6AC =8BD =OE 2.53.5AOD AD E AD 12OE AD =ABCD 68AC BD ==，113422OA AC OD BD ====，AC BD ⊥AOD5AD ===E AD∴， 故选：A ．8. 在四边形中，．下列说法能使四边形为矩形的是（ ）A. B. C. D. 【答案】C【解析】【分析】结合平行四边形的判定和性质及矩形的判定逐一分析即可．【详解】A ：，为平行四边形而非矩形故A 不符合题意B ：，为平行四边形而非矩形故B 不符合题意C ：∴∥四边形为矩形故C 符合题意D ：不是平行四边形也不是矩形故D 不符合题意故选：C ．【点睛】本题主要考查平行线的性质，平行四边形的判定和性质及矩形的判定等知识，熟练掌握以上知识1 2.52OE AD ==ABCD ,AD BC AB CD =∥ABCD AB CDAD BC =A B ∠=∠A D∠=∠ AB CD ,AD BC AB CD =∥∴ABCD AD BC =,AD BC AB CD=∥∴ABCD AD BC∥180A B ∴∠+∠=︒A B∠=∠∴90A B ∠=∠=︒AB CD= AB CD∴ABCD AD BC∥180A B ∴∠+∠=︒A D∠=∠180D B ∴∠+∠=︒∴ABCD并灵活运用是解题的关键．9. 如图，在矩形中，为对角线的中点，．动点在线段上，动点在线段上，点同时从点出发，分别向终点运动，且始终保持．点关于的对称点为；点关于的对称点为．在整个过程中，四边形形状的变化依次是（ ）A. 菱形→平行四边形→矩形→平行四边形→菱形B. 菱形→正方形→平行四边形→菱形→平行四边形C 平行四边形→矩形→平行四边形→菱形→平行四边形D. 平行四边形→菱形→正方形→平行四边形→菱形【答案】A【解析】【分析】根据题意，分别证明四边形菱形，平行四边形，矩形，即可求解．【详解】∵四边形是矩形，∴，，∴，，∵、，∴∵对称，∴，∴∵对称，∴，.是ABCD O BD 60ABD ∠=︒E OB F OD ,E F O ,B D OE OF =E ,AD AB 12,E E F ,BC CD 12,F F 1212E E F F 1212E E F F ABCD AB CD ∥90BAD ABC ∠=∠=︒60BDC ABD ∠=∠=︒906030ADB CBD ∠=∠=︒-︒=︒OE OF =OB OD =DF EB=21DF DF BF BF ==，21,BE BE DE DE ==1221E F E F =260F DC CDF ∠=∠=︒130EDA E DA ∠=∠=︒∴，同理，∴∴∴四边形是平行四边形，如图所示，当三点重合时，，∴即∴四边形是菱形，如图所示，当分别为的中点时，设，则，，在中，，连接，，∵，∴是等边三角形，∵为中点，∴，，160E DB ∠=︒160F BD ∠=︒11DE BF ∥1221E F E F ∥1212E E F F ,,E F O DO BO =1212DE DF AE AE ===1212E E EF =1212E E F F ,E F ,OD OB 4DB =21DF DF ==13DE DE ==Rt △ABD 2,AB AD ==AE AO 602ABO BO AB ，∠=︒==ABO E OB AE OB ⊥1BE =∴，根据对称性可得，∴，∴，∴是直角三角形，且，∴四边形是矩形，当分别与重合时，都是等边三角形，则四边形是菱形∴在整个过程中，四边形形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形，故选：A ．【点睛】本题考查了菱形的性质与判定，平行四边形的性质与判定，矩形的性质与判定，勾股定理与勾股定理的逆定理，轴对称的性质，含30度角的直角三角形的性质，熟练掌握以上知识是解题的关键．10. 已知的值是（ ）A. B. C. 5 D. 6【答案】C【解析】【分析】主要考查整式的化简求值及完全平方公式与二次根式的运算，熟练掌握各个运算法则是解题关AE ==1AE AE ==2221112,9,3AD DE AE ===22211AD AE DE =+1DE A 190E ∠=︒1212E E F F ,F E ,D B 11,BE D BDF 1212E E F F 1212E E F F 1x +=32321x x x +-+键．先求出，再把原式化为整体代入计算即可．【详解】解：，，，即，，故选：C ．二、填空题（共6 小题，每小题 3 分，共 18 分）11. 写出一个小于3的正无理数___________．（答案不唯一）【解析】【分析】根据无理数估算的方法求解即可.【详解】解：∵∴（答案不唯一）．【点睛】本题主要考查了无理数估算，准确计算是解题的关键．12.的结果是_________．【答案】2【解析】【分析】根据二次根式的性质进行化简即可．．故答案为：2．的224x x +=()22221x x x x x ++-+1x + ()2215x \+==2215x x \++=224x x +=32321x x x \+-+()22221x x x x x =++-+2421x x x =+-+221x x =++41=+5=0<<03<<2=．13. 多项式分解因式的结果是_____________．【答案】【解析】【分析】本题考查了乘法公式，二次根式的性质，因式分解，掌握运用乘法公式进行因式分解是解题的关键．根据二次根式的性质，再结合乘法公式进行因式分解即可求解．【详解】解：，故答案为： ．14. 如图，在正方形中，已知，，则的长是_____________，其对角线的交点坐标是_____________．【答案】 ①. 5 ②. 【解析】【分析】本题考查直角坐标、正方形和全等三角形的性质，解题的关键是证明．通过勾股定理求出，证明得到，即可求得点的坐标，再根据中点坐标公式得出结论即可．【详解】解：，，，在中，；如下图所示，过点D ，作垂直于x 轴，交x轴于点E ，()()(0000a a a aa a ⎧⎪===⎨⎪-⎩＞）＜27x-(x x +27=(2227x x x x -=-=(x x ABCD ()30A ，()04B ，AB 7722⎛⎫ ⎪⎝⎭，ABO ADE ≌△△AB ABO DAE ≌3,4DE OA AE OB ====D ()30A ，()04B ，3,4OA OB ∴==Rt AOB △5AB ==DE∵，，∴，在和中，∵，∴，∴，∴，∴点的坐标为，对角线的交点坐标是，即，故答案为：5，．15. 出入相补原理是我国古代数学的重要成就之一，最早是由三国时期数学家刘徽创建．“将一个几何图形，任意切成多块小图形，几何图形的总面积保持不变，等于所分割成的小图形的面积之和”是该原理的重要内容之一、如图，在矩形中，，，对角线与交于点O ，点E 为边上的一个动点，，，垂足分别为点F ，G ，则___________．【答案】##【解析】分析】连接，根据矩形的性质得到，，，根据勾股定理得到，求得，根据三角形的面积公式即可得到结论．【90OAB DAE ∠+∠=︒90OAB OBA∠+∠=︒DAE ABO ∠=∠ABO DAE ABO DAE BOA AED BA AD ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO DAE ≌3,4DE OA AE OB ====7OE OA AE =+=D ()7,3∴074322++⎛⎫ ⎪⎝⎭，7722⎛⎫ ⎪⎝⎭，7722⎛⎫ ⎪⎝⎭，ABCD 5AB =12AD =AC BD BC EF AC ⊥EG BD ⊥EF EG +=60138413OE 12BC AD ==AO CO BO DO ===90ABC ∠=︒13AC ==132OB OC ==【详解】解：连接，四边形是矩形，，，，，，，，，，，故答案为：．【点睛】此题考查了矩形的性质、勾股定理．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．16. 如图，在四边形中，，，，，则的长是________．【答案】【解析】【分析】本题考查了等边三角形的判定和性质，旋转的性质，全等三角形的判定和性质，勾股定理的综合运用，掌握旋转的性质，全等三角形的判定和性质是解题的关键．如图所示，连接可得是等边三角形，将绕点逆时针旋转可得，，是等边三角形，过点作延长线于点，可证是等腰直角三角形，根据勾股定理可求出的长，由此即可求解．OE ABCD 90ABC ∴∠=︒12BC AD ==AO CO BO DO ===5AB = 12BC =13AC ∴==132OB OC ∴==111115121522222BOC BOE COE ABC S S S OB EG OC EF S ∴=+=⨯⋅+⋅==⨯⨯⨯= ∴113113113()15222222EG EF EG EF ⨯+⨯=⨯+=6013EG EF ∴+=6013ABCD AB BC =60ABC ∠=︒75ADC ∠=︒=AD 3DC =BD AC ABC ABD A 60︒ABD ACE ≌BD CE =ADE C CF DE ⊥F CDF CE【详解】解：如图所示，连接，∵，，∴是等边三角形，则，将绕点逆时针旋转，∴与重合，与重合，∴，∴等边三角形，∴，，∵，即，∴，∴，过点作延长线于点，即，∴，∴是等腰直角三角形，且，∴，∴，∴，在中，∴故答案为： ．三、解答题（共8 小题，共72 分）是AC AB BC =60ABC ∠=︒ABC 60BAC BCA ABC ∠=∠=∠=︒ABD A 60︒AB AC AD AE 60DAE ∠=︒ADE AD AE DE ===60ADE ∠=︒BAC CAD CAD DAE ∠+∠=∠+∠BAD CAE ∠=∠()BAD CAE SAS ≌BD CE =C CF ED ⊥F 90F ∠=︒180180756045CDF ADC ADE ∠=︒-∠-∠=︒-︒-︒=︒CDF 3CD =CD =DF ==EF ED DF =+==Rt CEF CE ===BD =17. 计算：（1；（2【答案】（1（2）【解析】【分析】本题主要考查二次根式的性质化简，二次根式的混合运算，掌握二次根式混合运算法则是解题的关键．（1）运用二次根式的性质化简，再根据二次根式的加减运算即可求解；（2）运用二次根式的性质化简，再根据二次根式的加减运算即可求解．【小问1详解】【小问2详解】．18. 已知，（1）直接写出，的值；（2）求的值．【答案】（1），（2）【解析】--+=-=-3==+=3a =+3b =-a b +ab 22a ab b -+6715【分析】本题主要考查乘法公式的运用，二次根式的混合运算，掌握二次根式的混合运算法则是解题的关键．（1）根据二次根式的运算法则即可求解；（2）运用乘法公式，将（1）中的结果代入计算即可求解．【小问1详解】解：；；【小问2详解】解：，由（1）可知，，，∴原式．19. 如图，在四边形中，．（1）求证：（2）求四边形的面积．【答案】（1）见详解 （2）234【解析】【分析】（1）连接，根据勾股定理计算出长，再利用勾股定理逆定理判定是直角三角形，即可得到结论；（2）利用和的面积求和，即可．【小问1详解】(33a b +=6=(33ab =+223=-7=()2223a ab b a b ab -+=+-6a b +=7ab =2637362115=-⨯=-=ABCD 201572490AB BC CD AD B ====Ð=°，，，，CD AD ⊥ABCD AC AC ACD ACD ABC连接，∵ ，，∵ ，即，∴ ，∴；【小问2详解】解：四边形的面积=．故面积为：234．【点睛】本题主要考查了勾股定理和勾股定理逆定理．关键是掌握在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方；如果三角形的三边长a ，b ，c 满足，那么这个三角形就是直角三角形．20. 如图，在中，是边的中点，过点 作直线，交的角平分线于点E ，交的外角的角平分线于点，连接．（1）求证：四边形为矩形．（2）请添加一个条件，使四边形为正方形，直接写出该条件．【答案】（1）证明过程见详解（2），或（答案不唯一）【解析】【分析】（1）根据角平分线可得，可证，根据对角线相互平分的四边形是平AC 90B Ð=°∴22224725+=222AD CD AC +=90D Ð=°CD AD ⊥ABCD ΔΔ11+=×24×7+×20×15=23422ACD ACB S S 222+=a b c ABC O AC O MN BC ∥ACB ∠CE ABC ACG ∠CF F AE AF ，AECF AECF CE CF =45OCE ∠=︒90ECF ∠=︒OE OC OF ==行四边形，可得是平行四边形，再根据有一个角是直角的平行四边形是矩形，由此即可求证；（2）根据正方形的判定方法“有一组邻边相等的矩形是正方形”，“对角线相互垂直的平行四边形是正方形”即可求解．【小问1详解】证明：已知平分，平分，∴，∵，∴，∴，∵，∴，∴，∴，∵点是边的中点，∴，∴，∴四边形是平行四边形，∵，∴平行四边形是矩形；【小问2详解】解：由（1）可知四边形是矩形，∴根据“有一组邻边相等的矩形是正方形”，“对角线相互垂直的平行四边形是正方形”得，添加条件为：，或（答案不唯一），添加条件为：，∵四边形是矩形，，∴矩形是正方形；添加条件：，∵，∴，∵，AECF CE ACB ∠CF ACG ∠1122BCE ECA ACB ACF FCG ACG ====∠∠，∠∠180ACB ACG +=︒∠∠()1111180902222ACE ACF ACB ACF ACB ACG +=+=+=⨯︒=︒∠∠∠∠∠90ECF ∠=︒MN BC ∥BCE CEF GCF CFE ==∠∠，∠∠OEC OCE OCF OFC ==∠∠，∠∠OE OC OF ==O AC OA OC =OA OE OC OF ===AECF 90ECF ∠=︒AECF AECF CE CF =45OCE ∠=︒CE CF =AECF CE CF =AECF 45OCE ∠=︒45BCE ECO ==︒∠∠90BCO ∠=︒MN BC ∥∴，即，且四边形是矩形，∴矩形是正方形；综上所述，添加条件为：：，或（答案不唯一）．【点睛】本题主要考查角平分线的性质，平行线的性质，等腰三角形的判定和性质，矩形的证明，正方形的判定和性质的综合，掌握矩形判定和性质，正方形的判定和性质是解题的关键．21. 如图，在中，两点分别在边 上，连接， 且．（1）求证：四边形为平行四边形；（2）若平分，，且，，求的长．【答案】（1）证明过程见详解 （2）的长为【解析】【分析】（1）根据全等三角形的判定可得，，再根据平行四边形的性质，可得，由此即可求证；（2）根据题意可得，根据垂直可得平行四边形是矩形，设，在和中，运用勾股定理即可求解．【小问1详解】证明：∵四边形是平行四边形，∴，∵，∴，∴，∴，即，∴四边形为平行四边形；【小问2详解】解：∵平分，90EOA ∠=︒EF AC ⊥AECF AECF CE CF =45OCE ∠=︒ABCD Y E F ，AB CD ，DE BF AF ，，ADE CBF ∠=∠DEBF AF BAD ∠DE AB ⊥6AD =10AF =AE AE 73()ASA ADE CBF △≌△DE BF AE CF ==，BE DF =6BE DF ==DEBF AE CF x ==Rt ABF Rt BCF ABCD AD CB AB CD AB CD DAB C ==∠=∠∥，，，ADE CBF ∠=∠()ASA ADE CBF △≌△DE BF AE CF ==，AB AE CD BF -=-BE DF =DEBF AF BAD ∠∴，∵，∴，∴，∴，则，∵，且四边形为平行四边形，∴平行四边形是矩形，∴，设，则，在中，，在中，，则，∴，∴，解得，，∴的长为．【点睛】本题主要考查平行四边形的判定和性质，矩形的判定和性质，等角对等边，勾股定理的运用，掌握矩形的判定和性质是解题的关键．22. 如图是由小正方形组成的网格，每个小正方形的顶点叫做格点，的顶点都是格点，点 P 在AC 上，仅用无刻度的直尺在给定网格中完成画图．（1）在图1中，先画，再在上画点H ，使，然后在上画点Q ，使；（2）在图2中，先画的中线，再在上画点F ，使．【答案】（1）图见解析 DAF FAB ∠=∠AB CD FAB DFA ∠=∠DAF DFA ∠=∠6AD DF ==6BE DF ==DE AB ⊥DEBF DEBF BF CD ⊥AE CF x ==6AB AE BE x =+=+Rt ABF 222AF AB BF =+Rt BCF 222BC CF BF =+222BF BC CF =-()2222AF AB BC CF=+-()()22221066x x =++-73x =AE 7386⨯ABC ABDC BD BH CP =CD ∥QH BC ABC CE AC 12EF AC =（2）图见解析【解析】【分析】本题考查格点作图，平行四边形的性质，等腰三角形的性质．（1）根据平行四边形的性质，取格点D ，连接，使得，再连接，然后连接，交于点，连接并延长交于点H ，则得出，连接交于M ，连接并延长交于点Q ，连接，则，即为所求；（2）取格点，连接交于点E ，则的中点E ；再取格点，连接，交于点F ，可得，连接，利用直角三角形斜边上的中线等于斜边的一半得出，点E ，点F 即为所求．【小问1详解】解：如图所示，，点E 即为所求；【小问2详解】解：点E ，点F 即为所求．23. 如图1，在菱形中，E 是边上的点，是等腰三角形，，（）．（1）如图2，当时，连接交于点P，AD ,AD BC AD BC =∥CD BD AC O PO AD COP BOH ≌CP BH =PD BC AM CD HQ ABCD Y QH ,S R SR AB AB J BJ AC BJ AC ⊥EF 1122EF AB AC ==ABCD Y ABCD BC AEF △AE EF =AEF ABC α∠=∠=90α≥︒90α=︒BD AF①直接写出的度数；②求证：．（2）如图1，当时，若，求的值．【答案】（1）①②证明见解析（2）【解析】【分析】（1）①在上截取，连接，证明，再结合菱形性质得出结论；②作交于点N ，证明四边形是平行四边形，根据性质得出，再根据勾股定理得出结论；（2）延长使，连接，过F 作交延长线于点N ，先证求出，设，则，利用勾股定理求出，计算得出结论；【小问1详解】解：①在上截取，连接，，，，又，，四边形是菱形，且，∴四边形是正方形，，，DCF ∠2CF DP +=135DCF ∠=︒23BE EC =2CF CD ⎛⎫ ⎪⎝⎭45DCF ∠=︒2CF CD ⎛⎫= ⎪⎝⎭AB AM EC =ME MAE CEF ≌FN BC BD BCFN 2BD CF DP =+EC CM BE =MF FN BM ⊥BC BAE MEF ≌△△150α=︒2BE t =3,2,5EC t CM MF t CD CB t =====2CF AB AM EC =ME 90ABC AEF ∠=∠=︒ ABC BAE AEF CEF ∴∠+∠=∠+∠BAE CEF ∴∠=∠AE FE =MAE CEF ∴ ≌ ABCD 90ABC∠=︒ABCD AB BC ∴=90BCD ∠=︒又，，，，，；②作交于点N ，，，四边形是平行四边形，，，，，，在中，，；【小问2详解】解：延长使，连接，过F 作交延长线于点N ，，，，AM EC =BM BE ∴=90ABC ∠=︒ 45BME ∴∠=°135AME ECF ∴∠=∠=︒1359045DCF ∴∠=︒-︒=︒FN BC BD 45DCF BDC ∠=︒=∠ BD CF ∴ ∴BCFN ,,CF BN BC NF AD BC NF AD ∴===∥∥,DAP NFP ADP FNP ∴∠=∠∠=∠DAP NFP ∴ ≌DP PN ∴=2BD CF DP ∴=+Rt BCDBD=2CF DP ∴+=EC CM BE =MF FN BM ⊥BC AB BC EM∴==,BAE MEF AE EF ∠=∠= BAE MEF ∴ ≌,MF BE CM ABC EMF α∴==∠=∠=，，解得，设，则，，，由勾股定理，得，，【点睛】本题考查了菱形的性质、平行四边形是的判定与性质，全等三角形判定与性质及勾股定理的应用，熟练掌握相关性质及添加辅助线解决问题是解题关键．24. 在平面直角坐标系中，已知矩形，其中．（1）如图1，若点，E 在边上，将沿翻折，点C 恰好落在边上的点F 处，①直接写出点 F 的坐标及的长；②如图 2，将沿y 轴向上平移m 个单位长度得到，平面内是否存在点G ，使以、O 、、G 为顶点的四边形是菱形，若存在，求点G 的坐标，若不存在，请说明理由．（2）如图3，若点，连接，M ，N 两点分别是线段 上的动点，且，求的最小值．【答案】（1）①；②存在，，理由见解析 （2）的最小值为9【解析】180,1802MCF BCD αα︒-∴∠=∠=︒-3901352DCF α∴∠=-︒=︒150α=︒2BE t =3,2,5EC t CM MF t CD CB t =====18015030FMN ∠=︒-︒=︒ NF t ∴=MN =()(22222228CF CN NF t t t ∴=+=+=+2CF CD ⎛⎫∴= ⎪⎝⎭AOBC ()06A ，()100B ，BC ACE △AE OB EF AOF A O F ''' A 'F '()60B ，AB BC AB ，2AN CM =12OM ON +()8,0F 103EF =()()123328,6,8,6,8,3G G G ⎛⎫-- ⎪⎝⎭12OM ON +【分析】（1）①根据勾股定理求出点F 坐标，设，根据勾股定理列方程解决；②由平移得出，根据菱形性质分情况求出即可；（2）分别取中点E 、F ，连接，以为边构造，连接，推出当点O 、M 、P 在同一直线上时值最小，求出即可．【小问1详解】解：①矩形，，，，由翻折得：，在中，，；设，则，在中，，解得：，；②存在，，理由如下：将沿y 轴向上平移m 个单位长度得到，平面内是否存在点G ，使以、O 、、G 为顶点的四边形是菱形，，当时，，解得：，，则将点先向右平移8个单位，再向下平移6个单位得到到，同理将点O 先向右平移8个单位，再向下平移6个单位得到到；EF x =()()()0,,0,6,8,O m A m F m +''',OA AN EF CMCMP AFE ≌,OP OC OM MP +OP AOBC ()06A ，()100B ，10,6OB AC OA BC \====10AF AC ==Rt AOF 8OF ==()8,0F ∴EF x =,6CE EF x BE x ===-Rt BEF △()()2221086x x -+-=103x =103EF ∴=()()123328,6,8,6,8,3G G G ⎛⎫-- ⎪⎝⎭AOF A O F ''' A 'F '()()()0,,0,6,8,O m A m F m ∴+'''10OA A F '''===610m +=4m =()8,4F ∴'A 'F '()8,6G '-当时，，解得：，，则将先向左平移8个单位，再向上平移6个单位得到点，同理将点O 先向左平移8个单位，再向上平移6个单位得到到；当时，，解得：，，则将向上平移个单位得到点，同理将点向上平移个单位得到点；综上所述，存在，；【小问2详解】解：分别取中点E 、F ，连接，以为边构造，连接，，则，当点O 、M 、P 在同一直线上时值最小，最小值，，矩形为正方形，10OF A F '''==222810m +=6m =()8,6F ∴'F 'A '()8,6G '-6OF A O m ''==+()22286m m +=+73m =77258,,6333F OA ⎛⎫∴=+= ⎪⎝⎭''O 253A 'F '253328,3G '⎛⎫ ⎪⎝⎭()()123328,6,8,6,8,3G G G ⎛⎫-- ⎪⎝⎭,OA AN EF CM CMP AFE ≌,OP OC 12ON EF MP ∴==12ON OM OM MP +=+∴OM MP +OM MP ∴+OP =()()0,6,6,0A B ∴AOBC，且，在中，在中，，则的最小值为9．【点睛】本题考查了矩形及菱形性质、平移的性质、勾股定理的应用、坐标与图形，熟练掌握相关性质是解题关键．45EAF MCP OCB ∴∠=∠=∠=︒3AE CP ==90OCP ∴∠=︒Rt OBC△OC =Rt OCP9OP ===12OM ON +。