控制图(2011-11-12)

控制图1、概念控制图又叫做管制图，是用于分析和判断工序是否处于稳定状态所使用的带有控制界限的一种工序管理图。

控制图是一种对过程质量加以测定、记录从而进行控制管理的一种用科学方法设计的图，图上有中心线（CL ）、上控制线（UCL ）、下控制线（LCL ），并有按时间顺序抽取的样本计量值的描点序列。

控制图主要用于：过程分析及过程控制。

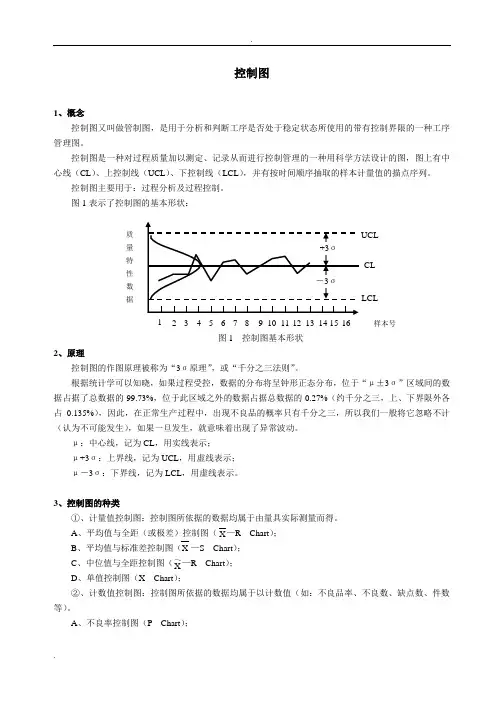
图1表示了控制图的基本形状：2、原理控制图的作图原理被称为“3σ原理”，或“千分之三法则”。

根据统计学可以知晓，如果过程受控，数据的分布将呈钟形正态分布，位于“μ±3σ”区域间的数据占据了总数据的99.73%，位于此区域之外的数据占据总数据的0.27%（约千分之三，上、下界限外各占0.135%），因此，在正常生产过程中，出现不良品的概率只有千分之三，所以我们一般将它忽略不计（认为不可能发生），如果一旦发生，就意味着出现了异常波动。

μ：中心线，记为CL ，用实线表示； μ+3σ：上界线，记为UCL ，用虚线表示； μ－3σ：下界线，记为LCL ，用虚线表示。

3、控制图的种类①、计量值控制图：控制图所依据的数据均属于由量具实际测量而得。

A R Chart ）； B S Chart ）；C Chart ）；D 、单值控制图（X Chart ）；②、计数值控制图：控制图所依据的数据均属于以计数值（如：不良品率、不良数、缺点数、件数等）。

A 、不良率控制图（P Chart ）；质 量 特 性 数 据B、不良数控制图（Pn Chart）；C、缺点数控制图（C Chart）；D、单位缺点数控制图（U Chart）。

4、控制图的用途根据控制图在实际生产过程中的运用，可以将其分为分析用控制图、控制用控制图：①、分析用控制图（先有数据，后有控制界限）：用于制程品质分析用，如：决定方针、制程解析、制程能力研究、制程管制之准备。

分析用控制图的主要目的是：（1）分析生产过程是否处于稳态。

管制图简介[计算][应用范围][实施步骤][使用原因]管制图基本原理统计理论认为母体参数可由随机抽取的样本来估计，SPC图的统计基础即在于此。

但是，SPC图并不能控制一个制程，它只是提供制程重要的信息，这个信息可以作为质量决策与修正制程的基础。

一般SPC图提供三条制程信息的管制线：上管制线(upper control limit, UCL)﹑中心线(center line, CL)﹑下管制线(lower control limit, LCL)。

不同制程管制对象有不同的数据，所有的数据都可归类到下列其中一种：1.分类数据－将产品质量分为「好或不好」、「合格或不合格」等计数数据－记录某产品的某个特性发生次数，例如错误次数﹑意外次数﹑销售领先次数等3.连续数据－某个质量特征的量测值，例如尺寸﹑成本﹑时间等前两种数据为计数值数据，第三种为计量值资料。

收集数据时，如果可能应该尽量收集定量数据，因为定量管制图所需的比较性计算较少，而且能提供较多的信息。

基本计算管制图可用一通式来表示，假设y为量测质量特性之样本统计量，y之平均数为μy，标准差为δy，则UCL＝μy＋kδy中心线＝μyLCL=μy－kδy其中kδy为管制界限至中心线之距离。

此管制图之理论首先由美国之Waiter A. Shewhart 博士提出，任何依据此原理发展出之管制图都称为Shewhart (苏华特)管制图。

应用范围管制图之应用有许多方式，在大多数之应用上，管制图是用来做制程之在线(on-line)监视。

亦即收集制程样本数据用来设立管制图，若样本值落在管制界限内且没有任何系统性之变化，则称制程在管制内。

管制图也可以用来决定过去之制程数据是否在管制内，及末来之制程是否将在管制内。

管制图也可用来做为估计之工具，当制程是在管制内时，则可预测一些制程参数，例如平均数、标准差、不合格率等。

此种制程能力分析对于管理者之决策分析有相当大之影响，例如自制或外购之决策，工厂及制程之改善以降低变异，及与供货商或顾客间之合约。

控制图的基本原理质量特性数据具有波动性，在没有进行观察或测量时，一般是未知的，但其又具有规律性，它是在一定的范围内波动的，所以它是随机变量。

一、正态分布如果随机变量受大量独立的偶然因素影响，而每一种因素的作用又均匀而微小，即没有一项因素起特别突出的影响，则随机变量将服从正态分布。

正态分布是连续型随机变量最常见的一种分布。

它是由高斯从误差研究中得出的一种分布，所以也称高斯分布。

随机变量服从正态分布的例子很多。

一般来说，在生产条件不变的前提下，产品的许多量度，如零件的尺寸、材料的抗拉强度、疲劳强度、邮件的内部处理时长、随机测量误差等等都是如此。

定义若随机变量的概率密度函数为：则称的分布为正态分布，记为。

正态分布的概率密度函数如图5—1所示。

图5-l正态分布概率密度曲线从图中我们叫以看出正态分布有如下性质：(1)曲线是对称的，对称轴是x=μ；(2)曲线是单峰函数，当x=μ时取得最大值；(3)当曲时，曲线以x轴为渐近线；(4)在处，为正态分布曲线的拐点；(5)曲线与x轴围成的面积为1。

另外，正态分布的数字特征值为：平均值标准偏差数字特征值的意义：平均值μ规定了图形所在的位置。

根据正态分布的性质，在x=μ处，曲线左右对称且为其峰值点。

标准偏差，规定了图形的形状。

图5-2给出了3个不同的值时正态分布密度曲线。

当小时，各数据较多地集中于μ值附近，曲线就较“高”和“瘦”；当大时，数据向μ值附近集中的程度就差，曲线的形状就比较“矮”和“胖”。

这说明正态分布的形状由的大小来决定。

在质量管理中，反映了质量的好坏，越小，质量的一致性越好。

图5-2大小不同时的正态分布在正态分布概率密度函数曲线下，介于坐标,,,间的面积，分别占总面积的58.26%，95.45%，99.73%和99.99%。

它们相应的几何意义如图5-3听示。

图5-3各种概率分布的几何意义二、控制图的轮廓线控制图是画有控制界限的一种图表。

如图5-4所示。

通过它可以看出质量变动的情况及趋势，以便找出影响质量变动的原因，然后予以解决。

§5.3.2　工程项目质量控制方法控制图（又称管理图）:——它是在直角坐标系内画有控制界限，描述生产过程中质量波动状态的图形。

利用控制图区分质量波动原因，判明生产过程是否处于稳定状态的方法称为控制图法。

控制下限控制上限中心线T1 2 3 4 5 6 7 8 9 10 11 12··········§5.3.2　工程项目质量控制方法控制图的用途：1、过程分析——分析生产过程是否稳定。

2、过程控制——控制生产过程质量状态。

其原理： 衡量生产过程是否稳定，只需观察产品的分布情况，即：分布中心的位置μ和分布的离散程度σ。

§5.3.2　工程项目质量控制方法 当控制图同时满足以下两个条件：一是点子几乎全部落在控制界限之内；二是控制界限内的点子排列没有缺陷。

我们就可以认为生产过程基本上处于稳定状态。

如果点子的分布不满足其中任何一条，都应判断生产过程为异常。

1、点子几乎全部落在控制界线内，是指应符合下述三个要求：1)连续25点以上处于控制界限内；2)连续35点中仅有1点超出控制界限；3)连续100点中不多于2点超出控制界限。

§5.3.2　工程项目质量控制方法2、点子排列没有缺陷，是指点子的排列是随机的，而没有出现异常现象。

这里的异常现象是指点子排列出现了“链”、“多次同侧”、“趋势或倾向”、“周期性变动”、“接近控制界限”等情况。

1)链:是指点子连续出现在中心线一侧的现象。

出现五点链，应注意生产过程发展状况。

出现六点链，应开始调查原因：出现七点链，应判定工序异常，需采取处理措施，如图7—12(a)所示。

§5.3.2　工程项目质量控制方法2)多次同侧：是指点子在中心线一侧多次出现的现象，或称偏离。

下列情况说明生产过程已出现异常：在连续11点中有10点在同侧，如图7—12(b)所示。

控制图(control charts)又名：统计过程控制( statistical process control)方法演变：EQ \o(\s\up5(－),\s\do2(x))计量值控制图：⎺X－R控制图（又名均值极差控制图），⎺X－s控制图，单值控制图（又名X 控制图，X-R控制图，IX-MR控制图，XmR控制图，移动极差控制图），移动均值-移动极差控制图（又名MA-MR控制图），目标偏差控制图（又名差异控制图、偏差控制图、名义值偏差控制图），CUSUM（又名累计和控制图），EWMA（又名指数加权移动平均控制图），多元控制图（又名Hotelling T2控制图）。

计数值控制图：p控制图（又名不良品率控制图），np控制图，c控制图（又名缺陷数控制图），u控制图。

两种数据都适用的控制图：短期过程控制图（又名稳定控制图或者Z控制图），组控制图（又名多属性值控制图）。

概述控制图是一种对过程变异进行分析和控制的图形工具。

数据按时间顺序绘制在图上，控制图一般有一条代表均值的中心线，一条上控制限位于中心线上方，一条下控制限位于中心线下方，这些线是根据过程数据确定的。

通过当前数据和由历史数据计算所得的控制限的比较，我们可以判定当前过程变异是稳定的（受控制）还是不稳定的（不受控制，受到某个特定因素的干扰）。

控制图分为很多种，不同的过程、不同的数据，我们采用不同的控制图。

计量值数据的控制图经常是成对应用，其中常绘制在上方的一张控制图监测均值，或者说过程数据的分布中心，而绘制在下方的一张控制图监测极差，或者说分布的波动程度。

如果借助于练习打靶的例子来说明，那么均值就是靶子上射击集中的地方，极差是射击点的离散程度。

计量值数据要成对使用控制图，计数值数据则通常只使用一张控制图就足够了。

适用场合·当你希望控制当前过程，问题出现时能察觉并能对其采取补救措施时；·当你希望对过程输出的变化范围进行预测时：·当你判断一个过程是否稳定（处于统计受控状态）时；·当你分析过程变异来源是随机性（偶然事件）还是非随机性（过程本身固有）时；·当你决定怎样完成一个质量改进项目时——防止特殊问题的出现，或对过程进行基础性的改变。

控制图（Control Chart）又叫管制图，是对过程质量特性进行测定、记录、评估，从而监察过程是否处于控制状态的一种用统计方法设计的图。

有三条平行于横轴的直线：中心线（CL，Central Line）、上控制线（UCL，Upper Control Line）和下控制线（LCL，Lower Control Line），并有按时间顺序抽取的样本统计量数值的描点序列。

UCL、CL、LCL统称为控制线（Control Line），通常控制界限设定在±3标准差的位置。

根据控制图使用目的不同，控制图可分为：分析用控制图和控制用控制图。

根据统计数据的类型不同，控制图可分为：计量控制图和计数控制图（包括计件控制图和计点控制图）。

计量型控制图平均数与极差控制图( -X-R Chart )平均数与标准差控制图( -X-S Chart )中位数与极差控制图( ~X-R Chart )个別值与移动极差控制图( X-Rm Chart )计数值控制图不良率控制图(P chart)不良数控制图(nP chart，又称np chart 或d chart)缺点数控制图(C chart)单位缺点数控制图(U chart) 控制图种类及应用场合控制图的分析与判定应用控制图的目的，就是要及时发现过程中出现的异常，判断异常的原则就是出现了“小概率事件”，为此，判断的准则有两类。

第一类：点子越出界限的概率为0.27% 。

准则1属于第一类。

第二类：点子虽在控制界限内，但是排列的形状有缺陷。

准则2-8属于第二类。

控制图八大判异准则（口诀）2/3A （连续3点中有2点在中心线同一侧的B区外<即A区内>）4/5C （连续5点中有4点在中心线同一侧的C区以外）6连串（连续6点递增或递减，即连成一串）8缺C （连续8点在中心线两侧，但没有一点在C区中）9单侧（连续9点落在中心线同一侧）14交替（连续14点相邻点上下交替）15全C （连续15点在C区中心线上下，即全部在C区内1界外（1点落在A区以外）▶ 2/3A （连续3点中有2点在中心线同一侧的B区外<即A区内>）判读：1、控制过严；2、材料品质有差异；3、检验设备或方法之大不相同；4、不同制程之资料绘于同一控制图上；5、不同品质材料混合使用。

控制图的原理及其分类引言控制图是一种常用的质量管理工具，在工业生产和过程控制中广泛应用。

控制图可以用于监测和分析过程的稳定性、变异性和质量水平，从而帮助企业进行控制和改进。

本文将介绍控制图的原理及其分类。

首先，我们将解释控制图的基本原理，然后详细讨论三种常用的控制图分类：X-Bar 控制图、R 控制图和P 控制图。

控制图的原理控制图的原理基于统计过程控制（SPC）理论。

SPC 理论认为，任何可测量的过程或系统都存在一定的变异性。

控制图通过对过程数据的统计分析，判断这种变异性是否超出可接受的范围，从而帮助工程师获取关于过程的可靠信息。

控制图的构建基于以下几个关键原则：1.任何过程可测量的特性都可以用统计数据来描述：控制图的基础是使用统计数据描述过程的变异性。

2.过程的变异性存在常态分布：根据中心极限定理，大部分过程的变异性都可以近似地呈现正态分布。

3.随机变异与特殊原因变异：过程变异性可以分为两种类型，随机变异（常态变异）和特殊原因变异（非常态变异）。

控制图的目标是从这两种变异中区分出来。

4.过程的稳定性：稳定的过程是指在统计范围内，没有特殊原因导致的变异性。

控制图的作用是监控过程的稳定性，及时发现过程中的异常情况。

5.控制上下限：控制图上下限的选择是基于统计数据，目标是覆盖大部分的随机变异，并确定过程不受特殊原因的影响。

X-Bar 控制图X-Bar 控制图是最常用的控制图之一，用于监控过程的平均值。

X-Bar 控制图的构建步骤如下：1.收集样本数据：从过程中选择一组样本，并记录样本的平均值。

2.计算平均值和范围：计算所有样本的平均值，并计算样本平均值的平均值和范围。

3.衡量中心线和控制限：根据样本平均值的平均值和范围来确定中心线和控制限。

4.绘制控制图：根据计算结果，将中心线和控制限绘制在控制图上。

通过观察样本平均值是否在控制限范围内，可以判断过程的稳定性。

如果样本平均值超出控制限，表示过程存在特殊原因变异，需要进行调查和纠正。