五年级几何图形测试提高卷
- 格式:doc
- 大小:43.00 KB
- 文档页数:2

专题7 多边形的面积(图形与几何)1、把每组中不规则的图形进行转化,再和规则的图形比较面积,更为简捷。
2、把平行四边形转化成长方形,先沿着平行四边形的一条高将其剪成两部分,然后平移,拼成一个长方形。
3、如果用S表示平行四边形的面积,用a表示平行四边形的底,用h表示平行四边形的高,那么平行四边形的面积公式可以写成S=ah。
4、用两个完全一样的三角形可以拼成一个平行四边形,三角形的面积是它所拼成的平行四边形面积的一半。
5、如果用S表示三角形的面积,用a表示三角形的底,用h表示三角形的高,那么三角形的面积公式可以写成S=ah÷2。
6、用两个完全一样的梯形拼成一个平行四边形,梯形的面积是所拼成的平行四边形面积的一半。
7、梯形的面积=(上底+下底)×高÷2。
8、边长为100米的正方形土地,面积是1公顷,1公顷=10000平方米。
9、测量或计量大面积的土地,通常用平方千米作单位,变成为1000米的正方形土地,面积是1平方千米。
10、1平方千米=1000000平方米=100公顷。
11、遇到较复杂的图形时,可以将这些图形转化成已经学过的正方形、长方形、平行四边形或梯形等图形。
一般采用“割补法”,可以将图割成几个简单图形,先算出这几个简单图形的面积,再加起来,也可以将图形补成规则图形,用这个规则图形的面积减去补上的部分的面积,就是原图形的面积。
12、不规则图形的面积:先数出整格个数和半格个数,然后根据整格个数和半格个数÷2来计算不规则图形的面积。
一、选择题1.(2022上·江苏泰州·五年级统考期中)红光小学占地面积大约是60亩,1亩≈667平方米,1公顷=15亩,这所小学的占地面积还可以说成大约是()。
A.4公顷B.667平方米C.6670平方米D.6.67平方千米2.(2022上·河南平顶山·五年级统考期中)一张长方形纸,长18厘米,宽12厘米,把它剪成直角边分别是3厘米、4厘米的直角三角形小旗,最多可以剪()面。
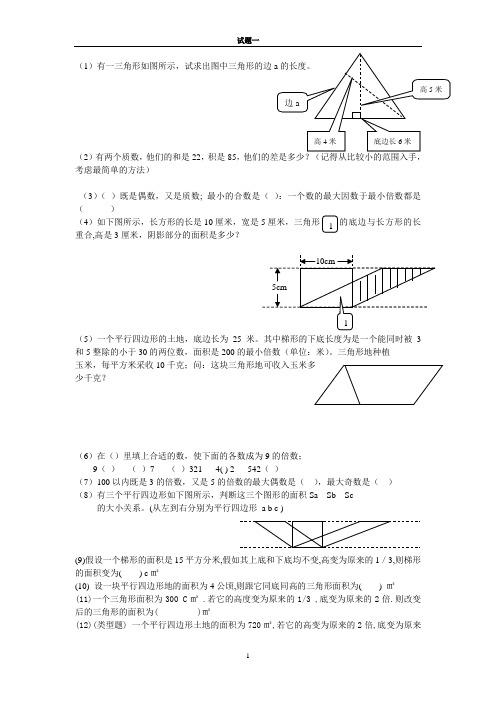
(1)有一三角形如图所示,试求出图中三角形的边(2)有两个质数,他们的和是22,积是85,他们的差是多少?(记得从比较小的范围入手,考虑最简单的方法)(3)( )既是偶数,又是质数; 最小的合数是( ):一个数的最大因数于最小倍数都是( )(4)如下图所示,长方形的长是10厘米,宽是5厘米,三角形的底边与长方形的长重合,高是3厘米,阴影部分的面积是多少?(5)一个平行四边形的土地,底边长为25米。
其中梯形的下底长度为是一个能同时被3和5整除的小于30的两位数,面积是200的最小倍数(单位:米)。
三角形地种植玉米,每平方米采收10少千克?(6)在()里填上合适的数,使下面的各数成为9的倍数;9( ) ( )7 ( )321 4( ) 2 542( )(7)100以内既是3的倍数,又是5的倍数的最大偶数是( ),最大奇数是( )(8)有三个平行四边形如下图所示,判断这三个图形的面积Sa Sb Sc的大小关系。
(从左到右分别为平行四边形 a b c )(9)假设一个梯形的面积是15平方分米,假如其上底和下底均不变,高变为原来的1/3,则梯形的面积变为( ) c ㎡(10) 设一块平行四边形地的面积为4公顷,则跟它同底同高的三角形面积为( ) ㎡(11)一个三角形面积为300 C ㎡ .若它的高度变为原来的1/3 ,底变为原来的2倍.则改变后的三角形的面积为( )㎡(12)(类型题) 一个平行四边形土地的面积为720㎡,若它的高变为原来的2倍,底变为原来的1/4,则改变后的平行四边形的面积是( )公顷(13)已知一个梯形的面积为80 C ㎡,高为1分米,上底为0.6分米,则它的下底长度为( )cm(14)现有三个连续的偶数,它们的和为72.则这三个偶数分别为( ) ( ) ( )判断题(15)若一个梯形的上底和高均不变,下底变为原来的1/2,则它的面积是原来的1/2.( )(16)面积相同的两个三角形形状完全相同.( )(17)平行四边形的面积一定是梯形面积的2倍( )(18)面积相同高相等的两个梯形,形状完全相同.( )(19)两个质数相乘,所得结果为质数 ( )(20)质数一定不是偶数 ( )(21)合数一定是偶数( )偶数一定是合数( )(22)合数至少有3个因数 ( )(23)两个数相加的和是13,且这两个数均为小于15的质数,则这两个数分别是( ) ( )(24)30以内的4的倍数有( ) ,6 的倍数有( ) 则30以内同时为4和6的倍数有( )由此得出,30以内4和6的最小公倍数是( )(25)如图,梯形的高为4米,下底长度为5米.空白部分大的三角形的高为3米.分别求出图中阴影部分的两个三角形的面积.(26)如图,在一面墙的周围筑一圈篱笆,已知篱笆总长度为40米,求这块篱笆围起的土地的面积..(27)类型题: 如图,在一面墙的周围筑一圈篱笆,已知篱笆总长度为40米,求这块篱笆围起的平行四边形土地的面积..。

第1篇一、选择题(每题2分,共20分)1. 下列图形中,不是轴对称图形的是()A. 正方形B. 等边三角形C. 平行四边形D. 圆2. 一个长方形的长是6cm,宽是4cm,那么它的周长是()A. 10cmB. 12cmC. 16cmD. 18cm3. 下列分数中,最大的是()A. $\frac{1}{2}$B. $\frac{3}{4}$C. $\frac{2}{3}$D. $\frac{4}{5}$4. 一个圆的半径是5cm,那么它的直径是()A. 5cmB. 10cmC. 15cmD. 20cm5. 下列图形中,面积最大的是()A. 正方形B. 长方形C. 等边三角形D. 等腰梯形6. 一个长方体的长、宽、高分别是3cm、2cm、1cm,那么它的体积是()A. 5cm³B. 6cm³C. 7cm³D. 8cm³7. 下列图形中,有4条对称轴的是()A. 正方形B. 等边三角形C. 等腰梯形D. 正六边形8. 下列分数中,约分后最简的是()A. $\frac{12}{16}$B. $\frac{18}{24}$C. $\frac{15}{20}$D. $\frac{10}{12}$9. 一个圆的周长是31.4cm,那么它的半径是()A. 5cmB. 6cmC. 7cmD. 8cm10. 下列图形中,有3条对称轴的是()A. 正方形B. 等边三角形C. 等腰梯形D. 正五边形二、填空题(每题2分,共20分)11. 一个长方形的面积是24cm²,如果它的长是6cm,那么它的宽是____cm。
12. 下列分数中,约分后与$\frac{3}{5}$相等的是____。
13. 一个圆的直径是10cm,那么它的半径是____cm。
14. 下列图形中,面积最小的是____。
15. 一个长方体的体积是24cm³,如果它的长是4cm,那么它的宽和高分别是____cm。
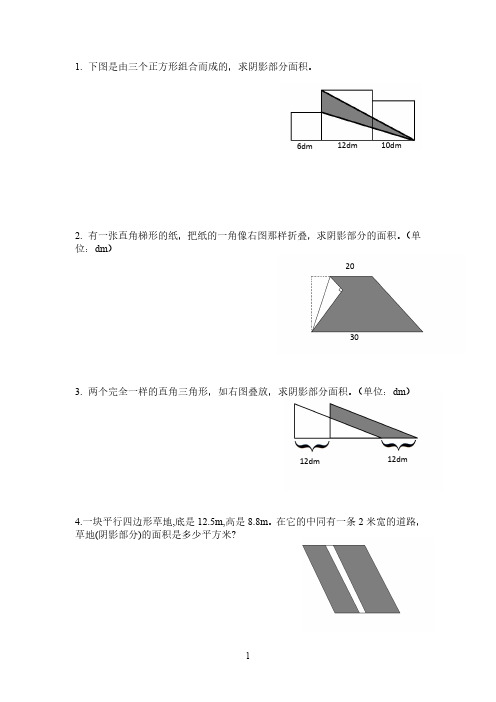
1.下图是由三个正方形组合而成的,求阴影部分面积。
2.有一张直角梯形的纸,把纸的一角像右图那样折叠,求阴影部分的面积。
(单位:dm )3.两个完全一样的直角三角形,如右图叠放,求阴影部分面积。
(单位:dm )4.一块平行四边形草地,底是12.5m,高是8.8m 。
在它的中同有一条2米宽的道路,草地(阴影部分)的面积是多少平方米?6dm 12dm 10dm12dm 12dm20305.一个用四条木条钉成的长方形框架,长是36cm ,宽是20cm ,将它拉伸成一个平行四边形后,面积减少了108cm 2,平行四边形较长边上的高是多少厘米?6.求阴影部分面积。
(单位:dm )7.两个正方形的面积分别是10dm 和4dm ,求阴影部分的面积。
8.大正方形的周长为104厘米,且四个三角形的长边都是17厘米。
求空白部分的面积。
41049.由五个周长为24dm的正方形拼成右图图形,求阴影部分面积。
10.有一块直角梯形菜地,它的下底长76米,如果下底减少24米,这块地就变成了正方形,请你算一算这块直角梯形菜地的面积是多少平方米?11.求阴影部分面积。
(单位:dm)12.如右图,ABCD是一个直角梯形,AD和BC的和是5.6,EF=1.3厘米,三角形ABE的面积是1.43平方厘米。
求直角梯形ABCD的面积。
13.两个都要直角三角形ABC和DEF的直角边分别是10厘米和8厘米。
求阴影部分面积。
14.求阴影部分面积。
(单位:dm)15.如图,靠一面墙用篱笆围成一块菜地,篱笆全长42米,这块菜地的面积是多设平方米?16.已知,AB=14dm,BC=22dm,四边形EFGH的面积是36dm2。
求阴影部分面积。
17.如右图,三角形ABC的面积是32.4,是三角形EFB面积的三倍。
平行四边形EFCD的面积是多少?18.求下列组合图形的面积。
(单位:dm)。

图形与几何专题测试卷一、估计下面图形的面积。
(每个小方格的面积为1cm2)(共9分)树叶的面积约占()cm2桃的面积约占()cm2花瓶的面积约占()cm2二、填空题。
(除标注外,每空1分,共20分)1.一个平行四边形面积是38 cm2,底是9.5 cm,高是()cm。
2.一个平行四边形的面积是10 m2,若底和高都扩大到原来2倍,它的面积是()m2。
3.一个梯形的面积是6.5 dm2,上下底之和是13 cm,这个梯形的高是()。
4.左图是由一个()形和一个()形组合成的,也可以看作由两个 ()组合而成的。
5.图中,阴影部分甲的面积比乙大4 cm2。
求三角形ABC的面积是()cm2。
6.一个三角形原来的底是14cm,如果将底增加2cm,面积就增加2cm2。
原来三角形的面积是()cm2。
7.一个直角梯形的上底、下底和高分别是10 cm、12 cm、8 cm,在里面画一个最大的正方形,正方形的面积是()cm2。
8.写出下列图形的面积。
(小方格的边长是 1 cm)(8分)9.在两条平行线间有三个不同的图形(如图),把它们按面积从大到小的顺序排列,依次是图( )>图()>图()。
三、选择题。
(共10分)1.一个梯形的面积是27cm2,高是4cm,上底长是下底长的2倍,这个梯形的上底是()cm。
A.4B.6C.8D.92.在下图中,若三角形甲的面积是20cm2,则三角形乙的面积是()cm2。
A.80 B.60 C.40 D.1603.右图中的正方形和平行四边形面积相比,()。
A.相等 B.正方形的面积大C.平行四边形的面积大 D.不能确定4.正方形、等边三角形、半圆形的对称轴的条数分别为x条,y条,z条,则x+y+z等于()。
A.5 B.7 C.8 D.195.如下图,如果梯形的面积是960cm2,上底是30cm,下底是50cm,那么阴影部分的面积是()。
A.120cm2 B.60cm2C.240cm2 D.180cm2四、按要求做题。

小学五年级数学几何图形试题及参考答案试题一:判断题1. 正方形的四条边长度相等,对角线互相垂直。
2. 直角三角形的两条直角边长度相等。
3. 三角形至少有一个锐角。
4. 平行四边形的对边相等,对角线互相垂直。
5. 圆的直径是圆的两个切线的长度之和。
参考答案:1. 正确2. 错误3. 正确4. 正确5. 正确试题二:选择题1. 梯形ABCD中,AB∥CD,AB=5cm,CD=8cm,AC=3cm,BD=7cm,求梯形的面积是多少?A. 18平方厘米B. 20平方厘米C. 24平方厘米D. 30平方厘米2. 在长方形ABCD中,AB=6cm,BC=8cm,E为对角线BD的中点,连结AE。
求△ADE的面积是多少?A. 12平方厘米B. 18平方厘米C. 24平方厘米D. 36平方厘米3. 一个等边三角形的边长是3cm,一个正方形的边长是4cm。
两者的面积比是多少?A. 1:2B. 1:3C. 1:4D. 9:16参考答案:1. B. 20平方厘米2. A. 12平方厘米3. D. 9:16试题三:计算题1. 如图所示,求长方形ABCD的面积。
(图形描述:一个长方形,AB为底边,AB=6cm,BC为高,BC=4cm)2. 如图所示,求正方形EFGH的周长。
(图形描述:一个正方形,EFGH为四条边,EF=5cm)参考答案:1. 长方形ABCD的面积为6cm × 4cm = 24平方厘米。
2. 正方形EFGH的周长为4 × 5cm = 20厘米。
以上是小学五年级数学几何图形试题及参考答案,希望对您有帮助。
专题4 轴对称和平移(图形与几何)1、轴对称图形和对称轴。
轴对称图形的意义:将一个图形沿着一条直线对折,折痕两侧的部分能够完全重合,这个图形就叫作轴对称图形。
折痕所在的直线叫作对称轴。
2、在方格纸上画轴对称图形的另一半与画某个图形的轴对称图形。
在方格纸上画轴对称图形的另一半与画某个图形的轴对称图形的步骤:(1)确定所给图形的几个关键点;(2)输出关键点到对称轴的距离分别是几格;(3)在对称轴的另一侧找出与各关键点对称的点;(4)按所给图形的形状顺次联结各对称点。
3、画平移后的图形。
图形平移的步骤:(1)找出图形的关键点(或关键线段);(2)按制定方向和格数把关键点(或关键线段)平移到新位置,描出各点(或画出各线段);(3)把各点(或各线段)按原图顺次联结,就得到平移后的图形。
4、平移的特点。
平移只改变图形的位置,不改变图形的形状和大小5、图形的多次平移。
画把图形多次平移后的图形时,应按照要求一次一次平移。
6、轴对称、平移在图案设计中的应用。
轴对称、平移在图案设计中的应用:一个简单图形经过平移、轴对称等方法,可得到美妙的图案。
7、在方格纸上接着画图形。
接着画一组图形的方法:先确定基本图形,再根据需要按一定的规律进行图形的变换。
8、利用平移、轴对称在方格纸上设计简单的图案。
利用平移、轴对称设计图案时,可以只用一种方法,也可以两种方法都用。
平移图形时,要记住方向和距离;画轴对称图形时,要先找准关键点的对称点,再连线。
一、选择题1.笑笑在左图对折的纸上剪了两个洞,打开后的样子是下面的()。
A.B.C.2.(2023上·广东揭阳·五年级校考期中)下列图形中,对称轴最多的是()。
A.B.C.3.(2023上·黑龙江大庆·五年级校联考期中)下列不属于平移的是()。
A.电梯运行B.拨动钟表的分针C.抽拉办公桌的抽屉4.(2023上·辽宁朝阳·五年级统考期中)像这样把一张纸连续对折三次,剪出来的图形展开后是()。
小学五年级数学几何图形练习题及答案一、长方形练习题1. 画一个长方形,使得它的两条边长度分别为3 cm和5 cm。
2. 画一个长方形,使得它的周长为16 cm,宽度为2 cm。
3. 画一个长方形,使得它的面积为20 平方厘米。
答案:1. 长方形的两条边长度分别为3 cm和5 cm的示意图如下:```------------| || |------------3 cm```2. 长方形的周长为16 cm,宽度为2 cm的示意图如下:```------------| |2| |------------6 cm```3. 长方形的面积为20 平方厘米的示意图如下:```------------| |4| |------------5 cm```二、正方形练习题1. 画一个正方形,使得它的边长为4 cm。
2. 画一个正方形,使得它的周长为20 cm。
3. 画一个正方形,使得它的面积为36 平方厘米。
答案:1. 正方形的边长为4 cm的示意图如下:```------| || || |------4 cm```2. 正方形的周长为20 cm的示意图如下:```------| |8 | | 8| |------4 cm```3. 正方形的面积为36 平方厘米的示意图如下:```------| |6 | | 6| |------6 cm```三、三角形练习题1. 画一个等边三角形,其中每条边的长度为5 cm。
2. 画一个等腰三角形,其中两条腰的长度为4 cm,底边的长度为6 cm。
3. 画一个直角三角形,其中直角边的长度为3 cm,另外两条边的长度分别为4 cm和5 cm。
答案:1. 等边三角形每条边的长度为5 cm的示意图如下:```** ** ** * * * * *```2. 等腰三角形两条腰的长度为4 cm,底边的长度为6 cm的示意图如下:```** ** ** * * * * * *```3. 直角三角形直角边的长度为3 cm,另外两条边的长度分别为4 cm和5 cm的示意图如下:```** |* |* |* * * * *```四、圆形练习题1. 画一个半径为2 cm的圆。
图形与几何测试卷(2)时间:90分钟满分:100分分数:一、填空。
(22分)1.一个圆柱和与它等底等高的圆锥的体积和是144 cm3。
圆柱的体积是( )cm3,圆锥的体积是( )cm3。
2.有一个圆环,外圆半径是6厘米,内圆半径是4厘米,圆环的面积是( )平方厘米。
3.看图数一数,填一填。
(如右图,每个方格的面积按1 cm2计算)A图( )cm2B图( )cm2C图( )cm2D图大约( )cm24.把一个高为10厘米的圆柱沿底面半径切成若干等份,拼成一个近似的长方体。
如果这个长方体的底面积是50平方厘米,那么圆柱的体积是( )立方厘米。
5.一个梯形的面积是8 cm2 ,如果它的上底、下底和高各扩大到原来的2倍,它的面积是( )cm2 。
(导学号03766120)6.两个圆的半径分别是3厘米和5厘米,它们周长的比是( ),面积的比是( )。
二、判断。
(对的在括号里画“√”,错的画“✕”)(12分)1.在一个三角形中,只要两个内角和小于另一个内角,这个三角形一定是钝角三角形。
( )2.一条直线上的两点把这条直线分成两条射线和一条线段,所以射线比直线短。
( )3.长方形、正方形、圆、等腰梯形都是轴对称图形。
( )4.圆有无数条对称轴,而半圆只有一条对称轴。
( )三、选择。
(把正确答案的选项填在括号里)(12分)1.下面各组线段中,能围成三角形的是( )。
A. 1 cm 1 cm 2 cmB. 1 cm 2.5 cm 3 cmC. 0.9 dm 1 dm 2 dmD. 4 m7 m 2 m2.一个正方形的边长和圆的半径相等,已知正方形的面积是20平方米,则圆的面积是( )平方米。
A. 15.7B. 62.8C. 12.56D. 25.123.学校传达室的门坏了,下图分别是木工师傅修门的4种方案,( )种修理方案可以使这扇门最牢固。
四、画出下图关于直线的轴对称图形。
(10分)五、看图计算。
(14分)1.求右图阴影部分的面积。
平面几何图形的面积1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米,则平行四边形的面积是(24 )平方分米,三角形的面积是(12 )平方分米。
2、李叔叔在院子里靠着墙边围城了一个鸡笼,围鸡笼的网子长20.5米,求这个鸡笼的占地面积是多少平方米?上底+下底=20.5-8.5=12(米)梯形面积=12×8.5÷2=51(平方米)3、有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的是是多少平方米?32原长方形的长:24÷2=12(米)原长方形的宽:24÷3=8(米)原来长方形的面积:12×8=96(平方米)4、如图是由边长分别为4厘米、8厘米的两个正方形组成的图形,求阴影部分面积。
方法一:可以分割成两个钝角三角形第一个钝角三角形的底是4,高是4,第二个钝角三角形的高是8,底是8-4=4,所以总共的面积是:4×4÷2+8×(8-4)÷2=24(平方厘米)方法二:两个正方形的面积-2处空白的面积=4×4+8×8-8×8÷2-4×(4+8)÷2=24(平方厘米)5、如图是由边长分别为4、8、6厘米的三个正方形组成的图形,求阴影部分面积。
方法一:可以分割成三个钝角三角形第一个钝角三角形的底是4,高是4,面积是:4×4÷2=8(平方厘米)第二个钝角三角形的高是8,底是(8-4),面积:8×(8-4)÷2=16(平方厘米)第三个钝角三角形的高是8,底是6,面积是:6×8÷2=24(平方厘米)一共的面积:8+16+24=48(平方厘米)方法二:把右上角补起来阴影面积=三个正方形的面积+小长方形面积-两处空白的面积=4×4+8×8+6×6+6×(8-6)-(8+4)×4÷2-8×(6+8)÷2=48(平方厘米)6、下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.208 5阴影部分+中间空白=中间空白+下面空白所以阴影部分=下面空白20-5=15(厘米)(15+20)×8÷2=140(平方厘米)7、右图中甲的面积比乙的面积大__________平方厘米.乙甲6厘米8厘米4厘米利用同增同减差不变甲-乙=(甲+空白)-(乙+空白)=大三角形面积-小三角形面积=6×8÷2-4×8÷2=24-16=8(平方厘米)8、右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF 的面积大9平方厘米,求ED 的长.A B CDEF利用同增同减差不变三角形ABF-三角形EDF 的面积=9平方厘米同时增加梯形BCDF 的面积,则:长方形ABCD-三角形BCE=9长方形ABCD 的面积=4×6=24(平方厘米)则三角形BCE 的面积=24-9=15(平方厘米)EC=15×2÷6=5(厘米)ED=5-4=1(厘米)9、如图所示,CA=AB=4厘米,△ABE 比△CDE 的面积小2平方厘米,求CD 的长为多少厘米?A BECD利用同增同减差不变三角形CDE-三角形ABE 的面积=2平方厘米同时增加三角形BCE 的面积,则:三角形BCD-三角形ABC=2三角形ABC 的面积=4×4÷2=8(平方厘米)则三角形BCD 的面积=8+2=10(平方厘米)CD=10×2÷4=5(厘米)10、一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?原来的面积=15×12=180(平方分米)现在的的面积=(15-2)×(12-2)=130(平方厘米)减少的面积:180-130=50(平方厘米)11、一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?5×22566-2×5=56(平方厘米)设剩下的部分正方形的边长为x厘米5x+2x=56X=8原来长方形的长:8+5=13(厘米)原来长方形的宽:8+2=10(厘米)原来长方形的面积:13×10=130(平方厘米)12、下面图形中,长方形ABCD的面积是32平方厘米,EF都是所在边的中点,求三角形AEF的面积。
(1)有一三角形如图所示,试求出图中三角形的边
(2)有两个质数,他们的和是22,积是85,他们的差是多少?(记得从比较小的范围入手,考虑最简单的方法)
(3)( )既是偶数,又是质数; 最小的合数是( ):一个数的最大因数于最小倍数都是( )
(4)如下图所示,长方形的长是10厘米,宽是5厘米,三角形的底边与长方形的长重合,高是3厘米,阴影部分的面积是多少?
(5)一个平行四边形的土地,底边长为25米。
其中梯形的下底长度为是一个能同时被3和5整除的小于30的两位数,面积是200的最小倍数(单位:米)。
三角形地种植
玉米,每平方米采收10少千克?
(6)在()里填上合适的数,使下面的各数成为9的倍数;
9( ) ( )7 ( )321 4( ) 2 542( )
(7)100以内既是3的倍数,又是5的倍数的最大偶数是( ),最大奇数是( )
(8)有三个平行四边形如下图所示,判断这三个图形的面积Sa Sb Sc
的大小关系。
(从左到右分别为平行四边形 a b c )
(9)假设一个梯形的面积是15平方分米,假如其上底和下底均不变,高变为原来的1/3,则梯形的面积变为( ) c ㎡
(10) 设一块平行四边形地的面积为4公顷,则跟它同底同高的三角形面积为( ) ㎡
(11)一个三角形面积为300 C ㎡ .若它的高度变为原来的1/3 ,底变为原来的2倍.则改变后的三角形的面积为( )㎡
(12)(类型题) 一个平行四边形土地的面积为720㎡,若它的高变为原来的2倍,底变为原来
的1/4,则改变后的平行四边形的面积是( )公顷
(13)已知一个梯形的面积为80 C ㎡,高为1分米,上底为0.6分米,则它的下底长度为
( )cm
(14)现有三个连续的偶数,它们的和为72.则这三个偶数分别为( ) ( ) ( )
判断题
(15)若一个梯形的上底和高均不变,下底变为原来的1/2,则它的面积是原来的1/2.( )
(16)面积相同的两个三角形形状完全相同.( )
(17)平行四边形的面积一定是梯形面积的2倍( )
(18)面积相同高相等的两个梯形,形状完全相同.( )
(19)两个质数相乘,所得结果为质数 ( )
(20)质数一定不是偶数 ( )
(21)合数一定是偶数( )偶数一定是合数( )
(22)合数至少有3个因数 ( )
(23)两个数相加的和是13,且这两个数均为小于15的质数,则这两个数分别是( ) ( )
(24)30以内的4的倍数有( ) ,6 的倍数有( ) 则30以内同时为4和6的倍数有( )由此得出,30以内4和6的最小公倍数是( )
(25)如图,梯形的高为4米,下底长度为5米.空白部分大的三角形的高为3米.分别求出图中阴影部分的两个三角形的面积.
(26)如图,在一面墙的周围筑一圈篱笆,已知篱笆总长度为40米,求这块篱笆围起的土地的面积..
(27)类型题: 如图,在一面墙的周围筑一圈篱笆,已知篱笆总长度为40米,求这块篱笆围起的平行四边形土地的面积..。